A numerical comparison of spherical, spheroidal and ellipsoidal harmonic gravitational field models for small non-spherical bodies: examples for the Martian moons

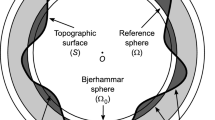
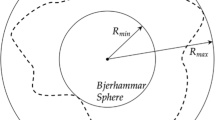
Abstract

We present a comprehensive numerical analysis of spherical, spheroidal, and ellipsoidal harmonic series for gravitational field modeling near small moderately irregular bodies, such as the Martian moons. The comparison of model performances for these bodies is less intuitive and distinct than for a highly irregular object, such as Eros. The harmonic series models are each associated with a distinct surface, i.e., the Brillouin sphere, spheroid, or ellipsoid, which separates the regions of convergence and possible divergence for the parent infinite series. In their convergence regions, the models are subject only to omission errors representing the residual field variations not accounted for by the finite degree expansions. In the regions inside their respective Brillouin surfaces, the models are susceptible to amplification of omission errors and possible divergence effects, where the latter can be discerned if the error increases with an increase in the maximum degree of the model. We test the harmonic series models on the Martian moons, Phobos and Deimos, with moderate oblateness of $<$0.4. The possible divergence effects and amplified omission errors of the models are illustrated and quantified. The three models yield consistent results on a bounding sphere of Phobos in their common convergence region, with relative errors in potential of $\sim$0.01 and $\sim$0.001 % for expansions up to degree 10 and degree 20 respectively. On the surface of Phobos, the spherical and spheroidal models up to degree 10 both have maximum relative errors of $\sim$1 % in potential and $\sim$100 % in acceleration due ostensibly to divergence effect. Their performances deteriorate more severely on the more irregular Deimos. The ellipsoidal model exhibits much less distinct divergence behavior and proves more reliable in modeling both potential and acceleration, with respective maximum relative errors of $\sim$1 and $\sim$10 %, on both bodies. Our results show that for the Martian moons and other such moderately irregular bodies, the ellipsoidal harmonic series should be considered preferentially for gravitational field modeling.

Appendix: Quantifying numerical errors in modeled potential

The numerical approximation of quadratures of (2), (7), and (13) introduce errors in the derived field coefficients. This appendix addresses how to assess the impact of such numerical coefficient errors on our simulation results and conclusions. The following discussion is based on Phobos but the conclusion applies to Deimos as well.

1.1 Model errors in potential

The field coefficients for the SH model are obtained via a numerical approximation of (2) as follows,

$$\begin{aligned} \left[ {{\begin{array}{l} {\hat{{C}}_{nm} } \\ {\hat{{S}}_{nm} } \\ \end{array} }} \right]&= \frac{r^{(0)}}{4\pi GM}\sum _i^{200} \sum _j^{100} V(r^{(0)},\varphi _j ,\lambda _i)\nonumber \\&\times \bar{{P}}_{nm} (\sin \varphi _j )\left[ {{\begin{array}{l} {\cos m\lambda _i } \\ {\sin m\lambda _i } \\ \end{array} }} \right] \cos \varphi _j \Delta \varphi _j \Delta \lambda _{i}, \end{aligned}$$

(21)

where we use a grid of $200~\times ~100$ evaluation points, specified by $(\lambda _i ,\varphi _j )$ on the Brillouin sphere. $\Delta \lambda _i$, $\Delta \varphi _j$ are the longitudinal and latitudinal increments, respectively. The boundary values given by the PM, $V(r^{\left( 0 \right) },\varphi _j ,\lambda _i )$, are considered free of errors. The overhead symbol “${}^{\wedge }$” indicates that the derived coefficients contain numerical errors. To prevent cluttering of overhead symbols, the overbar formerly used to indicate normalization, as in $\bar{{C}}_{nm} ,\bar{{S}}_{nm}$, has been suppressed.

In the region of uniform series convergence, the SH modeled potential is

$$\begin{aligned}&\hat{{V}}_{\mathrm{SH}} (r,\varphi ,\lambda ;\;\hat{{C}}_{nm} ,\hat{{S}}_{nm} ) \nonumber \\&=\frac{GM}{r}\sum _{n=0}^{n_{\max } } \sum _{m=0}^n \left( {\frac{r^{(0)}}{r}} \right) ^{n}\nonumber \\&\quad \times \bar{{P}}_{nm} (\sin \varphi )\left( {\hat{{C}}_{nm} \cos m\lambda +\hat{{S}}_{nm} \sin m\lambda } \right) . \end{aligned}$$

(22)

The model errors are defined as

$$\begin{aligned} \delta V_{\mathrm{SH}} =\hat{{V}}_{\mathrm{SH}} -V=\delta V_{\mathrm{SH}}^{(\mathrm{OM})} +\delta V_{\mathrm{SH}}^{(\mathrm{CF})} , \end{aligned}$$

(23)

where the omission errors, $\delta V_{\mathrm{SH}}^{\mathrm{(OM)}}$, are given by

$$\begin{aligned} \delta V_{\mathrm{SH}}^{(\mathrm{OM})}&= -\frac{GM}{r}\sum _{\begin{array}{c} n= \\ n_{\max } +1 \end{array}}^\infty \sum _{m=0}^{n} \left( {\frac{r^{(0)}}{r}} \right) ^{n}\nonumber \\&\times \bar{{P}}_{nm} (\sin \varphi )(C_{nm} \cos m\lambda +S_{nm} \sin m\lambda ) , \end{aligned}$$

(24)

and $\delta V_{\mathrm{SH}}^{(\mathrm{CF})}$, which we call the numerical potential errors, arise from the numerical coefficient errors, $\delta C_{nm} ,\delta S_{nm}$ (defined below), i.e.,

$$\begin{aligned} \delta V_{\mathrm{SH}}^{(\mathrm{CF})}&= \frac{GM}{r}\sum _{n=0}^{n_{\max } } \sum _{m=0}^n \left( {\frac{r^{(0)}}{r}} \right) ^{n}\nonumber \\&\times \bar{{P}}_{nm} (\sin \varphi )(\delta C_{nm} \cos m\lambda +\delta S_{nm} \sin m\lambda ). \end{aligned}$$

(25)

It should be stressed that (23) is only valid in the region of uniform convergence for the SH, because inside the Brillouin sphere the model may introduce errors due to divergence effects. The errors for the RH and EH modeled potentials in their respective regions of uniform convergence can be defined similarly.

1.2 Definition of numerical coefficient errors

Substituting Eq. (1) into (21) yields

$$\begin{aligned} \left[ {{\begin{array}{l} {\hat{{C}}_{nm} } \\ {\hat{{S}}_{nm} } \\ \end{array}}} \right]&= \frac{r^{(0)}}{4\pi GM}\sum _i^{200} \sum _j^{100} \frac{GM}{r^{(0)}}\sum _{p=0}^\infty \sum _{q=0}^{p}\nonumber \\&\times \bar{{P}}_{pq} (\sin \varphi _j )(C_{pq} \cos q\lambda _i +S_{pq} \sin q\lambda _i ) \nonumber \\&\times \bar{{P}}_{nm} (\sin \varphi _j )\left[ {{\begin{array}{l} {\cos m\lambda _i } \\ {\sin m\lambda _i } \\ \end{array} }} \right] \cos \varphi _j \Delta \varphi _j \Delta \lambda _i \nonumber \\&= \sum _{p=0}^{\infty } {\sum _{q=0}^{p} {\left[ {{\begin{array}{l} {\Theta _{nmpq}^{(\mathrm{C})} C_{pq} +\Theta _{nmpq} S_{pq} } \\ {\Theta _{nmpq}^{(\mathrm{S})} S_{pq} +{\Theta }{^\prime }_{nmpq} C_{pq} } \\ \end{array} }} \right] }}, \end{aligned}$$

(26)

with the shorthand numerical operators

$$\begin{aligned} \Theta _{nmpq}^{\mathrm{(C)}}&= \frac{1}{4\pi }\!\sum _i^{200} \sum _j^{100} \left\{ {\bar{{P}}_{nm} (\sin \varphi _j)\bar{{P}}_{pq} (\sin \varphi _j )\cos m\lambda _i \cos q\lambda _i } \right\} \nonumber \\&\times \cos \varphi _j \Delta \varphi _j \Delta \lambda _i , \nonumber \\ \Theta _{nmpq}^{\mathrm{(S)}}&= \frac{1}{4\pi }\sum _i^{200} \sum _j^{100} \left\{ {\bar{{P}}_{nm} (\sin \varphi _j )\bar{{P}}_{pq} (\sin \varphi _j )\sin m\lambda _i \sin q\lambda _i } \right\} \nonumber \\&\times \cos \varphi _j \Delta \varphi _j \Delta \lambda _i, \nonumber \\ \Theta _{nmpq}&= \frac{1}{4\pi }\sum _i^{200} \sum _j^{100} \left\{ {\bar{{P}}_{nm} (\sin \varphi _j )\bar{{P}}_{pq} (\sin \varphi _j )\cos m\lambda _i \sin q\lambda _i } \right\} \nonumber \\&\times \cos \varphi _j \Delta \varphi _j \Delta \lambda _i , \nonumber \\ {\Theta }{^\prime }_{nmpq}&= \frac{1}{4\pi }\sum _i^{200} \sum _j^{100} \left\{ {\bar{{P}}_{nm} (\sin \varphi _j )\bar{{P}}_{pq} (\sin \varphi _j )\sin m\lambda _i \cos q\lambda _i } \right\} \nonumber \\&\times \cos \varphi _j \Delta \varphi _j \Delta \lambda _i. \end{aligned}$$

(27)

The orthogonality of the SH suggests that $\Theta _{nmpq}^{(\cdot )} \approx \delta _{np} \delta _{mq}$, where $\delta _{kl}$ is the Kronecker delta, and $\Theta _{nmpq} ,{\Theta }{^\prime }_{nmpq} \approx 0$. The numerical coefficient errors can be defined formally as

$$\begin{aligned} \left[ {{\begin{array}{l} {\delta C_{nm} } \\ {\delta S_{nm} } \\ \end{array} }} \right]&= \left[ {{\begin{array}{l} {\hat{{C}}_{nm} } \\ {\hat{{S}}_{nm} } \\ \end{array} }} \right] -\left[ {{\begin{array}{l} {C_{nm} } \\ {S_{nm} } \\ \end{array} }} \right] \nonumber \\&= \sum _{p=0}^\infty {\sum _{q=0}^p {\left[ {{\begin{array}{l} {(\Theta _{nmpq}^{(C)} -\delta _{np} \delta _{mq} )C_{pq} +\Theta _{nmpq} S_{pq} } \\ {(\Theta _{nmpq}^{(S)} -\delta _{np} \delta _{mq} )S_{pq} +{\Theta }{^\prime }_{nmpq} C_{pq} } \\ \end{array} }} \right] }},\nonumber \\ \end{aligned}$$

(28)

which are affected by all true coefficients, $C_{pq} ,S_{pq}$. It is instructive to rearrange (28) as follows

$$\begin{aligned} \left[ {{\begin{array}{l} {\delta C_{nm} } \\ {\delta S_{nm} } \\ \end{array} }} \right]&= \left[ {{\begin{array}{l} {\delta C_{nm}^{(\mathrm{I})} } \\ {\delta S_{nm}^{(\mathrm{I})} } \\ \end{array} }} \right] +\left[ {{\begin{array}{l} {\delta C_{nm}^{(\mathrm{II})} } \\ {\delta S_{nm}^{(\mathrm{II})} } \\ \end{array} }} \right] \nonumber \\&= \sum _{p=0}^{n_{\max }} {\sum _{q=0}^p {\left[ {{\begin{array}{l} {(\Theta _{nmpq}^{(\mathrm{C})} \!-\!\delta _{np} \delta _{mq} )C_{pq} \!+\!\Theta _{nmpq} S_{pq} } \\ {(\Theta _{nmpq}^{(\mathrm{S})} \!-\!\delta _{np} \delta _{mq} )S_{pq} \!+\!{\Theta }{^\prime }_{nmpq} C_{pq} } \\ \end{array} }} \right] } }\nonumber \\&+ \sum _{\begin{array}{c} p= \\ n_{\max } +1 \end{array}}^\infty {\sum _{q=0}^p {\left[ {{\begin{array}{l} {\Theta _{nmpq}^{(\mathrm{C})} C_{pq} +\Theta _{nmpq} S_{pq} } \\ {\Theta _{nmpq}^{(\mathrm{S})} S_{pq} +{\Theta }{^\prime }_{nmpq} C_{pq} } \\ \end{array} }} \right] } }.\nonumber \\ \end{aligned}$$

(29)

Note that while the numerical coefficient errors of the first kind, $\delta C_{nm}^{(\mathrm{I})} ,\delta S_{nm}^{(\mathrm{I})}$, can be assessed if we assume $\hat{{C}}_{pq} ,\hat{{S}}_{pq} \approx C_{pq} ,S_{pq}$, those of the second kind, $\delta C_{nm}^{(\mathrm{II})} ,\delta S_{nm}^{(\mathrm{II})}$, are not obtainable via (29) directly because $C_{pq} ,S_{pq}$ are unknown ($\hat{{C}}_{pq} ,\hat{{S}}_{pq}$ are not derived) for $p>n_{\max }$.

The numerical coefficient errors for the RH and EH models can be expressed similarly and thus are not elaborated here.

1.3 Assessing the numerical potential errors $\delta V^{\mathrm{(CF)}}$

We shall treat the two components of the numerical coefficient errors separately. To assess $\delta C_{nm}^{(\mathrm{I})} ,\delta S_{nm}^{(\mathrm{I})}$, we derive a “surrogate” SH model via (22) up to the same maximum degree, $n_{\max }$, namely,

$$\begin{aligned} \left[ {{\begin{array}{l} {\tilde{C}_{nm} } \\ {\tilde{S}_{nm} } \\ \end{array} }} \right]&= \frac{r^{(0)}}{4\pi GM}\sum _i^{200} {\sum _j^{100} {\hat{{V}}_{\mathrm{SH}} \left( {r^{(0)},\varphi _j ,\lambda _i ;\;\hat{{C}}_{pq} ,\hat{{S}}_{pq} } \right) } } \nonumber \\&\times \bar{{P}}_{nm} (\sin \varphi _j )\left[ {{\begin{array}{l} {\cos m\lambda _i } \\ {\sin m\lambda _i } \\ \end{array} }} \right] \cos \varphi _j \Delta \varphi _j \Delta \lambda _i ,\;\nonumber \\&\quad p,n\le n_{\max }. \end{aligned}$$

(30)

Then, $\tilde{C}_{nm} ,\tilde{S}_{nm}$ introduce only numerical errors of the first kind,

$$\begin{aligned} \left[ {{\begin{array}{l} {\delta \hat{{C}}_{nm}^{(\mathrm{I})} } \\ {\delta \hat{{S}}_{nm}^{(\mathrm{I})} } \\ \end{array} }} \right] =\left[ {{\begin{array}{l} {\tilde{C}_{nm} } \\ {\tilde{S}_{nm} } \\ \end{array} }} \right] -\left[ {{\begin{array}{l} {\hat{{C}}_{nm} } \\ {\hat{{S}}_{nm} } \\ \end{array} }} \right] , \end{aligned}$$

(31)

with respect to $\hat{{C}}_{pq} ,\hat{{S}}_{pq}$, since there are no $\hat{{C}}_{pq} ,\hat{{S}}_{pq}$ for $p>n_{\max }$. We approximate the numerical potential errors due to $\delta C_{nm}^{(\mathrm{I})} ,\delta S_{nm}^{(\mathrm{I})}$ as $\delta V_{\mathrm{SH}}^{\mathrm{(I)}} \approx \delta \hat{{V}}_{\mathrm{SH}}^{\mathrm{(I)}} (r,\varphi ,\lambda ;\;\delta \hat{{C}}_{nm}^{(\mathrm{I})} ,\delta \hat{{S}}_{nm}^{(\mathrm{I})} )\;.$ However, we do not evaluate $\delta \hat{{C}}_{nm}^{(\mathrm{I})} ,\delta \hat{{S}}_{nm}^{(\mathrm{I})}$ explicitly, but instead derive $\delta \hat{{V}}_{\mathrm{SH}}^{\mathrm{(I)}}$ directly as

$$\begin{aligned} \delta \hat{{V}}_{\mathrm{SH}}^{\mathrm{(I)}}&= \tilde{V}_{\mathrm{SH}} (r,\varphi ,\lambda ;\;\tilde{C}_{nm} ,\tilde{S}_{nm})\nonumber \\&-\hat{{V}}_{\mathrm{SH}} (r,\varphi ,\lambda ;\;\hat{{C}}_{nm} ,\hat{{S}}_{nm} ). \end{aligned}$$

(32)

To evaluate $\delta C_{nm}^{\mathrm{(II)}} ,\delta S_{nm}^{\mathrm{(II)}}$ we refer back to (23) and assume that our PM model has infinite resolution. It is reasonable to expect that $\left| {\delta V_{\mathrm{SH}}^{\mathrm{(OM)}}} \right| \le \left| {\delta V_{\mathrm{SH}} } \right|$. Moreover, $\delta V_{\mathrm{SH}}$ are accessible in the region of uniform convergence. ${\delta V_{\mathrm{SH}} }/V$ and ${\delta V_{\mathrm{RH}}}/V$ (i.e., $e_V$ for the SH and RH models) up to degree 20 on the respective Brillouin surfaces are given in Fig. 10 (${\delta V_{\mathrm{EH}} }/V$ up to degree 20 on the Brillouin ellipsoid is given in Fig. 6f). Therefore, these represent upper bounds of the magnitude of omission errors. As a reasonable consequence, the following inequality,

$$\begin{aligned} \left[ {{\begin{array}{l} {\left| {\delta C_{nm}^{(\mathrm{II})} } \right| } \\ {\left| {\delta S_{nm}^{(\mathrm{II})} } \right| } \\ \end{array} }} \right]&\le \left[ {{\begin{array}{l} {\left| {\delta \hat{{C}}_{nm}^{(\mathrm{II})} } \right| } \\ {\left| {\delta \hat{{S}}_{nm}^{(\mathrm{II})} } \right| } \\ \end{array} }} \right] \nonumber \\&= \left| {-\frac{r^{(0)}}{4\pi GM}\sum _i^{200} {\sum _j^{100} {\delta V_{\mathrm{SH}} (r^{\left( 0 \right) },\varphi _j ,\lambda _i )} } } \right. \nonumber \\&\quad \times \left. {\bar{{P}}_{nm} (\sin \varphi _j )\left[ {{\begin{array}{l} {\cos m\lambda _i } \\ {\sin m\lambda _i } \\ \end{array} }} \right] \cos \varphi _j \Delta \varphi _j \Delta \lambda _i } \right| , \end{aligned}$$

(33)

holds for $n\le n_{\max }$. Note that $\hat{{C}}_{pq} ,\hat{{S}}_{pq} \approx C_{pq} ,S_{pq}$ is necessarily assumed. Then the numerical potential errors due to $\delta \hat{{C}}_{nm}^{(\mathrm{II})} ,\delta \hat{{S}}_{nm}^{(\mathrm{II})}$ are defined as

$$\begin{aligned} \delta \hat{{V}}_{\mathrm{SH}}^{\mathrm{(II)}}&= \;\frac{GM}{r}\sum _{n=0}^{n_{\max } } \sum _{m=0}^n \left( {\frac{r^{(0)}}{r}} \right) ^{n}\nonumber \\&\times \bar{{P}}_{nm} (\sin \varphi )(\delta \hat{{C}}_{nm}^{\mathrm{(II)}} \cos m\lambda +\delta \hat{{S}}_{nm}^{\mathrm{(II)}} \sin m\lambda ). \end{aligned}$$

(34)

Finally, we estimate the upper bounds of the numerical potential errors as follows,

$$\begin{aligned} \left| {\delta V_{\mathrm{SH}}^{\mathrm{(CF)}} } \right| \le \left| {\delta \hat{{V}}_{\mathrm{SH}}^{\mathrm{(CF)}} } \right| =\left| {\delta \hat{{V}}_{\mathrm{SH}}^{\mathrm{(I)}} } \right| +\left| {\delta \hat{{V}}_{\mathrm{SH}}^{\mathrm{(II)}} } \right| , \end{aligned}$$

(35)

with $\delta \hat{{V}}_{\mathrm{SH}}^{\mathrm{(I)}} ,\delta \hat{{V}}_{\mathrm{SH}}^{\mathrm{(II)}}$ given by (32) and (34), respectively. $\left| {\delta \hat{{V}}_{\mathrm{RH}}^{\mathrm{(CF)}} } \right| ,\,\left| {\delta \hat{{V}}_{\mathrm{EH}}^{\mathrm{(CF)}} } \right|$ for the RH and EH models can be evaluated in a similar fashion and are not explicated here.

Fig. 10

Relative model errors in potential in the case of Phobos: a SH model up to degree 20 on the Brillouin sphere, b RH model up to degree 20 on the Brillouin spheroid

1.4 Results

The numerical potential errors for SH model up to degree 20 are given in Fig. 11. For the purpose of comparison, relative errors, i.e., the ratios, ${\left| {\delta \hat{{V}}_{\mathrm{SH}}^{(\cdot )} } \right| }/V$, are provided. On the Brillouin sphere, ${\left| {\delta \hat{{V}}_{\mathrm{SH}}^{\mathrm{(I)}} } \right| }/V$ are greater near the poles with a maximum of 0.0002 %, while in other areas they are at the level of 10$^{-5}$ % (Fig. 11a). ${\left| {\delta \hat{{V}}_{\mathrm{SH}}^{\mathrm{(II)}} } \right| }/V$ exhibit a distinct pattern of omission errors, with larger errors occurring near Stickney (Fig. 11b). The maximum error in this case is 0.0001 %. The total numerical potential errors, $\left| {\delta \hat{{V}}_{\mathrm{SH}}^{\mathrm{(CF)}} } \right|$, are dominated by $\left| {\delta \hat{{V}}_{\mathrm{SH}}^{\mathrm{(I)}} } \right|$, especially in higher latitudes (Fig. 11c). The errors are negligible compared to total errors shown in Fig. 10a. On the surface of the body ${\left| {\delta \hat{{V}}_{\mathrm{SH}}^{\mathrm{(CF)}} } \right| }/V$ become significant in higher latitudes that corresponds to the greatest depth below the Brillouin sphere (Fig. 11d). However, the maximum error of 2.2 % constitutes an insignificant portion to the total error of 86 % for the degree-20 SH model (Fig. 7b).

Fig. 11

Relative numerical potential errors of the SH model up to degree 20 in the case of Phobos: a ${\left| {\delta \hat{{V}}_{\mathrm{SH}}^{\mathrm{(I)}} } \right| }\Big /V$ on the Brillouin sphere, b ${\left| {\delta \hat{{V}}_{\mathrm{SH}}^{\mathrm{(II)}} } \right| }\Big /V$ on the Brillouin sphere, c ${\left| {\delta \hat{{V}}_{\mathrm{SH}}^{\mathrm{(CF)}} } \right| }\Big /V$ on the Brillouin sphere, d ${\left| {\delta \hat{{V}}_{\mathrm{SH}}^{\mathrm{(CF)}} } \right| }\Big /V$ on the body surface

The relative numerical potential errors for the degree-20 RH model, ${\left| {\delta \hat{{V}}_{\mathrm{RH}}^{\mathrm{(CF)}}} \right| }\Big /V$, on the Brillouin spheroid show a pattern similar to that of ${\left| {\delta \hat{{V}}_{\mathrm{SH}}^{\mathrm{(CF)}} } \right| }\Big /V$ on the Brillouin sphere (Fig. 12a). It likely results from the similarity of (2) and (7) for the derivation of respective field coefficients. ${\left| {\delta \hat{{V}}_{\mathrm{RH}}^{\mathrm{(CF)}}} \right| }\Big /V$ is not as distinct above Stickney, which is not surprising since the Brillouin spheroid overall fits the body more closely than the Brillouin sphere, as suggested by Fig. 10. The maximum error of 0.0003 % occurs at the poles, which is slightly larger than the maximal ${\left| {\delta \hat{{V}}_{\mathrm{SH}}^{\mathrm{(CF)}}} \right| }\Big /V$ at the same locations. On the surface of Phobos the pattern of errors over 0.01 % is analogous to that in Fig. 7d (Fig. 12b); the maximum error is 0.35 %. The pattern of ${\left| {\delta \hat{{V}}_{\mathrm{EH}}^{\mathrm{(CF)}} } \right| }\Big /V$ on the Brillouin ellipsoid differs from that of either ${\left| {\delta \hat{{V}}_{\mathrm{SH}}^{\mathrm{(CF)}} } \right| }\Big /V$ or ${\left| {\delta \hat{{V}}_{\mathrm{RH}}^{\mathrm{(CF)}} } \right| }\Big /V$ on the respective Brillouin surfaces (Fig. 13a). It can be inferred that this is due to the different prescription of (13) compared to (2) and (7). The location of outstanding errors, e.g., above 0.001 %, on the surface of Phobos corresponds to that of the most pronounced model errors, i.e., Stickney, near ($0^{\circ }, \,0^{\circ }$) and ($180^{\circ },\, 0^{\circ }$) (Figs. 13b, 7f). The maximum error is 0.003 %. In general, we have $\left| {\delta \hat{{V}}_{\mathrm{SH}}^{\mathrm{(CF)}} } \right| >\left| {\delta \hat{{V}}_{\mathrm{RH}}^{\mathrm{(CF)}} } \right| >\left| {\delta \hat{{V}}_{\mathrm{EH}}^{\mathrm{(CF)}} } \right|$ on the body surface, obviously governed by the depths below the respective Brillouin surfaces. In all cases, these (upper bounds of) numerical potential errors are smaller than the total errors by at least one order of magnitude, and therefore have little impact on our analysis and conclusions.

Fig. 12

Relative numerical potential errors of the RH model up to degree 20 in the case of Phobos: a ${\left| {\delta \hat{{V}}_{\mathrm{RH}}^{\mathrm{(CF)}} } \right| }\Big /V$ on the Brillouin spheroid, b ${\left| {\delta \hat{{V}}_{\mathrm{RH}}^{\mathrm{(CF)}} } \right| }\Big /V$ on the body surface

Fig. 13

Relative numerical potential errors of the EH model up to degree 20 in the case of Phobos: a ${\left| {\delta \hat{{V}}_{\mathrm{EH}}^{\mathrm{(CF)}} } \right| }\Big /V$ on the Brillouin ellipsoid, b ${\left| {\delta \hat{{V}}_{\mathrm{EH}}^{\mathrm{(CF)}} } \right| }\Big /V$ on the body surface