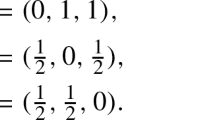Decentralization and mutual liability rules

Abstract

This paper builds on the recent work of Groote Schaarsberg et al. (Math Methods Oper Res 87(3):383–409, 2018) on mutual liability problems. In essence, a mutual liability problem comprises a financial network in which agents may have both monetary individual assets and mutual liabilities. Here, mutual liabilities reflect rightful monetary obligations from past bilateral transactions. To settle these liabilities by reallocating the individual assets, mutual liability rules are analyzed that are based on centralized bilateral transfer schemes which use a certain bankruptcy rule as its leading allocation mechanism. In this paper we derive a new characterization of mutual liability rules by taking a decentralized approach instead, which is based on a recursive individual settlement procedure. We show that for bankruptcy rules that satisfy composition, this decentralized procedure always leads to the same allocation as the one prescribed by the corresponding mutual liability rule based on centralized bilateral transfer schemes. Finally, we introduce a new reduction method for mutual liability problems and prove that any bankruptcy-rule-based mutual liability rule is invariant with respect to such a reduction.

1 Introduction

The Wall Street Crash of October 1929 sparked widespread despair among American consumers and firms about their investments. In fact, the confidence of American investors in the financial system was shaken to such an extent that it ultimately led to a wave of bank runs which put the solvency of banks at risk. When facing a bank run, banks often need to liquidate their assets, such as their outstanding loans to other banks, because banks typically hold a fraction of deposits as cash reserves. This can have dire consequences when bank runs occur simultaneously. For example, in the United States the number of operating banks nearly halved from 1929 to 1933 (Bernanke 1983). In addition, the fact that highly intertwined financial institutions wish to liquidate their assets and settle their claims brings about a practical problem too: how can one allocate the total available assets of the financial institutions among them? Although bank runs were not as apparent during the most recent global financial and banking crises between mid 2007 and early 2009, the allocation problem remains relevant. In September 2008 the financial stress reached a peak when Lehman Brothers, at that time the fourth-largest investment bank in the United States, filed for bankruptcy. Had it not been for governments bailing out other financial institutions in financial distress, the financial system would have been on the verge of collapse.¹

The allocation issue described above can be modeled as a mutual liability problem as introduced by Groote Schaarsberg et al. (2018). Mutual liability problems are a generalization of the well-studied notion of a bankruptcy problem as introduced by O’Neill (1982). In a bankruptcy problem there is a single non-negative monetary estate that has to be allocated among a finite set of claimants, where each claimant has a non-negative claim on the estate. In order to determine an allocation of the estate, one can use so-called bankruptcy rules. Such rules prescribe for each bankruptcy problem how to allocate the estate among the claimants. For an extensive survey on bankruptcy rules and their properties, see (Thomson 2003, 2013, 2015).

In a similar fashion, mutual liability problems can be represented by a non-negative estate vector containing each agent’s monetary estate and a non-negative claims matrix where entries indicate liabilities between (ordered) pairs of agents. In other words, a mutual liability problem comprises a financial network of economic agents (like banks) that interact by means of monetary transactions. Furthermore, as result of these interactions, each agent has assets, debtors and creditors. Mutual liability rules prescribe for each mutual liability problem how to allocate the total available estate among the agents. An example of a mutual liability rule is a $\varphi$-based mutual liability rule that relies on a specific bankruptcy rule ${\varphi }$. In fact, $\varphi$-based mutual liability rules will be the focus of this paper. A $\varphi$-based mutual liability rule put forward by Groote Schaarsberg et al. (2018) prescribes that, for each mutual liability problem, the final allocation of the total estate should be the direct consequence of a $\varphi$-transfer scheme of bilateral payments that satisfies an internal consistency property.

This paper builds on the work of Groote Schaarsberg et al. (2018) and provides new insights into $\varphi$-based mutual liability rules. The approach of Groote Schaarsberg et al. (2018) can be regarded as a centralized mechanism, i.e., an independent authority is assigned the task to allocate the total estate among the agents. We move away from this and look at mutual liability rules from a decentralized perspective instead. This perspective is particularly interesting in light of recent discussions about privacy. For instance, agents may rather not fully disclose their debts. We show that agents can take matters into their own hands and still reach a consensus on how to allocate the total estate when using a $\varphi$-based individual settlement allocation procedure. In this recursive procedure agents settle their claims individually, that is, in each step of the recursion the estate of each agent is reallocated by using a fixed specific bankruptcy rule $\varphi$. As a result of these individual reallocations, the total estate is reallocated and, correspondingly, mutual liabilities are reduced. This procedure terminates in finitely many steps if no further reallocations occur in a certain step. Nevertheless, such a step need not exist. We prove that, if reallocations go on indefinitely, the sequence of estate vectors that is generated by the individual settlement allocation procedure has a limit.

In Csóka and Herings (2017, (2018) bankruptcy rules also form the basis for payment matrices, which then, in fact, are viewed as solutions to mutual liability problems. Csóka and Herings (2017) focus on the proportional rule and corresponding payment matrices in particular, for which they provide an axiomatization. Moreover, Csóka and Herings (2018) take a recursive decentralized approach to mutual liability problems. Their idea of decentralization differs from ours, that is, in each step one agent is selected that has to make payments to other agents. Therefore, agent-specific payments occur sequentially instead of simultaneously. Again, they put emphasis on payment matrices rather than on the resulting allocation.

Interestingly, there is a particular property of a bankruptcy rule that bridges the gap between the allocation prescribed by a $\varphi$-based mutual liability rule and the outcome of the corresponding individual settlement allocation procedure. Our main result is that these allocations coincide when one applies bankruptcy rules that satisfy composition.² If a bankruptcy rule satisfies composition, then, in any bankruptcy problem, the allocation remains the same when first allocating an estimate of the estate which is lower than the realization and next, allocating the surplus estate.

Finally, this paper introduces a new reduction method for mutual liability problems, which is based on the concept of bankruptcy-stable sets. A bankruptcy stable set consists of agents that can already pay off all their debts by receiving their full claim on agents within the same set. As these agents do not rely on agents outside of the set, we let them settle all claims first. We prove that any $\varphi$-based mutual liability rule is invariant with respect to a reduction on a bankruptcy stable set.

This paper is organized as follows. In Sect. 2 we review bankruptcy problems, mutual liability problems and $\varphi$-based mutual liability rules. It also contains the leading example that is used throughout this paper. Next, Sect. 3 introduces and discusses the individual settlement allocation procedure and contains our main result. Section 4 discusses the invariance of $\varphi$-based mutual liability rules on bankruptcy-stable sets. Finally, Sect. 5 concludes.

2 Bankruptcy and mutual liability problems

In a bankruptcy problem, each claimant i within a finite set N has a non-negative justifiable claim $c_i$ on a common non-negative estate e that has to be allocated among these claimants.³ When the estate is insufficient to cover all claims, a natural, leading question is how to allocate the estate among the claimants in an adequate way. So-called bankruptcy rules are a helpful tool in answering this question as each of such rules prescribes a way to solve any bankruptcy problem. Let $\mathcal {B}^N$ denote the set of all bankruptcy problems (e, c), with $c=(c_i)_{i \in N}$, on N. A bankruptcy rule $\varphi :\mathcal {B}^N \rightarrow \mathbb {R}_{+}^N$ assigns to each bankruptcy problem $(e,c) \in \mathcal {B}^N$ a non-negative allocation vector $\varphi (e,c) \in \mathbb {R}_{+}^N$ such that

$$\begin{aligned} \sum _{j \in N} \varphi _j(e,c) = \min \{e , \sum _{j\in N} c_j \}, \end{aligned}$$

(2.1)

and $\varphi _j(e,c) \le c_j$ for all $j \in N$. The minimum operator in (2.1) distinguishes bankruptcy situations from situations in which there is essentially no problem. That is, if the estate exceeds the total claims, then each bankruptcy rule $\varphi$ prescribes that each claimant receives his full claim. In such cases there is a leftover estate value that stays with the entity on which the claimants had a rightful claim.

From the outset we assume that a bankruptcy rule satisfies estate monotonicity.

Definition 2.1

A bankruptcy rule $\varphi$ satisfies estate monotonicity if for all $(e,c) \in \mathcal {B}^N$ and $(e',c) \in \mathcal {B}^N$ with $e \le e'$ it holds that $\varphi (e,c) \le \varphi (e',c)$.

Estate monotonicity states that no claimant should receive less than what he did receive initially when it turns out there is more to be allocated. A well-known implication of estate monotonicity of a bankruptcy rule is that the bankruptcy rule is continuous in the estate.

Definition 2.2

A bankruptcy rule $\varphi$ satisfies estate continuity if for all $(e,c) \in \mathcal {B}^N$ and for any sequence of non-negative estates $\{e^k\}_{k=1}^{\infty }$ that converges to e, the sequence $\{\varphi (e^k,c)\}_{k=1}^{\infty }$ converges to $\varphi (e,c)$.

For an extensive survey of bankruptcy rules see Thomson (2003, (2013, (2015). In this paper we focus our attention on the constrained equal awards rule CEA and the Talmud rule $\tau$. The constrained equal awards rule CEA allocates the estate as equally as possible among the claimants provided that the allocation to each claimant is not more than what he claims. It is, for all $(e,c) \in \mathcal {B}^N$, defined by

$$\begin{aligned} CEA_i(e,c) = \min \{ c_i, \lambda \} \end{aligned}$$

for all $i \in N$ with $\lambda \in \mathbb {R}$ such that $\sum _{j \in N} \min \{ c_j, \lambda \} = \min \{e, \sum _{j \in N} c_j \}$.

The Talmud rule $\tau$ (Aumann and Maschler 1985) is, for all $(e,c) \in \mathcal {B}^N$, defined in terms of the constrained equal awards rule as follows:

$$\begin{aligned} \tau (e,c) = {\left\{ \begin{array}{ll} \begin{aligned} &{} c &{} \quad &{} \text { if } \sum _{j \in N} c_j \le e, \\ &{} c - CEA(\sum _{j \in N} c_j - e, \frac{1}{2}c) &{} \quad &{} \text { if } e \le \sum _{j \in N} c_j \le 2e, \\ &{} CEA(e,\frac{1}{2}c) &{} \quad &{} \text { if } \sum _{j \in N } c_j \ge 2e. \end{aligned} \end{array}\right. } \end{aligned}$$

For our purpose, we consider two additional bankruptcy rule properties. First, the concede-and-divide CD principle.

Definition 2.3

A bankruptcy rule $\varphi$ satisfies concede-and-divide if for all $(e,c) \in \mathcal {B}^N$ with $N = \{1,2\}$ it holds that $\varphi (e,c) = CD(e,c)$ with⁴

$$\begin{aligned} CD_1(e,c) = {\left\{ \begin{array}{ll} (e-c_2)^{+} + \frac{e - (e-c_1)^{+} - (e-c_2)^{+} }{2} &{} \text { if } c_1 + c_2 \ge e, \\ c_1 &{} \text { if } c_1 + c_2 < e, \end{array}\right. } \end{aligned}$$

and

$$\begin{aligned} CD_2(e,c) = {\left\{ \begin{array}{ll} (e-c_1)^{+} + \frac{e - (e-c_1)^{+} - (e-c_2)^{+} }{2} &{} \text { if } c_1 + c_2 \ge e, \\ c_2 &{} \text { if } c_1 + c_2 < e. \end{array}\right. } \end{aligned}$$

Concede-and-divide states that in a bankruptcy problem with two claimants both first get the amount not claimed by the other claimant after which the remaining estate is allocated equally. The Talmud rule $\tau$ does satisfy concede-and-divide while the constrained equal awards rule CEA does not.

Second, the composition principle.

Definition 2.4

A bankruptcy rule $\varphi$ satisfies composition if for all $(e,c) \in \mathcal {B}^N$ and all $e' \le e$ it holds that

$$\begin{aligned} \varphi (e,c) = \varphi (e',c) + \varphi (e-e',c-\varphi (e',c)). \end{aligned}$$

If a bankruptcy rule satisfies composition, then this property ensures that in any bankruptcy problem the allocation remains the same when first allocating an estimate of the estate which is lower than the realization and next, allocating the surplus estate. In contrast to concede-and-divide, the Talmud rule $\tau$ does not satisfy composition while the constrained equal awards rule CEA does.

A mutual liability problem can be represented by a triple (N, E, C) where N denotes a finite set of agents; $E = (e_i)_{i \in N} \in \mathbb {R}_{+}^N$ denotes a non-negative estates vector where coordinate $e_i$ indicates the estate belonging to agent i; $C = (c_{ij})_{i,j \in N} \in \mathbb {R}_{+}^{N \times N}$ denotes a non-negative claims matrix where cell $c_{ij}$ indicates the claim of agent j on agent i, $i \ne j$, and $c_{ii} =0$ for all $i \in N$. In other words, each agent $i \in N$ has a non-negative estate $e_i$, at most $|N|-1$ creditors as represented by positive numbers in the ith row of C, and at most $|N| - 1$ debtors as represented by positive numbers in the ith column of C. Note that there is no condition on the relation between the claims $c_{ij}$ and $c_{ji}$ with $i \ne j$. The set of all mutual liability problems on N is denoted by $\mathcal {L}^N$. A mutual liability rule $\mu :\mathcal {L}^N \rightarrow \mathbb {R}_{+}^N$ assigns to each mutual liability problem $(E,C) \in \mathcal {L}^N$ a non-negative allocation vector $\mu (E,C) \in \mathbb {R}_{+}^N$ such that $\sum _{j \in N} \mu _j(E,C) = \sum _{j \in N} e_j$.  Groote Schaarsberg et al. (2018) present a method of solving mutual liability problems that makes use of so-called payment matrices. A payment matrix is a non-negative matrix $P = (p_{ij})_{i,j \in N}$ where cell $p_{ij}$ indicates the payment of agent i to agent j. When a bankruptcy rule $\varphi$ forms the basis for such a payment matrix, it is called a (bilateral) ${\varphi }$-transfer scheme. In a $\varphi$-transfer scheme the payments adhere to a specific form of internal consistency.

Definition 2.5

Let $(E,C) \in \mathcal {L}^N$ and let $\varphi$ be a bankruptcy rule. For all $i \in N$, let $\bar{c}_i \in \mathbb {R}^N_{+}$ indicate the ith row of claims matrix C. The payment matrix $P = (p_{ij}) \in \mathbb {R}^{N \times N}_{+}$ is called a ${\varphi }$-transfer scheme for (E, C) if, for all $i \in N$,

$$\begin{aligned} p_{ij} = \varphi _j(e_i + \sum _{m \in N} p_{mi} \;, \; \bar{c}_i) \end{aligned}$$

(2.2)

for all $j \in N$. The set of all possible $\varphi$-transfer schemes for (E, C) is denoted by $\mathcal {P}^{\varphi }(E,C)$.

Note that in any $(E,C) \in \mathcal {L}^N$,

$$\begin{aligned} (e_i + \sum _{m \in N} p_{mi} \; , \; \bar{c}_i) \in \mathcal {B}^N \end{aligned}$$

is the bankruptcy problem corresponding to agent $i \in N$, and additionally that, for all $i \in N$,

$$\begin{aligned} p_{ii} = 0 \end{aligned}$$

since $(\bar{c}_i)_i = c_{ii} = 0$. A $\varphi$-transfer scheme is internally consistent in the following sense. The amount agent $i \in N$ pays to agent $j \in N$ follows from the allocation vector provided by $\varphi$ of the bankruptcy problem in which the estate equals the current estate $e_i$ of agent i plus the amount $\sum _{m \in N} p_{mi}$ agent i receives from the other agents and with claims vector $\bar{c}_i$ as given by the ith row of C. Clearly, in any $\varphi$-transfer scheme $P = (p_{ij})_{i,j \in N} \in \mathcal {P}^{\varphi }(E,C)$

$$\begin{aligned} 0 \le p_{ij} \le c_{ij} \end{aligned}$$

for all $i,j \in N$, $i \ne j$, and

$$\begin{aligned} \sum _{j \in N} p_{ij} \le e_i + \sum _{j \in N} p_{ji} \end{aligned}$$

for all $i \in N$.

A $\varphi$-transfer scheme $P \in \mathcal {P}^\varphi (E,C)$ can directly be translated into a transfer allocation vector $\alpha ^P \in \mathbb {R}_{+}^N$, given by

$$\begin{aligned} \alpha ^P_i = e_i + \sum _{j \in N} p_{ji} - \sum _{j \in N} p_{ij} \end{aligned}$$

(2.3)

for all $i \in N$. Hence, in a transfer allocation vector the allocation to an agent equals his estate plus his net payments. Groote Schaarsberg et al. (2018) show that there always exists at least one $\varphi$-transfer scheme and that all $\varphi$-transfer schemes corresponding with a mutual liability problem yield the same transfer allocation vector.

Theorem 2.1

(cf. Groote Schaarsberg et al. 2018) Let $(E,C) \in \mathcal {L}^N$ and let $\varphi$ be a bankruptcy rule. Then,

• (i) $\mathcal {P}^{\varphi }(E,C) \ne \emptyset$,

• (ii) $P^1, P^2 \in \mathcal {P}^{\varphi }(E,C) \implies \alpha ^{P^1} = \alpha ^{P^2}$.

Therefore, the resulting allocation vector is only based on the bankruptcy rule and not on the exact $\varphi$-transfer scheme.

Definition 2.6

Let $\varphi$ be a bankruptcy rule. The ${\varphi }$-based mutual liability rule $\rho ^{\varphi } :\mathcal {L}^N \rightarrow \mathbb {R}_{+}^N$ is defined by setting, for all $(E,C)\in \mathcal {L}^N$,

$$\begin{aligned} \rho ^{\varphi }(E,C) = \alpha ^P, \end{aligned}$$

where P is a $\varphi$-transfer scheme for (E, C).

The following example explicitly computes the allocation vector $\rho ^{\tau }(E,C)$ prescribed by the $\tau$-based mutual liability rule for a specific mutual liability problem with three agents. In fact, the mutual liability problem of Example 2.1 is the leading mutual liability problem throughout this paper.

Example 2.1

Consider a mutual liability problem $(E,C) \in \mathcal {L}^N$, with $N=\{1,2,3\}$,

In this problem, agent 1 has an estate of 2 while agents 2 and 3 both have an estate of 1. Neither of the agents has sufficient funds to pay off all debts on their own. Thus, each agent is dependent on payments from others. Agent 1 owes 1 to agent 2 and 2 to agent 3. Agent 2 owes 1 to both agents 1 and 3. Agent 3 owes 5 to agent 1 and 2 to agent 2.

A $\tau$-transfer scheme $P=(p_{ij})_{i,j \in N}$ can be obtained by considering the three conditions imposed by (2.2):

$$\begin{aligned} (p_{11},p_{12},p_{13})&= \tau (2+p_{21}+p_{31},(0,1,2)), \quad \quad \quad \quad ({\mathrm{Agent \ 1}}) \\ (p_{21},p_{22},p_{23})&= \tau (1+p_{12}+p_{32},(1,0,1)), \quad \quad \quad \quad ({\mathrm{Agent \ 2}})\\ (p_{31},p_{32},p_{33})&= \tau (1+p_{13}+p_{23},(5,2,0)). \quad \quad \quad \quad ({\mathrm{Agent \ 3}}) \end{aligned}$$

Hence, obviously

$$\begin{aligned} {\left\{ \begin{array}{ll} \, p_{11} = p_{22} = p_{33} = 0, \\ \, p_{12} \le 1, p_{13} \le 2, \\ \, p_{21} \le 1, p_{23} \le 1, \\ \, p_{31} \le 5, p_{32} \le 2. \end{array}\right. } \end{aligned}$$

Because agents pay nothing to and claim nothing from themselves, solving a three-agent bankruptcy problem boils down to solving a two-agent bankruptcy problem. As a result, we apply the concede-and-divide principle.

With respect to agent 3, note that $0 \le p_{13} + p_{23} \le 3$. Additionally, suppose that $p_{13} + p_{23} \ge 1$, then

$$\begin{aligned} (p_{31},p_{32})&= CD(1+p_{13}+p_{23},(5,2)) \\&= (p_{13}+p_{23}-1,0) + \frac{1}{2}(2,2) \\&= (p_{13}+p_{23},1). \end{aligned}$$

Hence, $p_{32} = 1$. Agent 2 needs to receive at least a total payment of 1 to pay all his debts. Hence, for agent 2 we now get $(p_{21},p_{23}) = (1,1)$. Likewise, for agent 1 we then get $(p_{12},p_{13}) = (1,2)$. Finally, we get $p_{31} = p_{13}+p_{23} = 2 + 1 = 3$. A $\tau$-transfer scheme for (E, C) is thus equal to

$$\begin{aligned} P = \begin{bmatrix} 0 &{} 1 &{} 2 \\ 1 &{} 0 &{} 1 \\ 3 &{} 1 &{} 0 \end{bmatrix}. \end{aligned}$$

Correspondingly, the transfer allocation is equal to

$$\begin{aligned} \rho ^\tau (E,C) = (2+4-3,1+2-2,1+3-4) = (3,1,0). \end{aligned}$$

3 Individual settlement allocation procedure

As Example 2.1 shows, computing $\varphi$-transfer schemes can be complex in general as we typically deal with them on an ad hoc basis. Nonetheless, (Groote Schaarsberg et al. 2018) show that for a special subclass of mutual liability problems, so-called hierarchical mutual liability problems, $\varphi$-transfer schemes can be determined recursively. We will build on this recursive approach, albeit we extend it to general mutual liability problems and base it on a decentralized mechanism. Roughly speaking, given a bankruptcy rule $\varphi$, in each step of the recursion each agent independently solves a bankruptcy problem using $\varphi$ to determine his payments to others. The estate vector and claims matrix can be updated accordingly as a consequence of these payments. The result is a new mutual liability problem to which the same procedure can be applied. The recursive procedure is formally defined in Definition 3.1 and hereafter referred to as the individual settlement allocation procedure, or ISAP in short.

Definition 3.1

Let $(E,C)\in \mathcal {L}^N$ and let $\varphi$ be a bankruptcy rule. The individual settlement allocation procedure generates a sequence of estate vectors $\{E^k\}_{k \in \mathbb {N}}$, a sequence of claims matrices $\{C^k\}_{k \in \mathbb {N}}$ and a sequence of payment matrices $\{\Phi ^k\}_{k \in \mathbb {N}}$ with $\Phi ^k = (\Phi ^k_{ij})_{i,j \in N}$ in the following way:

• 1. Initially, set $E^1 = (e^1_i)_{i \in N} = E$ and $C^1 = (c^1_{ij})_{i,j \in N} = C$

Then, recursively for $k=2,3, \ldots$

• 2. For each agent $i\in N$ the payment to agent $j \in N$ in step $k-1$ is equal to

  $$\begin{aligned} \Phi ^{k-1}_{ij} = \varphi _j(e^{k-1}_i,\bar{c}^{k-1}_i), \end{aligned}$$

  where $\bar{c}^{k-1}_i \in \mathbb {R}^N_{+}$ is the ith row of claims matrix $C^{k-1}$

• 3. Subsequently, update the estate vector to $E^k = (e^k_i)_{i\in N}$ with

  $$\begin{aligned} e_i^k = e_i^{k-1} + \sum _{m \in N} \Phi ^{k-1}_{mi} - \sum _{m \in N} \Phi ^{k-1}_{im} \end{aligned}$$

• 4. Correspondingly, the claims matrix is updated to $C^k = (c^k_{ij})_{i,j\in N}$ with

  $$\begin{aligned} c^k_{ij} = c^{k-1}_{ij} - \Phi ^{k-1}_{ij} \end{aligned}$$

Note that in the ISAP there are no further subsequent updates if at some step $k \in \mathbb {N}$ either $e^k_i = 0$ or $\bar{c}^k_i = 0$ for all $i \in N$. Yet this need not always happen, in which case updates go on indefinitely. The next theorem shows that these updates are negligible in the limit. In other words, the sequence of estate vectors $\{E^k \}_{k \in \mathbb {N}}$ that is generated by the ISAP has a limit.

Theorem 3.1

Let $(E,C) \in \mathcal {L}^N$ be a mutual liability problem and let $\varphi$ be a bankruptcy rule. Then, the limit of the sequence $\{E^k\}_{k \in \mathbb {N}}$ generated by the individual settlement allocation procedure exists.

Proof

In each step $k \in \{2,3, \ldots \}$ of the ISAP |N| bankruptcy problems are solved. Therefore, the claim of agent j on agent i in step k is equal to

$$\begin{aligned} c^{k}_{ij} = c^{k-1}_{ij} - \varphi _j(e_i^{k-1},\bar{c}_i^{k-1}) \end{aligned}$$

for all $i,j \in N$. By definition of a bankruptcy rule,

$$\begin{aligned} 0 \le \varphi _j(e_i^{k-1},\bar{c}_i^{k-1}) \le c_{ij}^{k-1} \end{aligned}$$

for all $k \in \{2,3, \ldots \}$ and for all $i,j \in N$. Hence,

$$\begin{aligned} 0 \le c^{k}_{ij} \le c^{k-1}_{ij} \end{aligned}$$

for all $k \in \{2,3, \ldots \} \text { and for all } i,j \in N$. Therefore, for all $i,j \in N$, the sequence $\{c_{ij}^k\}_{k \in \mathbb {N}}$ is non-increasing and bounded from below by zero. Thus, by the Monotone Convergence Theorem⁵ for sequences, this sequence has a limit. Note that in step $k \in \mathbb {N}$ the estate of agent $i \in N$ is equal to

$$\begin{aligned} e_i^k = \dots = e^1_i + \underbrace{\sum _{j \in N} (c^1_{ji}-c_{ji}^k)}_{(1)} - \underbrace{\sum _{j \in N} (c^1_{ij}-c_{ij}^k)}_{(2)}. \end{aligned}$$

(3.1)

That is, at step k agent $i\in N$ has received (1) and has paid (2) to other agents so far. Thus, $e^k_i$ is a continuous function of $c^k_{ij}$ and $c^k_{ji}$, for all $j\in N$. This implies that also the limit of the sequence $\{ e_i^k\}_{k \in \mathbb {N}}$ exists for every $i \in N$. $\square$

Thus, as a result of Theorem 3.1, for every bankruptcy rule $\varphi$, the ISAP leads to a new type of mutual liability rule, called the recursive $\varphi$-based mutual liability rule, in the following way.

Definition 3.2

Let $\varphi$ be a bankruptcy rule. The corresponding recursive ${\varphi }$-based mutual liability rule $r^{\varphi } :\mathcal {L}^N \rightarrow \mathbb {R}_{+}^N$ is defined by setting, for all $(E,C) \in \mathcal {L}^N$,

$$\begin{aligned} r^{\varphi }(E,C) = \lim _{k \rightarrow \infty } \{E^k \}, \end{aligned}$$

where $\{E^k\}_{k \in \mathbb {N}}$ is the sequence generated by the ISAP on $(E,C) \in \mathcal {L}^N$ with respect to $\varphi$.

Next, we provide an alternative characterization of the allocation vector prescribed by a recursive $\varphi$-based mutual liability rule which is based on payment matrices.

Lemma 3.1

Let $(E,C) \in \mathcal {L}^N$, let $\varphi$ be a bankruptcy rule, and let the payment matrix $P=(p_{ij})_{i,j \in N }$ be given by

$$\begin{aligned} p_{ij} = \sum _{k = 1}^{\infty } \Phi ^k_{ij} \end{aligned}$$

for all $i,j \in N$, where $\{\Phi ^k \}_{k \in \mathbb {N}}$ is the sequence of payment matrices generated by the ISAP in (E, C) with respect to $\varphi$. Then, $r^{\varphi }(E,C) = \alpha ^P$.

Proof

Let $\{E^k\}_{k \in \mathbb {N}}$ be the sequence of estate vectors generated by the ISAP on (E, C) with respect to $\varphi$ and let $E^k=(e^k_i)_{i \in N}$. Let $i \in N$ and $m \in \{2,3, \ldots \}$. By definition of the ISAP we have that

$$\begin{aligned} e_i^m = \dots = e_i^1 + \sum _{k=1}^{m-1}\sum _{j\in N} \Phi _{ji}^k - \sum _{k=1}^{m-1}\sum _{j\in N} \Phi _{ij}^k. \end{aligned}$$

(3.2)

Hence, for all $i \in N$,

$$\begin{aligned} r_i^\varphi (E,C)&= \lim _{m \rightarrow \infty } e_i^m \\&{{\mathop {=}\limits ^{(3.2)}}} \lim _{m \rightarrow \infty } \bigg (e_i^1 + \sum _{k=1}^{m-1}\sum _{j\in N} \Phi _{ji}^k - \sum _{k=1}^{m-1}\sum _{j\in N} \Phi _{ij}^k \bigg ) \\&= e_i^1 + \sum _{j \in N}\sum _{k=1}^{\infty }\Phi ^k_{ji} - \sum _{j \in N} \sum _{k=1}^{\infty } \Phi ^k_{ij} \\&= e_i^1 + \sum _{j \in N} p_{ji} - \sum _{j \in N} p_{ij} \\&= \alpha _i^P. \end{aligned}$$

$\square$

The ISAP is illustrated in the following two examples. Example 3.1 additionally provides the allocation following from a decentralized clearing process as given in Csóka and Herings (2018). In a decentralized clearing process, agents settle their claims sequentially instead of simultaneously like in the ISAP. In each step of a decentralized clearing process, an eligible agent is selected that pays other agents a certain amount. Both the selection process and the payment process are possibly history dependent or stochastic. Naturally, the resulting allocation depends on the selection process as well as the payment process. For our purpose, we assume agents are selected in a deterministic and consistent way and agents pay according to a bankruptcy rule $\varphi$. In this way, the decentralized clearing process is identical to the ISAP except for the fact that agent-specific payments occur sequentially.

Example 3.1

Reconsider the mutual liability problem $(E,C) \in \mathcal {L}^N$ of Example 2.1 with $N=\{1,2,3 \}$,

$$\begin{aligned} E = \begin{pmatrix} 2 \\ 1 \\ 1 \end{pmatrix}, \quad \text {and} \quad C = \begin{bmatrix}0 &{}\quad 1 &{}\quad 2 \\ 1 &{}\quad 0 &{}\quad 1 \\ 5 &{}\quad 2 &{}\quad 0 \end{bmatrix}. \end{aligned}$$

We explicitly compute the allocation vector $r^{\tau }(E,C)$ prescribed by the recursive $\tau$-based mutual liability rule. Set $E^1 = E$ and $C^1 = C$. We have

$$\begin{aligned} \Phi ^1 = \begin{bmatrix}0 &{}\quad \frac{1}{2} &{}\quad 1 \frac{1}{2} \\ \frac{1}{2} &{}\quad 0 &{}\quad \frac{1}{2} \\ \frac{1}{2} &{} \quad \frac{1}{2} &{}\quad 0 \end{bmatrix} \end{aligned}$$

since

$$\begin{aligned} \tau (2, (0,1,2))&= (0,\frac{1}{2},1 \frac{1}{2}), \quad \quad \quad \quad ({\mathrm{Agent \ 1}}) \\ \tau (1, (1,0,1))&= (\frac{1}{2},0, \frac{1}{2}), \quad \quad \quad \quad ({\mathrm{Agent \ 2}}) \\ \tau (1, (5,2,0))&= (\frac{1}{2},\frac{1}{2},0). \quad \quad \quad \quad ({\mathrm{Agent \ 3}}) \end{aligned}$$

Hence,

$$\begin{aligned} E^2&= \begin{pmatrix} 2 \\ 1 \\ 1 \end{pmatrix} + \begin{pmatrix}1 \\ 1 \\ 2 \end{pmatrix} - \begin{pmatrix}2 \\ 1 \\ 1 \end{pmatrix} = \begin{pmatrix}1 \\ 1 \\ 2 \end{pmatrix} \end{aligned}$$

and

$$\begin{aligned} C^2&= \begin{bmatrix}0 &{} 1 &{} 2 \\ 1 &{} 0 &{} 1 \\ 5 &{} 2 &{} 0 \end{bmatrix} - \begin{bmatrix}0 &{} \frac{1}{2} &{} 1\frac{1}{2}\\ \frac{1}{2} &{} 0 &{} \frac{1}{2} \\ \frac{1}{2} &{} \frac{1}{2} &{} 0 \end{bmatrix} = \begin{bmatrix}0 &{} \frac{1}{2} &{} \frac{1}{2} \\ \frac{1}{2} &{} 0 &{} \frac{1}{2} \\ 4 \frac{1}{2} &{} 1 \frac{1}{2} &{} 0 \end{bmatrix}. \end{aligned}$$

Next,

$$\begin{aligned} \Phi ^2 = \begin{bmatrix}0 &{} \frac{1}{2} &{} \frac{1}{2} \\ \frac{1}{2} &{} 0 &{} \frac{1}{2} \\ 1 \frac{1}{4} &{} \frac{3}{4} &{} 0 \end{bmatrix} \end{aligned}$$

since

$$\begin{aligned} \tau (1, (0,\frac{1}{2},\frac{1}{2}))= & {} (0,\frac{1}{2}, \frac{1}{2}), \\ \tau (1, (\frac{1}{2},0,\frac{1}{2}))= & {} (\frac{1}{2},0, \frac{1}{2}), \\ \tau (2, (4\frac{1}{2},1 \frac{1}{2},0))= & {} (1 \frac{1}{4},\frac{3}{4},0). \end{aligned}$$

Therefore,

$$\begin{aligned} E^3&= \begin{pmatrix} 1 \\ 1 \\ 2 \end{pmatrix} + \begin{pmatrix}1 \frac{3}{4} \\ 1 \frac{1}{4} \\ 1 \end{pmatrix} - \begin{pmatrix}1 \\ 1 \\ 2 \end{pmatrix} = \begin{pmatrix} 1 \frac{3}{4} \\ 1 \frac{1}{4} \\ 1 \end{pmatrix} \end{aligned}$$

and

$$\begin{aligned} C^3&= \begin{bmatrix}0 &{} \frac{1}{2} &{} \frac{1}{2} \\ \frac{1}{2} &{} 0 &{} \frac{1}{2} \\ 4 \frac{1}{2} &{} 1 \frac{1}{2} &{} 0 \end{bmatrix} - \begin{bmatrix}0 &{} \frac{1}{2} &{} \frac{1}{2}\\ \frac{1}{2} &{} 0 &{} \frac{1}{2} \\ 1\frac{1}{4} &{} \frac{3}{4} &{} 0 \end{bmatrix} = \begin{bmatrix}0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ 3 \frac{1}{4} &{} \frac{3}{4} &{} 0 \end{bmatrix}. \end{aligned}$$

Now the first two rows of $C^3$ are zero, that is, agents 1 and 2 are debt free. On the other hand, agent 3 has a positive estate and outstanding debts. Hence, we only have to consider the reallocation of the estate of agent 3. Since $\tau (1, (3 \frac{1}{4}, \frac{3}{4},0)) = (\frac{5}{8}, \frac{3}{8},0)$, we have

$$\begin{aligned} \Phi ^3 = \begin{bmatrix} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ \frac{5}{8} &{} \frac{3}{8} &{} 0 \end{bmatrix}. \end{aligned}$$

Hence,

$$\begin{aligned} E^4&= \begin{pmatrix} 1 \frac{3}{4} \\ 1 \frac{1}{4} \\ 1 \end{pmatrix} + \begin{pmatrix} \frac{5}{8} \\ \frac{3}{8} \\ 0 \end{pmatrix} - \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} = \begin{pmatrix} 2 \frac{3}{8} \\ 1 \frac{5}{8} \\ 0 \end{pmatrix} \end{aligned}$$

and

$$\begin{aligned} C^4&= \begin{bmatrix}0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ 3 \frac{1}{4} &{} \frac{3}{4} &{} 0 \end{bmatrix} - \begin{bmatrix}0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ \frac{5}{8} &{} \frac{3}{8} &{} 0 \end{bmatrix} = \begin{bmatrix}0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ 2 \frac{5}{8} &{} \frac{3}{8} &{} 0 \end{bmatrix}. \end{aligned}$$

Clearly, in subsequent steps nothing changes because now $e^4_3 = 0$, i.e.,

$$\begin{aligned} \begin{bmatrix} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \end{bmatrix} = \Phi ^4 = \Phi ^5 = \dots \end{aligned}$$

such that $E^4 = E^5 = \dots$ and $C^4 = C^5 = \dots$. Thus, the allocation vector $r^{\tau }(E,C)$ is obtained in a finite number of steps:

$$\begin{aligned} r^{\tau }(E,C) = E^4 = (2\frac{3}{8},1\frac{5}{8},0). \end{aligned}$$

In Example 2.1, the allocation vector prescribed by the $\tau$-based mutual liability rule was shown to be equal to $\rho ^{\tau }(E,C) = (3,1,0)$. Note that

$$\begin{aligned} \rho ^{\tau }(E,C) \ne r^{\tau }(E,C). \end{aligned}$$

If agents pay each other sequentially instead of simultaneously (ceteris paribus), the prescribed allocation need not be the same. For instance, suppose that the order in which agents are selected is as follows: agent 1, agent 3, agent 2, agent 1, agent 3, .... In the first step, agent 1 pays $\tau (2,(0,1,2)) = (0,\frac{1}{2},1\frac{1}{2})$, thereby reallocating his estate and reducing his debts. The estate vector becomes $(0,1\frac{1}{2},2\frac{1}{2})$ and agent 1’s debts become $(0,\frac{1}{2},\frac{1}{2})$. Proceeding in a similar fashion, one can show that the sequence of estate vectors generated by this decentralized clearing process is given by

$$\begin{aligned} \begin{pmatrix}2 \\ 1 \\ 1 \end{pmatrix},\begin{pmatrix} 0 \\ 1 \frac{1}{2} \\ 2 \frac{1}{2} \end{pmatrix},\begin{pmatrix}1 \frac{1}{2} \\ 2 \frac{1}{2} \\ 0 \end{pmatrix},\begin{pmatrix}2 \frac{1}{2} \\ \frac{1}{2} \\ 1 \end{pmatrix},\begin{pmatrix}1 \frac{1}{2} \\ 1 \\ 1 \frac{1}{2} \end{pmatrix},\begin{pmatrix}2 \frac{1}{2} \\ 1\frac{1}{2} \\ 0 \end{pmatrix},\begin{pmatrix}2 \frac{1}{2} \\ 1\frac{1}{2} \\ 0 \end{pmatrix}, \ldots , \end{aligned}$$

thus converging in a finite number of steps to an allocation of $(2\frac{1}{2},1\frac{1}{2},0)$. Note that this allocation differs from the allocation prescribed by the ISAP.

The following example illustrates that the allocation vector $r^{\varphi }(E,C)$ prescribed by the recursive $\varphi$-based mutual liability rule will not always be attained in a finite number of steps.

Example 3.2

Consider the mutual liability problem $(E,C) \in \mathcal {L}^N$ with $N= \{1,2,3 \}$,

$$\begin{aligned} E = \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix}, \quad \text {and} \quad C = \begin{bmatrix}0 &{} 1 &{} 1 \\ 1 &{} 0 &{} 1 \\ 0 &{} 0 &{} 0 \end{bmatrix}. \end{aligned}$$

Due to the structure of C, both the constrained equal awards rule and the Talmud rule prescribe that in each step of the ISAP the estate of agents 1 and 2 will be allocated equally among their two claimants, which implies that both receive half of their estate. Moreover, in each step of the ISAP agent 3 receives half the estate of both agents 1 and 2, but at the same time does not make any payments at all. Hence, for $k\in \mathbb {N}$,

$$\begin{aligned} E^k = \left( \left( \frac{1}{2}\right) ^{k-1},\left( \frac{1}{2}\right) ^{k-1}, 3- 2\left( \frac{1}{2}\right) ^{k-1} \right) , \end{aligned}$$

and the ISAP takes an infinite number of steps. It readily follows that

$$\begin{aligned} r^{\tau }(E,C) = r^{CEA}(E,C) = (0,0,3). \end{aligned}$$

As seen in Examples 2.1 and 3.1, $\rho ^{\varphi }(E,C)$ and $r^{\varphi }(E,C)$ can differ. The reason for this is that, in contrast to $\rho ^\varphi$(E,C), $r^{\varphi }(E,C)$ entails partitioning a mutual liability problem into a series of sub-problems. In the individual settlement allocation procedure, the ultimate payment an agent makes is the sum of payments in each sub-problem (cf. Lemma 3.1). On the other hand, payments that follow from a $\varphi$-transfer scheme are determined by solving a system of equations using the original mutual liability problem only. Our main result states that the property of composition guarantees $\rho ^{\varphi }(E,C)$ and $r^{\varphi }(E,C)$ to be equal for any $(E,C) \in \mathcal {L}^N$.

Theorem 3.2

Let $(E,C) \in \mathcal {L}^N$ and let $\varphi$ be a bankruptcy rule that satisfies composition. Then, $\rho ^{\varphi }(E,C)= r^{\varphi }(E,C)$.

Proof

Let $\{E^k\}_{k \in \mathbb {N}}$, $\{C^k\}_{k \in \mathbb {N}}$ and $\{\Phi ^k\}_{k \in \mathbb {N}}$ be the sequences generated by the ISAP on (E, C) with respect to $\varphi$. As usual, set $E^k = (e^k_i)_{i \in N}$, $C^k = (c^k_{ij})_{i,j \in N}$ and $\Phi ^k = (\Phi ^k_{ij})_{i,j \in N}$. By Lemma 3.1, $r^{\varphi }(E,C)$ corresponds to a payment matrix P with elements

$$\begin{aligned} p_{ij} = \sum _{k=1}^{\infty } \Phi _{ij}^k \end{aligned}$$

(3.3)

for all $i,j \in N$. To show that $\rho ^{\varphi }(E,C) = r^{\varphi }(E,C)$ it suffices to show that $P \in \mathcal {P}^{\varphi }(E,C)$. For this it suffices to verify that (see (2.2)), for all $i\in N$,

$$\begin{aligned} p_{ij} = \varphi _j(e^1_i + \sum _{m \in N} p_{mi} \;, \; \bar{c}^1_i) \end{aligned}$$

for all $j \in N$. In order to do so, define

$$\begin{aligned} B = \{i \in N | \sum _{m \in N} c_{im}^k > e_i^k \text { for all } k \in \mathbb {N} \}. \end{aligned}$$

First, let $i \in B$. Since i never has sufficient funds to pay off all remaining debts, it holds that

$$\begin{aligned} e_i^k = e_i^{k-1} + \sum _{m \in N} \Phi _{mi}^{k-1} - \sum _{m \in N} \Phi _{im}^{k-1} = \sum _{m \in N} \Phi _{mi}^{k-1} \end{aligned}$$

(3.4)

for all $k \in \{2,3, \ldots \}$. Furthermore, from the definition of the ISAP we know that

$$\begin{aligned} \bar{c}_i^k = \bar{c}_i^{k-1} - \varphi (e_i^{k-1}, \bar{c}_i^{k-1}). \end{aligned}$$

(3.5)

Hence, for all $j \in N$,

$$\begin{aligned} \varphi _j(e^1_i + \sum _{m \in N} p_{mi} \;, \; \bar{c}^1_i)&{{\mathop {=}\limits ^{(3.3)}}} \varphi _j(e^1_i + \sum _{m \in N} \sum _{k=1}^{\infty } \Phi _{mi}^k \;, \; \bar{c}^1_i) \\&= \varphi _j(e^1_i + \sum _{m \in N} \sum _{k=2}^{\infty } \Phi _{mi}^{k-1} \;, \; \bar{c}^1_i) \\&{{\mathop {=}\limits ^{(3.4)}}} \varphi _j(e^1_i + \sum _{k=2}^{\infty } e_i^k \;, \; \bar{c}^1_i) \\&= \varphi _j(\lim _{K \rightarrow \infty } \sum _{k=1}^K e_i^k \; , \; \bar{c}^1_i) \\&= \lim _{K \rightarrow \infty } \varphi _j(\sum _{k=1}^K e_i^k \; , \; \bar{c}^1_i) \\&= \lim _{K \rightarrow \infty } \bigg ( \varphi _j(e_i^1, \bar{c}_i^1) + \varphi _j\big (\sum _{k=2}^K e_i^k \; , \; \bar{c}^1_i - \varphi (e_i^1, \bar{c}_i^1) \big ) \bigg )\\&{{\mathop {=}\limits ^{(3.5)}}} \lim _{K \rightarrow \infty } \bigg ( \varphi _j(e_i^1, \bar{c}_i^1) + \varphi _j(\sum _{k=2}^K e_i^k \; , \; \bar{c}^2_i ) \bigg ) \\&= \lim _{K \rightarrow \infty } \sum _{k=1}^K \varphi _j(e_i^k, \bar{c}_i^k) \\&= \lim _{K \rightarrow \infty } \sum _{k=1}^K \Phi _{ij}^k \\&= \sum _{k=1}^{\infty } \Phi _{ij}^k \\&= p_{ij}. \end{aligned}$$

The fifth equality follows from continuity of $\varphi$ in the estate which stems from the result that a bankruptcy rule is continuous in the estate if it satisfies composition.⁶ The sixth equality follows from applying composition, and the eighth by repeatedly applying the previous arguments again.

Second, let $i \notin B$. Then, take $\ell \in \mathbb {N}$ such that

$$\begin{aligned} e_i^{\ell } \ge \sum _{m \in N} c_{im}^{\ell } . \end{aligned}$$

Thus, $c_{ij}^{k} = 0$ and $\Phi _{ij}^{k} = 0$ for all $j \in N$ and $k \in \{\ell +1,\ell +2, \ldots \}$. Hence,

$$\begin{aligned} p_{ij}&= \sum _{k=1}^{\infty } \Phi ^k_{ij} \\&= \sum _{k=1}^{\ell } \Phi ^k_{ij} \\&= \sum _{k=1}^{\ell } (c^k_{ij}-c^{k+1}_{ij}) \\&= c^1_{ij} - c^{\ell +1}_{ij} \\&= c^1_{ij}. \end{aligned}$$

Moreover,

$$\begin{aligned} e^{\ell }_i \ge \sum _{m \in N} c_{im}^{\ell }&\iff e_i^{\ell -1} + \sum _{m \in N} \Phi _{mi}^{\ell -1} - \sum _{m \in N} \Phi _{im}^{\ell -1} \ge \sum _{m \in N} \left( c_{im}^{\ell -1} - \Phi _{im}^{\ell -1} \right) \\&\iff e_i^{\ell -1} + \sum _{m \in N} \Phi _{mi}^{\ell -1} \ge \sum _{m \in N} c_{im}^{\ell -1} \\&\iff e_i^{\ell -2} + \sum _{k = \ell -2}^{\ell -1} \sum _{m \in N} \Phi _{mi}^{k} - \sum _{m \in N} \Phi _{im}^{\ell -2} \ge \sum _{m \in N} \left( c_{im}^{\ell -2} - \Phi _{im}^{\ell -2} \right) \\&\iff e_i^1 + \sum _{k=1}^{\ell -1} \sum _{m \in N} \Phi _{mi}^{k} \ge \sum _{m \in N} c_{im}^1 \\&\iff e_i^1 + \sum _{m \in N} \sum _{k=1}^{\ell -1} \Phi _{mi}^{k} \ge \sum _{m \in N} c_{im}^1. \end{aligned}$$

This result implies that

$$\begin{aligned} e_i^1 + \sum _{m \in N} p_{mi} \ge e_i^1 + \sum _{m \in N} \sum _{k=1}^{\ell -1} \Phi _{mi}^{k} \ge \sum _{m \in N} c^1_{im}. \end{aligned}$$

(3.6)

Hence,

$$\begin{aligned} p_{ij} = c^1_{ij} {{\mathop {=}\limits ^{(3.6)}}} \varphi _j(e^1_i + \sum _{m \in N} p_{mi} \;, \; \bar{c}^1_i) \end{aligned}$$

for all $j \in N$. $\square$

As mentioned before, the Talmud rule $\tau$ does not satisfy composition while the constrained equal awards rule CEA does. Two other well-known bankruptcy rules, the proportional rule PROP and constrained equal losses rule CEL, satisfy composition too (cf. Herrero and Villar 2001).

4 On the invariance of mutual liability rules

To reduce or simplify the analysis of mutual liability problems a rather natural approach would seem to first settle all bilateral claims before applying a mutual liability rule. However, the outcome that follows from a mutual liability rule may change as a result of settling all bilateral claims.

Example 4.1

Reconsider the mutual liability problem $(E,C) \in \mathcal {L}^N$ of Example 2.1 with $N=\{1,2,3 \}$,

$$\begin{aligned} E = \begin{pmatrix} 2 \\ 1 \\ 1 \end{pmatrix}, \quad \text {and} \quad C = \begin{bmatrix}0 &{} 1 &{} 2 \\ 1 &{} 0 &{} 1 \\ 5 &{} 2 &{} 0 \end{bmatrix}. \end{aligned}$$

If the agents were to settle claims bilaterally first, agent 1 pays 1 to agent 2 and 2 to agent 3, agent 2 pays 1 to agent 1 and 1 to agent 3, and agent 3 pays 2 to agent 1 and 1 to agent 2. This would lead to the following reduced mutual liability problem:

$$\begin{aligned} E = \begin{pmatrix} 2 \\ 1 \\ 1 \end{pmatrix}, \quad \text {and} \quad \check{C} = \begin{bmatrix}0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ 3 &{} 1 &{} 0 \end{bmatrix}. \end{aligned}$$

One can readily check that

$$\begin{aligned} \rho ^{\tau }(E,\check{C}) = \rho ^{CEA}(E,\check{C}) = r^{\tau }(E,\check{C}) = r^{CEA}(E,\check{C}) = (2 \frac{1}{2}, 1 \frac{1}{2},0). \end{aligned}$$

Note that this allocation is different from $\rho ^\tau (E,C) = (3,1,0)$ and $r^\tau (E,C) = (2 \frac{3}{8}, 1 \frac{5}{8}, 0)$ as derived in Examples 2.1 and 3.1, respectively. Additionally, the allocation of the reduced mutual liability problem differs from $\rho ^{CEA}(E,C) = r^{CEA}(E,C) = (2,2,0)$.

We now propose a new reduction method that is based on so-called bankruptcy-stable sets that guarantees the invariance of any $\varphi$-based mutual liability rule. A bankruptcy-stable set is a set of agents such that for every agent in this set the total claims on other agents in this same set suffice to become debt-free with respect to all agents. In other words, for each agent in a bankruptcy-stable set, the initial estate plus the claims on other agents in this same set cover all debts of that agent.

Definition 4.1

Let $(E,C) \in \mathcal {L}^N$. A set $S \subseteq N$, $S \ne \emptyset$, is called bankruptcty-stable for (E, C) if

$$\begin{aligned} e_i + \sum _{m \in S} c_{mi} \ge \sum _{m \in N} c_{im} \end{aligned}$$

for all $i \in S$. Let $\mathcal {S}(E,C)$ denote the set of all bankruptcy-stable sets for (E, C).

From the definition it readily follows that the union of two bankruptcy-stable sets is bankruptcy stable.

Lemma 4.1

Let $(E,C) \in \mathcal {L}^N$ and let $S,T \in \mathcal {S}(E,C)$. Then, $S \cup T \in \mathcal {S}(E,C)$.

Agents in a bankruptcy-stable set S do not depend on agents outside of S in order to pay all their debts. Therefore, to reduce or simplify a mutual liability problem one could let agents in a bankruptcy-stable set S first settle all bilateral claims among themselves and also pay the full claim to all agents outside of S.

Definition 4.2

Let $(E,C) \in \mathcal {L}^N$ and let $S \in \mathcal {S}(E,C)$. The corresponding reduced mutual liability problem $(E^S,C^S) \in \mathcal {L}^N$ with $E^S = (e_i^S)_{i \in N}$ and $C^S = (c_{ij}^S)_{i,j \in N}$ is defined by

$$\begin{aligned} e^S_i = {\left\{ \begin{array}{ll} \begin{aligned} &{} \; e_i + \sum _{m\in S}c_{mi} - \sum _{m\in N} c_{im} &{} \quad &{} \text { if } i \in S, \\ &{} \; e_i + \sum _{m\in S} c_{mi} &{} \quad &{} \text { if } i \in N\backslash S, \end{aligned} \end{array}\right. } \end{aligned}$$

(4.1)

and

$$\begin{aligned} c^S_{ij} = {\left\{ \begin{array}{ll} \begin{aligned} &{} \; 0 &{} \quad &{} \text { if } i \in S \text { and } j\in N, \\ &{} \; c_{ij} &{} \quad &{} \text { if } i \in N \backslash S \text { and } j\in N . \end{aligned} \end{array}\right. } \end{aligned}$$

(4.2)

The following example illustrates the reduction method based on bankruptcy-stable sets.

Example 4.2

Reconsider the mutual liability problem $(E,C) \in \mathcal {L}^N$ of Example 2.1 with $N=\{1,2,3 \}$,

$$\begin{aligned} E = \begin{pmatrix} 2 \\ 1 \\ 1 \end{pmatrix}, \quad \text {and} \quad C = \begin{bmatrix}0 &{} 1 &{} 2 \\ 1 &{} 0 &{} 1 \\ 5 &{} 2 &{} 0 \end{bmatrix}. \end{aligned}$$

Even if agent 3 receives his full claims on agents 1 and 2, he is still not able to pay off his debts. On the other hand, when agents 1 and 2 receive the full claim they have on each other it suffices to pay off all their debts. Therefore, a bankruptcy-stable set is given by $S = \{1,2 \}$. The reduced mutual liability problem $(E^{S},C^{S})$ is given by

$$\begin{aligned} E^{S} = \begin{pmatrix} 0 \\ 0 \\ 4 \end{pmatrix}, \quad \text {and} \quad C^{S} = \begin{bmatrix}0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ 5 &{} 2 &{} 0 \end{bmatrix}. \end{aligned}$$

Clearly, the allocation vector is equal to

$$\begin{aligned} \rho ^{\tau }(E^{S},C^{S}) = (3,1,0) = \rho ^{\tau }(E,C). \end{aligned}$$

However,

$$\begin{aligned} r^{\tau }(E^{S},C^{S}) = (3,1,0) \ne (2 \frac{3}{8}, 1 \frac{5}{8}, 0 ) = r^\tau (E,C). \end{aligned}$$

In fact, for any bankruptcy rule $\varphi$ the allocation vector prescribed by the $\varphi$-based mutual liability rule for any given mutual liability problem is invariant with respect to a reduction on any bankruptcy-stable set.

Theorem 4.1

Let $(E,C) \in \mathcal {L}^N$, let $\varphi$ be a bankruptcy rule and let $S \in \mathcal {S}(E,C)$. Then, $\rho ^{\varphi }(E^S,C^S) = \rho ^{\varphi }(E,C)$.

Proof

Let $\tilde{P} = (\tilde{p}_{ij}) \in \mathbb {R}_{+}^{N \times N}$ be a $\varphi$-transfer scheme for $(E^S,C^S)$. Define $P = (p_{ij}) \in \mathbb {R}_{+}^{N \times N}$ by

$$\begin{aligned} p_{ij} = {\left\{ \begin{array}{ll} \begin{aligned} &{} c_{ij} &{} \quad &{} \text { if } i \in S \text { and } j\in N, \\ &{} \tilde{p}_{ij} &{} \quad &{} \text { if } i \in N \backslash S \text { and } j\in N. \end{aligned} \end{array}\right. } \end{aligned}$$

(4.3)

We will prove that $P \in \mathcal {P}^\varphi (E,C)$ and that $\alpha ^{\tilde{P}} = \alpha ^P$. Then, as a direct result $\rho ^{\varphi }(E^S,C^S) = \rho ^{\varphi }(E,C)$.

To show that $P \in \mathcal {P}^\varphi (E,C)$ we have to prove that, for all $i \in N$,

$$\begin{aligned} p_{ij} = \varphi _j(e_i + \sum _{m \in N} p_{mi} \;, \; \bar{c}_i) \end{aligned}$$

for all $j \in N$, where $\bar{c}_i$ denotes the ith row of C.

First, let $i \in S$. Then, for all $j \in N$,

$$\begin{aligned} \varphi _j(e_i + \sum _{m \in N} p_{mi} \;, \; \bar{c}_i)&{{\mathop {=}\limits ^{(4.3)}}} \varphi _j(e_i + \sum _{m \in S} c_{mi} + \sum _{m \in N \backslash S } \tilde{p}_{mi} \;, \; \bar{c}_i) \\&= c_{ij} \\&{{\mathop {=}\limits ^{(4.3)}}} p_{ij}, \end{aligned}$$

where the last but one equality follows from the fact that $i \in S$ and thus

$$\begin{aligned} e_i + \sum _{m \in S} c_{mi} \ge \sum _{m \in N} c_{im}. \end{aligned}$$

Second, let $i\in N \backslash S$. Then, with $\bar{c}^S_i$ denoting the ith row of $C^S$, for all $j \in N$,

$$\begin{aligned} \varphi _j(e_i + \sum _{m \in N} p_{mi} \;, \; \bar{c}_i)&{{\mathop {=}\limits ^{(4.3)}}} \varphi _j(e_i + \sum _{m \in S} c_{mi} + \sum _{m \in N \backslash S } \tilde{p}_{mi} \;, \; \bar{c}_i) \\&= \varphi _j(e^S_i + \sum _{m \in N \backslash S } \tilde{p}_{mi} \;, \; \bar{c}^S_i) \\&= \varphi _j(e^S_i + \sum _{m \in N \backslash S } \tilde{p}_{mi} + \sum _{m \in S } \tilde{p}_{mi} \;, \; \bar{c}^S_i) \\&= \varphi _j(e^S_i + \sum _{m \in N } \tilde{p}_{mi} \;, \; \bar{c}^S_i) \\&= \tilde{p}_{ij} \\&{{\mathop {=}\limits ^{(4.3)}}} p_{ij}, \end{aligned}$$

where the second equality follows from the fact that, by definition [see (4.1) and (4.2)] in the reduced problem $(E^S,C^S)$, for all $i \in N \backslash S$

$$\begin{aligned} e_i^S = e_i + \sum _{m \in S} c_{mi} \text { and } c^S_{im} = c_{im} \end{aligned}$$

for all $m \in N$; the third equality follows from the fact that, by definition of $C^S$, $c^S_{mi} = 0$ for all $m \in S$, and consequently $\tilde{p}_{mi} = 0$ for all $m \in S$; the last but one equality follows from $\tilde{P} \in \mathcal {P}^\varphi (E^S,C^S)$.

Next, to show that $\alpha ^{\tilde{P}} = \alpha ^P$ we again discriminate between agents in S and $N \backslash S$. In both cases we use that $\tilde{p}_{ij} = 0$ for all $i \in S$ and $j\in N$, which readily follows from the fact that $c^S_{ij} = 0$ for all $i \in S$ and $j \in N$.

First, let $i \in S$. Then,

$$\begin{aligned} \alpha ^{\tilde{P}}_i&= e^S_i + \sum _{j \in N} \tilde{p}_{ji} - \sum _{j \in N} \tilde{p}_{ij} \\&= e^S_i + \sum _{j \in N \backslash S } \tilde{p}_{ji} + \sum _{j \in S } \tilde{p}_{ji} - \sum _{j \in N} \tilde{p}_{ij} \\&= e^S_i + \sum _{j \in N \backslash S } \tilde{p}_{ji} \\&{{\mathop {=}\limits ^{(4.1)}}} e_i + \sum _{j \in S} c_{ji} - \sum _{j \in N} c_{ij} + \sum _{j \in N \backslash S } \tilde{p}_{ji} \\&{{\mathop {=}\limits ^{(4.3)}}} e_i + \sum _{j \in S} p_{ji} - \sum _{j \in N} p_{ij} + \sum _{j \in N \backslash S } p_{ji}\\&= e_i + \sum _{j \in N} p_{ji} - \sum _{j \in N} p_{ij} \\&= \alpha ^P_i. \end{aligned}$$

Second, let $i \in N \backslash S$. Then,

$$\begin{aligned} \alpha ^{\tilde{P}}_i&= e^S_i + \sum _{j \in N} \tilde{p}_{ji} - \sum _{j \in N} \tilde{p}_{ij} \\&= e^S_i + \sum _{j \in N \backslash S } \tilde{p}_{ji} + \sum _{j \in S } \tilde{p}_{ji} - \sum _{j \in N} \tilde{p}_{ij} \\&= e^S_i + \sum _{j \in N \backslash S } \tilde{p}_{ji} - \sum _{j \in N} \tilde{p}_{ij} \\&{{\mathop {=}\limits ^{(4.1)}}} e_i + \sum _{j \in S} c_{ji} + \sum _{j \in N \backslash S } \tilde{p}_{ji} - \sum _{j \in N} \tilde{p}_{ij} \\&{{\mathop {=}\limits ^{(4.3)}}} e_i + \sum _{j \in S} p_{ji} + \sum _{j \in N \backslash S } p_{ji} - \sum _{j \in N} p_{ij} \\&= e_i + \sum _{j \in N} p_{ji} - \sum _{j \in N} p_{ij} \\&= \alpha ^P_i. \end{aligned}$$

$\square$

As seen in Example 4.2, the allocation vector prescribed by a recursive $\varphi$-based mutual liability rule need not be invariant with respect to a reduction on a bankruptcy-stable set. However, for every bankruptcy rule $\varphi$ that satisfies composition, Theorem 3.2 and Theorem 4.1 imply that invariance is guaranteed.

Corollary 4.1

Let $(E,C) \in \mathcal {L}^N$, let $\varphi$ be a bankruptcy rule that satisfies composition and let $S \in \mathcal {S}(E,C)$. Then, $r^{\varphi }(E,C) = r^{\varphi }(E^S,C^S)$.

5 Concluding remarks

The majority of the existing literature on bankruptcy situations comprises bankruptcy problems which are of a unilateral nature: all claimants claim from one entity (e.g. a bank) only. When claims are of a more bilateral nature, i.e., when agents have claims on each other, we arrive at the model of mutual liability problems. It can serve as a model for financial networks with bilateral claims between several agents like banks, governments, and insurance companies, in which, at a certain point time (e.g. due to a financial crisis) agents want to cash their claims.

This paper introduces a recursive $\varphi$-based individual settlement procedure for mutual liability problems, which we call the individual settlement allocation procedure (ISAP). The ISAP focuses on agents as individuals and how these agents can individually contribute to an overall settlement of claims, which then leads to a unique redistribution of the agent’s assets. In the ISAP, a bankruptcy rule $\varphi$ forms the basis for payments between agents. Our main result states that the composition property of bankruptcy rules bridges the gap between the allocation prescribed by a $\varphi$-based mutual liability rule and the outcome of the corresponding ISAP.

In a follow-up paper we will extend fundamental properties of bankruptcy rules to mutual liability rules and provide a general axiomatic characterization of mutual liability rules (Ketelaars 2020). Groote Schaarsberg et al. (2018) made a start on this by providing a characterization of a $\varphi$-based mutual liability rule on the basis of the consistency and concede-and-divide axioms (cf. Aumann and Maschler 1985).

Even though this paper focuses on mutual liability rules with an underlying bankruptcy rule $\varphi$ that specifies bilateral payments, mutual liability rules need not rely on bankruptcy rules per se. Several bankruptcy rules, like the proportional rule, lend themselves to be naturally extended to a network setting, although such an extension need not be unique (Ketelaars 2020). Another interesting approach to mutual liability problems is a game-theoretic one. In the setting of mutual liability problems, we believe that the non-cooperative approach is the most fruitful one due to the interdependencies between agents.