Performance analysis of a reflected fluid production/inventory model

Abstract

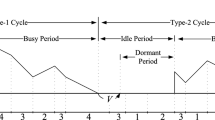
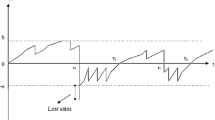
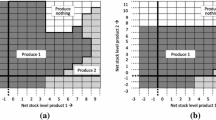
We study the performance of a reflected fluid production/inventory model operating in a stochastic environment that is modulated by a finite state continuous time Markov chain. The process alternates between ON and OFF periods. The ON period is switched to OFF when the content level reaches a predetermined level q and returns to ON when it drops to 0. The ON/OFF periods generate an alternative renewal process. Applying a matrix analytic approach, fluid flow techniques and martingales, we develop methods to obtain explicit formulas for the cost functionals (setup, holding, production and lost demand costs) in the discounted case and under the long-run average criterion. Numerical examples present the trade-off between the holding cost and the loss cost and show that the total cost appears to be a convex function of q.

Appendix

In this “Appendix” we introduce the algorithm developed in Ramaswami (2006) for the computation of the matrix $\Psi (\beta )$ associated with the MMFF process $(\mathcal {F}(t),\mathcal {J}(t),t\ge 0)$, as described in Sect. 3.2. Let $\sigma (x)=\inf \{t>0,\mathcal {F}(t)=x\}$ be the first passage time to level x and define the following LST

$$\begin{aligned}{}[\Psi (\beta )] _{ij}=E\left( e^{-\beta \sigma (0)},\mathcal {J} (\sigma (0))=j\mid \mathcal {F}(0)=0,\mathcal {J}(0)=i\right) \quad i\in S_{1},\quad j\in S_{2}. \end{aligned}$$

(58)

$[\Psi (\beta )] _{ij}$ represents the LST of $\sigma (0)$ restricted to the event that the fluid process hits level 0 at state $j\in S_{2},$ given $\mathcal {F}(0)=0$ and $J(0)=i\in S_{1}.$ Ramaswami (2006, Appendix 1, p. 512) shows how to compute the matrix $\Psi (\beta )$ and provides a good algorithm for this. The algorithm for $\Psi (\mathfrak {\beta })$ is given as follows.

For $\lambda >0,$ let

$$\begin{aligned} P_{\lambda }=\frac{1}{\lambda }U^{-1}Q+I \end{aligned}$$

where U and Q define in Sect. 3.2. Choose (fixed) positive numbers $\lambda$ and $\delta$ such that

$$\begin{aligned}&\lambda \ge \max _{i\in s}\left\{ -[U^{-1}Q]_{ii}\right\} \\&\max _{i\in S}\left[ \frac{{\text {Re}}(\mathfrak {\beta })}{\lambda } U^{-1}\right] _{ii}\le \delta <1,\quad \hbox {and}\\&\max _{i\in S}\left[ P_{\lambda }-\frac{{\text {Re}}(\mathfrak {\beta } )}{\lambda }U^{-1}\right] _{ii}>0 \end{aligned}$$

Define the matrices

$$\begin{aligned} A_{2}(\mathfrak {\beta },\lambda )= & {} \left( \begin{array} [c]{cc} 0 &{}\quad 0\\ 0 &{}\quad \lambda U_{2}\left( \mathfrak {\beta }I+2\lambda U_{2}\right) ^{-1} \end{array} \right) \\ A_{1}(\mathfrak {\beta },\lambda )= & {} \Lambda U(\mathfrak {\beta }I+\Lambda U)^{-1}\left( \begin{array} [c]{cc} 0 &{}\quad 0\\ \frac{1}{2}P_{21} &{}\quad \frac{1}{2}P_{22} \end{array} \right) \\ A_{0}(\mathfrak {\beta },\lambda )= & {} \left( \begin{array} [c]{cc} P_{11}-\frac{\beta }{\lambda }U_{1}^{-1} &{}\quad P_{12}\\ 0 &{}\quad 0 \end{array} \right) \end{aligned}$$

where $\Lambda =diag(\lambda I_{\vert S_{1}\vert },2\lambda I_{\vert S_{2}\vert })$ and $P=P_{\lambda }.$ Consider now the following algorithm.

1.1 Algorithm

Fix $\epsilon >0$ and set $diff=100$;

$$\begin{aligned}&H^{**}(1,\mathfrak {\beta },\lambda )=\left( I-A_{1}(\mathfrak {\beta } ,\lambda )\right) ^{-1}A_{0}(\mathfrak {\beta },\lambda );\\&L^{**}(1,\mathfrak {\beta },\lambda )=\left( I-A_{1}(\mathfrak {\beta } ,\lambda )\right) ^{-1}A_{2}(\mathfrak {\beta },\lambda );\\&G^{**}(1,\mathfrak {\beta },\lambda )=L^{**}(1,\mathfrak {\beta },\lambda );\\&T(1)=H^{**}(1,\mathfrak {\beta },\lambda );\\&Dowhile (diff>\epsilon )\\&\begin{array} [c]{cl} &{} k=k+1;\\ &{} U^{**}(k,\mathfrak {\beta },\lambda )=H^{**}(k-1,\mathfrak {\beta },\lambda )L^{**}(k-1,\mathfrak {\beta },\lambda )\\ &{} \quad \quad \quad \quad \quad \quad \qquad +\,L^{**}(k-1,\mathfrak {\beta },\lambda )H^{**}(k-1,\mathfrak {\beta },\lambda );\\ &{} M=(H^{**}(k-1,\mathfrak {\beta },\lambda ))^{2};\\ &{} H^{**}(k,\mathfrak {\beta },\lambda )=(I-U^{**}(k,\mathfrak {\beta },\lambda ))^{-1}M;\\ &{} M=(L^{**}(k-1,\mathfrak {\beta },\lambda ))^{2};\\ &{} L^{**}(k,\mathfrak {\beta },\lambda )=(I-U^{**}(k,\mathfrak {\beta },\lambda ))^{-1}M;\\ &{} G^{**}(k,\mathfrak {\beta },\lambda )=G^{**}(k-1,\mathfrak {\beta },\lambda )+T(k-1)L^{**}(k,\mathfrak {\beta },\lambda );\\ &{} T(k)=T(k-1)H^{**}(k,\mathfrak {\beta },\lambda );\\ &{} diff=\mathop {max}\limits _{j,k\in S}\left\{ [G^{**}(k,\mathfrak {\beta },\lambda )]_{j,k}-[G^{**}(k-1,\mathfrak {\beta },\lambda )]_{j,k}\right\} ; \end{array} \\&end\\&\Psi (\mathfrak {\beta })\cong G_{12}^{**}(k,\mathfrak {\beta } ,\lambda )G_{22}^{**}(k,\mathfrak {\beta },\lambda )^{-1}. \end{aligned}$$

Table 3 Transform matrices

Table 4 LST of first-passage times

Once we have computed $\Psi (\beta )$, the LST matrix of other hitting times are straightforward to evaluate; we list these matrices and their sizes in Tables 3 and 4. All matrices have nice probabilistic interpretations. For more details see Ahn et al. (2007).

The following LSTs of first-passage times are needed in our analysis: