Modelling and diagnostic tests for Poisson and negative-binomial count time series

Abstract

When modelling unbounded counts, their marginals are often assumed to follow either Poisson (Poi) or negative binomial (NB) distributions. To test such null hypotheses, we propose goodness-of-fit (GoF) tests based on statistics relying on certain moment properties. By contrast to most approaches proposed in the count-data literature so far, we do not restrict ourselves to specific low-order moments, but consider a flexible class of functions of generalized moments to construct model-diagnostic tests. These cover GoF-tests based on higher-order factorial moments, which are particularly suitable for the Poi- or NB-distribution where simple closed-form expressions for factorial moments of any order exist, but also GoF-tests relying on the respective Stein’s identity for the Poi- or NB-distribution. In the time-dependent case, under mild mixing conditions, we derive the asymptotic theory for GoF tests based on higher-order factorial moments for a wide family of stationary processes having Poi- or NB-marginals, respectively. This family also includes a type of NB-autoregressive model, where we provide clarification of some confusion caused in the literature. Additionally, for the case of independent and identically distributed counts, we prove asymptotic normality results for GoF-tests relying on a Stein identity, and we briefly discuss how its statistic might be used to define an omnibus GoF-test. The performance of the tests is investigated with simulations for both asymptotic and bootstrap implementations, also considering various alternative scenarios for power analyses. A data example of daily counts of downloads of a TeX editor is used to illustrate the application of the proposed GoF-tests.

1 Introduction

There is a huge literature on goodness-of-fit (GoF) tests for count distributions, i. e., which refer to a quantitative random variable (rv) with range being contained in the set of non-negative integers, $\mathbb {N}_0=\{0,1,\ldots \}$. More precisely, if the counts might become arbitrarily large (range $\mathbb {N}_0$), they are referred to as unbounded counts, whereas bounded counts can never exceed a specified upper bound $N\in \mathbb {N}=\{1,2,\ldots \}$ (range $\{0,1,\ldots ,N\}\subset \mathbb {N}_0$). The large majority of papers refer to independent and identically distributed (i. i. d.) counts, and most often, the GoF-tests are designed with respect to the null hypothesis of a Poisson (Poi) distribution, which constitutes the most well-known model for unbounded counts, see Gürtler and Henze (2000) for a comprehensive comparison. Some authors also allow for non-Poisson null hypotheses such as the negative-binomial (NB) distribution (also unbounded counts) or the binomial (Bin) distribution (bounded counts), see Kyriakoussis et al. (1998), Rueda and O’Reilly (1999), Meintanis (2005), Beltrán-Beltrán and O’Reilly (2019), and GoF-tests for bivariate count distributions have been developed as well, see Novoa-Muñoz and Jiménez-Gamero (2014) and Hudecová et al. (2021) as examples. The proposed GoF-tests can be roughly classified into three groups. Some try to use as much information as possible by defining test statistics relying on, e. g., the cumulative distribution function (cdf) or the probability generating function (pgf), see Gürtler and Henze (2000) and Luong (2020); Puig and Weiß (2020) for examples. These may lead to broadly applicable tests that are, however, difficult to use in practice (bootstrap- or simulation-based implementations). Also the GoF-test by Betsch et al. (2022) based on a Stein characterization of the Poi-distribution belongs to this class; see Anastasiou et al. (2023) for related references. Others consider statistics relying on frequency distributions such as the famous Pearson statistic, further members of the power-divergence family, or statistics from the family of scaled Bregman divergences (Cressie and Read 1984; Kißlinger and Stummer 2016). These statistics commonly lead to simple $\chi ^2$-asymptotics under the i. i. d.-assumption and are thus easily applied by practitioners. Even more facile are statistics relying on moment properties, such as Fisher’s index of dispersion or related statistics (Kyriakoussis et al. 1998), which are easy to compute and have simple normal asymptotics. While GoF-tests from the first two groups are often consistent against large classes of alternatives (omnibus tests), they are not necessarily particularly powerful for any such alternative. Furthermore, it is not possible to conclude from a rejection on the type of violation of the null hypothesis. Therefore, the moment-based GoF-tests from the third group are valuable complements as they may allow for a kind of “targeted diagnosis”. For example, if Fisher’s index of dispersion exceeds the upper critical value and thus rejects the Poi-null, we diagnose an overdispersed alternative distribution. Certainly, such moment-based GoF-tests lack broad consistency by construction. They also cannot be expected to be perfectly selective as, for example, features like skewness and excess are not fully separated, see Horswell and Looney (1992) for such results. Nevertheless, the pattern of rejections might give valuable insights into the type of violation(s) of the null model.

The situation gets more complex if the data generating process (DGP) is not i. i. d. but exhibits serial dependence, i. e., if the GoF-test is applied to a count time series; see Weiß (2018a) for a comprehensive discussion. Then, pgf-based GoF-tests such as those of Meintanis and Karlis (2014), Schweer (2016) still require bootstrap implementations, now certainly an adequate type of time-series bootstrap such as those discussed by Jentsch and Weiß (2019). But for non-i. i. d. count time series, also Pearson-type GoF tests are more demanding, because although closed-form asymptotics might still be available, these are typically given by sophisticated quadratic-form distributions rather than just simple $\chi ^2$-distributions (Weiß 2018b). Only for the third group of GoF-tests, there is still a chance for ending up with simple normal asymptotics, see the dispersion and skewness tests analyzed by Schweer and Weiß (2014), Schweer and Weiß (2016) as an example.

In what follows, we focus on this third group of GoF-tests, i. e., on test statistics relying on moment properties, and these are applied to time series consisting of unbounded counts having Poi- or NB-marginals. However, we do not restrict ourselves to specific (low-order) moments like in Schweer and Weiß (2014), Schweer and Weiß (2016), but we consider quite general moment statistics and their asymptotics instead. More precisely, we discuss marginal GoF-statistics of the form $\hat{T }=\tau \big (\frac{1}{T}\,\sum _{t=1}^T \varvec{g}(X_t)\big )$ for a vector-valued function $\varvec{g}$ and some smooth function $\tau$ (“functions of generalized means”), and these are compared to $T _0=\tau \big (E[\varvec{g}(X)]\big )$ computed under some null hypothesis. As an example, for specific cases of Poisson null hypotheses, Aleksandrov et al. (2022) defined statistics utilizing the Stein–Chen identity. Setting $\tau (u,v,w)=\frac{v}{u\,w}$ and $\varvec{g}(x)=\big (x,x\,f(x),f(x+1)\big ){}^\top$ for some bounded function $f:\mathbb {N}_0\rightarrow \mathbb {R}$, such as $f(x)=\exp (-x)$, the resulting statistic falls within the aforementioned class of marginal GoF-statistics. In a similar spirit, one may generalize the idea of Kyriakoussis et al. (1998), who consider second-order factorial moments for defining $T$. The use of factorial moments instead of, e. g., raw or central moments is motivated by the fact that for many common count distributions, such as the aforementioned Poi- or NB-distribution, there exist simple closed-form formulae for factorial moments of any order. These can even be extended to the bivariate case, see Sect. 2 for a concise summary. While Kyriakoussis et al. (1998) only discussed the second-order case, we shall consider quite general statistics defined by $\tau (u,v,w)=\frac{u}{v\,w}$ and $\varvec{g}(x)=\big (x_{(r)},x_{(r-s)},x_{(s)}\big ){}^\top$ for some $1\le s<r$. Here, $x_{(k)}=x\cdots (x-k+1)$, $k\in \mathbb {N}$, denotes the kth falling factorial (with $x_{(0)}:=1$). So $E[\varvec{g}(X)] = \big (\mu _{(r)},\mu _{(r-s)},\mu _{(s)}\big ){}^\top$, where $\mu _{(k)}=E[X_{(k)}]$ is the kth factorial moment. It should be noted that several alternative notations for falling factorials and factorial moments exist in the literature, see Johnson et al. (2005, pp. 2, 53). We also emphasize that throughout this article, $x_{(k)}$ always denotes a falling factorial and should not be confused with an order statistic.

Our GoF-tests for unbounded counts are developed for the following null scenarios: either a marginal Poi-distribution, or a marginal NB-distribution. The motivation for considering the Poi-distribution is obvious, as it plays the role of the “normal distribution” for unbounded counts. From a practical point of view, however, the Poi-distribution is often not realistic, as it requires the variance being equal to the mean (equidispersion). Instead, one is commonly confronted with a variance larger than the mean (overdispersion), and in this case, the NB-distribution serves as the default choice. There is a large literature on GoF-tests that distinguish between distributions with different dispersion characteristics (such as the Poi-null against an NB-alternative), see the aforementioned references. But it is also relevant (and actually more demanding) to test between distributions having identical first- and second-order properties. For example, the Poi-distribution is not the only one being equidispersed, also the Good distribution may share this property (Weiß 2018a). Similarly, several further distributions exist for overdispersed unbounded counts (Johnson et al. 2005), such as the Poisson-Inverse Gaussian (PIG), Consul’s generalized Poisson (GPoi), the Conway–Maxwell (COM) Poisson, or the zero-inflated Poisson (ZIP) distribution. Thus, for being able to identify an appropriate model for the given count data, it could be relevant to test a Poi-null against a Good-alternative, or an NB-null against a PIG- or ZIP-alternative.

When turning to the time-series case and when looking at the asymptotics of the GoF-statistics, also the respective bivariate extensions turn out to be important. Therefore, we start our discussion with a concise survey of bivariate Poi- and NB-distributions, see Sect. 2. Then, we turn to corresponding count time series models in Sect. 3. Later, closed-form asymptotics for the GoF-statistics can be derived if the lag-h bivariate distributions are sufficiently “well-behaved,” in the sense that these are equal to either a bivariate Poi- or bivariate NB-distribution (BPoi or BNB, respectively). Therefore, the survey in Sect. 3 concentrates on such types of count time series models where lagged pairs are BPoi- or BNB-distributed (note the analogy to the common requirement for Gaussian processes in the real-valued case, where joint distributions are multivariate normal).

During our research, we realized that there is a lot of confusion in the literature regarding the most relevant NB-model in the aforementioned class; this is carefully clarified in Sect. 3 and Appendix A. In Sect. 4, we present the general approach for constructing moment-based statistics, and we propose and analyze several novel GoF-tests relying on factorial moments or Stein-type identities. In addition, Sect. 4.4 sketches how the Stein approach might be extended to develop omnibus GoF-tests for counts. The performance of the novel GoF-tests is investigated with simulations in Sect. 5, and an illustrative data example is discussed in Sect. 6. Finally, Sect. 7 concludes the article and discusses several directions for future research. Proofs are provided in the Supplementary Materials to this article.

2 On bivariate Poisson and negative-binomial distributions

The three most well-known distributions for a univariate count rv X are the Bin-, Poi-, and NB-one, see Chapters 3–5 in Johnson et al. (2005) for a detailed survey. A compact summary of definition and relevant properties is provided by Table 1. Recall that the special case $Y\sim NB (1,\pi )$ leads to the geometric distribution, while the variable $Z:=1+Y$ is said to follow the shifted geometric distribution with $pgf _Z(z) = z\,pgf _Y(z)$.

Table 1 Basic univariate count distributions: probability generating function $pgf (z) = E\big [z^X\big ]$ and kth factorial moment, $\mu _{(k)} = E[X_{(k)}]$ with $k\in \mathbb {N}$

2.1 The bivariate Poisson distribution

The bivariate Poisson distribution $BPoi (\lambda _1,\lambda _2, \lambda _{0})$ with parameters $\lambda _1,\lambda _2, \lambda _{0}>0$ is defined as the distribution of the vector $\varvec{X}:= (\varepsilon _1+\varepsilon _{0},\varepsilon _2+\varepsilon _{0})^{\top }$ with range $\mathbb {N}_0^2$, where $\varepsilon _1,\varepsilon _2,\varepsilon _{0}$ are independent rv’s with $\varepsilon _i\sim Poi (\lambda _i)$ for $i=0,1,2$. Thus, by the additivity of the Poi-distribution, the marginals satisfy $X_i\sim Poi (\lambda _0+\lambda _i)$ for $i=1,2$, with marginal factorial moments $\mu _{i,(k)}=E[(X_i)_{(k)}]$ given by $\mu _{i,(k)} = (\lambda _0+\lambda _i)^k$. The following properties of the BPoi-distribution are taken from Section 4 in Kocherlakota and Kocherlakota (2014). $BPoi (\lambda _1,\lambda _2, \lambda _0)$ is determined by the bivariate pgf

$$\begin{aligned} \textstyle pgf _{X_1,X_2}(z_1,z_2) := E\big [z_1^{X_1}\, z_2^{X_2}\big ] \ =\ \exp {\Big ( \lambda _1\, z_1 + \lambda _2\, z_2 + \lambda _0\, z_1 z_2 - \lambda _{\bullet } \Big )}, \end{aligned}$$

(1)

where $\lambda _{\bullet }:=\sum _{i=0}^{2}\lambda _i$. The conditional distribution of $X_1|X_2=x_2$, in turn, has the pgf

$$\begin{aligned} pgf _{X_1|x_2}(z)\ =\ \Big (\frac{\lambda _2+\lambda _0\,z}{\lambda _2+\lambda _0}\Big )^{x_2}\, \exp \Big (\lambda _1\,(z-1)\Big ), \end{aligned}$$

(2)

i. e., it is a convolution of $Bin (x_2,\frac{\lambda _0}{\lambda _2+\lambda _0})$ and $Poi (\lambda _1)$. The joint factorial moments $\mu _{(r,s)} = E\big [(X_1)_{(r)}\,(X_2)_{(s)}\big ]$, $r,s\in \mathbb {N}_0$, are

$$\begin{aligned} \mu _{(r,s)} - \mu _{1,(r)}\, \mu _{2,(s)} \ =\ \mu _{1,(r)}\, \mu _{2,(s)}\! \sum _{i=1}^{\min {\{r,s\}}}\left( {\begin{array}{c}r\\ i\end{array}}\right) \,\left( {\begin{array}{c}s\\ i\end{array}}\right) \,i!\,\left( \frac{\lambda _0}{(\lambda _0+\lambda _1)(\lambda _0+\lambda _2)}\right) ^i, \end{aligned}$$

(3)

also see Supplement S.1. An expression for the probability mass function (pmf) of $BPoi (\lambda _1,\lambda _2, \lambda _0)$ is provided in Section 4 of Kocherlakota and Kocherlakota (2014).

2.2 The bivariate negative-binomial distribution

A bivariate extension of the NB-distribution was introduced by Edwards and Gurland (1961), Subrahmaniam (1966), see Kocherlakota and Kocherlakota (2014) for a detailed survey. With $n>0$, $\pi _1,\pi _2\in (0,1)$, and $\pi _{0}\in (-\pi _1\,\pi _2,1)$ such that $\pi _{\bullet }:=\sum _{i=0}^{2} \pi _i <1$ holds, the distribution $BNB (n,\pi _1,\pi _2,\pi _{0})$ is defined by the bivariate pgf

$$\begin{aligned} pgf _{X_1,X_2}(z_1,z_2)= & {} \left( \frac{1-\pi _{\bullet }}{1-\pi _1\,z_1-\pi _2\,z_2-\pi _{0}\,z_1 z_2}\right) ^n \nonumber \\= & {} \Big (1+\tfrac{\pi _{\bullet }}{1-\pi _{\bullet }}-\tfrac{\pi _1}{1-\pi _{\bullet }} \,z_1-\tfrac{\pi _2}{1-\pi _{\bullet }}\,z_2-\tfrac{\pi _{0}}{1-\pi _{\bullet }}\,z_1 z_2\Big )^{-n}. \end{aligned}$$

(4)

We have a Poi-limit for $n\rightarrow \infty$ (Subrahmaniam 1966), namely $BPoi (\lambda _1,\lambda _2, \lambda _{0})$ if $n\,\pi _{i}/(1-\pi _{\bullet })\rightarrow \lambda _{i}$ for $n\rightarrow \infty$.

Remark 1

Note that the original definition of $BNB (n,\pi _1,\pi _2,\pi _{0})$ in Edwards and Gurland (1961), Subrahmaniam (1966) requires a truly positive $\pi _0$, i. e., $\pi _{0}\in (0,1)$. But as shown in Proposition 3.1 (c) of Bar-Lev et al. (1994), we get a valid pgf (4) even if we allow for $\pi _{0}\in (-\pi _1 \pi _2,1)$. This can be seen by applying the (negative-)binomial series to (4):

$$\begin{aligned} pgf _{X_1,X_2}(z_1,z_2)= & {} (1-\pi _{\bullet })^n\, \Big ((1-\pi _1\,z_1)(1-\pi _2\,z_2)-(\pi _{0}+\pi _1 \pi _2)\,z_1 z_2\Big )^{-n}\\= & {} \sum _{k=0}^\infty \left( {\begin{array}{c}n+k-1\\ k\end{array}}\right) \frac{(1-\pi _{\bullet })^n\,(\pi _{0}+\pi _1 \pi _2)^k\,z_1^k z_2^k}{(1-\pi _1\,z_1)^{n+k}(1-\pi _2\,z_2)^{n+k}} \end{aligned}$$

has positive series coefficients as long as $\pi _{0}+\pi _1 \pi _2>0$ (note that the negative-binomial series $(1-\pi _i\,z_i)^{-n-k}$, $i=1,2$, have positive series coefficients as well).

Inserting $z_1=1$ or $z_2=1$, respectively, into (4), it is clear that the components of $\varvec{X}\sim BNB (n,\pi _1,\pi _2,\pi _{0})$ are univariately NB-distributed, namely $X_1\sim NB \big (n,\frac{1-\pi _{\bullet }}{1-\pi _2}\big )$ and $X_2\sim NB \big (n,\frac{1-\pi _{\bullet }}{1-\pi _1}\big )$. Thus, the marginal factorial moments are $\mu _{i,(r)} = (n+r-1)_{(r)}\,\big (\frac{\pi _i+\pi _{0}}{1-\pi _{\bullet }}\big )^r$ for $i=1,2$. The joint factorial moments $\mu _{(r,l)}$ satisfy

$$\begin{aligned}{} & {} \mu _{(r,s)} - \mu _{1,(r)}\,\mu _{2,(s)}[1ex]\nonumber \\{} & {} \qquad =\mu _{1,(r)}\,\mu _{2,(s)}\!\sum \limits _{i=1}^{\min \{r,s\}} \frac{\left( {\begin{array}{c}n+r+s-i-1\\ s-i\end{array}}\right) \left( {\begin{array}{c}r\\ i\end{array}}\right) }{\left( {\begin{array}{c}n+s-1\\ s\end{array}}\right) }\,\left( \left( \frac{\pi _{0}\,(1-\pi _{\bullet })}{(\pi _1+\pi _{0})(\pi _2+\pi _{0})}\right) ^i-(-1)^i \right) ,\nonumber \\ \end{aligned}$$

(5)

see the proof in Supplement S.1. Finally, if $\pi _0>0$, then the pgf of the conditional distribution of $X_1|X_2=x_2$ can be decomposed as

$$\begin{aligned} pgf _{X_1|x_2}(z)\ =\ \left( \frac{\pi _2+\pi _{0}\,z}{\pi _2+\pi _{0}}\right) ^{x_2} \left( \frac{1-\pi _1}{1-\pi _1\,z}\right) ^{n+x_2}, \end{aligned}$$

(6)

i. e., the distribution of $X_1|x_2$ is a convolution of the distributions $Bin (x_2,\frac{\pi _{0}}{\pi _2+\pi _{0}})$ and $NB (n+x_2, 1-\pi _1)$. These and further properties of the BNB-distribution are provided by Kocherlakota and Kocherlakota (2014).

3 On Poisson and negative-binomial count processes

In Sect. 3.1, we briefly survey important members of the Poisson integer-valued autoregressive moving-average (Poi-INARMA) family, namely such having a BPoi-distribution for any pair $(X_t,X_{t-h})$ with time lag $h\in \mathbb {N}$. Analogously, Sect. 3.2 discusses a model, where we have BNB-distributions for any pair $(X_t,X_{t-h})$. This model has been proposed for (at least) five times in the literature until now. We show the agreement of these five proposals and discuss further relevant properties.

3.1 Poi-INARMA models

The first thinning-based models for count time series have been proposed by McKenzie (1985), among others the first-order Poisson integer-valued autoregressive (Poi-INAR(1)) model for unbounded counts. It uses the random operator “$\theta \,\circ$” of binomial thinning (Bin-thinning) with thinning parameter $\theta \in (0,1)$, see Steutel and van Harn (1979), as a discrete-valued counterpart to the arithmetic operation “$\theta \,\cdot$” (multiplication). With X being a count rv, Bin-thinning is defined by requiring a conditional Bin-distribution, namely $\theta \circ X|X\ \sim Bin (X,\theta )$. The additivity of the Bin-distribution implies that we can rewrite $\theta \circ X = \sum _{i=1}^X Q_i$, where the counting series $(Q_i)$ comprises i. i. d. $Bin (1,\theta )$-variates being independent of X.

Definition 1

Let $\lambda >0$ and $\rho \in (0,1)$, and let the innovations $(\epsilon _t)_{\mathbb {Z}}$ be i. i. d. according to $Poi (\lambda )$. Assume that all thinnings are performed independently of each other, independent of $(\epsilon _t)_{\mathbb {N}}$, and that the thinnings at time t and $\epsilon _t$ are independent of $(X_s)_{s<t}$. Then, the process $(X_t)_{\mathbb {Z}}$ defined by

$$\begin{aligned} X_t\ =\ \rho \circ X_{t-1}\ +\ \epsilon _t \end{aligned}$$

(7)

is said to be a Poi-INAR(1) process.

The Bin-thinning operator in Definition 1 might be interpreted as determining the number of survivors from the previous population $X_{t-1}$, see Section 2 in Weiß (2018a) for a detailed discussion. The Poi-INAR(1) process constitutes an ergodic Markov chain with limiting marginal distribution $Poi (\mu )$ with $\mu =\lambda /(1-\alpha )$. Thus, if initialized by $X_0\sim Poi (\mu )$, the process is stationary with $\mu =\sigma ^2=\lambda /(1-\alpha )$ (equidispersion), and its autocorrelation function (acf) equals $\rho (h) = Corr[X_t,X_{t-h}] = \rho ^h$, $h\in \mathbb {N}$. In particular, the pairs $(X_t,X_{t-h})$ are BPoi-distributed, namely as

$$\begin{aligned} (X_t,X_{t-h})\ \sim \ BPoi \Big (\big (1-\rho (h)\big )\,\mu ,\ \big (1-\rho (h)\big )\,\mu ,\ \rho (h)\,\mu \Big ); \end{aligned}$$

(8)

see Alzaid and Al-Osh (1988), Weiß (2018a) for these and further properties. Therefore, properties of $(X_t,X_{t-h})$ can be deduced from Sect. 2.1. In particular, we can compute the factorial moments $\mu _{(r,s)}(h):= E\big [(X_t)_{(r)}\,(X_{t-h})_{(s)}\big ]$ via (3):

$$\begin{aligned} \mu _{(r,s)}(h) - \mu _{(r)}\,\mu _{(s)} \ =\ \mu ^{r+s}\, \sum _{i=1}^{\min {\{r,s\}}}\left( {\begin{array}{c}r\\ i\end{array}}\right) \,\left( {\begin{array}{c}s\\ i\end{array}}\right) \,i!\,\left( \frac{\rho (h)}{\mu }\right) ^i, \end{aligned}$$

(9)

see Supplement S.2. Also note that (2) implies the decomposition $Bin (x_{t-1},\rho )+Poi (\lambda )$ for $X_t|x_{t-1}$, in agreement with Definition 1. Finally, the bivariate distribution (8) for lag $h=1$ agrees with the distribution in Section 2(c) of Phatarfod and Mardia (1973), i. e., the Poi-INAR(1) model was already considered by these authors.

The BPoi-property (8) holds in exactly the same way also for different types of Poi-INARMA processes (plugging-in the respective acf), namely for higher-order autoregressions in the sense of Alzaid and Al-Osh (1990), see Weiß (2018b) for details, as well as for the moving-average-type Poi-INMA models (Al-Osh and Alzaid 1988; Weiß 2008a). Because of this universal relevance of (8), when later discussing the Poi-GoF-tests in Sect. 4, we derive the asymptotics not for a specific time series model, but for any time series model satisfying the BPoi-property (8).

Example 1

As a further illustrative example from the Poi-INARMA family, consider the Poi-INMA(1) model defined by

$$\begin{aligned} X_t\ =\ \epsilon _t\ +\ \beta \circ \epsilon _{t-1} \qquad \text {with } \beta \in (0,1), \end{aligned}$$

(10)

where $Poi (\lambda )$-innovations lead to $Poi (\mu )$-observations with $\mu =\lambda \,(1+\beta )$. Here, the acf satisfies $\rho (1)=\beta /(1+\beta )$ and $\rho (h)=0$ for $h\ge 2$ (Al-Osh and Alzaid 1988).

3.2 NB-IINAR(1) model

If being concerned with counts exhibiting overdispersion, i. e., where the marginal variance $\sigma ^2$ exceeds the mean $\mu$, the NB-distribution is the default model, recall Sect. 2.2. The Poi-INAR(1) model discussed in Sect. 3.1 can be modified in such a way that the observations’ marginal distribution is NB, but the innovations’ distribution as well as joint distributions are non-standard in this case (Weiß 2008b). Since the asymptotics for marginal GoF-statistics rely on the joint bivariate distribution of the pairs $(X_t,X_{t-h})$, a sufficiently simple bivariate model for $(X_t,X_{t-h})$ (in analogy to the BPoi-distribution (8) for several types of Poi-INARMA processes) is required for being able to derive closed-form asymptotic expressions. Such a model for AR(1)-like NB-counts is the iterated-thinning INAR(1) (IINAR(1)) model proposed by Al-Osh and Aly (1992, Section 2); also see Wolpert and Brown (2011), Leisen et al. (2019), Guerrero et al. (2022) as well as Phatarfod and Mardia (1973). The IINAR(1) model recursion is similar to the INAR(1) recursion in Definition 1, but it uses a different thinning operator, namely the iterated-thinning operator “$\circledast$”. It can be understood as two nested thinnings (Weiß 2008b), where first a Bin-thinning “$\circ$” with parameter $\theta _1\in (0,1)$ is applied, and then another operator “$*$” with parameter $\theta _2$ such that $\theta _1\,\theta _2\in (0,1)$ holds (the last condition is later required for achieving stationarity). More precisely,

$$\begin{aligned} \textstyle (\theta _1,\theta _2)\circledast X\ :=\ \theta _2 *\big (\theta _1\circ X\big )\ :=\ \sum \limits _{i=1}^{\theta _1\circ X} Y_i, \end{aligned}$$

(11)

where the i. i. d. counting series $(Y_i)$ of the second operator has the mean $\theta _2$. Conditioned on $X=x$, we have

$$\begin{aligned} pgf _{(\theta _1,\theta _2)\circledast x}(z)\ =\ pgf _{\theta _1\circ x}\Big (pgf _Y(z)\Big )\ =\ \Big (1-\theta _1+\theta _1\,pgf _Y(z)\Big )^x, \end{aligned}$$

(12)

and the conditional mean equals $E\big [(\theta _1,\theta _2)\circledast x\big ] = \theta _1\,\theta _2\,x$. Again, the relevance of the requirement $\theta _1\,\theta _2\in (0,1)$ becomes clear, because for $\theta _1\,\theta _2\ge 1$, the operator “$\circledast$” would not act as a “thinning” in the literal sense. It is possible, however, that the second operator “$\theta _2*$” has $\theta _2\ge 1$ (as long as $\theta _1\,\theta _2<1$), whereas the Bin-thinning “$\theta _1\circ$” is well-defined only for $\theta _1\in (0,1)$.

In Al-Osh and Aly (1992) and Weiß (2008b), the special case of iterated thinning together with a geometric counting series is considered, while Wolpert and Brown (2011), Leisen et al. (2019) use the shifted geometric distribution (recall Sect. 2) for this purpose. In Appendix A, it is shown that both constructions of the iterated-thinning operator are equal in distribution, but the second approach has a less restrictive parametrization. Thus, in what follows, we define the geometric iterated-thinning operator with a shifted-geometric counting series $(Y_i)$, namely $Y_i\sim 1+NB (1,\frac{\alpha }{1+\alpha })$ with $pgf _Y(z) = \alpha \,z/(\alpha +1-z)$, and by setting $\theta _1 = \frac{\alpha }{1+\alpha }\,\rho$ and $\theta _2=\frac{1+\alpha }{\alpha }$. Furthermore, to keep the notations simple, we shall use the shorthand symbol $\rho \circledast _\alpha x:= (\frac{\alpha }{1+\alpha }\,\rho ,\frac{1+\alpha }{\alpha })\circledast x$ for this operator. Altogether, see Appendix A,

$$\begin{aligned} pgf _{\rho \circledast _\alpha x}(z)\ =\ \left( 1-\frac{\alpha \rho \,(1-z)}{\alpha +1-z}\right) ^x \end{aligned}$$

(13)

holds, with conditional mean $E\big [(\frac{\alpha }{1+\alpha }\,\rho ,\frac{1+\alpha }{\alpha })\circledast x\big ] = \rho \,x$.

Remark 2

Note that for $\alpha >1/\rho$, we can decompose the pgf (13) as

$$\begin{aligned} \textstyle pgf _{\rho \circledast _\alpha x} \ =\ \left( 1-\frac{\alpha \rho \,(1-z)}{\alpha +1-z}\right) ^x \ =\ \left( \frac{\alpha +(\alpha \rho -1)\,(z-1)}{\alpha +1-z}\right) ^x \ =\ \left( \frac{1 +\frac{\alpha \rho -1}{\alpha }\,(z-1)}{1+\frac{1}{\alpha }\,(1-z)}\right) ^x, \end{aligned}$$

which is the product of the pgfs of $Bin (x,\frac{\alpha \rho -1}{\alpha })$ and $NB (x,\frac{\alpha }{1+\alpha })$. So for $\alpha >1/\rho$, we can represent the operator $\rho \circledast _\alpha x$ as the sum of two independent operators, namely a Bin- and NB-thinning applied to x. This is analogous to the convolution (6), also see the discussion of (A.3) below.

The geometric iterated-thinning operator was first used by Al-Osh and Aly (1992) to define the NB-IINAR(1) model.

Definition 2

Let $n,\alpha >0$ and $\rho \in (0,1)$. Let the innovations $(\epsilon _t)_{\mathbb {Z}}$ be i. i. d. according to $NB (n,\frac{\alpha }{1+\alpha })$ with mean $\mu _{\epsilon }=n/\alpha$ and variance $\sigma _{\epsilon }^2=\frac{1+\alpha }{\alpha }\,\mu _{\epsilon }$. Assume that all thinnings are performed independently of each other, independent of $(\epsilon _t)_{\mathbb {N}}$, and that the thinnings at time t and $\epsilon _t$ are independent of $(X_s)_{s<t}$. Then, the process $(X_t)_{\mathbb {Z}}$ defined by

$$\begin{aligned} X_t\ =\ \rho \circledast _\alpha X_{t-1}\ +\ \epsilon _t \end{aligned}$$

(14)

is said to be an NB-IINAR(1) process.

As shown in Appendix A, the NB-IINAR(1) process according to Definition 2 agrees with the models in Wolpert and Brown, (2011, Theorem 1(4)), Leisen et al. (2019, Eq. (3)) and Guerrero et al. (2022, Section 2.3) except a different parametrization, and there is also a relation to the model in Gouriéroux and Lu (2019, Section 2). It also agrees with a proposal by Phatarfod and Mardia (1973), although these authors do not provide the data-generating mechanism in Definition 2 but define the model by its bivariate pgf, see Appendix A for details.

Remark 3

Note that the DGP of Definition 2 has a quite intuitive interpretation as a branching process with immigration. From the previous population $X_{t-1}$, the fraction $(\frac{\alpha }{1+\alpha }\,\rho )\circ X_{t-1}$ survives until time t and, in addition, may also reproduce itself, as controlled by the count $Z_{t,i}\sim 1+NB (1,\frac{\alpha }{1+\alpha })$ for the ith survivor at time t. So altogether, the part $\rho \circledast _\alpha X_{t-1}$ origins from the previous population $X_{t-1}$, and it is complemented by an independent immigration $\epsilon _t$ at time t. For $\alpha \rightarrow \infty$, the reproduction mechanism degenerates to just preserving the survivors $\rho \circ X_{t-1}$, i. e., the IINAR(1) recursion (14) reduces to the INAR(1) recursion (7) in this case. If, in addition, $n/\alpha \rightarrow \lambda$ for a fixed $\lambda >0$, then the innovations $\epsilon _t$ get $Poi (\lambda )$-distributed, i. e., altogether, the NB-IINAR(1) process converges to a Poi-INAR(1) process.

Al-Osh and Aly (1992) showed that the NB-IINAR(1) process according to Definition 2 constitutes an ergodic Markov chain with limiting marginal distribution $NB (n,\frac{\alpha (1-\rho )}{1+\alpha (1-\rho )})$. The stationary NB-IINAR(1) process has the mean $\mu =n/\big (\alpha (1-\rho )\big )$, variance $\sigma ^2=\frac{1+\alpha (1-\rho )}{\alpha (1-\rho )}\,\mu$, and acf $\rho (h) = \rho ^h$. As shown in Supplement S.3, we obtain the joint bivariate pgf of $(X_t,X_{t-h})$ as

$$\begin{aligned} pgf _{X_h,X_0}(z_1,z_2)\ =\ \left( \frac{1-\pi _{\bullet }}{1-\pi _1\,z_1-\pi _2\,z_2-\pi _{0}\,z_1 z_2}\right) ^n \end{aligned}$$

(15)

with $\pi _1=\pi _2=\frac{1-\rho ^h}{1-\rho }/\big (\alpha +\frac{1-\rho ^h}{1-\rho }\big ) \in (0,1)$ and $\pi _{0}=\big (\alpha /(1+\alpha -\alpha \rho )-\frac{1-\rho ^h}{1-\rho }\big )/\big (\alpha +\frac{1-\rho ^h}{1-\rho }\big )$. So comparing to (4), we recognize that (15) is the pgf of the BNB-distribution. In view of Remark 1, it is worth pointing out that $\pi _0>-\pi _1\pi _2$ is always satisfied, and that $\pi _{0}>0$ iff $\alpha > \frac{1-\rho ^h}{1-\rho }\,\frac{1}{\rho ^h}$.

Properties of $(X_t,X_{t-h})$ can be deduced from Sect. 2.2. In particular, we can compute the factorial moments $\mu _{(r,s)}(h)$ via (5), see Supplement S.2:

$$\begin{aligned}{} & {} \mu _{(r,s)}(h) - \mu _{(r)}\,\mu _{(s)} \ \ [-1ex] \nonumber \\{} & {} \qquad =\mu _{(r)}\,\mu _{(s)}\,\sum \limits _{i=1}^{\min \{r,s\}} \frac{\left( {\begin{array}{c}n+r+s-i-1\\ s-i\end{array}}\right) \left( {\begin{array}{c}r\\ i\end{array}}\right) }{\left( {\begin{array}{c}n+s-1\\ s\end{array}}\right) }\sum \limits _{j=1}^i \left( {\begin{array}{c}i\\ j\end{array}}\right) \, \rho ^{jh}\,\big (1+\alpha (1-\rho )\big )^{j}\, (-1)^{i-j},\nonumber \\ \end{aligned}$$

(16)

where $\mu _{(r)}\,\mu _{(s)}=(n+r-1)_{(r)}(n+s-1)_{(s)}\big /\big (\alpha (1-\rho )\big )^{r+s}$.

4 GoF-tests for time series of Poi- or NB-counts

In what follows, we develop different types of GoF-tests for count time series $X_1,\ldots ,X_T$, which test the null hypothesis of either a $Poi (\mu )$- or $NB (n,\pi )$-marginal distribution. To derive asymptotic normality based on the central limit theorem (CLT) by Ibragimov (1962), we impose the following condition throughout this section:

Assumption A::

$(X_t)_{\mathbb {Z}}$ is $\alpha$-mixing with geometrically decreasing weights.

Assumption A commonly holds for INAR-type models like those in Sect. 3 (see Doukhan and Fokianos 2012), and certainly for i. i. d. and M-dependent processes. Furthermore, for being able to derive feasible closed-form asymptotics, we later also require that lagged pairs of observations, $(X_t,X_{t-h})$, are BPoi-distributed in the case of a Poi-null, and BNB-distributed for a NB-null (as satisfied by the models in Sect. 3); these assumptions (which also imply the existence of moments) are detailed in Sect. 4.2 below.

4.1 General approach

As outlined in Sect. 1, we focus on marginal GoF-statistics of the form $\hat{T }=\tau \big (\frac{1}{T}\,\sum _{t=1}^T \varvec{g}(X_t)\big )$, i. e., being functions of generalized means, where the function $\varvec{g}: \mathbb {N}_0\rightarrow \mathbb {R}^k$ and the smooth function $\tau : \mathbb {R}^k\rightarrow \mathbb {R}$ with some $k\in \mathbb {N}$ have to be specified, and where the test decision relies on deviations of $\hat{T }$ from $T _0=\tau \big (E[\varvec{g}(X)]\big )$. The asymptotic distribution as well as a bias correction for $\hat{T }$ are derived in two steps (assuming that all involved moments exist). First, the CLT in Ibragimov (1962) is used to conclude that under the null hypothesis, $\overline{\varvec{g}(X)} = \frac{1}{T}\,\sum _{t=1}^T \varvec{g}(X_t)$ is asymptotically normally distributed with (exact) mean $\varvec{\mu }_{\varvec{g}}=E[\varvec{g}(X)]$, i. e.,

$$\begin{aligned}{} & {} \sqrt{T}\,\Big (\overline{\varvec{g}(X)}-\varvec{\mu }_{\varvec{g}}\Big )\ \overset{d }{\rightarrow }\ N \big (\varvec{0},\varvec{\Sigma }_{\varvec{g}}\big ), \quad \text {where } \varvec{\Sigma }_{\varvec{g}}=\big (\sigma _{\varvec{g};ij}\big )_{i,j=1,\ldots ,k} \text { has} \nonumber \\ \sigma _{\varvec{g};ij}\ {}{} & {} = E\big [ g_i(X_{t})\, g_j(X_{t}) \big ] - \mu _{g;i}\, \mu _{g;j}\ \nonumber \\{} & {} \quad \qquad +\sum \limits _{h=1}^\infty \Big (E\big [ g_i(X_{t})\, g_j(X_{t-h}) \big ] + E\big [ g_j(X_{t})\, g_i(X_{t-h}) \big ] - 2\, \mu _{g;i}\, \mu _{g;j} \Big ).\nonumber \\ \end{aligned}$$

(17)

If, in addition, the bivariate distributions of $(X_t,X_{t-h})$ are symmetric, in the sense that $pgf _{X_t,X_{t-h}}(z_1,z_2) = pgf _{X_t,X_{t-h}}(z_2,z_1)$ (“time reversibility”, as it holds for the models in Sect. 3), then we even get

$$\begin{aligned} \textstyle \sigma _{\varvec{g};ij}\ =\ E\big [ g_i(X_{t})\, g_j(X_{t}) \big ] - \mu _{g;i}\, \mu _{g;j}\ +\ 2\,\sum \limits _{h=1}^\infty \Big (E\big [ g_i(X_{t})\, g_j(X_{t-h}) \big ] - \mu _{g;i}\, \mu _{g;j} \Big ). \end{aligned}$$

(18)

In the second step, we use the first-order Taylor expansion $\tau (\varvec{y})\approx \tau (\varvec{\mu }_{\varvec{g}}) + {{\textbf {D}}}\,(\varvec{y}-\varvec{\mu }_{\varvec{g}})$, where $\tau (\varvec{\mu }_{\varvec{g}})=T _0$ and ${{\textbf {D}}}=grad \,\tau (\varvec{\mu }_{\varvec{g}})$, to conclude that (“Delta method”)

$$\begin{aligned} \sqrt{T}\,\Big (\hat{T }-T _0\Big )\ \overset{d }{\rightarrow }\ N \big (\varvec{0}, \sigma _{T }^2\big ) \quad \text {with } \sigma _{T }^2 = {{\textbf {D}}}\,\varvec{\Sigma }_{\varvec{g}}\,{{\textbf {D}}}^\top . \end{aligned}$$

(19)

Finally, while $\overline{\varvec{g}(X)}$ is an exactly unbiased estimator of $\varvec{\mu }_{\varvec{g}}$, the final statistic $\hat{T }$ usually has a finite-sample bias with respect to $T _0$. Thus, a bias correction is useful, which follows from the second-order Taylor expansion $\tau (\varvec{y})\approx \tau (\varvec{\mu }_{\varvec{g}}) + {{\textbf {D}}}\,(\varvec{y}-\varvec{\mu }_{\varvec{g}}) + \frac{1}{2}\, (\varvec{y}-\varvec{\mu }_{\varvec{g}})^\top \,{{\textbf {H}}}\,(\varvec{y}-\varvec{\mu }_{\varvec{g}})$, where ${{\textbf {H}}}$ is the Hessian of $\tau$ in $\varvec{\mu }_{\varvec{g}}$:

$$\begin{aligned} E\big [\hat{T }\big ]\ \approx{} & {} T _0 + \frac{1}{2}\, E\Big [\big (\,\overline{\varvec{g}(X)}-\varvec{\mu }_{\varvec{g}}\big )\!^\top \,{{\textbf {H}}}\,\big (\,\overline{\varvec{g}(X)}-\varvec{\mu }_{\varvec{g}}\big )\Big ][2ex] \nonumber \\ \approx{} & {} T _0 + \frac{1}{2\,T}\, \sum _{i=1}^k h_{ii}\,\sigma _{\varvec{g};ii} + \frac{1}{T}\, \sum _{i<j} h_{ij}\,\sigma _{\varvec{g};ij} \ =:\ \mu _{T }. \end{aligned}$$

(20)

Using (19) and (20), the asymptotic implementation of the (two-sided) GoF-test at level $\gamma$ looks as follows. With $z_\gamma$ denoting the $(1-\gamma /2)$-quantile of the standard normal distribution, $N (0,1)$, the null hypothesis is rejected if $\hat{T }$ violates the critical values $\mu _{T } \mp z_\gamma \, T^{-1/2}\,\sigma _{T }$. Here, the parameter values required for computing the critical values are obtained by plugging-in the respective parameter estimates (see the details below).

4.2 GoF-tests using factorial moments

The first class of tests is inspired by the dispersion test of Kyriakoussis et al. (1998). But instead of considering only second-order factorial moments, we use factorial moments up to order $r\in \mathbb {N}$ for arbitrary $r\ge 2$ by defining $\tau (u,v,w)=\frac{u}{v\,w}$ and $\varvec{g}(x)=\big (x_{(r)},x_{(r-s)},x_{(s)}\big ){}^\top$ for some $1\le s<r$. So the test statistic becomes

$$\begin{aligned} \hat{T }_{(r,s)}\ =\ \frac{\overline{X_{(r)}}}{\,\overline{X_{(s)}}\,\overline{X_{(r-s)}}\,} \quad \text {with}\quad T _{(r,s)}\ =\ \frac{\mu _{(r)}}{\mu _{(s)}\,\mu _{(r-s)}}, \end{aligned}$$

(21)

where the values of r, s are selected by the user. This choice can be guided by common interpretations of rth-order moments: $\hat{T }_{(r,s)}$ with $r=2$ is a kind of dispersion statistic, while $r=3$ and $r=4$ might be interpreted as skewness and excess statistics, respectively. If, for example, the relevant alternative scenario has similar dispersion properties like the null model but differs in terms of skewness, the choice $r=3$ appears reasonable.

Adapting (18) to (21), we get

$$\begin{aligned} \textstyle \sigma _{\varvec{g};(k,l)}\ =\ \mu _{(k,l)}(0) - \mu _{(k)}\, \mu _{(l)}\ +\ 2\,\sum \limits _{h=1}^\infty \big (\mu _{(k,l)}(h) - \mu _{(k)}\, \mu _{(l)} \big )\ =:\ \sigma _{(k,l)}. \end{aligned}$$

(22)

Applying (22) to (19) and (20), we achieve the following result.

Theorem 1

Let the DGP $(X_t)_{\mathbb {Z}}$ satisfy the $\alpha$-mixing assumption of Sect. 4, and define $A_{k,l}=\sigma _{(k,l)}/(\mu _{(k)}\,\mu _{(l)})$. Then, the distribution of the statistic $\hat{T }_{(r,s)}$ according to (21) can be approximated by the normal distribution $N (\mu _{\hat{T }_{(r,s)}},\ \tfrac{1}{T}\,\sigma _{\hat{T }_{(r,s)}}^2)$, where the bias-corrected mean is given by

$$\begin{aligned} \mu _{\hat{T }_{(r,s)}}= & {} T _{(r,s)}\,\Big (1 + \tfrac{1}{T}\,\big (A_{r-s,r-s} +A_{s,s}-A_{r,r-s}-A_{r,s}+A_{r-s,s}\big )\Big ), \end{aligned}$$

and the variance by

$$\begin{aligned} \sigma _{\hat{T }_{(r,s)}}^2= & {} T _{(r,s)}^2\, \Big (A_{r,r}+A_{r-s,r-s} +A_{s,s}-2A_{r,r-s}-2A_{r,s}+2A_{r-s,s}\Big ). \end{aligned}$$

The proof of Theorem 1 is provided by Supplement S.4. Note that in the special case $r=2\,s$ (“symmetric statistic”), so $r-s=s$ and $T _{(2s,s)}=\mu _{(2s)}/\mu _{(s)}^2$, Theorem 1 simplifies to

$$\begin{aligned}{} & {} \mu _{\hat{T }_{(2s,s)}}\! = T _{(2s,s)}\,\Big (1 + \tfrac{1}{T}\,(3\,A_{s,s}-2\,A_{2s,s})\Big ), \\{} & {} \sigma _{\hat{T }_{(2s,s)}}^2\! = T _{(2s,s)}^2\, \Big (A_{2s,2s}+4\,(A_{s,s}-A_{2s,s})\Big ). \end{aligned}$$

As outlined in the beginning of Sect. 4, we now consider two null scenarios, namely

• Poi-null: $(X_t,X_{t-h})\, \sim \, BPoi \big (\lambda (h),\, \lambda (h),\, \lambda _0(h)\big )$ with $\lambda (h)=\big (1-\rho (h)\big )\,\mu$ and $\lambda _0(h)=\rho (h)\,\mu$ like in Sect. 3.1, then

  $$\begin{aligned} T _{(r,s)}\ =\ 1;\qquad \text {or} \end{aligned}$$

  (23)

• NB-null: $(X_t,X_{t-h})\, \sim \, BNB \big (n,\, \pi (h),\, \pi (h),\, \pi _0(h)\big )$ with

  $$\begin{aligned} \pi (h) = \frac{1-\rho (h)}{n/\mu + 1-\rho (h)} \quad \text {and}\quad \pi _0(h) = \frac{n/(n+\mu )-1+\rho (h)}{n/\mu +1-\rho (h)} \end{aligned}$$

  like in Sect. 3.2, then

  $$\begin{aligned} T _{(r,s)} \ =\ \frac{(n+r-1)_{(r)}}{(n+s-1)_{(s)}\,(n+r-s-1)_{(r-s)}} \ =\ \frac{\left( {\begin{array}{c}n+r-1\\ s\end{array}}\right) }{\left( {\begin{array}{c}n+s-1\\ s\end{array}}\right) }. \end{aligned}$$

  (24)

  (Note that for the NB-IINAR(1) model according to Definition 2, we get $\pi (h)=\frac{1-\rho ^h}{\alpha (1-\rho )+1-\rho ^h}$ and $\pi _0(h)=\frac{\alpha (1-\rho )/(1+\alpha -\alpha \rho )-(1-\rho ^h)}{\alpha (1-\rho )+1-\rho ^h}$.)

Here, (23) or (24) serve as the null value $T _0$ according to Sect. 4.1 if testing the Poi-null or NB-null, respectively. The factorial moments $\mu _{(r,s)}(h)$ required for (22) have already been computed in (9) and (16). In Supplement S.5, we derive the following result.

Corollary 1

The $A_{k,l}$ required for Theorem 1 compute as follows:

• (i) For the Poi-null, it holds that

  $$\begin{aligned} A_{k,l}\ =\ \sum \limits _{i=1}^{\min \{k,l\}} \left( {\begin{array}{c}k\\ i\end{array}}\right) \left( {\begin{array}{c}l\\ i\end{array}}\right) \frac{i!}{\mu ^i} {\textstyle \Big (1+2\,\sum \limits _{h=1}^{\infty }\rho (h)^i \Big )}. \end{aligned}$$

  Moreover, in the case of the Poi-INAR(1) process, we get

  $$\begin{aligned} A_{k,l}\ =\ \sum \limits _{i=1}^{\min \{k,l\}} \left( {\begin{array}{c}k\\ i\end{array}}\right) \left( {\begin{array}{c}l\\ i\end{array}}\right) \frac{i!}{\mu ^i} \frac{1+\rho ^i}{1-\rho ^i}. \end{aligned}$$

• (ii) For the NB-null, it holds that

  $$\begin{aligned} A_{k,l}\ =\ \sum \limits _{i=1}^{\min \{k,l\}} \frac{\left( {\begin{array}{c}n+k+l-i-1\\ l-i\end{array}}\right) \left( {\begin{array}{c}k\\ i\end{array}}\right) }{\left( {\begin{array}{c}n+l-1\\ l\end{array}}\right) }\,\sum _{j=1}^i \left( {\begin{array}{c}i\\ j\end{array}}\right) \,(1+n/\mu )^{j}\,(-1)^{i-j}\,{\textstyle \Big (1+2\,\sum \limits _{h=1}^{\infty }\rho (h)^j \Big )}. \end{aligned}$$

  Moreover, in the case of the NB-IINAR(1) process, we get

  $$\begin{aligned} A_{k,l}\ =\ \sum \limits _{i=1}^{\min \{k,l\}} \frac{\left( {\begin{array}{c}n+k+l-i-1\\ l-i\end{array}}\right) \left( {\begin{array}{c}k\\ i\end{array}}\right) }{\left( {\begin{array}{c}n+l-1\\ l\end{array}}\right) }\,\sum _{j=1}^i \left( {\begin{array}{c}i\\ j\end{array}}\right) \, \big (1+\alpha (1-\rho )\big )^{j}\, (-1)^{i-j}\, \frac{1+\rho ^j}{1-\rho ^j}. \end{aligned}$$

Example 2

In Kyriakoussis et al. (1998), only the case of the second-order statistic $\hat{T }_{(2,1)}$ is considered. For the AR(1)-like acf $\rho (h)=\rho ^h$, see Supplement S.6, Theorem 1 together with Corollary 1 then yields for the

• (i) Poi-null:

  $$\begin{aligned} \textstyle \mu _{\hat{T }_{(2,1)}}\ =\ 1-\frac{1}{T\mu }\,\frac{1+\rho }{1-\rho },\qquad \sigma _{\hat{T }_{(2,1)}}^2\ =\ \frac{2}{\mu ^2}\,\frac{1+\rho ^2}{1-\rho ^2}; \end{aligned}$$

• (ii) NB-null:

  $$\begin{aligned} \textstyle \mu _{\hat{T }_{(2,1)}}\ =\ \frac{n+1}{n}\Big (1-\frac{2}{T}\,\frac{1+\alpha (1-\rho )}{n}\,\frac{1+\rho }{1-\rho }\Big ),\quad \sigma _{\hat{T }_{(2,1)}}^2\ =\ \frac{2(n+1)\big (1+\alpha (1-\rho ) \big )^2}{n^3}\,\frac{1+\rho ^2}{1-\rho ^2}. \end{aligned}$$

In fact, Kyriakoussis et al. (1998) restrict to the special case of i. i. d. counts, and they do not consider the above bias correction. Plugging-in $\rho =0$ into the expressions for $\sigma _{\hat{T }_{(2,1)}}^2$, and using the notation $\theta =\frac{\alpha }{1+\alpha }$ for the NB-null, we confirm the results in Sections 3.1 and 3.3 of Kyriakoussis et al. (1998).

Fig. 1

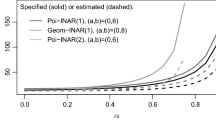
Asymptotic power curves of $\hat{T }_{(r,s)}$-tests (5 %-level) for null hypotheses a Poi-INAR(1) (so $n_0=\infty$) and b NB-IINAR(1) with $n_0=10$ (see dotted lines). NB-IINAR(1) alternatives with $n\not =n_0$ and $\sigma ^2/\mu = 1 + \mu /n$, where $\mu =5$, $\rho =0.3$, and $T=250$ are kept fixed

Corollary 1 can be used for testing the null hypothesis of a Poi-INAR(1) or NB-IINAR(1) model, respectively (or of i. i. d. Poi- or NB-counts), as outlined in the end of Sect. 4.1. In particular, if we take the alternative from the same model families, Corollary 1 also allows to do an asymptotic power analysis. While comprehensive simulation-based analyses are later presented in Sect. 5, let us now have a first look at some asymptotic power curves. Figure 1 considers the null hypothesis of a Poi-INAR(1) model in (a), and of an NB-IINAR(1) model in (b). Here, the alternatives are taken from the NB-IINAR(1) family in such a way that mean $\mu$ and acf parameter $\rho$ remain fixed, and only the dispersion structure changes (as controlled by n or $\sigma ^2/\mu = 1 + \mu /n$, respectively). We consider the “dispersion statistic” $\hat{T }_{(2,1)}$, the “skewness statistic” $\hat{T }_{(3,1)}$, and the “excess statistics” $\hat{T }_{(4,1)}, \hat{T }_{(4,2)}$. Among these test statistics, always $\hat{T }_{(2,1)}$ shows the best power in Fig. 1 (followed by $\hat{T }_{(3,1)}$). Note that in (b), we have better power properties regarding increases of dispersion (decreasing n), i. e., for detecting relative overdispersion. The dominance of the dispersion statistics in Fig. 1 is not surprising as the alternatives primarily differ from the null in terms of dispersion; this also agrees with the findings in earlier studies such as Schweer and Weiß (2016); Puig and Weiß (2020); Aleksandrov et al. (2022). Thus, later in Sect. 5, we shall focus on such alternative scenarios where the dispersion does not differ from the null scenario, but the remaining shape properties do. Then, the higher-order $\hat{T }_{(r,s)}$-statistics shall turn out to be more useful than $\hat{T }_{(2,1)}$.

We conclude this section with a note on how to apply Corollary 1 in practice. In the case of AR(1)-like counts, the $A_{k,l}$ depend on $\mu$ and $\rho =\rho (1)$, the true values of which we do not know in real applications. Thus, it is necessary to plug-in parameter estimates instead, where we use the sample mean $\hat{\mu }:=\overline{x}$ and the lag-1 sample acf $\hat{\rho }=\hat{\rho }(1)$ (if the tests are applied to i. i. d. counts, only $\mu$ and $\overline{x}$ are required). These moment estimators of $\mu ,\rho$ are $\sqrt{T}$-consistent, so Slutsky’s theorem implies that $\sqrt{T}\,\big (\hat{T }_{(r,s)}-\mu _{\hat{T }_{(r,s)}}\big )/ \sigma _{\hat{T }_{(r,s)}} \overset{d }{\rightarrow } N (0,1)$ still holds if $\mu , \rho$ are replaced by $\hat{\mu },\hat{\rho }$ in the formulae for $\mu _{\hat{T }_{(r,s)}}, \sigma _{\hat{T }_{(r,s)}}$.

4.3 GoF-tests using Stein’s identity

Stein (1972, 1986) developed the idea to characterize (discrete or continuous) distributions by types of moment identities. Such Stein identities are available for several common discrete distributions, see Sudheesh and Tibiletti (2012) and Betsch et al. (2022), including the Poi-case (then it is referred to as the Stein–Chen identity) and the NB-case. In Aleksandrov et al. (2022), the Stein–Chen identity

$$\begin{aligned} E\big [X\, f(X)\big ]\ =\ \mu \, E\big [f(X+1)\big ] \end{aligned}$$

(25)

of the $Poi (\mu )$-distribution is utilized to develop moment-based GoF-tests for Poi-count time series. Among others, they considered the statistic (referred to as “ $\hat{T}_2$ ” in their article)

$$\begin{aligned} \hat{T }\!_{f}^{\,Poi } \ =\ \frac{\overline{Xf(X)}}{\, \overline{X}\ \overline{f(X+1)} \,}, \end{aligned}$$

(26)

where

$$\begin{aligned} T \!_{f}^{\,Poi }\ =\ \frac{E\big [X\,f(X)\big ]}{E[X]\,E\big [f(X+1)\big ]} \quad \text {equals~1 under the Poi-null}. \end{aligned}$$

(27)

As discussed by Aleksandrov et al. (2022), f can be interpreted as a weight function and should be chosen by the user with respect to the anticipated alternative scenario. For overdispersed alternatives, for example, it is reasonable to assign increasing weight to increasing counts – note that (26) with $f(x)=x$ is closely related to Fisher’s dispersion index. For equi- and underdispersed as well as zero-inflated alternatives, by contrast, the choice $f(x)=\exp (-x)$ showed a promising power performance in the simulations of (Aleksandrov et al. 2022), where now most weight concentrates on low counts. Later, we focus on this special case for asymptotic calculations, but our general approach is applicable to different choices of f as well.

In the sequel, we complement the approach of Aleksandrov et al. (2022) by developing Stein-type GoF-tests for NB-count time series. According to Sudheesh and Tibiletti (2012), the Stein identity for the NB-distribution with mean $\mu >0$ and parameter $n>0$ (recall from Table 1 that an NB-distribution parametrized in $n,\mu >0$ has $\pi =\frac{n}{n+\mu }$) can be denoted as

$$\begin{aligned} (n+\mu )\,E\big [X\,f(X)\big ]\ =\ \mu \, E\big [(n+X)\,f(X+1)\big ], \end{aligned}$$

(28)

which (after having divided both sides of (28) by n) converges to (25) for $n\rightarrow \infty$. In analogy to (26)–(27), using the hypothetical value $n=n_{0}$, we now define

$$\begin{aligned} \hat{T }\!_{f}^{\,NB } \ =\ \frac{\big (n_{0}+\overline{X}\big )\,\overline{Xf(X)}}{\, \overline{X}\ \overline{(n_{0}+X)\,f(X+1)} \,}, \end{aligned}$$

(29)

where

$$\begin{aligned} T \!_{f}^{\,NB }\ =\ \frac{\big (n_{0}+E[X]\big )\,E\big [X\,f(X)\big ]}{E[X]\,E\big [(n_{0}+X)\,f(X+1)\big ]} \quad \text {equals~1 under the NB-null}. \end{aligned}$$

(30)

In Aleksandrov et al. (2022), it was shown for statistic $\hat{T }\!_{f}^{\,Poi }$ under the Poi-null that it is possible to find a general closed-form expression for the asymptotic distribution of such a Stein-type statistic. The asymptotic implementation of the corresponding tests in practice, however, is often demanding such that a parametric-bootstrap implementation is clearly preferable (see Sect. 5 for further details). Thus, in the sequel, we present asymptotic derivations only for the illustrative case of i. i. d. counts using the particular choice $f(x)=\exp (-x)$. Note that Stein-type statistics using $f(x)=\exp (-x)$ are closely related to the rv’s moment generating function (mgf) $\psi (u):= E[e^{u\,X}] = pgf (e^u)$, because then $E\big [f(X+1)\big ]=e^{-1}\,\psi (-1)$ and $E\big [X\,f(X)\big ]=\psi '(-1)$. Relevant examples are summarized in Table 2; also see Eqs. (S.8)–(S.10) in Supplement S.7.

Table 2 Examples of mgf $\psi (u) = E[e^{u\,X}]$ and its derivatives

Let us begin with the Stein–Chen statistic (26). Then, the following asymptotics hold for the case of i. i. d. Poi-counts and i. i. d. NB-counts (for the parametrization used in Sect. 3.2, this implies $\rho =0$ and $\alpha =n/\mu$), respectively.

Theorem 2

Let $(X_t)_{\mathbb {Z}}$ be i. i. d. with existing moments, set $f(x)=\exp (-x)$. The asymptotic distribution of $\hat{T }\!_{\exp }^{\,Poi }$ from (26) is $N (\mu _{\hat{T }\!_{\exp }^{\,Poi }},\ \tfrac{1}{T}\,\sigma _{\hat{T }\!_{\exp }^{\,Poi }}^2)$, where:

• (i) If $(X_t)_{\mathbb {Z}}$ is i. i. d. according to $Poi (\mu )$, then

  $$\begin{aligned} \mu _{\hat{T }\!_{\exp }^{\,Poi }}= & {} 1+\tfrac{1}{T}\,\exp \!\big (\mu \,(1-e^{-1})^2\big )\,(1-e^{-1}),\\ \sigma _{\hat{T }\!_{\exp }^{\,Poi }}^2= & {} \exp \!\big (\mu \,(1-e^{-1})^2\big )\,\Big ( \tfrac{1}{\mu }+(1-e^{-1})^2\Big )-\tfrac{1}{\mu }. \end{aligned}$$

• (ii) If $(X_t)_{\mathbb {Z}}$ is i. i. d. according to $NB \big (n,\frac{n}{n+\mu }\big )$ with mgf $\psi (u)$, see the second row in Table 2, then

  $$\begin{aligned} \textstyle \mu _{\hat{T }\!_{\exp }^{\,Poi }}= & {} \textstyle T \!_{\exp }^{\,Poi } + \textstyle \tfrac{1}{T}\,\frac{e}{\mu \,\psi (-1)}\\{} & {} \Big (\frac{\psi '(-1)\,\sigma ^2}{\mu ^2} -\frac{\psi ''(-1)}{\mu }+ \frac{ \psi '(-1)^2}{\mu \psi (-1)}-\frac{\psi '(-2)}{\psi (-1)}+\frac{\psi '(-1)\psi (-2)}{\psi (-1)^2}\Big ),\\ \sigma _{\hat{T }\!_{\exp }^{\,Poi }}^2= & {} \textstyle \Big (\frac{e }{\mu \,\psi (-1)}\Big )^2\Big (\frac{\psi '(-1)^2\,\sigma ^2}{\mu ^2} - 2\, \frac{\psi '(-1)\,\psi ''(-1)}{\mu }+\psi ''(-2) +2\, \frac{\psi '(-1)^3}{\psi (-1)\mu }\\{} & {} \textstyle -2\, \frac{\psi '(-1)\,\psi '(-2)}{\psi (-1)}+ \frac{\psi '(-1)^2\,\psi (-2)}{\psi (-1)^2}\Big ), \end{aligned}$$

  where   $T \!_{\exp }^{\,Poi } = \big (1+\frac{\mu }{n}\,(1-e^{-1})\big )^{-1}$.

The proof of Theorem 2 is provided by Supplement S.7. Note that the results of part (ii) converge to those of (i) for $n\rightarrow \infty$. Next, we consider the NB’s Stein statistic (29) and derive its asymptotics for the same scenarios as in Theorem 2.

Theorem 3

Let $(X_t)_{\mathbb {Z}}$ be i. i. d. with existing moments, set $f(x)=\exp (-x)$. The asymptotic distribution of $\hat{T }\!_{\exp }^{\,NB }$ from (29) is $N (\mu _{\hat{T }\!_{\exp }^{\,NB }},\ \tfrac{1}{T}\,\sigma _{\hat{T }\!_{\exp }^{\,NB }}^2)$, where:

• (i) If $(X_t)_{\mathbb {Z}}$ is i. i. d. according to $Poi (\mu )$, then

  $$\begin{aligned} \mu _{\hat{T }\!_{\exp }^{\,NB }}= & {} \textstyle T \!_{\exp }^{\,NB }+\frac{1}{T}\,\Bigg (e^{\mu \,(1-e^{-1})^2}\cdot \frac{n_{0}\, (n_{0}+\mu )\, \big ((1-e^{-1}) \, (n_{0}+ e^{-2}\mu )-e^{-1}\big )}{(n_{0}+e^{-1}\mu )^3} + \frac{e\, n_{0}}{(e\, n_{0}+\mu )^2} \Bigg ), \\ \sigma _{\hat{T }\!_{\exp }^{\,NB }}^2= & {} \textstyle e^{\mu \,(1-e^{-1})^2}\cdot \frac{n_{0}^2\, (n_{0}+\mu )^2}{(n_{0}+e^{-1}\mu )^4}\,\Big (\frac{1}{\mu }+(1-e^{-1})^2 \Big ) -\frac{n_{0}^2 \big (n_{0}+\mu \,(2-e^{-1})\big ) }{\mu (n_{0}+e^{-1}\mu )^3}, \end{aligned}$$

  where   $\displaystyle T \!_{\exp }^{\,NB } = \frac{n_{0}+\mu }{n_{0}+e^{-1}\mu }$.

• (ii) If $(X_t)_{\mathbb {Z}}$ is i. i. d. according to $NB \big (n,\frac{n}{n+\mu }\big )$ with mgf $\psi (u)$, see the second row in Table 2, and if $A (u):=\psi '(u)+n_{0}\,\psi (u)$, then

  $$\begin{aligned} \mu _{\hat{T }\!_{\exp }^{\,NB }}= & {} \textstyle T \!_{\exp }^{\,NB }+\tfrac{1}{T}\,\frac{e\,n_{0}}{\mu \,A (-1)^2}\,\Bigg (\frac{\psi '(-1)\,A (-1)\,\sigma ^2}{\mu ^2} +\tfrac{n_{0}}{\mu }\big (\psi '(-1)^2-\psi (-1)\psi ''(-1)\big )\\{} & {} \textstyle +\tfrac{(n_{0}+\mu )}{A (-1)}\Big (\psi '(-1)\,A (-2)-\psi (-1) \big (\psi ''(-2)+n_{0}\psi '(-2)\big )\Big )\Bigg ), \\ \sigma _{\hat{T }\!_{\exp }^{\,NB }}^2= & {} \textstyle \Big (\frac{e\, n_{0}}{\mu \,A (-1)}\Big )^2\Bigg (\frac{\psi '(-1) ^2\,\sigma ^2}{\mu ^2} + \frac{2(n_{0}+\mu )\psi '(-1)}{\mu \,A (-1)}\big (\psi '(-1)^2-\psi (-1)\psi ''(-1)\big )\\{} & {} \textstyle +\frac{(n_{0}+\mu )^2}{\,A (-1)^2}\Big (\psi (-1)^2\psi ''(-2)-2\psi (-1)\psi '(-1)\psi '(-2) +\psi '(-1)^2\psi (-2)\Big )\Bigg ), \end{aligned}$$

  where   $\displaystyle T \!_{\exp }^{\,NB } = \frac{e\,(n_{0}+\mu )\,\psi '(-1)}{\mu \,A (-1)}$.

The proof of Theorem 3 is again provided by Supplement S.7. The results of Theorem 3 converge to those of Theorem 2 for $n_0\rightarrow \infty$. Note that the DGP’s parameter value n in part (ii) might differ from the null value $n_0$ used form computing the Stein statistic (29). Also note that for applications in practice, the sample mean $\overline{x}$ is plugged-in instead of $\mu$ in the asymptotics of Theorems 2 and 3, recall the analogous discussion in the last paragraph of Sect. 4.2.

Fig. 2

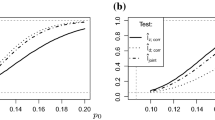
Asymptotic power curves of Stein tests and some $\hat{T }_{(r,s)}$-tests (5 %-level) against NB-alternatives with $n\not =n_0$ and $\sigma ^2/\mu = 1 + \mu /n$, where $\mu =2.5$. a Poi-null with $T=100$ using $\hat{T }\!_{\exp }^{\,Poi }$, and b geometric null ($n_0=1$) with $T\in \{100,250\}$ using $\hat{T }\!_{\exp }^{\,NB }$

Like in Sect. 4.2, Theorems 2 and 3 can now be used for asymptotic power analyses: using Theorem 2, we can test the Poi-null against an NB-alternative, while Theorem 3 allows to test an NB-null against Poi- and NB-alternatives. This is illustrated by Fig. 2. In part (a), the Poi-null is violated in favour of increasing dispersion, and as expected from Sect. 4.2, the dispersion test $\hat{T }_{(2,1)}$ performs best. But it is interesting to note that the Stein–Chen test $\hat{T }\!_{\exp }^{\,Poi }$ performs similarly well for strong overdispersion, where the NB-distribution also exhibits considerable zero inflation. Part (b) refers to the opposite situation, where $\hat{T }_{(2,1)}$ and $\hat{T }\!_{\exp }^{\,NB }$ are applied to a geometric null (i. e., NB with $n_0=1$), and where increasing n causes decreasing dispersion (i. e., underdispersion w. r. t. a geometric distribution). Now, the Stein test is superior, which agrees with analogous findings for a Poi-null in Aleksandrov et al. (2022).

4.4 Omnibus GoF-tests using Stein’s identity

As outlined in Sect. 1, the main aim of this article is to present a variety of moment-based GoF-tests for Poi- and NB-counts that can be used for a kind of targeted diagnosis. But especially the flexible Stein approach described in Sect. 4.3 could also be used to construct omnibus GoF-tests being powerful against a large class of alternatives. This shall be briefly demonstrated in this section for the special case of testing the null hypothesis of i. i. d. Poi-counts, and for a particular class of weight functions (see the details below), while a more comprehensive analysis is recommended for future research, see Sect. 7.

While the construction of the GoF-tests in Sect. 4.3 is based on a single weight function f (where we focused on $f(x)=\exp (-x)$ for illustration), we extend this approach and equip the functions $\varvec{g}$ and f, respectively, with an additional index $s\in [a,b]$, where $a,b\in \mathbb {R}$ with $a<b$. That is, we consider $\hat{T }(s)=\tau \big (\frac{1}{T}\,\sum _{t=1}^T \varvec{g}_s(X_t)\big )$ for a class of vector-valued function $\varvec{g}_s$ with $s\in [a,b]$ and some smooth function $\tau$. Then, to construct a marginal GoF-statistic, we compare the whole function $\big (\hat{T }(s)\big )_{s\in [a,b]}$ with $\big (T _0(s)\big )_{s\in [a,b]}$, where $T _0(s)=\tau \big (E[\varvec{g}_s(X)]\big )$ is computed under some null hypothesis. There are different ways to do this comparison, see Gürtler and Henze (2000) for an overview. For instance, one could consider the maximum distance

$$\begin{aligned} \max _{s\in [a,b]} \big |\hat{T }(s)-T _0(s)\big |, \end{aligned}$$

(31)

the (integrated) $L^2$-distance

$$\begin{aligned} \int _a^b\left( \hat{T }(s)-T _0(s)\right) ^2\, d s, \end{aligned}$$

(32)

or the weighted $L^2$-distance

$$\begin{aligned} \int _a^b\left( \hat{T }(s)-T _0(s)\right) ^2\, w(s)\ d s \end{aligned}$$

(33)

for some weight function $w:\mathbb {R}\rightarrow [0,\infty )$. As mentioned above, we shall focus on the null of i. i. d. Poi-counts for illustration, i. e., on GoF-test statistics utilizing the Stein–Chen identity (25). Like in Sect. 4.3, we set $\tau (u,v,w)=\frac{v}{u\,w}$, but allow for a whole class of vector-valued functions $\big (\varvec{g}_s\big )_{s\in [a,b]}$ with $\varvec{g}_s(x)=\big (x,x\,f_s(x),f_s(x+1)\big ){}^\top$ for a family of bounded functions $\big (f_s\big )_{s\in [a,b]}$ with $f_s:\mathbb {N}_0\rightarrow \mathbb {R}$. For example, considering the function $f(x)=\exp (-x)$ discussed before, a natural class of functions could be defined by setting $f_u(x)=\exp (u\,x)$, which would lead to mgf-based GoF-tests. But other choices leading to well-known quantities are also possible, such as pgf-based GoF-tests based on $f_s(x)=s^x$, which are related to the mgf-based ones by setting $u=\ln {s}$. In this regard, the Stein–Chen identity (25) can be extended to read

$$\begin{aligned} E\big [X\, f_s(X)\big ]\ =\ \mu \, E\big [f_s(X+1)\big ], \quad s\in [a,b], \end{aligned}$$

(34)

which can be accordingly utilized to construct a whole class of moment-based GoF-test statistics for i. i. d. Poi-rv’s. For instance, adopting the approach from Sect. 4.3 with $\tau$ defined above, (26) leads to the statistic

$$\begin{aligned} \hat{T }\!_{f}^{\,Poi }(s) \ =\ \frac{\overline{Xf_s(X)}}{\, \overline{X}\ \overline{f_s(X+1)} \,}, \quad s\in [a,b], \end{aligned}$$

(35)

and

$$\begin{aligned} T \!_{f}^{\,Poi }(s)\ =\ \frac{E\big [X\,f_s(X)\big ]}{E[X]\,E\big [f_s(X+1)\big ]} \quad \text {equals~1 under the Poi-null} \end{aligned}$$

(36)

for all $s\in [a,b]$. In what follows, we focus on the special case of $f_s(x)=s^x$ for asymptotic calculations, but our general approach is applicable to different choices of $f_s$ as well. Then, the following asymptotics of the Stein–Chen statistic (35) hold for the case of i. i. d. Poi-counts.

Theorem 4

Let $(X_t)_{\mathbb {Z}}$ be i. i. d. with existing moments, set $f_s(x)=s^x$ for $s\in [a,b]$, where $a>0$. Then, $\sqrt{T}\,\big (\hat{T }\!_{s^x}^{\,Poi }(s)-T \!_{s^x}^{\,Poi }(s)\big )_{s\in [a,b]}$ converges weakly to a centered Gaussian process $\big (G\!_{s^x}(s)\big )_{s\in [a,b]}$ with mean function $\big (\mu _{\hat{T }\!_{s^x}^{\,Poi }}(s)\big )_{s\in [a,b]}$ and covariance kernel $\big (\sigma _{\hat{T }\!_{s^x}^{\,Poi }}(s_1,s_2)\big )_{s_1,s_2\in [a,b]}$.

In particular, if $(X_t)_{\mathbb {Z}}$ is i. i. d. according to $Poi (\mu )$, then $T \!_{s^x}^{\,Poi }(s)=1$, and we get

$$\begin{aligned} \mu _{\hat{T }\!_{s^x}^{\,Poi }}(s)= & {} \frac{1}{T}\,(1-s)\,\exp \!\big (\mu (s-1)^2\big ), \\ \sigma _{\hat{T }\!_{s^x}^{\,Poi }}(s_1,s_2)= & {} \left( \frac{1}{\mu }+(s_1-1)(s_2-1)\right) \exp \!\big (\mu (s_1-1)(s_2-1)\big ) -\frac{1}{\mu }. \end{aligned}$$

The proof of Theorem 4 is provided by Supplement S.8. Note that Theorem 4 implies Theorem 2 (i) by setting $s=s_1=s_2=e^{-1}$.

Now, we can make use of Theorem 4 for testing the null hypothesis of $(X_t)_{\mathbb {Z}}$ being i. i. d. according to $Poi (\mu )$. In analogy to Rueda and O’Reilly (1999) and Meintanis (2005), we consider the integrated $L^2$-distance (32), where the integration runs from 0 to 1. To avoid division by zero in (35), however, the lower integration bound is chosen as some $\varepsilon >0$, where $\varepsilon$ is close to zero (for our simulations in Sect. 5.3, we used $\varepsilon =10^{-3}$). Then, by the continuous mapping theorem, we immediately get

$$\begin{aligned} T\int _\varepsilon ^1 \left( \hat{T }\!_{s^x}^{\,Poi }(s)-1\right) ^2\, d s \ \Rightarrow \ \int _\varepsilon ^1 G_{s^x}^2(s)\, d s\quad \text {under the Poi-null}. \end{aligned}$$

(37)

For the practical implementation of the omnibus GoF-test (37), we follow Meintanis (2005) and use a parametric bootstrap scheme, see Sect. 5 for details.

5 Simulation experiments

In Sects. 5.1–5.2, we analyze the finite-sample performance of the GoF-tests developed in Sects. 4.2 and 4.3 by simulations. We consider both asymptotic and bootstrap implementations, where the reported rejection rates rely on $10^4$ replications. We always use two-sided critical values with level 5 %, which are computed as the 2.5 %- and 97.5 %-quantiles from either the asymptotic normal distribution according to Sects. 4.2 and 4.3 (plugging-in parameter estimates instead of the population values), or from the generated bootstrap sample (with 500 bootstrap replicates). The used bootstrap scheme depends on the type of DGP: If the tests are applied to i. i. d. counts as discussed in Sect. 5.1, the parametric i. i. d.-bootstrap is considered (where $\mu$ is estimated by the sample mean), while for the AR(1)-like counts of Sect. 5.2, the parametric INAR bootstrap of Jentsch and Weiß (2019) is used (with parameters estimated based on sample mean and lag-1 sample acf), which has been proven to be consistent for statistics belonging to the class of functions of generalized means (as they are considered here). Note that for the bootstrap implementations of the GoF-tests developed in Sects. 4.2 and 4.3, $10^4$ replications are still possible as only sample moments have to be computed for executing the tests, but neither numerical optimization nor integration are necessary.

For the power scenarios (recall the discussions in Sects. 4.2 and 4.3), we restrict to alternative scenarios of “relative equidispersion”, i. e., the dispersion (as well as mean and acf) agree with the respective null model, but further shape properties (such as higher-order moments or zero probability) differ. Here, our main focus is on the NB-case, as tests for a Poisson null (against equidispersed alternatives) have already been investigated to some part by Schweer and Weiß (2016), Aleksandrov et al. (2022). For the NB-null, where suitable, we use the NB-index (NBI) test by Aleksandrov (2019) as a further moment-based benchmark. Additional competitor tests are considered in Sect. 5.3, where we also provide some simulation experiments regarding the omnibus Stein GoF-test of Sect. 4.4. The subsequent discussion refers to the rejection rates being tabulated in Appendix B.

5.1 Size and power for i.i.d. counts

Table 5 shows simulated sizes for the null hypothesis of i. i. d. $Poi (\mu )$ counts, where the low mean scenarios, $\mu \in \{0.5,1,2,4\}$, are the same as in Schweer and Weiß (2016), and these are supplemented by the larger means $\mu \in \{10,15\}$. For the very low means $\mu \in \{0.5,1\}$, the $\hat{T }_{(r,s)}$-test with $r=3$ and especially $r=4$ tends to strong undersizing if implemented asymptotically, and at least for $r=4$, we still have undersizing if using a bootstrap implementation. This can be explained by the fact that the factorial $x_{(4)}$ becomes zero if $x\le 3$, which often happens for $\mu \in \{0.5,1\}$. Therefore, rejections are essentially only possible if the upper critical value is violated.¹ Furthermore, the true distribution of the higher-order $\hat{T }_{(r,s)}$-statistics is somewhat skewed for low sample sizes T, which implies a deviation from the asymptotic normal distribution, but which is captured well by the bootstrap implementation. With increasing $\mu$ and T, however, the sizes of the $\hat{T }_{(r,s)}$-test clearly improve for both implementations. For the Stein–Chen test $\hat{T }\!_{\exp }^{\,Poi }$, the opposite pattern is observed, namely a deterioration of the asymptotic implementation’s size for the large means $\mu \in \{10,15\}$. This is caused by the fact that the weighting function $f(x)=\exp (-x)$ puts most weight on low counts (close to zero), but these are hardly observed for $\mu \in \{10,15\}$. It should be noted that the bootstrap implementation of the $\hat{T }\!_{\exp }^{\,Poi }$-test leads to reliable sizes throughout. Table 6 shows corresponding sizes for the null of i. i. d. $NB \big (n,\frac{n}{n+\mu }\big )$-counts. Generally, we observe the same pattern as in the Poisson case, i. e., the asymptotic implementation of the $\hat{T }_{(r,s)}$-test shows undersizing for low $\mu$, while this happens for the $\hat{T }\!_{\exp }^{\,NB }$-test for large $\mu$. The bootstrap implementation guarantees good size properties throughout. For means $\mu \le 5$, we also considered the NBI-test of Aleksandrov (2019) as a further competitor (for larger $\mu$, the NBI is not computed as it relies on the frequency of zeros, which are hardly ever observed in such a case). However, the sizes of the NBI’s asymptotic implementation are often much larger than 5 %, i. e., we have a severely increased rate of false rejections. Again, a bootstrap implementation leads to reliable sizes (but not for the large means skipped in Table 6). Altogether, the newly proposed $\hat{T }_{(r,s)}$-, $\hat{T }\!_{\exp }^{\,Poi }$-, and $\hat{T }\!_{\exp }^{\,NB }$-tests have rather reliable sizes, and if deteriorations are observed, these are mainly lower deviations, leading to a conservative test.

Let us now turn to a power analysis of the proposed tests. Table 7 shows power values for the i. i. d. $Poi (\mu )$-null, but where the i. i. d. counts follow a Good distribution (Weiß 2018a, p. 219) with mean and variance being equal to $\mu$. Such an alternative scenario was also investigated by Schweer and Weiß (2016), who demonstrated that the equidispersed Good distribution has larger skewness and excess than a Poisson distribution. For the very low means $\mu \in \{0.5,1\}$, the skewness test $\hat{T }_{(3,1)}$ performs best, although the power is generally rather low. For the medium means $\mu \in \{2,4\}$, the $\hat{T }\!_{\exp }^{\,Poi }$-test is the best choice, in accordance with Aleksandrov et al. (2022), whereas we have an ambivalent picture with the large means $\mu \in \{10,15\}$: if using asymptotic implementations, the $\hat{T }_{(4,2)}$-test is preferable, whereas the $\hat{T }\!_{\exp }^{\,Poi }$-test succeeds again under bootstrap implementation. For the $\hat{T }_{(r,s)}$-tests with $r\ge 3$, the results of Table 7 indicate that the use of the bootstrap implementation is even detrimental: the power values are usually somewhat lower than for the asymptotic implementation, whereas the sizes are larger, recall Table 5.

For the null of the $NB \big (n,\frac{n}{n+\mu }\big )$-distribution, we consider two types of alternative with “relative equidispersion” (i. e., having the same mean and variance as the NB-null): the Poisson-Inverse Gaussian (PIG) distribution exhibiting strong skewness to the right (Willmot 1987), and the ZIP distribution with its additional point mass in zero (Weiß 2018a, p. 220). The power values for the PIG-alternative in Table 8 show that the $\hat{T }\!_{\exp }^{\,NB }$-test has superior performance for low mean and strong overdispersion, $(\mu ,n)\in \big \{(1.5,1), (5, 3.\overline{3})\big \}$; recall that the power values of the NBI are well interpretable only for the bootstrap implementation because of the size distortions in the asymptotic case. With increasing $\mu$ and decreasing overdispersion (i. e., increasing n), we generally have lower power values, and now $\hat{T }_{(4,2)}$ often has the best power. However, in analogy to the Poi-case of Table 7, the asymptotic implementation of the $\hat{T }_{(r,s)}$-tests appears preferable in practice, as we get a larger power together with lower sizes (although leading to a conservative test).

The power values in Table 9 refer to the ZIP-alternative. As already noted above, the statistics $\hat{T }_{(r,s)}$ with $r\ge 3$ can hardly violate their lower critical value for low $\mu$, which explains their bad power in this case. With increasing $\mu$, however, their power improves and reaches rather high values. By contrast to our previous power analyses, the use of the bootstrap implementation clearly improves the power of the $\hat{T }_{(r,s)}$-tests regarding the ZIP-alternative. Nevertheless, the clearly best choice for uncovering the apparent zero inflation is the Stein statistic $\hat{T }\!_{\exp }^{\,NB }$, which agrees with the analogous findings of Aleksandrov et al. (2022) for the Stein–Chen test in the Poisson case. For $\mu \le 5$ and if using a bootstrap implementation, the NBI performs similarly well, but the Stein statistic $\hat{T }\!_{\exp }^{\,NB }$ is more widely applicable and performs very well also if using the more simple asymptotic implementation.

5.2 Size and power for AR(1)-like counts

As the next step, we analyze the additional effect of serial dependence on size and power of the proposed tests. For this purpose, we extend our simulations to AR(1)-like counts with dependence parameter $\rho$, namely to the null hypotheses of either $Poi (\mu )$-counts generated by an INAR(1)-DGP, or $NB \big (n,\frac{n}{n+\mu }\big )$-counts by an IINAR(1)-DGP, recall Sect. 3. As computations are more demanding in the dependent case (especially the bootstrap implementations are much more time consuming now), we restrict our simulations to selected scenarios from Sect. 5.1. While the choice of the null models is obvious, the selection of alternative scenarios is more demanding. The common way of causing non-Poisson counts $X_t$ within the INAR(1) model is to choose non-Poisson innovations $\epsilon _t$ according to a specific model. For example, if $\epsilon _t$ has the equidispersed Good distribution like in Sect. 5.1, then the $X_t$ are also equidispersed and non-Poisson (but not following a Good distribution anymore, i. e., only the Poisson distribution is preserved by the INAR(1) DGP). Special features of the innovations $\epsilon _t$ (beyond mere dispersion) reach the observations $X_t$ more and more dampened with increasing $\rho$. For example, zero inflation fades out with increasing $\rho$, see Weiß et al. (2019). In numerical experiments with the IINAR(1) model, however, where even two thinnings are executed one after the other, this dampening effect was further intensified. While we can easily choose ZIP-distributed $\epsilon _t$ such that mean and variance of the IINAR(1) model are preserved, the resulting $X_t$ hardly exhibit any zero inflation. For this reason, we decided to use again the INAR(1) DGP for defining alternative scenarios. More precisely, we define the NB-, PIG-, and ZIP-INAR(1) alternatives (all having a non-NB marginal distribution) such that they have the same mean, variance, and acf as the null NB-IINAR(1) model. Just to avoid confusion: even the NB-INAR(1) process (with its NB-distributed innovations) has a non-NB marginal, although the difference to the null’s $NB \big (n,\frac{n}{n+\mu }\big )$-distribution is quite small.

Let us start with the null of Poi-INAR(1) counts and the alternative of INAR(1) counts having equidispersed-Good innovations $\epsilon _t$, for $\rho =0.25$. Comparing the sizes in the upper block of Table 10 to the corresponding i. i. d.-sizes in Table 5, we recognize a rather similar pattern: The asymptotic implementations of the $\hat{T }_{(r,s)}$-tests tend to undersizing for low $\mu$ and T, whereas the bootstrap implementations of all tests are uniquely close to the nominal 5%-level, but with a slight tendency to oversizing. Altogether, the effect of serial dependence on the sizes appears negligible. This is different for the power values in the lower block of Table 10 compared to Table 7: in accordance with analogous findings in previous studies (e. g., Schweer and Weiß 2014 and Schweer and Weiß (2016)), an increase in serial dependence causes a decrease in power. Besides this general loss in performance, the other conclusions of Sect. 5.1 remain valid: the bootstrap implementation of the $\hat{T }\!_{\exp }^{\,Poi }$-test usually leads to the best power, and the $\hat{T }_{(r,s)}$-tests have a higher power and lower size under asymptotic implementation.

Next, let us turn to the NB-case. For the sizes in the upper part of Table 11 (to be compared to the i. i. d.-sizes in Table 6), we draw an analogous conclusion as in the Poi-case, namely that there is hardly any effect of the apparent serial dependence. The asymptotic implementations of the $\hat{T }_{(r,s)}$-tests tend to undersizing for low $\mu$ and T, whereas the bootstrap implementations of all tests are close to (but somewhat larger than) the nominal 5%-level. For the power simulations, we get a more complex picture. The power values in the lower part of Table 11 are more of theoretical rather than practical interest, as the NB-INAR(1)’s marginal distribution is very similar to the NB-null. Nevertheless, the $\hat{T }_{(r,s)}$-tests with $r\ge 3$ and especially the $\hat{T }\!_{\exp }^{\,NB }$-test exhibit mild power, caused by the different data-generating mechanism.

The practically relevant alternative scenarios, namely PIG- and ZIP-INAR(1), are summarized in Table 12 (to be compared to Tables 8 and 9, respectively). The power values for the PIG-alternative generally show the same pattern as in the i. i. d.-case, i. e., a superior performance of $\hat{T }\!_{\exp }^{\,NB }$-test for low mean and strong overdispersion, while $\hat{T }_{(4,2)}$ makes up with increasing $\mu$ and decreasing overdispersion (i. e., increasing n). But interestingly, the power values for $\rho =0.25$ are usually larger than in the i. i. d.-case, which can be explained by the combined effect of the change in the marginal distribution and that in the data-generating mechanism (for the latter, recall the power values in the lower part of Table 11). This is different from the ZIP-case, where we have worse power in the presence of serial dependence (caused by the aforementioned dampening effect of the thinnings). Nevertheless, the $\hat{T }\!_{\exp }^{\,NB }$-test is very powerful in detecting zero inflation, and also the bootstrap implementation of the $\hat{T }_{(4,2)}$-test does rather well.

5.3 Power analysis of competitor tests

In Sects. 5.1 and 5.2, we recognized that the novel GoF-tests have attractive power properties, where, by design of the GoF-statistics, the individual performance depends on the type of violation of the null hypothesis. To be able to judge their performance with respect to existing GoF-tests, this section discusses simulated power values for some well-established competitors (if available at all for the considered null hypothesis). As most competitors are computationally much more demanding, we restrict our analyses to selected competitors and alternative scenarios, but we still use $10^4$ replications per scenario (and 500 bootstrap replications where necessary). All tests of this section are equipped with an upper critical value only.

For testing the Poi-null under i. i. d. assumptions, many possible competitors are surveyed by Gürtler and Henze (2000). In what follows, we focus on the pgf-based tests presented there, as these are among the most powerful tests, and as the Stein-type GoF-tests $\hat{T }\!_{\exp }^{\,Poi }, \hat{T }\!_{\exp }^{\,NB }$ are related to the pgf as well, recall Sect. 4.4. While the pgf under the null, $pgf (u|\mu )$, depends on the mean $\mu$, estimated by $\hat{\mu }:=\overline{x}$ as before, the sample pgf $\widehat{pgf }(u)$ is itself computed as a type of sample mean, namely $\widehat{pgf }(u) = \overline{u^X}$. The two types of pgf-based GoF-tests in Section 2.3 of Gürtler and Henze (2000) are

$$\begin{aligned} \begin{array}{rl} R_{a}\ =&{} \displaystyle T\int _0^1 \Big (\widehat{pgf }(u) - pgf (u|{\hat{\mu }})\Big )^2\,u^a\,d u,\\ \\ [-2ex] B_{a}\ =&{} \displaystyle T\int _0^1 \Big (\hat{\mu }\,\widehat{pgf }(u) - \widehat{pgf }'(u)\Big )^2\,u^a\,d u. \end{array} \end{aligned}$$

(38)

Here, $a=0$ corresponds to not using any weight, whereas $a>0$ puts more weight near the end of the integration interval; if weights are useful at all, Gürtler and Henze (2000) recommend the choice $a=5$. Besides (38), we also consider the traditional Pearson statistic $\chi ^2$ (see Weiß 2018b) as well as the GoF-test in Section 5 of Betsch et al. (2022). The latter test has been selected as a further competitor as it also utilizes the Stein–Chen identity (25) in some way:

$$\begin{aligned} S\ =\ \sum _{k=0}^\infty \Big (\overline{\big (1-{\hat{\mu }}/(X+1)\big )\,\mathbbm {1}(X\ge k)}\ -\ \overline{\mathbbm {1}(X=k)}\Big )^2, \end{aligned}$$

(39)

Here, $\mathbbm {1}(\cdot )$ denotes the indicator function.

For testing the NB-null under i. i. d. assumptions, again the Pearson statistic $\chi ^2$ (see Weiß 2018b) is considered, as well as the modified versions of (38) proposed by Rueda and O’Reilly (1999) and Meintanis (2005). While $R_a$ looks like in (38) but using the NB’s pgf, the NB-counterpart to $B_a$ in (38) is

$$\begin{aligned} B_{a}\ =\ T\int _0^1 \Big (\hat{\mu }\,\widehat{pgf }(u) - \big (1+\tfrac{1}{n}\,\hat{\mu }\,(1-u)\big )\,\widehat{pgf }'(u)\Big )^2\,u^a\,d u. \end{aligned}$$

(40)

While we are not aware of any GoF-test for the null of an NB-IINAR(1) model, two competitors for the Poi-INAR(1) null are considered: on the one hand again the Pearson statistic $\chi ^2$ (see Weiß 2018b), on the other hand the test by Meintanis and Karlis (2014), which is defined in analogy to $B_a$ in (38) but using the bivariate pgf of the pairs $(X_t,X_{t-1})$:

$$\begin{aligned} W_{a}\ =\ T\int _0^1 \int _0^1 \Big (\hat{\lambda }\,(u-v)\,\widehat{pgf }(u,v) - \big (u\,\tfrac{\partial \widehat{pgf }(u,v)}{\partial u}-v\,\tfrac{\partial \widehat{pgf }(u,v)}{\partial v}\big )\Big )^2\,u^a v^a\,d u\,d v.\nonumber \\ \end{aligned}$$

(41)

Meintanis and Karlis (2014) recommend to use $a=2$ as the weight parameter.

The simulated power values are summarized in Table 13. The upper left block in Table 13 has to be compared to the row $\mu =4$ in Table 7, the upper right block to the corresponding row in Table 10, both corresponding to a Poi-null. It becomes clear that our novel $\hat{T }\!_{\exp }^{\,Poi }$-test has the best power without exception, and also the $\hat{T }_{(4,2)}$-test shows competitive performance. Analogous conclusions hold for the NB-null in the lower block of Table 13, which has to be compared to $(\mu ,n)=(5,3.333)$ in Tables 8 and 9. Now the $\hat{T }\!_{\exp }^{\,NB }$-test dominates all competitors, which again demonstrates the appealing performance of our moment-based approach for defining GoF-tests.

As a final comparison, we consider the omnibus Stein-GoF test discussed in Sect. 4.4. While we restricted our derivations to the case of the unweighted $L_2$-distance and the null of i. i. d. Poi-counts with $f_s(x)=s^x$, see (37), we explore the power of such integrated Stein-pgf tests more comprehensively, namely by allowing for additional weights and by also considering the null of i. i. d. NB-counts. In the latter case, the integration is done with respect to (29), i. e.,

$$\begin{aligned} \hat{T }\!_{s^x}^{\,NB }(s) \ =\ \frac{\big (n_{0}+\overline{X}\big )\,\overline{Xf_s(X)}}{\, \overline{X}\ \overline{(n_{0}+X)\,f_s(X+1)} \,}. \end{aligned}$$

Altogether, we use the GoF-test statistics

$$\begin{aligned} T\int _\varepsilon ^1 \left( \hat{T }\!_{s^x}^{\,Poi }(s)-1\right) ^2\,s^a\, d s\quad \text {for testing the Poi-null}, \end{aligned}$$

(42)

and

$$\begin{aligned} T\int _\varepsilon ^1 \left( \hat{T }\!_{s^x}^{\,NB }(s)-1\right) ^2\,s^a\, d s\quad \text {for testing the NB-null}, \end{aligned}$$

(43)

where we set $\varepsilon =10^{-3}$ in both cases. In view of the above experiences, we tried $a\in \{0,2,5\}$, and we used the parametric i. i. d.-bootstrap sketched in the beginning of Sect. 5 for implementation.

The simulated power values are summarized in Table 14. Comparing to the competitor tests of Table 13, we recognize a superior power for the integrated Stein-pgf tests, where highest power is achieved for the medium weights $a=2$. In fact, the corresponding power values are often slightly larger than those of the $\hat{T }\!_{\exp }^{\,Poi }$-test in Table 7 or $\hat{T }\!_{\exp }^{\,NB }$-test in Tables 8–9, respectively. This clearly shows that such integrated Stein-pgf tests constitute a promising direction for future research.

Fig. 3

Time series plot and sample pacf of download counts

Table 3 Download counts: statistics $\hat{T }_{(r,s)}$ and their critical regions

Table 4 Download counts: ML estimates (standard errors) and values of AIC and BIC for different models

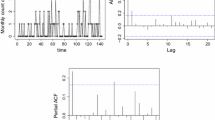
6 Illustrative data example

In what follows, we analyze a time series of daily counts of downloads of a TeX-editor (period June 2006 to February 2007, thus $T=267$), see Fig. 3. These data have been introduced by Weiß (2008b) and further analyzed by Weiß (2018a). They have an AR(1)-like sample partial acf (pacf), and the sample dispersion index $s_X^2/\overline{x}\approx 3.138$ is much larger than the Poisson value 1, but close to the geometric value $1+\overline{x}\approx 3.401$. Similarly, the zero frequency $\approx 0.277$ is much larger than the corresponding Poisson’s zero probability of $\approx 0.091$, but again close to the geometric value $\approx 0.319$. Therefore, it is very natural to test the null hypothesis $H_0$ of an NB-IINAR(1) process with geometric marginal distribution (i. e., with $n=1$, abbreviated as Geom-IINAR(1) process) for these data. For the sake of completeness, we also report the results if testing the null $\tilde{H}_0$ of a Poi-INAR(1) process, although $\tilde{H}_0$ seems rather inappropriate in view of the aforementioned sample properties. All tests are done on the 5 %-level.

Let us begin with the factorial-moment-based statistics $\hat{T }_{(r,s)}$, which are uniquely defined for both $H_0$ and $\tilde{H}_0$, but with different critical values. Here, an asymptotic implementation is possible, recall Example 2, where we have to plug-in the moment estimates for $(\mu ,\rho )$, namely $\big (\overline{x}, \hat{\rho }(1)\big )\approx (2.401, 0.245)$, instead of the unknown population values. We obtain the statistics and critical regions shown in columns 1–4 of Table 3. The values $\hat{T }_{(r,s)}$ clearly differ from the hypothetical Poisson value 1, but they are fairly close to the geometric values 2, 3, 4, and 6, respectively. Indeed, $\tilde{H}_0$ is rejected for each of these statistics, whereas we do not get any rejection for $H_0$. For comparison, we also considered a bootstrap implementation (with 500 bootstrap replicates) in columns 5–6 of Table 3, but the test decisions are identical. Note that the bootstrap’s lower critical values $c_l$ for $r\ge 3$ under $H_0$ differ notably from the asymptotic ones, which is plausible in view of Sect. 5, where we noted problems with $c_l$ for low means $\mu$.

Next, we consider both types of Stein test. The Stein–Chen statistic $\hat{T }\!_{\exp }^{\,Poi }$ takes the value $\approx 0.427$ being much smaller than the $\tilde{H}_0$-value 1, whereas $\hat{T }\!_{\exp }^{\,NB }\approx 1.055$ is very close to the $H_0$-value 1. In fact, the respective critical regions (obtained via bootstrap) are $\mathbb {R}{\setminus }(0.851, 1.191)$ for $\hat{T }\!_{\exp }^{\,Poi }$, leading to a rejection of $\tilde{H}_0$, and $\mathbb {R}{\setminus }(0.846, 1.144)$ for $\hat{T }\!_{\exp }^{\,NB }$, which does not contradict $H_0$. So altogether, our diagnostic tests lead to unique conclusions, namely to reject $\tilde{H}_0$ of a Poi-INAR(1) process, but not contradicting $H_0$ of a Geom-IINAR(1) process.

In view of these diagnostic results, let us conclude this section with a final model fitting. Table 4 shows the results of maximum likelihood (ML) estimation for the Poi-INAR(1) model ($\tilde{H}_0$, rejected), the Geom-IINAR(1) model ($H_0$, not rejected), and, in addition, also for the general NB-IINAR(1) model with variable n. The values in parentheses are the respective approximate standard errors (computed from the numerical Hessian of the log-likelihood function), and Akaike’s and the Bayesian information criterion (AIC and BIC, respectively) are shown for model selection. Both criteria prefer the Geom-IINAR(1) model, and it should be noted that the NB-IINAR(1) model’s estimate for n is not significantly different from 1. Finally, we computed the standardized Pearson residuals for checking the adequacy of the fitted Geom-IINAR(1) model. The residuals have the mean $\approx -0.009$ close to zero, the variance $\approx 0.969$ close to one, and they are serially uncorrelated. So altogether, the Geom-IINAR(1) model seems to be an appropriate choice for the download-counts time series. According to Remark 3, a possible interpretation might be as follows: In the first step of iterated thinning, the fraction $\hat{\alpha }\,\hat{\rho }/(1+\hat{\alpha })\approx 0.126$ of persons downloading the TeX-editor at day $t-1$ decide to give a recommendation to other persons for day t. Here, the mean number of recommendations (caused by the second step of iterated thinning) is equal to $(1+\hat{\alpha })/\hat{\alpha }\approx 2.623$. In addition, the innovation $\epsilon _t$ causes $1/\hat{\alpha }\approx 1.623$ further downloads in the mean, now by the users’ own initiative (without recommendation).

7 Conclusions and future research

Unbounded-counts data are often modelled by using the Poi- or NB-distribution. In this paper, we proposed GoF-tests for testing the null hypothesis of Poi- or NB-marginals in a time-series context. The considered classes of time series are defined in analogy to the class of Gaussian processes, by requiring bivariate Poi- or NB-distributions, respectively, for the lagged pairs $(X_t,X_{t-h})$. In this context, we also clarified some confusion in the literature regarding the NB-IINAR(1) model. In our research, we focused on two types of moment-based GoF-tests: tests relying on factorial moments, and tests using the so-called Stein’s identity. We considered both asymptotic and bootstrap implementations, and we studied i. i. d. counts as well as count data with serial dependence. In Monte–Carlo simulations, we illustrated the performance of the different tests under the null and under various alternatives. Under the null, the newly proposed tests showed rather reliable sizes, and if deteriorations were observed, these were mainly lower deviations leading to a conservative test. Most tests also showed a decent power (although decreasing for increasing dependence in the data), where the different GoF-statistics are sensitive to different features of the alternative distribution. If the GoF-statistic is chosen appropriately in view of the considered alternative scenario, the achieved power exceeds that of existing competitor tests. This sensitivity towards the considered alternative also implies that using a set of our GoF-statistics allows for a targeted diagnosis regarding the type of violation of the respective null hypothesis. Finally, we successfully applied our novel GoF-tests to a time series of download counts, where a geometric IINAR(1) model was identified as the best choice for these data.

This article opens up several opportunities for future research. One of these directions was already briefly investigated in Sects. 4.4 and 5.3, namely the use of Stein-type GoF-statistics for constructing an omnibus GoF-test. While we restricted our derivations to the null of i. i. d. Poi-counts and to one particular GoF-statistic (using the weight function $f(x)=s^x$ such that the test statistic is related to the pgf), the appealing simulation results of Sect. 5.3 indicate that such GoF-tests should also be considered more generally, including the case of i. i. d. NB-counts. It would also be relevant to analyze if an extension to serially dependent counts is possible. At this point, a second research direction becomes clear. In the Poi-case studied by Aleksandrov et al. (2022), it was shown that multiple Stein statistics can be combined into a single, asymptotically $\chi ^2$-distributed statistic. This would allow to create a pgf-based Stein GoF-test, where the pgf is jointly evaluated at only finitely many points $0<s_1<\ldots<s_k<1$. The exact asymptotics and performance of such a test, also for the NB-null, deserves further investigation in future research. Finally, the presented GoF-tests are designed for count time series having a marginal Poi- or NB-distribution and are, thus, relevant for INARMA-type processes. Another large class of models for count time series are integer-valued generalized autoregressive conditional heteroscedasticity (INGARCH) models, which are defined based on a conditional Poi- or NB-distribution (or other parametric distributions, see Weiß (2018a) for a survey). In this case, neither the proposed test statistics nor their asymptotics are applicable. Hence, it would be relevant for future research to develop conditional Stein-type GoF-tests for such INGARCH count processes.

Appendices

Appendix A: On alternative formulations of the NB-IINAR(1) model

In Al-Osh and Aly (1992) and Weiß (2008b), the special case of iterated thinning together with a geometric counting series is considered, i. e., “$\circledast$” corresponds to the sequential execution of Bin-thinning “$\circ$” and the NB-operator “$*$” of Ristić et al. (2009). More precisely, using $\rho ,\alpha \rho \in (0,1)$ and setting $\theta _1 = \alpha \rho$ and $\theta _2=1/\alpha$, so $Y_i\sim NB (1,\frac{\alpha }{1+\alpha })$ and $pgf _Y(z) = \alpha /(\alpha +1-z)$ according to Table 1, we get from (12) that

$$\begin{aligned} pgf _{(\alpha \rho ,1/\alpha )\circledast x}(z)\ =\ \Big (1+\alpha \rho \,\big (pgf _Y(z)-1\big )\Big )^x\ =\ \left( 1-\frac{\alpha \rho \,(1-z)}{\alpha +1-z}\right) ^x, \end{aligned}$$

(A.1)

with conditional mean $E\big [(\alpha \rho ,1/\alpha )\circledast x\big ] = \rho \,x$. Note that the boundary case $\alpha \rho =1$ was also considered by Gouriéroux and Lu (2019, Section 2).

In Wolpert and Brown (2011), Leisen et al. (2019), by contrast, another i. i. d. counting series for “$*$” is assumed, say $(Z_i)$, which follows the shifted geometric distribution (recall Sect. 2). Setting $\theta _1 = \frac{\alpha }{1+\alpha }\,\rho$ and $\theta _2=\frac{1+\alpha }{\alpha }$, so $Z_i\sim 1+NB (1,\frac{\alpha }{1+\alpha })$ with $pgf _Z(z) = \alpha \,z/(\alpha +1-z)$, Eq. (12) implies that

$$\begin{aligned} pgf _{(\frac{\alpha }{1+\alpha }\,\rho ,\frac{1+\alpha }{\alpha })\circledast x}(z)\ =\ \Big (1+\tfrac{\alpha }{1+\alpha }\,\rho \,\big (pgf _Z(z)-1\big )\Big )^x\ =\ \left( 1-\frac{\alpha \rho \,(1-z)}{\alpha +1-z}\right) ^x, \end{aligned}$$

(A.2)

again with conditional mean $E\big [(\frac{\alpha }{1+\alpha }\,\rho ,\frac{1+\alpha }{\alpha })\circledast x\big ] = \rho \,x$. So both approaches lead to the same pgf, i. e., both constructions of the iterated-thinning operator are equal in distribution. However, the second approach (A.2) has a practical advantage: $\theta _1 = \frac{\alpha }{1+\alpha }\,\rho \in (0,1)$ holds for any $\rho \in (0,1)$ and $\alpha >0$, i. e., the parameter space of $(\rho ,\alpha )$ is less restricted. Therefore, we always use the second version (A.2) of the geometric iterated-thinning operator, together with the shorthand notation $\rho \circledast _\alpha x:= (\frac{\alpha }{1+\alpha }\,\rho ,\frac{1+\alpha }{\alpha })\circledast x$, see (13).

In Wolpert and Brown (2011), Leisen et al. (2019), two different ways of defining an NB-IINAR(1) model are provided. But as we shall see, after appropriate reparametrizations, they lead to the same model as given in Definition 2.

In Leisen et al. (2019), the NB-IINAR(1) model recursion uses the shifted geometric counting series $Z_i\sim 1+NB \big (1, 1-q(1-\Theta )\big )$ and the innovations $\epsilon _t\sim NB \big (n, 1-q(1-\Theta )\big )$, together with the Bin-thinning “$\Theta \circ$”. Substituting $1-q(1-\Theta ) \mapsto \frac{\alpha }{1+\alpha }$ and $\Theta \mapsto \frac{\alpha }{1+\alpha }\,\rho$, it becomes clear that their thinning operator is equivalent to (A.2). Since also the innovations are distributed the same as in Definition 2, the model (3) of Leisen et al. (2019) agrees with the model in Definition 2. Note that $(1-q)(1-\Theta ) = \frac{\alpha (1-\rho )}{1+\alpha }$ and $q(1-\Theta ) = \frac{1}{1+\alpha }$, so $\alpha (1-\rho )=(1-q)/q$. Consequently, the stationary marginal distribution $NB \big (n,\frac{\alpha (1-\rho )}{1+\alpha (1-\rho )}\big )$ is expressed as $NB (n,1-q)$ in agreement with Leisen et al. (2019).

Also in Wolpert and Brown (2011), the NB-IINAR(1) model is defined based on a shifted geometric counting series, so using again (A.2). This time, the parameter of the Bin-thinning operator is $\rho p/(1-\rho +\rho p)$ (corresponding to $\frac{\alpha }{1+\alpha }\,\rho$ in our parametrization), and counting series as well as innovations use the geometric parameter $p/(1-\rho +\rho p)$ (corresponding to $\frac{\alpha }{1+\alpha }$ in Definition 2). So $\rho$ plays the same role in both model definitions, while $\alpha ^{-1} = \frac{1+\alpha }{\alpha }-1 = (1-\rho )(1-p)/p$ and, thus, $\alpha (1-\rho )=p/(1-p)$. Therefore, the stationary marginal distribution $NB \big (n,\frac{\alpha (1-\rho )}{1+\alpha (1-\rho )}\big )$ is expressed as $NB (n,p)$ in agreement with Wolpert and Brown (2011).

Note that Wolpert and Brown (2011), Leisen et al. (2019) do not explicitly point out the iterated-thinning operator in Definition 2, but they define their model by the recursion $X_t = B_{t-1}+N_{t-1}$ with $B_{t-1}\sim Bin \big (X_{t-1},\frac{\alpha }{1+\alpha }\,\rho \big )$ and $N_{t-1}\sim NB \big (n+B_{t-1},\frac{\alpha }{1+\alpha }\big )$. Utilizing the additivity of the NB-distribution, the equivalence to the iterated-thinning formulation becomes clear.

For lag $h=1$, we have $\frac{1-\rho ^h}{1-\rho }=1$. Thus, the bivariate pgf (15) reduces to (2.6) in Al-Osh and Aly (1992), namely to

$$\begin{aligned} \textstyle pgf _{X_1,X_0}(z_1,z_2)\ =\ \left( \tfrac{\alpha ^2(1-\rho )}{(1+\alpha -\alpha \rho )\,(1+\alpha -z_1-z_2) -(\alpha \rho -1)\,z_1 z_2}\right) ^n. \end{aligned}$$

(A.3)

Note that (A.3) leads to the formula given in Theorem 1(4) of Wolpert and Brown (2011) by using the aforementioned parameter substitution.

Another thinning-based characterization of the NB-IINAR(1) model (but which avoids the step of nesting two thinnings) was recently given in Section 2.3 of Guerrero et al. (2022). Their parametrization is translated into the one used here by mapping their $r\mapsto n$, $\mu \mapsto \frac{n}{\alpha (1-\rho )}$, and $\mu (1-\alpha )\mapsto \frac{n}{\alpha }$. This can be seen by comparing the expression for $pgf _{\rho \circledast _\alpha x}(z)$ in (13) with the one for $\Psi _G(z)^x$ in Section 2.3 of Guerrero et al. (2022).

Comparing (A.3) to (4), we have $(X_t,X_{t-1})\sim BNB \big (n, \frac{1}{1+\alpha },\frac{1}{1+\alpha }, \frac{\alpha \rho -1}{(1+\alpha -\alpha \rho )\,(1+\alpha )}\big )$. Note that $\pi _0/(\pi _1\pi _2) = \big (\frac{\alpha }{1+\alpha (1-\rho )}-1\big ) \,(1+\alpha ) >-1$ holds, and $\pi _0>0$ if $\alpha >1/\rho$. The latter condition is also necessary for the decomposition discussed in Remark 2, recall (6). From (A.3), it also becomes clear that the NB-IINAR(1) model was considered in a further article, namely in Section 2(a) of Phatarfod and Mardia (1973). These authors define the model by the bivariate pgf in (A.3) with the parametrization $\rho$ and $a^{-1}=\alpha (1-\rho )$.

Appendix B: Tabulated simulation results of Sect. 5

See Tables 5, 6, 7, 8, 9, 10, 11, 12, 13 and 14.

Table 5 Simulated sizes for i. i. d. $Poi (\mu )$-null, where two-sided tests with nominal level 0.05; see Sect. 5.1

Table 6 Simulated size for i. i. d. $NB \big (n,\frac{n}{n+\mu }\big )$-null, where two-sided tests with nominal level 0.05; see Sect. 5.1

Table 7 Simulated power for i. i. d. $Poi (\mu )$-null and equidispersed Good-alternative with mean $\mu$, where two-sided tests with nominal level 0.05; see Sect. 5.1

Table 8 Simulated power for i. i. d. $NB \big (n,\frac{n}{n+\mu }\big )$-null and PIG-alternative with same mean and variance, where two-sided tests with nominal level 0.05; see Sect. 5.1

Table 9 Simulated power for i. i. d. $NB \big (n,\frac{n}{n+\mu }\big )$-null and ZIP-alternative with same mean and variance, where two-sided tests with nominal level 0.05; see Sect. 5.1

Table 10 Simulated size and power for INAR(1) DGP with $\rho =0.25$, for $Poi (\mu )$-null and equidispersed Good-alternative with mean $\mu$, where two-sided tests with nominal level 0.05; see Sect. 5.2

Table 11 Simulated size for NB-IINAR(1) DGP with mean $\mu$ and $\rho =0.25$, and power for corresponding NB-INAR(1) alternative, where two-sided tests with nominal level 0.05; see Sect. 5.2

Table 12 Simulated power for PIG- and ZIP-INAR(1) alternative with mean $\mu$ and $\rho =0.25$, where NB-IINAR(1) null and two-sided tests with nominal level 0.05; see Sect. 5.2

Table 13 Simulated power for diverse competitor tests with nominal level 0.05; see Sect. 5.3

Table 14 Simulated power for integrated Stein-pgf tests with nominal level 0.05; see Sect. 5.3