On generalized progressive hybrid censoring in presence of competing risks

Abstract

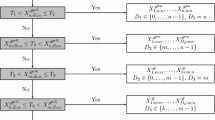
The progressive Type-II hybrid censoring scheme introduced by Kundu and Joarder (Comput Stat Data Anal 50:2509–2528, 2006), has received some attention in the last few years. One major drawback of this censoring scheme is that very few observations (even no observation at all) may be observed at the end of the experiment. To overcome this problem, Cho et al. (Stat Methodol 23:18–34, 2015) recently introduced generalized progressive censoring which ensures to get a pre specified number of failures. In this paper we analyze generalized progressive censored data in presence of competing risks. For brevity we have considered only two competing causes of failures, and it is assumed that the lifetime of the competing causes follow one parameter exponential distributions with different scale parameters. We obtain the maximum likelihood estimators of the unknown parameters and also provide their exact distributions. Based on the exact distributions of the maximum likelihood estimators exact confidence intervals can be obtained. Asymptotic and bootstrap confidence intervals are also provided for comparison purposes. We further consider the Bayesian analysis of the unknown parameters under a very flexible beta–gamma prior. We provide the Bayes estimates and the associated credible intervals of the unknown parameters based on the above priors. We present extensive simulation results to see the effectiveness of the proposed method and finally one real data set is analyzed for illustrative purpose.

Appendix: the proof of the main theorem

First we derive the distribution function of $\widehat{\theta }_1$ which is given below.

$$\begin{aligned} F_{\widehat{\theta }_1| D_1>0}(x)= & {} P(\widehat{\theta }_1 \le x | D_1>0) \nonumber \\= & {} P(\widehat{\theta }_1 \le x, A | D_1>0)+P(\widehat{\theta }_1 \le x, B | D_1>0) +P(\widehat{\theta }_1 \le x, C | D_1>0) \nonumber \\= & {} \sum _{j=k}^{m-1} \sum _{i=1}^j P(\widehat{\theta }_1 \le x| J=j, D_1=i)P(J=j, D_1=i | D_1>0) \nonumber \\&+\sum _{i=1}^k P(\widehat{\theta }_1 \le x| B, D_1=i) P(B, D_1=i | D_1>0) \nonumber \\&+ \sum _{i=1}^m P(\widehat{\theta }_1 \le x| C, D_1=i) P(C, D_1=i | D_1>0), \end{aligned}$$

(7)

where,

$$\begin{aligned}&A=\{Z_{k:m:n}<T<Z_{m:m:n}\},\quad B=\{T<Z_{k:m:n}<Z_{m:m:n}\}, \\&C=\{Z_{k:m:n}<Z_{m:m:n}<T\}. \end{aligned}$$

Now to compute the terms on the right hand side of (7), we need the following Lemmas.

Lemma 1

The joint distribution of $Z_{1:m:n},\ldots , Z_{J:m:n}$ given $J=j, D_1=i$ for $i=1,\ldots ,j$ and $j=k,\ldots , m-1$ at $z_1,\ldots , z_j$, is given by,

$$\begin{aligned}&f_{Z_{1:m:n},\ldots , Z_{j:m:n}|J=j, D_1=i}(z_1, \ldots , z_j)\nonumber \\&=\frac{\prod _{v=1}^j \gamma _v}{P(J=j, D_1=i)} \Big (\frac{1}{\theta _1}\Big )^i \Big (\frac{1}{\theta _2}\Big )^{j-i} e^{-\frac{1}{\theta } (\sum _{s=1}^j z_s (1+R_s) + TR^*_j)}. \end{aligned}$$

(8)

Proof of Lemma 1

For $j=k,k+1,\ldots m \ \ {\text {and}} \ \ i=1,2,\ldots , j$, consider left side of (8),

$$\begin{aligned}&P(z_1<Z_{1:m:n}<z_1+dz_1,\ldots ,z_j<Z_{j:m:n}<z_j+dz_j|J=j, D_1=i) \nonumber \\&\quad =\frac{P(z_1<Z_{1:m:n}<z_1+dz_1,\ldots ,z_j<Z_{j:m:n}<z_j+dz_j,J=j, D_1=i)}{P(J=j, D_1=i)} \end{aligned}$$

(9)

Note that, the event $\{z_1<Z_{1:m:n}<z_1+dz_1,\ldots ,z_j<Z_{j:m:n}<z_j+dz_j,J=j, D_1=i)\}$ for $i=1,\ldots ,j; j=k,k+1,\ldots ,m$ is nothing but the failure times of j units till time point T and out of them i units have failed due to Cause-1. The probability of this event is the likelihood contribution of the data when $T^*=T$. Thus (9) becomes,

$$\begin{aligned} \prod _{v=1}^j \gamma _v \bigg (\frac{1}{\theta _1}\bigg )^i \bigg (\frac{1}{\theta _2}\bigg )^{j-i}\frac{e^{-\frac{1}{\theta }\big [\sum _{s=1}^{j} (1+R_s)z_s + TR^*_j\big ]}}{P(J=j,D_1=i)} \; dz_1\ldots dz_j. \end{aligned}$$

$\square$

Lemma 2

The joint distribution of $Z_{1:m:n},\ldots , Z_{k:m:n}$ given $T<Z_{k:m:n}<Z_{m:m:n}, D_1=i$ for $i=1,\ldots ,k$ at $z_1,\ldots , z_k$, is given by

$$\begin{aligned}&f_{Z_{1:m:n},\ldots , Z_{k:m:n}|T<Z_{k:m:n}<Z_{m:m:n}, D_1=i}(z_1, \ldots , z_k) \nonumber \\&\quad =\frac{\prod _{v=1}^k \gamma _v}{P(T<Z_{k:m:n}<Z_{m:m:n}, D_1=i)} \Big (\frac{1}{\theta _1}\Big )^i \Big (\frac{1}{\theta _2}\Big )^{k-i} e^{-\frac{1}{\theta } (\sum _{s=1}^{k-1} z_s (1+R_s) + z_k (1+R^*_k))}. \end{aligned}$$

(10)

Proof of Lemma 2

For $i=1,2, \ldots , k$, consider left side of (10),

$$\begin{aligned}&P(z_1<Z_{1:m:n}<z_1+dz_1,\ldots ,z_k<Z_{k:m:n}<z_k+dz_k|T<Z_{k:m:n}<Z_{m:m:n},D_1=i)\nonumber \\&\quad =\frac{P(z_1<Z_{1:m:n}<z_1+dz_1,\ldots ,z_k<Z_{k:m:n}<z_k+dz_k,T<Z_{k:m:n}<Z_{m:m:n},D_1=i)}{P(T<Z_{k:m:n}<Z_{m:m:n},D_1=i)} \end{aligned}$$

(11)

Note that, the event $\{z_1<Z_{1:m:n}<z_1+dz_1,\ldots ,z_k<Z_{k:m:n}<z_k+dz_k,T<Z_{k:m:n}, D_1=i)\}$ for $i=1,\ldots ,k$ is nothing but the failure times of k units till the experiment termination point $Z_{k:m:n}$ and out of them i units have failed due to Cause-1. The probability of this event is the likelihood contribution of the data when $T^*=Z_{k:m:n}$. Thus (11) becomes,

$$\begin{aligned} \prod _{v=1}^k \gamma _v\bigg (\frac{1}{\theta _1}\bigg )^i \bigg (\frac{1}{\theta _2}\bigg )^{k-i}\frac{e^{-\frac{1}{\theta }\big [\sum _{s=1}^{k-1} (1+R_s)z_s + z_k(1+R^*_k)\big ]}}{P(T<Z_{k:m:n}<Z_{m:m:n},D_1=i)} \; dz_1\ldots dz_k. \end{aligned}$$

$\square$

Lemma 3

The joint distribution of $Z_{1:m:n},\ldots , Z_{m:m:n}$ given $Z_{k:m:n}<Z_{m:m:n}<T, D_1=i$ for $i=1,\ldots ,m$ at $z_1,\ldots , z_m$, is given by,

$$\begin{aligned}&f_{Z_{1:m:n},\ldots , Z_{m:m:n}|Z_{k:m:n}<Z_{m:m:n}<T, D_1=i}(z_1, \ldots , z_m) \nonumber \\&\quad =\frac{\prod _{v=1}^m \gamma _v}{P(Z_{k:m:n}<Z_{m:m:n}<T, D_1=i)} \Big (\frac{1}{\theta _1}\Big )^i \Big (\frac{1}{\theta _2}\Big )^{m-i} e^{-\frac{1}{\theta }\sum _{s=1}^{m} (1+R_s)z_s}. \end{aligned}$$

(12)

Proof of Lemma 3

For $i=1,2,\ldots m$, consider left side of (12),

$$\begin{aligned}&P(z_1<Z_{1:m:n}<z_1+dz_1,\ldots ,z_m<Z_{m:m:n}<z_m+dz_m|Z_{k:m:n}<Z_{m:m:n}<T,D_1=i) \nonumber \\&\quad =\frac{P(z_1<Z_{1:m:n}<z_1+dz_1,\ldots ,z_m<Z_{m:m:n}<z_m+dz_m,Z_{k:m:n}<Z_{m:m:n}<T,D_1=i)}{P(Z_{k:m:n}<Z_{m:m:n}<T,D_1=i)} \end{aligned}$$

(13)

Note that, the event $\{z_1<Z_{1:m:n}<z_1+dz_1,\ldots ,z_m<Z_{m:m:n}<z_m+dz_m,Z_{k:m:n}<Z_{m:m:n}<T, D_1=i)\}$ for $i=1,\ldots ,m$ is nothing but the failure times of m units till the experiment termination point $Z_{m:m:n}$ and out of them i units have failed due to Cause-1. The probability of this event is the likelihood contribution of the data when $T^*=Z_{m:m:n}$. Thus (13) becomes,

$$\begin{aligned} \prod _{v=1}^m \gamma _v\bigg (\frac{1}{\theta _1}\bigg )^i \bigg (\frac{1}{\theta _2}\bigg )^{m-i}\frac{e^{-\frac{1}{\theta }\sum _{s=1}^{m} (1+R_s)z_s}}{P(Z_{k:m:n}<Z_{m:m:n}<T,D_1=i)} \; dz_1\ldots dz_m. \end{aligned}$$

(14)

$\square$

Theorem 3

The conditional moment generating function of $\widehat{\theta }_1$ given $J=j, D_1=i$ for $i=1,\ldots , j$ and $j=k,\ldots , m-1$ is given by

$$\begin{aligned}&\quad E(e^{t\widehat{\theta }_1}|J=j, D_1=i)\\&\quad = \prod _{v=1}^j \frac{\gamma _v}{P(J=j,D_1=i)} \bigg (\frac{1}{\theta _1}\bigg )^i\bigg (\frac{1}{\theta _2}\bigg )^{j-i} \Big (\frac{1}{\theta }-\frac{t}{i}\Big )^{-j} \\&\qquad \times \sum _{v=0}^j \frac{(-1)^v e^{-T(\frac{1}{\theta }-\frac{t}{i})\gamma _{j-v+1}}}{\{\prod _{h=1}^v (\gamma _{j+1-v}-\gamma _{j+1-v+h})\}\{\prod _{h=1}^{j-v} (\gamma _h-\gamma _{j-v+1})\}}. \end{aligned}$$

Proof

$$\begin{aligned}&E[e^{t\widehat{\theta }_1}|J=j,D_1=i]\\&\quad =\frac{\prod _{v=1}^j \gamma _v}{P(J=j,D_1=i)} \bigg (\frac{1}{\theta _1}\bigg )^i\bigg (\frac{1}{\theta _2}\bigg )^{j-i}\\&\qquad \times \int _{0}^T \int _{0}^{z_j}\ldots \int _{0}^{z_2} e^{-z_1(1+R_1)(\frac{1}{\theta }-\frac{t}{i})} \ldots e^{-z_j(1+R_j)(\frac{1}{\theta }-\frac{t}{i})} e^{-TR^*_j(\frac{1}{\theta } -\frac{t}{i})} \ dz_1\ldots dz_j \end{aligned}$$

The above equality follows using Lemma 1,

$$\begin{aligned}&\quad =\frac{\prod _{v=1}^j \gamma _v}{P(J=j,D_1=i)} \bigg (\frac{1}{\theta _1}\bigg )^i\bigg (\frac{1}{\theta _2}\bigg )^{j-i} e^{-TR^*_j(\frac{1}{\theta }-\frac{t}{i})}\\&\qquad \times \int _{0}^T \int _{0}^{z_j}\ldots \int _{0}^{z_2} e^{-z_1} e^{-z_1(1+R_1)(\frac{1}{\theta }-\frac{t}{i})-1} \ldots e^{-z_j} e^{-z_{j}(1+R_{j})(\frac{1}{\theta }-\frac{t}{i})-1}dz_1\ldots dz_j\\&=\frac{\prod _{v=1}^j \gamma _v}{P(J=j,D_1=i)} \bigg (\frac{1}{\theta _1}\bigg )^i\bigg (\frac{1}{\theta _2}\bigg )^{j-i} \Big (\frac{1}{\theta }-\frac{t}{i}\Big )^{-j} \\&\qquad \times \sum _{v=0}^j \frac{(-1)^v e^{-T(\frac{1}{\theta }-\frac{t}{i})\gamma _{j-v+1}}}{\{\prod _{h=1}^v (\gamma _{j+1-v}-\gamma _{j+1-v+h})\}\{\prod _{h=1}^{j-v} (\gamma _h-\gamma _{j-v+1})\}} \end{aligned}$$

The last equality follows using Lemma 1 of Balakrishnan et al. (2002).$\square$

Corollary 1

The conditional distribution of $\widehat{\theta }_1$ given $J=j, D_1=i$ for $i=1,\ldots ,j$ and $j=k,\ldots ,m-1$ is given by,

$$\begin{aligned} f_{\widehat{\theta }_1|J=j,D_1=i}(x)&=\prod _{v=1}^j \frac{\gamma _v}{P(J=j,D_1=i)} \bigg (\frac{1}{\theta _1}\bigg )^i\bigg (\frac{1}{\theta _2}\bigg )^{j-i} \Big (\frac{1}{\theta }\Big )^{-j}\\&\qquad \times \sum _{v=0}^j \frac{(-1)^v e^{-\frac{T}{\theta }\gamma _{j-v+1}}}{\{\prod _{h=1}^v (\gamma _{j+1-v}-\gamma _{j+1-v+h})\}\{\prod _{h=1}^{j-v} (\gamma _h-\gamma _{j-v+1})\}}\\&\qquad \times f_G\Big (x;\frac{T}{i}\gamma _{j-v+1},j,\frac{i}{\theta }\Big ). \end{aligned}$$

Theorem 4

The conditional moment generating function of $\widehat{\theta }_1$ given $T<Z_{k:m:n}<Z_{m:m:n}, D_1=i$ for $i=1,\ldots , k$ is given by,

$$\begin{aligned}&\quad E(e^{t\widehat{\theta }_1}|T<Z_{k:m:n}<Z_{m:m:n}, D_1=i)\\&\quad =\frac{\prod _{v=1}^k \gamma _v}{P(T<Z_{k:m:n}<Z_{m:m:n},D_1=i)} \bigg (\frac{1}{\theta _1}\bigg )^i\bigg (\frac{1}{\theta _2}\bigg )^{k-i} \Big (\frac{1}{\theta }-\frac{t}{i}\Big )^{-k} \\&\qquad \times \sum _{v=0}^{k-1} \frac{(-1)^v e^{-T(\frac{1}{\theta }-\frac{t}{i})\gamma _{k-v}}}{\{\prod _{j=1}^v (\gamma _{k-v}-\gamma _{k-v+j})\}\{\prod _{j=1}^{k-1-v} (\gamma _j-\gamma _{k-v})\}\gamma _{k-v}}. \end{aligned}$$

Proof

$$\begin{aligned}&E[e^{t\widehat{\theta }_1}|T<Z_{k:m:n}<Z_{m:m:n},D_1=i]\\&\quad =\frac{\prod _{v=1}^k \gamma _v}{P(T<Z_{k:m:n}<Z_{m:m:n},D_1=i)} \bigg (\frac{1}{\theta _1}\bigg )^i\bigg (\frac{1}{\theta _2}\bigg )^{k-i}\\&\qquad \times \int _{T}^\infty \int _{0}^{z_k}\ldots \int _{0}^{z_2} e^{-z_1(1+R_1)(\frac{1}{\theta }-\frac{t}{i})} \ldots e^{-z_{k-1}(1+R_{k-1})(\frac{1}{\theta }-\frac{t}{i})}e^{-z_k(1+R^*_k)(\frac{1}{\theta }-\frac{t}{i})} dz_1\ldots dz_k \end{aligned}$$

The above equality follows using Lemma 2,

$$\begin{aligned}&\quad =\frac{\prod _{v=1}^k \gamma _v}{P(T<Z_{k:m:n}<Z_{m:m:n},D_1=i)} \bigg (\frac{1}{\theta _1}\bigg )^i\bigg (\frac{1}{\theta _2}\bigg )^{k-i}\\&\qquad \times \int _{T}^\infty \Big [\int _{0}^{z_k}\ldots \int _{0}^{z_2} e^{-z_1} e^{-z_1(1+R_1)(\frac{1}{\theta }-\frac{t}{i})-1} \ldots e^{-z_{k-1}} e^{-z_{k-1}(1+R_{k-1})(\frac{1}{\theta }-\frac{t}{i})-1}dz_1\ldots dz_{k-1} \Big ]\\&\ \ \ \ \ \ \ \times e^{-z_k(1+R^*_k)(\frac{1}{\theta }-\frac{t}{i})} dz_k\\&\quad =\frac{\prod _{v=1}^k \gamma _v}{P(T<Z_{k:m:n}<Z_{m:m:n},D_1=i)} \bigg (\frac{1}{\theta _1}\bigg )^i\bigg (\frac{1}{\theta _2}\bigg )^{k-i} \frac{1}{(\frac{1}{\theta }-\frac{t}{i})^{k-1}}\\&\qquad \times \int _T^\infty \sum _{v=0}^{k-1} \frac{(-1)^v e^{-z_k(\frac{1}{\theta }-\frac{t}{i})\gamma _v}}{\{\prod _{j=1}^v (\gamma _{k-v}-\gamma _{k-v+j})\}\{\prod _{j=1}^{k-1-v} (\gamma _j-\gamma _{k-v})\}} dz_k \end{aligned}$$

The last equality follows using Lemma 1 of Balakrishnan et al. (2002)

$$\begin{aligned}&\quad =\frac{\prod _{v=1}^k \gamma _v}{P(T<Z_{k:m:n}<Z_{m:m:n},D_1=i)} \bigg (\frac{1}{\theta _1}\bigg )^i\bigg (\frac{1}{\theta _2}\bigg )^{k-i} \Big (\frac{1}{\theta }-\frac{t}{i}\Big )^{-k} \\&\qquad \times \sum _{v=0}^{k-1} \frac{(-1)^v e^{-T(\frac{1}{\theta }-\frac{t}{i})\gamma _{k-v}}}{\{\prod _{j=1}^v (\gamma _{k-v}-\gamma _{k-v+j})\}\{\prod _{j=1}^{k-1-v} (\gamma _j-\gamma _{k-v})\}\gamma _{k-v}}. \end{aligned}$$

$\square$

Corollary 2

The conditional distribution of $\widehat{\theta }_1$ given $T<Z_{k:m:n}<Z_{m:m:n}, D_1=i$ for $i=1,\ldots , k$ is given by,

$$\begin{aligned}&f_{\widehat{\theta }_1|T<Z_{k:m:n}<Z_{m:m:n},D_1=i}(x)\\&\quad =\frac{\prod _{v=1}^k \gamma _v}{P(T<Z_{k:m:n}<Z_{m:m:n},D_1=i)} \bigg (\frac{1}{\theta _1}\bigg )^i\bigg (\frac{1}{\theta _2}\bigg )^{k-i} \Big (\frac{1}{\theta }\Big )^{-k}\\&\qquad \times \sum _{v=0}^{k-1} \frac{(-1)^v e^{-\frac{T}{\theta }\gamma _{k-v}}}{\{\prod _{j=1}^v (\gamma _{k-v}-\gamma _{k-v+j})\}\{\prod _{j=1}^{k-1-v} (\gamma _j-\gamma _{k-v})\}\gamma _{k-v}}\\&\qquad \times f_G\Big (x;\frac{T}{i}\gamma _{k-v},k,\frac{i}{\theta }\Big ). \end{aligned}$$

Theorem 5

The moment generating function of $\widehat{\theta }_1$ given $Z_{k:m:n}<Z_{m:m:n}<T, D_1=i$ for $i=1,\ldots ,m$ is given by,

$$\begin{aligned}&E(e^{t\widehat{\theta }_1}|Z_{k:m:n}<Z_{m:m:n}<T, D_1=i)\\&\quad =\frac{\prod _{v=1}^m \gamma _v}{P(Z_{k:m:n}<Z_{m:m:n}<T,D_1=i)} \bigg (\frac{1}{\theta _1}\bigg )^i\bigg (\frac{1}{\theta _2}\bigg )^{m-i} \Big (\frac{1}{\theta }-\frac{t}{i}\Big )^{-m}\\&\qquad \times \sum _{v=0}^{m} \frac{(-1)^v e^{-T(\frac{1}{\theta }-\frac{t}{i})(\gamma _{m-v+1}-\gamma _{m+1})}}{\{\prod _{j=1}^v (\gamma _{m-v+1}-\gamma _{m-v+j+1})\}\{\prod _{j=1}^{m-v} (\gamma _j-\gamma _{m-v+1})\}}. \end{aligned}$$

Proof

$$\begin{aligned}&E[e^{t\widehat{\theta }_1}|Z_{k:m:n}<Z_{m:m:n}<T,D_1=i]\\&\quad =\frac{\prod _{v=1}^m \gamma _v}{P(Z_{k:m:n}<Z_{m:m:n}<T,D_1=i)} \bigg (\frac{1}{\theta _1}\bigg )^i\bigg (\frac{1}{\theta _2}\bigg )^{m-i}\\&\qquad \times \int _{0}^T \int _{0}^{z_m}\ldots \int _{0}^{z_2} e^{-z_1(1+R_1)(\frac{1}{\theta }-\frac{t}{i})} \ldots e^{-z_{m-1}(1+R_{m-1})(\frac{1}{\theta }-\frac{t}{i})}e^{-z_m(1+R_m)(\frac{1}{\theta }-\frac{t}{i})} dz_1\ldots dz_m \end{aligned}$$

The above equality follows using Lemma 3,

$$\begin{aligned}&\quad =\frac{\prod _{v=1}^m \gamma _v}{P(Z_{k:m:n}<Z_{m:m:n}<T,D_1=i)} \bigg (\frac{1}{\theta _1}\bigg )^i\bigg (\frac{1}{\theta _2}\bigg )^{m-i}\\&\qquad \times \int _{0}^T \ldots \int _{0}^{z_2} e^{-z_1} e^{-z_1(1+R_1)(\frac{1}{\theta }-\frac{t}{i})-1} \ldots e^{-z_m} e^{-z_m(1+R_m)(\frac{1}{\theta }-\frac{t}{i})-1} dz_1\ldots dz_m\\&\quad =\frac{\prod _{v=1}^m \gamma _v}{P(Z_{k:m:n}<Z_{m:m:n}<T,D_1=i)} \bigg (\frac{1}{\theta _1}\bigg )^i\bigg (\frac{1}{\theta _2}\bigg )^{m-i} \Big (\frac{1}{\theta }-\frac{t}{i}\Big )^{-m}\\&\qquad \times \sum _{v=0}^{m} \frac{(-1)^v e^{-T(\frac{1}{\theta }-\frac{t}{i})(\gamma _{m-v+1}-\gamma _{m+1})}}{\{\prod _{j=1}^v (\gamma _{m-v+1}-\gamma _{m-v+j+1})\}\{\prod _{j=1}^{m-v} (\gamma _j-\gamma _{m-v+1})\}} \end{aligned}$$

The last equality follows using Lemma 1 of Balakrishnan et al. (2002).$\square$

Corollary 3

The conditional distribution of $\widehat{\theta }_1$ given $Z_{k:m:n}<Z_{m:m:n}<T, D_1=i$ for $i=1,\ldots , m$ is given by,

$$\begin{aligned}&f_{\widehat{\theta }_1|Z_{k:m:n}<Z_{m:m:n}<T,D_1=i}(x)\\&\quad =\frac{\prod _{v=1}^m \gamma _v}{P(Z_{k:m:n}<Z_{m:m:n}<T,D_1=i)} \bigg (\frac{1}{\theta _1}\bigg )^i\bigg (\frac{1}{\theta _2}\bigg )^{m-i} \Big (\frac{1}{\theta }\Big )^{-m}\\&\qquad \times \sum _{v=0}^{m} \frac{(-1)^v e^{-\frac{T}{\theta }(\gamma _{m-v+1}-\gamma _{m+1})}}{\{\prod _{j=1}^v (\gamma _{m-v+1}-\gamma _{m-v+j+1})\}\{\prod _{j=1}^{m-v} (\gamma _j-\gamma _{m-v+1})\}}\\&\qquad \times f_G\left( x;\frac{T}{i}(\gamma _{m-v+1}-\gamma _{m+1}),m,\frac{i}{\theta }\right) . \end{aligned}$$

Proof of Theorem 1

Combining corollaries 1–3, we get the first part of Theorem 1. $\square$

$\mathrm{Derivation of} P(D_1=0).$

$$\begin{aligned} P(D_1=0)=&P(D_1=0,Z_{k:m:n}<T<Z_{m:m:n})+P(D_1=0,T<Z_{k:m:n}<Z_{m:m:n})\\&+P(D_1=0,Z_{k:m:n}<Z_{m:m:n}<T)\\ =&P(Z_{k:m:n}<T<Z_{m:m:n})P(D_1=0|Z_{k:m:n}<T<Z_{m:m:n})\\&+P(T<Z_{k:m:n}<Z_{m:m:n})P(D_1=0|T<Z_{k:m:n}<Z_{m:m:n})\\&+P(Z_{k:m:n}<Z_{m:m:n}<T)P(D_1=0|Z_{k:m:n}<Z_{m:m:n}<T). \end{aligned}$$

We find each of the above probabilities separately.

$$\begin{aligned}&P(Z_{k:m:n}<T<Z_{m:m:n}) =\sum _{j=k}^{m-1} P(Z_{j:m:n}<T<Z_{j+1:m:n})\\&\quad =\sum _{j=k}^{m-1} \prod _{v=1}^{j+1} \gamma _v \Big (\frac{1}{\theta }\Big )^{j+1}\int _{T}^{\infty }\int _{0}^T\ldots \int _{0}^{z_2}e^{-\frac{1}{\theta }\sum _{i=1}^{j} z_i(1+R_i)} e^{-\frac{1}{\theta } z_{j+1}(1+R^*_{j+1})} dz_1 \ldots dz_j dz_{j+1}\\&\quad =\sum _{j=k}^{m-1} \prod _{v=1}^{j+1} \gamma _v \sum _{u=0}^{j} \frac{(-1)^u e^{-\frac{T}{\theta }\gamma _{j-u+1}}}{\{\prod _{v=1}^u (\gamma _{j-u+1}-\gamma _{j+v-u+1})\}\{\prod _{v=1}^{j-u} (\gamma _v-\gamma _{j-u+1})\}\{\gamma _{j-u+1}-u\}}. \end{aligned}$$

$$\begin{aligned} P(D_1=0|J=j)=\Big (\frac{\theta _1}{\theta _1+\theta _2}\Big )^j. \end{aligned}$$

$$\begin{aligned}&P(T<Z_{k:m:n}<Z_{m:m:n})\\&\quad =\prod _{v=1}^k \gamma _v \Big (\frac{1}{\theta }\Big )^k \int _T^{\infty } \int _{0}^{z_k}\ldots \int _0^{z_2} e^{-\frac{1}{\theta }\Big (\sum _{i=1}^k z_i(1+R_i)+z_k\gamma _k\Big )} dz_1\ldots dz_{k-1} dz_k\\&\quad =\prod _{v=1}^k \gamma _v \sum _{v=0}^{k-1} \frac{(-1)^v e^{-\frac{T}{\theta }\gamma _{k-v}}}{\{\prod _{j=1}^v (\gamma _{k-v}-\gamma _{k-v+j})\}\{\prod _{j=1}^{k-1-v} (\gamma _j-\gamma _{k-v})\}\gamma _{k-v}}.\\&P(D_1=0|T<Z_{k:m:n}<Z_{m:m:n}) =\Big (\frac{\theta _1}{\theta _1+\theta _2}\Big )^k\\&P(Z_{k:m:n}<Z_{m:m:n}<T)\\&\quad =\prod _{v=1}^m \gamma _v \Big (\frac{1}{\theta }\Big )^m \int _0^{T} \int _{0}^{z_m}\ldots \int _0^{z_2} e^{-\frac{1}{\theta }\sum _{i=1}^m z_i(1+R_i)}dz_1\ldots dz_{m-1} dz_m\\&\quad =\prod _{v=1}^m \gamma _v \sum _{v=0}^{m} \frac{(-1)^v e^{-\frac{T}{\theta }(\gamma _{m-v+1}-\gamma _{m+1})}}{\{\prod _{j=1}^v (\gamma _{m-v+1}-\gamma _{m-v+j+1})\}\{\prod _{j=1}^{m-v} (\gamma _j-\gamma _{m-v+1})\}}.\\&P(D_1=0|Z_{k:m:n}<Z_{m:m:n}<T)=\Big (\frac{\theta _1}{\theta _1+\theta _2}\Big )^m. \end{aligned}$$