Abstract
We study correspondences that choose an interval of alternatives when agents have single-peaked preferences over locations and ordinally extend their preferences over intervals. We extend the main results of Moulin (Public Choice 35:437–455, 1980) to our setting and show that the results of Ching (Soc Choice Welf 26:473–490, 1997) cannot always be similarly extended. First, strategy-proofness and peaks-onliness characterize the class of generalized median correspondences (Theorem 1). Second, this result neither holds on the domain of symmetric and single-peaked preferences, nor can in this result min/max continuity substitute peaks-onliness (see counter-Example 3). Third, strategy-proofness and voter-sovereignty characterize the class of efficient generalized median correspondences (Theorem 2).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
We study the problem where an interval of alternatives is chosen from the interval [0, 1] based on the preferences of a finite number of agents. This interval can be considered as the political spectrum, while the chosen interval can in turn be considered as the legislative constitution or the governmental coalition (in the sense that some “extreme” views are not accounted for by the constitution or are not represented by any member(s) of the governmental coalition). We assume that agents have single-peaked preferences defined over all alternatives on [0, 1]; that is, an agent’s welfare is strictly increasing up to his “peak” (his favorite alternative), and is strictly decreasing thereafter. Other examples for the type of social choice problems we are interested in would be the planning of public parking zones where an agent knows that he will (eventually) find a parking spot in the designated parking zone but he does not know where this will be, or the drafting of an “if-needed” list of candidate locations to build a public facility, e.g., a hospital. The motivation behind our model also resembles that of two-stage voting procedures such as, for example, Black’s procedure (e.g. Fishburn 1977) or the “rule of k names” (e.g. Barberà and Coelho 2000), or situations where voters select subsets of the outcome space (e.g. Nuñez and Xefteris 2017). We assume that decisions are made under ignorance (Peterson 2009, p. 40) and that agents, when comparing sets, focus on their best (most favorite) point(s) and their worst (least favorite) point(s) in each set.
We consider voting mechanisms that guarantee that the agents announce their true preferences; in other words, we are interested in voting mechanisms or (choice) correspondences, that are strategy-proof. Although the classic result of Gibbard and Satterthwaite establishes that on the full domain of preferences -with more than two possible outcomes- strategy-proofness and non-dictatorship are incompatible (Gibbard 1973; Satterthwaite 1975), this is not true for the domain of single-peaked preferences. This compatibility between the two aforementioned properties has been well studied in the context of (choice) functions that, based on agents’ (single-peaked) preferences, chose one alternative. Specifically, it has been shown that strategy-proofness and peaks-onliness (the agents only announce their peak) characterize the class of generalized median rules (Moulin 1980). Moreover, when also requiring (Pareto) efficiency, the sub-class of efficient generalized median rules is characterized (Moulin 1980). A similar result also holds when the range of the function is closed and not connected (Barberà and Jackson 1994). For symmetric single-peaked preferences, peaks-onliness can be substituted by unanimity (when a common best alternative exists, it is chosen) (Border and Jordan 1983); furthermore, it turns out that in these results two of the required properties can be weakened; specifically, peaks-onliness and efficiency can be substituted by continuity (a small change in the announced preferences does not change the outcome a lot) and voter-sovereignty (no alternative is a priori excluded from being chosen) respectively (Ching 1997).Footnote 1
Our main results also make use of either the additional property of peaks-onliness or a version of continuity adapted for our context (i.e., where an interval of alternatives is chosen). Furthermore, we also study the case where correspondences are efficient. Concisely, our results are the following. First, strategy-proofness and peaks-onliness characterize the class of generalized median correspondences (Theorem 1). Second, this result does not hold on the subdomain of symmetric and single-peaked preferences, nor can in this result continuity substitute peaks-onliness (see counter-Example 3). Third, strategy-proofness, voter-sovereignty, and either peaks-onliness or continuity characterize the class of efficient generalized median correspondences (Theorem 2).
The paper proceeds as follows. We introduce the model and choice correspondences and their properties in Sect. 2. Section 3 contains the definition of generalized median correspondences and efficient generalized median correspondences and their characterizations. We conclude with a discussion of some model assumptions and by reviewing some related literature (Sect. 4).
2 The model
Consider a coalition (of agents) \(N\equiv \{1,\ldots ,n\}\) (\(n\ge 2\)) and a set of alternatives \(A\equiv [0,1]\). We denote generic agents by i and j and generic alternatives by x and y. Each agent i is equipped with complete, transitive, and reflexive preferences \(R_i\) over A. As usual, \(x\mathbin {R_i}y\) is interpreted as “x is at least as desirable as y”, \(x\mathbin {P_i}y\) as “x is preferred to y”, and \(x\mathbin {I_i}y\,\) as “x is indifferent to y”. Moreover, for preferences \(R_i\) there exists a number \(p(R_i)\in {\mathbb {R}}\), called the peak (level) of i, with the following property: for each pair \(x,\,y\in {\mathbb {R}}\) such that either \(y<x\le p(R_i)\), or \(y>x\ge p(R_i)\), we have \(x\mathbin {P_i}y\). We call such preferences single-peaked and denote the domain of single-peaked preferences by \({\mathcal {R}}\). Preferences \(R_{i}\in {\mathcal {R}}\) are symmetric if for each pair \(x,y\in {\mathbb {R}}\), \(|x-p(R_i)|=|y-p(R_i)|\) implies \(x\mathbin {I_i}y\). Let \({\mathcal {R}}^N\) be the set of profiles \(R\equiv (R_i)_{i\in N}\) such that for each \(i\in N\), \(R_i\in {\mathcal {R}}\). Given \(R\in {\mathcal {R}}^N\) and \(j\in N\), we use R and \((R_{-j},R_j)\) interchangeably. For each \(R\in {\mathcal {R}}^N\), we denote the vector of peaks by \(p \equiv (p_i)_{i\in N}\), the smallest peak by  , the largest peak by \({\bar{p}}\equiv \max \{p_i\}_{i\in N}\), and the convex hull of peaks by
, the largest peak by \({\bar{p}}\equiv \max \{p_i\}_{i\in N}\), and the convex hull of peaks by  .
.
Denote the class of closed intervals in A by \({\mathcal {A}}\), generic sets in \({\mathcal {A}}\) by X and Y, the minimum of X by \(X_{_{-}}\), and the maximum of X by \({\bar{X}}\). For each \(R_i\in {\mathcal {R}}\) denote the set of best alternative(s) of i in X by \(b_{R_i}(X)\equiv \{x\in X:\text{ for } \text{ each } y\in X\text{, } x\mathbin {R_i}y\}\) and the set of worst alternative(s) of i in X by \(w_{R_i}(X)\equiv \{x\in X:\text{ for } \text{ each } y\in X\text{, } y\mathbin {R_i}x\}\). By single-peakedness,  and \(|b_{R_i}(X)|=1\). By single-peakedness,
and \(|b_{R_i}(X)|=1\). By single-peakedness,  and if
and if  (only if
(only if  ), then
), then  . With some abuse of notation, we treat sets \(b_{R_i}(X)\) and \(w_{R_i}(X)\) as if they are points and for each \(x\in X\), we write \(b_{R_i}(X)\mathbin {R_i}x\mathbin {R_i}w_{R_i}(X)\).
. With some abuse of notation, we treat sets \(b_{R_i}(X)\) and \(w_{R_i}(X)\) as if they are points and for each \(x\in X\), we write \(b_{R_i}(X)\mathbin {R_i}x\mathbin {R_i}w_{R_i}(X)\).
We will consider choice correspondences that assign outcomes in \({\mathcal {A}}\) under complete uncertainty (or ignorance) with the interpretation that any agent “knows the set of possible outcomes \(\ldots \), but has no information about the probabilities of those outcomes or about their likelihood ranking” (Bossert et al. 2000, p. 295).Footnote 2 We assume that agents when evaluating outcomes focus exclusively on the best and worst points of the outcomes. Various preference extensions with different degrees of optimism or pessimism do so: consider, for example,
-
either very optimistic agents who only focus on the best alternative(s) in the outcome set (max extension) or (lexicographically) first on the best alternative(s) and then on the worst alternative(s) (max-min extension)
-
or very pessimistic agents who only focus on the worst alternative(s) in the outcome set (min extension) or (lexicographically) first on the worst alternative(s) and then on the best alternative(s) (min-max extension),
see Klaus and Protopapas (2020, Appendix A) for a more detailed discussion. All these preference extensions have in common that given \(X,Y\in {\mathcal {A}}\), if an agent prefers his best alternative(s) in X to his best alternative(s) in Y and his worst alternative(s) in X to his worst alternative(s) in Y, then he prefers X to Y. To strike a balance between the opposite assumptions of optimistic versus pessimistic preferences, we use the following best-worst extension of preferences over sets (we use the same symbols to denote preferences over points and preferences over sets).
Best-worst extension of preferences to sets
For each \(i\in N\) with \(R_i\in {\mathcal {R}}\) and each \(X,Y\in {\mathcal {A}}\), we have
and
This extension of preferences is transitive; however, it is not complete (there exist sets \(X,Y\in {\mathcal {A}}\) such that neither \(X\mathbin {R_{i}}Y\) nor \(Y\mathbin {R_{i}}X\)). In Klaus and Protopapas (2020, Appendix A) we also give a normative foundation of our preference extension based on Bossert et al. (2000, Theorem 1) and illustrate it with the example of public parking allocation.
We use the standard notion of Pareto optimality/efficiency as our efficiency notion.
Efficient sets
Given \(R\in {\mathcal {R}}^N\), set \(X\in {\mathcal {A}}\) is (Pareto) efficient if and only if there is no set \(Y\in {\mathcal {A}}\) such that for each \(i\in N\), \(Y\mathbin {R_i}X\), and for at least one \(j\in N\), \(Y\mathbin {P_j}X\); we denote the class containing all efficient sets at R by \(\mathrm {E}(R)\).
The next characterization of efficient sets follows from Klaus and Protopapas (2020) and it coincides with the well-known characterization of (Pareto) efficient points for choice functions. Note that the original result is a little more complicated since it holds for all compact sets.
Proposition 1
(Klaus and Protopapas (2020)) At \(R\in {\mathcal {R}}^N\), a closed interval is efficient if and only if it is a subset of the convex hull of peaks.
A (choice) correspondence F assigns to each \(R\in {\mathcal {R}}^N\) a set \(F(R)\in {\mathcal {A}}\), i.e., \(F:{\mathcal {R}}^N\rightarrow {\mathcal {A}}\). Given \(R\in {\mathcal {R}}^N\), we denote the minimum of F(R) by  and the maximum of F(R) by \({\bar{F}}(R)\). We denote the family of correspondences by \({\mathcal {F}}\). Moreover, if \(F\in {\mathcal {F}}\) assigns to each \(R\in {\mathcal {R}}^N\) an interval consisting of a single point we will refer to it as a function and use notation \(f\in {\mathfrak {f}}\), i.e., \(f:{\mathcal {R}}^N\rightarrow A\).
and the maximum of F(R) by \({\bar{F}}(R)\). We denote the family of correspondences by \({\mathcal {F}}\). Moreover, if \(F\in {\mathcal {F}}\) assigns to each \(R\in {\mathcal {R}}^N\) an interval consisting of a single point we will refer to it as a function and use notation \(f\in {\mathfrak {f}}\), i.e., \(f:{\mathcal {R}}^N\rightarrow A\).
The first two properties we consider are related; the first is (Pareto) efficiency for correspondences while the second, being weaker than the first, requires no alternative in A to be a priori excluded from being selected.
Efficiency
For each \(R\in {\mathcal {R}}^N\), \(F(R)\in \mathrm {E}(R)\).
Voter-sovereignty
For each \(x\in A\), there exists \(R\in {\mathcal {R}}^N\) such that \(F(R)=\{x\}\).
The next property, which is central in our results, requires no agent to gain by deviating; it also implies comparability between the chosen sets before and after an agent’s deviation. Note that it is a strong extension of strategy-proofness to correspondences in line with the one introduced by Duggan and Schwartz (2000) (see Barberà 2011, for a comprehensive survey on strategy-proof social choice correspondences).
Strategy-proofness
For each \(i\in N\), each \(R\in {\mathcal {R}}^N\), and each \(R^{\prime }_i\in {\mathcal {R}}\), \(F(R)\mathbin {R_i}F(R_{-i},R^{\prime }_i)\).
The next property expresses a considerable reduction or simplification of the information used by a correspondence by requiring the chosen set to depend only on the vector of peaks.
Peaks-onliness
For each pair \(R,R^{\prime }\in {\mathcal {R}}^N\) such that \(p=p^{\prime }\), \(F(R)=F(R^{\prime })\).
So far we have introduced typical “economic” properties. Our last two properties are a bit more technical (although commonly considered in various economic contexts). First, we adapt continuity to our context; loosely speaking, it requires that when the announced preferences of an agent change “a little”, the minimum and maximum alternatives chosen do not change “a lot”. Before describing it formally, we first define the three following notions. First, the indifference relation \(r_{R_i}:[0,1]\rightarrow [0,1]\), given preferences \(R_i\in {\mathcal {R}}\), loosely speaking maps each alternative x to an alternative y that i finds indifferent to x, according to \(R_i\), i.e., for each \(x\in [0,p_i]\), \(r_{R_i}(x)=y\) if \(y\in [p_i,1]\) exists such that \(y\mathbin {I}_ix\), or \(r_{R_i}(x)=1\) otherwise; while for each \(x\in [p_i,1]\), \(r_{R_i}(x)=y\) if \(y\in [0,r_i]\) exists such that \(y\mathbin {I}_ix\), or \(r_{R_i}(x)=0\) otherwise. Second, the distance between a pair \(R_i,R^{\prime }_i\in {\mathcal {R}}\) is measured by \(\mathrm {d}(R_i,R^{\prime }_i)\equiv \max _{x\in [0,1]}|r_{R_i}(x)-r_{R^{\prime }_i}(x)|\). Finally, a sequence \(\{R_i^k\}_{k\in {\mathbb {N}}^+}\) in \({\mathcal {R}}\) converges to \(R_i\), if \(k\rightarrow \infty \) implies that distance \(\mathrm {d}(R_i,R_i^k)\rightarrow 0\). We denote this convergence by \(R_i^k\rightarrow R_i\).
Min/max continuity
For each \(R\in {\mathcal {R}}^N\), each \(i\in N\), and each \(\{R_i^k\}_{k\in {\mathbb {N}}^+}\) in \({\mathcal {R}}\),

Min/max continuity for functions is equivalent to the regular continuity property for functions and Protopapas (2018, Appendix A) shows that it is equivalent to upper-hemi continuity and lower-hemi continuity for correspondences.
A choice correspondence satisfies uncompromisingness (Border and Jordan 1983) if whenever an agent’s preferences change such that his peaks, before and after this change, both lie on the same side of the minimum (maximum) point chosen, then the minimum (maximum) point chosen does not change.
Uncompromisingness
For each \(i\in N\) and each pair \(R,R^{\prime }\in {\mathcal {R}}^N\) such that \(R^{\prime }_{-i}=R_{-i}\),
- (i):
-
if [
 and
and  ] or [
] or [ and
and  ], then
], then  and
and - (ii):
-
if [\(p_i<{\bar{F}}(R)\) and \(p^{\prime }_i\le {\bar{F}}(R)\)] or [\(p_i>{\bar{F}}(R)\) and \(p^{\prime }_i\ge {\bar{F}}(R)\)], then \({\bar{F}}(R)={\bar{F}}(R^{\prime })\).
3 Generalized median rules and correspondences
Before defining the classes of functions and correspondences that our results revolve around, the following definition is necessary: for each odd and positive integer k, and each vector \(T\in {\mathbb {R}}^k\), label the coordinates of T such that \(t_1\le \dots \le t_k\); we define the median (coordinate) of T by \(\mathrm {med}{(T)}\equiv t_{\frac{k+1}{2}}\).
The class of functions we consider was introduced and characterized by strategy-proofness and peaks-onliness (Moulin 1980, Proposition 3). It was later shown that peaks-onliness can be substituted with the “weaker” property of continuity (Ching 1997, Theorem). In order to provide an intuition in understanding this class, we present an example inspired by the one provided in Arribillaga and Massó (2016, p. 564).
Example 1
Let \(N=\{1,2\}\) and \(\alpha =(\alpha _\emptyset ,\alpha _{\{1\}},\alpha _{\{2\}},\alpha _{N})\) such that \(\alpha _N\le \alpha _{\{1\}}\le \alpha _{\{2\}}\le \alpha _\emptyset \). Define \(f^\alpha \in {\mathfrak {f}}\) as follows. For each \(R\in {\mathcal {R}}^N\), if \(p_1\le p_2\), choose \({\tilde{\alpha }}_p=(\alpha _\emptyset ,\alpha _{\{1\}},\alpha _N)\) and set \(f^\alpha (R)=\mathrm {med}{({\tilde{\alpha }}_p,p)}\), and if \(p_1>p_2\), choose \({\tilde{\alpha }}_p=(\alpha _\emptyset ,\alpha _{\{2\}},\alpha _N)\) and set \(f^\alpha (R)=\mathrm {med}{({\tilde{\alpha }}_p,p)}\). The range of \(f^{\alpha }\) equals \([\alpha _N,\alpha _\emptyset ]\). Note that if \(\alpha _{\{1\}}\not =\alpha _{\{2\}}\), then the agents have asymmetric power in influencing the chosen alternative; since \(\alpha _{\{1\}}\le \alpha _{\{2\}}\), agent 1 has a greater power than agent 2 in influencing the chosen alternative: agent 1 can make sure that the chosen alternative is not larger than \(\alpha _{\{1\}}\) and not smaller than \(p_1\) (by announcing \(p_1\le \alpha _{\{1\}}\)), or that it is not larger than \(p_1\) and not smaller than \(\alpha _{\{1\}}\) (by announcing \(p_1\ge \alpha _{\{1\}}\)). In addition, he is a dictator on the interval \([\alpha _{\{1\}},\alpha _{\{2\}}]\).
Next, agent 2 only has the power to influence the chosen alternative if agent 1 “allows” him to do so. That is, if \(\alpha _N\le p_1\le \alpha _{\{1\}}\), then agent 2 can choose an alternative in \([p_1, \alpha _{\{1\}}]\), and if \( p_1\le \alpha _N\le \alpha _{\{1\}}\), then agent 2 can choose an alternative in \([\alpha _N, \alpha _{\{1\}}]\). Similarly, if \( \alpha _{\{2\}}\le p_1\le \alpha _\emptyset \), then agent 2 can choose an alternative in \([\alpha _{\{2\}}, p_1]\), and if \( \alpha _{\{2\}}\le \alpha _\emptyset \le p_1\), then agent 2 can choose an alternative in \([\alpha _{\{2\}}, \alpha _\emptyset ]\). \(\square \)
The general n-agent case is defined next. We use the terminology of generalized median rules (see Border and Jordan 1983). Moulin (1980) was the first to introduce this class of rules using a “minmax representation.” Ching (1997) refers to augmented median voter schemes and explains “Moulin (1980) first characterized the class of solutions satisfying strategy-proofness and peak only as the class of minmax solutions. We show how to relate a minmax solution and an augmented median-voter solution in terms of their parameters.”
Generalized median rules
Let \(\alpha \in A^{2^n}\) be such that \(\alpha \equiv (\alpha _M)_{M\subseteq N}\), where for each pair of sets \(L\subseteq M\subseteq N\), \(\alpha _L\ge \alpha _M\). Also, for each \(R\in {\mathcal {R}}^N\), let bijection \(\pi :N\rightarrow N\) be such that \(p_{\pi (1)}\le \cdots \le p_{\pi (n)}\) and construct vector \({\tilde{\alpha }}_p=(\alpha _{\emptyset },\alpha _{\{\pi (1)\}},\alpha _{\{\pi (1),\pi (2)\}},\ldots ,\alpha _N)\). We denote the generalized median rule associated with vector \(\alpha \) by \(f_G^{\alpha }\), where for each \(R\in {\mathcal {R}}^N\), \( f_G^{\alpha }(R)\equiv \mathrm {med}{(p,{\tilde{\alpha }}_v)}\). We denote the class of generalized median rules by \({\mathfrak {f}}_G\).
Clearly, if all agents announce different peaks, a unique ordering of them by their announced peak exists. Moreover, for the case where some agents announce the same peak and hence such a unique ordering does not exist, the chosen alternative does not depend on the particular ordering chosen; as shown in Ching (1997, Remark 1) (see also Protopapas 2018, Lemma 1).
The following class of correspondences extends the spirit of generalized median rules to correspondences.
Generalized median correspondences
Let \(\alpha ,\beta \in A^{2^n}\) be such that \(\alpha \equiv (\alpha _M)_{M\subseteq N}\) and \(\beta \equiv (\beta _M)_{M\subseteq N}\), with \(\alpha \le \beta \), where for each pair of sets \(L\subseteq M\subseteq N\), \(\alpha _L\ge \alpha _M\) and \(\beta _L\ge \beta _M\). Also, for each \(R\in {\mathcal {R}}^N\), let bijection \(\pi :N\rightarrow N\) be such that \(p_{\pi (1)}\le \cdots \le p_{\pi (n)}\) and construct vectors \({\tilde{\alpha }}_p =(\alpha _{\emptyset },\alpha _{\{\pi (1)\}},\alpha _{\{\pi (1),\pi (2)\}},\ldots ,\alpha _N)\) and \({\tilde{\beta }}_p =(\beta _{\emptyset },\beta _{\{\pi (1)\}},\beta _{\{\pi (1),\pi (2)\}},\ldots ,\beta _N)\). We denote the generalized median correspondence associated with vectors \(\alpha \) and \(\beta \) by \(F_G^{\alpha ,\beta }\), where for each \(R\in {\mathcal {R}}^N\), \( F_G^{\alpha ,\beta }(R)\equiv [\mathrm {med}{(p,{\tilde{\alpha }}_p)},\mathrm {med}{(p,{\tilde{\beta }}_p)}]\). We denote the class of generalized median correspondences by \({\mathcal {F}}_G\).
Remark 1
By definition of \({\mathcal {F}}_G\) and \({\mathfrak {f}}_G\), a generalized median correspondence \(F^{\alpha ,\beta }_G\) can be decomposed into two generalized median rules \(f^\alpha _G\) and \(f^\beta _G\), i.e., for each \(R\in {\mathcal {R}}^N\), \(F^{\alpha ,\beta }_G(R)\equiv [\mathrm {med}{(p,{\tilde{\alpha }}_p)},\mathrm {med}{(p,{\tilde{\beta }}_p)}]= [f^\alpha _G(R),f^\beta _G(R)]\). \(\square \)
Given \(F^{\alpha ,\beta }_G\in {\mathcal {F}}_G\), if for each \(R\in {\mathcal {R}}^N\), \(F^{\alpha ,\beta }_G(R)\in \mathrm {E}(R)\), we say that \(F^{\alpha ,\beta }_G\) is an efficient generalized median correspondence and denote the class of efficient generalized median correspondences by \({\mathcal {F}}_{EG}\). We obtain the following characterization.
Proposition 2
A generalized median correspondence \(F^{\alpha ,\beta }_G\) is an efficient generalized median correspondence if and only if \(\alpha ,\beta \) are such that \(\alpha _\emptyset =\beta _\emptyset =1\) and \(\alpha _N=\beta _N=0\).
Proof
Let \(F^{\alpha ,\beta }_G\in {\mathcal {F}}_G\). First, assuming that \(F_G^{\alpha ,\beta }\in {\mathcal {F}}_{EG}\) such that \(\alpha ,\beta \) are not as described above, results in a contradiction as follows. If \(\alpha _N\not =0\) or \(\beta _N\not =0\), choose \(R\in {\mathcal {R}}^N\) such that \(p=(0,\ldots , 0)\). By Proposition 1, \(\mathrm {E}(R)=\{0\}\) and by the definition of \({\mathcal {F}}_G\), \(F_G^{\alpha ,\beta }(R)=[\alpha _N,\beta _N]\). Hence, \(F_G^{\alpha ,\beta }(R)\not \in \mathrm {E}(R)\). Similarly, if \(\alpha _\emptyset \not =1\) or \(\beta _\emptyset \not =1\), choose \(R\in {\mathcal {R}}^N\) such that \(p=(1,\ldots , 1)\), \(\mathrm {E}(R)=\{1\}\), \(F_G^{\alpha ,\beta }(R) =[\alpha _\emptyset ,\beta _\emptyset ]\), and \(F_G^{\alpha ,\beta }(R)\not \in \mathrm {E}(R)\).
Second, if \(\alpha _N=\beta _N=0\) and \(\alpha _\emptyset =\beta _\emptyset =1\), then for each \(R\in {\mathcal {R}}^N\), \(\mathrm {med}{(p,{\tilde{\alpha }}_p)}\in \mathrm {Conv}(p)\) and \(\mathrm {med}{(p,{\tilde{\beta }}_p)}\in \mathrm {Conv}(p)\). Hence, \(F_G^{\alpha ,\beta }(R)\subseteq \mathrm {Conv}(p)\), and thus, by Proposition 1, \(F_G^{\alpha ,\beta }(R)\in \mathrm {E}(R)\). \(\square \)
Generalized median correspondences are strategy-proof, similar to the results on functions by Moulin (1980). However, in contrast to Moulin’s results these correspondences are not group strategy-proof.Footnote 3 The following example illustrates this.
Example 2
(Group strategy-proofness counter-example) Let \(N=\{1,2,3\}\) and define \(F^{\prime }\in {\mathcal {F}}\) such that for all \(R\in {\mathcal {R}}^N\), \(F^{\prime }(R)=[\mathrm {med}(0,0,0,p_1,p_2,p_2,1),\mathrm {med}(0,0,p_1,p_2,p_3,1,1)]\), i.e.,  selects the smallest peak and \(\bar{F^{\prime }}\) the second smallest peak. Note that \(F^{\prime }=F^{\alpha ,\beta }_G\in {\mathcal {F}}_{EM}\) with \(\alpha _\emptyset =\beta _\emptyset =1\), \(\alpha _{\{i\}}=0\), \(\beta _{\{i\}}=1\), \(\alpha _{\{i,j\}}=\beta _{\{i,j\}}=1\), and \(\alpha _N=\beta _N=0\).
selects the smallest peak and \(\bar{F^{\prime }}\) the second smallest peak. Note that \(F^{\prime }=F^{\alpha ,\beta }_G\in {\mathcal {F}}_{EM}\) with \(\alpha _\emptyset =\beta _\emptyset =1\), \(\alpha _{\{i\}}=0\), \(\beta _{\{i\}}=1\), \(\alpha _{\{i,j\}}=\beta _{\{i,j\}}=1\), and \(\alpha _N=\beta _N=0\).
Now, consider symmetric \(R,R^{\prime }\in {\mathcal {R}}^N\) such that \(p_1=p^{\prime }_1=0\), \(p_2=0.5\), \(p^{\prime }_2=0.6\), and \(p_3=p^{\prime }_3=1\). Then, \(F^{\prime }(R)=[0,0.5]\) and \(F^{\prime }(R^{\prime })=[0,0.6]\). Hence, agent 2 is indifferent when changing preferences from \(R_2\) to \(R^{\prime }_2\) while agent 3 is strictly better off after this deviation; a contradiction to group strategy-proofness. \(\square \)
We now present our first main result, which generalizes Moulin (1980, Proposition 3).Footnote 4
Theorem 1
The following three statements for a correspondence \(F\in {\mathcal {F}}\) are equivalent.
- (i):
-
F satisfies strategy-proofness and peaks-onliness.
- (ii):
-
F satisfies uncompromisingness.
- (iii):
-
F is a generalized median correspondence.
We prove Theorem 1 in Appendix A. The properties in the above characterization are independent: first, correspondence \(F^*\) proposed in the following example satisfies strategy-proofness but neither peaks-onliness nor uncompromisingness; second,  satisfies peaks-onliness but neither strategy-proofness nor uncompromisingness.
satisfies peaks-onliness but neither strategy-proofness nor uncompromisingness.
Ching (1997, Theorem) provided an alternative characterization to Moulin (1980, Proposition 3) by replacing peaks-onliness with continuity. Next, we show that this result does not extend to correspondences. We illustrate this with a correspondence satisfying strategy-proofness and min/max continuity but violating peaks-onliness and uncompromisingness. Moreover, the example also demonstrates that the equivalence of (i) and (ii) in Theorem 1 does not hold on the subdomain of symmetric single-peaked preferences (see also Remark 2).
Example 3
(Counter-example corresponding to Ching (1997, Theorem)) Let \(|N|\!\ge \! 1\) and define \(r^*_R \equiv \max \{r_{R_i}(0)\}_{i\in N}\), that is, at profile R, among the indifferent announced alternatives to 0 of each agent \(i\in N\), \(r^*_R\) is the largest one. Next, define \(F^*\in {\mathcal {F}}\) as follows. For each \(R\in {\mathcal {R}}^N\), \(F^*(R)=[0, r^*_R]\). By definition, it follows that \(F^*\) satisfies min/max continuity. Note that \(F^*\) satisfies neither peaks-onliness, nor voter-sovereignty, nor efficiency.
To show that \(F^*\) satisfies strategy-proofness let \(R\in {\mathcal {R}}^N\) and \(R^{\prime }_i\in {\mathcal {R}}\) such that \(R^{\prime }_i\not =R_i\).
Case 1 \((r_{R_i}(0)=r^*_R)\). By single-peakedness, \(b_{R_i}(F^*(R))=\{p_i\}\), implying i’s best point does not improve by deviating at R, and \(0\in w_{R_i}(F^*(R))\). By the definition of \(F^*\), \(0\in F^*(R_{-i},R^{\prime }_i)\), hence i’s worst point(s) does not improve by deviating at R. Therefore, \(F^*(R)\mathbin {R_i}F^*(R_{-i},R^{\prime }_i)\).
Case 2 \((r_{R_i}(0)<r^*_R)\). By single-peakedness, \(b_{R_i}(F^*(R))=\{p_i\}\), implying i’s best point does not improve by deviating at R, and \(w_{R_i}(F^*(R))=\{r^*_R\}\). By the definition of \(F^*\), \(r^*_R\in F^*(R_{-i},R^{\prime }_i)\), hence i’s worst point does not improve by deviating at R. Therefore, \(F^*(R)\mathbin {R_i}F^*(R_{-i},R^{\prime }_i)\).
To show that \(F^*\) does not satisfy uncompromisingness let \(N=\{1,2,3\}\) and consider symmetric profiles \(R,R^{\prime }\in {\mathcal {R}}^N\) such that \(p_1=0.2\), \(p^{\prime }_1=0.3\), and \(p_2=p^{\prime }_2=p_3=p^{\prime }_3=0\). Hence, \(r^*_R=r_{R_1}(0)=0.4\) and \(r^*_{R^{\prime }}=r_{R^{\prime }_1}(0)=0.6\). Therefore, \(F(R)=[0,0.4]\) and \(F(R^{\prime })=[0,0.6]\) and \(F^*\) does not satisfy uncompromisingness. \(\square \)
We conclude this section by presenting the “efficient version” of Theorem 1. Notice that now strategy-proofness and voter sovereignty imply peaks-onliness and min/max continuity; this generalizes a result by Ching (1997, Proposition 2).
Theorem 2
The following three statements for a correspondence \(F\in {\mathcal {F}}\) are equivalent.
- (i):
-
F satisfies strategy-proofness and voter-sovereignty.
- (ii):
-
F satisfies uncompromisingness and voter-sovereignty.
- (iii):
-
F is an efficient generalized median correspondence.
We prove Theorem 2 in Appendix B. The properties in the above characterization are independent: first, a constant choice correspondence that always chooses a fixed set satisfies strategy-proofness and uncompromisingness, but not voter-sovereignty. Second,  satisfies voter-sovereignty but neither strategy-proofness nor uncompromisingness.
satisfies voter-sovereignty but neither strategy-proofness nor uncompromisingness.
4 Conclusion
We have presented two characterization results when agents have single-peaked preferences over locations and ordinally extend their preferences over intervals. First, strategy-proofness and peaks-onliness characterize the class of generalized median correspondences (Theorem 1). Second, strategy-proofness and voter-sovereignty characterize the class of efficient generalized median correspondences (Theorem 2). Furthermore, in both characterizations, strategy-proofness (and peaks-onliness) can be replaced by uncompromisingness. We next discuss two extensions of these results.
Remark 2
(Results for symmetric single-peaked preferences) On the subdomain of symmetric single-peaked preferences, peaks-onliness is vacuously satisfied. Then, Example 3 illustrates that Theorem 1 does not hold on the subdomain of symmetric single-peaked preferences since correspondence \(F^*\) satisfies strategy-proofness but neither satisfies uncompromisingness, nor is it a generalized median correspondence. In contrast, Theorem 2 does hold on the subdomain of symmetric single-peaked preferences ( Protopapas 2018, Theorem 5). \(\square \)
Remark 3
(Results with anonymity) Moulin (1980, Proposition 3) also characterized the set of choice functions satisfying strategy-proofness, peaks-onliness, and anonymityFootnote 5 (introduced as strategy-proof and anonymous voting schemes). The extension to our model is as follows: let vectors \(a,b\in A^{n+1}\) be such that \(a\equiv (a_1,\ldots ,a_{n+1})\) and \(b\equiv (b_1,\ldots ,b_{n+1})\), with \(a\le b\), \(a_1\le \cdots \le a_{n+1}\), and \(b_1\le \cdots \le b_{n+1}\). We define the median correspondence associated with vectors a and b for each \(R\in {\mathcal {R}}^N\) by \(F_M^{a,b}(R)\equiv [\mathrm {med}{(p,a)},\mathrm {med}{(p,b)}].\)
Based on Theorem 1 and Moulin (1980, Proposition 3) (anonymity also applies to the functions  and \({\bar{F}}\)), we obtain the following characterization: a choice correspondence satisfies strategy-proofness, peaks-onliness, and anonymity if and only if it is a median correspondence (Protopapas 2018, Theorem 2). By adding voter sovereignty and using Theorem 2, an “efficient version” of this characterization where \(a_1=b_1=0\) and \(a_{n+1}=b_{n+1}=1\) is obtained (Protopapas 2018, Theorem 4). Finally, on the domain of symmetric single-peaked preferences, the class of efficient median correspondences is characterized by strategy-proofness (uncompromisingness), voter-sovereignty, and anonymity (Protopapas 2018, Theorem 6). \(\square \)
and \({\bar{F}}\)), we obtain the following characterization: a choice correspondence satisfies strategy-proofness, peaks-onliness, and anonymity if and only if it is a median correspondence (Protopapas 2018, Theorem 2). By adding voter sovereignty and using Theorem 2, an “efficient version” of this characterization where \(a_1=b_1=0\) and \(a_{n+1}=b_{n+1}=1\) is obtained (Protopapas 2018, Theorem 4). Finally, on the domain of symmetric single-peaked preferences, the class of efficient median correspondences is characterized by strategy-proofness (uncompromisingness), voter-sovereignty, and anonymity (Protopapas 2018, Theorem 6). \(\square \)
4.1 Related literature
When choosing a single alternative from a finite set (of alternatives), strategy-proofness and voter-sovereignty characterize, on the domain of strict preferences, a class of functions similar to the class of efficient generalized median rules (Barberà et al. 1993). Moreover, the admissible preferences of all agents being top-connectedFootnote 6 characterizes the maximal domain in which (i) every strategy-proof and unanimous function is a generalized median rule, and (ii) every generalized median rule is strategy-proof (Achuthankutty and Roy 2018).
When departing from the setting where agents have single-peaked preferences and only one alternative is chosen, a few more results should be mentioned. First, in the case of probabilistic functions,Footnote 7 where the agents’ single-peaked preferences are ordinarily extended over probability distributions via first-order stochastic dominance, similar results to Moulin’s results (1980) were achieved (Ehlers et al. 2002). Next, if agents have single-dipped preferences,Footnote 8strategy-proofness and unanimity characterize the class of collections of 0-decisive sets with a tie-breakerFootnote 9 (Manjunath 2014). Klaus and Storcken (2002) consider location problems in Euclidean space when agents have separable quadratic single-peaked preferences but in contrast to Border and Jordan (1983), they consider choice correspondences and characterize the class of “coordinatewise median voting schemes” as an extension of the median without using additional and fixed coordinates (so-called phantom voters in Border and Jordan 1983). Klaus and Storcken (2002) also use the best-worst extension of preferences to sets we use here. In a predecessor paper, Klaus and Protopapas (2020), for the same model as in this paper, considered so-called solidarity properties and show that efficiency and replacement-dominanceFootnote 10 characterize the class of target point functions while efficiency and population-monotonicityFootnote 11 characterize the larger class of target set correspondences.
Finally, we would like to discuss two results when preferences are single-peaked and two alternatives can be chosen, with the agents comparing different pairs of alternatives using the max-extension, i.e., when comparing two pairs of alternatives \(X=\{x_1,x_2\}\) and \(Y=\{y_1,y_2\}\), an agent first locates in each pair the alternative he ranks higher, say \(x^*\) and \(y^*\). If he prefers \(x^*\) to \(y^*\), then he also prefers X to Y. If he is indifferent between \(x^*\) and \(y^*\), then he is also indifferent between X and Y.
(Heo 2013, Theorem 1) Strategy-proofness, continuity, anonymity, and users-onlyFootnote 12 characterize the class of double median functions.Footnote 13
(Miyagawa 2001, Theorem 1) If \(|N|> 3\), then efficiency and replacement-dominance characterize the class of rules comprised of the left-peaks function and the right-peaks function.Footnote 14
The class of generalized median correspondences and the class of median correspondences discussed in Remark 3 share the property of decomposability into two functions with the double median functions characterized in Heo (2013) and the left-peaks (right-peaks) functions characterized in Miyagawa (2001). However, there are some notable differences between our and their results.
First, by using the max-extension of preferences in our setting, as is the case in the two aforementioned papers, the only efficient correspondence would be the one always choosing the interval of the peaks, that is, for all \(R\in {\mathcal {R}}\),  . This follows from the fact that agents only care about their best alternative in a set and that in our setting we do not a priori limit the number of alternatives that may be chosen at a given profile.
. This follows from the fact that agents only care about their best alternative in a set and that in our setting we do not a priori limit the number of alternatives that may be chosen at a given profile.
Second, the class of double median functions of Heo (2013) seems to be equivalent to the class of median correspondences (see Remark 3). Specifically, the pair of alternatives \((x_1, x_2)\) chosen by a double median function are essentially the minimum and maximum alternatives of the interval chosen by a median correspondence. However, Heo’s characterization result makes use of users-only, a property that partitions each coalition of agents into two sub-coalitions; one preferring \(x_1\) over \(x_2\), and everyone else, with only the first partition (second partition) influencing the choice of alternative \(x_1\) (\(x_2\)). In our setting, for each \(F^{a,b}\in {\mathcal {F}}_M\), the choice of both vectors a and b depends on the preferences of all agents.
Third, although the left-peaks function of Miyagawa (2001) seems to be a special case of a median correspondence (see Remark 3), this is not the case; the left-peaks function always chooses the two distinct left-most peaks, and moreover, Miyagawa’s setting requires that at least two distinct peaks exist in each profile. In our setting, the median correspondence that looks “similar” to the left-peaks function is \(F^{a,b}\in {\mathcal {F}}\) where \(a=(0,\ldots , 0)\) and \(b=(0,\ldots ,0,1)\). Although this correspondence seems to choose the two left-most peaks, when two or more agents share the minimum peak, it only chooses the minimum peak. Furthermore, in Klaus and Protopapas (2020) the same properties as in Miyagawa (2001) (namely, efficiency and replacement-dominance) are considered, for (almost) the same setting as in this paper. There, it is shown that each correspondence satisfying said properties is essentially a function, reconfirming a characterization of Vohra (1999) for target-point functions.Footnote 15
Notes
Although technically continuity is not weaker than peaks-onliness, loosely speaking, it imposes fewer restrictions on the result.
For a survey of criteria and methods for ranking subsets of a set of outcomes under complete uncertainty we refer to Barberà et al. (2004, Section 3).
No group of agents can deviate such that all members of the group are weakly better off and at least one member of the group is strictly better off.
Note that this result only holds on the full domain of single-peaked preferences that we consider here but not on the subdomain of symmetric single-peaked preferences. We explain this aspect of our result after discussing the logical independence of characterizing properties and in Remark 2.
The names of the agents do not affect the chosen alternative.
For every agent and every pair of “neighboring” alternatives (a, b), there exist admissible preferences such that a is the most favorite alternative and b is the second most favorite alternative.
Given the agents’ preferences, a probability distribution over all alternatives is chosen.
An agent’s welfare is strictly decreasing up to his “dip” (his least favorite alternative), and is strictly increasing thereafter.
Each such function chooses either the minimum or the maximum alternative. Loosely speaking, if all agents are indifferent between the two alternatives the choice depends on the preference profile (over all other alternatives). Otherwise, the choice depends on the number of agents preferring the minimum over the maximum alternative, their identities, and their preferences.
Replacement-dominance: if the preferences of an agent change, then the other agents, whose preferences remained unchanged, should all be made at least as well off as they were initially, or they should all be made at most as well off.
Population-monotonicity: if additional agents join a population, then the agents who were initially present should all be made at least as well off as they were initially, or they should all be made at most as well off.
For each pair of chosen alternatives (a, b), the choice of a depends only on agents preferring a over b.
A double median function can be decomposed into two median rules, where for each preference profile each one selects one alternative.
The left (right) peaks function chooses the two unique left-most (right-most) peaks.
Each target point function is determined by its target point: if the target point is efficient, it is chosen; if it is not efficient, the closest efficient point is chosen.
This is done to distinguish different types of profiles in Step 3 of the proof.
References
Achuthankutty G, Roy S (2018) On single-peaked domains and min-max rules. Soc Choice Welf 51:753–772
Arribillaga RP, Massó J (2016) Comparing generalized median voter schemes according to their manipulability. Theor Econ 11:547–586
Barberà S (2011) Handbook of Social Choice and Welfare, chapter 25 “Strategyproof social choice”. Elsevier, Amsterdam
Barberà S, Bossert W, Pattanaik PK (2004) Handbook of Utility Theory, chapter 17 “Ranking sets of objects”. Springer, Boston
Barberà S, Coelho D (2000) On the rule of \(k\) names. Games Econ Behav 70:44–61
Barberà S, Gül F, Stacchetti E (1993) Generalized median voter schemes and committees. J Econ Theory 61:262–289
Barberà S, Jackson M (1994) A characterization of strategy-proof social choice functions for economies with pure public goods. Soc Choice Welf 11:241–252
Border K, Jordan J (1983) Straightforward elections, unanimity and phantom voters. Rev Econ Stud 50:153–170
Bossert W, Pattanaik P, Xu Y (2000) Choice under complete uncertainty: axiomatic chacterizations of some decision rules. Econ Theor 16:295–312
Ching S (1997) Strategy-proofness and “median-voters”. Soc Choice Welf 26:473–490
Duggan J, Schwartz T (2000) Strategic manipulability without resoluteness or shared beliefs: Gibbard-Satterthwaite generalized. Soc Choice Welf 17:85–93
Ehlers L, Peters H, Storcken T (2002) Strategy-proof probabilistic decision schemes for one-dimensional single-peaked preferences. J Econ Theory 105:408–434
Fishburn PC (1977) Condorcet social choice functions. SIAM J Appl Math 33:469–489
Gibbard A (1973) Manipulation of voting schemes: a general result. Econometrica 41:587–601
Heo EJ (2013) Strategy-proof rules for two public goods: double median rules. Soc Choice Welf 41:895–922
Klaus B, Protopapas P (2020) Solidarity for public goods under single-peaked preferences: characterizing target set correspondences. Soc Choice Welf (in press). https://doi.org/10.1007/s00355-020-01245-3
Klaus B, Storcken T (2002) Choice correspondences for public goods. Soc Choice Welf 19:127–154
Manjunath V (2014) Efficient and strategy-proof social choice when preferences are single-dipped. Int J Game Theory 43:579–597
Miyagawa E (2001) Locating libriaries on a street. Soc Choice Welf 18:527–541
Moulin H (1980) On strategy-proofness and single peakedness. Public Choice 35:437–455
Nuñez M, Xefteris D (2017) Implementation via approval mechanisms. J Econ Theory 17:169–181
Peterson M (2009) An introduction to decision theory. Cambridge University Press, Cambridge
Protopapas P (2018) On strategy-proofness and single-peakedness: median-voting over intervals. MPRA Working Paper 83939. https://mpra.ub.uni-muenchen.de/83939/1/MPRA_paper_83939.pdf
Satterthwaite M (1975) Strategy-proofness and Arrow’s condition: existence and correspondence theorems for voting procedures and social welfare functions. J Econ Theory 10:187–217
Vohra R (1999) The replacement principle and tree structured preferences. Econ Lett 63:175–180
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
We gratefully acknowledge financial support from the Swiss National Science Foundation (SNFS) for project \(100018\_156201\). This work has also been partly supported by COST Action IC1205 on Computational Social Choice. We would like to thank Sidartha Gordon, Flip Klijn, Jordi Massó, William Thomson, and two anonymous referees and an associate editor for their very valuable feedback.
Appendices
Appendix
Proof of Theorem 1
Before starting the proof of Theorem 1 we show that following an agent’s preference deviation, there are restrictions on the chosen set.
Lemma 1
For each \(F\in {\mathcal {F}}\) satisfying strategy-proofness and peaks-onliness, each \(i\in N\), and each \(R,R^{\prime }\in {\mathcal {R}}^N\) such that \(R_{-i}=R^{\prime }_{-i}\), the following hold.
- (a):
-
If \(p_i<{\bar{F}}(R)\), then \({\bar{F}}(R)\le {\bar{F}}(R^{\prime })\), and if in addition
 , then
, then  .
. - (b):
-
If
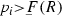 , then
, then  , and if in addition \(p_i>{\bar{F}}(R)\), then \({\bar{F}}(R)\ge {\bar{F}}(R^{\prime })\).
, and if in addition \(p_i>{\bar{F}}(R)\), then \({\bar{F}}(R)\ge {\bar{F}}(R^{\prime })\).
Proof
(a) Let \(F\in {\mathcal {F}}\) satisfy strategy-proofness and peaks-onliness. Let \(R,R^{\prime }\in {\mathcal {R}}^N\) and \(i\in N\) be such that \(R_{-i}=R^{\prime }_{-i}\) and \(p_i<{\bar{F}}(R)\). By peaks-onliness it is without loss of generality to assume that \(R_i\) is such that \(0\mathbin {P}_i {\bar{F}}(R)\). Hence, \(w_{R_i}(F(R))={\bar{F}}(R)\). Then, by strategy-proofness, \({\bar{F}}(R)\mathbin {R_i}w_{R_i}(F(R^{\prime }))\). Hence, since for all \(y\in [0,{\bar{F}}(R))\), \(y\mathbin {P_i}{\bar{F}}(R)\), we have \(w_{R_i}(F(R^{\prime }))\ge {\bar{F}}(R)\) and \({\bar{F}}(R^{\prime })\ge {\bar{F}}(R)\).
If in addition  , then by peaks-onliness it is without loss of generality to additionally assume that \(R_i\) is such that
, then by peaks-onliness it is without loss of generality to additionally assume that \(R_i\) is such that  . Hence,
. Hence,  . Then, by strategy-proofness,
. Then, by strategy-proofness,  . Hence, since for all
. Hence, since for all  , we have
, we have  and
and  .
.
The proof of statement (b) is based on symmetric arguments. \(\square \)
Proof of Theorem 1
\({\varvec{(i)\Rightarrow (ii)}}\) Let \(F\in {\mathcal {F}}\) satisfy strategy-proofness and peaks-onliness. We show that F satisfies uncompromisingness. Let \(R,R^{\prime }\in {\mathcal {R}}^N\) and \(i\in N\) be such that \(R_{-i}=R^{\prime }_{-i}\). Since by peaks-onliness \(p_i=p^{\prime }_i\) implies \(F(R)=F(R^{\prime })\), let \(p_i<p^{\prime }_i\). There are four (partially overlapping) cases.
Case 1.1  . By Lemma 1(a),
. By Lemma 1(a),  . Moreover, assuming
. Moreover, assuming  results in a contradiction since then
results in a contradiction since then  and by Lemma 1(a),
and by Lemma 1(a),  . Therefore,
. Therefore,  .
.
Case 1.2  . By Lemma 1(b),
. By Lemma 1(b),  . Hence,
. Hence,  and by Lemma 1(b),
and by Lemma 1(b),  . Therefore,
. Therefore,  .
.
Case 2.1 \((p_i<p^{\prime }_i\le {\bar{F}}(R))\). By Lemma 1(a), \({\bar{F}}(R)\le {\bar{F}}(R^{\prime })\). Moreover, assuming \({\bar{F}}(R)<{\bar{F}}(R^{\prime })\) results in a contradiction since then \(p^{\prime }_i<{\bar{F}}(R^{\prime })\) and by Lemma 1(a), \({\bar{F}}(R^{\prime })\le {\bar{F}}(R)\). Therefore, \({\bar{F}}(R)={\bar{F}}(R^{\prime })\).
Case 2.2 \(({\bar{F}}(R)<p_i<p^{\prime }_i)\). By Lemma 1(b), \({\bar{F}}(R^{\prime })\le {\bar{F}}(R)\). Hence, \({\bar{F}}(R^{\prime })<p^{\prime }_i\) and by Lemma 1(b), \({\bar{F}}(R)\le {\bar{F}}(R^{\prime })\). Therefore, \({\bar{F}}(R)={\bar{F}}(R^{\prime })\). \(\square \)
Before continuing the proof of Theorem 1 we prove the following result.
Lemma 2
If \(F\in {\mathcal {F}}\) satisfies uncompromisingness, then it satisfies peak-monotonicity, i.e., for each \(i\in N\) and each \(R,R^{\prime }\in {\mathcal {R}}^N\) such that \(R^{\prime }_{-i}=R_{-i}\), if \(p_i\le p^{\prime }_i\), then  and \({\bar{F}}(R)\le {\bar{F}}(R^{\prime })\).
and \({\bar{F}}(R)\le {\bar{F}}(R^{\prime })\).
Note that peak-monotonicity implies peaks-onliness.
Proof
Let \(F\in {\mathcal {F}}\) satisfy uncompromisingness. Let \(i\in N\) and \(R,R^{\prime }\in {\mathcal {R}}^N\) be such that \(R^{\prime }_{-i}=R_{-i}\) and \(p_i\le p^{\prime }_i\). There are three cases.
Case 1  . We first consider
. We first consider  . If
. If  , then by uncompromisingness,
, then by uncompromisingness,  . Let \(R_i^1\in {\mathcal {R}}\) be such that
. Let \(R_i^1\in {\mathcal {R}}\) be such that  . Then, by uncompromisingness,
. Then, by uncompromisingness,  . If
. If  , then assuming
, then assuming  leads to a contradiction as follows. Beginning from \(R^{\prime }\), change i’s preference to \(R_i^1\). Since
leads to a contradiction as follows. Beginning from \(R^{\prime }\), change i’s preference to \(R_i^1\). Since  , by uncompromisingness,
, by uncompromisingness,  . However, since \(R^{\prime }_{-i}=R_{-i}\), we also have
. However, since \(R^{\prime }_{-i}=R_{-i}\), we also have  , contradicting
, contradicting  . Therefore, we have
. Therefore, we have  .
.
Next, we consider \({\bar{F}}(R)\). Note that \(p_i< {\bar{F}}(R)\). Then, the arguments to show that \({\bar{F}}(R^{\prime })\ge {\bar{F}}(R)\) are the same as above with \({\bar{F}}\) in the role of  .
.
Case 2  . First, \({\bar{F}}(R^{\prime })\ge {\bar{F}}(R)\) follows by Case 1 (the argument there was based on \(p_i< {\bar{F}}(R))\). Next, if
. First, \({\bar{F}}(R^{\prime })\ge {\bar{F}}(R)\) follows by Case 1 (the argument there was based on \(p_i< {\bar{F}}(R))\). Next, if  , then
, then  and uncompromisingness imply
and uncompromisingness imply  , a contradiction. Hence,
, a contradiction. Hence,  .
.
Case 3 \(({\bar{F}}(R)\le p_i)\). If \({\bar{F}}(R^{\prime })<{\bar{F}}(R)\), then \({\bar{F}}(R^{\prime })<{\bar{F}}(R)\le p_i\le p^{\prime }_i\) and uncompromisingness imply \({\bar{F}}(R^{\prime })={\bar{F}}(R)\), a contradiction. Hence, \({\bar{F}}(R)\le {\bar{F}}(R^{\prime })\).
Next, we consider  . Note that
. Note that  . Then, the arguments to show that
. Then, the arguments to show that  are the same as above with
are the same as above with  in the role of \({\bar{F}}\). \(\square \)
in the role of \({\bar{F}}\). \(\square \)
Proof of Theorem 1
\({\varvec{(ii)\Rightarrow (iii)}}\) Let \(F\in {\mathcal {F}}\) satisfy uncompromisingness. By Lemma 2, F satisfies peak-monotonicity and hence peaks-onliness. For each \(i\in N\), let \(R_i^{\min },R_i^{\max }\in {\mathcal {R}}\) be such that \(p_i^{\min }=0\) and \(p_i^{\max }=1\). We proceed in three steps.
Step 1. Let \(i\in N\), \(R\in {\mathcal {R}}^N\), and consider profiles \(R^{\min }:=(R_{-i},R_i^{\min })\) and \(R^{\max }:=(R_{-i},R_i^{\max })\). Since \(R_{-i}=R_{-i}^{\min }=R_{-i}^{\max }\) and \(p_i^{\min }\le p_i\le p_i^{\max }\), by Lemma 2,

We show that

Case 1  . Then,
. Then,  . Since
. Since  , uncompromisingness implies
, uncompromisingness implies  . Therefore,
. Therefore,  .
.
Case 2  . Then,
. Then,  . Since
. Since  , uncompromisingness implies
, uncompromisingness implies  . Therefore,
. Therefore,  .
.
Case 3  . Then,
. Then,  . Assuming
. Assuming  and thus
and thus  results in a contradiction as follows. Since
results in a contradiction as follows. Since  , uncompromisingness implies
, uncompromisingness implies  . Similarly, assuming
. Similarly, assuming  and thus
and thus  results in a contradiction as follows. Since
results in a contradiction as follows. Since  , uncompromisingness implies
, uncompromisingness implies  . Therefore,
. Therefore,  .
.
The arguments to show that
are the same as above with \({\bar{F}}\) in the role of  .
.
Step 2. We construct two vectors \(\alpha \) and \(\beta \). We will use a different letter (U instead of R) to label the following profiles.Footnote 16 For each \(M\subseteq N\), let \(U^M\in {\mathcal {R}}^N\) be such that all agents in M announce 0 as their peak and all other agents announce 1 as their peak, i.e.,
Next, let vectors \(\alpha =(\alpha _M)_{M\subseteq N}\) and \(\beta =(\beta _M)_{M\subseteq N}\) be such that

Let \(L,M\subseteq N\) be such that \(L\subsetneq M\). Then, for each \(i\in M{\setminus } L\), \(U_i^L\ne U_i^M\) (because \(u_i^L=1>0=u_i^M\)), and for each \(i\not \in M{\setminus } L\), \(U_i^L=U_i^M\). Beginning from profile \(U^L\), (sequentially) change the preferences of agents \(i\in M{\setminus } L\) to \(U_i^M\). Since for each \(i\in M{\setminus } L\), \(u_i^L>u_i^M\), by (sequentially) applying peak-monotonicity, we conclude that \(\alpha _L\ge \alpha _M\) and \(\beta _L\ge \beta _M\).
Step 3. We show that F is a generalized median correspondence associated with vectors \(\alpha \) and \(\beta \) that were constructed in Step 2.
Let \(R\in {\mathcal {R}}^N\). Without loss of generality, index the agents in N such that \(p_{1}\le p_{2}\le \cdots \le p_{n}\). Recall vectors \(\alpha ,\beta \) and profiles \(U^M\) (\(M\subseteq N\)) defined in Step 2. Let vectors \({\tilde{\alpha }}_p,{\tilde{\beta }}_p\in A^{n+1}\) be such that
Since the coordinates of \({\tilde{\alpha }}_p\) and \({\tilde{\beta }}_p\) are such that \(0\le \alpha _N\le \cdots \le \alpha _{\emptyset }\le 1\) and \(0\le \beta _N\le \cdots \le \beta _{\emptyset }\le 1\), and \(u^{\emptyset }=(1,\ldots ,1)\), we have  and \({\bar{F}}(U^{\emptyset }) =\mathrm {med}{(u^{\emptyset },{\tilde{\beta }}_p)} =\beta _{\emptyset }\). Moreover, for each \(i\in \{1,\ldots ,n\}\),
and \({\bar{F}}(U^{\emptyset }) =\mathrm {med}{(u^{\emptyset },{\tilde{\beta }}_p)} =\beta _{\emptyset }\). Moreover, for each \(i\in \{1,\ldots ,n\}\),
implies

Next, for each \(i\in \{1,\ldots , n\}\), let \(R^i\in {\mathcal {R}}^N\) be such that
Note that at profiles \(R^i\) the order of agents’ peaks does not change, i.e., for each \(i\in \{1,\ldots , n\}\), we have \(p^{i}_{1}\le p^{i}_{2}\le \cdots \le p^{i}_{n}\). Hence, for each \(i\in \{1,\ldots , n\}\), \({\tilde{\alpha }}_{p^{i}}={\tilde{\alpha }}_p\) and \({\tilde{\beta }}_{p^{i}}={\tilde{\beta }}_p\); in the sequel we will therefore use \({\tilde{\alpha }}_p\) and \({\tilde{\beta }}_p\) instead of \({\tilde{\alpha }}_{p^{i}}\) and \({\tilde{\beta }}_{p^{i}}\).
We show that \(F(R)=F_G^{\alpha ,\beta }(R)=[\mathrm {med}{(p,{\tilde{\alpha }}_p)},\mathrm {med}{(p,{\tilde{\beta }}_p)}]\) by induction.
Induction basis. We show that \(F(R^{1})=F_G^{\alpha ,\beta }(R^{1})\).
Consider profile \(R^{1}=(R_{1},R_{2}^{\max },\ldots ,R_{n}^{\max })\). Recall profiles \(U^{\{1\}}=(R_{1}^{\min },R_{2}^{\max }, \ldots ,R_{n}^{\max })\) and \(U^{\emptyset }=(R_{1}^{\max },\ldots ,R_{n}^{\max })\). Hence, \(U^{\{1\}}=(R^{1}_{-1},R_{1}^{\min })\) and \(U^{\emptyset }=(R^{1}_{-1},R_{1}^{\max })\). By Step 1,

Hence,

Moreover, since
we have that

Therefore, \(F(R^{1})=F_G^{\alpha ,\beta }(R^{1})\).
Induction hypothesis. For \(i\in \{2,\dots ,n\}\), \(F(R^{i-1})=F_G^{\alpha ,\beta }(R^{i-1})\).
Induction step. We show that \(F(R^{i})=F_G^{\alpha ,\beta }(R^{i})\). More specifically, we show  . The proof that \({\bar{F}}(R^{i})={\bar{F}}_G^{\alpha ,\beta }(R^{i})\) is obtained by using the same arguments with \({\bar{F}}\) in the role of
. The proof that \({\bar{F}}(R^{i})={\bar{F}}_G^{\alpha ,\beta }(R^{i})\) is obtained by using the same arguments with \({\bar{F}}\) in the role of  and \({\tilde{\beta }}_{p}\) in the role of \({\tilde{\alpha }}_{p}\). Recall that
and \({\tilde{\beta }}_{p}\) in the role of \({\tilde{\alpha }}_{p}\). Recall that
There are three cases.
Case 1  . Since \(R^{i-1}_{-i}=R^{i}_{-i}\) and
. Since \(R^{i-1}_{-i}=R^{i}_{-i}\) and  , by uncompromisingness,
, by uncompromisingness,  . Thus, \(R^{i-1}_{-i}=R^{i}_{-i}\) and \(\mathrm {med}{(p^{i-1},{\tilde{\alpha }}_{p})}<p_{i}=p_{i}^{i}\le p_i^{i-1}=1\) implies \(\mathrm {med}{(p^{i-1},{\tilde{\alpha }}_{p})}=\mathrm {med}{(p^{i},{\tilde{\alpha }}_{p})}\). Hence,
. Thus, \(R^{i-1}_{-i}=R^{i}_{-i}\) and \(\mathrm {med}{(p^{i-1},{\tilde{\alpha }}_{p})}<p_{i}=p_{i}^{i}\le p_i^{i-1}=1\) implies \(\mathrm {med}{(p^{i-1},{\tilde{\alpha }}_{p})}=\mathrm {med}{(p^{i},{\tilde{\alpha }}_{p})}\). Hence,  .
.
Case 2  . Recall that \(U^{\{1,\ldots ,i\}}=(R_{1}^{\min },\ldots , R_i^{\min },R_{i+1}^{{\max }},\ldots ,R_{n}^{\max })\). Since \(p_{1}\le \cdots \le p_{n}\) and
. Recall that \(U^{\{1,\ldots ,i\}}=(R_{1}^{\min },\ldots , R_i^{\min },R_{i+1}^{{\max }},\ldots ,R_{n}^{\max })\). Since \(p_{1}\le \cdots \le p_{n}\) and  , for each \(j\in \{1,\ldots ,i\}\),
, for each \(j\in \{1,\ldots ,i\}\),  . Hence, by uncompromisingness,
. Hence, by uncompromisingness,  . Beginning from profile \(R^i_{}\), (sequentially) change the preferences of agents \(j\in \{1,\ldots ,i\}\) to \(R_j^{\min }\). Then, by (sequentially applying) uncompromisingness,
. Beginning from profile \(R^i_{}\), (sequentially) change the preferences of agents \(j\in \{1,\ldots ,i\}\) to \(R_j^{\min }\). Then, by (sequentially applying) uncompromisingness,  . We have shown at the beginning of Step 3 that
. We have shown at the beginning of Step 3 that  . Thus,
. Thus,  . Then, \(p_1^i\le \cdots \le p_i^i<\alpha _{\{1,\ldots ,i\}}\) and \(p_{i+1}^i=\cdots = p_n^i=1\ge \alpha _{\{1,\ldots ,i\}}\). This implies \(\mathrm {med}{(p^{i},{\tilde{\alpha }}_{p})}=\alpha _{\{1,\dots ,i\}}\). Hence,
. Then, \(p_1^i\le \cdots \le p_i^i<\alpha _{\{1,\ldots ,i\}}\) and \(p_{i+1}^i=\cdots = p_n^i=1\ge \alpha _{\{1,\ldots ,i\}}\). This implies \(\mathrm {med}{(p^{i},{\tilde{\alpha }}_{p})}=\alpha _{\{1,\dots ,i\}}\). Hence,  .
.
Case 3  . Since \(R^{i-1}_{-i}=R^{i}_{-i}\) and \(p_i=p_i^{i}\le p_i^{i-1}=p_i^{\max }=1\), by peak-monotonicity,
. Since \(R^{i-1}_{-i}=R^{i}_{-i}\) and \(p_i=p_i^{i}\le p_i^{i-1}=p_i^{\max }=1\), by peak-monotonicity,  . Thus, \(p_{1}\le \dots \le p_{n}\) and
. Thus, \(p_{1}\le \dots \le p_{n}\) and  imply
imply  . There are two sub-cases.
. There are two sub-cases.
Case 3.1  . Thus,
. Thus,  . Hence,
. Hence,  implies \(\mathrm {med}{(p^{i-1},{\tilde{\alpha }}_{p})}=p_{i}=p_i^{i}\le p_i^{i-1}=1\). This implies \(\mathrm {med}{(p^{i},{\tilde{\alpha }}_{p})}=\mathrm {med}{(p^{i-1},{\tilde{\alpha }}_{p})}\). Hence,
implies \(\mathrm {med}{(p^{i-1},{\tilde{\alpha }}_{p})}=p_{i}=p_i^{i}\le p_i^{i-1}=1\). This implies \(\mathrm {med}{(p^{i},{\tilde{\alpha }}_{p})}=\mathrm {med}{(p^{i-1},{\tilde{\alpha }}_{p})}\). Hence,  .
.
Case 3.2  . Recall that \(U^{\{1,\ldots ,i-1\}}=(R_{1}^{\min },\ldots , R_{i-1}^{\min },R_{i}^{{\max }},\ldots ,R_{n}^{\max })\) with
. Recall that \(U^{\{1,\ldots ,i-1\}}=(R_{1}^{\min },\ldots , R_{i-1}^{\min },R_{i}^{{\max }},\ldots ,R_{n}^{\max })\) with  . By the same arguments as at the beginning of Case 2,
. By the same arguments as at the beginning of Case 2,  implies that
implies that  . Since
. Since  , it follows that \(p_i\le \alpha _{\{1,\ldots ,i-1\}}\).
, it follows that \(p_i\le \alpha _{\{1,\ldots ,i-1\}}\).
Recall that \(U^{\{1\ldots ,i\}}=(R_{1}^{\min },\ldots , R_{i}^{\min },R_{i+1}^{{\max }},\ldots ,R_{n}^{\max })\) with  . Beginning from profile \(U^{\{1,\ldots ,i\}}\), (sequentially) change the preferences of all agents \(j\in \{1,\ldots ,i\}\) to \(R_j\) and obtain profile \(R^i=(R_{1},\ldots ,R_i,R_{i+1}^{\max },\ldots ,R_{n}^{\max })\). Since for each \(j\in \{1,\ldots ,i\}\), \(p^i_j\ge p_j^{\min }=0\), by (sequentially) applying peak-monotonicity, we obtain
. Beginning from profile \(U^{\{1,\ldots ,i\}}\), (sequentially) change the preferences of all agents \(j\in \{1,\ldots ,i\}\) to \(R_j\) and obtain profile \(R^i=(R_{1},\ldots ,R_i,R_{i+1}^{\max },\ldots ,R_{n}^{\max })\). Since for each \(j\in \{1,\ldots ,i\}\), \(p^i_j\ge p_j^{\min }=0\), by (sequentially) applying peak-monotonicity, we obtain  . Hence, \(p_i\ge \alpha _{\{1,\ldots ,i\}}\) and it follows that \(\alpha _{\{1,\ldots ,i\}}\le p_i\le \alpha _{\{1,\ldots ,i-1\}}\).
. Hence, \(p_i\ge \alpha _{\{1,\ldots ,i\}}\) and it follows that \(\alpha _{\{1,\ldots ,i\}}\le p_i\le \alpha _{\{1,\ldots ,i-1\}}\).
Thus, since \(\alpha _N\le \dots \le \alpha _{\emptyset }\), vector \({\tilde{\alpha }}_{p}\) contains at least \(n+1-i\) coordinates not larger than \(p_i\) (i.e., coordinates \(\alpha _{\{1,\ldots ,i\}}, \dots ,\alpha _N\)) and at least i coordinates not smaller than \(p_i\) (i.e., coordinates \(\alpha _{\emptyset },\dots ,\alpha _{\{1,\ldots ,i-1\}}\)). In addition, since \(p_{1}\le \cdots \le p_{n}\), at least i agents announce peaks not larger than \(p_i\) (i.e., agents \(1,\dots , i\)) and \(n-i+1\) agents announce peaks not smaller than \(p_i\) (i.e., agents \(i,\ldots ,n\)). This implies \(\mathrm {med}{(p^{i},{\tilde{\alpha }}_{p})}=p_i\). Hence,  . \(\square \)
. \(\square \)
Proof of Theorem 1
\({\varvec{(iii)}\mathbb {\Rightarrow } \varvec{(i)}}\) Let \(F_G^{\alpha ,\beta }\in {\mathcal {F}}_G\). By definition, \(F_G^{\alpha ,\beta }\) satisfies peaks-onliness. By Moulin (1980, Proposition 3),  and \({\bar{F}}_G^{\alpha ,\beta }\) are strategy-proof and by Border and Jordan (1983, Proposition 1),
and \({\bar{F}}_G^{\alpha ,\beta }\) are strategy-proof and by Border and Jordan (1983, Proposition 1),  and \({\bar{F}}_G^{\alpha ,\beta }\) satisfy uncompromisingness. Then, by Lemma 2,
and \({\bar{F}}_G^{\alpha ,\beta }\) satisfy uncompromisingness. Then, by Lemma 2,  and \({\bar{F}}_G^{\alpha ,\beta }\) satisfy peak-monotonicity. To show that \(F_G^{\alpha ,\beta }\) satisfies strategy-proofness let \(i\in N\), \(R,R^{\prime }\in {\mathcal {R}}^N\) such that \(R_{-i}=R^{\prime }_{-i}\).
and \({\bar{F}}_G^{\alpha ,\beta }\) satisfy peak-monotonicity. To show that \(F_G^{\alpha ,\beta }\) satisfies strategy-proofness let \(i\in N\), \(R,R^{\prime }\in {\mathcal {R}}^N\) such that \(R_{-i}=R^{\prime }_{-i}\).
Case 1  . First, if \(p_i>p^{\prime }_i\), by uncompromisingness,
. First, if \(p_i>p^{\prime }_i\), by uncompromisingness,  and \({\bar{F}}_G^{\alpha ,\beta }(R)={\bar{F}}_G^{\alpha ,\beta }(R^{\prime })\). Hence, \(F_G^{\alpha ,\beta }(R)=F_G^{\alpha ,\beta }(R^{\prime })\).
and \({\bar{F}}_G^{\alpha ,\beta }(R)={\bar{F}}_G^{\alpha ,\beta }(R^{\prime })\). Hence, \(F_G^{\alpha ,\beta }(R)=F_G^{\alpha ,\beta }(R^{\prime })\).
Second, if \(p_i\le p^{\prime }_i\), by peak-monotonicity,  and \({\bar{F}}_G^{\alpha ,\beta }(R)\le {\bar{F}}_G^{\alpha ,\beta }(R^{\prime })\), which implies \(F_G^{\alpha ,\beta }(R)\mathbin {R_i}F_G^{\alpha ,\beta }(R^{\prime })\).
and \({\bar{F}}_G^{\alpha ,\beta }(R)\le {\bar{F}}_G^{\alpha ,\beta }(R^{\prime })\), which implies \(F_G^{\alpha ,\beta }(R)\mathbin {R_i}F_G^{\alpha ,\beta }(R^{\prime })\).
Case 2 \((p_i\ge {\bar{F}}_G^{\alpha ,\beta }(R))\). Symmetric to Case 1.
Case 3  . Then, \(b_{R_i}(F_G^{\alpha ,\beta }(R)) =p_i\mathbin {R_i}b_{R_i}(F_G^{\alpha ,\beta }(R^{\prime }))\). Next,
. Then, \(b_{R_i}(F_G^{\alpha ,\beta }(R)) =p_i\mathbin {R_i}b_{R_i}(F_G^{\alpha ,\beta }(R^{\prime }))\). Next,  . By strategy-proofness of
. By strategy-proofness of  and \({\bar{F}}^{\alpha ,\beta }_{G}\),
and \({\bar{F}}^{\alpha ,\beta }_{G}\),  and \({\bar{F}}_G^{\alpha ,\beta }(R)\mathbin {R_i}{\bar{F}}_G^{\alpha ,\beta }(R^{\prime })\), which implies \(w_{R_i}(F_G^{\alpha ,\beta }(R)) \mathbin {R_i}w_{R_i}(F_G^{\alpha ,\beta }(R^{\prime }))\). Hence, \(F_G^{\alpha ,\beta }(R)\mathbin {R_i}F_G^{\alpha ,\beta }(R^{\prime })\).\(\square \)
and \({\bar{F}}_G^{\alpha ,\beta }(R)\mathbin {R_i}{\bar{F}}_G^{\alpha ,\beta }(R^{\prime })\), which implies \(w_{R_i}(F_G^{\alpha ,\beta }(R)) \mathbin {R_i}w_{R_i}(F_G^{\alpha ,\beta }(R^{\prime }))\). Hence, \(F_G^{\alpha ,\beta }(R)\mathbin {R_i}F_G^{\alpha ,\beta }(R^{\prime })\).\(\square \)
Proof of Theorem 2
Before proving Theorem 2, we prove some intermediate results.
Lemma 3
If \(F\in {\mathcal {F}}\) satisfies strategy-proofness and voter-sovereignty, then it satisfies unanimity, i.e., for each \(R\in {\mathcal {R}}^N\) such that \(p=(x,\ldots ,x)\), \(F(R)=\{x\}\).
Proof
Let \(F\in {\mathcal {F}}\) satisfy strategy-proofness and voter-sovereignty. We show that F satisfies unanimity. Let \(a\in A\) and \(R^{a}\in {\mathcal {R}}^N\) be such that \(p^{a}=(a,\ldots ,a)\). By voter-sovereignty, there exists \(R^0\in {\mathcal {R}}^N\) such that \(F(R^0)=\{a\}\). First, consider profile \(R^1:=(R^{a}_{1},R^0_{-1})\). By strategy-proofness, \(F(R^1)\mathbin {R^{a}_1}F(R)\). Since \(F(R^0)=\{a\}=\{p^{a}_1\}\), we then have \(F(R^1)=\{a\}\). Next, for each \(i\in \{2,\ldots ,n\}\) (sequentially) consider profile \(R^i:=(R^{a}_i ,R^{i-1}_{-i})\). By strategy-proofness we again obtain \(F(R^i)=F(R^{i-1})=\{a\}\). Therefore, since \(R^n=R^{a}\), \(F(R^a)=\{a\}\). \(\square \)
Lemma 4
If \(F\in {\mathcal {F}}\) satisfies strategy-proofness and voter-sovereignty, then F satisfies efficiency.
Proof
Let \(F\in {\mathcal {F}}\) satisfy strategy-proofness and voter-sovereignty. By Lemma 3, F satisfies unanimity. We show that F satisfies efficiency. The proof proceeds in two steps.
Step 1. Let \(R\in {\mathcal {R}}^N\) such that \(p_1=p_2\le \cdots \le p_n\) and \(F(R)\in \mathrm {E}(R)\). By Proposition 1,  . Consider \(R^{\prime }_1\in {\mathcal {R}}\) such that \(p^{\prime }_1\ge p_n\) and let \(R^{\prime }:=(R^{\prime }_1 ,R_{-1})\). If \(p^{\prime }_1=p_1\), then \(p_1=\cdots =p_n\) and by unanimity, \(F(R^{\prime })=\{p_1\}\in \mathrm {E}(R^{\prime })\). Assume \(p^{\prime }_1>p_1\). We show that \(F(R^{\prime })\in \mathrm {E}(R)\).
. Consider \(R^{\prime }_1\in {\mathcal {R}}\) such that \(p^{\prime }_1\ge p_n\) and let \(R^{\prime }:=(R^{\prime }_1 ,R_{-1})\). If \(p^{\prime }_1=p_1\), then \(p_1=\cdots =p_n\) and by unanimity, \(F(R^{\prime })=\{p_1\}\in \mathrm {E}(R^{\prime })\). Assume \(p^{\prime }_1>p_1\). We show that \(F(R^{\prime })\in \mathrm {E}(R)\).
If  , then
, then  . Hence,
. Hence,  . Thus, \(w_{R^{\prime }_1}(F(R)) \mathbin {P^{\prime }_1}w_{R^{\prime }_1}(F(R^{\prime }))\), contradicting strategy-proofness. Therefore,
. Thus, \(w_{R^{\prime }_1}(F(R)) \mathbin {P^{\prime }_1}w_{R^{\prime }_1}(F(R^{\prime }))\), contradicting strategy-proofness. Therefore,  .
.
Recall that \(p_1=p_2<p^{\prime }_1\). If \({\bar{F}}(R^{\prime })>p^{\prime }_1=\bar{p^{\prime }}\), then  and \(w_{R_2}(F(R^{\prime }))={\bar{F}}(R^{\prime })\). Consider \({\hat{R}}_2\in {\mathcal {R}}\) such that \({\hat{p}}_2=p^{\prime }_1\) and \(p_2\mathbin {{\hat{I}}_2}{\bar{F}}(R^{\prime })\). Note that \(w_{{\hat{R}}_2}(F(R^{\prime }))\mathbin {{\hat{I}}_2}{\bar{F}}(R^{\prime })\). Let \({\hat{R}} :=({\hat{R}}_2,R^{\prime }_{-2})\). By strategy-proofness, \(w_{{\hat{R}}_2}(F({\hat{R}}))\mathbin {{\hat{R}}_2}w_{{\hat{R}}_2}(F(R^{\prime }))\). Hence, \(w_{{\hat{R}}_2}(F({\hat{R}}))\mathbin {{\hat{I}}_2}{\bar{F}}(R^{\prime })\mathbin {{\hat{R}}_2}p_2\). Thus, \(w_{{\hat{R}}_2}(F({\hat{R}}))\in [p_2,{\bar{F}}({\hat{R}})]\). Then, \(w_{R_2}(F({\hat{R}}))={\bar{F}}({\hat{R}})\). If \({\bar{F}}({\hat{R}})\le {\hat{p}}_2\), then \(w_{R_2}(F({\hat{R}}))\mathbin {P_2}w_{R_2}(F(R^{\prime }))\), contradicting strategy-proofness. Hence, \({\bar{F}}({\hat{R}})>{\hat{p}}_2=p^{\prime }_1\).
and \(w_{R_2}(F(R^{\prime }))={\bar{F}}(R^{\prime })\). Consider \({\hat{R}}_2\in {\mathcal {R}}\) such that \({\hat{p}}_2=p^{\prime }_1\) and \(p_2\mathbin {{\hat{I}}_2}{\bar{F}}(R^{\prime })\). Note that \(w_{{\hat{R}}_2}(F(R^{\prime }))\mathbin {{\hat{I}}_2}{\bar{F}}(R^{\prime })\). Let \({\hat{R}} :=({\hat{R}}_2,R^{\prime }_{-2})\). By strategy-proofness, \(w_{{\hat{R}}_2}(F({\hat{R}}))\mathbin {{\hat{R}}_2}w_{{\hat{R}}_2}(F(R^{\prime }))\). Hence, \(w_{{\hat{R}}_2}(F({\hat{R}}))\mathbin {{\hat{I}}_2}{\bar{F}}(R^{\prime })\mathbin {{\hat{R}}_2}p_2\). Thus, \(w_{{\hat{R}}_2}(F({\hat{R}}))\in [p_2,{\bar{F}}({\hat{R}})]\). Then, \(w_{R_2}(F({\hat{R}}))={\bar{F}}({\hat{R}})\). If \({\bar{F}}({\hat{R}})\le {\hat{p}}_2\), then \(w_{R_2}(F({\hat{R}}))\mathbin {P_2}w_{R_2}(F(R^{\prime }))\), contradicting strategy-proofness. Hence, \({\bar{F}}({\hat{R}})>{\hat{p}}_2=p^{\prime }_1\).
Set \({\hat{R}}^2\equiv {\hat{R}}\). Thus, \({\bar{F}}({\hat{R}}^2)>{\hat{p}}^2_2=p^{\prime }_1\). We now (sequentially) consider for each \(j\in \{3,\ldots ,k\}\) with \(p_j<p^{\prime }_1\) preferences \({\hat{R}}_j\in {\mathcal {R}}\) such that \({\hat{p}}_j=p^{\prime }_1\) and \(p_j\mathbin {{\hat{I}}_j}{\bar{F}}({\hat{R}}^{j-1})\). Let \({\hat{R}}^{j}:=({\hat{R}}_j,{\hat{R}}_{-j}^{j-1})\). Then, by the same arguments as above for \({\hat{R}}^{j}\) instead of \({\hat{R}}^{2}\), we obtain that \({\bar{F}}({\hat{R}}^{j})>p^{\prime }_1\). In particular, for the final profile \({\hat{R}}^{k}\), \({\bar{F}}({\hat{R}}^{k})>p^{\prime }_1\). However, profile \({\hat{R}}^{k}\) is such that for all agents \(i\in N\), \(p({\hat{R}}^{k}_i)=p^{\prime }_1\). Thus, by unanimity, \(F({\hat{R}}^{k})=\{p^{\prime }_1\}\), a contradiction. Hence, \({\bar{F}}(R^{\prime })\le p^{\prime }_1=\bar{p^{\prime }}\).
Therefore,  and \(F(R^{\prime })\in \mathrm {E}(R^{\prime })\).
and \(F(R^{\prime })\in \mathrm {E}(R^{\prime })\).
Step 2. Let \(R\in {\mathcal {R}}^N\) such that \(p_1\le \cdots \le p_n\). Let \(R^1\in {\mathcal {R}}^N\) be such that \(R^1:=(R_1,\ldots ,R_1)\). By unanimity, \(F(R^1)=\{p_1\}\). Hence, by Proposition 1, \(F(R^1)\in \mathrm {E}(R^1)\). Next, consider profile \(R^2:=(R_2,R^1_{-2})\) where \(p_2\ge p^1_2=p_1\),  , and \(\bar{p^2}\ge \bar{p^1}\). Since \(F(R^1)\in \mathrm {E}(R^1)\), by Step 1 (with agent 2 in the role of agent 1) we conclude \(F(R^2)\in \mathrm {E}(R^2)\). We (sequentially) consider for each \(i=\{3,\ldots ,n\}\) profile \(R^i:=(R_i,R^{i-1}_{-i})\). Since \(F(R^{i-1})\in \mathrm {E}(R^{i-1})\), by Step 1 (with agent i in the role of agent 1) we conclude \(F(R^{i})\in \mathrm {E}(R^{i})\). Therefore, since \(R^n\equiv R\), \(F(R)\in \mathrm {E}(R)\). \(\square \)
, and \(\bar{p^2}\ge \bar{p^1}\). Since \(F(R^1)\in \mathrm {E}(R^1)\), by Step 1 (with agent 2 in the role of agent 1) we conclude \(F(R^2)\in \mathrm {E}(R^2)\). We (sequentially) consider for each \(i=\{3,\ldots ,n\}\) profile \(R^i:=(R_i,R^{i-1}_{-i})\). Since \(F(R^{i-1})\in \mathrm {E}(R^{i-1})\), by Step 1 (with agent i in the role of agent 1) we conclude \(F(R^{i})\in \mathrm {E}(R^{i})\). Therefore, since \(R^n\equiv R\), \(F(R)\in \mathrm {E}(R)\). \(\square \)
Lemma 5
If \(F\in {\mathcal {F}}\) satisfies strategy-proofness and voter-sovereignty, then for each \(R,R^{\prime }\in {\mathcal {R}}^N\) and each \(i\in N\) such that \(R_{-i}=R^{\prime }_{-i}\) the following holds:
- (a):
-
if
 and
and  , then \(F(R)=F(R^{\prime })\) and
, then \(F(R)=F(R^{\prime })\) and - (b):
-
if \(p_i>{\bar{F}}(R)\) and \(p^{\prime }_i\ge {\bar{F}}(R)\), then \(F(R)=F(R^{\prime })\).
Proof
Let \(F\in {\mathcal {F}}\) satisfy strategy-proofness and voter-sovereignty. By Lemma 4, F satisfies efficiency. Let \(R,R^{\prime }\in {\mathcal {R}}^N\) and \(i\in N\) be such that \(R_{-i}=R^{\prime }_{-i}\). Assume that \(p_1\le \cdots \le p_n\).
(a) Let  and
and  . We have that
. We have that  and \(w_{R_i}(F(R))={\bar{F}}(R)\). If
and \(w_{R_i}(F(R))={\bar{F}}(R)\). If  , then
, then  , contradicting strategy-proofness. Hence,
, contradicting strategy-proofness. Hence,  . If
. If  , then
, then  , contradicting strategy-proofness. Hence,
, contradicting strategy-proofness. Hence,  or
or  .
.
Assuming  leads to a contradiction as follows. If \({\bar{F}}(R^{\prime })\ge p_i\), then
leads to a contradiction as follows. If \({\bar{F}}(R^{\prime })\ge p_i\), then  , contradicting strategy-proofness. Hence, \({\bar{F}}(R^{\prime })< p_i\). By efficiency,
, contradicting strategy-proofness. Hence, \({\bar{F}}(R^{\prime })< p_i\). By efficiency,

Hence, \(1\ne i\). Consider \({\hat{R}}_1\in {\mathcal {R}}\) such that \({\hat{p}}_1=p_i\) and  and let \(R^1:=({\hat{R}}_1,R_i,R_{-1,i})\) and \({\tilde{R}}^1 =({\hat{R}}_1,R^{\prime }_i,R_{-1,i})\). Note that \({\tilde{R}}^1=({\hat{R}}_1,R^{\prime }_{-1})=({\hat{R}}_i,R^1_{-i})\). By efficiency,
and let \(R^1:=({\hat{R}}_1,R_i,R_{-1,i})\) and \({\tilde{R}}^1 =({\hat{R}}_1,R^{\prime }_i,R_{-1,i})\). Note that \({\tilde{R}}^1=({\hat{R}}_1,R^{\prime }_{-1})=({\hat{R}}_i,R^1_{-i})\). By efficiency,  . Then,
. Then,  and strategy-proofness imply \(F(R^1)=F(R)\).
and strategy-proofness imply \(F(R^1)=F(R)\).
Now, starting from \({\tilde{R}}^1=({\hat{R}}_1,R^{\prime }_{-1})\), strategy-proofness implies that \(b_{{\hat{R}}_1}(F({\tilde{R}}^1))\mathbin {{\hat{R}}_1}b_{{\hat{R}}_1}(F(R^{\prime })) ={\bar{F}}(R^{\prime })\). Since  , we have
, we have  . Hence,
. Hence,  . Recall that \({\tilde{R}}^1=({\hat{R}}_i,R^1_{-i})\). Hence, if
. Recall that \({\tilde{R}}^1=({\hat{R}}_i,R^1_{-i})\). Hence, if  , then
, then  , contradicting strategy-proofness. Thus, \(b_{{\hat{R}}_1}(F({\tilde{R}}^1))\in [{\bar{F}}({\hat{R}}),p_i)\) and
, contradicting strategy-proofness. Thus, \(b_{{\hat{R}}_1}(F({\tilde{R}}^1))\in [{\bar{F}}({\hat{R}}),p_i)\) and  .
.
We now (sequentially) consider for each \(j\in \{2,\ldots ,k\}\) with  preferences \({\hat{R}}_j\in {\mathcal {R}}\) such that \({\hat{p}}_j=p_i\) and
preferences \({\hat{R}}_j\in {\mathcal {R}}\) such that \({\hat{p}}_j=p_i\) and  . Let \(R^j:=({\hat{R}}_j,R^{j-1}_{-j})\) and \({\tilde{R}}^j:=({\hat{R}}_j,{\tilde{R}}^{j-1}_{-j})\). Then, for each pair of profiles \(R^j\) and \({\tilde{R}}^j\), by the same arguments as above, we obtain that
. Let \(R^j:=({\hat{R}}_j,R^{j-1}_{-j})\) and \({\tilde{R}}^j:=({\hat{R}}_j,{\tilde{R}}^{j-1}_{-j})\). Then, for each pair of profiles \(R^j\) and \({\tilde{R}}^j\), by the same arguments as above, we obtain that  . However, final profile \({\tilde{R}}^{k}\) is such that
. However, final profile \({\tilde{R}}^{k}\) is such that  , contradicting efficiency.
, contradicting efficiency.
We can now conclude that  . Then,
. Then,  and strategy-proofness imply \({\bar{F}}(R^{\prime })={\bar{F}}(R)\). Hence, \(F(R^{\prime })=F(R)\).
and strategy-proofness imply \({\bar{F}}(R^{\prime })={\bar{F}}(R)\). Hence, \(F(R^{\prime })=F(R)\).
(b) Let \(p_i>{\bar{F}}(R)\) and \(p^{\prime }_i\ge {\bar{F}}(R)\). By symmetric arguments to the ones presented in Part (a) for \({\bar{F}}\) instead of  it follows that \(F(R)=F(R^{\prime })\). \(\square \)
it follows that \(F(R)=F(R^{\prime })\). \(\square \)
Lemma 6
If \(F\in {\mathcal {F}}\) satisfies strategy-proofness and voter-sovereignty, then F satisfies peaks-onliness.
Proof
Let \(F\in {\mathcal {F}}\) satisfy strategy-proofness and voter-sovereignty. By Lemma 4, F satisfies efficiency. Let \(R,R^{\prime }\in {\mathcal {R}}^N\) and \(i\in N\) be such that \(R_{-i}=R^{\prime }_{-i}\). Assume that \(p_1\le \dots \le p_n\) and that \(p_i=p^{\prime }_i\). We prove that \(F(R)=F(R^{\prime })\). There are three cases.
Case 1  . Hence,
. Hence,  and by Lemma 5 (a), \(F(R)=F(R^{\prime })\).
and by Lemma 5 (a), \(F(R)=F(R^{\prime })\).
Case 2 \((p_i>{\bar{F}}(R))\). Hence, \(p^{\prime }_i>{\bar{F}}(R)\) and by Lemma 5 (b), \(F(R)=F(R^{\prime })\).
Case 3  . If
. If  , then \(b_{R^{\prime }_i}(F(R))=w_{R^{\prime }_i}(F(R))=p_i=p^{\prime }_i\) and by strategy-proofness, \(b_{R^{\prime }_i}(F(R^{\prime }))=w_{R^{\prime }_i}(F(R^{\prime }))=p^{\prime }_i\). Hence, \(F(R)=F(R^{\prime })\).
, then \(b_{R^{\prime }_i}(F(R))=w_{R^{\prime }_i}(F(R))=p_i=p^{\prime }_i\) and by strategy-proofness, \(b_{R^{\prime }_i}(F(R^{\prime }))=w_{R^{\prime }_i}(F(R^{\prime }))=p^{\prime }_i\). Hence, \(F(R)=F(R^{\prime })\).
Without loss of generality, assume that  (the case
(the case  is proven symmetrically). Then, \(b_{R^{\prime }_i}(F(R))=p_i=p^{\prime }_i\) and by strategy-proofness, \(b_{R^{\prime }_i}(F(R^{\prime }))=p^{\prime }_i\). Hence,
is proven symmetrically). Then, \(b_{R^{\prime }_i}(F(R))=p_i=p^{\prime }_i\) and by strategy-proofness, \(b_{R^{\prime }_i}(F(R^{\prime }))=p^{\prime }_i\). Hence,  . We prove that
. We prove that  by contradiction. Assume that
by contradiction. Assume that  . More specifically, assume that
. More specifically, assume that  (the case
(the case  is then proven by exchanging the roles of R and \(R^{\prime }\)). If \({\bar{F}}(R^{\prime })<{\bar{F}}(R)\), then
is then proven by exchanging the roles of R and \(R^{\prime }\)). If \({\bar{F}}(R^{\prime })<{\bar{F}}(R)\), then  and \(w_{R_i}(F(R^{\prime }))\mathbin {P_i}w_{R_i}(F(R))\), contradicting strategy-proofness. Hence, \({\bar{F}}(R)\le {\bar{F}}(R^{\prime })\). By Lemma 5, it is without loss of generality to assume that
and \(w_{R_i}(F(R^{\prime }))\mathbin {P_i}w_{R_i}(F(R))\), contradicting strategy-proofness. Hence, \({\bar{F}}(R)\le {\bar{F}}(R^{\prime })\). By Lemma 5, it is without loss of generality to assume that  and \(p_n={\bar{F}}(R^{\prime })\). Hence,
and \(p_n={\bar{F}}(R^{\prime })\). Hence,

If \(p_i=p_n={\bar{p}}\), then by efficiency,  . Thus,
. Thus,  , contradicting strategy-proofness. Hence, \(p_i<p_n\).
, contradicting strategy-proofness. Hence, \(p_i<p_n\).
Consider \({\hat{R}}_n\in {\mathcal {R}}\) such that \({\hat{p}}_n=p_i\) and  . Then,
. Then,  . Let \(R^n:=(R_i,{\hat{R}}_n,R_{-n,i})\) and \({\tilde{R}}^n:=(R^{\prime }_i,{\hat{R}}_n,R_{-n,i})\). Note that \(R^n=({\hat{R}}_n,R_{-n})\) and \({\tilde{R}}^n=({\hat{R}}_n,R^{\prime }_{-n})\).
. Let \(R^n:=(R_i,{\hat{R}}_n,R_{-n,i})\) and \({\tilde{R}}^n:=(R^{\prime }_i,{\hat{R}}_n,R_{-n,i})\). Note that \(R^n=({\hat{R}}_n,R_{-n})\) and \({\tilde{R}}^n=({\hat{R}}_n,R^{\prime }_{-n})\).
Since \(b_{{\hat{R}}_n}(F(R))={\hat{p}}_n\), by strategy-proofness, \(b_{{\hat{R}}_n}(F(R^n))={\hat{p}}_n\) and  . Since \(R^n=({\hat{R}}_n,R_{-n})\) and
. Since \(R^n=({\hat{R}}_n,R_{-n})\) and  , by strategy-proofness,
, by strategy-proofness,  . Then, by efficiency,
. Then, by efficiency,  .
.
Since \({\tilde{R}}^n=({\hat{R}}_n,R^{\prime }_{-n})\) and \(b_{{\hat{R}}_n}(F(R'))={\hat{p}}_n\), by strategy-proofness, \(b_{{\hat{R}}_n}(F({\tilde{R}}^n))={\hat{p}}_n\) and  . By efficiency,
. By efficiency,  . Recall that
. Recall that  . Hence, if
. Hence, if  , then \(w_{{\hat{R}}_n}(F(R^{\prime }))\mathbin {{\hat{P}}_n}w_{{\hat{R}}_n}(F({\tilde{R}}^n))\), contradicting strategy-proofness. Hence,
, then \(w_{{\hat{R}}_n}(F(R^{\prime }))\mathbin {{\hat{P}}_n}w_{{\hat{R}}_n}(F({\tilde{R}}^n))\), contradicting strategy-proofness. Hence,  . Similarly as before, by Lemma 5, we can assume that
. Similarly as before, by Lemma 5, we can assume that

We now (sequentially) consider for each \(j\in \{n-1,n-2,\ldots ,k\}\) with \(p_i<p_j\) preferences \({\hat{R}}_j\in {\mathcal {R}}\) such that \({\hat{p}}_j=p_i\) and  . Let \(R^j=({\hat{R}}_j,R^{j+1}_{-j})\) and \({\tilde{R}}^j =({\hat{R}}_j,{\tilde{R}}^{j+1}_{-j})\). Then, for each pair of profiles \(R^j\) and \({\tilde{R}}^j\), by the same arguments as above, we obtain that
. Let \(R^j=({\hat{R}}_j,R^{j+1}_{-j})\) and \({\tilde{R}}^j =({\hat{R}}_j,{\tilde{R}}^{j+1}_{-j})\). Then, for each pair of profiles \(R^j\) and \({\tilde{R}}^j\), by the same arguments as above, we obtain that

However, the final profiles \(R^k\) and \({\tilde{R}}^{k}\) are such that \(R^k_{-i}={\tilde{R}}^{k}_i\) and

Thus,  , contradicting strategy-proofness. We can now conclude that
, contradicting strategy-proofness. We can now conclude that  . Assuming \({\bar{F}}(R^{\prime })\ne {\bar{F}}(R)\) leads to a contradiction in a symmetric fashion. Hence, \(F(R^{\prime })=F(R)\).\(\square \)
. Assuming \({\bar{F}}(R^{\prime })\ne {\bar{F}}(R)\) leads to a contradiction in a symmetric fashion. Hence, \(F(R^{\prime })=F(R)\).\(\square \)
Proof of Theorem 2
We start with statement (i) and F satisfying strategy-proofness and voter sovereignty. Then, by Lemma 6, F satisfies peaks-onliness. Hence, by Theorem 1 ((i) \(\Rightarrow \) (iii)), \(F\in {\mathcal {F}}_{G}\). Since F satisfies peaks-onliness, by Lemma 4, F satisfies efficiency. Hence, \(F\in {\mathcal {F}}_{EG}\) and statement (i) implies statement (iii).
Second, we show that statement (iii) implies statement (ii). By Theorem 1 ((iii) \(\Rightarrow \) (ii)), each \(F\in {\mathcal {F}}_G\) satisfies uncompromisingness. Since F satisfies efficiency it also satisfies the weaker property of voter-sovereignty. Hence, statement (iii) implies statement (ii).
Finally, by Theorem 1 ((ii) \(\Rightarrow \) (i)), uncompromisingness implies strategy-proofness and peaks-onliness. Hence, statement (ii) implies statement (i). \(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Klaus, B., Protopapas, P. On strategy-proofness and single-peakedness: median-voting over intervals. Int J Game Theory 49, 1059–1080 (2020). https://doi.org/10.1007/s00182-020-00728-y
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00182-020-00728-y




 and
and  ] or [
] or [ and
and  ], then
], then  and
and , then
, then  .
.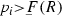 , then
, then  , and if in addition
, and if in addition  and
and  , then
, then