Cyclic dominance in a two-person rock–scissors–paper game

Abstract

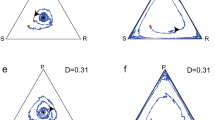
The Rock–scissors–paper game has been studied to account for cyclic behaviour under various game dynamics. We use a two-person parametrised version of this game. The cyclic behaviour is observed near a heteroclinic cycle, in a heteroclinic network, with two nodes such that, at each node, players alternate in winning and losing. This cycle is shown to be as stable as possible for a wide range of parameter values. The parameters are related to the players’ payoff when a tie occurs.

Appendices

Transitions near the RSP cycles

In this section we describe the construction of Poincaré maps (also called return maps) from and to cross sections of the flow near each node once around an entire heteroclinic cycle. The Poincaré maps are the composition of local and global maps. The local maps approximate the flow in a neighbourhood of a node. The global maps approximate the flow along a heteroclinic connection between two consecutive nodes.

Near $\xi _j$ we introduce an incoming section $H_{j}^{in,i}$ across the heteroclinic connection $\left[ \xi _{i}\rightarrow \xi _{j}\right]$ and an outgoing section $H_{j}^{out,k}$ across the heteroclinic connection $\left[ \xi _{j}\rightarrow \xi _{k}\right]$, $j \ne i,k$. By definition, these are five-dimensional subspaces in ${\mathbb {R}}^6$. Krupa and Melbourne (2004) have shown that not all dimensions are important in the study of stability of heteroclinic cycles as follows.

1.1 Poincaré maps

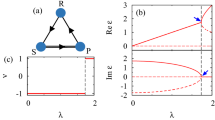
Assume that the flow is linearisable about each node (see Proposition 4.1. in Aguiar and Castro (2010) for detailed conditions). Locally at $\xi _j$, we denote by $-c_{ji}<0$ the eigenvalue in the stable direction through the heteroclinic connection $\left[ \xi _{i}\rightarrow \xi _{j}\right]$ and $e_{jk}>0$ the eigenvalue in the unstable direction through the heteroclinic connection $\left[ \xi _{j}\rightarrow \xi _{k}\right]$. As illustrated in Fig. 4a each node has two incoming connections and two outgoing connections. Looking at $\xi _j$ from the point of view of the sequence of heteroclinic connections $\left[ \xi _i\rightarrow \xi _j\rightarrow \xi _k\right]$, we say that $-c_{ji}$ is contracting, $e_{jk}$ is expanding, $-c_{jl}$ and $e_{jm}$ are transverse with $j \ne i,k,l,m$, $i \ne l$ and $k \ne m$ (see Garrido-da-Silva and Castro 2019; Krupa and Melbourne 2004; Podvigina 2012; Podvigina and Ashwin 2011).

Fig. 4

Representation of a the eigenvalues and b the cross sections near a node $\xi _j$ with $j \ne i,k,l,m$, $i \ne l$ and $k \ne m$

The linearised flow in the relevant local coordinates near $\xi _j$ is given by

$$\begin{aligned} \begin{aligned} {\dot{v}}&= \; -c_{ji}v\\ {\dot{w}}&= \; e_{jk}w\\ {\dot{z}}_{1}&= \; -c_{jl}z_{1}\\ {\dot{z}}_{2}&= \; e_{jm}z_{2}, \end{aligned} \end{aligned}$$

(10)

such that v, w and $(z_1,z_2)$ correspond, respectively, to the contracting, expanding and transverse directions. Table 2 provides all eigenvalues restricted to these directions for the three nodes $\xi _0$, $\xi _1$ and $\xi _2$.

All cross sections are reduced to a three-dimensional subspace and can be expressed as (see Fig. 4b)

$$\begin{aligned} \begin{aligned} H_{j}^{in,i}&=\left\{ \left( 1,w,z_{1},z_{2}\right) :\; 0 \le w,z_{1},z_{2}<1\right\} \\ H_{j}^{out,k}&=\left\{ \left( v,1,z_{1},z_{2}\right) :\; 0\le v,z_{1},z_{2}<1\right\} . \end{aligned} \end{aligned}$$

We construct local maps $\phi _{ijk}:H_{j}^{in,i}\rightarrow H_{j}^{out,k}$ near each $\xi _j$, global maps $\psi _{jk}:H_{j}^{out,k}\rightarrow H_{k}^{in,j}$ near each heteroclinic connection $\left[ \xi _{j}\rightarrow \xi _{k}\right]$, and their compositions $g_{j}=\psi _{jk} \circ \phi _{ijk}:H_{j}^{in,i}\rightarrow H_{k}^{in,j}$, $j \ne i,k$. Composing the latter successively along an entire heteroclinic cycle yields the Poincaré maps $\pi _j:H_j^{in,i} \rightarrow H_{j}^{in,i}$, one for each heteroclinic connection belonging to the heteroclinic cycle.

Integrating (10) we find

$$\begin{aligned} \phi _{ijk}\left( w,z_{1},z_{2}\right) =\left( w^{{\textstyle \frac{c_{ji}}{e_{jk}}}},\; z_{1}w^{{\textstyle \frac{c_{jl}}{e_{jk}}}},\; z_{2}w^{-{\textstyle \frac{e_{jm}}{e_{jk}}}}\right) , \quad \text {for }0<z_2<w^{\textstyle \frac{e_{jm}}{e_{jk}}}. \end{aligned}$$

Table 2 Eigenvalues of the linearisation of the flow about each node in a system of local coordinates in the basis of the associated contracting, expanding and transverse eigenvectors

On the other hand, expressions for global maps depend both on which heteroclinic connection and heteroclinic cycle one considers. Following the Remark on p. 1603 of Aguiar and Castro (2010), in the leading order any global map $\psi _{jk}$ is well represented by a permutation.

We describe the details for the cycle $C_0=\left[ \xi _0\rightarrow \xi _1\rightarrow \xi _0\right]$. The other cases are similar, and therefore, we omit the calculations. Notice that

$$\begin{aligned} \Gamma \left( (\text {R},\text {P}) \rightarrow (\text {S},\text {P}) \rightarrow (\text {S},\text {R}) \right) =C_0. \end{aligned}$$

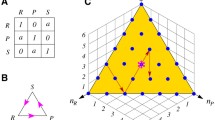
We pick, respectively, the heteroclinic connections $\left[ (\text {R},\text {P}) \rightarrow (\text {S},\text {P}) \right]$ and$\left[ (\text {S},\text {P}) \rightarrow (\text {S},\text {R}) \right]$ as representatives of $\left[ \xi _0 \rightarrow \xi _1\right]$ and $\left[ \xi _1 \rightarrow \xi _0\right]$, see Table 1. Considering the flow linearised about each representative heteroclinic connection the global maps have the form

$$\begin{aligned} \begin{aligned} \psi _{01}:\,&H_{0}^{out,1} \rightarrow H_{1}^{in,0}, \quad&\psi _{10} \left( v,z_1,z_2\right)&=\left( z_1,z_2,v\right) \\ \psi _{10}:\,&H_{1}^{out,0} \rightarrow H_{0}^{in,1}, \quad&\psi _{01} \left( v,z_1,z_2\right)&=\left( z_1,z_2,v\right) . \end{aligned} \end{aligned}$$

The pairwise composite maps $g_{0}=\psi _{01} \circ \phi _{101}$ and $g_{1}=\psi _{10} \circ \phi _{010}$ are

$$\begin{aligned} \begin{aligned} g_{0}:\,&H_{0}^{in,1} \rightarrow H_{1}^{in,0}, \quad&g_{0}\left( w,z_1,z_2\right)&= \left( z_{1}w^{{\textstyle \frac{1-\varepsilon _y}{2}}},\; z_{2}w^{-{\textstyle \frac{1+\varepsilon _x}{2}}}, \; w \right) , \\&\text {for }&0<z_{2}<w^{\textstyle \frac{1+\varepsilon _x}{2}}, \\ g_{1}:&H_{1}^{in,0} \rightarrow H_{0}^{in,1}, \quad&g_{1}\left( w,z_1,z_2\right)&= \left( z_{1}w^{{\textstyle \frac{1-\varepsilon _x}{2}}},\; z_{2}w^{-{\textstyle \frac{1+\varepsilon _y}{2}}},\; w \right) , \\&\text {for }&0<z_{2}<w^{\textstyle \frac{1+\varepsilon _y}{2}}. \end{aligned} \end{aligned}$$

(11)

The dynamics in the vicinity of the $C_0$-cycle is accurately approximated by the two Poincaré maps $\pi _{0}=g_{1} \circ g_{0}$ and $\pi _{1}=g_{0} \circ g_{1}$ with

$$\begin{aligned} \begin{aligned} \pi _{0}&: H_{0}^{in,1} \rightarrow H_{0}^{in,1}, \\ \pi _{0}&\left( w,z_1,z_2\right) = \left( z_2 z_{1}^{\textstyle \frac{1-\varepsilon _x}{2}}w^{\textstyle \frac{-1-3\varepsilon _x-\varepsilon _y+\varepsilon _x \varepsilon _y}{4}},\; z_{1}^{-{\textstyle \frac{1+\varepsilon _y}{2}}}w^{\textstyle \frac{3+\varepsilon _y^2}{4}}, \; z_1 w^{\textstyle \frac{1-\varepsilon _y}{2}} \right) , \end{aligned} \end{aligned}$$

(12)

for $0<z_{2}<w^{\textstyle \frac{1+\varepsilon _x}{2}}$ and $z_1>w^{\textstyle \frac{3+\varepsilon _y^2}{2\left( 1+\varepsilon _y\right) }}$,

$$\begin{aligned} \begin{aligned} \pi _{1}&: H_{1}^{in,0} \rightarrow H_{1}^{in,0}, \\ \pi _{1}&\left( w,z_1,z_2\right) = \left( z_2 z_{1}^{\textstyle \frac{1-\varepsilon _y}{2}}w^{\textstyle \frac{-1-\varepsilon _x-3\varepsilon _y+\varepsilon _x \varepsilon _y}{4}},\; z_{1}^{-{\textstyle \frac{1+\varepsilon _x}{2}}}w^{\textstyle \frac{3+\varepsilon _y^2}{4}}, \; z_1 w^{\textstyle \frac{1-\varepsilon _x}{2}} \right) , \end{aligned} \end{aligned}$$

(13)

for $0<z_{2}<w^{\textstyle \frac{1+\varepsilon _y}{2}}$ and $z_1>w^{\textstyle \frac{3+\varepsilon _x^2}{2\left( 1+\varepsilon _x\right) }}$.

1.2 Transition matrices

Consider the change of coordinates

$$\begin{aligned} \varvec{\eta }\equiv \left( \eta _{1},\eta _{2},\eta _{3}\right) =\left( \ln v,\ln z_{1},\ln z_{2} \right) . \end{aligned}$$

(14)

The maps $g_{j}:H_j^{in,i}\rightarrow H_k^{in,j}$, $j \ne i,k$, become linear

$$\begin{aligned} g_j\left( \varvec{\eta }\right) =M_j \varvec{\eta } \end{aligned}$$

and $M_j$ are called the basic transition matrices. For the Poincaré maps $\pi _j:H_j^{in,i} \rightarrow H_j^{in,i}$ the transition matrices are the product of basic transition matrices in the appropriate order. We denote them by $M^{(j)}$.

The basic transition matrices of the maps $g_0$ and $g_1$ in (11) with respect to $C_0$ are

$$\begin{aligned} M_{0} =\left[ \begin{array}{ccc} \dfrac{1-\varepsilon _y}{2} &{} 1 &{} 0\\ -\dfrac{1+\varepsilon _x}{2} &{} 0 &{} 1\\ 1 &{} 0 &{} 0 \end{array}\right] , \; \; \; \; M_{1} =\left[ \begin{array}{ccc} \dfrac{1-\varepsilon _x}{2} &{} 1 &{} 0\\ -\dfrac{1+\varepsilon _y}{2} &{} 0 &{} 1\\ 1 &{} 0 &{} 0 \end{array}\right] . \end{aligned}$$

Then, the products $M^{(0)}=M_1 M_0$ and $M^{(1)}=M_0 M_1$ provide the transition matrices (see Fig. 5) of the Poincaré maps $\pi _0$ in (12) and $\pi _1$ in (13):

$$\begin{aligned} \begin{aligned} M^{(0)}&=\left[ \begin{array}{ccc} \dfrac{-1-3\varepsilon _x-\varepsilon _y+\varepsilon _x\varepsilon _y}{4} &{} \dfrac{1-\varepsilon _x}{2} &{} 1\\ \dfrac{3+\varepsilon _y^2}{4} &{} -\dfrac{1+\varepsilon _y}{2} &{} 0\\ \dfrac{1-\varepsilon _y}{2} &{} 1 &{} 0 \end{array}\right] \\ M^{(1)}&=\left[ \begin{array}{ccc} \dfrac{-1-\varepsilon _x-3\varepsilon _y+\varepsilon _x\varepsilon _y}{4} &{} \dfrac{1-\varepsilon _y}{2} &{} 1\\ \dfrac{3+\varepsilon _x^2}{4} &{} -\dfrac{1+\varepsilon _x}{2} &{} 0\\ \dfrac{1-\varepsilon _x}{2} &{} 1 &{} 0 \end{array}\right] . \end{aligned} \end{aligned}$$

(15)

Fig. 5

Definition of the transition matrices a $M^{(0)}=M_1M_0$ and b $M^{(1)}=M_0M_1$ around the $C_0$-cycle. The matrix $M_0$ corresponds to the transformation represented by a dotted line and $M_1$ to that represented by a dashed line

Analogously, this process yields the transition matrices for the remaining heteroclinic cycles. We use different accents according to the heteroclinic cycle: for $C_1$,

$$\begin{aligned} \begin{aligned} {\widetilde{M}}^{(1)}:\,&H_1^{in,2} \rightarrow H_1^{in,2}, \quad&{\widetilde{M}}^{(1)}&= {\widetilde{M}}_2 {\widetilde{M}}_1\\ {\widetilde{M}}^{(2)}:\,&H_2^{in,1} \rightarrow H_2^{in,1}, \quad&{\widetilde{M}}^{(2)}&={\widetilde{M}}_1 {\widetilde{M}}_2 \end{aligned} \end{aligned}$$

where

$$\begin{aligned} {\widetilde{M}}_{1} =\left[ \begin{array}{ccc} \dfrac{2}{1+\varepsilon _y} &{} 1 &{} 0\\ \dfrac{1-\varepsilon _x}{1+\varepsilon _y} &{} 0 &{} 0\\ -\dfrac{2}{1+\varepsilon _y} &{} 0 &{} 1 \end{array}\right] , \; \; \; \; {\widetilde{M}}_{2} =\left[ \begin{array}{ccc} -\dfrac{1-\varepsilon _y}{1-\varepsilon _x} &{} 0 &{} 1\\ \dfrac{1+\varepsilon _x}{1-\varepsilon _x} &{} 1 &{} 0\\ \dfrac{1+\varepsilon _y}{1-\varepsilon _x} &{} 0 &{} 0 \end{array}\right] ; \end{aligned}$$

for $C_2$,

$$\begin{aligned} \begin{aligned} \widetilde{{\widetilde{M}}}^{(0)}:&H_0^{in,2} \rightarrow H_0^{in,2}, \quad&\widetilde{{\widetilde{M}}}^{(0)}&= \widetilde{{\widetilde{M}}_2} \widetilde{{\widetilde{M}}_0}\\ \widetilde{{\widetilde{M}}}^{(2)}:&H_2^{in,0} \rightarrow H_2^{in,0}, \quad&\widetilde{{\widetilde{M}}}^{(2)}&= \widetilde{{\widetilde{M}}_0} \widetilde{{\widetilde{M}}_2} \end{aligned} \end{aligned}$$

where

$$\begin{aligned} \widetilde{{\widetilde{M}}_{0}} =\left[ \begin{array}{ccc} \dfrac{2}{1+\varepsilon _x} &{} 1 &{} 0\\ \dfrac{1-\varepsilon _y}{1+\varepsilon _x} &{} 0 &{} 0\\ -\dfrac{2}{1+\varepsilon _x} &{} 0 &{} 1 \end{array}\right] , \; \; \; \; \widetilde{{\widetilde{M}}_{2}} =\left[ \begin{array}{ccc} -\dfrac{1-\varepsilon _x}{1-\varepsilon _y} &{} 0 &{} 1\\ \dfrac{1+\varepsilon _y}{1-\varepsilon _y} &{} 1 &{} 0\\ \dfrac{1+\varepsilon _x}{1-\varepsilon _y} &{} 0 &{} 0 \end{array}\right] ; \end{aligned}$$

for $C_3$,

$$\begin{aligned} \begin{aligned} {\widehat{M}}^{(1)}:\,&H_1^{in,0} \rightarrow H_1^{in,0}, \quad&{\widehat{M}}^{(1)}&= {\widehat{M}}_2 {\widehat{M}}_0 {\widehat{M}}_1\\ {\widehat{M}}^{(2)}:\,&H_2^{in,1} \rightarrow H_2^{in,1}, \quad&{\widehat{M}}^{(2)}&={\widehat{M}}_0 {\widehat{M}}_1 {\widehat{M}}_2\\ {\widehat{M}}^{(0)}:\,&H_0^{in,2} \rightarrow H_0^{in,2}, \quad&{\widehat{M}}^{(0)}&={\widehat{M}}_1 {\widehat{M}}_2 {\widehat{M}}_0 \end{aligned} \end{aligned}$$

where

$$\begin{aligned} {\widehat{M}}_{1} =\left[ \begin{array}{ccc} -\dfrac{2}{1+\varepsilon _y} &{} 0 &{} 1\\ \dfrac{1-\varepsilon _x}{1+\varepsilon _y} &{} 1 &{} 0\\ \dfrac{2}{1+\varepsilon _y} &{} 0 &{} 0 \end{array}\right] , \; \; \; \; {\widehat{M}}_{2} =\left[ \begin{array}{ccc} \dfrac{1+\varepsilon _x}{1-\varepsilon _y} &{} 1 &{} 0\\ \dfrac{1+\varepsilon _y}{1-\varepsilon _y} &{} 0 &{} 0\\ -\dfrac{1-\varepsilon _x}{1-\varepsilon _y} &{} 0 &{} 1 \end{array}\right] , \; \; \; \; {\widehat{M}}_{0} =\left[ \begin{array}{ccc} 1 &{} 1 &{} 0\\ -\dfrac{1+\varepsilon _x}{2} &{} 0 &{} 1\\ \dfrac{1-\varepsilon _y}{2} &{} 0 &{} 0 \end{array}\right] ; \end{aligned}$$

and, for $C_4$,

$$\begin{aligned} \begin{aligned} {\widehat{\widehat{M}}}^{(0)}:&H_0^{in,1} \rightarrow H_0^{in,1}, \quad&{\widehat{\widehat{M}}}^{(0)}&= {\widehat{\widehat{M}}_2} {\widehat{\widehat{M}}_1} {\widehat{\widehat{M}}_0}\\ {\widehat{\widehat{M}}}^{(2)}:&H_2^{in,0} \rightarrow H_2^{in,0}, \quad&{\widehat{\widehat{M}}}^{(2)}&= {\widehat{\widehat{M}}_1} {\widehat{\widehat{M}}_0} {\widehat{\widehat{M}}_2}\\ {\widehat{\widehat{M}}}^{(1)}:&H_1^{in,2} \rightarrow H_1^{in,2}, \quad&{\widehat{\widehat{M}}}^{(1)}&= {\widehat{\widehat{M}}_0} {\widehat{\widehat{M}}_2} {\widehat{\widehat{M}}_1} \end{aligned} \end{aligned}$$

where

$$\begin{aligned} {\widehat{\widehat{M}}}_{0} =\left[ \begin{array}{ccc} -\dfrac{2}{1+\varepsilon _x} &{} 0 &{} 1\\ \dfrac{1-\varepsilon _y}{1+\varepsilon _x} &{} 1 &{} 0\\ \dfrac{2}{1+\varepsilon _x} &{} 0 &{} 0 \end{array}\right] , \; \; \; \; {\widehat{\widehat{M}}_{2}} =\left[ \begin{array}{ccc} \dfrac{1+\varepsilon _y}{1-\varepsilon _x} &{} 1 &{} 0\\ \dfrac{1+\varepsilon _x}{1-\varepsilon _x} &{} 0 &{} 0\\ -\dfrac{1-\varepsilon _y}{1-\varepsilon _x} &{} 0 &{} 1 \end{array}\right] , \; \; \; \; {\widehat{\widehat{M}}_{1}} =\left[ \begin{array}{ccc} 1 &{} 1 &{} 0\\ -\dfrac{1+\varepsilon _y}{2} &{} 0 &{} 1\\ \dfrac{1-\varepsilon _x}{2} &{} 0 &{} 0 \end{array}\right] . \end{aligned}$$

The stability index

Each Poincaré map $\pi _j:{\mathbb {R}}^3\rightarrow {\mathbb {R}}^3$ induces a discrete dynamical system through the relation ${\varvec{x}}_{k+1}=\pi _j \left( {\varvec{x}}_k\right)$, where ${\varvec{x}}_k=\left( w_k,z_{1,k},z_{2,k}\right)$ denotes the state at the discrete time k. The stability of a heteroclinic cycle then follows from the stability of the fixed point at the origin of Poincaré maps around the former.

As in Podvigina (2012) and Podvigina and Ashwin (2011), for $\delta >0$ let ${{{\mathcal {B}}}}_{\delta }^{\pi _j}$ be the $\delta$-local basin of attraction of ${\varvec{0}}\in {\mathbb {R}}^3$ for the map $\pi _j$. Roughly speaking, ${{{\mathcal {B}}}}_{\delta }^{\pi _j}$ is the set of all initial conditions near $\xi _j$ whose trajectories remain in a $\delta$-neighbourhood of the heteroclinic cycle and converge to it.

We use $\left\| \cdot \right\|$ to express Euclidean norm on ${\mathbb {R}}^3$. Taking, for example, the Poincaré map $\pi _0$ in (12) with respect to the $C_0$-cycle the local basin ${{{\mathcal {B}}}}_{\delta }^{\pi _0}$ is defined to be

$$\begin{aligned} \begin{aligned} {{{\mathcal {B}}}}_{\delta }^{\pi _0}=\Big \{ {\varvec{x}} \in {\mathbb {R}}^3 :&\left\| \pi _0^k({\varvec{x}}) \right\|< \delta , \; \left\| g_0 \circ \pi _0^k({\varvec{x}}) \right\| < \delta \text { for all } k\in {\mathbb {N}}_0 \\ \text { and }&\lim _{k \rightarrow \infty } \left\| \pi _0^k({\varvec{x}})\right\| = 0, \; \lim _{k \rightarrow \infty } \left\| g_0 \circ \pi _0^k({\varvec{x}})\right\| = 0 \Big \}. \end{aligned} \end{aligned}$$

(16)

In the new coordinates $\varvec{\eta }$ (14) the origin in ${\mathbb {R}}^3$ becomes $-\varvec{\infty }$. For asymptotically small ${\varvec{x}}=\left( w,z_1,z_2\right) \in {{{\mathcal {B}}}}_{\delta }^{\pi _j}$ the requirement (as in (16)) that the iterates $\pi _j^k({\varvec{x}})$ approach ${\varvec{0}}$ (hence the heteroclinic cycle) as $k\rightarrow \infty$ corresponds to all asymptotically large negative $\varvec{\eta }$ such that

$$\begin{aligned} \lim _{k\rightarrow \infty } \left( M^{(j)}\right) ^k\varvec{\eta }=-\varvec{\infty }. \end{aligned}$$

(17)

For $M=M^{(j)}$ we denote the set of points satisfying (17) by $U^{-\infty }\left( M\right)$. Lemma 3 in Podvigina (2012), together with its reformulation as Lemma 3.2 in Garrido-da-Silva and Castro (2019), provide necessary and sufficient conditions for $U^{-\infty }\left( M\right)$ having a positive measure. The conditions depend on the dominant eigenvalue and the associated eigenvector of M. We transcribe the result in its useful form in the following

Lemma B.1

(adapted from Lemma 3 in Podvigina (2012)). Let $\lambda _{\max }$ be the maximum, in absolute value, eigenvalue of the matrix $M:{\mathbb {R}}^N \rightarrow {\mathbb {R}}^N$ and ${\varvec{w}}^{\max }=\left( w_1^{\max },\ldots ,w_N^{\max }\right)$ be an associated eigenvector. Suppose $\lambda _{\max } \ne 1$. The measure $\ell \left( U^{-\infty }(M)\right)$ is positive if and only if the three following conditions are satisfied:

• (i) $\lambda _{\max }$ is real;

• (ii) $\lambda _{\max }>1$;

• (iii) $w_{l}^{\max }w_{q}^{\max }>0$ for all $l,q=1,\ldots N$.

1.1 The function $F^\mathrm{{index}}$

The function $F^{\text {index}}:{\mathbb {R}}^N \rightarrow {\mathbb {R}}$ used to calculate the stability indices along heteroclinic connections is constructed in Garrido-da-Silva and Castro (2019).

For $N=3$ and any nonzero $\varvec{\alpha }=\left( \alpha _1,\alpha _2,\alpha _3\right) \in {\mathbb {R}}^3$ denote $\alpha _{\min }=\min \left\{ \alpha _1,\alpha _2,\alpha _3\right\}$ and $\alpha _{\max }=\max \left\{ \alpha _1,\alpha _2,\alpha _3\right\}$. From Appendix A.1 in Garrido-da-Silva and Castro (2019) we have

$$\begin{aligned} F^{\text {index}}(\varvec{\alpha })=F^{+}(\varvec{\alpha })-F^{-}(\varvec{\alpha }) \end{aligned}$$

with $F^{-}(\varvec{\alpha })=F^{+}(-\varvec{\alpha })$ where

$$\begin{aligned} F^{+}(\varvec{\alpha })= {\left\{ \begin{array}{ll} +\infty , &{} \text {if }\alpha _{\min } \ge 0\\ 0, &{} \text {if }\alpha _{1}+\alpha _{2}+\alpha _{3}\le 0\\ -\dfrac{\alpha _{1}+\alpha _{2}+\alpha _{3}}{\alpha _{\min }}, &{} \text {if }\alpha _{\min } <0\text { and }\alpha _{1}+\alpha _{2}+\alpha _{3}\ge 0, \end{array}\right. } \end{aligned}$$

and

$$\begin{aligned} F^{-}\left( \varvec{\alpha }\right) = {\left\{ \begin{array}{ll} +\infty , &{} \text {if }\alpha _{\max } \le 0\\ 0, &{} \text {if }\alpha _{1}+\alpha _{2}+\alpha _{3}\ge 0\\ -\dfrac{\alpha _{1}+\alpha _{2}+\alpha _{3}}{\alpha _{\max }}, &{} \text {if }\alpha _{\max } >0\text { and }\alpha _{1}+\alpha _{2}+\alpha _{3}\le 0. \end{array}\right. } \end{aligned}$$

It then follows that

$$\begin{aligned} F^{\text {index}}\left( \varvec{\alpha }\right) = {\left\{ \begin{array}{ll} +\infty , &{} \text {if }\alpha _{\min } \ge 0\\ -\infty , &{} \text {if }\alpha _{\max } \le 0\\ 0, &{} \text {if }\alpha _{1}+\alpha _{2}+\alpha _{3}=0\\ \dfrac{\alpha _{1}+\alpha _{2}+\alpha _{3}}{\alpha _{\max }}, &{} \text {if }\alpha _{\max }>0\text { and }\alpha _{1}+\alpha _{2}+\alpha _{3}<0\\ -\dfrac{\alpha _{1}+\alpha _{2}+\alpha _{3}}{\alpha _{\min }}, &{} \text {if }\alpha _{\min } <0\text { and }\alpha _{1}+\alpha _{2}+\alpha _{3}>0. \end{array}\right. } \end{aligned}$$