A semiparametric alternative to the Heckman correction: application with left-censored data on parental transfers

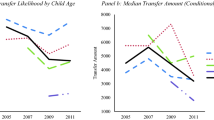
Abstract

Using a semiparametric estimator developed by Klein and Vella (J Appl Econom 24(5):735–762, 2009b), we study the motives for parental wealth transfers to living children using left-censored data from the Health and Retirement Study. We confirm the presence of heteroskedastic errors in our data and show that the inverse Mills ratio approach employed by the Heckman correction would be biased in such a setting. Using the more flexible semiparametic approach, we find evidence of a nonlinear relationship between amount of inter vivo transfers and recipient children’s household incomes, suggesting that parents’ motives for transferring wealth may vary depending on their child’s income level.

Appendices

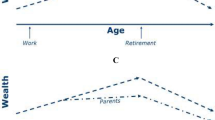
Appendix A Behavioral Framework (Cox 1987)

Let i and j index parents and children, respectively. The theoretical model assumes that a parent’s utility is driven by three arguments: his/her own consumption $C_{it}$, child $j's$ caring services (attention, companion, visits, calls, housework, etc.), and child $j's$ utility $U_j$. Parent $i's$ transfer decision $T_{it}$, namely how much money to give to child j, can be summarized in the following constrained problem:

$$\begin{aligned}&\underset{T_{i},S_{j}}{\text {max} } \quad U_{i}(C_{i},S_{j},U_{j}(C_{j},S_{j})) \end{aligned}$$

(6)

$$\begin{aligned}&\text {subject to} \;\; C_{i} = PI_{i}-T_{i} \end{aligned}$$

(7)

$$\begin{aligned}&C_{j} = CI_{j}+T_{i} \end{aligned}$$

(8)

$$\begin{aligned}&U_{j}(CI_{j}+T_{i},S_{j})\ge U_{j}(CI_{j},0) \end{aligned}$$

(9)

where $PI_{it}$,$CI_j$ represent the family income for parent i and child j and $S_j$ denotes demand of services of parent i from child j. The model additionally makes several shape restrictions on the utility functions. (i) Both parent’s and children’s consumptions, $C_{it}$ and $C_j$, are assumed to be normal goods, so that $\frac{\partial U_{i}}{\partial C_{i}}>0$, $\frac{\partial U_{j}}{\partial C_{j}}>0$. (ii) Providing caring services benefits the parents but is costly to children.⁸ Therefore, $\frac{\partial U_{j}}{\partial S_{j}}<0$,$\frac{\partial U_{i}}{\partial S_{j}}>0$. (iii) Parents care about children’s utility: $\frac{\partial U_{i}}{\partial U_{j}}>0$. (iv) Child j would provide $S_j$ service to parent i only if constraint (9) holds. That is, the net payoff of the transfer payment $T_{it}$ and committing the costly service $S_j$ is positive.

Imposing constraints (7)–(9), the problem described in (6) can be written as the following Lagrangian form:

$$\begin{aligned} {\mathcal {L}}(T_{it},S_j,\lambda )&= U_{i}(PI_{i}-T_{i}, S_{j},U_{j}(CI_{j}+T_{i},S_{j}))\nonumber \\&\quad +\lambda [U_{j}(CI_{j}+T_{i},S_{j})- U_{j}(CI_{j},0)] \end{aligned}$$

(10)

One important observation is that when transfer is purely motivated by the exchange motive, parents will set the transfer amount $T_{it}$ such that $U_{j}(CI_{j}+T_{i},S_{j})= U_{j}(CI_{j},0)$. In this case, a binding constraint (9) would imply $\lambda >0$. On the other hand, when the transfer behavior is effectively motivated by the altruistic motive, parents would transfer more than just balancing children’s utility, implying $U_{j}(CI_{j}+T_{i},S_{j})> U_{j}(CI_{j},0)$. In this case, a non-binding constraint (9) would imply $\lambda =0$.

After solving the Kuhn–Tucker conditions implied by Eq. (10) with the associated $\lambda$ values, Cox shows that the following conditions have to hold for the optimal transfer amount $T^*_{it}$:

$$\begin{aligned} \lambda > 0&\implies \frac{\partial T^*_{i}}{\partial CI_{j}}<0 \;\;\;\text {(if Altruistic Motive)} \end{aligned}$$

(11)

$$\begin{aligned} \lambda = 0&\implies \frac{\partial T^*_{i}}{\partial CI_{j}}>0 \;\;\;\text {(if Exchange Motive)} \end{aligned}$$

(12)

Should the transfer amount $T_{it}$ is observed in data, the sign of $\frac{\partial T_{i}}{\partial CI_{j}}$ can be exploited to formally test which motive denominates. If the transfer behavior is altruistically motived, a rise in child’s income would decrease the transfer amount. Under the exchange motive, the transfer amount, however, would increase as the child’s income rises, especially when the service demand of parents from children is relatively inelastic. As a final remark, Cox also shows that under either motive, the probability that a transfer occur is a decreasing function of the child’s income.⁹

Appendix B Estimation of the KV approach

Let $F(\cdot )$ denote the cumulative distribution function of $u^*$ in Eq. (4) and $\lambda (\cdot ) \equiv M \circ F^{-1} (\cdot )$; it is easy to show that

$$\begin{aligned} M(Z^*_{it}\alpha _0) = M \circ F^{-1} (F(Z^*_{it}\alpha _0)) = M \circ F^{-1} (P_{it}) = \lambda (P_{it}) \end{aligned}$$

(13)

where $P_{it}$ is the selection probability given by $P_{it} \equiv Prob(T_{it} = 1|Z_{it})$. Since we make no parametric assumptions with respect to the joint distribution of $u^*$ and v, the functional forms of $M(\cdot )$ and $\lambda (\cdot )$ are left unspecified. Substituting (13) to (3) gives,

$$\begin{aligned} E[TA_{it}|Z_{it}, T_{it} = 1] = Z_{it}\beta _0 + \lambda (P_{it}) \end{aligned}$$

(14)

We employ a two-step procedure to estimate $\beta$ in the above equation. In the first step, we estimate the transfer probability $P_{it}$ using quasi-maximum likelihood. When $S(Z_{it}) =exp(Z_{it}\pi _0)$, the probability can be estimated in a heteroskedastic probit. However, estimation of the transfer probability is in general complicated when the S function is unknown and the dimension of Z is large. To obtain reasonable estimates at moderate sample sizes, KV assumes that the Z’s enter the S function in an index form:

$$\begin{aligned} S(Z_{it}) = S(Z_{it}\pi _0) \end{aligned}$$

(15)

where $\pi _0$ are unknown parameters. The form of $S(\cdot )$ is left unspecified to permit a flexible mechanism that generates the heteroskedasticity. Given this index assumption, the transfer probability

$$\begin{aligned} P_{it} \equiv Prob[u_{it}> -Z_{it}\alpha _0] = Prob[S(Z_{it}\pi _0)u^* > -(Z_{it}\alpha _0)] = P(Z_{it}\alpha _0, Z_{it}\pi _0)\nonumber \\ \end{aligned}$$

(16)

can be characterized as a function of two indices $Z_{it}\alpha _0$ and $Z_{it}\pi _0$, one affecting the conditional mean response and the other affecting the conditional variance (Table 5).

Once the selection probability above is estimated, we employ method developed by Robinson (1988) to estimate $\beta _0$ in equation (14) in the second step. The idea is to first calculate the expectation of both sides of the equation conditional on the estimated selection probability $\widehat{P}_{it}$. Based on the identity that $\lambda (\widehat{P}) =E[\lambda (\widehat{P})| \widehat{P}]$, taking a difference would drop out the $\lambda (\widehat{P})$,

$$\begin{aligned} \underbrace{TA_{it} - E[TA_{it}|\widehat{P}]}_{TA^{\#}} = \underbrace{(Z_{it}-E[Z_{it}|\widehat{P}])}_{Z^{\#}}\beta _0 + \epsilon _{it} \end{aligned}$$

(17)

Estimators of the conditional expectations (e.g., $E[TA_{it}|\widehat{P}], E[Z_{it}|\widehat{P}]$) in this equation can be obtained using kernel estimators with bandwidth equals 1/5. Then, $\beta _0$ can be estimated by regressing $TA^{\#}$ on $Z^{\#}$.

Table 5 Summary of empirical tests of intergenerational transfer

One technical detail should be noted here. The parameters $\alpha 's$ and $\pi 's$ in Eq. (16) are not identified because both indices are driven by the same vector $Z_{it}$.¹⁰ However, KV shows the selection probability $P_{it}$ can be estimated consistently based on a re-parametrization of the two indices, provided that $Z_{it}$ contains two distinct continuous variables. To illustrate, let $Z_1, Z_2$ represent two distinct continuous variables in $Z_{it}$. With $Z_3$ representing all remaining explanatory variables (e.g., $Z_{it} \equiv [Z_{1i},Z_{2i},Z_{3i}]$), write the index vector

$$\begin{aligned} Q \equiv [Z\pi _0,Z\alpha _0]\equiv [Z_1, Z_2, Z_3] \left[ \begin{array}{cc} \Gamma _{c} &{} \\ \Gamma _{31} &{} \Gamma _{32} \end{array}\right] , \;\; \text {with}\;\; \Gamma _c\equiv \left[ \begin{array}{cc} \Gamma _{11} &{} \Gamma _{12} \\ \Gamma _{21} &{} \Gamma _{22} \end{array}\right] \end{aligned}$$

(18)

Assuming that the $2\times 2$ submatrix $\Gamma _c$ has full-rank, we can define

$$\begin{aligned} W\equiv Q*\Gamma _{c}^{-1} = [Z_1, Z_2, Z_3]\left[ \begin{array}{cc} 1 &{} 0 \\ 0 &{} 1 \\ \pi _{31} &{} \pi _{32} \end{array} \right] = [Z_1+ \pi _{31}Z_3, Z_2+\pi _{32}Z_3] \end{aligned}$$

(19)

Under this re-parameterization, note that $Prob[T_{it}=1|Q]=Prob[T_{it}=1|W]$. Importantly, each index in W now contains an excluded variable so that $\pi _{31},\pi _{32}$ can be identified and estimated consistently.

With $\widehat{P}$ as a kernel-type nonparametric conditional expectations estimator for the selectin probability in (16), a quasi-maximum-likelihood approach can be employed to estimate $\pi _{31}, \pi _{32}$. The kernel bandwidth is set to be $r = 1/9$ to ensure $\sqrt{N}-$normality because $\widehat{P}$ is a two-dimensional nonparametric expectation. Based on (16) and (19), the selection probability can be estimated by $\widehat{P}(Z_1+ \widehat{\pi _{31}}Z_3, Z_2+\widehat{\pi _{32}}Z_3)$.

Appendix C Bias from inverse Mills ratio

Let $\gamma (\cdot ) \equiv \phi (\cdot )/\Phi (\cdot )$ denote the inverse Mills ratio function. We note the inverse Mills ratio can be written as a function of the selection probability $P_{it}$,

$$\begin{aligned} \lambda ^*(P_{it}) = \gamma (\Phi ^{-1}(P_{it})) =\gamma (Z_{it}\alpha _0) \end{aligned}$$

(20)

Recall from the estimated transfer amount model in (14), in which we denote the true correction term as $\lambda (P_{it})$. If the inverse Mills ratio, $\lambda ^*(P_{it})$, is incorrectly employed, the misspecified model is subject to omitted variable bias:

$$\begin{aligned} E[TA_{it}|Z_{it},T_{it}=1]= & {} Z_{it}\beta _0 + \lambda (P_{it}) \end{aligned}$$

(21)

$$\begin{aligned}= & {} Z_{it}\beta _0+ \lambda ^*(P_{it}) +\underbrace{[\lambda (P_{it})-\lambda ^* (P_{it})]}_{\textrm{Omitted}\ \textrm{term}} \end{aligned}$$

(22)

As such, the correlation between $Z_{it}$ and $\lambda (P_{it})-\lambda ^*(P_{it})$ will dictate the direction of bias in estimating $\beta _0$.

It can be seen from Fig. 2 that $\lambda (P)$ is generally increasing with respect to the selection probability $P_{it}$. Since $\gamma (\cdot )$ is decreasing and $\Phi ^{-1}$ is increasing in their argument, respectively, $\lambda ^*(\cdot )$ is decreasing in $P_{it}$. Therefore, there is a positive relationship between $P_{it}$ and $\lambda (P_{it})-\lambda ^*(P_{it})$. Taken together, for variables that have a negative impact on $P_{it}$, the correlation between that variable and the omitted term $\lambda (P_{it}) -\lambda ^*(P_{it})$ is also negative, implying a downward bias in its regression coefficient. In the case of children’s income, which is known to have a negative impact on the selection probability, the inverse Mills ratio will underestimate the transfer–income derivative.