Estimation of the production profile and metafrontier technology gap: a quantile approach

Abstract

In this paper, a quantile function is suggested as an alternative description of a production technology. Since the quantile function may not share the same functional properties as the frontier function, it is argued that the quantile-based production function serves as a better benchmark for a firm’s production structure analysis. This argument is extended to the metafrontier analysis. The quantile metafrontier is defined as the envelopment of all groups’ quantile frontier at the same quantile level. The quantile technology gap serves as a more relevant indicator of efficiency in the adopted technology than the traditional measure of the metafrontier technology gap. The quantile approach is illustrated using survey data to estimate the earning profiles for men, and the impact of human capital on the industrial wage distributions in the service industry, the manufacturing industry, and all other industries in Taiwan.

Appendix

1.1 I. The quantile production function with homoscedastic and heteroscedastic errors

In output orientation, the quantile-$\tau$ function $Q_{Y|X} \left( {\tau |x} \right)$ corresponds to the quantile-$\tau$ frontier and the production frontier $\varPhi \left( x \right)$ corresponds to the quantile-one function. Figures 4 and 5 show the maps of the quantile-$\tau$ function $Q_{Y|X} \left( {\tau |x} \right)$ with homoscedastic and heteroscedastic errors.

Fig. 4

Quantile distribution of the homoscedastic error $\epsilon$. ${\text{TE}}_{\text{A}} = Q_{Y|X} \left( {0.98|x} \right) /\varPhi \left( x \right)$; ${\text{QTE}}_{\text{A}} \left( {0.98} \right) = {\text{QTE}}_{\text{B}} \left( {0.5} \right) = 1$

Fig. 5

Quantile distribution of the heteroscedastic error $\epsilon$. ${\text{TE}}_{\text{A}} = Q_{Y|X} \left( {0.98|x} \right) /\varPhi \left( x \right)$; ${\text{QTE}}_{\text{A}} \left( {0.98} \right) = {\text{QTE}}_{\text{B}} \left( {0.5} \right) = 1$

Figure 4 illustrates a profile of the quantile functions at various quantile levels with iid of $\epsilon$, i.e., $Q_{\epsilon |X} \left( {\tau |x} \right) = Q_{\epsilon } \left( \tau \right)$. The quantile function $Q_{Y|X} \left( {\tau |x} \right) = \varPhi \left( x \right)\exp \left( {Q_{\epsilon } \left( \tau \right)} \right)$ is simply a vertical displacement of one another as $\tau$ decreases, and the logarithmic quantile function $\ln Q_{Y|X} \left( {\tau |x} \right) = \ln \varPhi \left( x \right) + Q_{\epsilon } \left( \tau \right)$ is a parallel downward shift from $\ln \varPhi \left( x \right)$ with identical slope. Hence, estimation of the frontier function alone is then sufficient to reveal the properties of all other quantile production functions such as the returns to scale at $Q_{Y|X} \left( {0.75|x} \right)$ or at $Q_{Y|X} \left( {0.50|x} \right)$.

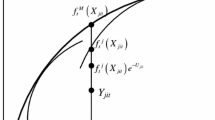
Figure 5 depicts a scenario where the one-side error $\epsilon$ is heteroscedastic. Consider, for example, the scaling model of Wang and Schmidt (2002) specifies $\epsilon = h\left( x \right)\epsilon^{*}$, where the scaling function $h\left( x \right) \ge 0$ and the basic distribution $F_{{\epsilon^{*} }} \left( {\epsilon^{*} } \right)$ of the nonpositive error $\epsilon^{*} \le 0$ does not depend on $x$. The quantile-$\tau$ function of the deterministic frontier becomes $Q_{Y|X} \left( {\tau |x} \right) = \varPhi \left( x \right)\exp \left( {h\left( x \right)Q_{{\epsilon^{*} }} \left( \tau \right)} \right)$. In this case, the quantile functions $Q_{Y|X} \left( {\tau |x} \right)$ would not share the same properties as the frontier function $\varPhi \left( x \right)$. Since

$$ \ln Q_{Y|X} \left( {\tau |x} \right) = \ln \varPhi \left( x \right) + h\left( x \right)Q_{{\epsilon^{*} }} \left( \tau \right), $$

(a)

we have

$$ \frac{{\partial \ln Q_{Y|X} \left( {\tau |x} \right)}}{\partial \ln x} = \frac{\partial \ln \varPhi \left( x \right)}{\partial \ln x} + \frac{{\partial h\left( x \right)Q_{{\epsilon^{*} \left( \tau \right)}} }}{\partial \ln x} \ne \frac{\partial \ln \varPhi \left( x \right)}{\partial \ln x}. $$

(b)

The logarithmic quantile function $\ln Q_{Y} \left( {\tau |x} \right)$ does not share the same slope as in $\ln \varPhi \left( x \right)$. Using the slope of the estimated frontier function $\ln \hat{\varPhi }\left( x \right)$ to predict, for example, the returns to scale for the third-quartile production function $\ln Q_{Y|X} \left( {0.75|x} \right)$ may give misleading results.

1.2 II: The graph illustration of the quantile-$\varvec{\tau}$ metafrontier technology gap

Figure 2 illustrates the definition of the quantile-$\tau$ metafrontier technology gap. At each quantile level, the quantile-$\tau$ metafrontier $Q_{Y|X}^{\text{meta}} \left( {\tau |x} \right)$ envelops all group-specific quantile-$\tau$ frontiers $Q_{Y|X}^{j} \left( {\tau |x} \right)$. Firm C of the first group ($j = 1$) lies on the group’s quantile-one frontier $\varPhi^{1} \left( {x_{0} } \right) = Q_{Y|X}^{1} \left( {1|x_{0} } \right)$, and its quantile metafrontier technology gap is ${\text{QMTG}}^{1} \left( 1 \right) = \frac{\hbox{CO}}{\hbox{DO}} = \frac{{Q_{Y|X}^{1} \left( {1|x_{0} } \right)}}{{Q_{Y|X}^{\text{meta}} \left( {1|x_{0} } \right)}}$, which is the conventional definition of technology gap, ${\text{MTG}}^{1} = \frac{{ \varPhi^{1} \left( {x_{0} } \right)}}{{ \varPhi^{\text{meta}} \left( {x_{0} } \right)}}$. On the other hand, the output of firm A of the first group lies on the group’s quantile-$\tau$ frontier $Q_{Y|X}^{1} \left( {\tau |x_{0} } \right)$, i.e., $y = Q_{Y|X}^{1} \left( {\tau |x_{0} } \right)$, and is therefore quantile-$\tau$ technical efficient, i.e., ${\text{QTE}}^{1} \left( \tau \right) = 1,$ even though it is not group-specific technically efficient as ${\text{TE}}^{1} = \frac{\hbox{AO}}{\hbox{CO}} = \frac{{Q_{Y|X}^{1} \left( {\tau |x_{0} } \right)}}{{ \varPhi^{1} \left( {x_{0} } \right)}} < 1.$ Furthermore, since the quantile-$\tau$ metafrontier $Q_{Y|X}^{\text{meta}} \left( {\tau |x} \right)$ envelops all groups’ quantile-$\tau$ frontiers, firm A’s ${\text{QMTG}}^{1} \left( \tau \right)$ is the vertical distance from $Q_{Y|X}^{1} \left( {\tau |x_{0} } \right)$ to $Q_{Y|X}^{\text{meta}} \left( {\tau |x_{0} } \right)$ at point A, i.e., ${\text{QMTG}}^{1} \left( \tau \right) = \frac{\hbox{AO}}{\hbox{BO}} = \frac{{Q_{Y|X}^{1} \left( {\tau |x_{0} } \right)}}{{Q_{Y|X}^{\text{meta}} \left( {\tau |x_{0} } \right)}}$. This alternative measure of technology gap differs from the vertical distance measured from the group frontier $\varPhi^{1} \left( x \right)$ to the metafrontier $\varPhi^{\text{meta}} \left( x \right)$.