Abstract
This paper outlines a methodology to test for structural break in a smooth time-varying cointegration model. We show how such a problem can be brought down to the standard procedure proposed by Hansen (J Bus Econ Stat 10:321–335, 1992). As an application, we investigate the long-run relationship between the crude oil price and the gasoline retail price for Switzerland.





Similar content being viewed by others
Notes
See Bierens (1997) for technical details on Chebyshev time polynomials.
Notice that the authors do not provide a formal proof of this consistency.
If equation (1) includes an intercept, this matrix should be \(M_{[T\tau ]}=\sum _{t=1}^{[T\tau ]}(x_t-\bar{x})(x_t-\bar{x})^{\prime }\).
Notice that the supremum is also favored here to minimize the consequences of the end-point problem, inherent to polynomial regression technics.
The values used for our experiments are the following: \(\xi =(1.5,0.2)^\prime \) and \(\xi _c=(0.2,-0.7)^\prime \) for \(m=1; \xi =(1.5,-1.2,0.2)^\prime \) and \(\xi _c=(-0.7,-0.1,0.2)^\prime \) for \(m=2\).
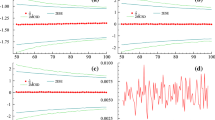
The crude oil recorded a price equals to 144USD in July 2008.
References
Bai J, Lumsdaine RL, Stock JH (1998) Testing for and dating common breaks in multivariate time series. Rev Econ Stud 65:395–432
Balke HS, Fomby TB (1997) Threshold cointegration. Int Econ Rev 38:627–645
Banerjee A, Lumsdaine RL, Stock JH (1992) Recursive and sequential tests of the unit-root and trend-break hypotheses: theory and international evidence. J Bus Econ Stat 10:271–287
Bierens HJ (1997) Testing the unit root with drift hypothesis against nonlinear trend stationarity, with an application to the US price level and interest rate. J Econom 81:29–64
Bierens HJ, Martins LF (2010) Time-varying cointegration. Econom Theory 26:1453–1490
Enders W, Siklos PL (2001) Cointegration and threshold adjustment. J Bus Econ Stat 19:166–176
Gonzalo J, Pitarakis PY (2006) Threshold effects in multivariate error correction models. In: Mill TC, Patterson K (eds) Palgrave handbook of econometrics, vol 1. Palgrave Macmillan, Hampshire, pp 578–609
Gregory AW, Hansen BE (1996) Residual-based test for cointegration in models with regime shifts. J Econom 70:99–126
Gregory AW, Nason JM, Watt D (1996) Testing for structural breaks in cointegrated relationships. J Econom 71:321–341
Hansen BE (1992) Tests for parameter instability in regressions with I(1) processes. J Bus Econ Stat 10:321–335
Hansen BE, Seo B (2002) Testing for two-regime threshold cointegration in vector error-correction models. J Econom 110:293–318
Krishnakumar J, Neto D (2011) Testing the inaction corridor in a three-regime threshold error correction model: an application to a Buffer-Stock model for U.S. money demand. Econ Notes 40:29–43
Krishnakumar J, Neto D (2012) Testing uncovered interest rate parity and term structure using three-regime threshold unit root VECM: an application to the Swiss interest rates islet. Oxf Bull Econ Stat 74:180–202
MacKinnon JG (2010) Critical values for cointegration tests. Queen’s Economics Department Working Paper, 1227
Neto D (2012) Testing and estimating time-varying elasticities of Swiss gasoline demand. Energy Econ 34:1755–1762
Park JY, Phillips PCB (1988) Statistical inference in regressions with integrated processes: part I. Econom Theory 4:468–497
Park JY (1992) Canonical cointegrating regression. Econometrica 60:119–143
Park JY, Hahn SB (1999) Cointegrating regressions with time varying coefficients. Econom Theory 15:664–703
Park SY, Zaho G (2010) An estimation of U.S. gasoline demand: a smooth time-varying cointegration approach. Energy Econ 32:110–120
Perron P (1989) The great crash, the oil price shock, and the unit root hypothesis. Econometrica 57:1361–1401
Phillips PCB, Hansen BE (1990) Statistical inference in instrumental variables regression with I(1) processes. Rev Econ Stud 57:99–125
Phillips PCB (1995) Fully modified least squares and vector autoregression. Econometrica 63:1023–1078
Kurozumi E, Arai Y (2005) Efficient estimation and inference in cointegrating regressions with structural change. J Time Ser Anal 28:545–575
Seo M (2006) Bootstrap testing for the null of no cointegration in a threshold vector error correction model. J Econom 134:129–150
Xiao Z, Phillips PCB (2002) A CUSUM test for cointegration using regression residuals. J Econom 108:43–61
Xiao Z (2009) Functional-coefficient cointegration models. J Econ 152:81–92
Zivot E, Andrews DWK (1992) Further evidence on the great crash, the oil-price shock, and the unit-root hypothesis. J Bus Econ Stat 10:251–270
Author information
Authors and Affiliations
Corresponding author
Additional information
The author was a Post-Doctoral Research Assistant at the Department of Economics, University of Geneva, when an early version of this paper was written.
Appendix
Appendix
The limiting distribution of \(\text {CS}_T\) under time-varying cointegration can be obtained using Lemma 2 in Bierens and Martins (2010) and Theorem 1 of Xiao and Phillips (2002).
Lemma A.1
Under the assumption of \(\Delta x_{t}\) being a strictly stationary zero-mean \(p\)-variate process such that \(\Delta x_{t}=e_{t}\) with \(e_{t}\) i.i.d \((0,\varOmega )\), defining \(Z_{t}\) as in equation (7) and denoting \(\varOmega ^{\frac{1}{2}}\) as the Cholesky factorization of \(\varOmega \), i.e. \(\varOmega =\varOmega ^{\frac{1}{2}}\varOmega ^{\frac{1}{2}\prime }\), using Lemma 2 of Bierens and Martins (2010), it comes the following limiting distributions:
where \(S^{(m)}(r)\) is defined as:
where \(W_2(r)\) is a \((p-1)\) vector Brownian motion.
Note that the above results are immediate if \(e_{t}\) is serially correlated such as \(e_{t}=\Phi (L)v_t=\sum _{s=0}^{\infty }\Phi _se_{t-s}\), and we assume that \(\sum _{s=0}^{\infty }s|\phi ^{(s)}_{ij}|<\infty \) for each i,j=1,...,n for \(\phi ^{(s)}_{ij}\), the row i, column j element of \(\Phi _s\) and that \((v_t)\) is an i.i.d. sequence with mean 0, variance \(\varOmega _v\) with the factorization \(\varOmega _v=\varOmega _v^{\frac{1}{2}}\varOmega _v^{\frac{1}{2}\prime }\), finite fourth moments. We have in this case:
and
where \(\varOmega _s=\mathbb {E}(e_te_{t-s}^\prime )=\sum _{k=0}^\infty \Phi _{s+k}\varOmega _v\Phi _{k}^\prime \) for \(s=0,1,2,\ldots \), and where \(\varLambda ^{\frac{1}{2}}=\Phi (1)\varOmega _{v}^{\frac{1}{2}}\) with \(\Phi (1)\) nonsingular.
Using the previous results and following Phillips and Hansen (1990) and Phillips (1995) to establish the limiting distribution of \(1/\sqrt{T}\left| \sum _{t=1}^{[Tr]}\hat{u}^+_t\right| \), with \(r\in [0,1]\), the convergence (12) can be stated, which is similar to the standard time-invariant case presented in Theorem 1 of Xiao and Phillips (2002). \(\square \)
Rights and permissions
About this article
Cite this article
Neto, D. Testing for and dating structural break in smooth time-varying cointegration parameters, with an application to retail gasoline price and crude oil price long-run relationship. Empir Econ 49, 909–928 (2015). https://doi.org/10.1007/s00181-014-0907-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00181-014-0907-6
Keywords
- Smooth time-varying cointegration
- Structural break
- FMLS
- Score test
- FM Wald test
- FMLS-based CUSUM test
- Crude oil price and retail price of gasoline