1 Introduction

In recent years, there has been a growing interest in modelling integer-valued time series of univariate and multivariate count data in a plethora of different scientific fields such as sociology, econometrics, manufacturing, engineering, agriculture, biology, biometrics, genetics, medicine, sports, marketing, and insurance. In particular, regarding the univariate case (Al-Osh and Alzaid 1987) and McKenzie (1985) were the first to consider an INAR(1) model based on the so-called binomial thinning operator. Subsequently, many articles focused on extending this setup by applying different thinning operators or by varying the distribution of innovations. For more details, the interested reader can refer to Weiß (2018), Davis et al. (2016), Scotto et al. (2015), Weiß (2008) among many more. The INAR(1) model with Poisson marginal distribution (Poisson INAR(1)) has been the most popular choice due to the simplicity of its log-likelihood function that implies that the formality of parameter estimation via maximum likelihood (ML) estimation is straightforward. Also, Freeland and McCabe (2004) considered an extension of the model by allowing for regression specifications on the mean of the Poisson innovation as well as parameter of binomial thinning operator. On the other hand, the literature which focuses on the multivariate case is less developed. In particular, Latour (1997) introduced a multivariate GINAR(p) model with a generalized thinning operator. Karlis and Pedeli (2013) and Pedeli and Karlis (2011, 2013a, b) focused on the diagonal case under which the thinning operators do not introduce cross correlation among different counts. In this case, the dependence structure introduced by innovations. Additionally, Ristić et al. (2012), Popović (2016), Popović et al. (2016) and Nastić et al. (2016) constructed multivariate INAR distributions with cross correlations among counts and random coefficients thinning. Finally, Karlis and Pedeli (2013) extended the setup of the previous articles by allowing for negative cross correlation via a copula-based approach for modelling the innovations.

In this paper, we extend the model proposed by Pedeli and Karlis (2011) by introducing the multivariate mixed Poisson-Generalized Inverse Gaussian INAR(1), MMPGIG-INAR(1), regression model for multivariate count time series data. The MMPGIG-INAR(1) is a general three parameter distribution family of INAR(1) models driven by mixed Poisson regression innovations where the mixing densities are chosen from the Generalized Inverse Gaussian class of distributions. Thus, the proposed modelling framework can provide the appropriate level of flexibility for modelling positive correlations of different magnitudes among time series of different types of overdispersed count response variables. In particular, depending on the values taken by the shape parameter, the MMPGIG-INAR(1) family includes many members, such as the mixed Poisson-Inverse Gaussian (PIG), as special cases and several others as limiting cases, such as the Negative Binomial, or Poisson-Gamma, the Poisson-Inverse Gamma (PIGA), the Poisson-Inverse Exponential, the Poisson-Inverse Chi Squared and the Poisson-Scaled Inverse Chi Squared distributions. Therefore, it can accommodate different levels of overdispersion depending on the chosen parametric form of the mixing density. Furthermore, the MMPGIG-INAR(1) family of models is constructed by assuming that the probability mass function (pmf) of the MMPGIG innovations is parameterized in terms of the mean parameter which results in a more orthogonal parameterization that facilitates maximum likelihood (ML) estimation when regression specifications are allowed for the mean parameters of the MMPGIG-INAR(1) regression model. For expository purposes, we derive the joint probability mass functions and the derivatives of several special cases of the MMPGIG-INAR(1) family which are used as innovations. These models are fitted to time series of claim count data from the Local Government Property Insurance Fund (LGPIF) data in the state of Wisconsin. At this point it is worth noting that modelling the correlation between different types of claims from the same and/or different types of coverage it is very important from a practical business standpoint. Many articles have been devoted to this topic, see for example, Bermúdez and Karlis (2011), Bermúdez and Karlis (2012), Shi and Valdez (2014a, b), Abdallah et al. (2016), Bermúdez and Karlis (2017), Pechon et al. (2018), Pechon et al. (2019), Bolancé and Vernic (2019), Denuit et al. (2019), Fung et al. (2019), Bolancé et al. (2020), Pechon et al. (2021), Jeong and Dey (2021), Gómez-Déniz and Calderín-Ojeda (2021), Tzougas and di Cerchiara (2021a, b). However, with the exception of very few articles, such as Bermúdez et al. (2018) and Bermúdez and Karlis (2021), the construction of bivariate INAR(1) models which can capture the serial correlation between the observations of the same policyholder over time and the correlation between different claim types remains a largely uncharted territory. This is an additional contribution of this study.

The rest of the paper proceeds as follows. Section 2 presents the derivation of the MMPGIG-INAR(1) model. Statistical properties of the MMPGIG innovations are discussed in Sect. 3. In Sect. 4, we present a description of the alternative special cases of the MMPGIG-INAR(1) family. Section 5 discusses the parameter estimation for these models based on the maximum likelihood method and integer-valued prediction. Section 6 contains our empirical analysis for the LGPIF data set. Finally, concluding remarks are given in Sect. 7.

2 Generalized setting

Let \(\mathbf {X}\) and \(\mathbf {R}\) be non-negative integer-valued random vectors in \({\mathbb {R}}^m\). Let \(\mathbf {P}\) be a diagonal matrix in \({\mathbb {R}}^{m \times m}\) with elements \(p_i \in (0,1)\). The multivariate Poisson-Generalized Inverse Gaussian INAR(1) is defined as

$$\begin{aligned} \mathbf {X}_t = \mathbf {P} \circ \mathbf {X}_{t-1} + \mathbf {R}_t =\begin{bmatrix} p_1 &{} 0 &{} \dots &{} 0&{} 0 \\ 0 &{} p_2 &{} \dots &{} 0 &{}0 \\ \vdots &{}&{}\ddots &{}&{}\vdots \\ 0&{}0&{}\dots &{} &{}p_m\\ \end{bmatrix} \circ \begin{bmatrix} X_{1,t-1}\\ X_{2,t-1} \\ \vdots \\ X_{m,t-1} \end{bmatrix} + \begin{bmatrix} R_{1,t}\\ R_{2,t} \\ \vdots \\ R_{m,t} \end{bmatrix} \end{aligned}$$
(2.1)

where the thinning operator \(\circ\) is the widely used binomial thinning operator such that \(p_i \circ X_{i,t} = \sum _{k=1}^{X_{i,t}} U_k\) where \(U_k\) are independent identically distributed Bernoulli random variables with success probability \(p_i\), i.e. \({\mathcal {P}}(U_k = 1) = p_i\). Hence \(p_i \circ X_{i,t}\) is binomially distributed with size \(X_{i,t}\) and success probability \(p_i\). Then the distribution function \(f_{p_i}(x, X_{i,t})\) can be easily written down as

$$\begin{aligned} f_{p_i}(x, X_{i,t}) = \left( {\begin{array}{c}X_{i,t}\\ x\end{array}}\right) p_i^ x (1 - p_i)^{X_{i,t} - x} \end{aligned}$$
(2.2)

Note that given \(X_{i,t}, X_{j,t} \ i \ne j\), \(p_i \circ X_{i,t}\) and \(p_j \circ X_{j,t},\) are independent of each other. To adapt the heteroscedasticity arising from the data, \(\{R_{i,t}\}_ {i=1,\ldots ,m}\) are mixed Poisson random variables \(Po(\theta _t \lambda _{i,t})\) with the random effect \(\theta _t\). The rate \(\lambda _{i,t}\) is characterized by its observed covariate \(z_{i,t} \in {\mathbb {R}}^{a_i \times 1 }\) for some positive integer \(a_i\) and they are connected through a log link function such that \(\log (\lambda _{i,t}) = z_{i,t}^{T} \beta _i\) where \(\beta _i \in {\mathbb {R}}^{a_i \times 1 }\). Furthermore, \(\{R_{i,t}\}_ {i=1,\ldots ,m}\) share the same random effect \(\theta _t\) with mixing distribution \(G(\theta )\), which means the dependent structure among \(X_{i,t}\) can be controlled by the choice of distribution and its corresponding size of parameters. The joint distribution of \(\mathbf {R}_t\) is

$$\begin{aligned} f_{\phi }(\mathbf {k},t)&= {\mathcal {P}}(R_{1,t} = k_1, \ldots , R_{m,t} = k_m) \nonumber \\&= {\mathbb {E}}\left[ {\mathcal {P}}(R_{1,t} = k_1, \ldots , R_{m,t} = k_m | \theta _t )\right] \nonumber \\&= \prod _{j=1}^m \frac{\lambda _{j,t}^{k_j}}{k_j!} \int _{0}^{\infty } e^{- \theta \sum _{i=1}^m \lambda _{i,t} } \theta ^{\sum _{i=1}^m k_i} dG(\theta ) \end{aligned}$$
(2.3)

We let \(\theta _t\) be a continuous random variable from the Generalized Inverse Gaussian distribution with density function \(g(\theta )\)

$$\begin{aligned} g(\theta ) = \frac{(\psi / \chi )^{\frac{\nu }{2}}}{2K_{\nu }(\sqrt{\psi \chi })} \theta ^{\nu -1} \exp \left\{ -\frac{1}{2} \left( \psi \theta + \frac{\chi }{ \theta } \right) \right\} , \end{aligned}$$
(2.4)

where \(-\infty \le \nu \le \infty , \psi>0, \chi >0\) and \(K_{\nu }(\omega )\) is the modified Bessel function of the third kind of order \(\nu\) and argument \(\omega\) such that

$$\begin{aligned} K_{\nu }(\omega ) = \int _{0}^{\infty } z^{\nu -1} \exp \left\{ - \frac{1}{2} \omega \left( z + \frac{1}{z}\right) \right\} dz \end{aligned}$$

The Generalized Inverse Gaussian distribution is a widely used family. For example, it includes the Inverse Gaussian as special case and the Gamma and Inverse Gamma as limiting cases. To avoid identification problems for mixed Poisson regression random variable \(\mathbf {R}_t\), the mean of \(\theta _t\) is restricted to one, i.e. \({\mathbb {E}}[\theta _t] = 1\), and all the parameters \(\nu , \psi , \chi\) will be either fixed or a function of another parameter \(\phi\). With these two constraints, there is only one parameter that is free to vary. (e.g. for Inverse Gaussian distribution, \(\nu = -\frac{1}{2}\) and \(\psi = \chi = \phi\)). The joint distribution of \(\mathbf {R}_t\) becomes an MPGIG distribution

$$\begin{aligned} f_{\phi }(\mathbf {k},t)&= \frac{(\psi / \chi )^{\frac{\nu }{2}}}{2K_{\nu }(\sqrt{\psi \chi })} \prod _{j=1}^m \frac{\lambda _{j,t}^{k_j}}{k_j!} \int _{0}^{\infty } e^{- \theta \sum _{i=1}^m \lambda _{i,t} } \theta ^{\sum _{i=1}^m k_i} \theta ^{\nu -1} \exp \left\{ -\frac{1}{2} \left( \psi \theta + \frac{\chi }{ \theta } \right) \right\} d\theta \nonumber \\&= \frac{(\psi / \chi )^{\frac{\nu }{2}}}{(\varDelta / \chi )^{\frac{\nu + \sum _{i} k_i}{2}}} \frac{K_{\nu + \sum _{i} k_i} (\sqrt{\varDelta \chi })}{K_{\nu }(\sqrt{\psi \chi })} \prod _{j=1}^m \frac{\lambda _{j,t}^{k_j}}{k_j!}, \end{aligned}$$
(2.5)

where \(\varDelta = \psi + 2 \sum _{i=1}^m \lambda _{i,t}\). In Sect. 5, we will discuss in detail the distribution function \(f_{\phi }(\mathbf {k},t)\) for some special cases. Finally, it should be noted that several articles discuss multivariate versions of MPGIG distribution and/or the MPIG distribution which is a special case for \(\nu =-0.5\), see, for instance, Barndorff-Nielsen et al. (1992), Ghitany et al. (2012) Amalia et al. (2017), Mardalena et al. (2020), Tzougas and di Cerchiara (2021b) and Mardalena et al. (2021). However, this is the first time that the MMPGIG-INAR(1) distribution family of INAR(1) models driven by mixed Poisson regression innovations are considered for modelling time series of count response variables.

3 Properties of innovations \(\mathbf {R}_t\)

Proposition 3.1

(The moments of \(\mathbf {R}_t\)) The mean, variance of \(R_{i,t}\) and covariance between \(R_{i,t}, R_{j,t}, i\ne j\) are given by

$$\begin{aligned} {\mathbb {E}}[R_{i,t}]&= {\mathbb {E}}[ {\mathbb {E}}[R_{i,t} | \theta _t] ] = \lambda _{i,t}\nonumber \\ Var(R_{i,t})&= Var({\mathbb {E}}[R_{i,t} | \theta _t]) + {\mathbb {E}}[Var(R_{i,t} | \theta _t) ]\nonumber \\&= \sigma ^2_{\theta } \lambda _{i,t}^2 + \lambda _{i,t} \nonumber \\ Cov(R_{i,t} , R_{j,t})&= Cov({\mathbb {E}}[R_{i,t} | \theta _t], {\mathbb {E}}[ R_{j,t} | \theta _t] ) + {\mathbb {E}}[Cov(R_{i,t}, R_{j,t} | \theta _t)] \nonumber \\&= \lambda _{i,t} \lambda _{j,t} \sigma _{\theta }^2 \end{aligned}$$
(3.1)

where \(\sigma _{\theta }^2\) is the variance for the random effect \(\theta _t\) and \(i,j = 1,\ldots ,m\).

Proposition 3.2

(Marginal property) The joint distribution function \(f_{\phi }(\mathbf {k},t)\) is closed to marginalization, i.e. the marginal distribution for \(R_{i,t}\) is given by \(f_{\phi }(k_i,t)\) such that

$$\begin{aligned} f_{\phi }(k_i,t)&= \int _0^{\infty } \frac{\lambda ^{k_i}_{i,t}}{k_i !} \theta ^{k_i} e^{-\lambda _{i,t}\theta } dG(\theta )\nonumber \\&= \frac{(\psi / \chi )^{\frac{\nu }{2}}}{( (\psi + \lambda _{i,t}) / \chi )^{\frac{\nu + k_i}{2}}} \frac{K_{\nu + k_i} (\sqrt{(\psi + \lambda _{i,t}) \chi })}{K_{\nu }(\sqrt{\psi \chi })} \frac{\lambda _{i,t}^{k_i}}{k_i!} \end{aligned}$$
(3.2)

which is a univariate mixed Poisson regression random variable. In general, this result is valid for any \(m'\)-variate mixed Poisson regression random variable with \(m' < m\)

Proof

We will show the result for univariate case. The \(m'\)-variate case can be derived similarly by reducing the number of following sum to \(m - m'\)

$$\begin{aligned} f_{\phi }(k_i,t)&= \sum _{k_1 = 0 } \cdots \sum _{k_{i-1} = 0} \sum _{k_{i+1}= 0} \cdots \sum _{k_m = 0} f_{\phi } (\mathbf {k},t) \\&= \int _0^{\infty } \prod _{j \ne i} \left( \sum _{k_j = 0}^{\infty } \frac{e^{-\theta \lambda _{j,t} } (\theta \lambda _{j,t})^{k_j} }{ k_j !} \right) \frac{e^{-\theta \lambda _{i,t} } (\theta \lambda _{i,t})^{k_i} }{ k_i !} dG(\theta ) \\&= \int _0^{\infty } \frac{\lambda ^{k_i}_{i,t}}{k_i !} \theta ^{k_i} e^{-\lambda _{i,t}\theta } dG(\theta ) \end{aligned}$$

\(\square\)

The marginalization property can enable, for example insurers, to easily price those policyholders who only engage in some but not all lines of business. The last property is about the identifiability of \(\mathbf {R}_t\), which will ensure the uniqueness of the model.

Proposition 3.3

(Identifiability of joint distribution \(\mathbf {R}_t\)) Assume that the covariate space \(\mathbf {z}_t = (z_{1,t}, \ldots , z_{m,t} )\) is of full rank. Denote the parameter set \(\varTheta _R = \{ \beta _i, \phi | i = 1,\ldots , m\}\) and \(\tilde{\varTheta }_R = \{ \tilde{\beta _i}, \tilde{\phi } | i = 1,\ldots , m\}\), the joint distribution \(f_{\phi }(\mathbf {k},t)\) is identifiable such that

$$\begin{aligned} f_{\phi }(\mathbf {k},t) = f_{\tilde{\phi }}(\mathbf {k},t) \end{aligned}$$

if and only if \(\varTheta _R = \tilde{\varTheta }_R\).

Proof

With the assumption that the covariate \(\mathbf {z}\) is of full rank and the log-link function is monotonic such that \(\log (\lambda _{i,t}) = z_{i,t}^T \beta _i\), it is obvious that the identification problem for the mixed Poisson regression random variable \(\mathbf {R}_t\) reduces to identification for mixed Poisson random variable (without regression), which means the set of parameter can be re-parametrized as \(\varTheta ^{*}_R = \{ \lambda _{i,t}, \phi | i = 1,\ldots , m\}\) and \(\tilde{\varTheta }^*_R = \{\tilde{\lambda }_{i,t}, \tilde{\phi } | i = 1,\ldots , m\}\).

Then the ’if’ statement is obvious since the same set of parameters will definitely lead to the same joint distribution function. For the ’only if’ statement, to match two distribution functions, all the moments (mean,variance, covariance) must reconcile. From the moment properties above, matching the \({\mathbb {E}}[R_{i,t}]\) will lead to \(\lambda _{i,t} = \tilde{\lambda }_{i,t}\). Likewise, given that the first moment is matched, only \(\phi = \tilde{\phi }\) will lead to the same \(Var(R_{i,t})\). Matching these moments already leads to \(\varTheta ^*_R = \tilde{\varTheta }^*_R\), then the covariance \(Cov(R_{i,t},R_{j,t})\) must match with each other. \(\square\)

4 Model specification

The distributional properties of \(\mathbf {X}_t\), in particular the correlation structure and ’tailedness’ of the distribution, are mainly determined by the innovation \(\mathbf {R}_t\), more specifically, the mixing density \(g(\theta )\). On the other hand, the explicit form of the derivatives of \(f_{\phi }(\mathbf {k},t)\) can significantly accelerate the computational speed when performing estimation. Hence, the distribution function \(f_{\phi }(\mathbf {k},t)\) as well as its derivatives are derived for two limiting cases (Gamma, Inverse Gamma) and some other special cases (GIG with unit mean and different values of \(\nu\)). Throughout this session, we define \(S^{\lambda }_t = \sum _{i=1}^m \lambda _{i,t}\) and \(S^{k} = \sum _{i=1}^m k_i\).

4.1 Mixing by Gamma distribution

If \(\mathbf {R}_t\) is univariate, the resulting distribution is known as the negative binomial distribution and this result can be easily extended to the multivariate case which is called the multivariate negative binomial distribution (see e.g. Marshall and Olkin 1990; Boucher et al. 2008; Cheon et al. 2009). The gamma density is obtained by letting \(\nu =\phi , \psi = 2\phi\) and \(\chi = 0\) in generalized Inverse Gaussian density in Sect. 2.4. The resulting mixing density has the following form:

$$\begin{aligned} g(\theta ) = \frac{\phi ^{\phi }}{\Gamma (\phi )} \theta ^{\phi -1} e^{- \phi \theta } \end{aligned}$$
(4.1)

with unit mean and variance \(\frac{1}{\phi }\). Then the expectation 2.3 can be evaluated explicitly

$$\begin{aligned} f_{\phi }(\mathbf {k},t)&= \prod _{i=1}^m \frac{\lambda _{i,t}^{k_i}}{k_i !} {\mathbb {E}}[ e^{-(S^{\lambda }_t)\theta } \theta ^{S^k} ] \nonumber \\&= \frac{\Gamma (\phi + S^k)}{ \Gamma (\phi ) \prod _{i=1}^m \Gamma (k_i + 1)} \frac{\phi ^{\phi }\prod _{i=1}^m \lambda _{i,t}^{k_i}}{(\phi +S^{\lambda }_t)^{\phi + S^k}} \end{aligned}$$
(4.2)

Proposition 4.1

The derivatives of the distribution function \(f_{\phi } (\mathbf {k},t)\) with respect to \(\varTheta _R = \{\phi , \beta _i \ | \ i =1,\ldots , m \}\) when \(\theta _t \sim\) Gamma\((\phi , \phi )\) are given by

$$\begin{aligned} \frac{\partial f_{\phi } (\mathbf {k},t)}{\partial \phi }&= f_{\phi } (\mathbf {k},t) \left( \sum _{n=1}^{S^k } \frac{1}{n+\phi -1 } + \log \left( \frac{\phi }{\phi +S^{\lambda }_t} \right) + \frac{\sum _{i=1}^m (\lambda _{i,t} - k_i) }{\phi + S^{\lambda }_t} \right) \nonumber \\ \frac{\partial f_{\phi } (\mathbf {k},t) }{\partial \beta _i}&= f_{\phi } (\mathbf {k},t) \left( \frac{k_i}{\lambda _{i,t}} - \frac{\phi + S^k}{\phi + S^{\lambda }_t}\right) \lambda _{i,t} z_{i,t} \ , \end{aligned}$$
(4.3)

where the sum \(\sum _{n=1}^{S^k } \frac{1}{n+\phi -1 } = 0\) when \(S^{k} = 0\).

Proof

The derivatives \(\frac{\partial f_{\phi } (\mathbf {k},t) }{\partial \beta _i}\) can be figured out easily except \(\frac{\partial f_{\phi }(\mathbf {k},t) }{\partial \phi }\) which involves the gamma function. The derivative of the gamma function can be derived by utilizing the alternative Weierstrass’s definition such that

$$\begin{aligned} \Gamma (z+1) = e^{-\gamma z }\prod _{n\ge 1} \left( 1 + \frac{z}{n}\right) ^{-1} e^{\frac{z}{n}}, \end{aligned}$$

which is valid for all complex number z except non-positive integers and \(\gamma\) is Euler–Mascheroni constant. Then the derivative can be derived by differentiating its log transform \(\log \Gamma (z+1)\), which leads to the series expansion of digamma function

$$\begin{aligned} \varPsi (z + 1) = \frac{\Gamma '(z+1)}{\Gamma (z+1)} = -\gamma + \sum _{n \ge 1} \left( \frac{1}{n} - \frac{1}{n + z} \right) \end{aligned}$$

Then the derivative \(\frac{\partial f_{\phi }(\mathbf {k},t) }{\partial \phi }\) can be derived steps by steps. First let us simplify the expression of \(f_{\phi }(\mathbf {k},t)\) such that

$$\begin{aligned} f_{\phi }(\mathbf {k},t)&= c_1 \frac{N(\phi )}{D(\phi )} \\ c_1 = \prod _{i=1}^m \frac{\lambda _{i,t}^{k_i}}{\Gamma (k_i + 1)}, \ N(\phi ) = \Gamma (\phi +&S^k) \phi ^{\phi }, \ D(\phi ) = \Gamma (\phi ) \left( \phi + S^{\lambda }_t \right) ^{\phi +S^k} \end{aligned}$$

The derivative is then

$$\begin{aligned} \frac{\partial f_{\phi }(\mathbf {k},t) }{\partial \phi }&= c_1 \frac{N'(\phi )D(\phi ) - N(\phi )D'(\phi )}{D^2(\phi )} \\&\quad = c_1 \frac{N(\phi )}{D(\phi )} \left( \sum _{n \ge 1} \left( \frac{1}{n + \phi - 1 } - \frac{1}{n + \phi + S^k-1} \right) + 1 + \log \phi - \log (\phi +S^{\lambda }_t) - \frac{\phi + S^k}{\phi +S^{\lambda }_t} \right) \end{aligned}$$

\(\square\)

4.2 Mixing by Inverse Gamma

The Inverse gamma distribution, which is another limiting case of generalized Inverse Gaussian distribution, is discussed in Sect. 9.3 (Johnson et al. 1995). Inverse gamma random variable has a relatively thicker right tail and a low probability in taking the values closed to 0. In this case, the density function \(g(\theta )\) is obtained by letting \(\psi = 0, \chi = 2\phi\) and \(\nu = -\phi -1\) such that

$$\begin{aligned} g(\theta ) = \frac{\phi ^{\phi +1}}{\Gamma (\phi + 1)} \theta ^{-\phi - 2} e^{-\frac{\phi }{\theta }} , \end{aligned}$$
(4.4)

with mean 1 and variance \(\frac{1}{\phi - 1}\) for \(\phi > 1\). It is also called the reciprocal gamma distribution such that \(\theta = 1/x\) where \(x \sim\) Gamma\((\phi + 1, \phi )\). The distribution function \(f_{\phi } (\mathbf {k},t)\) becomes

$$\begin{aligned} f_{\phi } (\mathbf {k},t)&=\prod _{i=1}^m \frac{ \lambda _{i,t}^{k_i} }{k_i ! } {\mathbb {E}} \left[ e^{ - S^{\lambda }_t \theta _t} \theta _t ^{S^k} \right] \nonumber \\&= \frac{ 2 K_{\nu } \left( \omega \right) }{\Gamma (\phi + 1) \prod _{i=1}^m \Gamma (k_i + 1)} \frac{\phi ^{\frac{\nu }{2} + \phi + 1} \prod _{i=1}^m \lambda _{i,t}^{k_i}}{ (S^{\lambda }_t)^{\frac{\nu }{2}}}, \end{aligned}$$
(4.5)

where \(\nu = S^k - \phi - 1\) and \(\omega = 2 \sqrt{\phi S^{\lambda }_t}\). The derivatives of \(f_{\phi } (\mathbf {k},t)\) with respect to the parameter set \(\varTheta _R = \{\phi , \beta _i \ | \ i =1,\ldots , m \}\) are given by

$$\begin{aligned} \frac{\partial f_{\phi } (\mathbf {k},t) }{\partial \phi }&=\left( \log \frac{\omega }{2} + \frac{ S^k+\phi + 1}{2\phi } +\frac{\partial \log K_{\nu } \left( \omega \right) }{\partial \phi } -\varPsi (\phi +1) \right) f_{\phi } (\mathbf {k},t) \nonumber \\ \frac{\partial f_{\phi } (\mathbf {k},t) }{\partial \beta _i}&= \left( \frac{k_i}{\lambda _{i,t}} f_{\phi } (\mathbf {k},t) -\frac{k_i+1}{\lambda _{i,t}} f_{\phi } (\mathbf {k} +\mathbf {1}_i, \phi ) \right) \lambda _{i,t} z_{i,t} \end{aligned}$$
(4.6)

In this case, numerical differentiation is applied to calculate \(\frac{\partial \log K_{\nu } \left( \omega \right) }{\partial \phi }\) since the parameter \(\phi\) appears both in the order \(\nu\) and argument \(\omega\) of the modified Bessel function \(K_{\nu }(\omega )\).

4.3 Mixing by Generalized Inverse Gaussian

Likewise, if \(\mathbf {R}_t\) is univariate, the distribution of \({\mathbf {R}}_t\) is known as the Poisson Generalized Inverse Gaussian distribution. To comply with constraints we made in Sect. 2, the mixing density function has following form

$$\begin{aligned} g(\theta ) = \frac{c^{\nu }}{2K_{\nu }(\phi )} \theta ^{\nu -1} \exp \left\{ -\frac{\phi }{2} \left( c\theta + \frac{1}{c \theta } \right) \right\} \end{aligned}$$
(4.7)

with unit mean and variance \(var(\theta _t) = \frac{1}{c^2} + \frac{2 (\nu +1)}{c\phi } - 1\), where \(c = \frac{K_{\nu + 1}(\phi )}{K_{\nu }(\phi )}\), \(\phi >0\) and \(\nu \in {\mathbb {R}}\). Then the distribution function \(f_{\phi } (\mathbf {k},t)\) becomes

$$\begin{aligned} f_{\phi } (\mathbf {k},t,\nu )&=\prod _{i=1}^m \frac{ \lambda _{i,t}^{k_i}}{k_i!} {\mathbb {E}} \left[ e^{ -\theta _t S^{\lambda }_t} \theta _t ^{S^k} \right] \nonumber \\&= \frac{K_{p}(\sqrt{ab})}{K_{\nu }(\phi )} c^{\nu } \left( \frac{b}{a}\right) ^{\frac{p}{2}} \prod _{i=1}^m \frac{\lambda _{i,t}^{k_i}}{k_i!} \end{aligned}$$
(4.8)

where \(a = \phi c + 2 S^{\lambda }_t\), \(b = \frac{\phi }{ c}\) and \(p = S^k+ \nu\). Furthermore, we let \(\nu\) be constant and fixed in order to avoid potential identification problems which may appear when performing estimation. In general, however, the derivative with respect to \(\phi\) is really hard to find since the constant c involves the Bessel function. On the other hand, it is worth noting that \(var(\theta _t)\) is roughly unbounded when \(\nu \in [-2,0]\) and the skewness and kurtosis are decreasing with respect to \(\nu\), which can be easily verified by some statistical software on computer. So, we will discuss cases where \(\nu = -\frac{1}{2}, -\frac{3}{2}, -\frac{3}{4}\), two of which have ‘explicit’ distributions in the sense that the constant c can be evaluated in closed form.

4.3.1 Generalized Inverse Gaussian with \(\nu = -\frac{1}{2}\)

In this case, the resulting distribution known as the Poisson Inverse Gaussian distribution is investigated by many authors (see,e.g Sichel 1974, 1982; Atkinson and Yeh 1982; Stein and Juritz 1988 among others). When \(\nu = -\frac{1}{2}\), \(c = 1\) and the distribution function f becomes

$$\begin{aligned} f_{\phi }(\mathbf {k},t) = \prod _{i=1}^m \frac{\lambda _{i,t}^{k_i}}{k_i !} \sqrt{\frac{2}{\pi }} \phi ^{\frac{1}{2}} e^{\phi } K_{p} (\sqrt{\phi (\phi + 2S^{\lambda }_t)}) \left( \frac{\phi }{\phi + 2S^{\lambda }_t}\right) ^{\frac{p}{2}} \end{aligned}$$
(4.9)

For convenience, we reparametrize the above density by squaring the parameter \(\phi\) such that

$$\begin{aligned} f_{\phi }(\mathbf {k},t) = \prod _{i=1}^m \frac{\lambda _{i,t}^{k_i}}{k_i !} \sqrt{\frac{2}{\pi }} \phi e^{\phi ^2} K_{p} (\phi \varDelta ) \left( \frac{\phi }{\varDelta }\right) ^{\nu } \end{aligned}$$
(4.10)

where \(p = S^k -\frac{1}{2}\) and \(\varDelta = \sqrt{\phi ^2 + 2S^{\lambda }}\). The derivatives of \(f_{\phi } (\mathbf {k},t)\) with respect to different parameters can be derived by making use of the derivative of \(K_{\nu }(\omega )\) with respect to its argument such that

$$\begin{aligned} \frac{\partial K_{\nu }(\omega )}{\omega } = \frac{\nu }{\omega } K_{\nu }(\omega ) - K_{\nu + 1}(\omega ), \end{aligned}$$
(4.11)

then it leads to the following derivatives

$$\begin{aligned} \frac{\partial f_{\phi } (\mathbf {k},t) }{\partial \phi }&= \left( 2\phi + \frac{1 + 2\nu }{\phi } \right) f_{\phi } (\mathbf {k},t) - \left( \phi + \frac{\varDelta ^2}{\phi }\right) \frac{k_1+1}{\lambda _{1,t}} f_{\phi } (\mathbf {k}+\mathbf {1}_1, \phi ),\nonumber \\ \frac{\partial f_{\phi } (\mathbf {k},t) }{\partial \beta _i}&= \left( \frac{k_i}{\lambda _{i,t}} f_{\phi } (\mathbf {k},t) - \frac{k_i+1}{\lambda _{i,t}} f_{\phi } (\mathbf {k} + \mathbf {1}_i, \phi ) \right) \lambda _{i,t} z_{i,t} \end{aligned}$$
(4.12)

where \(\mathbf {1}_i = (0,\ldots ,0,1,0,\ldots , 0)^T \in {\mathbb {R}}^{m \times 1}\) is vector with i-th element being one and 0 elsewhere.

4.3.2 Generalized Inverse Gaussian with \(\nu = -\frac{3}{2}\)

In this case, the constant \(c = \frac{\phi }{1+\phi }\) and the variance \(var(\theta _t) = \frac{1}{\phi }\) which is exactly the same as the variance of Inverse Gaussian case but the random effect \(\theta _t\) will in general have larger skewness and kurtosis. The resulting distribution function is

$$\begin{aligned} f_{\phi }(\mathbf {k},t) = \prod _{i=1}^m \frac{\lambda _{i,t}^{k_i}}{k_i !} \sqrt{\frac{2}{\pi }} (\phi + 1)^{S^k - 1} e^{\phi } \omega ^{-p} K_{p}(\omega ). \end{aligned}$$
(4.13)

where \(p = S^k - \frac{3}{2}\) and \(\omega = \sqrt{\phi ^2 + 2(\phi +1)S^{\lambda }_t}\). The derivatives with respect to different parameters can be derived similar to that of Inverse Gaussian case

$$\begin{aligned} \frac{\partial f_{\phi } (\mathbf {k},t) }{\partial \phi }&= \left( \frac{\phi + S^k}{\phi + 1}\right) f_{\phi }(\mathbf {k},t) -\left( \frac{k_1 + 1}{\lambda _{1,t}} \frac{\phi + S^{\lambda }_t}{\phi + 1} \right) f_{\phi }(\mathbf {k} + \mathbf {1}_1, t) \nonumber \\ \frac{\partial f_{\phi } (\mathbf {k},t) }{\partial \beta _i}&= \left( \frac{k_i}{\lambda _{i,t}} f_{\phi } (\mathbf {k},t) - \frac{k_i+1}{\lambda _{i,t}} f_{\phi } (\mathbf {k} + \mathbf {1}_i, \phi ) \right) \lambda _{i,t} z_{i,t} \end{aligned}$$
(4.14)

The remaining case where \(\nu = -\frac{3}{4}\) cannot be simplified since the \(c = \frac{K_{1/4}(\phi )}{K_{3/4}(\phi )}\) cannot be written down in terms of basic functions. Hence numerical differentiation has to be applied when evaluating \(\frac{\partial f_{\phi } (\mathbf {k},t) }{\partial \phi }\) and \(\frac{\partial f_{\phi } (\mathbf {k},t) }{\partial \beta _i}\). Finally, Table 1 summarise the parametrization of all mixing densities and Table 2 shows the moments formula for each mixing density.

Table 1 Parametrization of mixing density based on GIG density 2.4
Full size table
Table 2 Moments for the random effect \(\theta _t\). Ex.Kurtosis = Kurtosis − 3
Full size table

Although the formula for variances is slightly different due to its parametrization, they can be easily reparameterized and compared with each other. It turns out that the Inverse Gamma has the largest skewness and kurtosis while the Gamma density has the smallest, which means the ’tailedness’ of those density increases in a ‘top-down’ order according to the Table. Hence, one can choose different density to accommodate different tail structure encountered in real data.

5 Model fitting and prediction

5.1 Maximum likelihood estimation for the MMPGIG-INAR(1) model

In this section, we derive the log likelihood function and score function of the MMPGIG-INAR(1) model defined above for the general case. Let the whole parameter set be \(\varTheta = \{ p_i, \beta _i, \phi | i = 1,\ldots , m\}\) and then the log likelihood function \(\ell (\varTheta )\) for this discrete Markov chain is just the product of their conditional probability function such that \(\ell (\varTheta ) = \prod _{t} {\mathcal {P}}_{\varTheta }(\mathbf {X}_t | \mathbf {X}_{t-1})\), where the conditional probability is the convolution of m+1 distribution functions such that

$$\begin{aligned} {\mathcal {P}}(\mathbf {X}_t | \mathbf {X}_{t-1})&= {\mathbb {E}} \left[ \prod _{i=1}^2 {\mathcal {P}}(p_i \circ X_{i,t-1} +R_{i,t}= X_{i,t-1} | X_{i, t-1},\theta _t)\right] \nonumber \\&= {\mathbb {E}}\left[ \prod _{i=1}^m \sum _{k=0}^{s_i} f_{p_i}(k,X_{i,t-1}) f_{R_i}(X_{i,t}-k, t)\right] , \quad s_i =\min \{X_{i,t-1},X_{i,t}\} \nonumber \\&= \sum _{k_1=0}^{s_1} \dots \sum _{k_m=0}^{s_m} f_{\phi }(\mathbf {k},t) \prod _{i=1}^m f_{p_i}(X_{i,t} - k_i, X_{i,t-1}), \end{aligned}$$
(5.1)

where the expectation is taken with respect to the random variable \(\theta _t\). The following proposition gives \(\ell (\varTheta )\) and its score functions.

Proposition 5.1

Suppose there is a multivariate random sequence \((\mathbf {X}_1, \mathbf {X}_2, \dots \mathbf {X}_n)\) generated from the MMPGIG-INAR(1) model, the log likelihood function \(\ell (\varTheta )\) and score functions are given by

$$\begin{aligned} \ell (\varTheta )&= \sum _{t=1}^n \log {\mathcal {P}}(\mathbf {X}_t | \mathbf {X}_{t-1}) \nonumber \\&=\sum _{t=1}^n \log \sum _{k_1=0}^{s_1} \dots \sum _{k_m=0}^{s_m} f_{\phi }(\mathbf {k},t) \prod _{i=1}^m f_{p_i}(X_{i,t} - k_i, X_{i,t-1}) \nonumber \\ \frac{\partial \ell (\varTheta )}{\partial \vartheta }&= \sum _{t=1}^n \frac{1}{{\mathcal {P}}(\mathbf {X}_t | \mathbf {X}_{t-1})} \frac{\partial {\mathcal {P}}(\mathbf {X}_t | \mathbf {X}_{t-1}) }{\partial \vartheta }, \quad \vartheta \in \varTheta \end{aligned}$$
(5.2)

The derivatives inside the sum are given by

$$\begin{aligned}&\frac{\partial {\mathcal {P}}(\mathbf {X}_t | \mathbf {X}_{t-1})}{\partial p_j}= \sum _{k_1=0}^{s_1} \dots \sum _{k_m=0}^{s_m} f_{\phi }(\mathbf {k},t)\frac{\partial f_{p_j}(X_{ij,t}-k,X_{j,t-1}) }{\partial p_j }\prod _{i \ne j} f_{p_j}(X_{i,t} - k_i, X_{i,t-1}) \nonumber \\&\frac{\partial {\mathcal {P}}(\mathbf {X}_t | \mathbf {X}_{t-1})}{\partial \vartheta _1}= \sum _{k_1=0}^{s_1} \dots \sum _{k_m=0}^{s_m}\frac{\partial f_{\phi }(\mathbf {k},t)}{\vartheta _1} \prod _{i=1}^m f_{p_i}(X_{i,t} - k_i, X_{i,t-1}) \nonumber \\&\vartheta _1 \in \{\beta _1, \beta _2,\phi \} \end{aligned}$$
(5.3)

where the derivative \(\frac{\partial f_{p_j}(\omega ,X_{j,t-1}) }{\partial p_j }\) has the same form for all \(j = 1,...,m\).

$$\begin{aligned} \frac{\partial f_{p_j}(\omega , X_{j,t})}{\partial p_j} = f_{p_j}(\omega , X_{j,t})\frac{\omega - p_j X_{j,t}}{p_j(1 - p_j)} \end{aligned}$$

The derivatives \(\frac{\partial f_{\phi }(\mathbf {k},t) }{\vartheta _1}\) are already discussed in Sect. 4 for different cases. Hence, the maximum likelihood estimators can be obtained through numerical algorithms, for example Newton-raphson, Quasi-Newton and so on. However, optimization will be computational intensive as m increases. One can solve this issue by adopting the composite likelihood method introduced in Pedeli and Karlis (2013a), where the high dimensional likelihood function was reduced to a sum of bivariate cases.

5.2 Integer-valued prediction

Based on the estimates obtained by maximum likelihood and the random sequence \((\mathbf {X}_{1}, \dots , \mathbf {X}_n)\), the h-steps ahead distribution of \(\mathbf {X}_{n + h}\) conditional on \(\mathbf {X}_{n}\) is given by

$$\begin{aligned} \mathbf {X}_{n+h} \overset{D}{=} \hat{\mathbf {P}}^h \circ \mathbf {X}_n + \sum _{k=1}^h \hat{\mathbf {P}}^{h-k} \circ \mathbf {R}_{n+k}, \end{aligned}$$
(5.4)

where \(\hat{\mathbf {P}}\) is obtained from above estimation procedure. In the classical time series model, one would minimise MSE\((h) = {\mathbb {E}}[(\hat{\mathbf {X}}_{n+h} - \mathbf {X}_{n+h})^2 \vert \mathbf {X}_n]\) to obtain the optimal linear predictor such that \(\hat{\mathbf {X}}_{n + h} = {\mathbb {E}}[\mathbf {X}_{n+h} \vert \mathbf {X}_n]\). However, this would inevitably introduce real value for \(\hat{\mathbf {X}}_{n+h}\), which is not coherent to the integer-valued nature of MMPGIG-INAR(1) model. To solve this, one can instead use the median \(\tilde{\mathbf {X}}_{n+h}\) of \(\mathbf {X}_{n+h}\) , the 50% quantile, as prediction value for the model, which is also discussed by Pavlopoulos and Karlis (2008) and Homburg et al. (2019) . In the univariate case, the median is obtained by minimising the mean absolute error MAE\((h) = {\mathbb {E}}[|\tilde{X}_{n+h} - X_{n+h}| \vert X_n]\). The idea here can be extended to the multivariate case so that the median \(\tilde{\mathbf {X}}_{n+h}\) is called geometric median, which is calculated by minimising the expected Euclidean distance

$$\begin{aligned} MAE(h) = {\mathbb {E}}[ ||\tilde{\mathbf {X}}_{n+h} - \mathbf {X}_{n+h}||_2 \vert X_n] \end{aligned}$$
(5.5)

On the other hand, the expectation can be evaluated numerically by simulating the random samples of \(\mathbf {X}_{n+h}\).

6 Empirical analysis

The data used in this section come from the Local Government Property Insurance Fund (LGPIF) from the state of Wisconsin. This fund provides property insurance to different types of government units, which includes villages, cities, counties, towns and schools. The LGPIF contains three major groups of property insurance coverage, namely building and contents (BC), inland marine (IM) and motor vehicles (PN, PO, CN, CO). For exploratory purposes, we focus on modelling jointly the claim frequency of IM, denoted as \(X_{1,t}\), and comprehensive new vehicles collision (CN), denoted as \(X_{2,t}\). The insurance data cover the period over 2006–2011 with 1234 policyholder records in total. Only \(n_1 = 1048\) of them have complete data over the period 2006–2010 which will be used as the training data set. The last year 2011 with \(n_2 =1025\) policyholders out of 1048 in the data set will be the test data set. Denote the IM type and CN type claim frequency for a particular policyholder as \(X^{(j)}_{1,t}, X^{(j)}_{2,t}\) respectively, where j is the identifier for each policyholder. Then the relationship between \(X_{i,t}\) and \(X^{(j)}_{i,t}\) is simply \(X_{i,t} = \sum _{j=1}^{n_1} X_{i,t}^{(j)}\) with \(i = 1,2\) while t would take the values from 1 to 5 corresponding to the year 2006 to 2010.

In what follows, basic statistical analysis is shown in Table 3 and Figs. 1 and 2. The proportion of zeros for the two types of claims is higher than 90% during the period 2006–2010. Also, both types of claims exhibit overdispersion, since their variances exceeds their means during this period. Furthermore, the overdispersion for \(X_{2,t}\) is even stronger than that of \(X_{1,t}\), which indicates the need to employ an overdispersed distribution for this data. Additionally, the correlation tests for \(X_{1,t}\) and \(X_{2,t}\) show a positive correlation between the two claim types. At this point it is worth noting that modelling positively correlated claims has been explored by many articles. See for example, Bermúdez and Karlis (2011), Bermúdez and Karlis (2012), Shi and Valdez (2014a, b), Abdallah et al. (2016), Bermúdez and Karlis (2017), Bermúdez et al. (2018), Bermúdez et al. (2018), Pechon et al. (2018), Pechon et al. (2019), Bolancé and Vernic (2019), Denuit et al. (2019), Fung et al. (2019), Bolancé et al. (2020), Pechon et al. (2021), Jeong and Dey (2021), Gómez-Déniz and Calderín-Ojeda (2021), Tzougas and di Cerchiara (2021a, b) and Bermúdez and Karlis (2021). Finally, the proportion of zeros and kurtosis show that the marginal distributions of \(X_{1,t}, X_{2,t}\) are positively skewed and exhibit a fat-tailed structure which indicates the appropriateness of adopting a positive skewed and fat-tailed distribution (GIG distribution).

Table 3 Summary statistics of two types of claims over years
Full size table
Fig. 1
figure 1

summary statistics (mean, variance and correlation) for each type of claims across all the policyholders over years

Full size image

The description and some summary statistics for all the explanatory variables (covariates \(z_{1,t}, z_{2,t}\)) that are relevant to \(X_{1,t}, X_{2,t}\) are shown in Table 4. Variables 1–5 including ‘TypeVillage’ are categorical variables to indicate the entity types of a policyholder. Due to the strongly heavy-tailed structure appearing in variables 6 and 9 which can drastically distort the model fitting, those variables are transformed by means of the ’rank’ function in R software and then standardized, which can mitigate the effect of outliers. Variables 6–8 are relevant to IM claim \(X_{1,t}\) while variables 9,10 provide information for CN claims \(X_{2,t}\). The covariate \(z_{1,t}\) includes variables 1–8 and \(z_{2,t}\) contains variables 1–5 and variables 9, 10. These covariates act as the regression part for \(\lambda _{i,t}\) mentioned in Sect. 2, which may help explained part of the heterogeneity between \(X_{1,t}\) and \(X_{2,t}\).

Table 4 summary statistics for the explanatory variables
Full size table

The MMPGIG-INAR(1) with \(m = 2\), is applied to model the joint behaviour of \(X_{1,t}^{(j)}, X^{(j)}_{2,t}\) across all the policyholders. Note that when Gamma mixing density is used in MPGIG INAR(1), the resulting model will be the ”BINAR(1) Process with BVNB Innovations” in Pedeli and Karlis (2011), which we will used as comparison benchmark for other choices of mixing density. The the likelihood function would simply become

$$\begin{aligned} \ell (\varTheta ) = \sum _{j=1}^{n_1} \ell _j(\varTheta ) = \sum _{j=1}^{n_1} \sum _{t=1}^4 \log \Pr ( X^{(j)}_{1,t+1}, X^{(j)}_{2,t+1} | X^{(j)}_{1,t}, X^{(j)}_{2,t}), \end{aligned}$$
(6.1)

where \(\ell _j(\varTheta )\) is the likelihood function for policyholder j. Note that all the policyholders with the same type of claim \(X_{i,.}\) will share the same set of parameters \(p_i,\beta _i\) and \(\phi\) will be same for both claim types. In addition, it is necessary to show the appropriateness of introducing correlation and time-series component (binomial thinning) in MPGIG INAR(1). Then we also fit the data to following models.

  1. 1.

    The joint distribution of \(X^{(j)}_{1,t}\) and \(X^{(j)}_{2,t}\) are assumed to be bivariate mixed Poisson distribution (BMP) with probability mass function \(f_{\phi }(\mathbf {k},t)\) which we already discussed in Sect. 4.

  2. 2.

    The joint distribution of \(X^{(j)}_{1,t}\) and \(X^{(j)}_{2,t}\) are characterized by two independent INAR(1) models (TINAR)

    $$\begin{aligned} X^{(j)}_{1,t}&= p_1 \circ X^{(j)}_{1,t-1} + R_{1,t} \\ X^{(j)}_{2,t}&= p_2 \circ X^{(j)}_{2,t-1} + R_{2,t}, \end{aligned}$$

    where \(R_{i,t} \sim Pois(\lambda _{i,t} \theta _{i,t}), i=1,2\) and random effect \(\theta _{i,t}\) is independent of i.

Similarly, the likelihood functions for these models will have the same form as Eq. (6.1) but different joint distribution \(\Pr ( X^{(j)}_{1,t+1}, X^{(j)}_{2,t+1} | X^{(j)}_{1,t}, X^{(j)}_{2,t})\). For comparison purposes, we fit the bivariate Poisson mixture regression model with the training data starting from 2007 because BMP model does not need to consider lag responses.

All the estimations is implemented in R software by the ’optim’ function with method ’BFGS’ (quasi-Newton method). The gradient functions with respect to all the parameters are derived in Sects. 4 and 5 and they can be input as gradient argument in ’optim’ function, which will significantly decrease the amount of computational time compared to numerical gradient function in default setting.

Table 5 The AIC and BIC when fitting as two independent INAR model with different combination
Full size table
Table 6 The AIC and BIC when fitting bivariate sequence as bivarate mixed Poisson regression model and BINAR model
Full size table

Model fitting results are shown in Tables 5 and 6. All the results show a great improvement by adopting a time series model compared to BMP results in Table 6. When focusing on the results of BINAR in Table 6, except the case where the mixing density is GIG \(\nu = -\frac{3}{2}\), there is an significant improvement by introducing the fat-tailed distribution as mixing density in \(\mathbf {R}_t\) compared to Gamma case. On the other hand, the improvement from the optimal TINAR to the optimal BINAR (cells are in bold face) is obvious, which is indicated by lower AIC and BIC of BINAR with GIG \(\nu = -\frac{3}{4}\) compared to TINAR with GIG \(\nu = -\frac{3}{4}\) and Inverse Gaussian. It implies that there is significant correlation between two claim sequences. Maximum likelihood estimates for three cases are given in Table 7 as well as their standard deviations. The standard derivations are estimated by inverting the numerical Hessian matrix. From Table 7 we see that the estimates for \(p_i, \beta _i\) are very close to each other while the estimated \(\phi\) is significantly different among three mixing densities, which is expected because \(\phi\) influences the tail and correlation structure of the bivariate sequence \(X_{1,t}, X_{2,t}\). Furthermore, we see that the explanatory variables have a similar effect (positive and/or negative) and are almost identical for both response variables in the case of of all three models. Finally, the variables which are statistically significant at a 5 % threshold for \(X_{1,t}\) are TypeCounty, TypeMisc, TypeVillage, NoClaimCreditIM, and those which are statistically significant at a 5 % threshold for \(X_{2,t}\) are TypeCity, TypeCounty, TypeVillage, CoverageIM, and CoverageCN.

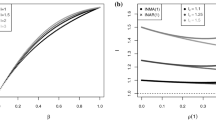
The Fig. 2 below presents prediction for both types of claims at \(t = 2011\) with \(n_2 = 1025\) policyholders based on geometric median Eq. (5.5). It seems that the prediction for number of policyholders who make no claims are reasonably good while the prediction for \(X_{1,t}\) are generally underestimated at tail and the prediction for \(X_{2,t}\) are overestimated at the tail. On the other hand, Table 8 shows the prediction sum of squared error (PSSE) and frequency of some basic combination of observations, namely (0, 0), (1, 0), (0, 1), (1, 1) for the best fitted models within three classes, bivariate mixed Poisson regression, Two independent INAR(1) and bivariate INAR(1). It is again clear that the introduction of autoregressive part makes sense as it greatly reduce the prediction error. Although the best TINAR model has the closet frequency of (0, 0), the best BINAR model has the lowest overall prediction error.

Table 7 Maximum likelihood estimation for MMPGIG-INAR(1) of insurance’s claim frequency data when \(m = 2\)
Full size table
Fig. 2
figure 2

Observed (dark) and Predicted (grey) frequency of the test data set based on estimated BINAR with GIG \(\nu = -\frac{3}{4}\) as mixing density

Full size image
Table 8 Summary of prediction on test data
Full size table

7 Concluding remarks

In this paper we proposed the MMPGIG-INAR(1) regression model for modelling multiple time series of different types of count response variables. The proposed model, which is an extension of BINAR(1) regression model that was introduced by Pedeli and Karlis (2011), can accommodate positive correlation and multivariate overdispersion in a flexible manner. In particular, the Generalized Inverse Gaussian class includes many distributions as its special and limiting cases that can be used for modelling the innovations \(\mathbf {R}_t\). Thus, the proposed modelling framework can efficiently capture the stylized characteristics of alternative complex data sets. Furthermore, due to the simple form of its density function, statistical inference for the MMPGIG-INAR(1) model is straightforward via the ML method, whereas other models that have been proposed in the literature, such as copula-based models, may result in numerical instability during the ML estimation procedure. For demonstration purposes different members of the proposed famly of models were fitted to LGPIF data from the state of Wisconsin. Finally, it is worth mentioning that a possible line of further research could be to also consider cross correlation, meaning that the non-diagonal elements of \(\mathbf {P}\) can take positive values.