1 Introduction

Powder bed fusion (PBF) metal additive manufacturing is well known for its capability of producing parts with highly complex shapes and with individual members of the parts down to sub-millimeter size. As PBF is maturing, the potential of the technology to be more widely applied to industry for designing and manufacturing of lattice structures has started to be realized [1]. A particular development of lattice structure PBF has been in the field of hip implant PBF, where promising results have demonstrated the potential of PBF manufactured Ti-alloy lattice structures capable of matching bones mechanically and biologically [2]. Although PBF is more and more widely applied for lattice structure manufacturing [3], there are challenges that need to be overcome for load-bearing implants as defects in PBF lattice structures affect significantly the mechanical integrity and thus their ability to match host body [4]. In PBF additive manufacturing, there is basically no limitation on how lattice structures can be built locally and thus unit cell distribution in a PBF lattice structure can be built according to design. This feasibility of PBF allows for the manufacture of gradient lattice structures [5,6,7], which in turn allows for the design of implant structures to meet the demand of natural and non-even distribution of stress in service conditions of the structures.

PBF for orthopedic implant applications has been viewed to have captured all the advantages of additive manufacturing [8]. For these implants, it is well understood that porous structures with pore sizes in the range of 0.3–0.6 mm are required for osseointegration and osteoconduction [9]. For a lattice structure to be implanted as a part in a location of a skeletal bone or bone replacement, the required and complex loading depending on the location needs to be adequately supported by the implant. Thus, a strong research effort has been made in recent years to test and to study the mechanical behavior of lattice structures produced by PBF [1, 3, 9,10,11]. However, in their recent and comprehensive review, Vyavahare et al. [3] conclude that additive manufacturing processes still need to be optimized for manufacturing porous structures in order for the required mechanical and biological properties to be satisfied. As explained in the review [3], mechanical properties of bone structures are directionally dependent. This feature of anisotropy can be followed in PBF made implant bones as PBF readily allows for complex structures to be produced, if the directionally dependent properties of PBF porous structures are understood and thus are designed for.

Electron powder bed fusion (EBPBF) is one of the two PBF additive manufacturing processes and the other is laser PBF. Although both PBF processes are highly capable of fabricating lattice structures, owing to the high base plate and powder bed temperatures, the level of residual stress or part distortion is low in parts additively manufactured using EBPBF. Continuous development of the EBPBF process has been made in the last decade [12], and as pointed out by the authors and as is well known, the dominant alloy used is Ti6Al4V. How mechanical properties of Ti-alloy lattice structures made by EBPBF are affected by the strut dimension, type of unit cell, and relative density have been the more recent research effort [13, 14]. The studies also have highlighted how EBPBF defects affect the mechanical properties of the lattice structures. Work on EBPBF has recently included lattice structures with solid shells to understand the mechanical behavior of the shell interacting with the lattices [15].

For biomedical implant applications, compressive loading is dominant and thus compression tests are conducted more often to determine the yield strength (σY-L), the ultimate compression strength (UCSL) and the elastic modulus (EL) of the lattice structures. Under compression testing of typical lattice structures, as has been well summarized and explained in the major review by du Plessis et al. [1], stress increases as strain increases through first the linear portion to reach σY-L and then stress continues to increase till UCSL. Soon after UCSL, stress decreases abruptly corresponding to the first collapse of cells in the lattice sample but stress increases again as strain increases. Then, stress decreases again when the second collapse occurs in other cell locations of the lattice sample. The collapsing and stress decrease-increase progress until all cells in the lattices have collapsed and the stress increases rapidly for further compression of the fully collapsed sample. For the structural purpose, as illustrated by Galati et al. [13], failure is defined when the stress decreases abruptly soon after UCSL, corresponding to the first collapse of the lattice sample.

As reviewed by Zhang et al. [16] and Del Guercio [17], many researchers have investigated the properties of EBPBF lattice structures and have conducted compression testing extensively. In the studies that have been reviewed [16, 17] and in the studies that have followed the reviews and carried out by Del Guercio et al. [18, 19], the effects of geometry, dimension, relative density, and heat treatment of the lattices have been the focuses of the studies. However, the effect of loading direction in relation to the orientation of unit cell of the lattice samples made using EBPBF on the properties of the lattices has not been a consideration. However, for an implant to support loading after implanting, actual compressive loading acting onto the implant can be in different directions and this needs to be considered in implant design. Thus, anisotropic properties of lattice structures and how cells in the structures behave under loading need to be understood.

As explained by Carolo and Cooper O. [20], inherent to EBPBF is the partially melted powder and layer stacking thus generating various micro-crack like defects such as “sharp protrusions, deep recesses, and undercuts” on both external and internal side surfaces. These side surface defects are considerably more pronounced in EBPBF lattice structures, as values of surface-to-volume ratio are very large due to the small sizes and large number of struts in the structures. Recently, Zhang et al. [21] have evaluated how the continuity of small struts down to 0.5 mm in diameter in lattice structures can be maintained in EBPBF. An important factor affecting how readily strut discontinuity may occur is the strut inclined angle and thus the strut orientation during EBPBF may also contribute to the anisotropic properties of the lattice structures. Clearly, severe surface defects and a high degree of discontinuity of struts may affect the compressive behavior of EBPBF lattice structures significantly and the effects are important to be understood.

The above discussion of literature has shown that, there has been a lack of research effort to study the effect of loading direction in relation to orientation of the unit cell of lattice structures on the compressive strength of the lattices. Thus, the anisotropic behavior of the structures has not been well understood. Furthermore, the effect of strut irregularity of lattice structures made using EBPBF on the compression strength of the structures has not been studied closely. Thus, the combined effects of loading direction (LD), unit cell orientation (UCO), and EBPBF defects of struts as referred to above on the compressive behavior of EBPBF lattice structures need to be studied. These combined effects can only be studied using simple cubic unit cells as in these cells each uniquely strut-LD can be defined and studied and the effects of various UCO-LD combinations can be determined. Furthermore, simple cubic lattice structures are routinely used in EBPBF products. Preliminary data showing [001] of lattice samples parallel to LD ([001]//LD) significantly stronger than [111]//LD samples have been presented in a conference proceeding [22].

In the present study, samples were built with the ratio of lattice density over solid density (ρL/ρS) equaling to 0.36 and thus ρL = 1.60 g/cm3 by design, close to the density of human femur cortical bone. Samples with three UCO-LD combinations were built and compressively tested. Samples were built in two different runs using the same production machine and thus reproducibility of the process could be checked. Post-test examination was conducted particularly considering the surface irregularity/defects of EBPBF struts. Interrupted tests were also conducted and samples were examined in order to provide further information to understand how crack may start to propagate. To further aid the understanding of the mechanical response of the lattices to loading, finite element simulation was performed.

2 Experimental procedures

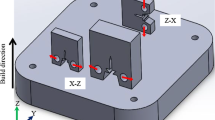
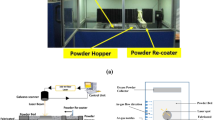
EBPBF lattice samples were built using Ti6Al4V alloy powder and an Arcam Q10 EBM production machine, which is used industrially for the production of orthopedic implants. The maximum beam power of the machine is 3000 W, minimum beam diameter is 100 μm, typical build atmosphere (vacuum) is 4 × 10−3 mbar, layer thickness is 100 μm, and axis resolution is 100 μm. The samples were built using the procedure of the standard Arcam EBPBF parameter control theme which is proprietary and used in industry. Three different types of simple cubic unit cell lattice samples were designed and built. The first refers to lattices with unit cell [001] parallel to build direction (BD thus LD), meaning [001]//LD. The second and third were [011]//LD and [111//LD respectively. Samples of [001]//LD, [011]//LD, or [111]//LD were built in a production run (EXPA). More [001]//LD and [111]//LD samples were made in a separate production run (EXPB) and thus the repeatability of the two runs apart for many runs (months) in the same EBPBF machine could also be checked. The cell size is the same for all samples and was 1.1 mm × 1.1 mm × 1.1 mm with the designed strut size being 0.5 mm in diameter, giving ρL/ρS = 0.36 (ρL = 1.60 g/cm3). In Fig. 1, the orientation of each unit cell is illustrated, and BD is vertically up.

Fig. 1
figure 1

EBPBF lattice samples: a illustrating unit cells [001]//BD (left), [011]//BD (mid), and [111]//BD (right), and b a [001]//BD (left), a [011]//BD (mid), and an [111] (right) built sample

Full size image

The built samples were compressively tested with LD//BD. In a [001]//BD (thus [001]//LD) sample, half of the total number of struts are parallel to BD and half normal to BD. A [011]//LD cell means that, with the original [001] cell having rotated about [100] for 45°, 1/3 of struts remain normal to BD. Rotating the original [001] unit cell about [\(1\overline{1 }0\)] for 54.74°, on the other hand, results in [111]//LD. Figure 1b shows one each of [001]//LD, [011]//LD, and [111]/LD built samples. For all samples, the height of the lattice portion is ~ 20 mm and the diameter is ~ 10 mm. Samples were built to include a solid portion on top and below the lattice so that deformation should only occur in the lattice portion of the sample. Samples were tested using a Tinius Olsen H50KS tester. This is a dual column tester with the frame capacity and the load cell both being 50 KN. The load measurement accuracy is ± 0.5% of the indicated load and the testing speed range of the machine is 0.001–500 mm/min with the speed accuracy of ± 0.005% of the indicated speed. For the current testing, a crosshead speed of 1.2 mm/min was used. Figure 2 shows the testing setup. A load–displacement data was recorded for each test. EL, σy-L, UCSL, and plastic strain (εp) were determined from the load–displacement test curves based on the nominal diameter being 10 mm and the nominal “gauge” length being 20 mm.

Fig. 2
figure 2

Images showing a compression testing and b a close-up view of the sample

Full size image

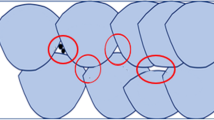
Selected lattice samples, both before testing and after testing, were examined using a Hitachi SU-70 scanning electron microscope (SEM) in secondary electron mode with the accelerating voltage set at 15 kV and with the focusing distance of 15–20 mm. SEM images were used to estimate the sizes of the lattice struts. To do this, image analysis was applied to the SEM images taken in un-tested samples using the ImageJ software. An example is given in Fig. 3 which shows struts being highly irregular and shows how a local area in a SEM image is taken for analysis using ImageJ to measure the diameter of the struts. In this way, a large number of cells in each sample can be measured. For each cell specifically orientated lattice structure, duplicate samples were used. During mechanical testing of the lattice samples, one each cell-orientated sample was interrupted meaning that the test was stopped before reaching UCSL and the sample was examined to possibly observe the initial stage of cracking.

Fig. 3
figure 3

Illustrations of how strut size is estimated: converting the SEM image to binary by applying an appropriate threshold in ImageJ then measuring the distance between black pixels using a Phyton code

Full size image

Finite element simulations of the lattices with three different UCOs were carried out using Static-Structural Module inside ANSYS Mechanical. A workstation with 36 logical processors coupled with an NVIDIA Quadro RTX6000 GPU accelerator was used for the simulations. 3D models from unit cells to the full lattice size samples were constructed in SolidWorks. The top and bottom boundary conditions were set by modeling a top and a bottom circular plate bonded to the lattice structure. The restricted boundary condition was set so that the bottom plate was fixed stationary, and axial displacement (up to 0.6 mm) was allowed in the top plate. Initially, the mesh sensitivity analysis was conducted and a mesh size of 0.1 mm, as illustrated in Fig. 4, has been shown to be appropriate. After setting up the model, values of yield strength, Young’s modulus, tangent modules (after yield point), and Poisson’s ratio were selected. These values are 120 GPa, 1001 MPa, 1098 MPa, and 0.323, respectively, and they are commonly used for the alloy. The simulated stress distribution in any location of the lattice and at any loading level can be examined. Stress and strain data were extracted from the simulation data to construct the strain–stress curves and to determine the simulated EL and σy-L (0.2% yield stress) values.

Fig. 4
figure 4

Illustration Loading and boundary condition used in the FE analysis

Full size image

3 Results and discussion

3.1 Orientation-dependent E L , σ y-L , UCS L , and ε p

The stress–strain test curves and one simulated curve for each group of specifically orientated lattice samples are shown in Fig. 5a, Fig. 5b, and Fig. 5c for [001]//LD, [011]/LD, and [111]//LD, respectively. In each simulated curve, stress initially increases stiffly as strain increases and then the stress increases slowly for the further increase in strain after yielding until ε = 3%. Failure strain cannot be reliably predicted as there is not a reliable failure criterion. As shown in Fig. 5d, from an experimentally determined load–displacement curve, EL can be determined using the linear region of the curve. For σy-L, the linear line is offset for 0.2% strain to intersect the curve and thus to obtain σy-L. Figure 5d also illustrates how apparent plastic strain (εp) is determined and this strain value is measured by the linear line intersecting the curve where the load starts to decrease after UCSL. During a test, there is initially a small plateau when σ≈10 MPa, likely resulting from the initial and small movement/adjustment in the regions between the solid top/bottom with the lattice.

Fig. 5
figure 5

Compressive strain–stress test (EXP) curves for a [001]//LD, b [011]//LD, and c [111]//LD lattice samples, and d examples illustrating how yield strength (σy-L) and plastic strain (εp) are determined for each type of lattices. In a, b, or c, one simulated (SIM) curve is also included

Full size image

For either [001]//LD or [111]//LD condition, samples are from two separate runs (run EXPA and run EXPB). As is clear in Fig. 5a, a curve from run EXPA of [001]//LD samples shows a lower EL and UCSL, compared to other [001]//LD samples. There are a sufficient number of samples tested for [111]//LD condition, 4 from run EXPA and 5 from EXPB run. Clearly, although there are scatters, all the curves have grouped closely together without an indication of one group of curves (from run EXPA) being different from the other (run EXPB). Overall, samples from the EBPBF machine may be viewed reasonably repeatable from one run to another, although a [001]//LD sample may have departed slightly in EL and UCSL.

For [001]//LD lattices, each test was terminated (manually) after UCSL was reached and when the load had clearly started decreasing, except for the one in which the test was stopped slightly after the linear portion. In these [001]//LD tests, the samples did not fracture but could be seen to start distorting after UCSL. For [011]//LD and [111]//LD samples, an interrupted test for one each was also conducted by stopping slightly after the linear portion. In all other tests of these samples, the load started to decrease a little after UCSL and this decrease was mostly quite rapid, as shown Fig. 5b and Fig. 5c. The sharp decrease corresponded to the collapsing of the sample meaning that the struts fractured quite quickly largely along a plane of the lattice. In each test, the test was terminated either soon after the collapse or continued a little longer so the load could be seen to increase again. This load re-increase was due to the top portion of the fractured sample totally collapsing on the lower portion so that further compression resulted in the increase under the compressive load.

From the experimental data plotted in Fig. 5a to Fig. 5c, EL, σy-L, UCSL, and εp values have been determined following the procedure explained using the plots in Fig. 5d and the determined values are listed in Table 1. Values of EL and σy-L predicted by simulation are also listed in Table 1. In the table, values are also listed for specific property (EL, σy-L, or UCSL) ratios of [001]//LD over [011]//LD or over [111]//LD and [011]//LD over [111]//LD. From the table, data from experiments show that EL[001] is significantly (1.6 times) higher than that of either EL[011] or EL[111]. Simulation data in the table show that EL[001] is 2.6 or 3.3 times higher than that of EL[011] or EL[111], respectively. EL[011] is almost the same as EL[111], determined experimentally. EL values for all three orientations determined experimentally are however considerably lower than the values determined by simulation. This is particularly so for the [001]//LD condition and will be discussed next (Section 3.2) below. Figure 5 and Table 1 show that the experimentally determined σy-L values are reasonably close to those from the simulation. Note UCSL values from experiments cannot be compared to simulated values as UCSL cannot be predicted reliably by simulation. A detailed discussion on the σy-L, UCS, and εp values listed in Table 1 will be made in Section 3.3.

Table 1 Experimentally determined (with one standard error values) and simulated compressive property values
Full size table

3.2 Discussion on [001]//LD property values

Although the present work focuses on the strength values of lattice structures and the influencing factors, modulus values are often presented using the stress–strain curves in literature. Thus, simulated and experimentally determined modulus values are discussed here. Predicted values from the present simulation including using two further relative density values are compared with several other studies in literature, as is shown in Fig. 6. Data from the present simulation work agree with the predicted values from Melhboob et al. [23], Niu et al. [24], and Zoubi et al. [25] although Tsai et al.’s EL values [26] are significantly lower. Thus, for ρL/ρS = 0.36, EL[001] = 23 GPa from the present simulation (Table 1) could be viewed as reasonable.

Fig. 6
figure 6

Data of relative modulus as a function of relative density predicted by simulation from this work and others in literature [23,24,25,26] for [001]//LD lattices

Full size image

Experimental determination of EL from compression testing and tests using a damping analyzer on EBPBF [001]/LD samples with lattice densities similar to that used in the current study have been conducted in three studies in literature. Their EL values plus the value from the present experiments are listed in Table 2. EL[001] values determined by compression testing are considerably lower than the values determined using the damping analysis method. Despite the lower EL values of lattice structures determined using compression testing, it has often been used [31,32,33,34], for lattice structures of various types of unit cells.

Table 2 Experimentally determined EL values from various sources
Full size table

For a further understanding, compression of a [001]//LD unit cell (Fig. 1a, left) is analytically considered. Also, to illustrate analytically and approximately, square (rs × rs) in shape instead of a circular shape is considered first for the struts. A relative density of a unit cell is:

$$\frac{{V}_{{\text{Struts}}}}{{V}_{{\text{Cell}}}}=\frac{{4\bullet {r}_{{\text{S}}}}^{2}\bullet {l}_{{\text{U}}}+8\bullet {{r}_{{\text{S}}}}^{2}\bullet {l}_{{\text{L}}}}{{{l}_{{\text{U}}}}^{3}}=\frac{{4\bullet r}^{2}\bullet \left({l}_{{\text{U}}}+2\bullet {l}_{{\text{L}}}\right)}{{{l}_{{\text{U}}}}^{3}}=\frac{{4\bullet {r}_{{\text{S}}}}^{2}\bullet \left(2{r}_{{\text{S}}}+{l}_{{\text{L}}}+2\bullet {l}_{{\text{L}}}\right)}{{{l}_{{\text{U}}}}^{3}}=\frac{{8\bullet {r}_{{\text{S}}}}^{3}+12\bullet {{r}_{{\text{S}}}}^{2}\bullet {l}_{{\text{L}}}}{{\left(2{r}_{{\text{S}}}+{l}_{{\text{L}}}\right)}^{3}}$$
(1)

where VStruts is the volume of all struts in a cell and VCell is the volume of the cell, rS, lU, and lL are graphically defined in Fig. 1a.

If \({r}_{{\text{S}}}=\frac{{l}_{{\text{U}}}}{2} {\text{ and }} {l}_{{\text{L}}}=0\) then \(\frac{{V}_{{\text{struts}}}}{{V}_{{\text{Cell}}}}=\frac{8\bullet {{r}_{{\text{S}}}}^{2}}{8\bullet {{r}_{{\text{S}}}}^{2}}=1\), meaning fully solid, and:

$$\frac{\Delta l}{{l}_{{\text{U}}}}\bullet E=\frac{F}{{{l}_{{\text{U}}}}^{2}}\to \frac{\Delta l}{{l}_{{\text{U}}}}=\frac{F}{{{E\bullet l}_{{\text{U}}}}^{2}}\mathrm{ or } F=\frac{\Delta l}{{l}_{{\text{U}}}}\bullet {{E\bullet l}_{{\text{U}}}}^{2}$$
(2)

where Δl is the compression displacement and F is the applied load.

\(\frac{{V}_{{\text{struts}}}}{{V}_{{\text{Cell}}}}=\frac{{8\bullet {r}_{{\text{S}}}}^{3}+12\bullet {{r}_{{\text{S}}}}^{2}\bullet {l}_{{\text{L}}}}{{\left(2{r}_{{\text{S}}}+{l}_{{\text{L}}}\right)}^{3}}=0.36\) means ρL = 1.60 g/cm3, which is the relative density used in the present work. Then:

$$5.12{{r}_{{\text{S}}}}^{3}+7.68{{r}_{{\text{S}}}}^{2}{l}_{{\text{L}}}-2.16{r}_{{\text{S}}}{{l}_{{\text{L}}}}^{2}-0.36{{l}_{{\text{L}}}}^{3}=0$$
(3)

A solution that also satisfies Vstruts/Vcell = 0.36 is \({{\varvec{l}}}_{\mathbf{L}}/{{\varvec{r}}}_{\mathbf{S}}=\) 2.9315. This ratio can be shown to be independent of cell size. Thus, \({{\varvec{l}}}_{\mathbf{U}}=2{{\varvec{r}}}_{\mathbf{S}}+{{\varvec{l}}}_{\mathbf{L}}=4.931{{\varvec{r}}}_{\mathbf{S}}\).

Assuming that the whole length (lU in Fig. 1a left) of the four vertical struts deforms uniformly without the constraint of the horizontal struts, thus referred to as the lower bound condition, F in Eq. (2) can be proportionally reduced to keep the same Δl/lU to derive the apparent modulus of the unit cell (EU), meaning that:

$$\frac{{\varvec{F}}\bullet \frac{4{{{\varvec{r}}}_{\mathbf{s}}}^{2}}{{{{\varvec{l}}}_{\mathbf{U}}}^{2}}}{{{{\varvec{l}}}_{\mathbf{U}}}^{2}}=\frac{\frac{\Delta {\varvec{l}}}{{{\varvec{l}}}_{\mathbf{U}}}\bullet {\varvec{E}}\bullet {{{\varvec{l}}}_{\mathbf{U}}}^{2}\bullet \frac{4{{{\varvec{r}}}_{\mathbf{s}}}^{2}}{{{{\varvec{l}}}_{\mathbf{U}}}^{2}}}{{{{\varvec{l}}}_{\mathbf{U}}}^{2}}=\frac{\Delta {\varvec{l}}}{{{\varvec{l}}}_{\mathbf{U}}}\bullet {{\varvec{E}}}_{\mathbf{U}}$$
(4)

Thus:

$${{\varvec{E}}}_{\mathbf{U}}=\frac{{{4{\varvec{E}}\bullet {\varvec{r}}}_{\mathbf{S}}}^{2}}{{{{\varvec{l}}}_{\mathbf{U}}}^{2}}$$
(5)

Then:

$${E}_{{\text{U}}}=\frac{{{4E\bullet r}_{{\text{S}}}}^{2}}{{{l}_{{\text{U}}}}^{2}}=\frac{{{4E\bullet r}_{{\text{S}}}}^{2}}{{(4.931r_{S})}^{2}}=0.1645E=0.1645\times 120{\text{GPa}}=19.7{\text{GPa}}$$

To illustrate through simulating a unit cell of [001]//LD, as shown in Fig. 7a and Fig. 7b, a full unit cell with a relative density ρc/ρs = 0.36 and a unit cell with vertical struts only were modeled with the same unit cell size and strut thickness. For the vertical-struts-only cell, the simulation has shown that EL[001]//LD = 19.7 GPa. This is the same as predicted and explained already using Eqs. 1–5, analytically based simply on the four vertical struts deforming without any influence from the hour horizontal struts. For the full unit cell meaning that the horizontal struts are included, EL[001]//LD = 21.8 GPa, slightly higher than the value obtained from considering only the vertical struts. The compression strain of the (lU − lL) portions is slightly resisted due to the horizontal struts that are connected. Thus, the total strain of the cell is slightly lower, resulting in a slightly higher E value. The single cell EL[001]//LD value is slightly lower than the full-size lattice EL[001]//LD (22.9 GPa) value as listed in Table 1.

Fig. 7
figure 7

Two load-supporting conditions of a unit cell used for simulation to determine unit cell EL[001]//LD, a only the four vertical struts used and b a normal unit cell

Full size image

Compression strength data of EBPBF [001]//LD samples from literature are now compared to the data (Table 1) in this study. In Parthasarathy et al.’s study [27], σy-L values were not provided. But examining their load–displacement curves and knowing their sample size have suggested that for their samples, σy-L[001]≈96 MPa and ≈130 MPa for samples having ρL = 1.39 and 1.69 g/cm3, respectively. Their UCSL[001] values are 117 and 163 MPa, respectively, for their two ρL values. Compared to data in Table 1, strength values from Parthasarathy et al.’s study are thus viewed low. Zhao et al. [29] did not report σy-L values and they also have not provided σ-ε curves. UCSL[001] at 196 MPa from Zhao et al.’s [29] with ρL = 1.63 g/cm3 and at 200 MPa from Li et al. [30] with ρL = 1.63 g/cm3 are lower than UCSL[001] = 235 MPa from the present work with ρL = 1.60 g/cm3. A σ-ε curve available in Li et al.’s work [30] also shows a stress plateau at peak stress with εp at ~ 0.077 is slightly higher than values with a mean value at 0.063 determined in the present work.

3.3 Cell orientation and stress distribution

The effect of cell orientation on the mechanical behavior of the cubic samples under compressive loading, which has not been studied previously, is now discussed in more detail based on the data obtained in the work as listed in Table 1. Both experimentally determined σy-L[001] and UCSL[001], respectively, are twice or almost twice the σy-L value and UCSL value of [011]//LD samples or the values of [111]//LD samples. σy-L[011] is very close to σy-L[111] and UCSL[011] is also very close to UCSL[111]. Experimentally determined σy-L values for each orientation differ from simulated values either slightly (for [001]//LD and [011]//LD conditions) or very little (for [111//LD condition). As for εp, the meaning of it for [001]//LD samples is the plastic strain before the start of lattice distortion. For [011]//LD or [111]//LD samples, εp represents the plastic strain before the start of lattice fracturing/collapsing. Noting this difference in the meaning of εp, the mean εp value of [001]//LD samples is 3.3 times and 5.3 times of the value for [011]//LD samples and for [111]//LD samples, respectively. This can also be viewed as that, comparatively, [001]//LD samples do not fracture and [011]//LD samples and [111]//LD samples fracture readily with low εp values. However, εp[011]/εp[111] = 1.6, meaning that [111]//LD samples significantly more readily fracture than [011]//LD samples do although EL and strength values, respectively, are largely the same.

To aid the understanding of why [011]//LD and [111]//LD samples are weak and readily fracture, compared to [001]//LD samples, stress distributions predicted by simulation are presented in Fig. 8. In the top row of the figure, in each case, the maximum von Misses stress (σvM-max) locally has reached σy (= 1001 MPa) meaning that yielding has commenced locally in the sample. The corresponding applied load (Fy-L-Sim) is also stated: − 13,277 N for [001]//LD, − 7592 N for [011]//LD, and − 7950 N for [111]//LD samples, respectively. These values may be viewed to agree with the values experimentally determined for the lattice samples. An example each can be seen in Fig. 5d: − 14,200 N for [001]//LD, − 7200 N for [011]//LD, and − 7800 N for [111]//LD sample, respectively, which are the load values after 0.2% strain offset. A feature in these σvM plots is that σvM is quite evenly distributed along the vertical and load-supporting struts of [001]//LD samples but is highly uneven within each strut in the other two differently orientated lattice samples. Locally high σvM values reaching σy of the alloy under low values of loading have resulted in low σy-L values for [011]//LD and [111]//LD samples, in comparison to [001]//LD samples.

Fig. 8
figure 8

Plots of stress distributions when the indicated load is applied for a [001]//LD, b [011]//LD, and c [111]//LD, with the top row showing von-Misses (σvM) stress and the bottom row showing first principal stress. Note: the highest value of σvM in each case has reached the yield stress (σy) of Ti6Al4V (≈1001 MPa)

Full size image

In the lower row of the plots in Fig. 8, the distributions of the first principal stress (σ1) are shown under the respective load value as those used for showing the σvM distributions in the top row. For [001]//LD, when the lattice yields (top-left plot of Fig. 8), σ1 locally in the connecting location of horizontal-vertical struts reaches ~ 600 MPa (in tension) as shown in the lower-left plot in Fig. 8. On the other hand, for both [011]//LD and [111]//LD lattices, as shown in the lower-mid and lower-right plots in Fig. 8, σ1 > 1600 MPa locally. As has already been explained in Introduction, various surface irregularities may act as defects that may result in a considerably higher stress concentration and in tension, providing a condition of crack growth and causing the struts to readily fracture. An examination of this possible fracturing behavior is presented below.

3.4 Fracture and deformation behavior

Figure 9 shows [011]//LD lattice samples, one before, and the other after testing and thus having fractured. The fracture path is along a row (a plane behind and inside the lattice sample) of struts in ~ 45° to the loading direction. The shear fracture of struts can be more clearly seen in the higher magnification SEM images. As has already been explained, σ1 locally in tension has reached a very high value in struts when yielding of the lattice has occurred. The irregularities in the form of sharp protrusions, deep recesses, and undercuts can readily further increase the stress concentration. Thus, the highly irregular struts readily fracture with a low εp value (< 0.02). As listed in Table 1, εp-[011]//LD (= 0.019) is significantly higher than εp-[111]//LD (= 0.012), although Fig. 8b and Fig. 8c indicate a similar and high level of stress locally. In [011]//LD samples, two out of three struts support the load primarily. In [111]//LD samples, all struts support the load equally thus there is a higher probability of strut defects assisting crack growth and fracturing. This may be the reason for a lower εp value.

Fig. 9
figure 9

SEM images of [011]//LD samples, a an un-tested sample and b a tested sample showing the fracturing of a raw (plane) of struts as indicated by the dotted lines in the left image, higher magnification images in three fractured locations (mid images) and a cross section of the sample showing clearly the fracture path in the right image

Full size image

The highly irregular struts also can be statistically shown by the measured sizes of the struts, with duplicate samples for each orientation, plotted in Fig. 10. The strut irregularity due to sharp protrusions, deep recesses, and undercuts that are indicative in Fig. 3 is consistent with the high values of one standard deviation (5–10%) and particularly with the high values of range (52–90%) of the strut size (width). The standard error values being only ~ 1% of the mean values are very small as a large number of strut size values have been used for the calculation; thus, the confidence is very high for the mean values. All the mean values are larger than the designed value of 0.5 mm. This larger strut size EBPBF samples than the designed strut size is consistent with the size difference between the measured strut size and the designed size reported in other studies [31,32,33,34]. The real strut size in the [001]//LD samples is slightly larger than the values of [011]//LD and [111]//LD samples and the reason is not clear.

Fig. 10
figure 10

Mean, standard deviation, standard error, and range values of strut sizes of the three different orientation samples calculated from measured strut size data

Full size image

An example of observing the samples from interrupted tests is shown in Fig. 11, using a [011]//LD sample. As shown in Fig. 5b, the test was stopped only slightly after the apparent yield point. Figure 11 demonstrates that, although the global plastic deformation is still low at ~ 0.003%, cracks have started to propagate. The locations of crack propagation should be those locally highly stressed, as predicted and shown in Fig. 8. Due to this crack initiation and propagation mechanism, the final fracturing as shown in Fig. 9 took place with a low εp value at ~ 0.02%. On the other hand, such a mechanism does not operate in [001]//LD samples. Thus, in these samples, εp values are high at > 0.06% when the sample starts to distort instead of fracturing.

Fig. 11
figure 11

SEM images showing the highly irregular strut surfaces of a [011]//LD sample with the test stopped before reaching UCSL, displaying a crack pointed to by an arrow locally having initiated and started to propagate

Full size image

4 Conclusions

Yield strength (σy-L) values determined experimentally for simple cubic unit cell lattice samples built using electron beam powder bed fusion (EBPBF) are generally in agreement with those predicted by simulation, for the same combination of loading direction (LD) and unit cell orientation (UCO). Thus, EBPBF defects do not affect σy-L. Both experimentally determined and simulated modules (EL) values have shown that EL of [001]//LD lattices is considerably higher than EL of [011]//LD lattices and EL of [111]//LD lattices. However, EL values determined using compression test are considerably lower than the true EL values, despite of the test values having been widely reported. σy-L, ultimate compression strength (UCSL) and failure strain (εp) of the lattice structures have been found to be strongly dependent on how LD and UCO combined. σy-L of [001]//LD lattices has been experimentally determined to be 1.8–2.0 times and εp to be 4–6 times, respectively, higher than those of [011]//LD and [111]//LD lattices. This is consistent with the simulation results that, in [011]//LD and [111]//LD lattices, stress concentration has resulted in the lattices hacing locally yielded and deformed when the load is 57% and 60%, respectively, of the load causing yielding in [001]//LD lattices. For [011]//LD and [111]//LD samples, simulation has illustrated the maximum principal stress (σ1) high in tension locally. This is consistent with the observation that micro-notches readily act as crack propagation locations for a plane of struts to fracture with low εp values in [011]//LD and [111]//LD samples.