Skip to main content
SpringerLink
Log in

A 2D filling and solidification benchmark test: validating smoothed particle hydrodynamics (SPH) simulations for sand gravity casting

  • ORIGINAL ARTICLE
  • Published:
The International Journal of Advanced Manufacturing Technology Aims and scope Submit manuscript

Abstract

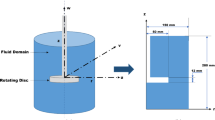
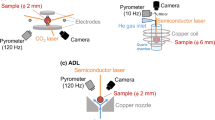
The simulation of the sand gravity casting process is complicated due to its multiscale and multiphysics nature. Although there are many commercial software options available, it remains extremely difficult to accurately predict the filling, solidification, and defects such as oxidation. Smoothed particle hydrodynamics (SPH) is a Lagrangian simulation approach that is particularly well-suited for modeling the gravity casting process. To validate the results of the filling, cooling, and solidification steps of the SPH method, it is interesting to introduce and design a 3D universal experimental test case of the gravity casting process that can be modeled in 2D. This universal test case is developed so that the hydrodynamic filling process can be analyzed in 2D while the cooling and solidification processes can be investigated in 1D. After comparing ProCAST, a commercial 3D mesh-based software, with the 2D SPH method, the results highlight the unique advantages of each approach in analyzing filling step and temperature evolution. The SPH simulations are better at capturing the essential aspects of fluid motion.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23
Fig. 24
Fig. 25
Fig. 26
Fig. 27

Similar content being viewed by others

Data Availability

The data supporting the conclusion of this article are included within the article. Any queries regarding these data may be directed to the corresponding author

References

  1. Bonollo F, Urban J, Bonatto B, Botter M (2005) Gravity and low pressure die casting of aluminium alloys: a technical and economical benchmark. ALLUMINIO E LEGHE 6:23–32

  2. Guofa MI, Hengtao ZHAO, Kuangfei WANG, Zhian XU, Jitai NIU (2008) Simulation of mold filling and solidification on gravity casting of Al-Si alloy (A357). Mater Sci Forum 575-578:1204–1209

    Article  Google Scholar 

  3. Sorte M (2017) Defects, root causes in casting process and their remedies: review. J Eng Res Appl 7(3):47–54

    Google Scholar 

  4. Viswanath A, Manu MV, Savithri S, Pillai UT (2017) Numerical simulation and experimental validation of free surface flows during low pressure casting process. J Mater Process Technol 244:320–330

    Article  Google Scholar 

  5. Jakumeit J, Subasic E, Bu¨nck M (2014) Shape casting: 5th International Symposium. Wiley, San Diego

    Google Scholar 

  6. Zhang B, Cockcroft SL, Maijer DM, Zhu JD, Phillion AB (2005) Casting Defects in Low-Pressure Die-Cast Aluminum AlloyWheels. JOM 57:36–43

    Article  Google Scholar 

  7. Ingle D, Narkhede BE (2018) A literature survey of methods to study and analyze the gating system design for its effect on casting quality. Mater Today: Proc 5:5421–5429

    Article  Google Scholar 

  8. Ellingsen K, Coudert T, M'Hamdi M (2015) SPH based modelling of oxide and oxide film formation in gravity die castings, IOP Conf Ser: Mater Sci Eng 84(1)

  9. Prakasha M, Cleary P, Grandfield J (2009) Modelling of metal flow and oxidation during furnace emptying using smoothed particle hydrodynamics. J Mater Process Technol 209:3396–3407

    Article  Google Scholar 

  10. Minaie B, Stelson KA, Voller VR (1991) Analysis of flow patterns and solidification phenomena in the die casting process. J Eng Mater Technol 113:296–302

    Article  Google Scholar 

  11. Liu S-g, Luo C-b, Li G-a, Gao W-l, Zheng L, Dai S-l (2018) Effect of pressurizing speed on filling behavior of gradual expansion structure in low pressure casting of ZL205A alloy. Res Dev 15(4):276–282

    Google Scholar 

  12. Im I-T, Kim W-S, Lee K-S (2001) A unified analysis of filling and solidification in casting with natural convection. Int J Heat Mass Transf 44:1507–1515

    Article  MATH  Google Scholar 

  13. Kreziak G, Rigaut C, Santarini M (1993) Low pressure permanent mould process simulation of a thin wall aluminium casting, Materials Science & Engineering A: Structural Materials: Properties. Microstructure and Processing A173(1–2):255–259

  14. Wenming Jiang, Zitian Fan (2014) Gating system optimization of low pressure casting A356 aluminum alloy intake manifoldbased on numerical simulation. China Foundry 11:119–124

    Google Scholar 

  15. Guofa Mi, Xiangyu Liu, Wang Kuangfei Fu, Hengzhi, (2009) Numerical simulation of low pressure die-casting aluminum wheel. China foundary 6(1):48–52

    Google Scholar 

  16. Ha J, Cleary P, Alguine V, Nguyen T (1999) Simulation of die filling in gravity die casting using sph and magmasoft. In: Second International Conference on CFD in the Minerals and Process Industries. CSIRO, Melbourne, Australia

    Google Scholar 

  17. Ye T, Pan D, Huang C, Liu M (2019) Smoothed particle hydrodynamics (SPH) for complex fluid flows: recent developments in methodology and applications. Phys Fluids 31(1)

  18. Hu MY, Cai JJ, Li N, Yu HL, Zhang Y, Sun B, Sun WL (2018) Flow modeling in high-pressure die-casting processes using sph model. Int J Met 12:97–105

    Google Scholar 

  19. Niu X, Zhao J, Wang B (2019) Application of smooth particle hydrodynamics (SPH) method in gravity casting shrinkage cavity prediction. Comput Part Mech 6:803–810

    Article  Google Scholar 

  20. Cleary P, Ha J, Sawley M (1999) Modelling industrial fluid flow application using SPH. Proceedings of the International Workshop on Bifurcation and Localisation

    Google Scholar 

  21. Wen-jiong CAO, Zhao-yao ZHOU, JIANG F-m (2015) Smoothed particle hydrodynamics modeling and simulation of foundry filling process. Trans Nonferrous Met Soc China 25:2321–2330

    Article  Google Scholar 

  22. Chandra U (1990) Benchmark problems and testing of a finite element code for solidification in investment castings. Int J Numer Methods Eng 30:1301–1320

    Article  Google Scholar 

  23. Sirrell B, Holliday M, Campbell J (1996) Benchmark testing the flow and solidification modeling of AI castings. JOM 48:20–23

    Article  Google Scholar 

  24. Carozzani T, Gandin CA, Digonnet H et al (2013) Direct Simulation of a Solidification Benchmark Experiment. Metall Mater Trans A 44(2):873-887

  25. Bublık O, Lobovsky L, Heidler V, Mandys T, Vimmr J (2021) Experimental validation of numerical simulation of free-surface flow within casting mold cavities. Eng Comput 38:4024–4046

    Article  Google Scholar 

  26. Coniglio N, Sivarupan T, El Mansori M (2018) Investigation of process parameter effect on anisotropic properties of 3D printed sand molds. Int J Adv Manuf Technol 94:2175–2185

    Article  Google Scholar 

  27. Zamani M (2017) Al-Si cast alloys -microstructure and mechanical properties at ambient and elevated temperature. Jönköping University, School of Engineering, Dissertation

    Google Scholar 

  28. Saada MB, El Mansori M (2021) Assessment of the effect of 3D printed sand mold thickness on solidification process of AlSi13 casting alloy. Int J Adv Manuf Technol 114:1753–1766

    Article  Google Scholar 

  29. Prakash C, Voller VR (1987) A fixed grid numerical modelling methodology for convection-diffusion mushy region phase-change problems. Int J Heat Mass Transf 30(8):1709–1719

    Article  Google Scholar 

  30. Monaghan JJ (1994) simulating free surface flows with sph. J Comput Phys 110(2):399–406

    Article  MATH  Google Scholar 

  31. Krimi A, Rezoug M, Khelladi S, Nogueira X, Deligant M, Ramírez L (2018) Smoothed Particle Hydrodynamics: a consistent model for interfacial multiphase fluid flow simulations. J Comput Phys 358:53–87

    Article  MathSciNet  MATH  Google Scholar 

  32. Liu MB, Liu GR (2010) Smoothed particle hydrodynamics (SPH): an overview and recent developments. Arch Comput Methods Eng 17:25–76

    Article  MathSciNet  MATH  Google Scholar 

  33. Cleary PW, Ha J, Sawley ML (2001) Modelling industrial fluid flow applications using SPH. Bifurcation and Localisation Theory in Geomechanics. CRC Press, p 8

    Google Scholar 

  34. Cleary PW, Ha J, Prakash M, Nguyen T (2006) 3D SPH flow predictions and validation for high pressure die casting of automotive components. Appl Math Model 30:1406–1427

    Article  Google Scholar 

  35. Sun PN, Colagrossi A, Marrone S, Zhanga AM (2017) The δplus-SPH model: simple procedures for a further improvement of the SPH scheme. Comput Methods Appl Mech Eng 315:25–49

    Article  MathSciNet  MATH  Google Scholar 

  36. Antuono M, Colagrossi A, Marrone S (2012) Numerical diffusive terms in weakly-compressible SPH schemes. Comput Phys Comm 183:2570–2580

    Article  MathSciNet  MATH  Google Scholar 

  37. Meringolo DD, Marrone S, Colagrossi A, Liua Y (2019) A dynamic δ-SPH model: how to get rid of diffusive parameter tuning. Comput Fluids 179:334–355

    Article  MathSciNet  MATH  Google Scholar 

  38. Meringolo DD, Liu Y, Wang X-Y, Colagrossi A (2018) Energy balance during generation, propagation and absorption of gravity waves through the δ-LES-SPH model. Coast Eng 140:355–370

    Article  Google Scholar 

  39. Antuonoa M, Colagrossi A, Marronea S (2012) Numerical diffusive terms in weakly-compressible SPH schemes. Comput Phys Commun 183:2570–2580

    Article  MathSciNet  MATH  Google Scholar 

  40. Monaghan JJ, Gingold RA (1983) Shock simulation by the particle method SPH. J Comput Phys 52:374–389

    Article  MATH  Google Scholar 

  41. Brent A, Voller V, Reid K (1988) Enthalpy-porosity technique for modeling convection-diffusion phase change: application to the melting of a pure metal. Numer Heat Transf A: Appl 13(3):297–318

    Google Scholar 

  42. Mackenzie JA, Robertson ML (2000) The numerical solution of one-dimensional phase change problems using an adaptive moving mesh method. J Comput Phys 161:537–557

    Article  MathSciNet  MATH  Google Scholar 

  43. Fachinotti VD, Cardona A, Huespe AE (1999) A fast convergent and accurate temperature model for phase-change heat conduction. Int J Numer Meth Eng 44:1863–1884

    Article  MathSciNet  MATH  Google Scholar 

  44. J. Crank, “Free and moving boundary problems,,” 1984.

    MATH  Google Scholar 

  45. Meyer GH (1973) Multidimensional stefan problems. SIAM J Numer Anal 10(3):522–538

    Article  MathSciNet  MATH  Google Scholar 

  46. Egolf W, Manz H (1994) Theory and modeling of phase change materials with and without mushy regions. Int J Heat Mass Transf 37(18):2917–2924

    Article  MATH  Google Scholar 

  47. Schwaiger HF (2008) An implicit corrected SPH formulation for thermal diffusion with linear free surface boundary conditions. Int J Numer Methods Eng 75:647–671

  48. Adami S, Hu X, Adams N (2012) A generalized wall boundary condition for smoothed particle hydrodynamics. J Comput Phys 231(21):7057–7075

    Article  MathSciNet  Google Scholar 

  49. Lan P, Zhang J (2014) Study on the mechanical behaviors of grey iron mould by simulation and. Mater Des 53:822–829

    Article  Google Scholar 

  50. Su-Ling L, Xiao F-R, Zhang S-J, Mao Y-W, Liao B (2014) Simulation study on the centrifugal casting wet-type cylinder liner based on ProCAST. Appl Therm Eng 73:512–521

    Article  Google Scholar 

  51. Hua W, Haiming S, Haifeng L, Zhenjia X (2012) Numerical simulation of flow field and temperature field on aluminium alloy engine cylinder in casting process. Mater Sci Forum 704-705:50–57

    Google Scholar 

Download references

Acknowledgements

The authors acknowledge the contribution of colleagues. Thanks are due to J. Bourgeois and J. Nègre of the Arts et Metiers ParisTech for their technical support.

Funding

Institut Carnot ARTS

Author information

Authors and Affiliations

  1. Arts et Metiers Institute of Technology CNAM, LIFSE, HESAM University F-75013, Paris, France

    Mohammad Zarbini Seydani & Sofiane Khelladi

  2. Department of Civil, Geological and Mining Engineering, Polytechnique Montréal, Montreal, QC, H3T 1J4, Canada

    Abdelkader Krimi

  3. MSMP Laboratory, EA-7350, Arts et Metiers ParisTech, 2 Cours des Arts et Metiers, 13617, Aix-en-Provence, France

    Marie Bedel & Mohamed El Mansori

Authors
  1. Mohammad Zarbini Seydani
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Abdelkader Krimi
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Marie Bedel
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Sofiane Khelladi
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Mohamed El Mansori
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

Mohammad Zarbini Seydani: numerical simulation, investigation, data curation, methodology, writing—original draft

Abdelkader Krimi: numerical simulation, methodology, conceptualization

Marie Bedel: experimental work, investigation, methodology, conceptualization

Sofiane Khelladi: numerical simulation, methodology, conceptualization

Mohamed El Mansori: supervision, conceptualization, methodology

Corresponding author

Correspondence to Mohammad Zarbini Seydani.

Ethics declarations

Ethical approval

Not applicable

Consent to participate

All the authors agree to participate in this research study.

Consent for publication

The authors consent to have the data published.

Competing interests

The authors declare no competing interests.

Additional information

Publisher’s note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zarbini Seydani, M., Krimi, A., Bedel, M. et al. A 2D filling and solidification benchmark test: validating smoothed particle hydrodynamics (SPH) simulations for sand gravity casting. Int J Adv Manuf Technol 128, 801–821 (2023). https://doi.org/10.1007/s00170-023-11892-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00170-023-11892-2

Keywords

Search

Navigation