1 Introduction

Fig. 1
figure 1

Shuttle-System

Full size image

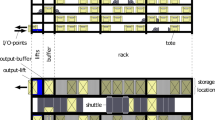
Shuttle-based storage and retrieval systems with tier-captive shuttles (SBS/RS) provide the highest throughput rates. The challenge with the design of systems like this is that the lifts usually become a bottleneck in those systems, and the utilization rate of the shuttles in the systems, is very low. [1,2,3]. To improve this, there are two possibilities: first, further to increase the performance of the lift or, second, to give the shuttle more tasks so that the relative performance decreases. Here is the primary mission to design a system efficiently utilizing every transporter (lifts and shuttles). One way to improve the relationship between lifts and shuttles is to add more lifts within a single aisle, as discussed by Ekren et al. [4]. This is useful if the additional aisle performance can be used; if not, this can cause downtimes of the whole system waiting for the pre-storage area. The second possibility to improve the relationship is to give the shuttle more work. The influence on the throughput per aisle is negative in most cases. Still, the question is whether the performance is needed or whether other effects offset this adverse effect, such as, e.g., the reduction of the aisle length. A possible additional task for shuttles is to increase storage depth. This increases the number of storage locations that must be served by a shuttle, leading to a longer cycle time. This, however, can only have a few adverse effects on the throughput in the entire system and, as Eder [5] shows can also have positive results. Another approach is to reduce the number of shuttles. This can happen in such a way that a shuttle no longer serves only one tier but has to serve several storage tiers. Eder [6] shows the influence on throughput with an adaptation, as described above. The two options listed so far have in common that the shuttle always stays in the same aisle. Another logical possibility is that the shuttle should change storage aisles. This means that a shuttle serves a certain number of aisles in one tier. The number of aisles is fixed, and only one shuttle is assigned to this area of multiple aisles and one tier. This paper aims to deliver an analytical approach to determining the throughput of a tier-captive aisle-changing SBS/RS. The depicted approach will be validated using simulation to show that this approach meets the common accuracy requirements. Another benefit of the developed method is the possibility of using it to optimize a storage system. The aim of this optimization can be, for example, to maximize performance by adapting the geometry of the storage system. The paper by Stojanovic [7] lists various optimization methods. A European material handling provider has offered such systems for some time. Such a system can be seen in Fig. 1.

This paper is organized as follows. The discussed system and the underlying assumptions are presented in Sect. 3. In Sect. 4, the analytical approach is presented. Especially the inter-arrival time, the service time of the shuttle with crossing the aisles, and the open queueing model with limited capacity. This queueing model takes the interactions between shuttles and lifts into account. Section 5 deals with a numerical study that shows the accuracy of the developed calculation model compared to a Monte-Carlo Simulation. Finally, Sect. 6 gives a conclusion of the paper and an outlook for future research.

2 Literature

The following section tries to give an overview of how the performance of SBS/RS can be evaluated. Here not only SBS/RS with aisle change shuttles are mentioned. To assess the performance of SBS/RS two ways are possible.

The first is a discrete-event simulation(DES) to determine the system’s performance measures. Several publications take this kind of approach (e.g., Ekren et al.[2,3,4, 8], Marchet et al.[9], Lerher et al. [10,11,12,13,14,15], Kriehn et al. [16], Ha et al. [17], Eroglu et al. [18] and Jerman et al. [19]). This kind of publication that discusses the storage system only via simulation is not mentioned in further detail because of their different focus on the topic.

The second way to discuss SBS/RS is by an analytical approach. This kind of discussion divides itself again into three different possibilities to discuss such a system.

The first analytical approach is a cycle time model. This approaches concern only the two subsystems: lifts and shuttles. However, the interactions between these two subsystems are not captured. There is a whole bunch of publications that deal with SBS/RS in a wide variety of forms (e.g., Sari et al. [20], Lerher [21,22,23,24], Lerher et al. [25, 26], Borovinšek [27], Ekren et al.[28], and Manzini et al. [29]). These papers are not discussed in further detail here, except for Lerher [22], who discusses a system with an aisle-changing shuttle. The significant point not covered in this paper is the interaction of lifts and shuttles. Lerher considered only one tier without any influence of the lifts.

The second analytical approaches are queueing networks. Methods of this kind take the interactions between lifts and shuttles into account. The primary outcome of such models is the time to retrieve a tote out of the storage system. The main disadvantage is that such a system can not determine the throughput of the system. Representative publications on this topic are from, e.g., Heragu et al. [30], Wang et al. [31], Marchet et al. [32], Ekren et al. [33], Epp et al. [34], and Tappia et al. [35]. Analytical approaches of this type have different goals and are not directly comparable to the method developed here.

The third kind discusses an SBS/RS by a single queueing model with limited capacity. Eder [5, 6, 36] discusses the different variations of SBS/RS by determining the cycle times of lifts and shuttles by a spacial discrete-time model. The further publications from Eder [37, 38] expand this analytical approach to different storage policies as the class-based storage policy. All these papers deal with aisle-captive systems, where a shuttle is dedicated to a specific aisle. Here the research gap is not to be found in neglecting the interactions between lifts and shuttles but in the fact that no system with a change of axis of the shuttle has yet been dealt with.

Except for Lerher [22], who discusses a multiple-aisle SBS/RS by a cycle time model, and Eroglu [18], who uses a simulation model to discuss a multiple-aisle SBS/RS, no other publication threat this kind of SBS/RS. The main disadvantage of the cycle time model is that the interactions between lifts and shuttles are left out. So the natural behavior of the system can not be described with this approach. The simulation model has the disadvantage that only a specific storage system can be simulated. Every change in dimension or technical data leads to a new simulation model. This literature overview shows that only a few papers discuss such systems. To close this research gap, Eder’s basic approach ([36]), which considers the interactions between lifts and shuttles via an open-queueing model with limited capacity, is to be expanded and adapted to a multiple-aisle tier-captive shuttle based storage and retrieval system. The main novelty of the presented approach is the ability to describe the influence of the multiple-aisle shuttle. This type of shuttle was not discussed before and is the main point of discussion in this paper. This additional degree of freedom compared to the two papers from Eder [5, 6] leads to new possibilities for the design of shuttle systems. Combined with various storage strategies discussed in this paper, a system with multiple new design parameters results.

Table 1 Notation of the tier-capative multiple-aisle AVS/RS
Full size table

3 System description

The system discussed in this paper is a tier-captive multiple-aisle SBS,/RS, as shown in Fig. 1. The I/O point ly on the first tier in front of the lifts. This lift transports the totes from the I/O point to the tier and back. In each tier are buffer slots between lifts and the cross-link. Each shuttle is assigned to one tier and a different number of aisles, so there are as many shuttle vehicles as tiers in a rack. The shuttles can change between the different aisles through the cross-link. These vehicles can handle one tote at a time. The position of the lift in relation to the axles is not fixed; it can be chosen from one side to the middle to the other side.

The main assumptions are based on an SBS/RS produced by a European material handling provider. These assumptions are similar to Eder [5, 6, 36].

  • There is one lift for the input and one for the output, which serves the transactions under a first come, first served rule in a single command cycle.

  • The shuttles serve the transactions under a first come, first served single and dual command cycle rule.

  • The I/O point is the dwell point of the input lift.

  • The point of service completion is the dwell point of the output lift and shuttles.

  • The lifts and shuttles accelerate/decelerate rates are averaged over time.

  • The lifts and shuttles’ velocities are averaged over time, exhibiting the same behavior as the real.

  • The time needed to transfer a tote to and from the lift is assumed.

  • The waiting queue before the I/O point is always filled. This assumption is necessary to eliminate the influence of the pre-storage area.

  • The totes are stored evenly distributed over the entire storage rack.

  • The order of totes is evenly distributed among all totes in the rack.

4 Analytical approach

The basis of this analytical approach is the paper of Eder [36]. This approach uses an open-queueing model with limited capacity (M\(\mid \)G\(\mid \)1\(\mid \)K). This model has three main parts to determine the throughput:

  • The inter-arrival time to a single tier

  • The shuttle service time

  • The open-queueing model M\(\mid \)G\(\mid \)1\(\mid \)K

Several changes are made to adopt this approach to an aisle-changing SBS/RS. The primary adoption of this approach is in discussing the shuttle service times. Here the multiple-aisle shuttle system influences the analytical approach compared to the basic paper of Eder [36]. Table 1 depicts all notations used in the following. In this section, the equations taken directly from Eder [36] are also listed to enable the entire approach’s comprehensibility.

4.1 Interarrival time

The first point of the analytical approach is the inter-arrival time determined by the lifts. The equations here can also be found in Eder [36]. This includes the time for the ride and the transfer times of totes to and from the lift are needed.

$$\begin{aligned} t_{lift}=2\cdot t_{R_{L}}+t_{t_{L}} \end{aligned}$$
(1)

The mean ride time is:

$$\begin{aligned} t_{R_{L}}=\frac{1}{n_{tier}}\sum _{k=1}^{n_{tier}} \textbf{t}(\mid l_{I/O}+(k-1)\cdot \Delta y \mid ) \end{aligned}$$
(2)

To consider the different speed profiles of the lift, the function \(\textbf{t}(l)\) has to be divided into two ranges. One range for distances less than \(l<\frac{v^2}{a}\):

$$\begin{aligned} \textbf{t}(l)=2\sqrt{\frac{l}{a_{lift}}} \end{aligned}$$
(3)

The other range for larger distances:

$$\begin{aligned} \textbf{t}(l)=\frac{l}{v_{lift}}+\frac{v_{lift}}{a_{lift}} \end{aligned}$$
(4)

The inter-arrival time to a tier is the cycle time times the number of tiers. This considers that one lift serves all tiers

$$\begin{aligned} t_A=t_{lift} \cdot n_{tier} \end{aligned}$$
(5)

4.2 Service time for a single deep rack

The second point is the service time of the shuttles. These equations contain the same arguments as the determination above and the extension for the aisle change. There are ride times A to B depending on the aisle change, the times for transferring the totes to and from the shuttle, and the time for changing the ride direction of the shuttle.

4.2.1 Single command cycle

For a single command cycle, the following equation is developed:

$$\begin{aligned} \begin{aligned} t_{shuttle_{SC}}= & {} 2 \cdot \frac{1}{n_{aisles}} \cdot t_{R_{S\_SC1}} \\{} & {} +2 \cdot \frac{n_{aisle}-1}{n_{aisles}} \cdot t_{R_{S\_SC2}} +2 \cdot t_{TR_{S\_SC}}\\{} & {} + 4 \cdot \frac{(n_{aisles}-1)}{n_{aisles}} \cdot t_{WC} + t_{t_{S}} \end{aligned} \end{aligned}$$
(6)

The first term of this equation stands for the ride in the longitudinal direction to a storage location. It contains two different parts depending on the need for an aisle change. The second term describes the needed time for an aisle shift. The third term stands for the time necessary for a change of direction. Here, the time for the wheel change in the two directions is described. The last term in this equation describes the time needed to load and unload the shuttle.

The mean time for the ride in the longitudinal direction in the aisles directly downstream is due to the following:

$$\begin{aligned} t_{R_{S\_SC1}}=\frac{1}{n_{slot}}\sum _{k=1}^{n_{slot}} \textbf{t}(k \cdot \Delta x +l_0) \end{aligned}$$
(7)

The mean time for the ride in the longitudinal direction in the aisles sidewards is:

$$\begin{aligned} t_{R_{S\_SC2}}= \textbf{t}(l_0)+ \frac{1}{n_{slot}}\sum _{k=1}^{n_{slot}} \textbf{t}(k \cdot \Delta x ) \end{aligned}$$
(8)

The difference between these two equations is that the shuttle has to stop a the cross-link when an aisle change is needed. To consider the different equations depending on the distances (3) and (4) have to be used again.

The mean time for the ride in the transverse direction in the cross-link is due to the:

$$\begin{aligned} t_{TR_{S\_SC}}=\frac{1}{n_{aisles}}\sum _{k=1}^{n_{aisles}}{} {\textbf {t}}(\mid l_{TP}+(k-1)\cdot \Delta z \mid ) \end{aligned}$$
(9)

The service time of the shuttles is as follows:

$$\begin{aligned} t_{S_{SC}}=2 \cdot t_{shuttle_{SC}} \end{aligned}$$
(10)

A dual handling cycle is the reference cycle, so this equation has to be multiplied by 2.

4.2.2 Dual command cycle and storage and retrieval in the random aisles

For the dual command cycle and a random aisle retrieval, the following equation is developed:

$$\begin{aligned} \begin{aligned} t_{shuttle_{DC}}= & {} 2 \cdot \frac{1}{n_{aisles}} \cdot t_{R_{S\_SC1}}\\{} & {} + 2 \cdot \frac{n_{aisle}-1}{n_{aisles}} \cdot t_{R_{S\_SC2}} \\{} & {} + \frac{1}{n_{aisles}}\cdot t_{R_{S\_DC1}} \\{} & {} +\frac{(n_{aisles}-1)}{n_{aisles}} \cdot t_{R_{S\_DC2}}\\{} & {} +2\cdot t_{TR_{S\_SC}}+t_{TR_{S\_DC}}\\{} & {} +6 \cdot \frac{(n_{aisles}-1)}{n_{aisles}} \cdot t_{WC}+ 2 \cdot t_{t_{S}} \end{aligned} \end{aligned}$$
(11)

The first term of this equation stands for the ride in the longitudinal direction to a storage location. It contains two different parts depending on the need for an aisle change. The second and third terms describe the time needed to ride between storage and retrieval locations. These terms are again different depending on the need for an aisle change. An aisle change from a storage location to an aisle change from a retrieval location takes time in the fourth term. The fifth term describes the time needed for the change of the aisle change of the shuttle on the ride between the storage location and the relocation location. The sixth term stands for the time needed for a direction change of the shuttle. The last term is for the time needed to load and unload the shuttle.

The mean time for the ride in the longitudinal direction between the storage location and the retrieval location within the same aisle is:

$$\begin{aligned} t_{R_{S\_DC1}}=\frac{1}{n_{slot}^2}\sum _{k=1}^{n_{slot}}\sum _{l=1}^{n_{slot}} \textbf{t}(\mid (k\cdot \Delta x-l\cdot \Delta x)\mid ) \end{aligned}$$
(12)

The mean time for the ride in the longitudinal direction between the storage location and the retrieval location over different aisles is:

$$\begin{aligned} t_{R_{S\_DC2}}=\frac{2}{n_{slot}}\sum _{k=1}^{n_{slot}} \textbf{t}(k \cdot \Delta x ) \end{aligned}$$
(13)

The mean time for the ride in a transversal direction between the aisle of the storage location and the aisle of the retrieval location is:

$$\begin{aligned} t_{TR_{S\_DC}}=\frac{1}{n_{aisles}^2}\sum _{k=1}^{n_{aisles}}\sum _{l=1}^{n_{aisles}}{} {\textbf {t}}( \mid k\cdot \Delta z-l\cdot \Delta z \mid ) \end{aligned}$$
(14)

The service time of the shuttles with dual command cycle is as follows:

$$\begin{aligned} t_{S_{DC}}=t_{shuttle_{DC}} \end{aligned}$$
(15)

4.2.3 Dual command cycle and storage and retrieval in the same aisle

For the dual command cycle and a storage location in the same aisle as the retrieval location n, the following equation is developed:

$$\begin{aligned} \begin{aligned} t_{shuttle_{DC}}=&2 \cdot \frac{1}{n_{aisles}} \cdot t_{R_{S\_SC1}} \\&+ 2 \cdot \frac{n_{aisle}-1}{n_{aisles}} \cdot t_{R_{S\_SC2}} + t_{R_{S\_DC1}}\\&+2\cdot t_{TR_{S\_SC}}\\&+ 4 \cdot \frac{(n_{aisles}-1)}{n_{aisles}} \cdot t_{WC}+2 \cdot t_{t_{S}} \end{aligned} \end{aligned}$$
(16)

The first term of this equation stands for the ride in the longitudinal direction to a storage location. It contains two different parts depending on the need for an aisle change. The second term describes the time needed to ride between storage and retrieval locations. The third term is the time needed for an aisle change to and from a storage/retrieval location. For the time of a direction change of the shuttle, the fourth term is required. The last term is for the time needed to load and unload the shuttle.

The service time of the shuttles with dual command cycle is as follows:

$$\begin{aligned} t_{S_{DC}}=t_{shuttle_{DC}} \end{aligned}$$
(17)

4.3 Open queueing model M\(\mid \)G\(\mid \)1\(\mid \)K

A time-continuous open queueing model with limited capacity is used to take the buffers’ influence and the interaction between lifts and shuttles into account. This queueing model represents the real behavior of a single tier through the mathematical description of a system with one service station, a limited number of buffer slots, and one inter-arrival time. The service station is a shuttle, and the lift gives the inter-arrivals. The inter-arrival time distribution is due to the distribution of rare events, a continuous time exponential time distribution. The service time is basic under a uniform time distribution for single command cycles and a triangle time distribution under a dual command cycle. The involvement of the aisle change changes the distributions to a certain extent and must therefore be determined numerically. With the help of this model the throughput \(\vartheta _{tier}\) of one single tier can be calculated [39]:

$$\begin{aligned} \vartheta _{tier}=\frac{1}{t_A}\cdot (1-p_k) \end{aligned}$$
(18)
$$\begin{aligned} \vartheta _{tier}=\frac{1}{t_S} \cdot (1-p_0) \end{aligned}$$
(19)

There are two ways to determine the throughput. One by the inter-arrival time and the blocking probability (18) and the second is by using the service time and the probability of emptiness of the queuing system (19).

Blocking probability describes the status that the system is filled so that no tote can enter the system. Applied to a shuttle system, the lift must wait for an empty slot in the input buffer. The probability of emptiness describes the status that the server has to wait because there is no tote in the queuing system. In an SBS/RS, this means that the shuttle has to wait for a tote.

The blocking probability of a queueing system is as follows [40]:

$$\begin{aligned} p_k=\frac{\rho ^{\frac{\sqrt{\rho \cdot e^{-s^2}}\cdot s^2 -\sqrt{\rho \cdot e^{-s^2}}+2K}{2+\sqrt{\rho \cdot e^{-s^2}}\cdot s^2 -\sqrt{\rho \cdot e^{-s^2}}}} \cdot (\rho -1)}{\rho ^{2\cdot \frac{\sqrt{\rho \cdot e^{-s^2}} \cdot s^2-\sqrt{\rho \cdot e^{-s^2}} +K+1}{2+\sqrt{\rho \cdot e^{-s^2}}\cdot s^2-\sqrt{\rho \cdot e^{-s^2}}}}-1} \end{aligned}$$
(20)

This equation describes the status that a system is filled, and no tote can enter the system.

Table 2 Tested parameter configurations of the tier-captive single-aisle SBS/RS
Full size table
Table 3 Cycle time of a shuttle in a single tier depending on the length of the aisle and the number of aisles
Full size table

The utilization rate of the shuttles is:

$$\begin{aligned} \rho =\frac{t_S}{t_A} \end{aligned}$$
(21)

K is the capacity of the queueing system. It is the sum of the number of buffer slots and the handling capacity of the shuttles.

$$\begin{aligned} K=n_{buf} + 1 \end{aligned}$$
(22)

s is the coefficient of variation of the service time distribution. This coefficient has to be gained by a simulation model. In the presented example in the following part, the coefficient of variation depends on the number of aisles and the number of slots within an aisle and has a value \(s=0.2-0.35\).

The probability of emptiness of the queueing system describes the status that the server has to wait because there is no tote in the queuing system [40]:

$$\begin{aligned} p_0=\frac{\rho -1}{\rho ^{2\cdot \frac{\sqrt{\rho \cdot e^{-s^2}} \cdot s^2-\sqrt{\rho \cdot e^{-s^2}} +K+1}{2+\sqrt{\rho \cdot e^{-s^2}} \cdot s^2-\sqrt{\rho \cdot e^{-s^2}}}}-1} \end{aligned}$$
(23)

The throughput of a storage section is equal to the throughput of one tier multiplied by the number of tiers:

$$\begin{aligned} \vartheta =\vartheta _{tier} \cdot n_{tier} \end{aligned}$$
(24)

5 Numerical study

The upcoming parts show the validation of the approach through a Monte-Carlo Simulation of a single tier with a different number of aisles served by one shuttle. Subsequently, an optimization example of the approach is presented to give an insight into the usage of such an approach and to show the influence of the different number of tiers on the throughput of the SBS/RS.

Fig. 2
figure 2

Comparison of a sample storage aisle between the analytical approach of this paper and Lerher [22]

Full size image

5.1 Numerical evaluation of the approximation quality

The performance of a single area with a different number of aisles served by a shuttle is essential during the design process of an SBS/RS. Understanding the influence of the different number of aisles per shuttle helps to determine an ecologically and economically ideal design of an SBS/RS. Specific parameter configuration was chosen to present various settings, as shown in Table 2. These parameters were specified by a European material handling provider of SBS/RS.

Fig. 3
figure 3

Cycle time of the shuttle with a retrieval position in a random aisle − Comparison analytical approach and Monte-Carlo simulation

Full size image
Fig. 4
figure 4

Cycle time of the shuttle with a retrieval position in the same aisle − Comparison analytical approach and Monte-Carlo simulation

Full size image

For validation, the results of the analytical model were compared with a simulation model. Therefore, a single tier with a different number of slots and a different number of aisles per shuttle/tier was selected. At each simulation run, 10000 totes were stored and retrieved. The number of stored totes is chosen with 10000 to avoid any transient phase mentioned in the simulation results. A Monte-Carlo Simulation performs the simulation runs. Here all storage and retrieval tasks were randomly distributed over all considered aisles. The only exception is the second strategy, where the storage process occurs in the same aisle as the retrieval. Table 2 shows the parameters used in this evaluation. Figures 3 & 4 and Table 3 show the comparison between the results of the analytical model and the simulation. The two different storage strategies are also included in this Table/Figure.

Table 4 Optimization example
Full size table
Fig. 5
figure 5

Example of a storage section with a storage capacity of 10000 storage locations

Full size image

This comparison shows that the analytical approach depicts reality. The estimation error is less than \(1\%\), independent of the storage strategy. Compared to other analytical methods in the literature [22], the presented approach has a high approximation quality. Here only the shuttle service times can be compared because Lerher does not mention the interactions between the lifts and the shuttles. In Fig. 2, the comparison of the approach from Lerher to the method discussed in this paper is depicted. It can be seen that the influence of the interactions between lifts and shuttles is not to be neglected. Table 2 defines the data used in this comparison. The length of the aisles is 100 m, and the number of aisles per shuttle is set to 1 so that only a shuttle has served one aisle. The restriction is made to show the main difference between the approaches.

The interaction description is unique for this kind of SBS/RS and can not be compared with other research, e.g., [22]. What can be seen is that the storage strategy with a storage and retrieval transaction in the same aisle has around \(20\%\) higher throughput compared to the random aisle storage and retrieval strategy. This leads to the fact that it is essential to know which storage strategy is used before you can design a storage system. You can also see that the right strategy can get more throughput from the same storage system without changing the technical conditions.

5.2 Application example

The depicted analytical approach allows an optimization of the geometry to achieve the highest throughput. An example of a system with a storage capacity of at least 10000 storage slots has been chosen to show this. The footprint was calculated without the space needed for buffers, lifts, and I/O points in front of the aisle. The parameters used assume the same values as in Sect. 5.1. The optimization process happens via a multi-parameter analysis, where the various parameters are used in the analytical calculation, and the results for the optimization are generated in this way. Another way of optimization not presented in this paper is, e.g., metaheuristic bat-inspired algorithm as described by Yang [41].

Table 4 depicts the results. The geometric ratio of height to length \(\left( \frac{n_{tier}}{n_{slot}} \right) \) is chosen for the highest throughput. This ratio is gained by numerical differentiation of the invented approach. Figure 5 depicts the throughput depending on the number of aisles per shuttle with a capacity of 10000 storage locations. Here it can be seen that with an increasing number of aisles per shuttle, the geometric form of the rack approaches a square. This is because, with an increase in aisles per shuttle, the length of these aisles decreases. For example, from 1 to three aisles, the length of the aisles is only a third to have the same storage capacity. The difference between the two storage strategies is less than that of a single aisle because of the influence of the lift and the waiting times between shuttles and lifts. Here, the difference is around \(5\%\) compared to a single tier where the difference is around \(20\%\).

6 Conclusion

The further development of SBS/RS has evolved in recent years. The primary type with two lifts and one shuttle per tier has become a multitude of variants. It is crucial to know their performance measures to compare these variants with each other or make the proper selection during the design process. Because of these many variants, not all systems are analytically accurately described. A variant with a non-aisle-captive shuttle has been discussed in more detail in this paper. There is almost no publication on this system in the scientific field, although it is offered for sale by a European manufacturer. It is, therefore, necessary to discuss this system. The determination of the performance measures, especially the throughput, is done by a continuous-time open-queueing system with limited capacity. This performance measure is chosen because of its relevance for the users of such storage systems. This approach takes the interactions between shuttles and lifts into account. The inter-arrival and service times were gained using a cycle-time model of lifts and shuttles with discrete spatial values. Here also, the time for the aisle changing process is mentioned through a probability-based approach. The accuracy of the developed analytical model compared to a Monte-Carlo simulation is validated. A limitation of the developed approach is that the influences of the conveyor way before and right after the storage aisle are not mentioned.

A key feature of the developed analytical approach is that a geometrical optimization can also be made. The advantage of the invented approach is that the calculation time is none compared to a simulation model. It is possible to determine the performance of a widbroadt of parameters and choose an optimal parameter configuration. This determination of the throughput can be handled by standard calculation software, and no special programs are necessary. Therefore, an example with a different number of aisles per shuttle and a fixed capacity has been depicted. The aim for every configuration was an optimal geometric dimension of the number of tiers and several slots to achieve the highest throughput. The process is carried out via a numerical parameter variation. The result is that the throughput increases with a further increase in the number of aisles per shuttle. This is not an expected result, but on a closer discussion, it becomes clear. The influence of the multiple aisles per shuttle on the length of an aisle and on the cycle time of the shuttle is more than the additional time spent changing aisles. Another result of the example is the difference in the throughput depending on the storage and retrieval locations. Here, two different strategies were chosen. The first strategy has a random storage location and a random retrieval location. This could randomly gain an aisle change within a dual command cycle. In the second storage strategy, the storage and retrieval locations are in the same aisle. This leads to a never necessary for aisle change within a dual command cycle. This strategy’s further performance/throughput is around \(5\%\) with no change in the physical parameters. The sensitivities of the approach to other sets of parameters are stable. What leads to a comparability of different parameter sets. The assumptions made in this paper are like an SBS/RS of a European material handling provider.

Further research will be dedicated to SBS/RS with alternative system configurations. Such a system may have a different number of lifts combined with an aisle-changing shuttle and a further increase in the number of shuttles per tier. This will lead to a complex SBS/RS with shuttles not dedicated to a certain number of aisles. As a further development of this system, the combination of multiple-aisle with multiple-depth storage can be discussed. All these points will be incorporated into future work.