1 Introduction

Core drilling is an abrasive process to open holes in civil construction structures. Depending on the core bit diameter, the process can be carried out with hand or stand-guided machines. In reinforced concrete core drilling, the core bit contains diamond-impregnated segments responsible for material removal. The composition of those segments, i.e., binder material and diamonds, is the most important factor in the process behavior and results. Process parameters, concrete type, and water supply are important factors as well [1]. Figure 1 summarizes and shows the common parameter range.

Fig. 1
figure 1

Core drilling characteristics overview

Full size image

Since diamond core drilling is one of the largest shares of diamond tools for construction, the development of new tools or tools that are more efficient is more than necessary in the near future. Such developments, pushed by the production of high crystal quality synthetic diamonds and new manufacturing strategies, culminated in the production of diamond-impregnated segments with defined patterns, since there is a general consensus that tools with a non-uniform diamond distribution have inconsistent performance and shorter tool life for most cases when cutting stone materials [2,3,4,5]. But still, only a few research works have investigated the correlation between the diamond-impregnated segment’s characteristics and the process results. According to Kansteiner and Biermann [6], a correlation between the diamond concentration and size with power consumption, feed rate, and segment wear was established. It was evidenced that these output results do not present a linear correlation with diamond size and concentration. So, the understanding of how concentration, size, and other characteristics affect the diamond layer drilling performance is incomplete and therefore the opportunities in the segment design not yet exploited. So far, in order to test the segment design performance, especially concerning core drilling feed rate, an experimental rig needs to be set up, demanding time and being costly. So, to reduce resource expenditures, process simulation models and tools need to be developed. According to Brinksmeier et al. [7], since core drilling is a bonded-abrasive process, the development of a kinematic-geometric model is one of the most applicable due to these models being able to calculate process characteristics and results from the tool path motion between tool and workpiece. Several industrial abrasive processes were modeled making use of this approach [8,9,10]. In the same manner, a new simulation for the design of segments for sawing was elaborated by Denkena et al. [11] in order to predict the comportment of the diamond distribution pattern to increase the feed rate, and consequently, to increase the material removal rate. However, this model is limited to linking the wear and removed material volume with the variation of diamond distances in tangential and axial directions without taking into account other important geometric characteristics of the abrasives, such as morphologies and orientation, which have a high impact on the amount of removed material, drilling feed rate, and process force. Recently, researchers started attempts to understand the behavior of diamond-impregnated segments under wear, in order to reduce resource expenditures. Quacquarelli et al. [12] developed a numerical-experimental approach for modeling the wear of diamond-impregnated tools for core drilling. The approach considers the tribological effects on the metallic surface caused by the debris suspended in the water, as known as slurry. Malevich et al. [13] performed an experimental and statistical analysis of the wear on such tools, by predicting the lifetime of single diamonds. The statistical model was used to extrapolate experimental results and forecast the tool performance considering its topography.

The main objective is to present a concept that uses a kinematic-geometric model for the reinforced concrete core drilling, which can be useful for drilling feed rate comparison between segment designs. The kinematic-geometric model will use detailed tool descriptions with stochastic and deterministic variables, as well as concrete (cement and agglomerates) and steel rebar as base materials. A kinematics process model, process force model, and a simplified material model are also included. This allows an evaluation of the impacts of both geometric characteristics of diamond-impregnated segments and process parameters, on the material removal amount, surface profile, cutting, and normal forces, which provides an indication and an estimation about the impregnated segment performance.

2 Geometric-kinematic model

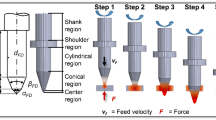
The geometric-kinematic model for reinforced concrete core drilling is a stochastic model of grain-level interactions with the workpiece surface. The sum of each grain-level interaction describes stochastically the behavior of the entire tool. The proposed model contains four different submodels that are closely connected to each other, as depicted by Fig. 2. The first is the detailed geometric description of the diamond-impregnated segment, followed by the kinematic model, material model, and force model. The kinematic added to the segment allows the diamonds’ interaction with the workpiece material, which modifies the material surface, consequently also feeds the input parameters for the force calculations, finalizing one simulation loop. After the one simulation loop, the kinematic model is again activated, repeating the calculation process.

Fig. 2
figure 2

Core drilling model calculations loop

Full size image

The following sections will describe in details how each of those individual models is equated and structured, and how the dependency from each other works in this loop-style interaction between them, in pursuance of the core drilling model representation and the segment design performance estimation.

2.1 Diamond-impregnated segment model

To allow a realistic distribution, the diamonds positioned inside the bond boundaries followed a pattern that was described by polar coordinates, with a given radius and angle, but stochastic positioning deviation (cell boundary), aiming for a trustworthy representation of the manufactured segment. The diamond pattern present in the segment model is very similar to the one used for reinforced concrete drilling segments. Additionally, the diamonds’ protrusion deviation, which varies around 150 μm from the surface, and the number of diamonds, ca. of 50 for 52 mm core bit and ca. of 25 for 102 mm core bit, were implemented based on X-ray tomography and microscopy characterization of the segment. To reproduce most of the tool geometrical influences, the diamond morphology was also taken into consideration based on Wilks and Wilks [14]. The morphological distribution of diamonds is well defined and is based on cubic and octahedral structures. The distortions in the synthetic diamond geometric due to the high-pressure sintering process were also implemented as aspect ratios. The grain size is characterized by the ISO 6106. The standard classifies the abrasives’ sizes by the size of the test sieves, which means that generally, the diameters follow a Gaussian distribution. After their generation, the diamonds can be rotated around the three orientation axes α, β, γ. The rotation of 𝜃, φ, and ψ about the three axes are respectively defined as:

$$ R_{x}(\theta) = \left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & cos(\theta) & -sin(\theta) \\ 0 & sin(\theta) & cos(\theta) \end{array}\right] $$
(1)
$$ R_{y}(\varphi) = \left[\begin{array}{ccc} cos(\varphi) & 0 & sin(\varphi) \\ 0 & 1 & 0 \\ -sin(\varphi) & 0 & cos(\varphi) \end{array}\right] $$
(2)
$$ R_{z}(\psi) = \left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & cos(\psi) & -sin(\psi) \\ 0 & sin(\psi) & cos(\psi) \end{array}\right] $$
(3)
$$ R (q) = R_{x} \cdot R_{y} \cdot R_{z} $$
(4)

It is supposed that each grain can assume arbitrary values for the orientation angles. Each angle determination occurs stochastically by a uniform distribution, which may be any angle between 0 and 360∘, and then they are distributed throughout the body of the tool. Figure 3 summarizes the characteristics implemented in the diamond-impregnated segment model.

Fig. 3
figure 3

Geometric characteristics of the diamond-impregnated segments

Full size image

One simplification aiming at the reduction of simulation efforts was the development of only one segment, as shown in Fig. 3. By defining the segment contour (see “top view”), the program only allows diamond abrasives to be distributed inside these limits.

2.2 Kinematic model

The kinematic model is responsible for providing movement to the segment in a three-dimensional space. Figure 4 illustrates the path that the diamond tool will take according to the parameters defined. The segment rotates around the x-axis and translates in feed-direction, similar to the drilling with drill bits kinematics.

Fig. 4
figure 4

Kinematic core drilling description

Full size image

The tool/diamond cutting speed vc and feed rate vf can be expressed as:

$$ \underline{v}_{c} = \pi \cdot \frac{n}{60} \cdot d \cdot \theta\hat{k} $$
(5)
$$ \underline{v}_{f} = -f \cdot n \cdot \hat{k} $$
(6)

where n is the number of tool rotations per minute, d diameter, and ae penetration per revolution. Another important parameter that belongs to the kinematic model is the discretization of the movements, the time step ts. This is determined with the material width mw, the core bit outer radius rcb, and the core bit rotation frequency fcb.

$$ t_{s} = \frac{m_{w}}{2\pi \cdot f_{cb} \cdot r_{cb}} $$
(7)

2.3 Force model

Based on the kinematic model, a proper solution for force calculation is the adapted Kienzle equation, which uses an analytical approach to estimate the forces during the cutting process that can be expressed as:

$$ F_{ci} = k_{c1.1} \cdot A_{i}^{1 - m_{c}} $$
(8)

where kc1.1 is the specific cutting force, A is the orthogonal cutting area, and mc is workpiece material coefficient of cutting force increase and μ is the forces ratio. These parameters are calculated based on single diamond interactions. For an expression of the entire tool, all the single forces need to be summed up as:

$$ F_{c} = {\sum\limits_{i}^{n}} F_{ci} $$
(9)

The normal force component perpendicular to the cutting direction results from the cutting force ratio μ as:

$$ F_{n} = \frac{F_{c}}{\mu} $$
(10)

The specific cutting force coefficient, the workpiece material coefficient, and the cutting force ratio are defined based on single diamond scratch tests in concrete and rebar steel (ASTM A615). Table 1 contains the coefficient values used in the Kienzle equation for both materials. The tests were performed with a peripheral speed (vc) of 4 m/s, with a depth of cut of 30 to 180μm for scratches in concrete and 5 to 30 μm for scratches in rebar. With the scratch experiments (concrete scratched sample shown in Fig. 5), it is possible to correlate the orthogonal projection of the scratch using the focus variation microscope, and the forces generated during the scratch using piezoelectric measurements.

Table 1 Specific cutting force and workpiece material coefficient
Full size table
Fig. 5
figure 5

Concrete scratched sample and scratching pin

Full size image

For the determination of the simulated engagement area, a cutting profile is defined using the orthogonal plane generated by the projection of the diamond in direction of the cutting speed vc is extracted from the 3D diamond geometry, as shown in Fig. 6.

Fig. 6
figure 6

Extraction of the diamond cutting profile

Full size image

The mesh points, given at the very beginning of the simulation, define the workpiece surface. Then, the orthogonal cutting profile travels over the mesh, from point A (blue profile) to B (red profile), with a defined kinematic within one simulation step, as demonstrated in Fig. 7. After verifying the points that were affected by the profile step, it provides the area of interaction between the mesh and the cutting profile, and the travel distance between points A and B. After this process, the surface is expected to be changed according to the cutting profile. By comparing the mesh before and after the simulation step, it is possible to identify the removed workpiece material volume. This approach transforms a three-dimensional grain into a two-dimensional grain, which brings a significant reduction in the simulation time for the model.

Fig. 7
figure 7

Travel distance between points A (blue) and B (red) over the mesh

Full size image

The modified Kienzle equation only provides the magnitude of the force, but it is also indispensable to know the direction of the force for the representation of the influence of the diamond morphology and orientation. Despite the 2D cutting profile consideration, every face of the diamond grain is associated with the normalized vectors used for the diamond morphology modeling. The total orthogonal cutting area is the sum of the orthogonal cutting area of each diamond face. The ratios of the cutting area of the faces through the volume extracted by the entire diamond are associated with the normal to determine the direction of the force. Equation 11 defines the direction of the force.

$$ \underline{F} = k_{c1.1} \cdot \sum\limits_{i=1}^{n} \frac{A_{i}}{A_{t}} \cdot \underline{n_{i}} $$
(11)

Here, the n is the total number of faces in a cutting profile, the Ai is the orthogonal cutting area are of of the face i, the At is the total orthogonal cutting area, and \(\underline {n_{i}}\) is the normal vector associated with the face number i.

2.4 Material removal model

Since the model is governed by geometrical characteristics and kinematics, it is certain that the material removal is strictly dependent on geometrical interaction between the diamond cutting profile and the workpiece. Thermal and mechanical influences, such as cutting temperature, rubbing, plowing, elastic material behavior, and crack propagation in material removal are neglected. The cutting process simulation is simplified considering the ideal kinematics and chip formation, adiabatic process; infinite machine and tool stiffness, negligible chip and water influence on the drilling process. For every simulation step, the volume of material removal, as mentioned in the force model section, relies on the area of interaction between the mesh (workpiece) and the cutting profile (diamond orthogonal projection normal to the cutting speed) and the diamond travel distance, resulting in a mesh groove, which its profile is an exact negative of the cutting profile. The superposition of the grooves, in the end, defines the surface roughness and the material removed volume. In Fig. 8, steel rebar and concrete surfaces are shown as an example of the mesh resulting from the geometric-kinematic interaction between abrasive particles and base material. Highlighted can be observed the grooves generated.

Fig. 8
figure 8

Steel rebar and concrete mesh surfaces after simulation

Full size image

The material removal model has not only the purpose of cutting forces calculation via Kienzle equation, but also to visualize the effects of the pattern design in the material removal capability, since the longitudinal and, mainly, the transversal distancing between diamonds are determining the superposition of grooves. In reinforced concrete core drilling, wrong diamond spacing, if too wide transversal distancing, can cause accelerated wear due to contact between material and bond surface, or if too narrow transversal distancing, can leave too little spacing for chipping formation between the diamonds.

3 Model validation

For the model validation, simulations were performed with the same process parameters as used in the reinforced concrete core drilling experiments. It was divided into two phases:

  • Phase one: Testing across different feed rate

  • Phase two: Testing of impregnated segments with different diamond sizes and concentrations

3.1 Model validation phase one

Alongside the results, Figs. 9 and 10 summarize the experimental conditions and parameters for the test for phase one. The force model depends on the process parameters and geometric properties of individual diamond interaction with the workpiece. The specific cutting force and the material coefficients were extracted from the scratch test experiments in concrete and steel rebar. In steel rebar (ASTM A615), the forces simulated showed a satisfactory correlation with the experimental results with the feed between 10 and 40 μm, as can be seen in Fig. 9.

Fig. 9
figure 9

Comparison between experimental and simulated forces in ASTM A615 steel

Full size image
Fig. 10
figure 10

Comparison between experimental and simulated forces in concrete

Full size image

In a shallow or in a deep depth of cut, phenomena like rubbing/plowing and crack propagation can occur, which is not considered by the model. For Utliberg concrete, where the range of depth of cut can vary from 50 to 300 μm per revolution, the presence of those phenomena can be intensified, which could explain the difference of up to 25% in the extremes portions of the depth of cut, as shown in Fig. 10. Besides, the simulation uses a single impregnated-segment approach, which is extrapolated to the entire core bit for comparison. The core bit rotational speed was kept constant throughout the experiment.

Despite the assumptions did not take into consideration such phenomena, the simulated results showed the same strong depth of cut dependency and the same linear behavior as the results obtained by the experiments, assuring an accurate core drilling process representation of forces by the geometric-kinematic model.

3.2 Model validation phase two

The next validation step observes how the simulation behaves by altering the diamond layer characteristics. For this, four different segment designs were manufactured and tested against the core drilling simulation, starting with a segment with 25/30 mesh and 4 rows, down to 35/40 mesh and 7 rows. As an example of a segment diamond layer design, Fig. 11 depicts the position of each diamond in the layer. All layer designs have the “zig-zag” aspect, differentiating from each other in the diamond size and number of rows, consequently altering the diamond concentration inside the metallic segment. Table 2 shows the diamond layer characteristics for each segment design.

Fig. 11
figure 11

Diamond layer for design 2 as example

Full size image
Table 2 Segments design tested during validation
Full size table

During the second phase core drilling validation experiments, each segment design drilled 20 holes in reinforced concrete, in order to have representative average results. The same number of holes was simulated since the model has a stochastic tool generation that can produce a deviation of ± 20% in cutting and normal forces. This means, before every hole is drilled in the simulation, a new tool with the same specification but stochastic characteristics is generated. Figures 12 and 13 show the results for normal force and input power needed to core drill concrete and steel rebar with a feed rate of 25 μm/rev and 175 μm/rev, respectively, as a comparison between simulation and experiment.

Fig. 12
figure 12

Comparison between experiments and simulation in ASTM A615 steel

Full size image
Fig. 13
figure 13

Comparison between experiments and simulation in concrete

Full size image

For both cases, concrete and steel rebar, the simulation presented consistent results in comparison with the core drilling average results, being able to provide a distinction on processes forces and input power between the segment design tested. According to the simulation, designs 2 and 3 are the ones that generated the lowest forces among the designs, indicating the most promising designs for increased feed rate for the tested condition. These results illustrate the effect of diamond size and number of diamond rows, which indicates that the recommended designs for such feed rates (25 μm/rev in steel and 175 μm/rev in concrete) are with mesh 35/40 (particle diameter of around 450 μm) with 5 to 6 diamond rows. Within the tested diamond layer configuration, normal forces and input power increases with the decrease of diamond size to mesh 40/45 (particle diameter of around 370 μm) and with the increase of diamond rows. The only simulated result that differs from the experiment trend is the input power needed for design 1 in steel rebar. The input power needed for cutting steel with the design 1 is supposed to have similar input power levels as design 4, but it presents significantly lower levels. This is incompatible with the results of normal forces for the same conditions. These differences between the behavior of normal force and input power can be caused by the fact that, invariably, the segments under experimentation are exposed to wear, which is not the case for the simulation. Wear on the impregnated segments can affect significantly the force ratio (μ), while in the simulation this ratio is constant. The results presented by the design 1 leads to a low forces ratio that occurs when normal forces are much higher then tangential forces. This is an effect generated by the diamonds’ dulling or flattening, which normally appears when the diamond size is larger than the ideal size for chip trickiness.

After all, the assumptions for the simulation are reasonably representing the core drilling process starting from the fundamental description of the microscopic properties of individual diamond interaction, up to the description of the entire diamond layer macroscopic properties.

4 Conclusion

The geometric-kinematic model stochastically provides macroscopic results based on the tool’s geometrical characteristics and on the core drilling kinematics. The model development and validation allowed the verification of the influence of the process parameters and diamond-impregnated segment geometric characteristics, which for abrasive processes are the most important impact factors on their performance. During the validation phase, the simulated core drilling forces mean values had up to ± 22% of deviation in comparison to the average experimental values, which indicates a satisfactory core drilling comparison among designs, considering the complexity of reinforced concrete cutting and the simplifications of cutting phenomena assumed for the geometric-kinematic model. The several outputs that can be generated by the simulation enable much faster identification of potential designs for certain conditions, in comparison with experiments, which demand not only the time spent on core drilling but also on the post-measurement procedures. With those outputs, it is possible to verify how the diamond layer will perform under the conditions proposed. Additionally, with the simplifications adopted, the simulation can be executed in personal computers, which facilitates the implementation of such development tools in the construction tool industry. Another point that counts in favor of the model for industrial application is its modularity. The addition of new submodels or modification of the existing ones, for example, substitutions of the base material description, can be effortlessly incorporated into the code library, expanding the possibilities of the model to be tested with distinct conditions.