1 Introduction

IC encapsulation can be divided into die saw, die bonding, wire bonding, molding, molding, post-mold cure, trim, marking, plating, and inspection. For the molding and post-mold cure (PMC) of IC encapsulation process, warpage and residual stress are critical issues, especially when the package has higher density and its thinness is thin. Then solder failure, crack, and delamination are the major reliability concerns for electronic products. During the transfer molding process, epoxy molding compound (EMC) is heated and filled into the mold cavity, and then cross-linking reaction in high temperature occurs and makes the thermosetting material cured and solidified. If EMC is not fully cured after the molding process, IC packages will be put into the oven and pressed for long-term high-temperature baking to make EMC fully cured. This step is called PMC process and makes the mechanical behavior and reliability of IC packages more stable.

As shown in Fig. 1, the main reason for warpage is uneven volume shrinkage or residual stress during manufacturing. There are two main reasons for the shrinkage phenomenon, one is curing volume shrinkage of material in the mold cavity due to chemical reaction of EMC, and another one is thermal volume shrinkage of coefficient of thermal expansion (CTE) mismatch of the components’ material during the cooling process.

Fig. 1
figure 1

Warpage problem

Full size image

In the previous studies, thermal shrinkage induced by different CTE values between materials was considered as the main reason for the warpage problem. However, in recent years, there are more evidence showing that the cure-induced shrinkage effect cannot be ignored. Kelly et al. [1, 2] predicted warpage by considering thermal-induced and cure-induced shrinkage of EMC. Chang and Hwang [3, 4] established a relationship between pressure, volume, temperature, and conversion of thermoset material, namely, P–V-T-C equation. Hong and Hwang [5] used the P–V-T-C relation to predict the warpage of bi-material after the molding process by mold flow analysis and finite element method (FEM). Teng [6] and Deng [7] considered both thermal and cure shrinkage to predict the warpage of IC package products (TSOP, LQFP, and FOWLP) by FEM, and verified the P–V-T-C relation by experiments. The results show that considering both temperature effect and chemical effect can more accurately predict package warpage.

Because of the high-temperature process, EMC would behave as a viscoelastic material during the PMC process. For this reason, it is necessary to take the viscoelastic properties of the material into consideration in the PMC analysis. As shown in Fig. 2, Wang [8] and Lin [9] used dynamic mechanical analysis (DMA) and time–temperature superposition (TTS) to verify WLF equation and generalized Maxwell viscoelastic model of EMC are available. Viscoelastic properties of EMC would be determined under different temperatures by using temperature shift factor. Similarly, the cure shift factor is determined by the same approach. Combined with the shift factors, the dual shift factors are defined to obtain the relaxation modulus at any temperature and degree of cure. Therefore, the viscoelastic model with time, temperature, and conversion as its parameters were established. In order to describe the warpage and residual stress caused by the effects of EMC during molding and PMC, Wang et al. [10] analyzed the warpage of the bi-material strip. Considering the P–V-T-C and viscoelastic properties, the influence of curing and PMC processes are discussed. Guo [11] considered P–V-T-C effect of the molding process, the viscoelastic effect of PMC process, and residual stress when performing the simulation analysis. Compared with the experiment results of the actual IC package products, the experiment results were close to the simulation results.

Fig. 2
figure 2

Cure curve schematic [8]

Full size image

Fatigue is defined as the process of progressive or permanent structural change occurring when materials subjected to some conditions such as thermal cycle which may lead to cracks or fracture finally. The life of IC packages can be predicted by reliability analysis. The data required for reliability analysis including plastic strain, creep, strain energy, etc. Then, select a suitable fatigue model to analyze reliability of IC packages.

Coffin proposed the Coffin-Manson model in 1954, which uses plastic strain as damage information to predict fatigue life [12]. Shi found that the fatigue ductility coefficient and fatigue ductility exponent in the model are not constants, but were affected by temperature and frequency [13]. Englemaier combined the cycle frequency, solder ball, and substrate temperature parameters to modified Coffin-Manson model. The modified model is also called the Modified Coffin-Manson model [14]. Lin used FEM and temperature cycling test (TCT) to perform two-dimensional (2D) and three-dimensional (3D) nonlinear analysis on the fatigue behavior of BGA solder balls [15]. Darveaux [16] developed a method to predict the fatigue life during the thermal cycle with crack growth experiment data. With the accumulated damage, the properties of materials do not remain the same but change all the time. Consequently, it is important to study the mechanism of damage accumulation in the material. In 1956, Miner proposed the approach of using stress amplitude to superposition the damage of materials under fatigue cycles [17]. Hamasha et al. [18] proved that Miner's rule is not available for predicting fatigue life because of two main reasons: one is solder material is stress-dependent, and another one is that damage accumulated could be changed by previously applied stress. Su et al. [19] reviewed and categorized the fatigue models into four groups based on the critical factor which lead to fatigue damage: plastic strain-based fatigue model, damage accumulation-based fatigue model, creep damage-based fatigue model, and energy-based fatigue model.

Although there are many life prediction methods have been proposed and tried to predict fatigue life from various aspects, the fatigue mechanism of materials is too complex and difficult to predict, which limits these fatigue models. Therefore, to improve the accuracy of the prediction model, the residual stress and strain generated by IC manufacturing process must be taken into consideration shown in Fig. 3.

Fig. 3
figure 3

Analysis procedure of IC package simulation

Full size image

2 Theory

2.1 Flow analysis theorem

Flow analysis was simulated to get the molding temperature, melting front, velocity, and conversion distribution in the cavity. The governing equations of flow analysis consisted of continuity equation, momentum equation, and energy equation [20].

  1. I.

    Conservation of mass

    $$\frac{\partial\rho}{\partial t}+\nabla\cdot\left(\rho\overset\rightharpoonup{\mathrm V}\right)=0$$
    (1)

    ρ, density of EMC; \(\overset\rightharpoonup V\), velocity; t, time; ∇, divergence calculator.

  2. II.

    Conservation of momentum

    $$\rho\left(\frac{\partial\overset\rightharpoonup{\mathrm V}}{\partial t}+\overset\rightharpoonup{\mathrm V}\cdot\nabla\overset\rightharpoonup{\mathrm V}\right)=-\nabla\cdot P+\nabla\cdot\overset\rightharpoonup{\overset\rightharpoonup\sigma}+\rho\overset\rightharpoonup{\mathrm g}$$
    (2)

    ∇, gradient; P, pressure; \(\overset\rightharpoonup g\), gravity; \(\overset\rightharpoonup{\overset\rightharpoonup\sigma}\), stress tensor.

  3. III.

    Conservation of energy

    $$\rho C_p\left(\frac{\partial T}{\partial t}+\overset\rightharpoonup{\mathrm V}\cdot\nabla T\right)=\nabla\cdot\left(k\cdot\nabla T\right)+\eta\dot\gamma^2+\dot\alpha\Delta H$$
    (3)

Cp, specific heat of EMC; T, temperature; k, heat conductivity of EMC; \(\dot{\gamma }\), shear rate; \(\Delta H\), enthalpy change; \(\dot{\alpha }\), cure rate.

2.2 Warpage analysis theorem

EMC material was assumed as linear elasticity, homogeneous, and isotropic. The basic stress–strain relation was expressed by Generalized Hook’s law [20]:

$$\left\{\sigma \right\}=\left[D\right]\left\{{\varepsilon }^{el}\right\}$$
(4)

{σ} = {σxx, σyy, σzz, σxy, σyz, σxz}T, stress matrix; [D], stiffness matrix;{εel}, elastic strain matrix.

For IC packages, warpage and residual stress result from thermal and cure shrinkage. Therefore, elastic strain could be written as:

$$\left\{{\varepsilon }^{el}\right\}=\left\{{\varepsilon }^{tot}\right\}-\left(\left\{{\varepsilon }^{th}\right\}+\left\{{\varepsilon }^{C}\right\}\right)$$
(5)

{εtot}, total strain matrix; {εth}, thermal-induced strain matrix; {εC}, cure-induced strain matrix.

Consequently, total strain can be written as:

$$\left\{{\varepsilon }^{tot}\right\}=\left\{{\varepsilon }^{C}\right\}+\left\{{\varepsilon }^{th}\right\}+\left\{{\varepsilon }^{el}\right\}=\left\{{\varepsilon }^{C}\right\}+\alpha\Delta T+{\left[D\right]}^{-1}\left\{\alpha \right\}$$
(6)
$${\left[D\right]}^{-1}=\left[\begin{array}{cc}\begin{array}{ccc}1/{E}_{xx}& -{\nu }_{xy}/{E}_{xx}& -{\nu }_{xz}/{E}_{xx}\\ -{\nu }_{yx}/{E}_{yy}& 1/{E}_{yy}& -{\nu }_{yz}/{E}_{yy}\\ -{\nu }_{zy}/{E}_{zz}& -{\nu }_{zy}/{E}_{zz}& 1/{E}_{zz}\end{array}& 0\\ 0& \begin{array}{ccc}1/{G}_{xy}& 0& 0\\ 0& 1/{G}_{yz}& 0\\ 0& 0& 1/{G}_{zx}\end{array}\end{array}\right]$$
(7)

[D]−1, inverse matrix of the stiffness matrix; Exx, Young’s modulus along x direction; νxy, Poisson’s ratio.

Then, the governing equations of stress–strain relationship were obtained:

$${\varepsilon }_{x}\alpha \Delta T+{\varepsilon }_{C}+\frac{{\sigma }_{xx}}{{E}_{xx}}-\frac{{v}_{xy}{\sigma }_{yy}}{{E}_{xx}}-\frac{{v}_{xy}{\sigma }_{zz}}{{E}_{xx}}$$
(8)
$$\varepsilon_y=\alpha\triangle T+\varepsilon_C-\frac{V_{xy}\;\delta_{xx}}{E_{yy}}+\frac{\delta_{yy}}{E_{yy}}-\frac{\delta_{zz}}{E_{yy}}$$
(9)
$${\varepsilon }_{z=}\alpha \Delta T+{\varepsilon }_{C}-\frac{{v}_{xz}{\sigma }_{xx}}{{E}_{zz}}-\frac{{{v}_{yz}\sigma }_{yy}}{{E}_{zz}}+\frac{{\sigma }_{zz}}{{E}_{zz}}$$
(10)

Assume EMC material is linear viscoelastic, homogeneous, and isotropic as well as load bearings, its stress tensor will be:

$$\overset\rightharpoonup{\overset\rightharpoonup\sigma}=\begin{bmatrix}\sigma_{xx}&\tau_{xy}&\tau_{xz}\\\tau_{yx}&\sigma_{yy}&\tau_{yz}\\\tau_{zx}&\tau_{zy}&\sigma_{zz}\end{bmatrix}=\begin{bmatrix}-P&0&0\\0&-P&0\\0&0&-P\end{bmatrix}+\begin{bmatrix}S_{xx}&S_{xy}&S_{xz}\\S_{yx}&S_{yy}&S_{yz}\\S_{zx}&S_{zy}&S_{zz}\end{bmatrix}$$
(11)
$$-P=\frac{1}{3}\left({\sigma }_{xx}+{\sigma }_{yy}+{\sigma }_{zz}\right)$$
(12)
$${S}_{xx}+{S}_{yy}+{S}_{zz}=0$$
(13)

P, mean stress; [S], deviatoric stress.

Similarly, the strain tensor will be:

$$\overset\rightharpoonup{\overset\rightharpoonup\varepsilon}=\begin{bmatrix}\varepsilon_{xx}&\varepsilon_{xy}&\varepsilon_{xz}\\\varepsilon_{yx}&\varepsilon_{yy}&\varepsilon_{yz}\\\varepsilon_{zx}&\varepsilon_{zy}&\varepsilon_{zz}\end{bmatrix}=\begin{bmatrix}\theta&0&0\\0&\theta&0\\0&0&\theta\end{bmatrix}+\begin{bmatrix}e_{xx}&e_{xy}&e_{xz}\\e_{yx}&e_{yy}&e_{yz}\\e_{zx}&e_{zy}&e_{zz}\end{bmatrix}$$
(14)
$$\theta =\frac{1}{3}\left({\varepsilon }_{xx}+{\varepsilon }_{yy}+{\varepsilon }_{zz}\right)$$
(15)
$${e}_{xx}+{e}_{yy}+{e}_{zz}=0$$
(16)

θ, mean strain; [e], deviatoric strain tensor.

When a viscoelastic material is load-bearing, its transient relation between stress and strain under time variation can be expressed as

$${\sigma }_{ij}={\varepsilon }_{kl}\left(0\right){R}_{\text{ijkl}}\left(t\right)+{\int }_{0}^{t}{R}_{\text{ijkl}}\left(t-\tau \right)\frac{\partial {\varepsilon }_{kl}\left(\tau \right)}{\partial \tau }d\tau$$
(17)

Rijkl(t), relaxation modulus of the material; εkl(0), material strain in the initial state.

Because the material is isotropic and homogeneous, the material relaxation modulus can be rewritten as:

$${R}_{\text{ijkl}}\left(t\right)=\frac{1}{3}\left[K\left(t\right)-G\left(t\right)\right]{\overset{\frown}{\sigma}}_{ij}{\overset{\frown}{\sigma} }_{kl}+\frac{1}{2}G\left(t\right)\left[{\overset{\frown}{\sigma} }_{ik}{\overset{\frown}{\sigma} }_{jl}-{\overset{\frown}{\sigma} }_{il}{\overset{\frown}{\sigma} }_{jk}\right]$$
(18)

K(t), volume relaxation modulus; G(t), shear relaxation modulus; \({\overset{\frown}{\sigma} }_{ij}\), kronecker delta function.

3 Material model

3.1 Viscosity model

Cross Castro-Macosko model is used for the viscosity calculation of EMC:

$$\eta =\frac{{\eta }_{0}{\left(\frac{{C}_{g}}{{C}_{g}-C}\right)}^{{k}_{1}+{k}_{2}C}}{1+{\left(\frac{{\eta }_{0}\dot{\gamma }}{{\tau }^{*}}\right)}^{1-n}}$$
(19)
$${\eta }_{0}=A\cdot exp\left(\frac{{T}_{b}}{T}\right)$$
(20)

C, degree of cure; η, viscosity; η0, zero-shear-rate viscosity; \(\dot{\gamma }\), shear strain rate; \({\tau }^{*}\), critical shear stress; n, power law index; Cg, degree of cure at gel point; k1, k2, A, Tb, model constants.

The constants of model were seen in Table 1, and the relationship of viscosity and temperature was illustrated in Fig. 4.

Table 1 Viscosity model constants
Full size table
Fig. 4
figure 4

Viscosity vs. temperature

Full size image

3.2 Cure kinetics model

Kamal’s model is used for the cure kinetics calculation of EMC:

$$\dot{C}=\frac{dC}{dt}=\left({K}_{a}+{K}_{b}\cdot {C}^{m}\right)\cdot {\left(1-C\right)}^{n}$$
(21)
$${K}_{a}=A\cdot exp\left(-\frac{{T}_{a}}{T}\right),{K}_{b}=B\cdot exp\left(-\frac{{T}_{b}}{T}\right)$$
(22)

\(\dot{C}\), cure reaction rate; A, B, m, n, Ka, Kb, model constants; Ea, Eb, activation energies; Ta, Tb, activation temperature.

The constants of the model are seen in Table 2, and the relationship of conversion and temperature is illustrated in Fig. 5.

Table 2 Cure kinetics model constants
Full size table
Fig. 5
figure 5

Conversion vs. temperature

Full size image

3.3 P–V-T-C model

Two-domain modified Tait model is used for the P–V-T-C relation of EMC:

$$\frac{1}{V}=\frac{1}{{V}_{\text{uncured}}}\cdot \left(1-C\right)+\frac{1}{{V}_{\text{cured}}}\cdot C$$
(23)
$$V_\text{uncured}/V_\text{cured}=V_0\left[1-\alpha\cdot\ln\;\left(1+\frac PB\right)\right]$$
(24)
$${V}_{0}=\left\{\begin{array}{c}{b}_{1S}+{b}_{2S}\left(T-{b}_{5}\right),{\text{i}}{\text{f}}\;T\le {T}_{\text{trans}}\\ {b}_{1L}+{b}_{2L}\left(T-{b}_{5}\right),{\text{i}}{\text{f}}\;T>{T}_{\text{trans}}\end{array}\right.$$
(25)
$$B=\left\{\begin{array}{c}b_{3S}\cdot\exp\;\left[-b_{4S}\cdot\left(T-b_5\right)\right],\;\mathrm{if}\;T\leq T_\text{trans}\\b_{3L}\cdot\exp\;\left[-b_{4L}\cdot\left(T-b_5\right)\right],\;\mathrm{if}\;T>T_\text{trans}\end{array}\right.$$
(26)
$${T}_{\text{trans}}\;\left(P\right)={b}_{5}+{b}_{6},\alpha =0.0894$$
(27)

C, degree of cure; V, specific volume; V0, specific volume at zero gauge pressure; B, accounts for pressure sensitivity of the material; b6, linear increase in Ttrans with pressure; b5, transition temperature at zero gauge pressure.

The constants of the model are seen in Table 3, and the P–V-T-C relationship is illustrated in Fig. 6.

Table 3 P–V-T-C model constants
Full size table
Fig. 6
figure 6

P–V-T-C relationship

Full size image

3.4 Viscoelastic model

Dual shift factor model is used for the viscoelastic calculation of EMC:

$$E\;\left(t\right)=E_\infty+\sum_{i=1}^NE_i\cdot\exp\;\left(-\frac t{\lambda_i}\right)$$
(28)
$$\lambda_i\;\left(T\right)=\lambda_i\;\left(T_f\right)\cdot a_T\;\left(T\right)\cdot a_C\;\left(C\right)$$
(29)
$$a_T=\left\{\begin{array}{l}\exp\left(\frac{-A_1\;\left(T-T_f\right)}{A_2\;+\;\left(T-T_f\right)}\right),\;\mathrm{for}\;T\geq T^\ast\\\exp\left(\frac{\Delta H_T}R\left(\frac1T-\frac1{T_0}\right)\right),\;\mathrm{for}\;T<T^\ast\end{array}\right.$$
(30)
$$a_C=\exp\left(\frac{\Delta H_C}R\left(\frac1{T_g\left(C\right)}-\frac1{T_{g1}}\right)\right)$$
(31)
$$T_g\;\left(C\right)=T_{g0}+\frac{\gamma C\left(T_{g1}-T_0\right)}{1-\left(1-\gamma\right)C}$$
(32)

E(t), stress relaxation modulus; Tf, reference temperature; T*, critical temperature; A1, A2, WLF model constants; ∆HT/R, ∆HC/R, active energy; Tg, glass transition temperature.

The constants of the model are seen in Tables 4 and 5, and the relationship of modulus and time is illustrated in Fig. 7.

Table 4 Viscoelastic model constants
Full size table
Table 5 Viscoelastic model parameters
Full size table
Fig. 7
figure 7

Master curve of the relaxation modulus

Full size image

4 Simulation

For the simulation of IC encapsulation process, Moldex3D can establish a series analysis procedure for IC packages. Through powerful parallel computing functions, complex calculations can be completed in a short time. It does not improve the efficiency of computer calculations because it can bear a larger number of mesh.

4.1 Mesh model and mechanical properties

As shown in Fig. 8, the case was TSOP 48L and supplied by ChipMOS. A unit consists of a lead frame, a tape, a die, wires, and EMC. To simplify the mesh model, tape and wires were ignored shown in Fig. 9.

Fig. 8
figure 8

Geometry of TSOP unit

Full size image
Fig. 9
figure 9

Mesh model of a unit

Full size image

Table 6 shows the material properties of each component in the IC package.

Table 6 Mechanical properties of each component
Full size table

4.2 Transfer molding analysis

Figure 10 shows the parameter settings of molding process, including mold temperature, material temperature, filling time, filling pressure, curing time, curing pressure, curing switch, and initial conversion. These following parameters were provided by ChipMOS.

Fig. 10
figure 10

Molding condition settings

Full size image

In order to observe the deformation trend of the unit, 19 measured nodes are set. There are 9 nodes in the long direction, 5 nodes in the short direction, and 7 nodes in the diagonal direction, as shown in Fig. 11.

Fig. 11
figure 11

Measured nodes

Full size image

Figure 12 shows the simulation results after molding. In general, a fine filling result should show balanced flow contribution of each gate and all flow paths should reach the cavity wall at the same time. When the filling rate reaches 80% and 95%, melting front does not reach cavity wall at the same time because of asymmetry of the lead frame structure.

Fig. 12
figure 12

Melting front results

Full size image

Figure 13 shows the results after curing process of the unit analysis indicated EMC conversion of approximately 90–95%, which was uncured. Therefore, PMC process must be carried out to make the EMC reach a fully cured state, also improve the mechanical properties and reliability.

Fig. 13
figure 13

Degree of cure

Full size image

The volumetric shrinkage after molding is about 2.2% shown in Fig. 14. When the unit is cooled from high temperature to room temperature after transfer molding, volume shrinkage of EMC is affected by P–V-T-C relationship. As shown in Fig. 15, maximum value (− 0.121 mm) is calculated by two-domain modified Tait model.

Fig. 14
figure 14

Volume shrinkage after molding

Full size image
Fig. 15
figure 15

Warpage after molding

Full size image

4.3 PMC analysis

Figure 16 and Table 7 show the environment condition for PMC process. The unit is placed in an oven at a temperature of 175 °C for 4 h to make package to be fully cured. Viscoelastic behavior and gravity are also considered. The convection coefficient is 25 W/m2-K.

Fig. 16
figure 16

PMC ambient condition settings

Full size image
Table 7 PMC temperature condition settings
Full size table

Figures 17 and 18 are the schematic figures simulated the sample always pressed on the board with 0.04 MPa. It is noted that the pressure is only applied at 175 °C, which is from the 200th second to 14180th second.

Fig. 17
figure 17

Loading schematic

Full size image
Fig. 18
figure 18

Boundary condition settings of PMC

Full size image

Observe the curing results of PMC analysis as shown in Fig. 19. The conversion of EMC is fully cured after PMC process. It is noted that at 400th second of PMC process, the analysis result shows the conversion of EMC has reached 100%. Subsequently, the effect on warpage of PMC time will be discussed.

Fig. 19
figure 19

Conversion results of PMC

Full size image

After PMC process, shows the unit deformed due to the long-term viscoelastic behavior of EMC. The deformation trend is asymmetrical and concave downward. Maximum value (− 0.119 mm) of warpage is calculated by the dual shift factor model (Fig. 20).

Fig. 20
figure 20

Warpage results of PMC simulation

Full size image

Figure 21 shows the deviations between experiments and simulations. There is about 5–30% error in the long direction, 40–50% error in the short direction, and 10–30% error in the diagonal direction.

Fig. 21
figure 21

Warpage comparison of three directions

Full size image

Next, the PMC time and PMC temperature will be changed individually to discuss how these factors affect the warpage simulation results.

4.4 Effect of PMC time

In the previous PMC simulation, EMC has reached 100% conversion at 400th second. If EMC does not require 4 h of baking to achieve fully cured, the baking time is shortened to 1 h shown in Table 8.

Table 8 One-hour PMC time of temperature settings
Full size table

Figure 22 shows the PMC time of 1 h and 4 h have no obvious influence on the warpage results, and the warpage amount is a micron-level variation range.

Fig. 22
figure 22

Effect of PMC time

Full size image

4.5 Effect of PMC temperature

Since the residual stress induced by the PMC process can affect the reliability prediction (Section 5.1), this section discusses whether the PMC temperature affects the residual stress, while observing the changes in the full curing time and warpage (Table 9). This section discusses three different PMC temperatures, which are 165 °C, 175 °C, and 185 °C, respectively. The actual condition of the PMC process is 175 °C.

Table 9 Comparing the effect of three PMC temperatures on the package
Full size table

4.5.1 Full curing time

The curing time decreases with increasing temperature, in order to clearly understand the effect of temperature on the time required for full curing, The PMC temperature of 165 °C and 185 °C were simulated. The conversion result of PMC temperature at 175 °C is shown in Fig. 19.

Figure 23 shows the full curing time of PMC temperature at 165 °C. It can be seen that the full curing time at 500 s after beginning of the PMC process.

Fig. 23
figure 23

Full curing time of PMC temperature at 165 °C

Full size image

Figure 24 shows the full curing time of PMC temperature at 185 °C. It can be seen that the full curing time at 350 s after beginning of the PMC process.

Fig. 24
figure 24

Full curing time of PMC temperature at 185 °C

Full size image

4.5.2 Warpage

The deformation trends of 165 °C PMC temperature and 185 °C PMC temperature is similar to 175 °C PMC temperature.

When the PMC temperature was set to be 165 °C, the maximum warpage is 0.112 mm, and it can be seen in Fig. 25.

Fig. 25
figure 25

Warpage results with 165 °C PMC temperature

Full size image

When the PMC temperature was set to be 185 °C, the maximum warpage is 0.119 mm, and it can be seen in Fig. 26.

Fig. 26
figure 26

Warpage results with 185 °C PMC temperature

Full size image

It can be found that when the PMC temperature was set to 165 °C or 185 °C, the change of warpage value is not obvious.

4.5.3 Residual stress

In order to understand the residual stress will be affected by temperature or not, the residual stress simulation is necessary. According to Section 5.1, the lead frame is the possible location of the failure. Here will discuss the PMC process-induced residual stress of the lead frame with 165 °C PMC temperature and 185 °C PMC temperature.

Figure 27 shows PMC process induced residual stress with 165 °C PMC temperature, it can be seen that the maximum Von Mises stress value is 443.92 MPa.

Fig. 27
figure 27

Von Mises stress after 165 °C PMC process

Full size image

Figure 28 shows PMC process induced residual stress with 185 °C PMC temperature, it can be seen that the maximum Von Mises stress value is 448.34 MPa.

Fig. 28
figure 28

Von Mises stress after 185˚C PMC process

Full size image

When the PMC temperature change to 165 °C and 185 °C, the PMC process-induced residual stress reduce 7 MPa and 2 MPa. It can be found that the Von Mises stress after the PMC process has a 1.5% variation, changing the PMC temperature has little effect on residual stress.

5 Thermal analysis

5.1 Thermal cycle

Refer to JEDEC specification [21] for temperature cycle conditions. After the end of PMC, the temperature drops from 25 to − 65 °C in 2 min. And the first thermal cycle starts: temperature rises from − 65 to 150 °C within 5 min and hold the temperature for 15 min; temperature reduces from 150 to − 65 °C within 6 min and hold the temperature for 15 min. As shown in Fig. 29, every cycle is 41 min.

Fig. 29
figure 29

Temperature profile

Full size image

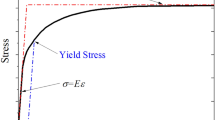
It can be seen from Fig. 30 that after two thermal cycles, the maximum von Mises stress occurs on the die: 778 MPa, which is far from the yield stress of Si: 7 GPa [22].

Fig. 30
figure 30

Von Mises stress result after thermal cycles (Z height: 0.167 mm)

Full size image

Observe the Von Mises results of lead frame. The focused place is at the circle location of the figures, where the maximum stress and assumed the firstly damage occurs. The types of damage that occurs accidently may be fatigue cracks, delamination.

From Fig. 31, it can be found that since thermal cycle simulation is performed after PMC simulation, there will be initial stress (450.8 MPa), which is the residual stress after PMC. Figure 32 shows the stress distribution of the lead frame after two temperature cycles. Its von Mises stress is 505.7 MPa. The value is close to the yield stress of lead frame material Alloy 42 of 634 MPa.

Fig. 31
figure 31

Von Mises stress distribution after PMC

Full size image
Fig. 32
figure 32

Von Mises stress distribution after thermal cycles

Full size image

At maximum Von Mises stress location where failure can occur, it was found maximum stress value of 730 MPa, minimum stress value of 80 MPa, and mean stress of 405 MPa during thermal cycling, as shown in Fig. 33a. When the process induced residual stress of the PMC process was not taken into account, the initial stress was assumed to be 0 at 25 °C, it was found maximum stress value of 279 MPa, minimum stress value of − 370 MPa, and the mean stress decreased to − 46 MPa. It can be found that stress states are very different when considering or not considering process induced residual stress. It is believed that the prediction of reliability will be strongly affected by the process induced residual stress since its value can be significant.

Fig. 33
figure 33

Von Mises stress vs. time vs. temperature

Full size image

6 Conclusion

As shown in Table 10, Moldex3D and mathematical model of EMC were used to discuss in detail warpage and residual stress caused by temperature effect and cure effect in molding and PMC processes of IC packages. And use the residual stress results of PMC simulation as the initial condition to analyze reliability of thermal cycles.

Table 10 Properties considered in each process analysis
Full size table

In the molding analysis, Cross Castro-Macosko model was used to describe the viscosity of EMC, and Kamal’s model was used to describe the cure kinetics of EMC, and two domain-modified Tait model was used to describe the P–V-T-C relation. In PMC analysis, dual shift factor model was used to describe viscoelastic properties of EMC. Comparing simulation results with experiment results, the prediction of the trend is correct. The amount of warping has an error of about 5–50%.

Regarding the effect of PMC on warpage, little differences were observed for different PMC duration and PMC temperature conditions. In addition, changing the PMC temperature has little effect on the residual stress. There is only a 1.5% variation in von Mises stress when changing the PMC process temperature. The stress states are very different when considering or not considering process induced residual stress. Taking into account the residual stress induced by the post-mold curing process will make the estimation of package reliability more reasonable.