Skip to main content
SpringerLink
Log in

Milling chatter detection of thin-walled parts based on GA-SE-SCK-VMD and RCMDE

  • ORIGINAL ARTICLE
  • Published:
The International Journal of Advanced Manufacturing Technology Aims and scope Submit manuscript

Abstract

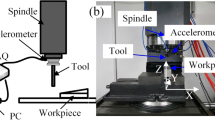
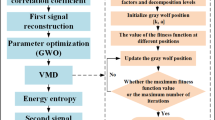
In the milling process, it is easy to produce chatter due to the low rigidity of the thin-walled structure, which leads to the deterioration of workpiece surface quality and reduces the service life of cutting tools and machine tools. Therefore, a new chatter detection method for thin-walled parts based on optimal variational mode decomposition (OVMD) and refined composite multi-scale dispersion entropy (RCMDE) is proposed in this paper. Firstly, to solve the problem that the decomposition effect of the variational mode decomposition (VMD) algorithm is greatly affected by its parameter, a genetic algorithm (GA) is used to iteratively optimize the parameter of the VMD algorithm, and a new index, square envelope spectral correlated kurtosis (SE-SCK), is introduced as the fitness function of the genetic algorithm. Then, the energy ratio of the decomposed signal is calculated as the principle of selecting sub-components, and the sub-components with rich chatter information are selected for signal reconstruction. To solve the problem that the multi-scale dispersion entropy (MDE) will miss some information in the multi-scale process, RCMDE is introduced to detect milling chatter. Finally, the experiment of the variable cutting depth in side milling of titanium alloy thin-walled parts is carried out. The experimental results show that the OVMD algorithm proposed can solve the problem of difficult separation of chatter frequency bands caused by mode aliasing and lay a foundation for subsequent chatter feature extraction. RCMDE is more conducive to chatter detection than the single-scale DE when the scale factor is 4. The distinguishing effect of RCMDE on the machining state is more than 50% higher than that of MDE when the scale factor is 4.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

Availability of data and material

The datasets used or analyzed during the current study are available from the corresponding author upon reasonable request.

Code availability

Not applicable.

Abbreviations

K :

Decomposition levels in VMD algorithm

\(\alpha\) :

Penalty factor in VMD algorithm

\(\partial_{t}\) :

Shear deformation energy consumption

\(u_{k} \left( t \right)\) :

The kth modal component

\(\omega_{k}\) :

The center frequency of the kth modal component

u :

The original signal

\(\delta \left( t \right)\) :

The pulse function

\(*\) :

The convolution operator

\(\lambda\) :

Lagrange multiplier

\(u_{k}^{n + 1}\) :

The n + 1 iteration of the kth modal component

\(\omega_{k}^{n + 1}\) :

The n + 1 iteration of the central frequency of the kth modal component

\(\lambda^{n + 1}\) :

The n + 1 iteration of Lagrange multiplier

\(\tau\) :

Scale factor in RCMDE

\(\overline{p} \left( {r_{{v_{0} v_{1} \cdots v_{m - 1} }} } \right)\) :

The average value of the probability of the dispersion mode corresponding to the coarse-grained sequence

\(p_{k}^{\left( \tau \right)}\) :

The probability of the dispersion model corresponding to the kth coarsening sequence under scale

\(\widetilde{X}\) :

The zero mean filtered signal

N :

The length of signal

\(r_{{\widetilde{X}}} \left( 0 \right)\) :

The value of the autocorrelation function

\(SE\left( {\widetilde{X}} \right)\) :

The square envelope signal

\(r_{SE} \left( 0 \right)\) :

The value of the autocorrelation function of the square envelope signal

\(f_{s}\) :

The sampling frequency

\(f_{r}\) :

The spindle rotation frequency

\(SES\left( f \right)\) :

The square envelope spectrum

f :

The spindle rotation frequency

\(\iota\) :

Delay in RCMDE

m :

Embedding dimension in RCMDE

References

  1. Yue CX, Gao HN, Liu XL, Liang SY, Wang LH (2019) A review of chatter vibration research in milling. Chin J Aeronaut 32(2):215–242

    Article  Google Scholar 

  2. Fu Y, Zhang Y, Zhou HM, Li DQ, Liu HQ, Qiao HY, Wang XQ (2016) Timely online chatter detection in end milling process. Mech Syst Signal Process 75:668–688

    Article  Google Scholar 

  3. Lamraoui M, Barakat M, Thomas M, Badaoui ME (2015) Chatter detection in milling machines by neural network classification and feature selection. J Vib Control 21(7):1250–1266

    Article  Google Scholar 

  4. Li DD, Zhang WM, Li YS, Xue F, Fleischer J (2020) Chatter identification of thin-walled parts for intelligent manufacturing based on multi-signal processing. Adv Manuf 1–12

  5. Wang WK, Wan M, Zhang WH, Yang Y (2022) Chatter detection methods in the machining processes: a review. J Manuf Process 77:240–259

    Article  Google Scholar 

  6. Gupta P, Singh B (2021) Exploration of tool chatter in CNC turning using a new ensemble approach. Maters Today: Proc 43(P1):640–645

    Google Scholar 

  7. Aslan D, Altintas Y (2018) On-line chatter detection in milling using drive motor current commands extracted from CNC. Int J Mach Tools Manuf 132:64–80

    Article  Google Scholar 

  8. Zhang CL, Li B, Chen BQ, Cao HR, Zi YY, He ZJ (2015) Weak fault signature extraction of rotating machinery using flexible analytic wavelet transform. Mech Syst Signal Process 64–65:162–187

    Article  Google Scholar 

  9. Cabrera CG, Araujo AC, Castello DA (2017) On the wavelet analysis of cutting forces for chatter identification in milling. Adv Manuf 5(2):130–142

    Article  Google Scholar 

  10. Gao J, Song QH, Liu ZQ (2018) Chatter detection and stability region acquisition in thin-walled workpiece milling based on CMWT. Int J Adv Manuf Technol 98(1–4):699–173

    Article  Google Scholar 

  11. Shrivastava Y, Singh B, Sharma A (2018) Identification of chatter in turning operation using WD and EMD. Maters today: Proc 5(11):23917–23926

    Google Scholar 

  12. Chen Y, Li HZ, Hou L, Wang J, Bu XJ (2018) An intelligent chatter detection method based on EEMD and feature selection with multi-channel vibration signals. Measurement 127:356–365

    Article  Google Scholar 

  13. Mou WP, Zhu SW, Jiang ZX, Song G (2020) Vibration signal-based chatter identification for milling of thin-walled structure. Chin J Aeronaut 35(1):204–214

    Article  Google Scholar 

  14. Liu CF, Zhu LD, Ni CB (2018) Chatter detection in milling process based on VMD and energy entropy. Mech Syst Signal Process 105:169–182

    Article  Google Scholar 

  15. Zhu LD, Liu CF, Ju CY, Guo MX (2020) Vibration recognition for peripheral milling thin-walled workpieces using sample entropy and energy entropy. Int J Adv Manuf Technol 108(9–10):3251–3266

    Article  Google Scholar 

  16. Yang K, Wang GF, Dong Y, Zhang QB, Sang LL (2019) Early chatter identification based on an optimized variational mode decomposition. Mech Syst Signal Process 115:238–254

    Article  Google Scholar 

  17. Ren JB, Sun GZ, Chen B, Luo M (2015) Multi-scale permutation entropy based on-line milling chatter detection method. J Mech Eng Sci 51(9):206–212

    Google Scholar 

  18. Liu XL, Wang ZX, Li MY, Liang SY, Wang LH (2021) Feature extraction of milling chatter based on optimized variational mode decomposition and multi-scale permutation entropy. Int J Adv Manuf Technol 114(9–10):2849–2862

    Article  Google Scholar 

  19. Chang CY, Wu TY (2018) Identification of milling status using vibration feature extraction techniques and support vector machine classifier. Inventions 3(2):25–25

    Article  Google Scholar 

  20. Rostaghi M, Azami H (2016) Dispersion entropy: a measure for time-series analysis. IEEE Signal Process Lett 23(5):610–614

    Article  Google Scholar 

  21. Azami H, Rosraghi M, Abasolo D, Escudero J (2017) Refined composite multiscale dispersion entropy and its application to biomedical signals. IEEE Trans Biomed Eng 64(12):2872–2879

    Article  Google Scholar 

  22. Cao HR, Zhou K, Chen XF (2015) Chatter identification in end milling process based on EEMD and nonlinear dimensionless indicators. Int J Mach Tools Manuf 92:52–59

    Article  Google Scholar 

  23. Lamraoui M, Badaoui ME, Guillet F (2015) Chatter detection in CNC milling processes based on Wiener-SVM approach and using only motor current signals. Springer Int Publishing 23:567–578

    Google Scholar 

  24. Liu HQ, Chen QH, Li B, Mao XY, Mao KM, Peng FY (2011) On-line chatter detection using servo motor current signal in turning. Sci Chin Technol Sci 54(12):11

    Article  MATH  Google Scholar 

  25. Dragomiretskiy K, Zosso D (2014) Variational mode decomposition. IEEE Trans Signal Proc A Pub IEEE Signal Proc Soc 62(3):531–544

    Article  MathSciNet  MATH  Google Scholar 

  26. Wang ZX, Liu XL, Li MY, Liang SY, Wang LH, Li YQ, Meng BY (2020) Intelligent monitoring and control technology of cutting chatter. J Mech Eng 56(24):1–23

    Article  Google Scholar 

  27. Liang T, Lu H (2020) A novel method based on multi-island genetic algorithm improved variational mode decomposition and multi-features for fault diagnosis of rolling bearing. Entropy 22(9):995

    Article  MathSciNet  Google Scholar 

  28. Chen XL, Feng FZ, Zhang BZ, Jiang PC (2018) Rolling bearing fault diagnosis with optimal resonant frequency band demodulation based on squared envelope spectral correlated kurtosis. J Mech Eng 54(21):90–100

    Article  Google Scholar 

  29. ANTONI J, (2007) Fast computation of the kurtogram for the detection of transient faults. Mech Syst Signal Process 21(1):108–124

    Article  Google Scholar 

  30. Huang NE (2000) New method for nonlinear and nonstationary time series analysis: empirical mode decomposition and Hilbert spectral analysis. NASA Goddard Space Flight Ctr (United States) 4056:197–209

    Google Scholar 

Download references

Funding

This research was funded by Projects of International Cooperation and Exchanges NSFC (Grant Number 51720105009).

Author information

Authors and Affiliations

  1. Key Laboratory of Advanced Manufacturing and Intelligent Technology, Ministry of Education, Harbin University of Science and Technology, Harbin, 150080, China

    Xianli Liu, Hanbin Wang, Maoyue Li, Zhixue Wang & Boyang Meng

Authors
  1. Xianli Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Hanbin Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Maoyue Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Zhixue Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Boyang Meng
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

Xianli Liu, Hanbin Wang, and Maoyue Li contributed to the conception of the study; Hanbin Wang studied the recognition of the machining state in the machining process of the thin-walled parts. Zhixue Wang contributed to the experimental verification. Boyang Meng helped perform the analysis with constructive discussions.

Corresponding author

Correspondence to Xianli Liu.

Ethics declarations

Ethics approval

The content studied in this article belongs to the field of metal processing and does not involve humans and animals. This article strictly follows the accepted principles of ethical and professional conduct.

Consent to participate

My co-authors and I would like to opt-in to In Review.

Consent for publication

I agree with the Copyright Transfer Statement.

Conflict of interest

The authors declare no competing interests.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Liu, X., Wang, H., Li, M. et al. Milling chatter detection of thin-walled parts based on GA-SE-SCK-VMD and RCMDE. Int J Adv Manuf Technol 124, 945–958 (2023). https://doi.org/10.1007/s00170-022-10235-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00170-022-10235-x

Keywords

Search

Navigation