1 Introduction

The demand for high-performance, recyclable structural components has promoted the development of thermoplastic composite technologies. Thermoplastic polymers offer the advantages of recyclability, easy joining methods [1], and the possibility to produce multi-functional and smart materials [2], and short fibers are often used as reinforcement to improve their strength and stiffness [3, 4]. In most cases, short fiber–reinforced composites (SFCs) are processed by injection molding (IM). Although IM seems unbeatable in productivity, it is not economical for custom production. Thus, fused filament fabrication (FFF) is emerging as a new potential.

The mechanical properties of SFCs are strongly dependent on their microstructure [5,6,7,8]. Fiber length distribution (FLD), fiber orientation distribution, and potential voids are all affected by the processing conditions; therefore, they are expected to differ for different technologies. Regarding orientation, IM composites have a sandwich-like morphology with fibers aligned parallel to the flow direction in the shell, and randomly oriented fibers in the core [9]. FFF composites, on the other hand, are highly oriented along the printing direction. The fiber length distribution is usually wide for IM and FFF as well, due to the fiber breakage caused by shear forces during melt processing. Lastly, the void content for IM is zero or negligible, while in FFF parts, it is significant [10,11,12,13,14].

Quantitative data on these microstructural features can be used to refine predictive models for SFCs.

There are several methods for the micromechanical modeling of IM composites.

Chin et al. [15] reported that statistical distribution functions can be used to describe FLD, and the ratio of the length-weighted and the numerical average length (the index of distribution) can be used for elastic modulus prediction. Hine et al. [16] investigated the effect of FLD numerically, and they found that the distribution function can be replaced by the numerical average length. Mortazavian and Fatemi [17] fitted a three-parameter probability density function to the fiber length and used it to modify the linear rule of mixtures for tensile strength prediction. Fiber orientation density was also taken into account. For elastic moduli prediction, they compared several analytical models and found that models that include the orientation distribution are more accurate. Lionetto et al. [18] described FLD with the two-parameter Weibull probability density function, then they used the mean value of fiber length in the modified Halpin–Tsai equation to calculate elastic moduli.

Being a younger technology, the micromechanical modeling of FFF composites is less discussed in literature yet. van de Werken et al. [4] used the distribution functions for length and orientation to refine the Halpin–Tsai model and the laminate analogy approach. They reported good agreement between the predicted and the experimental tensile strength and modulus. Somireddy et al. [19] applied the classical lamination theory (CLT) and the Tsai-Hill failure criteria, and they found that the voids degrade mechanical properties and reduce the accuracy of predictive methods. Papon et al. [20] identified three types of voids and considered their effects in a multi-level analytical modeling framework. They found that the void distribution can be obtained from stochastic void models, and it can be used with the CLT to give accurate predictions for the overall laminate properties. Besides the microstructural features, the fiber content is also important. Nasirov et al. [21] investigated short fiber–reinforced composites with a fiber content of up to 10 v% and they reported that the Mori–Tanaka homogenization method is very effective for higher fiber contents. However, their findings suggest that there might be differences in using homogenization models for composites with different fiber contents.

Micromechanical models are widely used for SFCs, and the goodness of the predictions can be refined by taking microstructural features into account. There are several metrics for describing fiber length and orientation, but which one gives more accurate results is less discussed. It is also known that different melt processing technologies create different microstructures in the products. However, differences in the applicability and the accuracy of the models are also rarely addressed in the literature.

In this study, we aim to compare the accuracy of the modified rule of mixtures (MROM) for SFCs prepared by IM and FFF. For this purpose, we prepared basalt fiber–reinforced polylactic acid filaments and granules with 5, 10, and 20 wt% fiber contents. We presented the microstructural differences between the technologies via X-ray micro-computed tomography, during which data on fiber length, orientation, and void content was collected. We used three different metrics to describe the fiber length and showed which gives the most accurate estimate for tensile strength. Lastly, we proposed a new approach for the mechanical modeling of products made with FFF technology.

2 Experimental procedure

2.1 Materials

The matrix of the composites was polylactic acid (PLA, Ingeo 3100 HP, Natureworks LLC, USA). Its density is 1.24 g/cm3 and its d-lactide content is approx. 0.5% [22].

Short basalt fibers were obtained from Kamenny Vek with an initial fiber length and diameter of 10 mm and 12 µm, respectively. The density of basalt fibers is 2.59 g/cm3. The fibers were cut from continuous yarn. The fibers are surface-treated with silane by the manufacturer, which can provide good adhesion with thermoplastic matrix materials [23,24,25]. To avoid possible hydrolytic degradation, we dried the raw materials at 80 °C for 4 h prior to processing. Further material parameters used for the shrinkage simulation can be seen in Table 1.

Table 1 Material parameters used for the shrinkage simulation [22, 26,27,28,29]
Full size table

2.2 Sample preparation

Composite compounds were prepared with a LabTech Scientific co-rotating twin-screw extruder (screw diameter = 26 mm, L/D = 44) with a temperature profile of 170–175-180–185-190 °C (from the hopper to the die) and a screw speed of 25 rpm. Dry mixtures with fiber contents of 5, 10, and 20 wt% were fed to the extruder, then the compounds were pelletized and extruded again for homogeneous fiber distribution. For filament fabrication, the compounds were extruded through a cylindrical die and the diameter required (1.75 mm) was controlled by draw speed.

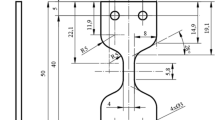
To investigate the differences between processing technologies, we prepared injection-molded and 3D-printed specimens as well. Samples for tensile testing (based on type 5B, ISO 527–1:2012 as can be seen in Fig. 1a) were produced on a Craftbot + type desktop FFF printer. We printed the samples with a nozzle temperature of 230 °C, a layer height of 0.2 mm, and an infill rate of 100%, with the printing orientation parallel to the longitudinal axis (0°). We also prepared neat PLA samples with a standing printing orientation (Fig. 1b) to determine interlayer bond strength.

Fig. 1
figure 1

Tensile specimen geometries. a FFF printed with flat printing orientation, b FFF printed with standing orientation, and c injection-molded specimens

Full size image

80 × 80 × 2 mm plates were injection molded with an Arburg Allrounder Advance 270S 400–170 (ARBURG GmbH, Lossburg) injection molding machine, with a melt temperature of 190 °C and a mold temperature of 25 °C, an injection rate of 50 cm3/s, and a holding pressure of 600 bar. The tensile specimen was cut by water jet cutting from the center of the parts with the longitudinal axis of the samples parallel to the flow direction (Fig. 1c).

2.3 Tensile testing

We conducted tensile tests to experimentally validate the analytical methods presented with a Zwick Z005 (Zwick Roell AG, Ulm) universal testing machine in accordance with the ISO 527–1:2012 standard, with a cross-head speed of 5 mm/min, and a gripping distance of 50 mm, at 25 °C and in 20% relative humidity. We tested 5 specimens for each sample type.

2.4 Interfacial shear strength measurements

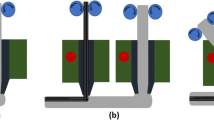
The adhesion between the fibers and the matrix has a great influence on the mechanical properties of the composites. One way to quantify adhesion is to measure the interfacial shear strength with microdroplet pullout tests [30]. For this purpose, we took single basalt fibers out of the continuous yard and fixed them onto paper frames for easier handling. Then, we placed a single drop of PLA melt on the fibers (as shown in Fig. 2a) using a soldering iron. The dimensions required to determine the strength (the embedded length (L) and fiber diameter (d)) were measured with an Olympus optical microscope. We placed the samples in a custom grip and performed the pull-out tests using a Zwick Z005 (Zwick Roell AG, Ulm) universal testing machine at a testing speed of 2 mm/min. Figure 2b, c shows a specimen and the experimental arrangement. We repeated the experiment on at least 20 samples.

Fig. 2
figure 2

a Micrograph of a PLA drop on basalt fiber and its relevant parameters (L (mm) is the embedded length, d1 and d2 (mm) are the fiber diameters); b schematic diagram of a test specimen; c experimental arrangement

Full size image

The interfacial adhesion is affected by pressure, which can differ by orders of magnitude between IM and FFF. To check if the test is representative of both technologies, we prepared a shrinkage simulation using Ansys R3 2019. A single fiber of 14-µm diameter and a 100-µm diameter polymer cylinder were modeled with overlap at the contact surface. Material parameters used as input can be seen in Table 1. We assumed isotropic material behavior for simplicity, and creep was not considered. We calculated shrinkage from an initial temperature of 200 °C with a 10 °C/min cooling rate which represents the conditions of sample preparation. The simulation showed that the pressure on the fiber surface is of the same magnitude as the pressure in the injection mold, with a maximum value of 263.5 MPa at 20 °C. Therefore, we expect no difference in the development of fiber-matrix adhesion as a function of processing technology.

Using the interfacial shear strength results, we determined the critical fiber length with the Kelly-Tyson equation (Eq. (1)) [31].

$${l}_{\mathrm{crit}}=\frac{{\sigma }_{f}{d}_{f}}{2\tau }$$
(1)

where lcrit (mm) is the critical fiber length, τ (MPa) is the interfacial shear strength of the fiber-matrix interface, σf (MPa) is the ultimate tensile strength of a single fiber, and df (mm) is the fiber diameter.

2.5 Microstructural analysis

We performed micro-computed tomography with a GE Phoenix Micromex 180 PCB (Baker Hughes Company, Houston) X-ray device to examine and quantify the internal morphological features of the composites. 4 × 2 × 5 mm samples were cut from the middle of the specimens and rotated 360° while being exposed to an X-ray beam (accelerating voltage: 180 kV; power: 20 W). We collected the images and reconstructed the 3D geometry with the Volume Graphics Studio Max software. After correcting image artifacts, a 5 × 3 × 1.6 mm region of interest was defined, which reduced the amount of data to be processed. Phases in the composites were segmented with gray level values based on the density differences of the materials (Fig. 3). Void content was determined by summing the volumes corresponding to gray levels of 6000 and below. We also determined the fiber orientation tensor components using fiber composite material analysis.

Fig. 3
figure 3

Regions of interest for X-ray μ-CT analysis in the case of (a) FFF and (b) IM composites. The matrix, the fibers and the voids in the composites are segmented according to their density differences and colored with gray, orange and blue, respectively

Full size image

For the fiber length distribution analysis, we approximated the fiber lengths with the major axis of the inscribed ellipse. Based on the data, we calculated the averages of fiber length (Eq. (2)), the length-weighted averages (Eq. (3)), and the fiber length distribution functions (Eq. (4)) as well [32].

$${L}_{n}=\frac{\sum {n}_{i}{L}_{i}}{\sum {n}_{i}}$$
(2)
$${L}_{w}=\frac{\sum {n}_{i}{{L}_{i}}^{2}}{\sum {n}_{i}{L}_{i}}$$
(3)

where Li (µm) is the length of fiber i and ni is the number of fibers of length Li.

$$f(l)=\frac{{N}_{i}/N}{\Delta l}$$
(4)

where N is the total number of the fibers within all intervals, Ni is the ith interval, and ∆l is the fiber length interval.

Scanning electron microscopy (SEM) was also used for further inspection and validation of the data collected with µ-CT analysis. Images of cryogenic fracture surfaces were acquired with a JEOL JSM 6380LA (JEOL Ltd., Tokyo) scanning electron microscope. The samples were coated with a thin layer of gold to prevent charging by the electron beam. Lastly, in order to determine the dimensions of the cross-sections, we used a Keyence VHX-5000 (Keyence Corporation, Mechelen) digital microscope with × 20 magnification and the ImageJ software.

3 Results and discussion

3.1 Fiber length distribution and critical fiber length

We determined the fiber length distribution after injection molding and 3D printing of the samples for each fiber content, and also calculated critical fiber length (Table 2). The fiber length distributions of the FFF-printed and the injection-molded composites are shown in Fig. 4, and the averages are presented in Table 3.

Table 2 Input data used to calculate the critical fiber length, and the result
Full size table
Fig. 4
figure 4

Fiber length distributions of the 5, 10, and 20 wt% composites prepared by a FFF and b injection molding

Full size image
Table 3 Numerical and length-weighted fiber length averages and standard deviations
Full size table

There was a large reduction in fiber length compared to the initial length of 10 mm during compounding, then further fiber breakage occurred during processing. The numerical averages and the weighted averages are all below the critical fiber length, so no increase in tensile strength can be expected. For FFF, these fiber length results are in line with the literature. Most data reported for fiber length is in the range of 50–300 microns [6, 14, 21, 33], with a maximum fiber length achieved in one instance being 480 microns [12]. In the case of injection molding, residual fiber length can be orders of magnitude longer with long-fiber granules [34, 35] or direct fiber feeding [36], but in this study, we aimed for uniform processing conditions to ensure comparability.

3.2 Fiber orientation

The performance of short-fiber composites greatly depends on the orientation distribution in the part. The orientation of the short fibers can vary from random to unidirectional depending on the processing conditions, so we compared the orientation of the 3D printed and the injection-molded samples based on the μ-CT analysis. To characterize the distribution, the fiber orientation tensor (Eq. (5)) is often used, where the diagonal elements are between 0 and 1 (1 indicating perfect alignment) [37].

$${A}_{ij}=\left[\begin{array}{ccc}{{\varvec{a}}}_{{\varvec{x}}{\varvec{x}}}& {a}_{xy}& {a}_{xz}\\ {a}_{yx}& {{\varvec{a}}}_{{\varvec{y}}{\varvec{y}}}& {a}_{yz}\\ {a}_{zx}& {a}_{zy}& {{\varvec{a}}}_{{\varvec{z}}{\varvec{z}}}\end{array}\right]$$
(5)

For visual representation, we plotted the principal diagonal values (axx, ayy, azz) of the second-order orientation tensor as a function of edge length (Fig. 5), thus describing orientation along the whole inspected region.

Fig. 5
figure 5

Fiber orientation distribution of FFF-printed and injection-molded composites with 5 and 10 wt% fiber content. The principal diagonal values of the second-order orientation tensor (axx, ayy, azz) are shown as a function of edge length (distance)

Full size image

The results show that in the case of 3D printing, the fibers are highly oriented in the printing direction, and the distribution does not seem to be affected by fiber content. For the injection-molded samples, the orientation vector along the x-axis was similar to that of the y-axis, which means that fibers are equally likely to be oriented parallel to and perpendicular to the injection direction. As the fiber content increases from 5 to 10 wt%, orientation also increases as the core–shell structure becomes more prominent.

3.3 Porosity

In addition to fiber length and orientation, the quality of composites is greatly affected by their void content. Using data obtained by μ-CT, we segmented and quantified the voids according to their volume (Fig. 6). There is no sign of porosity in the injection-molded samples, although the micro-voids that can occur at the fiber ends can only be detected up to the limit of the resolution of the X-ray microscope (6.5 μm).

Fig. 6
figure 6

Porosity of FFF-printed and injection-molded composites with 5 and 10 wt% fiber content. a The volume fraction of voids, fibers, and matrix phases; b the SEM micrograph of the fracture surface of the FFF 5 wt% sample and c the size distribution of voids in the FFF 5 wt% sample

Full size image

In the case of FFF samples, we observed smaller, uniformly distributed voids near the print bed and larger pores along the building direction. This may be due to the damping effect of the polymer layers. Near the print bed, higher pressure can be provided during extrusion thus creating a more compact structure. However, as the number of layers increases, damping can also increase but the applied pressure remains constant. We also observed that the voids between the printed filaments decreased with increasing fiber content, which is in agreement with the literature [6, 12].

3.4 Analytical modeling and experimental testing of tensile strength

The presented microstructural features (fiber length and orientation) can serve as input parameters for various analytical models to predict the mechanical properties of the composites. Since the average fiber lengths (Ln, Lw) are below the critical length for all the samples, the fiber length factor (χ1) can be determined with Eq. (6). In this case, uniform fiber length is assumed. We calculated the length correction factor using the arithmetic and the length-weighted fiber length averages as well [31].

$${\chi }_{1}=\frac{L}{2{L}_{\mathrm{crit}}}\;\mathrm{ for }\;L<{l}_{\mathrm{crit}}$$
(6)

where L (mm) is the average fiber length and Lcrit (mm) is the critical fiber length.

For samples with non-uniform fiber length, first we have to determine the fiber length distribution function. Then, the fiber length factor is modified according to Eq. (7). The second term is zero in this case, since the number of fibers exceeding the critical fiber length is zero for each sample.

$$\begin{aligned}{\chi }_{1}&=\int_{L_\mathrm{min}}^{L_\mathrm{crit}}\left[{l}^{2}/(2{L}_{\mathrm{crit}}{L}_{\mathrm{mean}}\right]f(l)dl\\&+\int_{L_\mathrm{crit}}^{L_\mathrm{max}}\left(\frac{l}{{L}_{\mathrm{mean}}}\right)\left[1-\frac{{L}_{\mathrm{crit}}}{2l}\right]f(l)dl\end{aligned}$$
(7)

where Lmean (mm) is the mean fiber length; Lcrit (mm) is the critical fiber length; Lmin and Lmax (mm) are the shortest and the longest fibers measured, respectively; and f(l) is the fiber length distribution function.

After the fiber length factor is calculated based on all three approaches, the MROM (Eq. (8)) can be used for the prediction of tensile strength. We made calculations with all three factors (χ1 based on Ln and Lw and determined with the fiber length distribution) in order to determine which gives a more accurate estimate.

$${\sigma }_{\mathrm{MROM}}={\chi }_{1}{\sigma }_{f}{v}_{f}+{\sigma }_{m}{v}_{m}$$
(8)

where χ1 (−) is the fiber length factor; σf (MPa) and σm (MPa) are the ultimate tensile strength of a fiber and the matrix, respectively; and vf (−) and vm (−) are the fiber and the matrix volume fractions, respectively.

Theoretically, a more accurate prediction can be achieved if we take into account fiber orientation as well. van de Werken et al. [4] reported a modeling framework based on the Halpin–Tsai equation (Eq. (9)), which includes the orientation factor (χ2). In this paper, the orientation factor is approximated by the principal diagonal value of the second-order orientation tensor in the direction of stress. For unidirectional composites, χ2 = 1.

$${\sigma }_{HT}={\chi }_{1}{\chi }_{2}{\sigma }_{f}{v}_{f}+{\sigma }_{\mathrm{m}}{v}_{\mathrm{m}}$$
(9)

where χ1 (−) is the fiber length factor; χ2 (−) is the orientation factor; σf (MPa) and σm (MPa) are the ultimate tensile strength of a fiber and the matrix, respectively; and vf (−) and vm (−) are the fiber and the matrix volume fractions, respectively.

The calculated and the experimental tensile strengths for IM and FFF composites are shown in Fig. 7. We also plotted the residuals (the error between the predicted values and the experimental data) to compare the accuracy of the different models (Fig. 8a, b), then we plotted the sum of the absolute values of the residuals in increasing order (Fig. 8c). For FFF composites, Fig. 9 shows the calculated and the experimental tensile strengths, and the residuals can be seen in Fig. 10.

Fig. 7
figure 7

Predicted tensile strengths based on the a MROM and b the Halpin–Tsai model, and experimental results for IM composites

Full size image
Fig. 8
figure 8

Residual plots for IM. a Halpin–Tsai and b MROM, c the sum of the residuals in increasing order

Full size image
Fig. 9
figure 9

Predicted tensile strengths based on the a MROM and b the Halpin–Tsai model, and experimental results for FFF composites

Full size image
Fig. 10
figure 10

Residual plots for FFF. a Halpin–Tsai and b MROM, c the sum of the residuals in increasing order

Full size image

In the case of injection molding, all methods besides MROM Lw give good prediction with a 5% deviation. Length-weighted average reduces accuracy, while the FLD function f(l) approximates the experimental results the best. The orientation factor further refines the estimate, and if it is used, the FLD function can be replaced by the numerical average length, which simplifies the calculations. These results underline that fiber orientation in IM composites influences mechanical properties strongly; therefore, it should not be neglected in analytical modeling.

For 3D printing, the application of the methods is not straightforward in terms of interpreting the strength of the neat matrix. Injection-molded PLA has a tensile strength of 60 MPa, while the strength measured on 3D printed samples only reaches 43.7 MPa. This raises the following question: which value for matrix strength gives a more accurate estimate for the composites? We made predictions using both and showed that approximations using the strength of the IM matrix overestimate and the neat FFF strength underestimates the experimental results. For neat PLA, the loss in strength is due to the voids, so calculations with the experimental matrix strength include their effect. Calculation with FFF strength defines a lower limit that can be applied safely for engineering parts.

Regarding the correction factors, it can be seen that similar to IM, the FLD function gives the best estimate; however, the numerical average closely follows. This means that f(l) can also be replaced with Ln for FFF calculations. Orientation, however, does not seem to have a significant effect on the accuracy of the model since fiber orientation in the extruded filaments is nearly unidirectional. The orientation, therefore, should not be corrected; rather, laminate mechanics can be used to take advantage of the unidirectional nature of the layers.

The difference between the accuracy of the models shows that application for 3D printed composites might require a different approach. In the FFF process, the material is deposited layer-by-layer, and molecular diffusion between layers is often incomplete. Thus, interlayer bonding strength does not reach the strength of the bulk material [38], which causes anisotropy in the strength of the 3D printed structure. Therefore, models that assume homogeneous strength for the matrix material may be inaccurate.

If the bond strength between the layers is below the strength within the filament, we can divide FFF printed parts into bulk material zones and contact zones (as shown in Fig. 11). Knowing the layer height and the number of layers, the size of the contact zones can be approximated based on optical microscopic images (Fig. 12). We defined the width of the contact zone as the minimum width of the cross-section, and the height was approximated by the height of the intersection of ellipses representing the elementary filaments. The volume fraction of all contact areas can be determined by Eq. (10).

$${v}_{c}=\frac{(n-1)({W}_{b}{H}_{b}L)}{{v}_{all}}$$
(10)

where n is the number of layers, L (mm) is the length, vall (mm3) is the volume of the specimen, Wb (mm) is the length, and Hb (mm) is the height of the interlayer contact.

Fig. 11
figure 11

Definition of contact zones. (a) Tested area of the tensile specimen; (b) interpretation of different strength zones in the cross-section; (c) general state of molecular diffusion between layers

Full size image
Fig. 12
figure 12

Definition of contact zones via optical microscopy

Full size image

The volume of the specimen is given by Eq. (11).

$${v}_{\mathrm{all}}={W}_{\mathrm{sample}}\cdot {H}_{\mathrm{sample}}\cdot L$$
(11)

Then we can calculate the strength of the matrix material based on the Rule of Mixtures (Eq. (12)) [39]. The tensile strength of the bulk material zones was assumed to be equal to injection-molded strength, and the bonding strength of the contact zones was determined experimentally (12.5 ± 5 MPa).

$${\sigma }_{\mathrm{mROM}}={\sigma }_{\mathrm{bulk}}(1-{v}_{c})+{\sigma }_{z}{v}_{c}$$
(12)

where σbulk (MPa) and σz (MPa) are the strength of the bulk material and the strength of the contact zones, respectively, and vc (−) is the volume fraction of the contact zones.

Tensile strength calculated this way considers the anisotropy of the matrix material of 3D printed structures. We entered the new matrix strength into the presented predictive models as shown in Eqs. (13) and (14). Matrix strength calculated with the ROM approximates the experimental values with an error of 5%, which suggests that the approach is appropriate for predicting the tensile strength of neat FFF parts. For composites, the accuracy of the analytical methods varies as a function of fiber content. This can be because as fiber content increases, more fibers are present in the contact area, thus changing interlayer strength. Further refinements should also cover the theoretical definition of interlayer strength and the size of the contact zones.

$${\sigma }_{\mathrm{MROMnew}}={\chi }_{1}{\sigma }_{f}{v}_{f}+(1-{v}_{f}){\sigma }_{\mathrm{mROM}}$$
(13)
$${\sigma }_{\mathrm{HTnew}}={\chi }_{1}{\chi }_{2}{\sigma }_{f}{v}_{f}+(1-{v}_{f}){\sigma }_{\mathrm{mROM}}$$
(14)

where χ1 (−) is the fiber length factor; χ2 (−) is the orientation factor; σf (MPa) is the ultimate tensile strength of a fiber; vf (−) and vm (−) are the fiber and the matrix volume fractions, respectively; and σmROM (MPa) is the matrix strength calculated with the rule of mixtures.

4 Conclusion

In this study, we compared the applicability of homogenization models for strength prediction of short fiber-reinforced composites prepared by injection molding (IM) and fused filament fabrication (FFF). We investigated basalt fiber–reinforced PLA composites with 5, 10, and 20 wt% fiber contents. We determined fiber length distribution, fiber orientation, and porosity via X-ray µ-CT, then we used this data for the analytical prediction of the tensile strength based on the modified rule of mixtures (MROM) and the Halpin–Tsai model. We found that in the case of IM, correction with the orientation factor gives the most accurate predictions. For FFF, the orientation factor is not significant due to the nearly unidirectional fiber arrangement in the layers. The FLD function can be replaced with the numerical length average for both technologies, which simplifies the calculations.

It was also shown that in the case of FFF, inserting the experimental matrix strength into models results in a lower tensile strength limit as the effect of voids is already considered. When designing load-bearing parts, the lower limit of strength is estimated for safety; therefore, calculations with the experimental tensile strength can provide good and useful results.

We also presented a new approach for refining predictive methods for FFF composites. As the bond strength between the layers is below the strength of the bulk material, the 3D printed structure can be segmented into bulk material zones and contact zones. Based on the rule of mixtures, we calculated tensile strength and found that the resulting value approximates the strength of the neat PLA with an error of 5%. Our findings provide a more precise approach for the modeling of FFF composites, thus contributing to industrial applicability. In our future studies, we aim to investigate the effect of fiber content on interlayer bond strength, and we also aim to further refine the model with theoretical calculations of bond strength.