Skip to main content
SpringerLink
Log in

Assembly accuracy prediction and optimization of aero-engine rotor under the separation condition of assembly and measurement

  • ORIGINAL ARTICLE
  • Published:
The International Journal of Advanced Manufacturing Technology Aims and scope Submit manuscript

Abstract

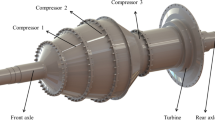
The measurement and assembly of the aero-engine rotor are separated from each other, which makes it difficult to keep the assembly datum consistent with the measurement datum; the existence of the datum error will cause the characteristic matrix to fail to truly reflect the geometric state of the rotor itself and cause the assembly model to be inaccurate, then ultimately affect the assembly accuracy prediction. Combined with the fact that the geometric characteristics of parts/components are not related to the measurement datum, the datum error elimination method has been proposed which makes the rotor characteristic matrix and assembly model more accurate, thereby improving the prediction effect of assembly accuracy. At the same time, the proposed direct optimization strategy is more efficient than the traditional genetic algorithm. The assembly experiment of the aero-engine rotor shows that the model and method proposed in this paper can better reflect the geometric characteristics of the rotor itself and are beneficial to reduce the coaxiality of the front and rear fulcrum. The related research also has reference significance for other large-scale and high-precision mechanical product assemblies.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

Availability of data and material and code

Not applicable.

References

  1. Zhu B, Yu NJ, Meng XH, Cheng YB, Ding SY, Shan FP (2015) Study on the tolerance analysis of aircraft engine assembly dimension chain. Journal of Test and Measurement Technology 29(02):177–184

    Google Scholar 

  2. Chen J, Li Y, Yu JF (2014) An effective tolerance allocation method for sheet metal assemblies. Manufacturing Automation 36(16):97–99

    Google Scholar 

  3. Whitney DE (2004) Mechanical assemblies. Oxford University Press, New York

    Google Scholar 

  4. Cai M, Yang JX, Wu ZT (2004) Mathematical model of cylindrical form tolerance. J Zhejiang Univ Sci 5(7):890–895. https://doi.org/10.1631/jzus.2004.0890

    Article  Google Scholar 

  5. Liu J, Wu FY, Wang J (2014) Optimization technique of aeroengine rotor assembly. Aero Engine 40(03):75–78

    Google Scholar 

  6. Ju YP, Wu FY, Jin B, Wei XP, Zu JG (2018) Multi-stage disc rotor structure assembly process based on rotor runout and initial unbalance optimization. Aero Engine 44(06):83–90

    Google Scholar 

  7. Sun SM, Li Y (2020) Research on the influence of aero-engine rotor installation edge manufacturing error on assembly performance. Modern Manufacturing Technology and Equipment 56(07):126–131

    Google Scholar 

  8. Rao SS, Wu W (2005) Optimum tolerance allocation in mechanical assemblies using an interval method. Eng Optim 37(3):237–257. https://doi.org/10.1080/0305215512331328240

    Article  MathSciNet  Google Scholar 

  9. Ding Y, Ceglarek D, Shi J (2000) Modeling and diagnosis of multistage manufacturing processes: part I state space model. Japan/USA Symposium of Flexible Automation:1–8.

  10. Thimm G, Britton GA, Cheong FS (2001) Controlling tolerance stacks for efficient manufacturing. Int J Adv Manuf Syst 18(1):44–48

    Article  Google Scholar 

  11. Zheng C, Jin S, Lai XM, Yu KG (2011) Assembly tolerance allocation using a coalitional game method. Eng Optim 43(7):763–778

    Article  MathSciNet  Google Scholar 

  12. Griffin P, Ballinger IA, Jaekle DE, Jackson A (2003) Design and manufacturing of a lightweight fuel tank assembly. 39th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Huntsville, Alabama, July 20–23, 2003, AIAA: 2003–4606. https://doi.org/10.2514/6.2003-4606

  13. Kulyk M, Lastivka I, Tereshchenko Y (2012) Effect of hysteresis in axial compressors of gas turbine engines. Aviation 16(4):97–102. https://doi.org/10.3846/16487788.2012.753679

    Article  Google Scholar 

  14. Klocke F, Veselovac D, Auerbach T, Seidner R (2008) Intelligent assembly for aero engine components. 1st International Conference Intelligent Robotics and Applications, Wuhan, PEOPLES R CHINA, OCT 15–17, 2008, 5315: 927–935. https://doi.org/10.1007/978-3-540-88518-4_99

  15. Yang Z, Hussain T, Popov AA, Mcwillam S (2011) A comparison of different optimization techniques for variation propagation control in mechanical assembly. IOP Conference Series: Mate Sci Eng 26(1)

  16. Yang Z, McWilliam S, Popov AA, Hussain T (2013) A probabilistic approach to variation propagation control for straight build in mechanical assembly. Int J Adv Manuf 64(5–8):1029–1047. https://doi.org/10.1007/s00170-012-4071-x

    Article  Google Scholar 

  17. Yang Z, Hussain T, Popov AA, Mcwillam S (2011) Novel optimization technique for variation propagation control in an aero-engine assembly. Proceedings of the Institution of Mechanical Engineers, Part B: Acad J Manuf Eng 225(1):100–111. https://doi.org/10.1243/09544054JEM2043

    Article  Google Scholar 

  18. Yang Z, McWilliam S, Popov AA, Hussain T (2013) Dimensional variation propagation analysis in straight-build mechanical assemblies using a probabilistic approach. J Manuf Syst 32(2):348–356. https://doi.org/10.1016/j.jmsy.2012.11.008

    Article  Google Scholar 

  19. Meng XH, Shan FP (2016) Assembling quality prediction of aero-engine rotor parts. Manufacturing Automation 38(05):61–65

    Google Scholar 

  20. Shan FP, Li ZM, Zhu B (2015) Modeling and analysis of assembly deviation of typical aero-engine rotor parts. Manufacturing Automation 37(07):100–103

    Google Scholar 

  21. Ai YY, Zhou HL, Sun D, Wang Z, Zhang FL, Tian J (2015) Vibration analysis and control of aero-engine. Journal of Shenyang University of Aeronautics and Astronautics 32(05):1–25

    Google Scholar 

  22. Jin S, Ding SY, Li ZM, Yang FY, Ma X (2018) Point-based solution using Jacobian-Torsor theory into partial parallel chains for revolving components assembly. J Manuf Syst 46:46–58. https://doi.org/10.1016/j.jmsy.2017.11.003

    Article  Google Scholar 

  23. Ding SY, Jin S, Li ZM, Wei ZQ, Yang FY (2018) Deviation propagation model and optimization of concentricity for aero-engine rotor assembly. Journal of Shanghai Jiao tong University 52(01):54–62

    Google Scholar 

  24. Ding SY, Zheng XH (2020) Rotor assembly accuracy control method based on improved Jacobian-Torsor theory. J of Aeronaut 1–16.

  25. Chen H, Jin S, Li ZM, Lai XM (2014) A comprehensive study of three-dimensional tolerance analysis methods. Comput Aided Des 53:1–13. https://doi.org/10.1016/j.cad.2014.02.014

    Article  Google Scholar 

  26. Chen ZY, Liu Y, Zhou P, Liu GT (2018) Assembly tolerance analysis based on improved Taguchi method. Comput Integr Manuf Syst 24(05):1200–1206

    Google Scholar 

  27. Chen ZY, Liu Y, Zhou P, Liu GT (2018) Assembly success rate calculation method for aero-engine based on improved Taguchi method. J Propuls Technol 39(3):653–659

    Google Scholar 

  28. Sun HB, Yan JX, Wei XH (2020) Chang Z. Aero-engine assembly technology driven by digital twin. Chin J Mech Eng 31(07):833–841.

  29. Asante JN (2009) A small displacement torsor model for tolerance analysis in a workpiece-fixture assembly Proceedings of the Institution of Mechanical Engineers. Part B, Acad J Manuf Eng 223(8):1005–1020. https://doi.org/10.1243/09544054JEM1337

    Article  Google Scholar 

  30. Li H, Zhu HP, Li PG, He F (2014) Tolerance analysis of mechanical assemblies based on small displacement torsor and deviation propagation theories. Int J Adv Manuf 72(1–4):89–99. https://doi.org/10.1007/s00170-014-5630-0

    Article  Google Scholar 

  31. Khan HA, Butt SU, Baqai AA, Saeed HA (2018) A new approach to predict the flexibility and precision of manufacturing systems using geometric constraints and small displacement torsors. Prcedia Manuf 17:294–301. https://doi.org/10.1016/j.promfg.2018.10.049

    Article  Google Scholar 

  32. Sun CZ (2017) Research on the measurement method of multi-stage rotor coaxiality based on vector projection. Harbin Institute of Technology.

  33. Rama H, Turek S, Rajmohan S, Anand S (2011) A comprehensive methodology for runout tolerance evaluation using discrete data. Int J Adv Manuf Technol 56(5–8):663–676. https://doi.org/10.1007/s00170-011-3218-5

    Article  Google Scholar 

  34. Mu XK, Sun QC, Sun W, Wang YL, Wang CH, Wang XB (2018) 3D Tolerance modeling and geometric precision analysis of plane features for flexible parts. Eng Comput 35(7):2557–2576. https://doi.org/10.1108/EC-10-2017-0388

    Article  Google Scholar 

  35. Sun QC, Zhao BB, Liu X, Mu XK, Zhang YL (2019) Assembling deviation estimation based on the real mating status of assembly. Computer-Aided Design:244–255. https://doi.org/10.1016/j.cad.2019.06.001

Download references

Funding

This work is financially supported by the National Natural Science Foundation of China (No. 51875081).

Author information

Authors and Affiliations

  1. School of Mechanical Engineering, Ganjingzi District, Dalian University of Technology, No. 2, Linggong Road, Dalian, Liaoning Province, China

    Minghua Li, Yunlong Wang, Qingchao Sun & Xiaokai Mu

Authors
  1. Minghua Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yunlong Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Qingchao Sun
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Xiaokai Mu
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

Minghua Li established the error elimination and assembly model; he also drafted the manuscript. Yunlong Wang carried out relevant experiments and data processing, Qingchao Sun and Xiaokai Mu made suggestions and reviewed the manuscript.

Corresponding authors

Correspondence to Qingchao Sun or Xiaokai Mu.

Ethics declarations

Ethics approval

Not applicable.

Consent to participate

Not applicable.

Consent for publication

Not applicable.

Conflict of interest

The authors declare no competing interests.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Li, M., Wang, Y., Sun, Q. et al. Assembly accuracy prediction and optimization of aero-engine rotor under the separation condition of assembly and measurement. Int J Adv Manuf Technol 120, 3103–3112 (2022). https://doi.org/10.1007/s00170-022-08912-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00170-022-08912-y

Keywords

Search

Navigation