Selected aspects of a cold forging process for hollow balls

Abstract

This paper presents the results of a study investigating a cold forging process for producing hollow balls with different wall thicknesses. The study was performed by FEM numerical modelling, which made it possible to obtain a wide spectrum of results. For the analysis of FEM results obtained for problematic cases (shape defects in forged balls), novel hypotheses for results interpretation are proposed. The FEM numerical model and hypotheses are then verified via experimental testing, and selected theoretical results are compared with experimental findings. Finally, obtained results are discussed (e.g. the effect of billet dimensions on forging conditions, wall thickness and hole size), a method for FEM results interpretation is presented, and design-related solutions ensuring the production of defect-free hollow balls are proposed.

1 Introduction

Balls are machine components that are widely used in everyday life. Owing to their relatively simple shape, balls have a wide range of applications and functions. A ball can have a conventional shape, i.e. it is produced as a standard solid part [1]. Balls can also be produced as hollow elements, with their shape only resembling that of conventional balls [2]. Depending on their application, these elements can be produced in a wide dimensional range, i.e. balls for ball mills have diameters of up to several hundred millimetres, whereas balls for bearings have diameters of only several millimetres. Balls are also used as elements for ball valves, with hollow balls of different dimensions used to that end. Finally, it should also be mentioned that balls can be made of different materials, both metallic and non-metallic [3].

The selection of a manufacturing technique for balls depends on the practical use of a ball, its size and material it is made of. There exists a great variety of manufacturing methods for producing balls. They can be generally divided into forging (forming) and finishing methods. The choice of a manufacturing method also depends on production volume. Mass and large-scale production in particular has considerable potential for development in the field of forming methods [4], because even the smallest improvement in manufacturing technique can improve economic (as well as ecological) results on a global scale.

This paper relates to one of the forming methods for producing hollow balls, namely—cold die forging. The ball under study is made of aluminium and is manufactured in series production. The ball is formed in one operation in order to reduce unit costs. At the same time, no particular application for the analysed element is specified, thus leaving the reader free to apply the results presented in the paper.

2 Popular forming methods for hollow balls

Widely used as machine and device components, hollow balls can be series or mass produced by casting and forming processes. In this paper, we will focus on the forming process, assuming that a hollow ball is made of a workable metal alloy. The literature review shows that there exist numerous forming methods for hollow balls, each of them having its advantages and disadvantages [5]. It should be emphasized that—in our opinion—machining is regarded as one of finishing methods, and, due to the fact that machining generates considerable material losses, it is not recommended for mass production.

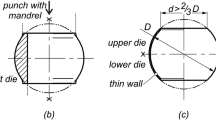
Let us begin with the die forging process. Figure 1 shows three conventional die forging methods for producing hollow balls. The first method is backward extrusion of a hollow part from bulk billet [6, 7]. The forged part has a web that is usually removed, e.g. by cutting. The second method, which is shown in Fig. 1b, consists of upsetting a sleeve (tube billet) between two dies. This method involves using a mandrel that is located inside the workpiece. The mandrel makes it possible to control the shape and dimensions of the internal surface of the workpiece. A shortcoming of this method is that the process requires the use of a third tool (mandrel). Also, numerous design and technology-related shortcomings must be overcome in this method, e.g. how to remove the mandrel without damaging the forging. Winiarski [8] showed that the use of this method leads to considerable increase in manufacturing costs of the upsetting device. In effect, it is easier to produce hollow balls by rolling with the use of a mandrel [11]. The third die forging method (Fig. 1c) involves upsetting a thin-walled billet (shell) using only two die halves. The method was designed by Seamless Hollow Ball Co. [9] at the early twentieth century, and it was further developed by Augustin and Hungerbach [3]. Unfortunately, however, very few studies in international literature have focused on this problem, as highlighted by Augustin and Hungerbach [3]. In general, it is easier to find patents relating to innovations in this field rather than comprehensive and interesting research studies. One example of such innovations is that designed by Kanazawa et al. [10]. A reason for the scarce number of studies on this forming method for hollow balls may be little interest therein on the part of industry. This stems from a lack of design guidelines, as well as from the fact that the process is characterized by a significant failure mode, namely buckling of thin-walled billet [7, 17]. The buckling phenomenon is very complex, particularly with respect to deformation of thin-walled parts [18].

Fig. 1

Basic forging methods for hollow balls: a) backward extrusion of a bulk billet using split die, b) upsetting of a tube billet (sleeve) on fixed mandrel using dies, c) upsetting of a thin-walled billet (shell) using only dies, without any additional tools

It is recommended that hollow balls should be die forged from tubes, as shown by Bartnicki et al. [4]. This process usually involves axial upsetting of a tube with the use of two dies, without any other tools such as mandrels. A schematic design of this process is shown in Fig. 2, while a comprehensive description of the process was given by Samołyk and Winiarski [7]. Unfortunately, however, this forming process produces an open ball whose dimensions (height, hole diameter, wall thickness) are limited, primarily by the occurrence of tube buckling during the forming process. Therefore, it is recommended that a closed ball be produced by a multi-operation process, e.g. that proposed by Eklund and Campbell [12]. In this process, the billet is subjected to upsetting first to obtain a semi-finished product of elliptical shape. Following the final forging operation, a sizing or mechanical working operation must be performed in order to smooth the joint. Owing to the use of several forming operations, additional tool sets must be produced, which has a negative effect on the cost-effectiveness of this forming method.

Fig. 2

Scheme illustrating the multi-operation manufacturing of a hollow ball according to the method proposed by Eklund et al. [12]

An alternative to forging process is the use of rolling and rolling-based processes [1, 2]. An ideal solution for forming hollow balls is the rotary compression process proposed by Skrochocki and Tomczak [13]. A schematic design of this process is shown in Fig. 3. This process is predominantly dedicated to mass production. One billet is sufficient to produce several parts that are then separated mechanically. Unfortunately, however, similarly to any other process [5], rotary compression too has its limitations [13]. First of all, there are constraints regarding the allowable wall thickness of forged parts, in combination with high costs of tools. In addition to that, rotary compression must be conducted in hot forming conditions.

Fig. 3

Scheme illustrating the multi-tool rotary compression process for a hollow ball according to the method proposed by Tomczak et al. [2]

An interesting solution is the production of a single hollow ball by multi-operation sheet metal forming. A schematic design of this process is shown in Fig. 4. Interestingly, this method is one of the oldest as it dates back to the early twentieth century [22]. One may, therefore, wonder why the method has not been applied on a wide scale and numerous studies are still being conducted to develop new forming methods for hollow balls. That can be explained by the fact that a hollow ball is difficult to manufacture, and its production requires performing several, if not several dozen operations. What is more, every operation must be performed using a separate set of tools, which considerably increases unit costs per product. Now wonder that alternative techniques were proposed over the next decades. Among these forming techniques it is worth mentioning that wherein a hollow ball is produced by deep drawing two ball halves first and then jo ining them via different joining methods.

Fig. 4

Scheme illustrating the multi-operation deep drawing process for a hollow ball

One example of the above technique is a method shown schematically in Fig. 5. This method consists of drawing (extruding) two spherical caps from metal sheet; in practice, it is limited to drawing parts that can be made in one operation. Following the smoothing of spherical cap edges, a permanent joint is made between them by welding. This can be done using two solutions. One solution is to put a connecting ring between the spherical caps [14]. The other is to apply direct thermal welding on the surfaces of the spherical cap edges [15]. Braginsky and Dashevsky [16] proposed that the deep drawn spherical caps were joined by friction bonding. Irrespective of the solution employed, thermal energy and clamping force are required to join the spherical caps. Also, the bonding joint always requires additional finishing.

Fig. 5

Scheme of producing a closed hollow ball from two extruded drawpieces bonded by welding (resistance or friction welding)

The production of hollow balls with given dimensions is no easy task. Like in the case of forming thin-walled balls from tubes, buckling is the most frequent failure mode in this process. This problem was thoroughly investigated and described by Alhussainy et al. [17] with respect to tube upsetting. Rots et al. [18] approached this problem in very broad terms. The problem of buckling in hollow ball forging processes was also described by Samołyk and Winiarski [7]. Generally, the problem can be solved by process design modification. Examples of such solutions are the aforementioned forming methods, particularly multi-operation methods.

An interesting technological solution for hollow balls is a forging process performed with the use of flexible inserts. This technique was proposed by Samołyk et al. [19]. A general scheme of this concept is shown in Fig. 6. A cast core is inserted into a thin-walled billet. For the cold forging process, the core can be made from a low-melting alloy [20]. During the forming process, both the workpiece and the core are deformed in such a way that it has a positive effect on process stability. In a previous study [19] it was proposed that the core had a specifically defined shape and was put inside the billet. A different solution for producing the core is proposed on the Russian Patents website [21]. According to this solution, a bar (or mandrel) is additionally inserted into the workpiece. After that, the space between the bar and the internal wall of the workpiece is filled with liquid metal. The solution proposed on [21] also recommends that the cast core can be used for compressing the workpiece in order to obtain a semi-closed hollow ball. A variation of this method is shown schematically in Fig. 7. It is also recommended that this process be performed with a mandrel (or rod) inserted inside the workpiece before letting liquid metal flow into the free space. Unfortunately, the literature review reveals that the solution proposed on the Russian Patents website [21] has remained only a concept.

Fig. 6

Scheme illustrating the manufacturing of a hollow ball using an additional tool (core) which is deformed during the forging process

Fig. 7

Modified method for producing a hollow ball from thin-walled extruded drawpiece with the use of a cast core made from workable alloy

3 Research method

The scientific objective of this study is to obtain complete data about the cold forging process for producing a hollow ball from a tube. As a result, it will be possible to determine the range of billet dimensions ensuring a correctly shaped forging, as well as stable forming conditions. The diameter of a forged ball is maintained constant at 30 mm. Tube dimensions (height, diameter and wall thickness) are variable. The study is performed in two stages. The first stage is a comprehensive numerical analysis that covers all possible cases of the forging process under study. The other stage involves experimental testing. The scope of these studies is limited to selected cases. The primary objective of experimental testing is to verify and validate the numerical model. It is worth mentioning that similar studies were successfully conducted and their results were reported in previous works [7, 19]. Moreover, results presented in this paper are a continuation of previous studies. In this way, they complement and extend the state of the art in both scientific and utilitarian terms.

3.1 FEM model

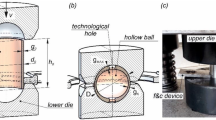
Numerical analysis was performed using the Deform-2D program which is based on the finite element method. The simulation was performed under axisymmetric deformation conditions. The billet material was described by a rigid-plastic model of material. On the other hand, the tools (two halves of the dies) were modelled as rigid objects. Since the process was performed under cold forging conditions, thermal calculations were omitted in the modelling. These assumptions reflect real conditions, and the degree of simplification helps significantly enhance the efficiency of calculations, while not affecting result quality at the same time. The applied geometrical model of the analysed forging process is shown in Fig. 8.

Fig. 8

Geometrical model of the analysed forging process for a hollow ball, as well as key information about the process: a) start of the simulation, b) end of the simulation

The top die moves with a constant speed of v = 1.67 mm/s. This speed is achieved by a slide of the Instron testing machine on which the experiments were conducted. The bottom die, on the other hand, is stationary. Contact conditions between the die cavity and the surface of the workpiece were described by the Coulomb friction model, for which the friction coefficient was set at μ = 0.24. The coefficient value complies with the lubrication conditions that were ensured in experimental testing. A method for determining this value (upsetting of ring samples) was discussed in more detail in previous studies [7, 19].

In the simulation, the tube was assigned the properties of AlMgSi0.5 aluminium alloy in an annealed state (EN Al6060-O, in compliance with EN 573–1: 2004). Due to the assumption of axisymmetric deformation, the tube could be reduced to a half of the axial section. The area of this cross-section was divided into at least 2,000 triangular elements. The number of elements used in the simulation varied due to remeshing. The material model was described by the following constitutive equation [19]:

$$\sigma_{p} = 949 \cdot \left( {0.0001 + \varepsilon } \right)^{0.248} \cdot \exp \left( { - 0.5209\varepsilon } \right) \cdot \dot{\varepsilon }^{0.1358}$$

(1)

where: σ_p—yield stress, ε—effective strain, ε^•—strain rate. The model was selected based on the results of previous studies. The above equation was established with the use of a self-made computer programme for plastometric test result analysis. The process under study was conducted by frictionless upsetting of cylindrical test samples using a laboratory testing machine.

The authors would like to emphasize that 3D FEM modelling of the analysed forging process for a hollow ball does not ensure a significant improvement in the quality of results obtained. However, it significantly increases calculation time and input data preparation. Therefore, the authors decided to use the simplest and most reliable modelling method that can be successfully used to analyse as many cases as possible in short time. An important advantage of the proposed model is the ease of obtaining unambiguous results for further processing and analysis. On the other hand, the data input operation can be automated.

3.2 Interpretation of FEM results

It is generally accepted that the finite element method is one of the most accurate methods of theoretical analysis. However, it has some drawbacks, too. First of all, it is only a mathematical method, the accuracy of which depends on many factors, and results obtained do not always reflect reality accurately. Fortunately, however, the mapping error can be estimated and results can be interpreted correctly by using, for example, special hypotheses.

The analysed forging process for a hollow ball may be disturbed by the occurrence of several failure modes such as underfill, overfill and material buckling [7]. The FEM model used for simulating the cases under analysis is not able to reproduce two key failure modes in the ball forging process, i.e. buckling and overfill leading to the formation of thin flash, fold or sometimes even overlap. Nevertheless, a thorough analysis of numerical results and their comparison with experimental findings made it possible to formulate hypotheses that allow accurate identification of cases wherein the probability of the above failure modes is sufficiently high.

The first hypothesis is a basis for formulating a method for numerical result interpretation, which makes it possible to assess the probability of buckling in the forging process under analysis. A diagram illustrating the proposed method is shown in Fig. 9. Under this method, it is assumed that the onset of buckling can be identified by observing changes in the shape of the outer contour of the forging. To that end, points p are defined on the ball contour; these points are arranged according to a predetermined constant scale Δy, with a point p₁ located halfway up the billet height (in the parting plane). This point is also a reference point because it marks the locus where the diameter of the ball should—theoretically—always be the largest. In the simulation, a radial coordinate x_n of all points is measured at every calculation step t_j, and then a difference Δx_n relative to the p₁ reference point is determined. Should the difference be positive for all points, it means that the outer contour of the forged ball is convex, and thus no buckling will occur. In an opposite case, i.e. the difference has a negative value for at least several points, some part of the ball contour becomes concave.

Fig. 9

Scheme illustrating the proposed method for FEM results interpretation in terms of assessment of material buckling probability in the forging process for a hollow ball; description in the text

Therefore, it is possible to formulate a hypothesis stating that if the external contour of the workpiece remains convex during the entire simulation, then there is zero probability of buckling occurrence. At this point one should ask why theoretical analysis poses any problems at all. Specifically, in the FEM simulation (performed according to the model described above), toward the end of the forming process, the outer contour of the forging always becomes convex for almost all analysed cases, even in those cases when buckling should actually occur. As a result, theoretical results are false. This means that the FEM simulation does not model this failure mode accurately and thus one cannot rely on final simulation results. The use of the proposed method for result interpretation, which is based on in-depth analysis of the entire FEM modelling history, makes it possible to accurately predict cases of the forging process in which the probability of buckling is greater than zero. It is also proposed that a matrix of so-called buckling signals be created. This matrix is a two-dimensional table showing points on the outline circumference and computation moments (which is the same as “signal” duration) where a negative difference Δx_n in relation to the p₁ reference point is obtained. The greater the number of such “signals” in the matrix, the greater the probability of buckling becomes. Finally, it must be emphasized that even the use of a more accurate 3D FEM model does not reproduce this defect in all simulated cases, and, at the same time, such model makes it difficult to collect data necessary for result interpretation. Hence the rationale for using a “simpler” FEM model.

Experimental results confirmed the validity of this hypothesis and the usefulness of the proposed method for FEM result interpretation. Figure 10 shows the photograph of an experimental forged ball formed from a billet with a diameter of 28 mm, a length of 27 mm, and a wall thickness of 2 mm. The FEM simulation for this particular case demonstrates that the final shape of the ball was correct (convex), which did not agree with the actual results. On the other hand, the application of the proposed result interpretation method shows that, between 15 and 68% completion of the forging process, a 7 mm wide central part of the ball contour becomes a concave line. The degree of concavity continues to increase until 48% completion of the forging process, reaching a value of Δx = 0.014 mm; after that, the concavity disappears, i.e. the contour becomes a convex line. Having created a signal matrix, the authors concluded that, for this case, the signal of buckling occurrence was very strong. A dozen or so such cases were observed in the theoretical analysis. Selected cases were subjected to experimental verification, and the experimental results confirmed that the proposed method for FEM results interpretation was suitable.

Fig. 10

Buckling of a ball forged from a billet with the dimensions of d₀ = 28 mm, h₀ = 27 mm, g₀ = 2 mm; description in the text

The second hypothesis concerns the prediction of overfill leading to the formation of thin flash (or fold) in the parting plane (in other words, along the “equator” of the forged ball). This phenomenon results from undesired flow of material into the space between the adjoining end faces of the die. A diagram that illustrates both this phenomenon and the method for result interpretation based on the second hypothesis is shown in Fig. 11. In this case, the problem is that the FEM simulation shows no such failure modes (i.e. small folds or thin flash). Initially, the material flows beyond the contour of the die cavity; after that, a forging free from the aforementioned defects on its outer surface is formed. Still, the experimental results show that the formation of fold or even thin flash is inevitable in such cases. A photograph of a forged part with such defect is shown in Fig. 12.

Fig. 11

Scheme illustrating the proposed method for FEM results interpretation in terms of overfill, overlap and flash formation probability assessment in the analysed forging process for a hollow ball; description in the text

Fig. 12

Hollow ball formed from a tube with the dimensions of d₀ = 28.5 mm, h₀ = 26 mm, g₀ = 2 mm; the ball has a small fold due to overfill; description in the text

Therefore, for the accurate interpretation of FEM results, a hypothesis was formulated: should, during the simulation, the conventional diameter D_E of the forging (measured in the “equatorial” plane) exceed the D_B value (i.e. the target diameter of the forged ball), then, even if in further calculations the D_E diameter will decrease to the expected value, the probability of overlap formation is sufficiently high. This interpretation method therefore consists of monitoring said forged ball diameter D_E. If this parameter exceeds the conventional value (here, the target ball diameter D_B = 30 mm; Fig. 11), the formation of overlap is very likely. The earlier this value is reached, the higher the probability of overfill causing overlap formation becomes. Figure 12 shows the forged part made from a billet with the dimensions of d₀ = 28.5 mm, h₀ = 26 mm and g₀ = 2 mm. In the simulation, the signal indicating the exceeding of the D_B value by the D_E diameter was obtained already at 86% completion of the forging process. The maximum diameter D_E obtained in the simulation is only 30.1 mm. A question arises whether this value is sufficiently high to predict the probability of defect formation. A detailed analysis of the numerical results for several different cases and their experimental verification have demonstrated that the extent of exceeding this diameter value is irrelevant. It is important that this value has been exceeded at all. What is far more important is the moment when this value is exceeded. The earlier it happens, the greater the probability of defect formation becomes, which means that the actual degree of overfill and thus the size of defect will be greater too. The experimental results show that, in extreme cases when—according to the numerical results—the signal of overfill should have been very strong, a thin ring of pressed flash-resembling material is formed, instead of the fold shown in Fig. 12.

3.3 Experimental validation of the FEM model

The FEM model was validated experimentally under laboratory conditions at the Lublin University of Technology. A device consisting of two halves of the dies made in accordance with Fig. 8 was used. Tubes were mounted and then upset forged in this device. Examples of tubes and forged parts are shown in Fig. 13. The upsetting operation was performed on a testing machine from Instron. The machine provides a maximum load of 1 MN and a constant tool speed of 1.67 mm/s. The testing machine was equipped with standard software for tool motion control, as well as displacement, speed and load measurement.

Fig. 13

Examples of billets and forged balls with different manufacturing quality (i.e. with and without defects)

Selected cases of the forging process for hollow balls were tested experimentally. The selection was based on the numerical results. The selected cases consisted of those in which the forged part had the correct shape and those wherein two failure modes occurred, i.e. buckling and overfill.

Regarding the first group, two parameters were compared: ball shape and forming force. It has been found that all forged parts show high qualitative agreement in terms of their shape. The outer surface of the forgings is smooth and regular, which results from correct filling of the die impression. Differences between the FEM and experimental results can only be observed in the region of central holes. The real holes are slightly larger than the holes obtained in the simulation, and sometimes their edges are slightly flattened. The diameter of the experimental holes is on average approx. 1 mm larger, which amounts to a relative difference of 8%. Figure 14 shows the most important dimensions of the axial section of a sample hollow ball forging obtained in experimental test and FEM calculation. A comparison of the numerical and experimental forces is shown in Fig. 15. At the initial stage of the forging process, the experimental force is greater than the numerical force. Over time, the difference becomes less visible, and then—in the midst of the forging process—the real force is lower than the simulated one. The difference is greater for the tube with a lower wall thickness. The observed difference between the numerical and experimental forces predominantly results from the area of the material–die cavity contact surface; the contact surface area changes during the forging process, and the numerical contact surface area differs from the real one. Toward the end of the process, due to closing of the dies, the real force sharply increases and significantly exceeds the calculated FEM value. This increase in force is typical of the die forging process. A detailed analysis of the diagram in Fig. 15 makes it possible to conclude that the FEM and experimental results show satisfactory agreement in qualitative and quantitative terms. This means that the proposed FEM model of the forging process for hollow balls has been validated. Additionally, the differences are related to, among others with the phenomenon of friction.

Fig. 14

Shape and important dimensions of a sample ball forging (forged from a billet with diameter ∅27 mm, wall thickness g₀ = 3 mm and height h₀ = 29 mm) obtained in the experiment and by FEM calculations

Fig. 15

FEM and experimental forming forces for 4 selected cases of forging a ball from a tube with the dimensions of d₀ x h₀ x g₀ (in mm); description in the text

The other group of experimentally tested cases of the forging process poses some problems, because all forged parts have defects. As mentioned in the previous section, these defects are very difficult to model accurately via FEM simulations. Therefore, this stage of experimental testing was aimed at verifying the previously formulated hypotheses that served for the development of two methods for FEM results interpretation. Given that this problem was discussed in the previous section of this paper, let us only summarize that the experimental findings have confirmed that the proposed method for FEM results interpretation is useful and that the formulated hypotheses are true.

4 Recommended forging parameters and failure modes

4.1 Ranges of dimensions for billet and forged part

In this study, a tube was used as a billet for the forging process. Figure 16a shows the shape and dimensions of the tube. The first key boundary parameter is an outside diameter of the billet, d₀, its value ranging from 26.5 mm to 29.5 mm. The maximum diameter must be smaller than the diameter of the finished ball, i.e. the diameter D_B of 30 mm. It should be mentioned that the diameter value was selected based on previous studies in this field. The results were reported in previous works [7, 19].

Fig. 16

Shape and dimensions of tube (a) and forged ball (b), with the dimensions being boundary or resulting parameters

The second boundary parameter is a billet height, h₀. In this study, the billet height ranged from 16 to 29 mm. This parameter is related to the diameter d₀, because a combination of the two parameters affects the forming process for a hollow ball. As a result, a h₀/d₀ ratio was defined, its allowable values ranging from 0.5 to 1.1. By the way, it is worth mentioning that the h₀/d₀ ratio is often used as a key variable for buckling assessment in the tube upsetting process [17].

The third boundary parameter is a billet wall thickness, g₀. In the cases analysed in this study the tube wall thickness ranged from 1.5 mm to 4 mm. This range is optimal relative to the analysed billet diameter and height ranges, as will be explained later in the paper. For the purpose of result analysis, wall thickness was related to tube diameter by means of a d₀/g₀ ratio. This ratio is also widely used in studies investigating the problem of buckling in tube upsetting [17].

During the forging process, the wall thickness of the workpiece changes in a non-uniform manner, hence the forged part has a variable wall thickness. Therefore, for the purpose of result analysis, this parameter was measured at different locations. As shown in Fig. 16, four thickness measurement points were selected, denoted by g₁, …, g₄. They are resulting parameters describing changes in workpiece wall thickness during the forging process.

The forged part has two characteristic holes described by a diameter D_H (Fig. 16b). Since the size of this diameter depends on billet dimensions, it is, therefore, possible to regard the diameter D_H as a parameter describing the forging process under analysis. As a rule, the central holes are expected to be the smallest; this, however, is difficult to achieve with the manufacturing technique in question. The achievement of the minimum value of D_H is only one of the many criteria that must be considered in combination with others. It is worth mentioning that a smaller diameter D_H means a higher height H_B (Fig. 16b), this height, too, being a resulting parameter. In contrast to the hole diameter D_H, the height H_B is easy to measure. Nevertheless, the above two parameters can be considered complementary when analysing results.

Another parameter for describing forged balls is a diameter D_E measured in the parting plane. The value of D_E lower than the nominal ball diameter D_B indicates underfill. Underfill is synonymous to the presence of underforged portion of material in a forging, and it is manifested as the formation of a narrow strip of slightly flattened surface with a width H_F. The dimensions D_E and H_F can be used simultaneously to describe this defect. The authors of the study also recommend using the parameter δ (Fig. 16b) to describe this defect. At this point it is worth mentioning that in a previous study [19], a novel forging method for hollow balls was proposed, wherein a flexible core was used to prevent underfill. The method consists of pushing out the workpiece wall and pressing it to the surface of the die cavity. In effect, the presence of underfill is less problematic (it can partly be reduced by forging process modification) than buckling or overfill (overlap, flash or fold formation). Therefore, in this study, underfill is consciously not considered on the same level as the other two defects.

4.2 FEM results and recommended tube dimensions

Numerical results are given in Fig. 17. This diagram shows the numerical results for the ratios d₀/g₀ and h₀/d₀, i.e. relationships between billet dimensions. Every point in this diagram denotes a specific analysed case of the forging process and, at the same time, describes the numerical results in qualitative terms. The forged parts are correct is they are free of defects (mentioned previously); it is, however, acceptable that the D_E diameter can be smaller than D_B (30 mm) yet not smaller than 29.8 mm. It was assumed that the value of δ (Fig. 16b) lower than 0.1 mm would indicate a defective forged part. For the extreme cases, the parameter δ is as high as 1 mm.

Fig. 17

Diagram showing the numerical results, where: d₀ – billet diameter, h₀ – billet height, g₀ – billet wall thickness, D_E – forged ball diameter as measured in the parting plane (see Fig. 16)

The diagram in Fig. 17 also shows the cases of the analysed forging process in which forged parts are defective. The forged parts were classified as defective based on the previously described novel methods for results interpretation. An analysis of the FEM results has revealed that the following undesired defects may occur: buckling; buckling with simultaneous overfill (local irregular overlap is formed in the parting plane); or overfill leading to the formation of thin flash or fold (regularly over the entire circumference of the forging). Also, the diagram shows the cases of the forging process in which—based on the result analysis—the occurrence of overfill leading to fold formation is quite probable; nevertheless, forgings with correct shape will be obtained, too. This is due to the fact that a very weak signal of this defect was detected when analysing the numerical results. The experimental ball does have the above-mentioned fold, but the defect is rather indistinct. Assuming that the forgings will undergo further finishing, e.g. by turning, their external shape can be corrected without any problems.

The numerical results were used to develop design guidelines for optimal billet dimensions ensuring defect-free forged parts. The recommended procedure is as follows. First, a wall thickness of the billet, g_0, must be determined. Next, an outside diameter of the billet, d₀, must be calculated and, finally, a billet height, h₀, must be determined. These recommendations are plotted in Figs. 18 and 19. On their basis, Eqs. (2) and (3) were established, ensuring optimal and unequivocal description of the relationship between tube dimensions, as evidenced by the high values of the coefficient of determination. However, the standard deviation (given in the diagrams) can be treated as a tolerance field for the value calculated from these equations. As a result, it is easier to determine billet dimensions with an accuracy reflecting the technological capabilities of a given machine park.

$$\frac{{d_{0} }}{{g_{0} }} = - 0.708 \cdot g_{0}^{3} + 7.742 \cdot g_{0}^{2} - 30.31 \cdot g_{0} + 49.64$$

(2)

$$\frac{{h_{0} }}{{d_{0} }} = - 0.0142 \cdot d_{0}^{2} + 0.6385 \cdot d_{0} - 5.8947$$

(3)

Fig. 18

Recommended ratio between billet dimensions d₀ and g₀ which ensures the production of a defect-free forged ball, where: R² – coefficient of determination, σ—standard deviation; description in the text

Fig. 19

Recommended ratio between billet dimensions h₀ and d₀ which ensures the production of a defect-free forged ball, where: R² – coefficient of determination, σ—standard deviation; description in the text

5 Effect of tube dimensions on selected dimensions of the forged ball

5.1 Wall thickness variations

In the forging process, the tube is compressed by two halves of the dies, which are characterized by a spherical shape of the die cavity. Due to compression, the tube undergoes complex deformation. First of all, it is subjected to axial compression by the axial component of force. At the same time, however, the tube is also reduced by the radial force component. Initially, this component acts only on the tube edge, which is precisely the thickness measurement point g₄ and the location of central hole formation. The shape of the billet changes—the tube becomes a spherical product, whose wall undergoes changes, too. In addition to changes in wall shape, there are also changes in wall thickness, which can be used to quantify obtained results.

Figure 20 shows the history of wall thickness variations for six selected cases. It was assumed that the forged part would be formed from a tube with an initial diameter of d₀ = 28.5 mm and a height of h₀ = 22 mm. The cases under analysis only differed with respect to tube wall thickness, g₀. In the FEM simulation, wall thickness variations were measured at 4 locations, in compliance with the assumptions shown in Fig. 16. After that, the measured wall thicknesses g₁, …, g₄ were compared with the initial wall thickness g₀, and the difference was expressed in percentage terms.

Fig. 20

Variations in forged ball wall thickness, as expressed in percentage terms, for six selected cases of the forging process conducted with different values of billet wall thickness g₀ (other dimensions of the billet: d₀ = 28.5 mm, h₀ = 22 mm – see Fig. 16); description in the text

It can be observed that wall thickness varies during the forging process and that the variations significantly depend on the initial thickness g₀. The thicknesses g₁ and g₂, i.e. those measured closest to the parting plane, increase as the forging process advances. The thin wall undergoes the smallest increase at these points. The increase in thickness is negligible at first, but then it becomes more rapid, ultimately amounting to about 2%. On the other hand, for a thicker wall (e.g. g₀ = 4 mm), the wall thickness increase at these points can be observed from the very beginning of the forging process, the ultimate increase being equal to about 5%. This behaviour pattern results from the fact that the material primarily undergoes upsetting at these measurement points and that the degree of increase significantly depends on the initial wall thickness. The thin wall is less rigid and thus prone more to radial displacement than to local upsetting. Therefore, buckling and overfill are more probable to occur in the forging process for thin-walled forged parts (as shown in Fig. 17).

At the thickness measurement point g₃ (i.e. approx. 2/3 of the billet height), the wall thickness begins to increase considerably right from the very beginning of the forging process, ultimately increasing by about 8%. A different behaviour pattern can be observed at the thickness measurement point g₄. At first, the wall thickness decreases, with the highest decrease observed for the thicker wall. After that, a considerable increase in the wall thickness is observed. The ultimate wall thickness increase amounts to 6–12%, compared to the initial thickness g₀. It must be highlighted that the wall thickness increase observed at this measurement point is higher for the thinner wall than for the thicker one. The behaviour pattern observed at g₄ results from the fact that this region of the workpiece also undergoes deformation. Also, it is in this region where a central hole is formed.

Summing up, the forged hollow ball is characterized by variations in its wall thickness during the forging process, these variations dependent on the region of the forging. Generally, wall thickness of the forged part is always higher than that of the billet material. An analysis of the numerical results (for the cases of the forging process wherein defect-free forged parts are produced) made it possible to establish a relationship between the forged part wall thicknesses g₁ and g₄ and the tube wall thickness g₀. This relationship is illustrated in Fig. 21. The plot can be used to determine the billet thickness that will ensure the production of a forged part with the required wall thickness. These relationships can also be expressed via Eqs. (4) and (5), and the calculated value can be changed within a tolerance range determined by the standard deviation σ which is 0.020 mm and 0.104 mm, respectively.

$$g_{0} = 1.0151 \cdot g_{1}^{0.9555}$$

(4)

$$g_{0} = 0.9082 \cdot g_{4}^{1.0078}$$

(5)

Fig. 21

Relationship between tube wall thickness g₀ and forged ball wall thicknesses g₁ and g₄ measured at two characteristic points (see Fig. 16)

5.2 Central hole diameter and forged ball height

In the analysed forging process for a hollow ball, a central hole is formed, its size depending on the initial dimensions of the billet, particularly the diameter d₀ and the height h₀. Figure 22 shows the results of central hole diameter (according to Fig. 16, the diameter D_H is the outside diameter of the central hole) obtained for the cases wherein defect-free forged parts are obtained. An analysis of the results reveals that the billet wall thickness g₀ has an insignificant effect on the central hole size. In fact, it only affects the value of D_H. On the other hand, the h₀/d₀ ratio has a considerable impact on the central hole diameter. This observation is confirmed by plotting the results to a diagram shown in Fig. 23. Additionally, based on the plot, it is possible to establish a relationship between the h₀/d₀ ratio and the central hole size in the forged part. The relationship can be expressed as Eq. (6):

$$D_{H} = 6.311 \cdot \left( {\frac{{h_{0} }}{{d_{0} }}} \right)^{2} - 25.618 \cdot \frac{{h_{0} }}{{d_{0} }} + 37.279$$

(6)

Fig. 22

Central hole diameter D_H (see Fig. 16b) in defect-free forged balls (for the forging process conducted with different billet dimensions) as a function of billet wall thickness g_0; description in the text

The above relationship (6) allows us to determine the predicted outside diameter of the central hole in the forged hollow ball, provided that the forging process is conducted using a billet with the recommended dimensions, which—in fact—ensures a defect-free forged part.

The measurement of central hole outside diameter may pose some problems. It is much easier to measure a forged ball height, H_B (as shown in Fig. 16b). Given that the measurement points for ball height are the same as those for the diameter D_H, the dimension H_B can be treated as an alternative way of discussing results in terms of the relationship between billet dimensions and central hole formation. It can be observed that the greater the height of the forged part is, the smaller the central hole becomes.

Figure 24 shows the plot illustrating the relationship between the h₀/d₀ ratio and the height H_B obtained for the cases of the forging process wherein defect-free balls are produced. This plot is an alternative to that shown in Fig. 23 and can be interpreted in an identical way. Like previously, it is possible to establish an equation describing forged part height, which is expressed as (7):

$$H_{B} = - 16.870 \cdot \left( {\frac{{h_{0} }}{{d_{0} }}} \right)^{2} + 42.514 \cdot \frac{{h_{0} }}{{d_{0} }} - 1.679$$

(7)

Fig. 23

Feasible central hole diameter D_H of a defect-free forged ball depending on the recommended billet dimensions h₀ and d₀

Fig. 24

Feasible height H_B of a defect-free forged ball depending on the recommended billet dimensions h₀ and d₀

6 Conclusions

This study investigated the die forging process for producing a hollow ball with an outside diameter D_B of 30 mm from a tube. This process requires the use of a tube with specified dimensions. The tube is described by ratios d₀/g₀ and h₀/d₀, and the allowable ranges of these ratios are strictly determined too. It has been shown that unsuitable tube dimensions lead to the formation of one or more defects in the forged part, which can be regarded as failure modes of this forging process. In this study, the forged part diameter D_B was assumed to be constant. Nevertheless, by using the recommended ratios and their relative values, the results obtained in this study can be successfully implemented to forge balls having a diameter other than 30 mm. It must be emphasized that the analysed range of billet dimensions is far from being exhaustive. The use of a tube with a wall thickness equal to or smaller than 1 mm does not produce a forged part with satisfactory dimensions. In contrast, the use of a tube with a thickness above 4.5 mm makes it possible to produce a defect-free ball; the realisation of this forging process poses, however, some problems, as higher wall thickness significantly limits the selection of other billet dimensions due to the specified maximum volume of the forged ball. From a certain point on, the ball being forged begins to become solid.

The results of this study lead to the following conclusions:

• the analysed forging process for a hollow ball poses some problems and may be disturbed by the occurrence of one or more failure modes, such as buckling, overfill causing thin flash formation, or underfill leading to the production of a ball with a smaller diameter than required as measured in the parting plane;

• the numerical results obtained with the use of a relatively simple FEM model in combination with the proposed methods for buckling and overfill probability assessment provide valuable data that can serve for comprehensive analysis of the forging process under study, which helps reduce research time and costs;

• the failure modes observed in the analysed forging process for hollow balls primarily depend on the h₀/d₀ ratio and—to a lesser degree—on the initial billet wall thickness g₀;

• one of the design-related objectives is to reduce central hole diameter; unfortunately, however, the hole is an indispensable element of the forged part, with its size depending on the h₀/d₀ ratio; since the occurrence of a failure mode in the process depends on this ratio too, it is, therefore, difficult to effectively reduce the central hole diameter.