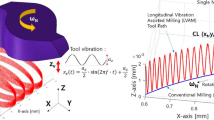
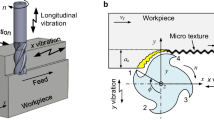
Abstract
To meet the modern demands for lightweight construction and energy efficiency, hard-to-machine materials such as ceramics, superalloys, and fiber-reinforced plastics are being used progressively. These materials can only be machined with great effort using conventional machining processes due to the high cutting forces, poor surface qualities, and the associated tool wear. Vibration-assisted machining has already proven to be an adequate solution in order to achieve extended tool lives, better surface qualities, and reduced cutting forces. This paper presents an analytical force model for longitudinal-torsional vibration-assisted milling (LT-VAM), which can predict cutting forces under intermittent and non-intermittent cutting conditions. Under intermittent cutting conditions, the relative contact ratio between the rake face and the sliding chip is utilized for modelling the shearing forces. Ploughing forces and shearing forces under non-intermittent cutting conditions are calculated by using an extended macroscopic friction reduction model, which can predict the reduced frictional forces under parallel and perpendicular vibration superimposition. The force model was implemented in MATLAB and can predict cutting forces without using any experimental vibration-assisted milling (VAM) data input.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Ti-6Al-4V, also called grade 5 titanium, is a heat-treatable α+β titanium alloy featuring biocompatibility, high strength to weight ratio, and high corrosion resistance. As a result, Ti-6Al-4V is used extensively in the aerospace industry, in marine applications and medical implants. In the aerospace industry, up to 95% of the raw part mass gets removed during machining operations resulting in high resource consumption and emissions during manufacturing [1].
In addition, the low thermal conductivity and high chemical reactivity with many cutting tool materials make titanium and its alloys difficult to machine materials [2]. Machining titanium is characterized by high tool-chip interface temperatures due to its high strength and low thermal conductivity, which generates high temperatures during plastic deformation. In addition, the low Young’s modulus of elasticity causes deflection and rubbing problems during machining, which further amplifies tool wear [3].
The term “vibration-assisted machining” refers to machining where an additional vibration is superimposed on the conventional kinematics of the cutting process. Vibration-assisted machining has been the subject of scientific investigation since the 1950s and is currently used to overcome the technical limitations of conventional machining [4, 5]. Figure 1 shows different types of vibration-assisted machining, which can be distinguished according to tangential, feed and radial vibration assistance (VA) depending on the resulting tooltip trajectory. When applied tangentially to the cutting direction, VA can cause the tool’s rake face to separate from the chip, resulting in “intermittent cutting.” If the applied VA is in the feed direction, chip thickness will vary during cutting, which results in intermittent cutting at low feed rates [6, 7]. VA in the radial direction can cause orthogonal cutting processes to behave like oblique cutting [8] and vibrations in different directions can be combined to create elliptical and 3-D paths.
Types of vibration-assisted machining [9]
Rinck et al. [9] studied the effects of longitudinal (vibration normal to the cutting direction) and longitudinal-torsional (vibration normal and in cutting direction) VAM under intermittent and non-intermittent cutting conditions when milling Ti-6Al-4V. Peripheral milling experiments have shown that increasing vibration amplitudes result in lower cutting forces and better surface finishes. During slotting, higher amplitudes produce harder surfaces with increased compressive residual stresses. The primary cutting edges of the tools used during VAM show 20% less wear, but minor cutting-edge wear is increased. Overall, LT-VAM performs better than longitudinal VAM. Gao and Altintas [10] modeled the chatter stability of synchronized elliptical VAM (vibrations normal to the surface and in cutting direction). Vibrations normal to the surface resulted in dynamic chip thickness and thus in forced vibrations. At low cutting speeds, vibrations in cutting direction caused the periodic separation of tool and chip, resulting in intermittent contact and eliminating chatter vibrations. At higher cutting speeds, intermittent contact no longer took place and the effects of vibration assistance diminished. In the case of Al 7050, the minimum stable depth of cut (DoC) increased from 1.2 to 2.0 mm. Similarly, during half immersion down milling of AISI 1045 steel, the minimum stable DoC increased from 0.2 mm to 0.35 mm. Most of the research done in the field of vibration assisted machining only concentrates on intermittent cutting conditions, where the influence of the VA is more obvious. However, research conducted by Suárez et al. [11] and Rinck et al. [9], presented the existence of a phase where the tool-chip contact is not interrupted, but a force reduction due to the vibration assistance is still evident.
Numerous methods exist for modeling cutting forces during machining processes. According to Arrazola et al. [12], these can be divided into artificial intelligence-based, empirical, analytical, and numerical approaches. Analytical models describe the physical relations between the input and output parameters, requiring no experimental calibration and allowing simpler expansion of the models. Merchant [13] modeled the cutting forces in 2-dimensional orthogonal cutting, where the cutting force is a function of the shear stress of the material (τs), the shear angle (Φ), the rake angle (αr) and the friction angle (βa) (see Fig. 5). In addition, Merchant [14] proposed a model to predict the shear angle (Φ), assuming the shearing of the material will happen at the minimum cutting power. Based on his work, numerous other analytical models were developed. These models were able to calculate cutting forces, temperatures, stresses, and strains based on material, workpiece and tool properties [15,16,17,18].
In the case of 3-dimensional oblique cutting, the cutting speed vector stands with the angle \(\gamma\) to the plane normal to the cutting edge of the tool (plane x1z1 in Fig. 6). The inclined cutting edge introduces forces in all 3 cartesian directions, which can be properly determined by knowing the 5 oblique cutting angles, namely the normal (Φn) and oblique (Φi) angle of the shear velocity (Vs), the normal (θn) and oblique (θi) angle of the resulting shearing force (FRes,s), and the chip flow angle (η) (see Fig. 6). Shamoto and Altıntas [19] developed a model to predict the 5 oblique cutting parameters by using the tool geometry and the friction angle (βa), allowing the prediction of shearing forces in oblique cutting operations.
The prediction of cutting forces by analytical or numerical models in vibration-assisted machining has been the subject of several research projects [20]. Most analytical models predict the cutting forces by multiplying the cutting forces during conventional machining with the relative contact ratio between tool and workpiece [21, 22]. In the case of vibration-assisted micro-milling, Ding et al. [6] modeled the cutting forces by calculating the relative contact ratio and the chip thickness resulting from the previous tool passes. However, this model only produces reliable results for micro-milling, where low feed rates are used. Shamoto et al. [8] developed a model which can predict the cutting forces in a 3D elliptical cutting process using the thin shear plane model. They assumed a constant shear direction and friction angle when the tool and workpiece were in contact. The shear angle calculation was applied either by using the minimum energy principle of Merchant [14] or by using the maximum shear stress principle of Krystoff [23]. Verma et al. [24] developed a cutting force model for axial ultrasonic assisted milling where the effect of acoustic softening of the workpiece material is considered with the help of a modified Johnson-Cook model. Arefin et al. [25] developed an analytical model that can predict the shear angle during vibration-assisted orthogonal cutting. The proposed model uses an energy-based approach that calculates the cutting force during elastic deformation, plastic deformation, and the elastic recovery steps in a vibration cycle to predict the equivalent shear angle.
In addition, there are numerical models in the literature that represent the chip formation process in VAM using the FEM [26]. The simulations are mostly limited to the two-dimensional orthogonal cut, where a vibration is superimposed on the tool cutting edge. Patil et al. [27] developed a numerical model for turning Ti 6Al 4V with a vibration superposition in the cutting direction. For the modeling, they use a combined Lagrangian-Euler approach with a Johnson-Cook material model. The friction between the cutting edge and the outgoing chip is assumed to be constant. A simulative parameter study was conducted to determine the influence of conventional process parameters and vibration parameters on the cutting force components. As the cutting speed increases from 10 to 30 m/min, a continuous cutting force reduction of 37 to 31 % is shown. According to the model, an increasing frequency and an increasing amplitude cause a higher cutting force reduction, which was attributed by the authors to a lower engagement time between the tool and the workpiece. A comparison of the simulation results with experimental investigations shows a good qualitative agreement of the results.
In the present work, a novel cutting force model for VAM is introduced that can calculate cutting forces under intermittent cutting and non-intermittent cutting conditions. It combines a model for friction reduction under the presence of ultrasonic vibrations with an analytical cutting force model. In the following section, the kinematics of a longitudinal-torsional vibration-assisted helical end mill will be modeled, the theory of macroscopic friction reduction will be explained, extended, and applied to model the cutting forces under orthogonal and oblique cutting conditions. Afterwards, the experimental settings and the used ultrasonic actuator will be presented. The model verification and the discussion of the results is explained in Sect. 4, followed by the conclusions in Sect. 5.
2 Model development
In this chapter, a new force model is discussed which can predict the cutting forces under longitudinal and longitudinal-torsional vibration superposition. The first section is for modeling the kinematics of a longitudinal-torsional vibration superimposition to calculate the relative contact time between the rake face of the cutting tool and the chip. Afterwards, the macroscopic friction reduction model of Storck et al. [28] will be extended for the case of simultaneous parallel and perpendicular vibration assistance. In the final section, the modeled relative contact ratio and the macroscopic friction coefficient is used to extend a force model for VAM.
2.1 Relative contact ratio between tool and workpiece during LT-VAM
In VAM, the effective movement of the cutting edge is modified by the vibration superimposition. Due to the longitudinal vibrations, each point of the milling tool experiences an oscillation along the tool axis. In the case of LT-VAM, an additional torsional vibration is superimposed again to act along the cutting direction. The resulting trajectory of the tooltip is given by
with
Al and At are the corresponding longitudinal and torsional vibration amplitudes at the tooltip, r is the radius of the tool, n is the spindle speed, fus is the ultrasonic vibration frequency and \(\Delta \phi\) stands for a possible phase shift difference between the longitudinal and the torsional vibrations.
To interrupt the contact between the tool’s rake face and the chip, the cutting edge must move away from the uncut workpiece. By formulating the trajectory of the cutting edge, the relative engagement during VAM can be calculated. The position of a point on the tools end cutting edge, which moves due to torsional vibration, is given by the following equations:
By differentiating Eq. (3) with respect to time, the resulting torsional vibration velocity vus,t and its maximum value vt,max can be calculated as follows:
The vector of the torsional vibration is parallel to the cutting speed vector (see Fig. 2). In the case of a torsional vibration, the cutting edge loses contact to the cutting zone when the vibration velocity vus,t exceeds the cutting speed. The vector of the longitudinal vibration, on the other hand, is perpendicular to the cutting speed vector. Because of the helix angle λH of the milling tool, the longitudinal vibration can still cause a loss of contact between the tool of the workpiece. The helix angle causes the cutting edge to move away from the cutting zone by the amount Δxus,l in the event of a longitudinal oscillation (see Fig. 2).
Figure 2 visualizes the trigonometric relationship between the helix angle λH, the longitudinal vibration amplitude Al, and the relative displacement between the rake face and the chip due to the longitudinal vibration Δxus,l. The relation can be formulated by the following equation:
The corresponding longitudinal vibration velocity at the cutting speed direction vus,l can be calculated as follows:
Thus, in case of a combined longitudinal and torsional vibration superimposition, the combined vibration velocity vus,lt can be obtained by combining Eqs. (4) and (7):
The maximum vibration velocity in cutting direction, which results from a combined longitudinal-torsional VA (vlt,max), can be determined according to Eq. (9) if the vibration amplitudes, frequency and phase shift are known:
If the value of vlt,max exceeds the cutting speed vc, separation between the chip and the rake face occurs during every vibration cycle. To calculate the contact time tc during a vibration period and the resulting relative engagement time, the times of contact loss and re-entry between the tool and the chip must be known. Figure 3 shows the path covered by the cutting edge in cutting direction with and without vibration superposition, illustrating the relationship between the vibration superimposition and the times of tool exit and re-entry.
Position of the cutting edge in cutting direction [9]
The separation occurs when the cutting edge moves against the cutting direction due to the vibration superposition. Since the cutting edge exits at time tex, the relative speed of the cutting edge is zero since the cutting speed and the vibration speed cancel each other out. Hence, the exit time tex can be calculated according to the following equation:
The re-entry to the cutting zone occurs at time ten, since the displacement due to VA is equal to the distance covered by the cutting motion with the speed vc. The simplified mathematical description is, therefore
where ∆xus.l stands for the displacement due to longitudinal vibration and ∆xus,t for the displacement due to torsional vibration. Once extended with the relevant input parameters, Eq. (11) becomes
which can be numerically approximated to find the entering time ta.
By knowing the exit (tex) and entry times (ten), the contact time (tc) and the relative contact ratio (Tc) during VAM with a helical end mill can be calculated by using the following equation, where tP represents the duration of one oscillation period:
When describing the kinematics and calculating the contact ratio, it must be considered that elastic deformations were neglected. In reality, the chip will first deform elastically and then plastically as the cutting edge enters the workpiece. Similarly, the chip will initially spring back elastically as the cutting edge exits, increasing the tool-workpiece contact and resulting in a higher relative contact time between tool and workpiece.
2.2 Macroscopic friction reduction at LT-VAM
If the vibration velocity in cutting speed direction (see Eq. 9) is lower than the cutting speed, the rake face and the chip will be in constant contact despite the vibration superimposition. However, due to the VA, the cutting speed and the chip flow velocity will be modulated at high frequency, leading to reduced mean friction between the cutting edge and the chip. Storck et al. [28] modeled the macroscopic friction reduction of a sliding body during parallel or perpendicular vibration superposition (see Fig. 4). The modeled reduction is due to the continuous change of the sliding direction and can only consider a parallel or a perpendicular vibration superposition. However, in case of LT-VAM, a combined parallel and perpendicular superposition occur simultaneously at the secondary (chip, rake face) and tertiary (machined surface, flank face) deformation zones. Therefore, in this section, the friction reduction model of Storck et al. [28] will be extended to model the macroscopic friction reduction in case of a combined parallel and perpendicular vibration superposition.
Macroscopic friction reduction under parallel and perpendicular vibration superimposition [28]
When a body slides over a surface with constant velocity vs with a superimposed vibration standing perpendicular to the sliding direction, the resulting velocity vector continuously changes its value and direction due to the current vibration velocity. Since the frictional force is independent of the speed and is always directed against the movement direction, any perpendicular vibration varies the direction of the friction vector, but not the magnitude.
Figure 4 visualizes the resulting friction reduction in case of a parallel or perpendicular vibration superposition. For a perpendicular vibration (index ⊥), even low vibration speeds result in a change of direction and thus a friction reduction as seen in Fig. 4. However, in case of a parallel vibration (index ∥), the vibration velocity must be greater than the sliding velocity to change the movement direction. Therefore, as can be seen in Fig. 4, a vibration in the main movement direction results in a friction reduction if the parallel vibration velocity exceeds the sliding velocity.
The perpendicular vibration velocity v⊥ is calculated by
where v⊥,max stands for the maximum perpendicular vibration velocity and can be calculated by using Eq. 5. The velocity in the main sliding direction v∥ remains constant. However, in case of a superimposed parallel vibration, the velocity in the main sliding direction v∥ no longer has a constant value. The resulting velocity in main sliding direction can be calculated using the equation
where v∥,max stands for the maximum parallel vibration velocity and Δϕ for a possible phase shift between the parallel and the perpendicular vibration. The absolute value of the velocity vector can be calculated according to the following equation:
By knowing the perpendicular and parallel components of the current velocity vector, the direction of the resulting frictional force can be determined at any given time. According to Coulomb’s law of friction, the magnitude of the kinetic friction is only dependent on the normal force FN and the kinetic friction coefficient µ. However, due to the parallel and perpendicular vibrations, the direction of the frictional vector changes continuously, causing a reduced mean frictional force in main sliding direction FF,⊥,∥ over a period T. The mean frictional force in the main movement direction can be calculated as follows:
The quotient within the integral is the ratio between the speed of the body in the main sliding direction and the overall speed of the body. By multiplying this quotient with the friction coefficient and the normal force, the frictional force acting on the main sliding direction can be found. After determining the mean frictional force, the friction reduction coefficient μus,⊥,∥ can be calculated by the following equation:
By using Eq. (18), it is now possible to calculate the macroscopic friction reduction coefficient in the sliding direction during a superimposed perpendicular and parallel vibration. In case of longitudinal-torsional VAM, Eq. (18) can be used to calculate the resulting friction reduction in the secondary and tertiary deformation zones.
2.3 Modelling of cutting forces in LT-VAM
In the following subsections, a new force model will be developed for vibration-assisted orthogonal and oblique cutting, which can be used to determine the cutting forces during longitudinal-torsional VAM. Both the orthogonal and oblique models start with the distinction if the vibration assistance results in intermittent cutting or non-intermittent cutting. In case of intermittent cutting, the reduced shearing forces will be modeled by using the relative contact ratio between the tool and the chip (Tc). For non-intermittent cutting, the reduced shearing forces will be modeled by utilizing the macroscopic friction reduction. For both cases, the reduced ploughing forces will be modeled by using macroscopic friction reduction, since the longitudinal-torsional vibration assistance does not result in separation of the clearance face and the machined workpiece during peripheral milling.
2.3.1 Modeling of cutting forces in orthogonal cutting
Due to simple, two-dimensional mechanics, the force model is first explained using the orthogonal cut. The force components in orthogonal cutting are calculated based on the geometric relationships between the rake angle αr, the shear angle Φs, and the friction angle βa. The friction angle is determined by the friction coefficient acting between the chip and the rake face of the tool, as described in Altintaş and Lee [29]. In Fig. 5, the vibration velocities resulting from longitudinal-torsional vibration superposition are illustrated on the right-hand side. The torsional component vus,t acts parallel to the cutting direction and the longitudinal component vus,l acts perpendicular to it.
If the maximum combined vibration velocity in cutting direction (see Eq. 9) is lower than the cutting speed, there will be no tool-workpiece separation due to the VA. However, the friction coefficient between the chip and the rake face will be reduced on a macroscopic scale (see Sect. 2.2). The lower average friction in the chip flow direction will allow chips to slide easier, reducing the shear angle and forming thinner chips with a higher chip flow velocity when compared to those in conventional cutting. The resulting forces and angles due to the VA are visualized in Fig. 5.
To model the macroscopic force reduction between the chip and the rake face, the chip flow velocity must first be determined. Assuming that the width of the deformed chip does not change, the chip flow velocity in vibration assisted machining vus,ch can be determined as a function of the cutting speed vc, the maximum torsional vibration component vus,t,max (see Eq. 5) and the chip thickness ratio rus,c:
Using the geometric relationships shown in Fig. 5, the chip compression ratio under VA rus,c can be expressed as a function of the shear angle Φus,s and the rake angle of the tool αr:
The shear angle during orthogonal cutting can be determined by using the theory of Krystoff [23]. The theory assumes that the shearing will happen in the plane where the shear stress is maximal, which occurs when the angle between the resultant force and the shear plane is 45°. Accordingly, the shear angle under VA Φus,s is calculated as follows:
Using the friction reduction coefficient μ⊥,∥,ch at the rake face and the conventional friction angle βa, the friction angle under VA βus,a can be calculated:
The average friction reduction coefficient μ⊥,∥,ch between the rake face and the chip is calculated by combining Eqs. 18 and 19, since the chip flow is the main sliding direction and longitudinal vibrations stand perpendicular to it. Thus, the macroscopic friction reduction at the rake face resulting from a longitudinal-torsional VA can be calculated as follows:
It must be considered that the chip flow velocity increases due to the lower friction between the rake face and the chip. However, an increase in chip flow velocity simultaneously leads to a lower friction reduction. Therefore, Eqs. (19), (20), (21), (22) and (23) must be calculated iteratively until the chip thickness ratio converges.
By knowing the vibration-assisted shear and the friction angles, vibration-assisted specific cutting pressures in tangential (Kus,tc) and feed (Kus,fc) directions can be determined for orthogonal cutting with
where τs is the shear yield stress of the respective material. To calculate the resulting cutting forces, the reduced friction between the flank face and the machined surface must be considered. The macroscopic friction reduction coefficient μ⊥,∥,e at the clearance face is calculated with the help of the cutting speed, which is modulated by the torsional vibration component and the longitudinal vibration assistance that stands perpendicular to it:
VA edge coefficients in tangential (Kus,te) and feed (Kus,fe) directions are obtained by multiplying the friction reduction coefficient with the conventional edge coefficients (Kte, Kfe), while the conventional edge coefficients can be determined according to Budak et al. [30]. Thus, the cutting forces under VA-assisted orthogonal cutting can be calculated as follows:
where b stands for the cutting width and h stands for the uncut chip thickness (see Fig. 6). If the maximum combined vibration velocity in cutting direction (see Eq. 9) exceeds the cutting speed, the chip and the rake face separate in every vibration cycle. Since the tool and workpiece are not in contact, shearing of the material does not occur and the shearing forces diminish. When the rake face meets the chip, the chip formation process resumes. Since the cutting force due to shearing is mostly independent of the cutting speed, it is assumed that the cutting forces during the contact phase are equal to those in conventional cutting. Therefore, vibration-assisted specific cutting coefficients are obtained by multiplying the contact ratio Tc with the conventional specific cutting pressures. The flank of the tool is in constant contact with the machined workpiece surface despite the intermittent cutting conditions at the rake face. The vibration-assisted edge coefficients can therefore be determined in an analogue way as without interruption of the cut (see Eqs. 26, 27 and 28). The resulting cutting force components during vibration assisted orthogonal cutting under intermittent cutting conditions are finally calculated as follows:
VA oblique cutting according to Altintas [31]
It must be noted here that this model does not consider elastic recovery of the chip during each vibration cycle. Due to elastic recovery, the contact time between the tool and the chip would be bigger in reality. Additionally, the model does not account for tool wear and uses the simplification of a uniform sliding contact between the rake face and the chip.
2.3.2 Modeling of cutting forces in oblique cutting
The simple, two-dimensional model of orthogonal cutting can be extended by inclining the cutting tool, causing force components to exist in all 3 Cartesian coordinates. Due to this fact, milling with an end mill with a helix angle greater than zero (λH > 0) results in a three-dimensional shearing force vector \({F}_{Res,s}\). Figure 6 illustrates the oblique cutting geometry with its forces and angles together with the respective longitudinal and torsional vibrations.
Like the case in orthogonal cutting, if the rake face and chip do not separate during oblique cutting, reduced shearing forces are modeled by using the macroscopic friction reduction. For this purpose, the chip flow velocity needs to be determined in the first step. The chip flow velocity in longitudinal-torsional VAM is a function of inclination γ or helix angle of the tool λH, the chip compression ratio rus,c and the longitudinal and torsional vibration components as in the following equation:
In contrast to orthogonal cutting, the direction of the chip flow and the direction of the longitudinal oscillations are no longer perpendicular in oblique cutting. The inclined cutting edge causes the chips to flow over the rake face with a chip flow angle ηus, which is the angle between the chip flow and the normal plane (see Fig. 6). To determine the macroscopic friction reduction at the rake face, it is necessary to determine the longitudinal vibration component that stands perpendicular to the chip flow direction. For this purpose, three additional coordinate systems are defined as shown in Fig. 6 with the associated angular relationships.
The 0th coordinate system is transformed into the 1st coordinate system by rotating the 0th coordinate system along its z-axis by γ. The 0th coordinate system is needed, since the longitudinal vibrations only act along the y0 axis and the torsional vibrations only act along the x0 axis. The 1st coordinate system is then transformed to the 2nd coordinate system by rotating the 1st coordinate system along the y1 axis by αn. Finally, the 2nd coordinate system is transformed into the 3rd coordinate system by rotating the 2nd coordinate system along the x2 axis by η. In the 3rd coordinate system, the rake face of the tool lies in the y3-z3 plane and the chips flow along the z3 axis. The longitudinal vibration speed can therefore be expressed by the following vector in the 3rd coordinate system basis (x3, y3, z3):
In the 3rd coordinate system, the y3 component of the longitudinal vibration velocity vector stands perpendicular to the chip flow velocity and thus can be used to calculate the macroscopic friction reduction between the rake face and the chip (µ⊥,∥,r) under longitudinal-torsional VA:
To calculate specific cutting pressures, the vibration-assisted normal friction angle βus,n must be determined according to Eq. (22). By knowing the friction angle under VA, the five oblique-cutting parameters (Φn, Φi, θi, θn, η) in VAM can be determined according to Shamoto and Altıntas [19]. The iterative calculation of the macroscopic friction reduction µ⊥,∥,r and the oblique cutting parameters are applied until the chip compression ratio under VA (rus,c) converges to a fixed value. In each iteration step, the chip flow angle η gets updated, which in turn results in a different friction reduction at the rake face and a different chip compression ratio under VA (rus,c), which can be calculated by using the following equation:
Finally, by using the vibration-assisted oblique cutting parameters, vibration-assisted specific cutting pressures in tangential (Kus,tc), feed (Kus,fc) and radial (Kus,rc) directions can be calculated by using the following equations which are derived from Altintas [31]:
with
The macroscopic friction reduction coefficient μ⊥,∥,e between the clearance face and the workpiece can be calculated in an analogue way as for the orthogonal cut using Eq. (26). Finally, the resulting cutting forces during longitudinal-torsional vibration-assisted oblique cutting can be calculated according to the following equations:
If the maximum combined vibration velocity in cutting direction (see Eq. 9) is higher than the cutting speed, the rake face of the tool and the sliding chip will periodically separate due to the VA. To predict the shearing forces, the conventional specific cutting pressures are multiplied by the contact ratio Tc. Since the clearance face of the tool does not separate despite the VA, the force reduction can be modeled by multiplying the macroscopic friction reduction at the flank face (see Eq. 26) with the respective edge coefficients. Thus, the resulting cutting forces during intermittent cutting can be calculated according to the following equations:
Finally, by knowing the instantaneous force components in tangential, feed and radial directions in oblique cutting, forces in x-, y-, and z-directions in end milling can be calculated according to Altintas [31].
For the sake of better understanding, a flowchart of the oblique cutting model is presented in Fig. 7.
3 Experimental setup
This chapter aims to explain the experimental setup and settings that were used during the validation of the proposed force model. For the VA peripheral milling experiments, the longitudinal-torsional vibrations are generated by a custom-made actuator, which has been previously used and described in Rinck et al. [9]. As seen in Figs. 8 and 9, the actuator is positioned between the spindle and the tool. It can be used to generate longitudinal or longitudinal-torsional vibrations depending on the tool configuration. The actuator was mounted on a Hermle UWF 900 3-Axis CNC milling center.
Actuator assembly with the longitudinal-torsional tool and longitudinal tool for VAM [9]
Experimental setup [9]
Hufschmied cemented carbide milling tools with identical cutting-edge geometry were used for both the longitudinal and longitudinal-torsional VAM experiments (see Fig. 10). However, the cutting-edge length and the total length of the tools differ due to different vibration characteristics. The tools used for longitudinal VAM milling had a total length of 97 mm and 10 mm length of the cutting edges, whereas the tools for longitudinal-torsional VAM had a total length of 36 mm and 20 mm length of the cutting edges. The tools were connected to the actuator via an M6 thread. The connection via thread ensures a good transfer of the vibration amplitude to the tool with minimal damping, but requires custom made tools. To ensure sufficient concentricity of the tool, axial centering was performed via a cylindrical surface. Longitudinal-torsional VAM tools were further connected to a slotted sonotrode to generate a torsional vibration output.
The workpiece was a 100 × 100 × 5 mm sized Ti-6Al-4V block and was fixed on the Kistler 9257A dynamometer.
Respective vibration amplitudes, frequencies and phase shift between longitudinal torsional vibrations were measured with a Polytec-3-D-laser-Doppler-vibrometer. When coupled with the actuator, the longitudinal-torsional mill vibrates at a resonance frequency of 32.24 kHz and yields a maximum longitudinal vibration amplitude of approximately 5.75 µm. Additionally, the longitudinal-torsional mill has a torsional vibration output at the end cutting edge that has 1.35 times the amplitude of longitudinal vibration. Resulting longitudinal and torsional vibrations do not have a phase shift (ΔΦ = 0).
The torsional vibration amplitude can thus be calculated with the following equation:
Similarly, the longitudinal mill vibrates at the resonance frequency of 31,645 kHz with a maximum amplitude of approximately 5.75 µm.
For the validation of the force model, one set of conventional milling (CM) experiment and three sets of longitudinal VAM (LVAM) and LTVAM experiments were conducted. All experiments were performed with an axial depth of cut of 5 mm (ap = 5 mm), radial depth of cut of 0.5 mm (ae = 0.5 mm), 0.035 mm feed per tooth (fz = 0.035 mm) and 80 m/min cutting speed (vc = 80 m/min). During the conventional and the VAM experiments, all parameters except for the vibration amplitude were kept constant.
4 Results and discussion
To validate the vibration-assisted force model, VAM experiments were carried out with longitudinal and longitudinal-torsional vibration superposition at varying vibration amplitudes. Each experiment was carried out three times and the mean cutting force components in x-, y-, and z-directions were determined. The resulting force components were then compared with the modeled values.
To find the edge coefficients in CM, the conventional specific cutting pressures in milling (Ktc, Krc, Kac) were determined using Eqs. (35)–(37). Therefore, the shear stress (τs) of Ti-6Al-4V and the friction angle (βa) were taken from Budak et al. [30] and used as inputs for the calculation of conventional and vibration-assisted specific cutting pressures. For the validation, the conventional edge coefficients (Kte, Kre, Kae) were calibrated directly from the ploughing forces. The ploughing forces were found by subtracting the shearing forces from the total cutting force. By calibrating the edge coefficients directly from the ploughing forces, accurate forces were modeled for CM (see Fig. 11).
After determining the conventional specific cutting pressures and the edge coefficients, the analytical procedure described in the previous chapter was used for calculating the vibration-assisted specific cutting pressures (Kus,tc, Kus,fc, Kus,rc) and edge coefficients (Kus,te, Kus,fe, Kus,re). In Table 1, the modeled specific cutting pressures and the corresponding edge coefficients for conventional and VAM are listed.
For a longitudinal vibration amplitude of 2.2 µm, the combined vibration velocity in cutting direction (\({v}_{us,lt})\) during both longitudinal and longitudinal-torsional VAM was less than the cutting speed (\({v}_{c}\)). Therefore, no separation of the chip and the rake face took place. In the case of both longitudinal and longitudinal-torsional VAM, vibration amplitudes above 2.2 µm resulted in intermittent cutting.
As can be seen in Table 1, the cutting coefficients decrease with increasing vibration amplitudes due to the vibration superposition. However, the specific cutting pressure in axial direction (Kac) slightly increases under non-intermittent cutting conditions. This noteworthy remark is associated with macroscopic friction reduction. The decreased friction angle (βa) results in an increased chip flow angle (η), which in turn causes a higher specific cutting coefficient in axial direction.
After modeling the specific cutting pressures and edge coefficients, the cutting forces in longitudinal and longitudinal-torsional VAM were calculated and compared with the experimental data in Fig. 11. The cutting force components can be predicted with good accuracy within the whole amplitude range. At an amplitude of 2.2 µm and thus within the range of non-intermittent cutting, there is an average error of 4% and 5% between the measured and modeled forces for longitudinal and longitudinal-torsional VAM, respectively. Thus, the increase of specific cutting pressure under non-intermittent cutting conditions is compensated by the decreased edge coefficient in axial direction. At a longitudinal vibration amplitude of 5.75 µm, the average error between the experimental and modeled forces is 5% for longitudinal VAM and 6% for longitudinal-torsional VAM. All modeled cutting force components are within the range of the standard deviation of the measured values.
5 Conclusion and outlook
This paper introduces a new analytical force model that can predict the cutting forces during longitudinal and longitudinal-torsional VAM. To achieve this, the relative contact between the tool’s rake face and the chip was modeled for a helical end mill, and an extended macroscopic friction reduction model was proposed. The macroscopic friction reduction model can calculate friction reduction under a simultaneous parallel and perpendicular vibration superimposition. The force model can predict the cutting forces under intermittent and non-intermittent cutting conditions. The predicted forces were in good agreement with the experimental forces. In future work, the model can be used to calculate the cutting forces for different workpiece materials and different milling tool geometries.
References
Helmecke TP (2018) Ressourceneffiziente Zerspanung von Ti-6Al-4V-Strukturbauteilen für Luftfahrtanwendungen. [Erstausgabe]. Edited by Berend Denkena. Garbsen: TEWISS Verlag (Berichte aus dem IFW, 2018, Vol. 14)
Che-Haron CH (2001) Tool life and surface integrity in turning titanium alloy. J Mater Process Technol 118(1–3):231–237. https://doi.org/10.1016/S0924-0136(01)00926-8
Machado AR, Wallbank J (1990) Machining of titanium and its alloys—a review. Proc Ins Mech Eng Part B J Eng Manuf 204(1):53–60. https://doi.org/10.1243/PIME_PROC_1990_204_047_02
Kumabe J, Masuko M (1958) Study on the ultrasonic cutting (1st Report). JSMET 24(138):109–114. https://doi.org/10.1299/KIKAI1938.24.109
Markov AI (1966) Ultrasonic machining of intractable materials. [by] A.I. Markov; Edited by E.A. Neppiras, Translated [from the Russian] by Scripta Technica, Ltd. London
Ding H, Chen S-J, Cheng K (2010) Two-dimensional vibration-assisted micro end milling: cutting force modelling and machining process dynamics. Proc Ins Mech Eng Part B J Eng Manuf 224(12):1775–1783. https://doi.org/10.1243/09544054JEM1984
Feng Y, Hsu FC, Lu YT, Lin YF, Lin CT, Lin CF et al (2020) Force prediction in ultrasonic vibration-assisted milling. Mach Sci Technol 1–24. https://doi.org/10.1080/10910344.2020.1815048
Shamoto E, Suzuki N, Hino R (2008) Analysis of 3D elliptical vibration cutting with thin shear plane model. CIRP Ann 57(1):57–60. https://doi.org/10.1016/j.cirp.2008.03.073
Rinck PM, Gueray A, Kleinwort R, Zaeh MF (2020) Experimental investigations on longitudinal-torsional vibration-assisted milling of Ti-6Al-4V. Int J Adv Manuf Technol 108(11–12):3607–3618. https://doi.org/10.1007/s00170-020-05392-w
Gao J, Altintas Y (2020) Chatter stability of synchronized elliptical vibration assisted milling. CIRP J Manuf Sci Technol 28:76–86. https://doi.org/10.1016/j.cirpj.2019.11.006
Suárez A, Veiga F, de Lacalle LNL, Polvorosa R, Lutze S, Wretland A (2016) Effects of ultrasonics-assisted face milling on surface integrity and fatigue life of Ni-alloy 718. J Mater Eng Perform 25(11):5076–5086. https://doi.org/10.1007/s11665-016-2343-6
Arrazola PJ, Özel T, Umbrello D, Davies M, Jawahir IS (2013) Recent advances in modelling of metal machining processes. CIRP Ann 62(2):695–718. https://doi.org/10.1016/j.cirp.2013.05.006
Merchant ME (1945a) Mechanics of the metal cutting process. I. Orthogonal cutting and a type 2 chip. J Appl Phys 16 (5):267–275. https://doi.org/10.1063/1.1707586
Merchant ME (1945b) Mechanics of the metal cutting process. II. Plasticity conditions in orthogonal cutting. J Appl Phys 16(6):318–324. https://doi.org/10.1063/1.1707596
Usui E, Hirota A, Masuko M (1978) Analytical prediction of three dimensional cutting process—part 1: basic cutting model and energy approach. J Eng Ind 100(2):222–228. https://doi.org/10.1115/1.3439413
Fang N (2003) Slip-line modeling of machining with a rounded-edge tool—part I: new model and theory. J Mech Phys Solids 51(4):715–742. https://doi.org/10.1016/S0022-5096(02)00060-1
Fang N (2003) Slip-line modeling of machining with a rounded-edge tool—part II: analysis of the size effect and the shear strain-rate. J Mech Phys Solids 51(4):743–762. https://doi.org/10.1016/S0022-5096(02)00061-3
Soo SL, Aspinwall DK (2007) Developments in modelling of metal cutting processes. Proc Ins Mech Eng Part L J Mater Des Appl 221(4):197–211. https://doi.org/10.1243/14644207JMDA163
Shamoto E, Altıntas Y (1999) Prediction of shear angle in oblique cutting with maximum shear stress and minimum energy principles. J Manuf Sci Eng 121(3):399–407. https://doi.org/10.1115/1.2832695
Nath C (2008) A study on ultrasonic vibration cutting of difficult-to-cut materials. Dissertation, National University Singapur. Singapur
Gao Y, Sun R, Leopold J (2015) Analysis of cutting stability in vibration assisted machining using ananalytical predictive force model. Procedia CIRP 31:515–520. https://doi.org/10.1016/j.procir.2015.03.014
Xiao M, Karube S, Soutome T, Sato K (2002) Analysis of chatter suppression in vibration cutting. In International Journal of Machine Tools and Manufacture 42(15):1677–1685. https://doi.org/10.1016/S0890-6955(02)00077-9
Krystoff J (1939) Technologische Mechanik der Zerspanung. Berichte über betriebswissenschaftliche Arbeiten. 12th ed.: VDI-Verlag
Verma GC, Pandey PM, Dixit US (2018) Modeling of static machining force in axial ultrasonic-vibration assisted milling considering acoustic softening. Int J Mech Sci 136:1–16. https://doi.org/10.1016/j.ijmecsci.2017.11.048
Arefin S, Zhang X, Anantharajan S, Liu K, Neo D (2019) An analytical model for determining the shear angle in 1D vibration-assisted micro machining. Nanomanuf Metrol 2:199–214. https://doi.org/10.1007/s41871-019-00049-z
Zhang J, Wang D (2019) Investigations of tangential ultrasonic vibration turning of Ti6Al4V using finite element method. Int J Mater Form 12(2):257–267
Patil S, Joshi S, Tewari A, Joshi SS (2014) Modelling and simulation of effect of ultrasonic vibrations on machining of Ti6Al4V. Ultrasonics 54(2):694–705
Storck H, Littmann W, Wallaschek J, Mracek M (2002) The effect of friction reduction in presence of ultrasonic vibrations and its relevance to travelling wave ultrasonic motors. Ultrasonics 40(1–8):379–383. https://doi.org/10.1016/S0041-624X(02)00126-9
Altintaş Y, Lee P (1996) A general mechanics and dynamics model for helical end mills. CIRP Ann 45(1):59–64. https://doi.org/10.1016/S0007-8506(07)63017-0
Budak E, Altintas, Y, Armarego EJA (1996) Prediction of milling force coefficients from orthogonal cutting data. J Manuf Sci Eng 118(2):216–224. https://doi.org/10.1115/1.2831014
Altintas Y (2012) Manufacturing automation. Cambridge University Press, Cambridge
Funding
Open Access funding enabled and organized by Projekt DEAL. This work was funded by the Deutsche Forschungsgemeinschaft (DFG) within the research project “Machining of high performance materials with ultrasonically modulated cutting speed” (Project number 406283248).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Ethics approval
Not applicable.
Consent to participate
Not applicable.
Consent for publication
Not applicable.
Conflict of interest
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Rinck, P.M., Gueray, A. & Zaeh, M.F. Modeling of cutting forces in 1-D and 2-D ultrasonic vibration-assisted milling of Ti-6Al-4V. Int J Adv Manuf Technol 119, 1807–1819 (2022). https://doi.org/10.1007/s00170-021-08355-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00170-021-08355-x