1 Introduction

Wire electrical discharge machining (WEDM) is a nontraditional machining technique which has been used for precision machining of complex shapes. The material removal process is based on the accumulation of successive craters formed from discharges between the two electrodes.

The discharges occur at a high frequency, each discharge producing a small crater on both electrodes. Since the crater is fundamental to the process, a model of the crater is important for its understanding and the definition of the parameters that influence the removal rate.

It is very difficult to model the crater formation. The physics behind electrical discharge machining (EDM) is not yet fully understood. A profound description of the process requires an interdisciplinary approach covering thermodynamics, electrodynamics and hydrodynamics.

The boundary conditions for the process, e.g. plasma diameter and its evolution through time, the power ratio between the anode and the cathode or the behavior at the plasma-material interface have not yet been defined theoretically, as pointed out by Hinduja and Kunieda [1]. One reason for this is the difficulty in simulating EDM arc plasmas. Besides that, the difference in the volumes removed between the anode and the cathode cannot be explained solely on the basis of energy distribution [2].

Nevertheless, there are several models in the literature attempting to describe the crater generation in EDM [1, 3,4,5,6,7]. Most models use a thermal approach and simplified boundary conditions. It is common for models to use as a heat source a Gaussian influx of energy that is radially symmetric. The shape of the crater is commonly determined by the melting isothermal surface created in the material as also mentioned by Feng et al. [3]. Under such assumptions, the craters are radially symmetric, thus not reflecting the observed shape of single craters created by WEDM, as seen in Fig. 1.

Fig. 1
figure 1

Single crater produced with WEDM

Full size image

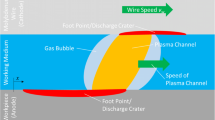
Another boundary condition that is simplified is the plasma diameter. Since Zingerman [8] it is commonly assumed the plasma diameter to be the same size as the craters.

Kojima et al. [9] made observations with high-speed cameras and established that the diameter of the plasma arc in air was five times greater than the crater diameter. In liquid dielectrics, the proportions were smaller, but still bigger than the crater diameter.

The observation of single craters produced by WEDM reveals that, under certain conditions, most of the craters are not radially symmetric. This fact cannot be explained with the current models. In addition to the asymmetry, there is a preferable direction for the crater elongation.

This paper tries to evaluate the craters’ dimensions, the level of asymmetry, determine the preferential direction of elongation and suggest its cause. To capture the observed asymmetry, it is chosen to model the crater with an ellipsoid equation instead of a spheric one. This is achieved through topography mapping of the craters with posterior modeling.

2 Overview of WEDM

2.1 Principle

WEDM is a non contact thermal machining process which uses a wire as tool–electrode, commonly made of brass. It can machine electrically conductive materials independently of its hardness. The material removal is based on local melting and ejection of the workpiece surface.

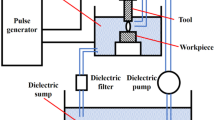
The electrodes are placed to maintain a small gap between them. This gap is filled with an insulation medium, which is usually de-ionized water. This medium prevents electrolysis to happen between the electrodes.

A plasma channel is formed once the voltage applied to the electrodes overcomes the dielectric strength. The plasma composing the spark is highly ionized and conductive, according to Descoeudres [10], capable of sustaining large currents around 104A. The plasma expands with time and at the end of the pulse, it collapses, leaving a small crater on both electrodes.

For every pulse, only a single discharge happens. Due to the small dimensions of the craters, they usually take place in a high frequency—commonly from 1kHz to 1MHz.

3 Materials and methods

3.1 Machine and workpiece

The experimental setup for creating single craters consists of a WEDM machine, AgieCharmilles CUT P350, with a 0.20-mm diameter Brass900 wire from Thermocompact. The craters are made using deionized water as dielectric. A stainlees steel, DIN 1.2379, is used as the workpiece. Its chemical composition is shown in Table 1 and some of its physical properties in Table 2.

Table 1 Steel 1.2379 chemical composition
Full size table
Table 2 Steel 1.2379 physical properties
Full size table

The machine uses a relaxation generator to produce the pulses. Table 3 shows the five different pulse energy levels along with the number of single craters that are analyzed in this paper.

Table 3 Pulse energy levels and the number of analyzed single craters
Full size table

The apparent elongation in the Y direction, that can be observed in the Fig. 1, cannot be explained by the unwinding speed of the wire. Since the pulses only last for around 1 μs and the wire unwinding speed is 9.9 m/min, the spark moves around 0.17 μm, which is much smaller than the dimension of any crater.

The InfiniteFocus microscope from Alicona is used to map the topography of the single craters created. Pictures of the single craters were taken with a ×100 (vertical resolution of 0.01 μm and lateral resolution of 0.85 μm) and ×50 (vertical resolution of 0.02 μm and lateral resolution of 1.20 μm) objective, which are selected according to the craters’ dimensions. The data from the microscope is exported and post processed.

3.2 Single crater

The single craters are produced on samples that consist of a flat surface with an area of 100×50 mm. To facilitate the identification and the measurements of the single craters’ topography, the flat surface is carefully cut to reach a smooth surface, with roughness (Ra) of 0.3 μm.

To create the single craters, the wire is oriented parallel to the surface. It is guided to pass in front of the prepared face of the workpiece with an increased gap, which reduces the total number of sparks while still keeping a more realistic process condition. Figure 2 illustrates the set up schematically.

Fig. 2
figure 2

Scheme for the production of single craters

Full size image

Images of the single craters are made with the microscope and exported for post processing. Figure 3 shows a single crater image taken by the microscope and the corresponding topography map.

Fig. 3
figure 3

Microscope image and topography perspective of a single crater

Full size image

3.3 Extracting the dimensions

To help interpretation, the microscope’s axes are aligned to the workpiece edges. This way, the Y -axis reading should be aligned to the wire direction, while the X-axis reading should be aligned to the cutting direction. Figure 4 displays this alignment. Furthermore, the region surrounding the crater is used to set the original, undamaged surface, which is set to zero level.

Fig. 4
figure 4

Microscope’s axis alignment to the workpiece

Full size image

To extract the crater dimensions, the data corresponding to the crater is supplied to a Levenberg–Marquardt algorithm, to fit an ellipsoid equation centered in (x0,y0,z0). The ellipsoidal equation is shown below:

$$ \frac{[x^{*}\cos(\theta)+y^{*}\sin(\theta)]^{2}}{a^{2}} + \frac{[x^{*}\sin(\theta)-y^{*}\cos(\theta)]^{2}}{b^{2}} + \frac{z^{2}}{c^{2}} = 1 $$
(1)

In Eq. 1, the variables a, b and c correspond to the semi-axis in the X, Y and Z directions respectively. The symbol x∗ and y∗ stand for (x − x0) and (y − y0), which designate the translation of the ellipsoid.

The ellipsoid’s center is placed on z0 = 0, it is assumed that the center lays on the undamaged surface.

The angle 𝜃 is the rotation angle of the ellipsoid on the X-Y plane. If the craters’ elongation is not exact aligned to the wire length, it is possible to capture this deviation through 𝜃. The search for this angle is constricted. It can only admit values from [− 45∘;45∘]. Values beyond this range would create ambiguity. The rims of the craters are not taken into consideration in the ellipsoidal equation.

Only the points of the image that belong to the crater must be supplied to the search algorithm. These points are clearly below the undamaged surface level. But just this criterion is not enough to select only the region of the crater.

After some trials, it was found the 15th percentile level on the Z-axis to be appropriate to define the points on the image that define the crater region. Figure 5 shows in black the crater region, under the 15th percentile level, selected to feed the search algorithm. Lower values would select a smaller region of the crater, which is not ideal for the search algorithm, while higher values might include points close to the surface that do not clearly belong to the crater.

Fig. 5
figure 5

The crater region identified by the 15th percentile is marked in black

Full size image

After fitting the ellipsoids, it is advised to evaluate how the ellipsoids’ volume distribute themselves. This is done through a normal Q-Q plot, which is a graphical method to evaluate the adherence of the data to a normal distribution, as can be seen in Fig. 6.

Fig. 6
figure 6

On the left, Q-Q plot for the crater volume to identify outliers. On the right, Q-Q plot for the crater volume after removing the outliers from the data

Full size image

With the help of the Q-Q plot, it is possible to identify outliers that would not be recognizable visually.

4 Results and discussion

4.1 Volume

Figure 7 shows the correlation between the craters’ volume and the energy pulse. The average volume of the craters is represented by the blue mark. The figure also shows the corresponding confidence interval with 95% confidence level.

Fig. 7
figure 7

Average crater volume as a function of the pulse energy. The bars express the 95% confidence interval

Full size image

As expected, the crater volume increases with the pulse energy. The data suggests a linear relationship. A regression on the data is performed and displayed on Fig. 7 as a red line. The equation used is the following:

$$ V = e_{c} \varepsilon + V_{0} $$
(2)

In Eq. 2, V is the crater volume, ε is the pulse energy in mJ, V0 the intercept and ec the specific energy per volume removed. The values were found to be:

$$ e_{c} = 3667.5 \frac{\mu m^{3}}{mJ} $$
(3)
$$ V_{0} = - 1164.7 \mu m^{3} $$
(4)

Replacing the values found in step Eqs. 3 and 4, yield Eq. 5 as the following:

$$ V = 3667.5 \frac{\mu m^{3}}{mJ} \varepsilon - 1164.7 \mu m^{3} $$
(5)

Solving the equation for crater volume zero, it is possible to established an energy threshold. Pulse energies smaller than 0.318 mJ should remove no volume.

4.2 Semi-axis in wire direction

The data regarding the length of the semi-axis in Y direction, represented by the symbol b in the ellipsoid Eq. 1, suggests a non-linear relationship to the pulse energy, as can be seen in Fig. 8.

Fig. 8
figure 8

Crater semi-axis b as a function of the pulse energy. The bars express the 95% confidence interval

Full size image

To capture this non-linear behavior, an exponential equation is fit to the data:

$$ b = k_{1}*\varepsilon^{k_{2}} - k_{3} $$
(6)

In Eq. 6, ε is the pulse energy in mJ and k1, k2 and k3 are constants. The regression yields Eq. 7 as following:

$$ b = 36.51 \varepsilon^{0.37} - 14.5 \mu m $$
(7)

4.3 Semi-axis in cutting direction

The semi-axis in the cutting direction, the symbol a in the ellipsoidal Eq. 1, has a similar behavior to the previous one, as shown in Fig. 9.

Fig. 9
figure 9

Crater semi-axis a as a function of the pulse energy. The bars express the 95% confidence interval

Full size image

The exponential relationship for the semi-axis in X direction, captured also through Eq. 6, is shown in the figure in red and gives the following Eq. 8:

$$ a = 21.48 \varepsilon^{0.32} - 2.51 \mu m $$
(8)

4.4 Semi-axis in Z direction

The semi axis in the Z direction corresponds to the c symbol in the ellipsoidal Eq. 1. This data can also be interpreted as the crater’s depth. Unlike the other dimensions of the crater, the depth seems to have a linear pattern with the increase of the pulse energy, Fig. 10.

Fig. 10
figure 10

Crater depth c as a function of the pulse energy. The bars express the 95% confidence interval

Full size image

The line that represents this relationship is shown in Eq. 9:

$$ c = 0.3284 \frac{\mu m}{mJ} \varepsilon + 2.70 \mu m $$
(9)

4.5 Aspect ratio

To represent the elongation of the craters, the aspect ratio ρ is defined in Eq. 10:

$$ \rho = \frac{b}{a} $$
(10)

Figure 11 displays the average aspect ratio per energy pulse along with the confidence interval.

Fig. 11
figure 11

Aspect ratio as a function of the pulse energy. The bars express the 95% confidence interval

Full size image

The aspect ratio grows consistently with the increase in the energy. A linear trend can be established with the following Eq. 11:

$$ \rho = 0.0687 \frac{1}{mJ} \varepsilon + 1.1347 $$
(11)

Even though there is an increase in the average aspect ratio for the pulse energies of 0.60 mJ, 1.02 mJ and 2.04 mJ, their confidence interval’s lower limit is smaller than one, which means that some of the craters are round and more symmetric or even compressed in the wire direction.

The 4.08 mJ energy pulses behave differently. The average aspect ratio is 1.5 and the lower boundary of the interval is above one. This means that the vast majority of the craters produced have a clear elongation in the Y semi-axis.

This becomes even more prominent in the 9.18 mJ energy pulses, with an average aspect ratio of 1.73 and the lower confidence interval at 1.2. However, such elongation values can be achieved with different angular deviation 𝜃 and might not represent craters that follow closely the wire geometry.

4.6 Angle of rotation

The elongation direction is evaluated through the rotation angle on the X-Y plane. Values close to zero mean that the main axes are well aligned to the cutting direction X and the wire direction Y. The 𝜃-values are presented in Fig. 12.

Fig. 12
figure 12

Angle of rotation as a function of the pulse energy. The bars express the 95% confidence interval

Full size image

The pulse energies of 0.60 mJ, 1.02 mJ and 2.04 mJ cover almost the whole interval [− 45∘;45∘]. This

means that they have no preferential elongation direction. Such behavior is expected since these craters are rounder and more symmetric.

As the pulse energy increases, the interval for the rotation angles becomes smaller. For more elongated craters, the rotation angle moves closer to zero, which indicates that the elongation does not deviate much from the wire longitudinal direction.

The elongation of the craters involves the effects of the wire geometry on the spark. In the direction of the wire, the gap stays as narrow as in the starting position of the ignited spark. This proximity means that the electrons and ions may more easily travel across the dielectric gap, which yields higher temperature and ionization along the wire direction.

5 Conclusion and outlook

The images of the single craters formed by WEDM have a significant elongation, which is dependent on the pulse energy level.

Craters from low energy pulses, until 2.04 mJ, have an increasing average aspect ratio , but their confidence interval is not above one. This indicates that their elongation is hidden by large stochastic effects superposed on an underlying deterministic dependence. Furthermore, these craters have shown a large range of angle rotations, reinforcing that their elongation is overwhelmed by the stochastic effects.

The craters generated by the higher energy levels have an aspect ratio considerably bigger and a confidence

interval above one. Thus, the majority of the craters produced at these energy levels are elongated. The angle of rotation has shown a smaller interval, indicating a preferable elongation direction, while still being superposed by stochastic effects.

The elongation of the craters arises from the effects of the wire geometry on the process. The plasma growth, after a certain energy level gets constricted by the wire geometry. Since the plasma column has dimensions which are bigger than the crater, it reaches values compatible to the wire diameter. The current is flowing preferentially in the highly ionized region of small gap height, which elongates the plasma column in the direction of the wire. An evaluation on the craters’ aspect ratio across different wire diameters will help to understand the origin of the observed elongation.

Current crater models need to be adapted to reproduce crater shapes for electrodes with large and non-isotropic curvatures.