Energy assessment of different cooling technologies in Ti-6Al-4V milling

Abstract

Manufacturing craves for more sustainable solutions for machining heat-resistant alloys. In this paper, an assessment of different cooling lubrication approaches for Ti6Al4V milling was carried out. Cryogenic cutting (liquid nitrogen) and conventional cooling (oil-based fluid) were assessed with respect to dry cutting. To study the effects of the main relevant process parameters, proper energy models were developed, validated and then used for comparing the analysed cooling lubrication strategies. The model parameters were identified exploiting data from specifically conceived experiments. The power assessment was carried out considering different perspectives, with a bottom-up approach. Indeed, it was found that cryogenic cooling, thanks to a better tribological behaviour, is less energy demanding (at least 25%) than dry and conventional cutting. If the spindle power is considered, lower saving percentages can be expected. Cryogenic cooling showed its best energy performance (from 3 to 11 times) with respect to conventional cutting if the machine tool perspective is analysed. Considering even the primary energy required for producing the cutting fluids, the assessment showed that cryogenic cooling requires up to 19 times the energy required for conventional cutting.

1 Introduction

Although titanium components are widely adopted in many high-performance applications, ranging from biomechanical to aerospace, its machinability is still a stimulating challenge both for manufacturing industries and for the research community [1]. Due to high chemical reactivity, low thermal conductivity and high material strength that is preserved at high temperatures, titanium and other heat-resistant alloys HRA are considered hard-to-cut materials. They can only be unprofitably processed [2] at low cutting speeds with the auxiliary of metalworking fluids (MWFs) [3]. Water miscible and oil-based cutting fluids (namely, conventional cooling) are the most widely diffused solutions for processing HRA in shop-floors. It was estimated that the costs associated to cutting fluids account for the 25% of the overall manufacturing costs [4].

Although productivity and machining costs are still the main drivers in machining technology development, in recent years, environmental sustainability [5] and health issues [6, 7] have been gaining an increasing attention. Adler et al. [8] analysed the main limitations of the existing cooling lubricating CL methodologies.

Several recent review papers focused on sustainability in machining [9, 10]. Gupta and Laubscher [11] give an overview of the most promising and advanced CL methods from pursuing the sustainability. The use of cryogenic fluids and minimum quantity lubrication MQL and the combination of MQL and cryogenic are subject of many research efforts. As summarized in Table 1, several aspects have been investigated, from the system development to the assessment of the different CL methodologies where different approaches were used. Most of the studies adopted experimental methods, some works combine numerical and experimental methods, while few works exploited already published data to perform comparative analyses.

Table 1 Sustainable machining - literature review map

Pervaiz et al. [12] resume the recent advances in MQL titanium machining. It was demonstrated that the cooling action of the oil is rather limited since the involved flow rates are very low (10–150 ml/h). The reduction of friction is the most relevant observed effect of MQL. Improvements in terms of surface integrity and tool life were observed even if in most of the studies the assessments were carried out with respect to dry cutting. In [13], an experimental assessment of surface roughness, chip morphology and energy consumption with respect to wet machining was carried out. Khan et al. in [14, 15] proposed an empirical model for studying the effect of the main parameters on the costs and overall energy demand. A comprehensive analysis considering process- and product-related performances (tool wear, productivity, surface roughness, etc.) and specific energy was carried out in [16].

In order to enhance the cooling potentialities of MQL, the development of a hybrid CL method that combines a cryogenic fluid with MQL (cryo-MQL) was carried out in many studies. Pereira et al. [17,18,19] designed specific nozzles for cryo-MQL. Computer fluid dynamics (CFD) simulations were performed to optimize the system performances. A preliminary assessment (tool life) with respect to other CL technologies was performed. It was found that the hybrid cryo-MQL showed lower performance than conventional cutting. Grguraš et al. [20] developed a solution for feeding the mixed LCO2-oil flow through the inner mill nozzles. Bergs et al. [21] studied the solubility of different oils in LCO2 jets. For this purpose, a specific mixing chamber was designed.

Several works carried out comparative analysis considering cryo-MQL and other CL methods. For instance, Superkar et al. [22] demonstrated the efficacy of supercritical CO2-MWFs jets in turning, drilling and tapping. Pereira et al. in [23] and [24, 25] respectively performed turning tests on steel and milling experiments on Inconel 718. Although remarkable results in terms of tool life and surface quality enhancement were observed, milling tests revealed that conventional cooling still assures the best performances. Similar results were observed by Tapoglou in [26]. In Bagherzadeh et al. [27] it was found that an optimized cryogenic (CO2) cooling is still more effective than cryo-MQL.

Shokrani et al. [28] performed milling tests on Ti6Al4V using an experimental set-up composed of four external nozzles for feeding, separately, both the C02 and the MQL jets on the tool. Maybe due to a non-optimized design, the observed tool life was comparable to the results achieved with MQL, especially at high cutting speed. Damir et al. [29] found that hybrid cryo-MQL assured tool life durations comparable to the ones achieved using high-pressure coolant HPC turning. Similar results were found by Gross et al. [30] in turning. Hanenkamp et al. [31] discovered that the mill duration (cryo + MQL) was strongly affected by the oil properties.

According to [32,33,34,35], the expected advantages of cryogenic machining are related to the potential increment of material removal rates (MRR), the extension of the tool life and the enhancement of the quality/integrity of processed surfaces [36, 37], and it prevents the oil contamination of the parts, chips and machine. Pusavec et al. in [38] tried to formalize all these aspects to compare different CL solutions. They proposed an overall cost function that considers even the contributions for cleaning the parts and the swarf, the cost for the MWFs disposal, the machine cost and the cost of energy. Although the results confirmed the great potentialities of cryogenic cooling, some difficulties need to be tackled.

For instance, the storage and delivery of LN2 is problematic. Indeed, a proper vacuum-insulated vessel and feeding system are necessary. The insulation of the most critical machine tool components (i.e. spindle bearings) and the need to prevent any early LN2 gasification are demanding challenges. Even a proper integration of the cryogenic solutions in real machine centres and shop-floors is tough. Paul in [39] analysed these aspects and presented some feasible solutions. On the contrary, CO2 can be more easily stored at ambient temperature but adopting higher pressures. CO2 is relatively cheap and for this reason is more attractive industrially than other cryogenic gases [40]. The drawbacks of cryogenic CO2 are related to a slightly irritating odour and higher density than air, and this can cause serious problems to workers unless proper air exchange is assured. For what concerns the cooling performance, it was estimated that LN2 assures a 20% higher refrigeration value than CO2 [41]. Moreover, when liquid CO2 sprayed through the nozzle, due to a high-pressure drop the liquid, CO2 changes phase into a mixture of a solid (dry ice) and gaseous state, thus reducing its cooling properties. This was confirmed by Shah et al. in [42]. The authors compared cryogenic CO2 and LN2 in titanium alloy drilling. It was found that LN2 made the drill life 45% longer than CO2. Conflicting results were reported in [43] since the results strongly depend on the cryogenic jet properties (i.e. position, orientation).

In some works, the development of a proper system [44] for feeding the cryogenic fluid was carried out even with the support of advanced simulations [45,46,47]. Shi et al. [48] developed a hybrid numerical approach that used CFD simulation results for properly setting the corresponding FE model. Augspurger et al. [49] combined an analytical formulation and temperature measurements for evaluating the cooling performance of CO2 in titanium milling.

Sadik et al. [50] performed wear tests in Ti6Al4V milling adopting cryogenic (C02) and conventional cutting. It was observed that cryogenic cutting assured higher tool life even changing the orifice size. Similar results were achieved in [51]. Khanna et al. [52] extended the analysis performing tests on precipitation hardening (PH) stainless steel (SS) adopting cryogenic CO2 and other CL methods. Even the reduction of the power consumption was observed in cryogenic condition.

Pusavec et al. in [41] carried out an experimental study on the main sustainable CL techniques for machining Inconel 718. They developed an empirical model using the response surface methodology RSM. In [53] an optimization process considering even the chip breakability was carried out.

Bordin et al. [54, 55] carried out comparative turning tests on Ti6Al4V produced by additive manufacturing. Cryogenic LN2 showed the better performance in terms of tool life with respect to conventional turning. Isakson et al. [56] compared cryogenic LN2 and conventional Ti6Al4V turning analysing the wear of the tool, the residual stresses and the surface roughness. It was found that wet turning assured a higher tool life.

Suhaimi et al. [57] experimented different LN2-assisted solutions for Ti6Al4V milling. It was found that in cryogenic milling, higher tool life occurred especially if with the developed indirect cooling strategy. Damir et al. [58] performed comparative turning tests adopting both LN2 and conventional cooling. With the auxiliary of LN, lower forces and a better surface finishing were observed. Moreover, it was demonstrated that with the adoption of LN2, a lower total single score, in terms of overall consumed energy, can be achieved.

Gupta et al. [59] proposed a study for comparing cryogenic (LN2) cutting turning with wet turning. In surface finishing, temperature add roughness were evaluated. Moreover, energy consumption and carbon emission were evaluated. The lowest energy consumption was observed for the combination LN2-MQL even if similar results were obtained just using LN2. Shokrani et al. [60] compared cryogenic milling with respect to conventional cooling. The authors used an experimental approach to assess the absorbed power with different machining parameters. They found that cryogenic cutting is more energy demanding, focusing on the energy absorbed by the machine, than dry cutting but less energy demanding than conventional cutting. Moreover, although the cutting tests were executed changing the parameters, only the average power was considered in the assessment.

According to the scientific literature (Table 1), most of the studies were focused on the process-product-related performances, while few research works really dealt with the environmental issues. Pusavec et al. in [35] stated that cryogenic machining is the sole cooling technology that has a disruptive effect on the indicators that are typically used for assessing the life cycle (LCA) of a process (CO2, water use, acidification, energy, solid waste, etc.). From this perspective, only dry cutting has similar environmental-oriented capabilities, but, according to the present tooling technology, it cannot be considered an industrial and profitable solution for processing hard-to-cut materials. Some of the already analysed papers (i.e. [59, 60]) experimentally observed an energy consumption reduction associated to the use of cryogenic in machining even if the analyses were typically carried out in specific cutting conditions. If the system boundaries were enlarged to the LN2 production, Pusavec et al. in [35] found that the energy demand in cryogenic machining is higher than in other CL methods since the LN2 liquefaction process is energy demanding. A different conclusion was outlined by Damir et al. in [58]. Another study on the overall energy request was carried out in [61]. It compared both conventional cutting and cryogenic cooling exploiting data from other research works. Since some data were missing, a specific procedure to assume them or to compare different scenarios, characterized by different processed materials, experimental set-ups, feeding systems, process parameters and machining operations, was adopted. Although the results were statistically analysed, they seem affected by the adopted procedure. In this research, it was found that CO2 is better than LN2 (averagely), but in many cases, much higher energy demands were observed.

In order to overcome the limitations described in the analysed research works, in this paper, a more structured approach was proposed for comparing cryogenic (LN2), conventional ad dry cutting. The assessment was performed at different levels adopting a bottom-up approach. The analysis started focusing on the tribological aspects involved in the cutting and then was extended up to the primary level where even the energy required to produce the cutting fluids was considered. For each perspective, a model was developed to analysed the effect of cutting parameters and other relevant process-related quantities. The models were properly characterized and validated through experiments. For this purpose, a reliable cryogenic set-up (developed in [45]) was exploited.

The proposed approach, together with the development of each sub-system model and the associated parameters identification procedure, was described in section “Materials and methods.” Moreover, a detailed description of both the experimental set-up and the performed tests was also provided. In the “Results and discussion” section, the main results and the sensitive analyses were reported and commented. Conclusions were also outlined.

2 Materials and methods

In this section, the procedure devised for carrying out the energy assessment of cryogenic milling and conventional cooling with respect to dry cutting was presented. Although dry cutting is far from being profitably used in titanium milling, it represents the reference from the environmental perspective. As schematized in Fig. 1, the analysis was performed at different levels. At the bottom one, the cutting power was considered. In addition, considerations about the effects of the cooling lubrication approach on cutting forces and on the tribological behaviour were outlined. The achieved results were compared to the results found in literature [62,63,64]. At the second level, the analysis was carried out considering the spindle system boundaries, while the machine boundaries were considered for the third assessment. Finally, at the top level, the primary global energy (cumulative energy demand (CED)) required for producing the cutting fluids was also considered in the analysis.

Fig. 1

The proposed approach for assessing the power of different cooling strategies in Ti6Al4V milling at different levels

At each level, for being able to study the effects of the main process-related parameters, an energy model was developed. Contextually, experimental test results (cutting force measurements and power measurements in different conditions) together with identification procedures were used to estimate the unknown model parameters. Proper tests were also carried out for model validation purposes.

A 4-axes machine centre was used for the experimentation. Since the results achieved in most of the papers that deal with cryogenic machining strongly depend on the specific adopted experimental set-up, an advanced through-tool cryogenic system [45] was used in this research. Although supplying a constant cryogenic coolant flow of liquid nitrogen LN2 through the inner channels of a rotating tool in a complex machine is a technological challenge since any small heat transfer or pressure drops inside the coolant feeding system [45] can evaporate a portion of the liquid with a combination of boiling and cavitation effects, this solution guaranties better cooling performance [65, 66, 73] with respect to flood cryogenic cooling both in terms of expected cutting performance (i.e. [63, 67]) and liquid nitrogen consumption. More details on the experimental set-up were reported in the following subsections.

2.1 Cutting power assessment

To accomplish the goal of this research, suitable models were properly developed. For the cutting process perspective, it was decided to start from one of the cutting force mechanistic models available in literature. More specifically, according to the representation of a generic peripherical milling operation reported in Fig. 2, the selected mechanistic model is described by Eqs. 1, 2, 3 and 4. This formulation is typically used for dealing with vibrational issues in machining [74]. As can be observed, the resulting cutting force on the engaged i^th insert/tooth can be projected along the radial direction F_ri, the tangential direction F_ti and the axial direction F_ai.

Fig. 2

Milling process and representation of the cutting forces acting on a generic insert

The force contributions on each insert can be computed according to Eq. 1.

$$ {\displaystyle \begin{array}{c}{F}_{ti}\left({\varphi}_i(t)\right)={K}_{tc}\cdot {a}_p\cdot {h}_i\left({\varphi}_i(t)\right)+{K}_{te}\cdot {a}_p\\ {}{F}_{ri}\left({\varphi}_i(t)\right)={K}_{rc}\cdot {a}_p\cdot {h}_i\left({\varphi}_i(t)\right)+{K}_{re}\cdot {a}_p\\ {}{F}_{ai}\left({\varphi}_i(t)\right)={K}_{ac}\cdot {a}_p\cdot {h}_i\left({\varphi}_i(t)\right)+{K}_{ae}\cdot {a}_p\end{array}} $$

(1)

K_tc, K_te, K_rc, K_te, K_ac, K_ae are the coefficients of the mechanistic model, a_p is the axial depth of cut and h_ithe instantaneous chip thickness that varies according to the angular coordinates φ_i, Eqs. 2 and 4.

$$ {h}_i\left({\varphi}_i(t)\right)={f}_z\cdot \sin \left({\varphi}_i(t)\right) $$

(2)

ω is the angular tool velocity assumed constant over time t, a_e is the radial depth of cut and f_z is the feed per tooth. These are the parameters typically set by the user before cutting. This mechanistic force model was selected because it considers, for the computation of the main cutting force components, a contribution due to the shear (proportional to the chip section A_i) and one linked to the friction/ploughing mechanism that, in this formulation, is considered proportional to the length of the cutting edge involved in the cutting.

$$ {A}_i\left({\varphi}_i(t)\right)={h}_i\left({\varphi}_i(t)\right)\cdot {a}_p $$

(3)

$$ {\varphi}_i(t)=\omega \cdot t $$

(4)

Since f_z is typically much lower that a_p, the length of the insert can be approximated with a_p. The formulation does not consider the tool radius.

$$ {A}_i\left({\varphi}_i(t)\right)={f}_z\cdot \mathit{\sin}\left({\varphi}_i(t)\right)\cdot {a}_p $$

(5)

Such a simple model has the desired features for the purposes of this research since it considers the main mechanisms responsible for the force generation, and it was expected that the CL strategy affects them together with the resulting cutting power.

Indeed, the instantaneous cutting power associated to each insert ${P}_{cu{t}_i}(t)$can be estimated through Eq. 6.

$$ {P_{cut}}_i(t)={F}_{ti}(t)\cdot {v}_c={K}_{tc}\cdot {a}_p\cdot {h}_i\left({\varphi}_i(t)\right)\cdot {v}_c+{K}_{te}\cdot {a}_p\cdot {v}_c $$

(6)

According to Eq. 7, the average cutting power can be estimated considering a period of time T associated to one revolution of the tool and the corresponding number of teeth Z. D is the tool diameter.

$$ {\overline{P}}_{cut}=\frac{1}{T}{\int}_0^TZ\cdot {F}_{ti}(t)\cdot {v}_c\cdot dt $$

(7)

T can be computed knowing the cutting speed and the spindle speed rotation Ω (Eq. 8):

$$ T=\frac{\pi D}{v_c}=\frac{2\pi }{\omega };\omega \left[\frac{\mathrm{rad}}{s}\right]=\frac{2\pi \varOmega \left[\mathrm{rev}/\min \right]}{60} $$

(8)

Substituting Eq. 6 in Eq. 7 and considering that the cutting force is not null only when the tooth is engaged in the workpiece, that is when the associated angular φ_i is in between φ_stand φ_ex (respectively the starting and exit immersion angle, Fig. 2), Eq. 9 can be written.

$$ {\overline{P}}_{cut}=\frac{1}{T}{\int}_0^TZ\cdot \left({K}_{tc}\cdot {a}_p\cdot {f}_z\cdot \mathit{\sin}\left({\varphi}_i(t)\right)+{K}_{te}\cdot {a}_p\right)\cdot {v}_c\cdot dt $$

(9)

The relationships can therefore be simplified as follows:

$$ {\overline{P}}_{cut}=\frac{1}{T}{\int}_0^{\frac{\varphi_{ex}}{\omega }}Z\cdot \left({K}_{tc}\cdot {a}_p\cdot {f}_z\cdot \mathit{\sin}\left(\omega \cdot t\right)+{K}_{te}\cdot {a}_p\right)\cdot {v}_c\cdot dt $$

(10)

Integrating the previous formulation, the average cutting power ${\overline{P}}_{cut}$ can be expressed as reported in Eq. 11.

$$ {\overline{P}}_{cut}=Z\cdot {K}_{tc}\cdot {a}_p\cdot {f}_z\cdot \left(\frac{a_e}{\pi \cdot D}\right)\cdot {v}_c+Z\cdot {K}_{te}\cdot {a}_p\cdot \frac{\varphi_{ex}}{2\pi}\cdot {v}_c $$

(11)

The relationship considers the non-dimensional ratio a_e/(D) and the φ_ex/(2π) that both give and indicate the radial tool-workpiece engagement. Moreover, the dependence upon the feed f_z is also visible.

Finally, the cutting power comparison linked to each specific cooling lubricating condition $\Delta {P}_{cut{t}_{j- dry}}$ can be formalized as reported in Eq. 12. ${\overline{P}}_{cut{t}_j}$ is the average cutting power linked to the specific cooling strategy (cryogenic or conventional cooling). The $\Delta {P}_{cut{t}_{j- dry}}$ was normalized, for both the conventional-dry and cryogenic-dry comparisons, with respect to the cutting power in dry cutting ${\overline{P}}_{cut{t}_{dry}}$.

$$ \varDelta {P}_{cut{t}_{j- dry}}\left[\%\right]=100\cdot \frac{{\overline{\varDelta P}}_{cut{t}_{j- dry}}}{{\overline{P}}_{cut{t}_{dry}}}=100\cdot \frac{\left({\overline{P}}_{cut{t}_j}-{\overline{P}}_{cut{t}_{dry}}\right)}{{\overline{P}}_{cut{t}_{dry}}} $$

(12)

According to Eq. 12, it is worth noting that $\Delta {P}_{cut{t}_{j- dry}}$ is twofold. Indeed, at the numerator, the first term is proportional to the difference of the tangential cutting coefficients, while the second depends on the difference of the edge tangential cutting coefficients. More in details, the first term considers the difference in terms of the shear contribution to chip formation, while the second one takes into account the different tribological conditions between the cutting edge and the processed material (i.e. friction, ploughing).

$$ \varDelta {P}_{cut{t}_{j- dry}}\left[\%\right]=100\cdot \frac{\left({K}_{t{c}_j}-{K}_{t{c}_{dry}}\right)\cdot {f}_z\cdot \left(\frac{a_e}{D}\right)+\frac{1}{2}\cdot \left({K}_{t{e}_j}-{K}_{t{e}_{dry}}\right)\cdot acos\left(1-\frac{2{a}_e}{D}\right)}{K_{t{c}_{dry}}\cdot {f}_z\cdot \left(\frac{a_e}{D}\right)+\frac{1}{2}\cdot {K}_{t{e}_{dry}}\cdot acos\left(1-\frac{2{a}_e}{D}\right)} $$

(13)

Equation 13 can be rewritten considering the cryogenic-dry comparison (Eq. 14) and the conventional-dry comparison respectively (Eq. 15).

$$ \varDelta {P}_{cut{t}_{cryo- dry}}\left[\%\right]=100\cdot \frac{\left({K}_{t{c}_{cryo}}-{K}_{t{c}_{dry}}\right)\cdot {f}_z\cdot \left(\frac{a_e}{D}\right)+\frac{1}{2}\cdot \left({K}_{t{e}_{cryo}}-{K}_{t{e}_{dry}}\right)\cdot acos\left(1-\frac{2{a}_e}{D}\right)}{K_{t{c}_{dry}}\cdot {f}_z\cdot \left(\frac{a_e}{D}\right)+\frac{1}{2}\cdot {K}_{t{e}_{dry}}\cdot acos\left(1-\frac{2{a}_e}{D}\right)} $$

(14)

$$ \varDelta {P}_{cut{t}_{conv- dry}}\left[\%\right]=100\cdot \frac{\left({K}_{t{c}_{conv}}-{K}_{t{c}_{dry}}\right)\cdot {f}_z\cdot \left(\frac{a_e}{D}\right)+\frac{1}{2}\cdot \left({K}_{t{e}_{conv}}-{K}_{t{e}_{dry}}\right)\cdot acos\left(1-\frac{2{a}_e}{D}\right)}{K_{t{c}_{dry}}\cdot {f}_z\cdot \left(\frac{a_e}{D}\right)+\frac{1}{2}\cdot {K}_{t{e}_{dry}}\cdot acos\left(1-\frac{2{a}_e}{D}\right)} $$

(15)

2.1.1 Cutting process model parameters identification

The identification of the cutting coefficients is typically performed exploiting experimental cutting force measurements, through a linear regression procedure. The force along the main machine axis direction can be experimentally measured (F_x(t), F_y(t) and F_z(t)) through force dynamometer, and the linked average contributions ($\overline{F_x},\overline{F_y},\overline{F_z}$) can even be analytically formulated (Eq. 16) [74].

$$ {\displaystyle \begin{array}{c}\overline{F_x}={\left\{\frac{Z\cdot {a}_p\cdot {f}_z}{8\pi}\cdot \left[{K}_{tc}\cdot \mathit{\cos}2{\varphi}_i-{K}_{rc}\left(2{\varphi}_i-\mathit{\sin}2{\varphi}_i\right)\right]+\frac{Z\cdot {a}_p}{2\pi}\cdot \left[-{K}_{te}\cdot \mathit{\sin}{\varphi}_i+{K}_{re}\cdot \mathit{\cos}{\varphi}_i\right]\right\}}_{\varphi_{st}}^{\varphi_{ex}}\\ {}\overline{F_y}={\left\{\frac{Z\cdot {a}_p\cdot {f}_z}{8\pi}\cdot \left[{K}_{tc}\cdot \left(2{\varphi}_i-\mathit{\sin}2{\varphi}_i\right)+{K}_{rc}\mathit{\cos}2{\varphi}_i\right]-\frac{Z\cdot {a}_p}{2\pi}\cdot \left[{K}_{te}\cdot \mathit{\cos}{\varphi}_i+{K}_{re}\cdot \mathit{\sin}{\varphi}_i\right]\right\}}_{\varphi_{st}}^{\varphi_{ex}}\\ {}\overline{F_z}=\frac{Z\cdot {a}_p}{2\pi}\cdot {\left[-{K}_{ac}\cdot {f}_z\cdot \mathit{\cos}{\varphi}_i+{K}_{ae}\cdot {\varphi}_i\right]}_{\varphi_{st}}^{\varphi_{ex}}\end{array}} $$

(16)

For the analysed milling operation, we can consider Eq. 17.

$$ {\displaystyle \begin{array}{c}{\varphi}_{st}=0;{\varphi}_{ex}\\ {}{\varphi}_{ex}=\mathrm{acos}\left(1-\frac{2{a}_e}{D}\right)\end{array}} $$

(17)

According to the multiple linear regression theory [75], the unknown cutting force coefficients can be estimated by solving Eq. 18:

$$ \boldsymbol{y}=\boldsymbol{X}\cdot \boldsymbol{\beta} +\boldsymbol{\epsilon} $$

(18)

where β is the vector of the unknown (p = 6) regression coefficients (cutting coefficients), X the vector of the regressor variables and y the vector that contains the response variables (average cutting forces). For the considered case, they can be formalized using Eq. 19. ϵ is the random error. n is the number of cutting tests that is the number of different experimental cutting conditions. As adequately described in Section 2.1.2, six different cutting conditions (n = 6) were tested for each tested CL solution.

$$ \boldsymbol{X}=\left\{\begin{array}{c}{X}_1^{\prime}\\ {}\\ {}\begin{array}{c}{X}_k^{\prime}\\ {}\\ {}{X}_n^{\prime}\end{array}\end{array}\right\};\kern0.5em \boldsymbol{\beta} =\left\{\begin{array}{c}{K}_{tc}\\ {}{K}_{rc}\\ {}\begin{array}{c}{K}_{ac}\\ {}{K}_{te}\\ {}\begin{array}{c}{K}_{re}\\ {}{K}_{ae}\end{array}\end{array}\end{array}\right\};\kern0.5em \boldsymbol{\epsilon} =\left\{\begin{array}{c}\begin{array}{c}\begin{array}{c}{\epsilon}_{x1}\\ {}{\epsilon}_{y1}\\ {}{\epsilon}_{z1}\end{array}\\ {}\cdots \\ {}\begin{array}{c}{\epsilon}_{xk}\\ {}{\epsilon}_{yk}\\ {}{\epsilon}_{zk}\end{array}\end{array}\\ {}\cdots \\ {}\begin{array}{c}{\epsilon}_{xn}\\ {}{\epsilon}_{yn}\\ {}{\epsilon}_{zn}\end{array}\end{array}\right\};\boldsymbol{y}=\left\{\begin{array}{c}\begin{array}{c}\begin{array}{c}\overline{F_{x1}}\\ {}\overline{F_{y1}}\\ {}\overline{F_{z1}}\end{array}\\ {}\cdots \\ {}\begin{array}{c}\overline{F_{xk}}\\ {}\overline{F_{yk}}\\ {}\overline{F_{zk}}\end{array}\end{array}\\ {}\cdots \\ {}\begin{array}{c}\overline{F_{xn}}\\ {}\overline{F_{yn}}\\ {}\overline{F_{zn}}\end{array}\end{array}\right\} $$

(19)

The k-th element X_k of vector X can be properly formulated using Eq. 16 and Eq. 20.

$$ \left[\begin{array}{ccc}{\left.\begin{array}{c}Z{a}_{pk}{f}_{zk}\\ {}/\left(8\pi \right)\mathit{\cos}\\ {}\left(2{\varphi}_k\right)\end{array}\right|}_{\varphi_{st\ k}}^{\varphi_{ex\ k}}& {\left.\begin{array}{c}Z{a}_{pk}{f}_{zj}\\ {}/\left(8\pi \right)\left(\begin{array}{c}2{\varphi}_k\\ {}-\mathit{\sin}\\ {}\left(2{\varphi}_k\right)\end{array}\right)\end{array}\right|}_{\varphi_{st\ k}}^{\varphi_{ex\ k}}& 0\\ {}{\left.\begin{array}{c}-Z{a}_{pk}{f}_{zk}\\ {}/\left(8\pi \right)\left(\begin{array}{c}2{\varphi}_k-\mathit{\sin}\\ {}\left(2{\varphi}_k\right)\end{array}\right)\end{array}\right|}_{\varphi_{st\ k}}^{\varphi_{ex\ k}}& {\left.\begin{array}{c}Z{a}_{pk}{f}_{zk}\\ {}/\left(8\pi \right)\mathit{\cos}\\ {}\left(2{\varphi}_i\right)\end{array}\right|}_{\varphi_{st\ k}}^{\varphi_{ex\ k}}& 0\\ {}0& 0& \begin{array}{c}-Z{a}_{pk}\\ {}/\left(2\pi \right)\cdot {f}_{zk}{\left.\begin{array}{c}\mathit{\cos}\\ {}\left(2{\varphi}_i\right)\end{array}\right|}_{\varphi_{st\ k}}^{\varphi_{ex\ k}}\end{array}\\ {}{\left.\begin{array}{c}-Z{a}_{pk}\\ {}/\left(2\pi \right)\mathit{\sin}\left({\varphi}_i\right)\end{array}\right|}_{\varphi_{st\ k}}^{\varphi_{ex\ k}}& {\left.\begin{array}{c}-Z{a}_{pk}\\ {}/\left(2\pi \right)\mathit{\cos}\left({\varphi}_i\right)\end{array}\right|}_{\varphi_{st\ j}}^{\varphi_{ex\ j}}& 0\\ {}{\left.\begin{array}{c}Z{a}_{pk}\\ {}/\left(2\pi \right)\mathit{\cos}\left({\varphi}_i\right)\end{array}\right|}_{\varPhi_{st\ k}}^{\varphi_{ex\ k}}& {\left.\begin{array}{c}-Z{a}_{pk}\\ {}/\left(2\pi \right)\mathit{\sin}\left({\varphi}_i\right)\end{array}\right|}_{\varphi_{st\ j}}^{\varphi_{ex\ j}}& 0\\ {}0& 0& \begin{array}{c}-Z{a}_{pk}\\ {}/\left(2\pi \right){\left.{\varphi}_k\right|}_{\varphi_{st\ k}}^{\varphi_{ex\ k}}\end{array}\end{array}\right]={X}_k $$

(20)

The minimization of the least square L = ϵ ′ ϵ brings to the unknown parameters (Eq. 21).

$$ \hat{\boldsymbol{\beta}}={\left({\boldsymbol{X}}^{\prime}\boldsymbol{X}\right)}^{-\mathbf{1}}\boldsymbol{X}^{\prime}\boldsymbol{y} $$

(21)

Moreover, it was computed the confidence interval of each estimated $\hat{\beta_q}$ parameter (Eq. 22):

$$ \hat{\beta_q}-{t}_{\frac{\alpha }{2},3n-p}\sqrt{{\hat{\sigma}}^2{C}_{qq}}\le {\beta}_q\le \hat{\beta_q}+{t}_{\frac{\alpha }{2},3n-p}\sqrt{{\hat{\sigma}}^2{C}_{qq}};\kern0.5em {C}_{qq}=\mathit{\operatorname{diag}}{\left({\boldsymbol{X}}^{\prime}\boldsymbol{X}\right)}^{-\mathbf{1}};\kern0.5em {\hat{\sigma}}^2=\frac{{\boldsymbol{y}}^{\prime}\boldsymbol{y}-\hat{\boldsymbol{\beta}}^{\prime}\boldsymbol{X}^{\prime}\boldsymbol{y}}{3n-p} $$

(22)

where C_qq is the qq^th element of the (X^′X)⁻¹matrix, ${\hat{\sigma}}^2$ the estimated variance and ${t}_{\frac{\alpha }{2},3n-p}$ is the t-Student with 3n-p degree of freedom with a confidence level α.

In order to analyse what are the cutting coefficients more sensitive to CL, a series of 2-sample t test considering the j1-j2 pairs were performed using Eq. 23 [75]. More specifically, the following pairs were considered: dry-conventional cooling, cryogenic-conventional and dry-cryogenic. For each 2-sample t, the p value was estimated. ν_q is the number of degrees of freedom.

$$ {\displaystyle \begin{array}{c}{t}_{0-q}=\frac{{\hat{\beta}}_{q-j1}-{\hat{\beta}}_{q-j2}}{\sqrt{\frac{C_{qq-j1}}{n_{j1}}+\frac{C_{qq-j2}}{n_{j2}}}}\ \\ {}{\nu}_q=\frac{{\left(\frac{C_{qq-j1}}{n_{j1}}+\frac{C_{qq-j2}}{n_{j2}}\right)}^2}{\frac{{\left(\frac{C_{qq-j1}}{n_{j1}}\right)}^2}{n_{j1}-1}+\frac{{\left(\frac{C_{qq-j2}}{n_{j2}}\right)}^2}{n_{j2}-1}}\end{array}} $$

(23)

2.1.2 Experiments and mechanistic model parameters identification

A Mandelli machine with a horizontal spindle (Fig. 3a) was used for the cutting tests. The machine was equipped with a Capellini Xevo electro-spindle with the maximum available torque of 160 Nm, and it can achieve up to Ω = 8000 rev/min. Both LN and lubricant were injected to the cutting zone through the nozzles of a commercial indexable cutter. For what concerns cryogenic cutting, a specific delivery system and a cryogenic head were used Fig. 3b).

Fig. 3

Experimental set-up for cutting tests: a force sensor and b cryogenic head

The cutting forces were measured through the Kistler dynamometer 9255B with the charge amplifier type 5070A. Preliminary dynamic tests on the dynamometer/piece system were performed in order to estimate the available bandwidth for the force measurements (70 Hz along X, 75 Hz along Z and 300 Hz along Y). Moreover, it was checked that the dynamometer performances were not compromised during cryogenic cutting since the dynamometer temperature was in the suggested working range. This was guaranteed machining the upper part of the piece (far from the dynamometer (Fig. 3a)) and using a properly designed system form vacuuming the evaporated nitrogen from the machine tool working area. A similar verification was made performing temperature measurements on the spindle side in order to prevent any spindle bearing damage.

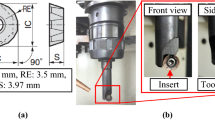
The tool used for the test was an indexable (Z = 2) commercial cutter (R390-020B20-11L) designed and manufactured by Sandvik Coromant. The nozzles diameter is equal to 2.5 mm. The tool was suitable both for contouring and for slotting due to its lead angle χ = 90°. The utilized inserts, the R390-11 T3 08M-MM S30T type is featured with a physical vapour deposition PVD TiAlN coating developed by Sandvik Coromant, and it is an industrial state-of-art solution for processing Ti6Al4V or other HRAs. Details on the tool geometry and on the cutting tool profile can be observed in Fig. 4a and b. More specifically, Fig. 4b shows the analysis performed with the scanning electron microscope SEM of the cross section of the cutting edge where it is clearly visible the TiAlN coating. According to the results already achieved, Fig. 4c and d show the estimated velocity profile and the liquid volumetric ratio close to the insert [45]. For what concerns the LN consumption, the overall mass flow rate ${\dot{m}}_{LN}$was roughly measured through differential measurements of the weight of the dewar during cutting tests. Setting the LN pressure inside the dewar to press = 3.5 bar, the mass flow rate was $\overline{{\dot{m}}_{LN}}\cong 45 kg/h$. Regarding conventional cutting, the lubricant flow rate was measured through a flow sensor ($\overline{Q_{lub}}=20.8\ l/\mathit{\min}$), refer to Section 2.3.2 for more details.

Fig. 4

Tool geometry and simulation of the adopted cryogenic cooling conditions [45]. a) is the insert geometry b) the cross-section of the cutting edge (Scanning Electron Microsccope) c) CFD velocity contour d) CFD simulation results (close to the cutting area)

An experimental campaign of milling tests was adequately designed for estimating the cutting coefficients ${\hat{\boldsymbol{\beta}}}_{\boldsymbol{j}}$ for each cooling lubricating condition “j”. As suggested by [74], the main cutting parameter to be varied for this purpose is the feed f_z. In this research, f_z was set in a range from 0.08 to 0.2 mm/tooth, and three discrete values were considered. Although the mechanistic model does not consider the cutting velocity dependence, two values for v_c were considered (50 m/min and 70 m/min). Without any loss of generality, other milling parameters were considered blocked factors (axial depth of cut a_p = 3 mm and radial depth of cut a_e = 5 mm).

As summarized in Table 2, the combination of the considered factors (f_z, three levels; v_c, two levels) brought to n = 6 different cutting conditions that were tested (in random order) just in a single pass in order to limit the tool wear. For this purpose, specific part programs in G-code in which the spindle speed Ω and the feed rate V_f = f_zZΩ were changed according to run order were developed. A similar strategy was adopted even for conventional cutting (Table 3). For each tested CL condition, brand-new inserts were used to prevent any effects due to the tool wear. Even the wear occurred at the end of each single pass can be considered negligible. Indeed, no specific trends in the cutting forces are visible in Fig. 5.

Table 2 Cutting test parameters and run order (cryogenic and dry cutting tests)

Table 3 Cutting test parameters and run order (conventional cooling tests)

Fig. 5

Cutting force measurements during conventional cutting tests (a) (a_p = 3 mm, a_e = 5 mm) and (b) F_y details f_z = 0.2 mm/tooth v_c = 50 m/min

In Fig. 5, the measured cutting forces acquired during the execution of conventional cutting tests were reported. Similar results were also available for dry and cryogenic cutting. The tested cutting conditions (n = 6) are clearly visible in Fig. 5a where the forces along the machine axis (F_x, F_y and F_z) are reported. In Fig. 5b, details of F_y at v_c = 50 m/min and adopting f_z = 0.2 mm/tooth can be appreciated.

Some preliminary considerations on the measured cutting forces need to be carried out. In order to analyse the effect of the CL technology on the cutting mechanisms, the cutting forces along y axis associated to dry, cryogenic and conventional milling were compared in Fig. 6b. Before comparing the forces, an average processing was first carried out: several cutting force profiles ${F}_{k_r}(t)$ (i.e. Fig. 6a) were synchronized and averaged using Eq. 24. k refers to the machine direction, r is the index for the cutting force profile and m = 30 is the number of profiles used for the averaging process. Moreover, the confidence interval 95% can even be computed using a relationship similar to the one reported in Eq. 22 and knowing ${{\hat{\sigma}}^2}_{F_k}(t)$ (see Eq. 24).

$$ {F}_k(t)=\frac{1}{m}\sum \limits_{r=1}^{r=m}{F}_{k_r}(t);\kern0.5em {{\hat{\sigma}}^2}_{F_k}(t)=\frac{1}{m-1}\sum \limits_{r=1}^{r=m}{\left({F}_{k_r}(t)-{F}_k(t)\right)}^2 $$

(24)

Fig. 6

(a) Forces on teeth and (b) cryogenic-dry-conventional cutting force comparison

It is worth noting that CL strategy heavily affected the experimental cutting forces. More specifically, it can be observed that cryogenic cooling made the cutting forces lower. This could bring to interesting results in terms of energy saving with respect to dry cutting, at least considering the cutting process level. So far, no similar studies focused on cutting forces in cryogenic milling have been found. Some research works (dealing with other machining processes) show conflicting results (i.e. [60, 63, 68, 69]. This could be related to the fact that the effects of the cryogenic cooling are very sensitive to the experimental set-up and to the LN injection specifications.

In order to identify the cutting coefficients ${\hat{\boldsymbol{\beta}}}_{\boldsymbol{j}}$ (Eq. 21) the measured cutting forces, in all the tested conditions, were averaged, and both the y_j vector and the matrix X_j were arranged according to Eq. 19 and Eq. 20. The average cutting forces and the regression curves were reported in Fig. 7. A good fitting is also confirmed by R² and R²_adj that are higher than 0.991 in all the cases. The hypotheses on the residuals (normality, homogeneity of the variance, independency of the residuals) were also checked. The identified parameters (Table 4), together with the 95% confidence intervals, of the mechanistic model are shown in Fig. 8.

Fig. 7

Experimental average cutting forces and fitting curves: conventional cooling - dry cutting - cryogenic cooling

Table 4 Identified cutting coefficients – dry-cryogenic – conventional cooling

Fig. 8

Identified cutting coefficients in different cooling lubrication conditions (dry, cryogenic and conventional cooling) with the corresponding 95% CI

The analysis confirms that the LN2 strongly affected the cutting mechanisms and the tribological aspects.

More in details, the results of the 2-sample t test carried out with Eq. 23 are reported in Fig. 9. The analysis shows that K_te and K_re are both statistically affected by the CL since the associated p values are very low. It can be even observed that K_tc cannot be considered different only for the dry-conventional pair.

Fig. 9

Effect of the CL methodology on the identified cutting coefficients – p values associated to the performed 2-sample t tests

K_tc, that is, the cutting coefficient used for considering the shear effect in the chip formation, was considerably reduced by the cryogenic coolant both with respect to dry and conventional cutting. This agrees with the results reported in [71] that used the coefficients for assessing the turning stability but disagrees with some considerations found in literature.

For instance, [72] guessed that cold strengthening of the material makes the cutting forces increasing, but generally this effect is contrasted and dominated by the friction reduction that makes the cutting forces reducing. Indeed, in the present research, such friction reduction was observed too. This was confirmed by the severe reduction noted in K_te and K_re. An plausible explanation of the origin of such effect was provided by [70]. The reduction of the coefficients was observed even for conventional cooling with respect to dry cutting even if it was expected due to the presence of the lubricant. Some analysed literature works (i.e. [32, 68]) guessed that the LN tends to evaporate, and consequently it creates a hydraulic cushion that reduces the friction between the contact surfaces. This research confirms the results found by [63] in turning that observed the reduction of the main force but a slight increment of the thrust force. Although milling is a different process, a similar effect was observed on the tangential force and the radial force as inferred by the identified coefficients K_tc and K_rc.

As a confirmation of the adequacy of the proposed modelling approach, in Fig. 10 the experimental and the simulated cutting forces (with the identified coefficients, Table 4) along X and Y were compared. The experimental forces only exhibit additional dynamics most likely linked to the machine and dynamometer resonances. Similar results were also achieved for dry and cryogenic cutting. The model validation was performed considering the following cutting parameters: v_c = 50 m/min, f_z = 0.2 mm/tooth, a_e = 5 mm and a_p = 3 mm.

Fig. 10

Cutting force X and Y direction – experimental and simulated comparison (conventional cutting – validation point)

2.2 Power assessment at the spindle level

To perform a power assessment at the spindle level, the contribution of the spindle (in the analysed case a permanent magnet synchronous motors PMSM, brushless) needs to be added to the cutting power that was already formalized. For this purpose, a spindle system model was developed (Section 2.2.1).

2.2.1 Spindle modelling

It was assumed, according to [76, 77], that the mechanical power Pmec_spindle and the Joule losses Ploss_spindle are the main contributions to the spindle power P_spindle (Eq. 25).

$$ {P}_{\mathrm{spindle}}= Pme{c}_{\mathrm{spindle}}+ Plos{s}_{\mathrm{spindle}} $$

(25)

Moreover, according to Eq. 26, static friction (associated to the parameter μ_s), viscous friction (linked to μ_v), the inertial term (through J_spindle) and the one linked to the cutting torque Torque_cut all contribute to the mechanical power Pmec_spindle computation.

$$ Pme{c}_{\mathrm{spindle}}=\left({\mu}_s\cdot \operatorname{sign}\left({\omega}_{\mathrm{spindle}}\right)+{\mu}_v\cdot {\omega}_{\mathrm{spindle}}+{J}_{\mathrm{spindle}}\cdot {\dot{\omega}}_{\mathrm{spindle}}+{Torque}_{\mathrm{cut}}\right)\cdot {\omega}_{\mathrm{spindle}}={k}_{t_{\mathrm{spindle}}}\cdot {i}_{q- rm{s}_{\mathrm{spindle}}}\cdot {\omega}_{\mathrm{spindle}} $$

(26)

The cutting torque Torque_cut is directly computed from the cutting power as follows: Torque_cut = P_cut/ω_spindle. The mechanical power can even be calculated considering the torque constant ${k}_{t_{\mathrm{spindle}}}$ and the root mean square (rms) quadrature current ${i}_{q- rm{s}_{\mathrm{spindle}}}$ [78]. The Joule losses can be analytically formalized through Eq. 27 where R_spindle is the motor phase resistance and ${i}_{q_{\mathrm{spindle}}}$ is the spindle quadrature current.

$$ Plos{s}_{\mathrm{spindle}}={R}_{\mathrm{spindle}}\cdot {i}_{q_{\mathrm{spindle}}}^2 $$

(27)

Considering Eq. 28, assuming that during cutting the inertial contribution can be neglected (${\dot{\omega}}_{\mathrm{spindle}}=0$) and introducing the dependence on the adopted cooling condition j, Eq. 25 can be re-written as follows (see Eq. 29):

$$ {i}_{q_{\mathrm{spindle}}}=\sqrt{2}\cdot \frac{Pme{c}_{\mathrm{spindle}}}{k_{t_{\mathrm{spindle}}}\cdot {\omega}_{\mathrm{spindle}}};{i}_{q- rm{s}_{\mathrm{spindle}}}=\frac{Pme{c}_{\mathrm{spindle}}}{k_{t_{\mathrm{spindle}}}\cdot {\omega}_{\mathrm{spindle}}} $$

(28)

Moreover, the main affecting cutting process parameters (v_c, a_e/D, f_z) were underlined

$$ {P}_{\mathrm{spindl}{\mathrm{e}}_j}\left({v}_c,{a}_e/D,{f}_z\right)={\omega}_{\mathrm{spindl}\mathrm{e}}\cdot \left({\mu}_s\cdot \operatorname{sign}\left({\omega}_{\mathrm{spindl}\mathrm{e}}\right)+{\mu}_v\cdot {\omega}_{\mathrm{spindl}\mathrm{e}}+\frac{P_{cu{t}_j}}{\omega_{\mathrm{spindl}\mathrm{e}}}\right)+{R}_{\mathrm{spindl}\mathrm{e}}\cdot {\left(\frac{\sqrt{2}}{K_{t_{\mathrm{spindl}\mathrm{e}}}}\cdot \left({\mu}_s\cdot \operatorname{sign}\left({\omega}_{\mathrm{spindl}\mathrm{e}}\right)+{\mu}_v\cdot {\omega}_{\mathrm{spindl}\mathrm{e}}+\frac{P_{cu{t}_j}}{\omega_{\mathrm{spindl}\mathrm{e}}}\right)\right)}^2 $$

(29)

Once the spindle motor power was formalized, the following power comparisons can be defined, and the power assessment can be performed (Eq. 30 and Eq. 31). Both $\Delta {P}_{\mathrm{spindl}{\mathrm{e}}_{\mathrm{conv}-\mathrm{dry}}}$ and $\Delta {\mathrm{P}}_{\mathrm{spindl}{\mathrm{e}}_{\mathrm{cryo}-\mathrm{dry}}}$ were normalized with respect to ${P}_{\mathrm{spindl}{\mathrm{e}}_{\mathrm{dry}}}$.

$$ \varDelta {P}_{\mathrm{spindl}{\mathrm{e}}_{\mathrm{conv}-\mathrm{dry}}}\left[\%\right]\left({v}_c,{a}_e/D,{f}_z\right)=100\frac{\left({{\mathrm{P}}_{\mathrm{spindl}\mathrm{e}}}_{\mathrm{conv}}\left({v}_c,{a}_e/D,{f}_z\right)\right)-\left({{\mathrm{P}}_{\mathrm{spindl}\mathrm{e}}}_{\mathrm{dry}}\left({v}_c,{a}_e/D,{f}_z\right)\right)}{P_{\mathrm{spindl}{\mathrm{e}}_{\mathrm{dry}}}\left({v}_c,{a}_e/D,{f}_z\right)} $$

(30)

$$ \varDelta {P}_{\mathrm{spindl}{\mathrm{e}}_{\mathrm{cryo}-\mathrm{dry}}}\left[\%\right]\left({v}_c,{a}_e/D,{f}_z\right)=100\frac{\left({{\mathrm{P}}_{\mathrm{spindl}\mathrm{e}}}_{\mathrm{cryo}}\left({v}_c,{a}_e/D,{f}_z\right)\right)-\left({{\mathrm{P}}_{\mathrm{spindl}\mathrm{e}}}_{\mathrm{dry}}\left({v}_c,{a}_e/D,{f}_z\right)\right)}{P_{\mathrm{spindl}{\mathrm{e}}_{\mathrm{dry}}}\left({v}_c,{a}_e/D,{f}_z\right)} $$

(31)

2.2.2 Experiments and spindle model parameters identification

In order to identify the spindle model parameters of Eq. 26, some experiments were carried out on Capellini electrospindle. According to the procedure describe in [78], no load (Torque_cut = 0) tests on the electrospindle were performed. Specifically, the following sequences of speeds were set to the spindle: 1000 rpm, 1500 rpm, 2000 rpm, 2500rmp, 3000 rpm, 2500 rpm, 2000 rpm, 1500 rpm, 1000 rpm and 0 rpm. During the tests, the spindle speed ω_spindle and the ${i}_{q-\mathrm{rm}{\mathrm{s}}_{\mathrm{s}\mathrm{pindle}}}$ were acquired through the numerical controller (NC) (Siemens Solution Line). The spindle acceleration ${\dot{\omega}}_{\mathrm{spindle}}$ was numerically computed deriving the ω_spindle.

$$ {K}_{t_{\mathrm{s}\mathrm{pindle}}}\cdot {i}_{q-\mathrm{rm}{\mathrm{s}}_{\mathrm{s}\mathrm{pindle}}}(t)={\mu}_s\cdot \operatorname{sign}\left({\omega}_{\mathrm{s}\mathrm{pindle}}(t)\right)+{\mu}_v\cdot {\omega}_{\mathrm{s}\mathrm{pindle}}(t)+{J}_{\mathrm{s}\mathrm{pindle}}\cdot {\dot{\omega}}_{\mathrm{s}\mathrm{pindle}}(t) $$

(32)

Rearranging Eq. 32, the unknown parameters ${\boldsymbol{\beta}}_{\mathbf{spindle}}=\left[{\mu}_s\kern0.5em {\mu}_v\kern0.5em {J}_{\mathrm{spindle}}\right]$ can be estimated through a least square regression (LSR), (Eqs. 33 and 34).

$$ {\boldsymbol{y}}_{\mathbf{spindle}}={\boldsymbol{X}}_{\mathbf{spindle}}\cdot {\boldsymbol{\beta}}_{\mathbf{spindle}};\kern0.5em {\hat{\boldsymbol{\beta}}}_{\boldsymbol{spindle}}=\left[\begin{array}{ccc}{\hat{\mu}}_s& {\hat{\mu}}_v& {\hat{J}}_{spindle}\end{array}\right]={\left({\boldsymbol{X}}_{\mathbf{spindle}}^{\prime }\ {\boldsymbol{X}}_{\mathbf{spindle}}\right)}^{-\mathbf{1}}{\boldsymbol{X}}_{\mathbf{spindle}}^{\prime }{\boldsymbol{y}}_{\mathbf{spindle}} $$

(33)

$$ {\boldsymbol{X}}_{\mathbf{spindle}}=\left[\begin{array}{ccc}\operatorname{sign}\left({\omega}_{\mathrm{s}\mathrm{pindle}}\left({t}_1\right)\right)& {\omega}_{\mathrm{s}\mathrm{pindle}}\left({t}_1\right)& {\dot{\omega}}_{spindle}\\ {}\begin{array}{c}\operatorname{sign}\left({\omega}_{\mathrm{s}\mathrm{pindle}}\left({t}_2\right)\right)\\ {}\vdots \end{array}& \begin{array}{c}{\omega}_{\mathrm{s}\mathrm{pindle}}\left({t}_2\right)\\ {}\vdots \end{array}& \begin{array}{c}{\dot{\omega}}_{spindle}\\ {}\vdots \end{array}\\ {}\operatorname{sign}\left({\omega}_{\mathrm{s}\mathrm{pindle}}\left({t}_n\right)\right)& {\omega}_{\mathrm{s}\mathrm{pindle}}\left({t}_n\right)& {\dot{\omega}}_{spindle}\end{array}\right];\kern0.5em {\boldsymbol{y}}_{\mathbf{spindle}}={K}_{t_{\mathrm{s}\mathrm{pindle}}}\left[\begin{array}{c}{i}_{q-\mathrm{rm}{\mathrm{s}}_{\mathrm{s}\mathrm{pindle}}}\left({t}_1\right)\\ {}\begin{array}{c}{i}_{q-\mathrm{rm}{\mathrm{s}}_{\mathrm{s}\mathrm{pindle}}}\left({t}_2\right)\\ {}\vdots \end{array}\\ {}{i}_{q-\mathrm{rm}{\mathrm{s}}_{\mathrm{s}\mathrm{pindle}}}\left({t}_n\right)\end{array}\right] $$

(34)

The identified parameters, together with the ${K}_{t_{\mathrm{spindle}}}$ and R_spindle are reported in Table 5. ${K}_{t_{\mathrm{spindle}}}$ and R_spindle were taken from the catalogue, but R_spindle value was also measured through a digital multimeter.

Table 5 Spindle model parameters

The identified model was also preliminary validated comparing the estimated electrical power ${\hat{P}}_{\mathrm{spindle}}(t)$ (Eq. 35) and the corresponding measured quantity. The comparison is reported in Fig. 11.

$$ {\hat{P}}_{\mathrm{spindle}}(t)={\omega}_{\mathrm{spindle}}(t)\cdot \left({\hat{\mu}}_s\cdot \operatorname{sign}\left({\omega}_{\mathrm{spindle}}(t)\right)+{\hat{\mu}}_v\cdot {\omega}_{\mathrm{spindle}}(t)+{\hat{J}}_{\mathrm{spindle}}\cdot {\dot{\omega}}_{\mathrm{spindle}}\right)+{R}_{\mathrm{spindle}}\cdot {\left(\sqrt{2}\cdot \frac{1}{K_{t_{\mathrm{spindle}}}}\cdot \left({\hat{\mu}}_s\cdot \operatorname{sign}\left({\omega}_{\mathrm{spindle}}(t)\right)+{\hat{\mu}}_v\cdot {\omega}_{\mathrm{spindle}}(t)+{\hat{J}}_{\mathrm{spindle}}\cdot {\dot{\omega}}_{\mathrm{spindle}}(t)\right)\right)}^2 $$

(35)

Fig. 11

Spindle power during no-load tests: estimated (identified model ID) and experimentally measured comparison

It can be noted that the estimated power matches quite well the experimentally measured power.

The electrical power absorbed by the spindle was acquired through a power meter. Figure 10 describes the adopted experimental set-up. The power meter can simultaneously acquire the powers of up to 5 three-phase loads. For each load, the three-phase currents and the corresponding voltages are acquired at a high sampling rate (up to 20 kHz), and the linked power can be computed. The currents are measured through LEM rings. In this specific case, the P_spindle is computed according to Eq. 36 where it can be observed the phase currents and the associated voltages.

$$ {P}_{\mathrm{spindl}\mathrm{e}}(t)={i}_{{\mathrm{spindl}\mathrm{e}}_1}(t)\cdot {V}_{{\mathrm{spindl}\mathrm{e}}_1}(t)+{i}_{{\mathrm{spindl}\mathrm{e}}_2}(t)\cdot {V}_{{\mathrm{spindl}\mathrm{e}}_2}(t)+{i}_{\mathrm{spindl}{\mathrm{e}}_3}(t)\cdot {V}_{{\mathrm{spindl}\mathrm{e}}_3}(t) $$

(36)

The signal acquisition was carried out by National Instruments© boards, and the power processing was performed in Labview© Fig. 12.

Fig. 12

Power measurements set-up

2.3 Power assessment at the machine level

In this section, the power assessment was carried out at the machine level. This means that even the feeding system was considered in the power computation. This perspective is rather common not only in literature (Rajemi et al. [79]) but even in industry (ISO 14955 – part II [80]).

Since for both dry and cryogenic cutting the feeding contribution is null, in this section, the sole feeding system model for conventional cooling was developed. Indeed, the liquid nitrogen is fed directly from the dewar without the need of supplementary auxiliaries.

2.3.1 Conventional cooling: feeding system modelling

In the analysed machine, the lubricant is fed in the cutting area through the inner tool nozzles by a high-pressure pump. Moreover, to get back the used lubricant from the machine, a suctioning pump (Brinkmann SFL 1350) is installed on the machine. Until the wasted lubricant is fully pumped back to the sump for being reused, the suctioning pump is kept switched on. The suctioning pump is switched off when the tank (characterized by its volume V_{tank − max}) is filled.

The power consumption of the high-pressure pump depends on the working condition (in terms of flow rate Q_lub, pressure Pres_HP and power absorption P_feed) that is related to the specific tool mounted on the spindle. If the tool is changed, even the corresponding hydraulic load changes and consequently the corresponding working condition. The high-pressure pump was described by Eqs. 37 and 38. More specifically, for the sake of simplicity, it was decided to adopt a quadratic model [81] to describe the dependence of the feeding pressure Pres_HP on the lubricant volumetric flow rate Q_lub.

$$ {Pres}_{\mathrm{HP}}\left({Q}_{\mathrm{lub}}\right)={a}_2\cdot {Q}_{\mathrm{lub}}^2+{a}_1\cdot {Q}_{\mathrm{lub}}+{a}_0 $$

(37)

a₀, a₁and a₂ are the model parameters that were properly identified exploiting specifically conceived experiments (see Section 2.3.2).

For what concerns the high-pressure pump power P_feed, a linear model that describes the dependence on the pressure and flow rate product Q_lub ∙ Pres_HP was proposed. Even in this case, the model parameters (b₀ and b₁) were identified through experimental measurements (Section 2.3.2).

$$ {P}_{\mathrm{feed}}\left({Q}_{\mathrm{lub}}\right)={b}_1\bullet {Q}_{\mathrm{lub}}\cdot Pre{s}_{\mathrm{HP}}+{b}_0 $$

(38)

Referring to the suctioning pump, its behaviour can be properly explained through Fig. 13 where both the amount of lubricant V_tank in the tank and the pump power were shown P_suct(t). According to the pump specifications, it was assumed that the power consumption is constant P_{suct − on} when the pump is active. More specifically, it was shown that, depending on the Q_lub, the suctioning pump can be switched on more or less frequently. For instance, if Q_lub1 < Q_lub2 (Q_lub3 < Q_lub1), the tank is filled slower Δt_off1 > Δt_off1 and it is taken less time to get back the lubricant Δt_on1 < Δt_on2. For sake of clarity, Δt_off is the time interval in which the suctioning pump is not working, while Δt_on is the time interval in which the suctioning pump is working. The explained behaviour can be analytically described by Eqs. 39 and 40. Q_suct is the suctioning flow rate and it was assumed to be constant.

$$ \Delta {t}_{\mathrm{off}}=\frac{V_{\mathrm{tank}-\max }}{Q_{\mathrm{lub}}\ } $$

(39)

$$ \Delta {t}_{\mathrm{on}}=\frac{-{V}_{\mathrm{tank}-\max }}{Q_{\mathrm{lub}}-{Q}_{\mathrm{suct}}\ } $$

(40)

Fig. 13

Suction pump behaviour

The average power of the suctioning pump ${P}_{\mathrm{suct}-\mathrm{a}{\mathrm{v}}_{\mathrm{conv}}}$ can be computed using Eq. 41.

$$ {P}_{\mathrm{suct}-\mathrm{a}{\mathrm{v}}_{\mathrm{conv}}}\left({Q}_{\mathrm{lub}}\right)=\frac{P_{\mathrm{suct}-\mathrm{on}}\cdot \varDelta {t}_{\mathrm{on}}}{\varDelta {t}_{\mathrm{on}}+\varDelta {t}_{\mathrm{off}}} $$

(41)

The overall power ${P}_{\mathrm{feed}-\mathrm{suc}{\mathrm{t}}_{\mathrm{conv}}}$ absorbed by the auxiliaries in conventional cooling can thus be expressed by Eq. 42.

$$ {P}_{feed- suc{t}_{conv}}\left({Q}_{lub}\right)={P}_{feed}+{P}_{suct- av} $$

(42)

Both for cryogenic cooling and dry cutting, the additional power contribution provided by the feeding system is null (${P}_{\mathrm{feed}-\mathrm{suc}{\mathrm{t}}_{\mathrm{dry}}}={P}_{\mathrm{feed}-\mathrm{suc}{\mathrm{t}}_{\mathrm{cryo}}}=0$).

The power assessment at the feeding level (machine) can therefore be carried out (Eq. 43).

$$ \varDelta {P}_{{\mathrm{feed}}_{j-\mathrm{dry}}}\left[\%\right]=100\frac{\left({P_{\mathrm{feed}}}_j+{P_{\mathrm{spindl}\mathrm{e}}}_j\right)-\left({P_{\mathrm{spindl}\mathrm{e}}}_{\mathrm{dry}}\right)}{P_{\mathrm{spindl}{\mathrm{e}}_{\mathrm{dry}}}} $$

(43)

If we focus first on the sole additional contribution due to the high-pressure pump, $\Delta {P}_{{\mathrm{feed}}_{\mathrm{conv}-\mathrm{dry}}}\left[\%\right]$ can be expressed by Eq. 44.

$$ \varDelta {P}_{{\mathrm{feed}}_{\mathrm{conv}-\mathrm{dry}}}\left[\%\right]\left({Q}_{\mathrm{lub}},\overline{v_c},{a}_e/D,{f}_z\right)=100\frac{\left({P_{\mathrm{feed}}}_{\mathrm{conv}}\left({Q}_{\mathrm{lub}}\right)+{P_{\mathrm{spindl}\mathrm{e}}}_{\mathrm{conv}}\left(\overline{v_c},{a}_{\mathrm{e}}/D,{f}_z\right)\right)-\left({P_{\mathrm{spindl}\mathrm{e}}}_{\mathrm{dry}}\left(\overline{v_c},{a}_e/D,{f}_z\right)\right)}{P_{\mathrm{spindl}{\mathrm{e}}_{\mathrm{dry}}}\left(\overline{v_c},{a}_e/D,{f}_z\right)} $$

(44)

It can be observed that the power assessment can be performed considering several process-related quantities such as Q_lub, v_c, a_e/D and f_z.

Since ${P}_{\mathrm{feed}-\mathrm{suc}{\mathrm{t}}_{\mathrm{dry}}}={P}_{\mathrm{feed}-\mathrm{suc}{\mathrm{t}}_{\mathrm{cryo}}}=0$, the cryogenic-dry power comparison at the feeding level coincides with the comparison performed at the spindle level (Eq. 45)

$$ \varDelta {P}_{{\mathrm{feed}}_{\mathrm{cryo}-\mathrm{dry}}}\left[\%\right]\left(\overline{v_c},{a}_e/D,{f}_z\right)\equiv \varDelta {P}_{{\mathrm{spindle}}_{\mathrm{cryo}-\mathrm{dry}}}\left[\%\right] $$

(45)

Even considering the contribution to the suctioning pump, the conventional-dry comparison can be formalized through the following relationships:

$$ \Delta {P}_{\mathrm{feed}-{\mathrm{suct}}_{\mathrm{conv}-\mathrm{dry}}}\left[\%\right]\left({Q}_{\mathrm{lub}},\overline{v_c},{a}_e/D,{f}_z\right)=100\frac{\left({P}_{\mathrm{feed}-\mathrm{suc}{\mathrm{t}}_{\mathrm{conv}}}\left({Q}_{\mathrm{lub}}\right)+{P_{\mathrm{spindl}\mathrm{e}}}_{\mathrm{conv}}\left(\overline{v_c},{a}_e/D,{f}_z\right)\right)-\left({P_{\mathrm{spindl}\mathrm{e}}}_{\mathrm{dry}}\left(\overline{v_c},{a}_e/D,{f}_z\right)\right)}{P_{\mathrm{spindl}{\mathrm{e}}_{\mathrm{dry}}}\left(\overline{v_c},{a}_e/D,{f}_z\right)} $$

(46)

While for the cryogenic-dry comparison, the previously considerations remain valid

$$ \varDelta {P}_{\mathrm{feed}-{\mathrm{suct}}_{\mathrm{cryo}-\mathrm{dry}}}\left[\%\right]\left(\overline{v_c},{a}_e/D,{f}_z\right)\equiv \varDelta {P}_{{\mathrm{spindle}}_{\mathrm{cryo}-\mathrm{dry}}}\left[\%\right] $$

(47)

2.3.2 Experiments and feeding system parameters identification

As previously anticipated, some experiments were carried out in order to identify the model parameters of Eqs. 37 and 38. More in details, to change the working condition of the high-pressure pump, some different tools were tested. Indeed, changing the tool (with different numbers and nozzle diameters), the related hydraulic losses change and consequently do the operating condition on the characteristic curve. For each tool, the high-pressure pump was switched on, and both the volumetric flow rate Q_lub and the feeding pressure Pres_HP were measured. The Q_lub was measured through a Rosemount 8705 flow sensor, while the lubricant pressure was measured with a Gefran 0-100 bar. The experimental set-up is reported in Fig. 14.

Fig. 14

Lubricant flow rate sensor and pressure sensor

During the tests, even the electrical power absorbed by the high-pressure pump was acquired through the already described power meter (see Fig. 10).

The achieved experiments results are reported in Fig. 15. More in details, Fig. 15 a shows that the experimental revealed Pres_HP − Q_lub pairs, while in Fig. 15b, the associated power consumptions can be observed. The black points correspond to the four tested conditions changing the tools. A red circle was used to underline the nominal condition used during the already described cutting tests.

Fig. 15

Conventional cooling: (a) high-pressure (HP) pump for lubricant – characteristic curve – experimental data and identified model and (b) absorbed electrical power – experimental data and identified model

On the same pictures, it can be observed the fitted models (Eqs. 37 and 38) obtained through a LSR approach. The estimated parameters (${\hat{a}}_0,{\hat{a}}_1,{\hat{a}}_2$, ${\hat{b}}_0$ and ${\hat{b}}_1$) are reported in Table 6.

Table 6 High-pressure pump – identified model parameters

For both the models, a quite high R-square value was obtained (close to 0.98). This demonstrates the adequacy of the proposed modelling approach.

For what concerns the suctioning pump, the performed power measurement confirmed the specifications reported on the catalogue P_suct. The other parameters of the model (from the pump and machine specifications) are reported in Table 7.

Table 7 Suction pump model parameters

2.4 Global power assessment

In this section, the analysis was extended to an upper level. Indeed, even the power required for producing the liquid nitrogen and the lubricant was considered (CED).

The global power can thus be computed through Eq. 48.

$$ {P}_{\mathrm{global}}={P}_{\mathrm{spindle}}+{P}_{\mathrm{feed}}+{P}_{\mathrm{suct}}+{P}_{\mathrm{CED}} $$

(48)

And the generic j^th comparison with respect to dry cutting can be formulated similar to what reported in the previous sections (Eq. 49);

$$ \varDelta {P}_{\mathrm{globa}{\mathrm{l}}_{j-\mathrm{dry}}}\left[\%\right]=100\frac{\left({P}_{\mathrm{CE}{\mathrm{D}}_j}+{P_{\mathrm{feed}}}_j+{P}_{\mathrm{suc}{\mathrm{t}}_j}+{P_{\mathrm{spindl}\mathrm{e}}}_j\right)-\left({P_{\mathrm{spindl}\mathrm{e}}}_{\mathrm{dry}}\right)}{P_{\mathrm{spindl}{\mathrm{e}}_{\mathrm{dry}}}} $$

(49)

where ${P}_{\mathrm{CE}{\mathrm{D}}_j}$is the cumulative power demand associated to the liquid nitrogen or the lubricant.

The assessment can be performed considering the conventional-dry pair (Eq. 50):

$$ \varDelta {P}_{\mathrm{globa}{\mathrm{l}}_{\mathrm{conv}-\mathrm{dry}}}\left[\%\right]\left({V}_{\mathrm{l}\mathrm{ub}},\overline{Q_{\mathrm{l}\mathrm{ub}}},\overline{v_c},{a}_e/D,{f}_z\right)=100\frac{\left({P}_{\mathrm{CE}{\mathrm{D}}_{\mathrm{conv}}}\left({V}_{\mathrm{l}\mathrm{ub}}\right)+{P}_{\mathrm{feed}-\mathrm{suc}{\mathrm{t}}_{\mathrm{conv}}}\left(\overline{Q_{\mathrm{l}\mathrm{ub}}}\right)+{{\mathrm{P}}_{\mathrm{spindl}\mathrm{e}}}_{\mathrm{conv}}\left(\overline{v_c},{a}_e/D,{f}_z\right)\right)-{{\mathrm{P}}_{\mathrm{spindl}\mathrm{e}}}_{\mathrm{dry}}\left(\overline{v_c},{a}_e/D,{f}_z\right)}{P_{\mathrm{spindl}{\mathrm{e}}_{\mathrm{dry}}}\left(\overline{v_c},{a}_e/D,{f}_z\right)} $$

(50)

The power associated to the CED linked to the production of lubricant depends on V_lub that is the lubricant used in a year. More specifically, Eq. 51 can be written:

$$ {V}_{\mathrm{lub}}={V}_{{\mathrm{H}}_2\mathrm{O}}+{V}_{{\mathrm{H}}_2\mathrm{O}}\cdot \mathrm{conc} $$

(51)

where ${V}_{{\mathrm{H}}_2\mathrm{O}}$ is the year consumption of water and conc is the concentration of oil in the lubricant.

Therefore, Eq. 52 can be written:

$$ {P}_{\mathrm{CE}{\mathrm{D}}_{\mathrm{conv}}}\left({V}_{\mathrm{lub}}\right)=\frac{\left({V}_{{\mathrm{H}}_2\mathrm{O}}\cdot {\rho}_{{\mathrm{H}}_2\mathrm{O}}\cdot \mathrm{CE}{\mathrm{D}}_{{\mathrm{H}}_2\mathrm{O}}+{V}_{\mathrm{oil}}\cdot {\rho}_{\mathrm{oil}}\cdot \mathrm{CE}{\mathrm{D}}_{\mathrm{oil}}\right)}{N_{\mathrm{days}/\mathrm{year}}\cdot {N}_{\mathrm{hours}/\mathrm{day}}\cdot 3600} $$

(52)

And both N_days/year and N_hours/day were used to get the right units. For this research, the following values were adopted: ${V}_{{\mathrm{H}}_2\mathrm{O}}=7000\ l/\mathrm{year}$ and conc = 12%. The annual consumption of water was experimentally measured on a machine centre (similar to the one adopted for the experimentation) used in a real shop-floor. The procedure adopted in the company is to periodically add water and oil to the machine to keep the concentration constant. The used oil concentration value is typical for conventional Ti6Al4V milling. The CED values both for water ($\mathrm{CE}{\mathrm{D}}_{{\mathrm{H}}_2\mathrm{O}}=0.00355\ \mathrm{MJ}/\mathrm{kg}$) and synthetic oil (CED_oil = 31.74 MJ/kg) were found in the database [82]. ρ_oil = 0.82 kg/l is the oil density.

Since P_{feed − suctcryo} = 0, the cryogenic-dry pair can be evaluated through Eq. 53.

$$ \varDelta {P}_{\mathrm{globa}{\mathrm{l}}_{\mathrm{cryo}-\mathrm{dry}}}\left[\%\right]\left({\dot{m}}_{LN},\overline{v_c},{a}_e/D,{f}_z\right)=100\frac{\left({P}_{\mathrm{CE}{\mathrm{D}}_{\mathrm{cryo}}}\left({\dot{m}}_{LN}\right)+{P_{\mathrm{spindl}\mathrm{e}}}_{\mathrm{cryo}}\left(\overline{v_c},{a}_e/D,{f}_z\right)\right)-\left({P_{\mathrm{spindl}\mathrm{e}}}_{\mathrm{dry}}\left(\overline{v_c},{a}_e/D,{f}_z\right)\right)}{P_{\mathrm{spindl}{\mathrm{e}}_{\mathrm{dry}}}\left(\overline{v_c},{a}_e/D,{f}_z\right)} $$

(53)

The power associated to the CED for the production of liquid nitrogen ${P}_{\mathrm{CE}{\mathrm{D}}_{\mathrm{cryo}}}$ depends on the liquid nitrogen mass flow rate ${\dot{m}}_{LN}$.

${P}_{\mathrm{CE}{\mathrm{D}}_{\mathrm{cryo}}}$ can be computed as follows:

$$ {P}_{\mathrm{CE}{\mathrm{D}}_{\mathrm{cryo}}}={P}_{\mathrm{CE}{\mathrm{D}}_{\mathrm{cryo}}}\left({\dot{m}}_{LN}\right)=\frac{{\dot{m}}_{LN}\cdot \mathrm{CE}{\mathrm{D}}_{LN}}{3600} $$

(54)

As anticipated, $\overline{{\dot{m}}_{LN}}=45\ \mathrm{kg}/\mathrm{h}$ is the liquid nitrogen mass flow rate measured in the nominal condition of pressure (press = 3.5 bar). The energy required for the production of the liquid nitrogen was set equal to CED_LN = 6.49 MJ [82].

It is worth noting that, according to [35, 82], the developed formulation does not consider the energy required for the lubricant disposal and the energy contribution linked to the production of the inserts that need to be substituted when worn. Indeed, it was assumed that the cutting performance, in terms of wear rate, can be considered comparable in all the analysed cases although a worse performance is expected for dry cutting. According to the literature, the comparison between conventional and cryogenic cutting in milling is often not in agreement [26, 60].

3 Results and discussion

In this section, the results of the performed power assessment as described in the previous subsections were presented. A proper validation of the proposed modelling approach was presented first (Section 3.1 and Section 3.3).

3.1 Model validation

The model validation was carried out comparing both the estimated cutting power and spindle power (Section 2.2.1) with the associated experimental values (see Fig. 16). The model validation was performed considering the following cutting condition: v_c = 50 m/min, f_z = 0.2 mm/tooth, a_e = 5 mm and a_p = 3 mm.

Fig. 16

Cutting power (a) and spindle power (b) – different cooling lubricating CL approaches – experimental and numerical model comparison (validation point, v_c = 50 m/min, f_z = 0.2 mm/tooth, a_e = 5 mm, a_p = 3 mm)

For what concerns the real cutting power, it was directly derived from cutting force measurements. Since for the adopted cutting condition (radial engagement a_e) at maximum one tooth is engaged in the piece, the following expressions can be used for computing the average cutting power:

$$ \left\{\begin{array}{c}{F}_{t{i}_{ex}}(t)\\ {}{F}_{r{i}_{ex}}(t)\end{array}\right\}={\boldsymbol{R}}_{\boldsymbol{i}}\cdot \left\{\begin{array}{c}{F}_x(t)\\ {}{F}_y(t)\end{array}\right\}=\left[\begin{array}{cc}-\sin {\varphi}_i(t)& \cos {\varphi}_i(t)\\ {}-\cos {\varphi}_i(t)& -\sin {\varphi}_i(t)\end{array}\right]\cdot \left\{\begin{array}{c}{F}_x(t)\\ {}{F}_{\mathrm{y}}(t)\end{array}\right\} $$

(55)

where the F_x and F_y are the measured experimental forces along X and Y and R_i is a rotation matrix that allows computing respectively the tangential ${F}_{t{i}_{ex}}$ and radial ${F}_{r{i}_{ex}}$ components (Eq. 55). Thus, the experimental cutting power ${P}_{cu{t}_{ex}}$, as a function of time, can be estimated using Eq. 56:

$$ {P}_{cu{t}_{ex}}(t)={F}_{t{i}_{ex}}(t)\cdot {v}_c/60 $$

(56)

And the average value $\overline{\overline{P_{cu{t}_{ex}}}}$ can be computed considering a defined number of tool rotations (q = 30).

$$ \overline{\overline{P_{cu{t}_{ex}}}}=\frac{1}{q\cdot T}{\int}_0^{q\cdot T}{P}_{cu{t}_{ex}}(t)\cdot d\mathrm{t} $$

(57)

Moreover, even the confidence intervals CI ±3σ of the experimental cutting power were estimated for all the experimented cooling conditions (Eq. 58):

$$ {\sigma}_{P_{cu{t}_{ex}}}=\sqrt{\frac{1}{q-1}\sum \limits_{p=1}^q{\left|\overline{{P_{cu{t}_{ex}}}_p}-\overline{\overline{P_{cu{t}_{ex}}}}\right|}^2\ } $$

(58)

where $\overline{P_{cu{t}_{e{x}_p}}}$ is the average cutting power in the p^th tool revolution.

It can be observed that the experimental cutting power (Eqs. 55, 56 and 57) matches the computed one through Eqs. 9, 10 and 11 and the identified cutting coefficients (Table 4). The best matching can be observed for conventional cooling. The maximum error is about 6% and it was observed for dry cutting.

Regarding the spindle power, in Fig. 16b, the analytically estimated value (Eq. 29) was compared with the measured one. The spindle power measurements were performed using the power meter depicted in Fig. 12. The comparison was done both for dry cutting, cryogenic and conventional cooling. Even in this case, the maximum error is rather limited (about 4% for the cryogenic cooling). According to the observed results, the model can be considered suitable for the purpose of the proposed analysis.

3.2 Cutting power assessment results

Since the cryogenic cooling exhibited a strong tendency in reducing the cutting forces, a structured analysis of the associated potentiality in terms of cutting power needs to be carried out. For this purpose, the analytical formulation devised and presented in Section 2.1 was exploited. Indeed, the cutting power assessment was performed exploiting Eq. 15 and Eq. 14. The identified cutting coefficients (Table 4) were used, while f_z was varied in a range 0.05–0.2 mm/tooth, and the dimensionless parameter (a_e/D) was assumed in the 0.2–1 range. According to the devised formulation, the assessment of cryogenic and conventional cooling was carried out with respect to dry cutting that represents the reference case in terms of environmental sustainability.

As can be easily observed in Fig. 17b, the expected cutting power saving (with respect to dry cutting) ranges from − 20% to more negative values depending on the selected cutting parameters (up to − 60% for low radial immersions and lower feeds (finishing operations)). When the tool is fully engaged on the workpiece and the feed is set to its maximum value (0.25 mm/tooth), the cutting power saving results in its minimum value. This is due the fact that in that condition, the tangential cutting force is dominated by the shear contribution (linked to K_tc) (see Eq. 14). On the contrary, when the feed f_z and the radial depth of cut a_e are both reduced, the friction contribution (linked to K_te) plays the main role, drastically decreasing the cutting power in comparison to dry cutting. For what concerns the conventional-dry comparison, Fig. 17 a shows that for rough milling, the cutting power is comparable, while for finishing operations (lower values of f_z and a_e/D), the conventional cutting seems less energy demanding than dry cutting mainly due to a better lubrication effectiveness, even explained by a lower K_te. Focusing on power associated to cutting, cryogenic cutting seems the most sustainable cooling lubricant solution.

Fig. 17

Cutting power assessment: (a) conventional-dry comparison and (b) cryogenic-dry comparison

3.3 Power assessment results at the spindle level and model validation

Similarly, in this section, the assessment was performed at a higher level. The spindle power was considered for this purpose. According to Eq. 30 and Eq. 31, the conventional-dry spindle power comparison (Fig. 18a) and the cryogenic-dry pair (Fig. 18b) were reported. Moreover, as a confirmation of the adequacy of adopted modelling approach, the corresponding measured quantities (also reported in Section 3.1) were put into evidence in Fig. 18. As summarized in Table 8, the lower and upper bound values for ΔP_spindle[%] were reported for both the comparisons, considering the nominal cutting speed that in this case was set ${\overline{v}}_c=50\mathrm{m}/\min$. A sensitive analysis considering different values of cutting velocity was also performed. More specifically, the following values were considered: v_c low = 30m/min and v_c high = 70m/min. It can be observed that for roughing operations (high radial immersions and high feeds), cryogenic cooling can assure savings up to 18% (at ${\overline{v}}_c\Big)$with respect to the power absorbed by the spindle in dry conditions. Higher percentage savings (up to 25%) occur when the feed is further decreased. The observed power savings are even more relevant if a lower cutting velocity is considered v_c low (Table 8).

Fig. 18

Spindle power assessment and model validation: (a) conventional-dry comparison and (b) cryogenic-dry comparison

Table 8 Spindle power assessment – sensitive analysis as a function of cutting speed

Conventional cutting showed that spindle power consumption P_spindle is similar to the corresponding one observed in dry cutting. Indeed, only slight differences can be observed (less than − 6%). If we consider this perspective, cryogenic cutting remains particularly convenient especially for operations in which the tool is rather engaged in the workpiece. This matches the typical needs of soe applications where, for instance in aerospace industry, up to 90% of the material is removed from the blank by machining operations.

For finishing operations, the energy savings with respect to conventional cooling are rather limited (less than 5%).

3.4 Power assessment results at the machine level

In this section, the focused was shifted to the machine. This means that the machine tool was considered the system boundary. From this perspective, the power assessment was carried out considering even the feed system (Eq. 44 and Eq. 46). More in details, Eq. 44 takes into consideration the power contribution due to high-pressure pump, while Eq. 46 considers in addition the power associated to the suctioning pump. The corresponding analyses were reported respectively in Fig. 19 a and b where the nominal $\overline{Q_{\mathrm{lub}}}$ and the nominal $\overline{{\mathrm{v}}_{\mathrm{c}}}$ were set.

Fig. 19

Power at the machine level (conventional-dry comparison) – (a) high-pressure pump and (b) high-pressure and suction pumps (both considering the nominal flow rate $\overline{Q_{\mathrm{lub}}}$ and the nominal $\overline{v_c}$)

Since for cryogenic cooling no additional power contributions need to be taken into account at the machine level, the analysis performed in the previous section still remains valid (Fig. 18b). A sensitive analysis as a function of the Q_lub was also carried out. Deviations from the nominal value $\overline{Q_{\mathrm{lub}}}$ (experimentally measured during the cutting test with the adopted tool) of ±15% were considered.

It can be observed that the high-pressure pump plays a relevant role (it absorbed about 1312 W in the nominal condition), while the suctioning pump power is quite limited with an average contribution of about 163 W. Even for roughing operations, the power percentage increment with respect to dry cutting is considerable (145%). Moreover, in both the cases (Tables 9, 10), reducing the Q_lub makes the conventional cutting even more power demanding (200% for roughing operations and 1387% for finishing operations).

Table 9 Conventional-dry comparison - power assessment at the machine level (high-pressure pump)

Table 10 Conventional-dry comparison - power assessment at the machine level (high-pressure and suctioning pump)

It can be concluded that if we consider the perspective of a manufacturing plant, without doubts, the choice of using cryogenic cutting as a cooling lubricating solution allows saving a lot of energy with respect to conventional cutting (close to 3 times for roughing machining and more than 11 times for finishing operations). This analysis and the analysed results are extremely relevant for manufacturing companies that deal with titanium alloys machining.

Table 11 Global power assessment (different CL technologies) ΔP_global [%] – sensitive analysis

3.5 Primary power assessment results

According to Section 2.4, the analysis was shifted to a global perspective. Indeed, the CED energy for producing lubricant and liquid nitrogen was also considered. More in details, Eq. 50 and Eq. 53 were used to plot the curves reported in Fig. 20.

Fig. 20

Global power assessment: (a) conventional-dry comparison (nominal conditions $\overline{V_{\mathrm{lub}}}$, $\overline{Q_{\mathrm{lub}}}$, $\overline{v_c}$) and (b) cryogenic-dry comparison (nominal conditions ($\overline{{\dot{m}}_{LN}}$, $\overline{v_c}$)

Specifically, the nominal conditions for what concerns the consumption of lubricant $\overline{V_{\mathrm{lub}}}$ (Fig. 20a) and the liquid nitrogen $\overline{{\dot{m}}_{LN}}$ flow rate (Fig. 20b) were considered. In addition, the nominal conditions for $\overline{Q_{\mathrm{lub}}}$ and $\overline{v_c}$.were also set. The analysis shows that due to a high consumption of liquid nitrogen that evaporates as soon as it cools the cutting region, the involved global power is much higher than dry cutting (about 19 times greater than conventional cutting for finishing and up to 16 times in case of rough milling).

The sensitive analysis shows (Table 11) that the achieved results seem less detrimental than the ones reported in [35, 61]. Even [61], that carried out an analysis considering the data gathered in literature for estimating the primary energy, found that cryogenic cooling averagely demands 39 time the energy requested by conventional cutting. Most likely this is due to the developed set-up that feeds the liquid nitrogen through the tool nozzles instead of using flood.

Since in conventional cutting the lubricant is continuously reused and only periodically refilled or substituted, the associated primary power is lower Thus, changing the perspective to a higher level makes the considerations outlined in Section 3.4 completely reviewed. It is important to observe that this analysis took into consideration the primary power consumption, but it was not focused on other environmental aspects like global warming, acidification, water usage and solid wasted [35] or features linked to the quality of the processed parts [36, 37].

The performed analyses (considering respectively ${P}_{\mathrm{cu}{\mathrm{t}}_{\mathrm{cryo}}}/{P}_{\mathrm{cu}{\mathrm{t}}_{\mathrm{conv}}}$, ${P}_{\mathrm{feed}-\mathrm{suc}{\mathrm{t}}_{\mathrm{conv}}}/{P}_{\mathrm{spindl}{\mathrm{e}}_{\mathrm{conv}}},$ ${P}_{\mathrm{globa}{\mathrm{l}}_{\mathrm{cryo}}}/{P}_{{\mathrm{globa}\mathrm{l}}_{\mathrm{conv}}}$) bring to the results summarized in Fig. 21.

Fig. 21

cryogenic cooling – conventional cooling comparison at different levels: (a) cutting power (b) machine level (c) primary power

4 Conclusions

In this paper, a comprehensive energy assessment of both cryogenic (LN2) cooling and conventional cooling was carried out with respect to dry cutting. Ti6Al4V milling was considered the reference application.

• The energy assessment was carried out at different levels. More specifically, the power involved in machining, the power absorbed by spindle, the power linked to the machine tool system and the primary power were considered.

• At each level, a proper energy model was developed to analyse the effect of the main cutting and process parameters (radial depth of cut, feed, cutting velocity, lubricant flow rate, LN2 flow rate).

• At the process level, cryogenic cooling makes Ti6Al4V cutting less energy demanding than dry cutting and conventional cooling. The results were explained through a mechanistic cutting model. Basically, LN2 lowers the friction between the tool and the workpiece.

• Cryogenic cooling assures energy saving even if the spindle losses were considered in the analysis.

• Relevant savings were also observed if the machine tool energy consumption was analysed. Indeed, the power absorbed by the machine auxiliaries makes conventional cutting from 3 to 11 times (depending on the cutting parameters) more energy demanding than cryogenic cutting. This result is extremely interesting for companies that process advanced material like HRA.

• Primary energy. Since the liquefaction of nitrogen is an energy demanding process, the overall requested energy in cryogenic cutting is close to be from 16 to 19 times higher than in conventional cutting.

• In order to make cryogenic LN2 even more environmental compliant, research efforts should be addressed to improve the efficiency of the feeding system that should assure a stable flow even with low LN2 rates. A more localized action of the jets needs to be pursued in order to avoid any waste of nitrogen and to enhance the cutting performance in terms of tool life and MRR.