1 Introduction

1.1 Centreless grinding

As Dhavlikar et al. [1] describe centreless grinding is a common manufacturing grinding process for round workpieces, thanks to its unique workpiece (WP) holding system. The WP is sustained along three contact lines, with the grinding wheel, the regulating wheel and the supporting blade (Fig. 1). This method removes the need to clamp the workpiece and create centring holes on the workpiece. WP loading and unloading is easier, which results in reduced cycle time and higher productivity. Nevertheless, Zhou et al. [2] mention, due to this setup, centreless grinding is exposed to roundness errors generated by two types of instabilities: dynamic regenerative chatter and geometric lobing.

Fig. 1
figure 1

Centreless grinding geometry

Full size image

Dynamic chatter, due to the interaction between the cutting process and the main resonances of the machine structure, is a very usual phenomenon in machining processes. Gallego [3] defines the geometric lobing as the product of the peculiar geometric setup of the WP, i.e. blade angle and WP height. As Klocke [4] shows in his study, it is one of the main constraints to WP roundness accuracy: WP centre can oscillate, provoking an irregular material removal which in turn increases WP waviness.

Dall [5] conducted the first significant research on the out-of-roundness WP problem, systematically relating the roundness error to the geometric configuration. Two main parameters were considered: the tangent angle and the top supporting blade angle. Then, Yonetsu [6] defined the interactions between pre- and post-grinding amplitudes of harmonics of the WP profile. And Rowe et al. [7] simulated the centreless grinding lobing problem on a digital computer taking into account all previous geometrical contemplations and presented the analytical model of the so-called geometric rounding mechanism. Later Marinescu et al. [8] used these results to explain the geometric roundness error regeneration process. After describing the basic geometrical connections of the process, it was possible to use different stability criteria, like Nyquist criterion, to show the theoretical instabilities produced by different configurations. Various researchers such as Bueno et al. [9] claimed that it is possible to create a stability map using the Nyquist criterion for each possible number of complete undulations that can be generated on the WP. Zhou et al. [2] presented the periodic characteristic roots distribution of the lobing loop and recommended a nominal stability diagram to suggest the range of the centre-height angle in order to lessen the lobing effect. Rowe et al. [10] introduced the geometric stability parameter derived from the Nyquist stability criterion, limited to integer lobes. Using these bases, Bianchi et al. [11] considered the nonlinearity due to the loss of contact under large waviness, investigating its effect on process stability. Also Lizarralde [12] has applied similar approaches to guide setup and optimization of centreless plunge grinding processes, in order to reduce setup time and avoid geometric instabilities as a function of WP height and blade angle, taking into account machine-WP dynamic interaction. These techniques lead to models that quantitatively predict the evolution of profile error for each geometric configuration.

The main objective of the previous works was to identify the region of instability, to be avoided during process setup configuration. It has to be noted that, depending on WP initial profile and process nonlinearities, final waviness can be negligible despite process instability, resulting in an acceptable WP. Time domain simulations have been exploited in literature for considering nonlinear phenomena and trying to predict the final WP roundness for unstable processes. Nevertheless, the limits of simulative approaches are well explained by Marinescu et al. [8]: “It is seen that the general [simulated] shapes have a similar tendency to those predicted […], but it would appear that other errors are additionally present in the experimental results”. As a matter of fact, limited quantitative comparisons are available in literature despite the significant research effort spent. As Zhou et al. [13] explain, different physical phenomena are involved in this phenomenon: while geometric variables roughly define the shape of the contact zone between WP and grinding wheel, measurements show that the actual contact length is much greater than the expected geometrical intersection. Furthermore Liu et al. [14] discuss that the main parameters influencing contact length are workpiece energy intensity, wear length and contact time of the abrasive grains, number of abrasive grains in contact, chip thickness and grain forces, wheel wear and nature of wheel wear, surface roughness and contact temperatures. In addition to the contact length, variability in material properties of the grinding wheel and workpiece, systematic precision/error of the manual setup done by the operator as a parameter, should be tackled in overall calculations with a robust approach, in order to reach accurate results.

Considering the various combinations of process geometry and grinding wheels, a proper estimation of all required parameters is very time-consuming and barely robust. Many researchers tried to develop algorithms to consider a reduced set of input data, such as workpiece diameter, wheel diameters and wheel properties, for suggesting an optimal grinding setup. Hashimoto [15] developed a model, named Opt-Setup Master that can generate the optimum setup conditions to ensure safe operations, better roundness and chatter-free grinding. This model, referring to Fig. 1, finds the sets of blade angle (γ), centre-height angle (β) and workpiece rotational speed (Ωw) satisfying all three stability criteria and then determines the optimum set by calculating the so-called PI (performance index) function, based on the process targets in terms of accuracy and productivity. Zakharov et al. [16] showed that the setup of centreless superfinishing machine tools entails the creation of geometric, kinematic and mechanical models of the shaping process and the use of formal optimization methods. Moreover Barrenetxea [17] developed an assistant tool for the setup and optimization of the centreless grinding process, optimizing productivity considering process data and machine characteristics (dynamics included).

All aforementioned approaches need a series of complex machine and process manual characterization in order to provide realistic output. Those characterizations are time-consuming and results uncertainty is usually not explicitly taken into account. Furthermore, traditional parametric identification does not allow to automatically alleviate epistemic errors by learning new functional relationships. These problems are amplified by the fact that the system is often inherently unstable and sensitive to initial states and parameters perturbation. A relevant known issue is concerned with nonlinear system identification, including structural dynamics, which is still an open problem in literature.

In addition to models based on first principles, as the one in the studies discussed above, an empirical approach is possible. We will focus on process characterization by artificial intelligence techniques in the following section.

1.2 Parameters selection based on AI

As Sjöberg et al. [18] suggest, a widespread approach to perform an input/output regression is based on artificial neural networks (NN). Many researchers have used those methodologies for prediction of chatter and surface roughness, both in grinding and other process domains. Rowe et al. [19] have suggested the application of AI technologies in grinding using modern computers and controllers as a way forward to produce higher quality components more efficiently. Junkar et al. [20] used machine learning technics for classification, through grinding signal detection, to assess performance classes, and discussed the possibility of upgrading this approach to a control algorithm by associating class assignments with appropriate control actions by a binary tree approach. Moreover Filipic et al. [21] used the same method to classify dielectric fluids in electrical discharge machining and for tool selection in an industrial grinding process, showing that the approach is beneficial in preventing poor process performance and improving product quality. Cherukuri [22] applied an artificial neural network (NN) to model stability in turning operations using analytical stability study to generate a dataset that trains the NN. Additionally, Khasawneh [23] had combined supervised machine learning with topological data analysis to obtain a descriptor of the process which can detect chatter in turning. And Zhang et al. [24] used Gaussian process regression (GPR) for modelling and predicting surface roughness in end face milling with accuracy of 84%. Furthermore, Aguiar et al. [25] have developed a neural network using a multisensor method to predict the final roughness on the grinded workpiece with 70% success rate. Lela et al. [26] examined the influence of cutting speed, feed and depth of cut on surface roughness in face milling by three different modelling methodologies, namely, regression analysis (RA), support vector machines (SVM) and Bayesian neural network (BNN), and found out that, when the training dataset is small, both BNN and SVR modelling methodologies are comparable with RA methodology and, furthermore, they can even offer better results. In particular, the best results were achieved by BNN, with less error with respect to SVR.

Human learning builds on observations and empirical evidence from the surrounding world: this accumulated knowledge is synthetized, through scientific development, in first principles (FP) models. Similarly, data-driven AI approaches use machine learning (ML) to derive models based on collected data. A combined model allows physical models to be enhanced by AI solutions, to enhance performance and trust. In this paper, a hybrid model structure is proposed: a FP model is built, based on known physical characteristics of the system, and coupled with three data-driven models, to minimize residual errors. In particular, an SVR model with polynomial kernel function, a back-propagation NN with Bayesian regularization and a GPR model with ardexponential kernel function are used as novel methods to attune the FP output to be closer to experimental results. The improved prediction capability of the proposed hybrid models could be profitably used to drive setup of process parameters.

2 Process model

2.1 First principle model

2.1.1 Nonlinear process kinematic

As Rowe [27] describes, considering a plunge centreless grinding, the shape of the cylindrical WP is defined by the radial reduction r(θ) occurring at the grinding point (i.e. at the contact between wheel and WP), where θ defines WP rotation, starting from zero at the beginning of grinding. The reduction r(θ) cumulates during grinding and it is equal to the reduction at the previous revolution r(θ − 2π) summed to the current wheel WP depth of cut I(θ) (also known as infeed). Namely:

$$ r\left(\theta \right)=I\left(\theta \right)+r\left(\theta -2\pi \right) $$
(1)

He [28] also mentions that, assuming a perfectly rigid system, the depth of cut is obtained from a pure kinematic model, computing the intersection between the grinding wheel and the WP, taking into account the feed movement X(θ), projected along the WP radius at grinding point, and WP centre displacement due to WP profile contacts at work rest and rubbing wheel.

Given its physical meaning, I (θ) cannot become negative, as the process either subtracts material, or leaves the surface unvaried when the wheel detaches: thus, the actual depth of cut must be “clipped” to zero if negative:

$$ I\left(\theta \right)={y}_{NL}\left(X\left(\theta \right)+{K}_1r\left(\theta -\alpha \right)-{K}_2r\left(\theta -\left(\pi -\beta \right)\right)-r\left(\theta -2\pi \right)\right) $$
(2)

where

  • K1 and K2 are the well-known coefficients relating WP displacement at the grinding contact to radius variation at work rest and rubbing wheel contacts, respectively: K1 ≜ sin β/ sin (α + β) and K2 ≜ sin α/ sin (α + β). The contact angles depend on work-height hw and work rest angle γ where α = π/2 − γ − β and β = βs + βc (Fig. 1). Angles βs and βc are given by βs = sin−1(2 · hw/(ds + dw)) and βc = sin−1(2 · hw/(dcw + dw)). By introducing υ ≜ β/βs, the grinding setup is completely defined by the 3-uple {γ, β, υ}.

  • yNL(·) is a two-segment piecewise function expressing the “clipping” nonlinearity due to wheel WP detachment:

$$ {y}_{NL}(u)\triangleq \left\{\begin{array}{cc}u& \mathrm{if}\ u\ge 0\\ {}0& \mathrm{otherwise}\end{array}\right. $$
(3)

Substituting Eq. (2) into Eq. (1), it yields:

$$ r\left(\theta \right)={y}_{NL}\left(X\left(\theta \right)+{K}_1r\left(\theta -\alpha \right)-{K}_2r\left(\theta -\left(\pi -\beta \right)\right)-r\left(\theta -2\pi \right)\right)+r\left(\theta -2\pi \right) $$
(4)

Knowing that θ = Ωt, the phase associated to a pulsation ω can be written as ωt = (ω/Ω)θ = nθ, where n is the number of oscillation cycles in a WP revolution, i.e. the number of lobes. Then, in order to study system stability, Eq. (4) can be rewritten in Fourier domain with s = jn (for sake of readability, the dependency on jn is omitted in the notation):

$$ r={y}_{NL}\left(X+{K}_1r{e}^{- jn\propto }-{K}_2r{e}^{- jn\left(\pi -\beta \right)}-r{e}^{-2 jn\pi}\right)+r{e}^{-2 jn\pi} $$
(5)

2.1.2 Wave filtering

Due to a well-known geometrical interference phenomenon, once a critical limit is exceeded, the amplitude of the waves engraved in WP profile becomes smaller than the amplitude of the relative vibration. According to Hashimoto, contact filtering occurring at regulating wheel/WP contact (denoted with cr) and at wheel/WP contact (denoted with cs) is modelled as:

$$ {Z}_{cs/ cr}(n)=\frac{1}{2}\left(1+\cos \left(\frac{l_{cs/ cr}}{d_w}n\right)\right) $$
(6)

where lcs/cr is the contact length at the interface and dw is the WP diameter.

The actual contact length depends both on geometrical factors and bodies compliance:

$$ {l}_{cs}=\sqrt{l_g^2+{l}_f^2} $$
(7)

where lg is the geometric contact length (\( {l}_g=\sqrt{I{\left({d}_w^{-1}+{d}_s^{-1}\right)}^{-1}} \)) and lf the deflection contact length, estimated as:

$$ {l}_f=\sqrt{\frac{8\cdotp {R}_r^2\cdotp {F}_n^{\prime}\cdotp {\left({d}_w^{-1}+{d}_s^{-1}\right)}^{-1}}{\pi {E}^{\ast }}} $$
(8)

where

  • Rr is a roughness factor equal to 1 for a smooth cylinder but typically ranges from 5 to 15 for a grinding wheel.

  • \( {F}_n^{\prime } \) is the normal grinding force per unit width.

  • E∗ is the combined elastic properties of the grinding wheel and workpiece, i.e. \( \frac{1}{E^{\ast }}=\frac{1-{\nu}_1}{E_1}+\frac{1-{\nu}_2}{E_2} \), where E1, E2, ν1, and ν2 are the Young modules and Poisson ratio, respectively.

2.1.3 Stiffness factor

Grinding machines static and dynamic compliance affects wheel-workpiece relative displacement. At very low frequencies—namely, lower than the first significant natural frequency—only static compliance can be considered; thus, deflection is approximately in phase with the depth of cut. Static deflection Δel is given by:

$$ {\varDelta}_{el}={K}_S/\left({K}_m{I}_e\right) $$
(9)

where KS (process stiffness) is the ratio between normal grinding force and actual infeed Ie and Km is the wheel-workpiece static stiffness. Whereas the actual infeed Ie depends on the nominal infeed I by Ie = I − Δel, Eq. (12) yields:

$$ {I}_e= KI $$
(10)
$$ \mathrm{with}\ K\triangleq \frac{K_m}{K_m+{K}_S}\left( stiffness\ factor\right) $$
(11)

2.1.4 Simulation model

The obtained process model is represented by the block diagram of Fig. 2. Based on it, a numeric simulation code has been developed in MATLAB™ to estimate the WP profile, discretized by a circular array of 7200 elements, representing WP radial reduction at a given angular position. The contact filtering illustrated in Section 2.2 has been implemented by a 0-phase symmetric FIR filter: a high order of 361 has been selected to fit properly the Zcs(n) of Eq. (8). Contact length lcs has been computed using Eqs. (9), (10) and (11). All the necessary parameters, such as Rr, Fn′, E1, E2, ν1 and ν2, have been taken from literature, given the WP material and grinding wheel type and status. Stiffness factor K has been estimated fitting an exponential decay on wheel spindle current signal during spark-out tests, as described in, par. 19.11.4.

Fig. 2
figure 2

Model block diagram

Full size image

Figure 3 depicts the Short-time Fourier transform (STFT) of the WP profile for a simulated unstable operation. It can be observed the transition from an initial linear unstable condition, with exponential growth, to a steady state condition due to clipping nonlinearity. Moreover, only one dominant harmonic component raises: the simulated profile, with “number of lobes” equal to 16 lobes, is plotted in Fig. 4 and used to compute the “simulated roundness”. Additionally, a “detach index” is evaluated, indicating the processing time percentage when detachment occurs. Exploiting the conceptual process model of Fig. 2, an analytical stability analysis is performed by the Nyquist criterion, delivering the exponential growth rate that, multiplied by the number of WP revolutions, produces the so-called “stability index”. The simulated roundness, detach index, simulated number of lobes and stability index plus dullness level of the grinding wheel, which is calculated after each test, will be used as additional inputs by the hybrid model described in the following.

Fig. 3
figure 3

Time-frequency analysis of the sample simulated WP profile

Full size image
Fig. 4
figure 4

Sample WP profile after 950 revolutions

Full size image

2.1.5 Experimental verification

To validate the obtained model, a series of experimental tests were done, varying seven independent control parameters (Table 1) by a randomly generated “latin hypercube” approach, while keeping 7 fixed parameters (Table 2), for a total of 100 samples. Ranges have been selected according to the industrial practice, by surveying technologists experience. The discrete variables (γ, WPD, WPL) have been chosen by discretizing the continuous random variables.

Table 1 DOE-controlled parameters
Full size table
Table 2 DOE-fixed parameters
Full size table

The test has been executed on a Monza 520 M6 century edition grinding machine by “Monzesi srl”, with manual work rest blade adjustment (Fig. 5). The WP roundness has been measured with a “Mitutoyo Roundpack 400” system, at three different highs along the WP, producing then an average roundness for each WP.

Fig. 5
figure 5

Monza 520 M6 century edition (working zone)

Full size image

When the process is unstable, waviness grows exponentially until grinding wheel/workpiece detachment occurs. Roundness final value, both experimentally and in simulations, is very sensitive to several system parameters. To effectively support industrial production, the analysis must be able to discriminate between acceptable and excessive roundness errors “RE”. Instead of adopting a discrete classification approach, this judgement is reproduced computing a normalized roundness error “REN” by a pseudo-sigmoid function, adapted from [29], that mitigates the disrupting effect of uncertainty and epistemic uncertainty:

$$ {RE}_N=\frac{RE}{RE^{0.6}+2} $$
(12)

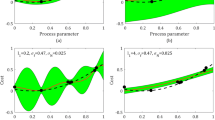
The relationship between normalized roundness RN predicted by the FP model and measured from the experiments is plotted, for all samples, in Fig. 6, showing an R correlation value around 0.45.

Fig. 6
figure 6

Correlation between simulated and experimental workpiece normalized roundness error RN

Full size image

3 Machine learning techniques

3.1 Learning setup

In the pre-processing stage, data has been checked for missing values and outliers and, in case of existence, they were removed which in this case only one point was eliminated. For reducing the effect of different scales across input variables on numerical conditioning during training, input data normalization has been performed to have values between −1 and 1. Then, a random selection of 20% of dataset was separated and kept aside as final test data, while the remaining 80% of original data was used to train the models. Furthermore, since the dataset was small, to improve prediction generality and remove effects of the initial random values, all algorithms were trained separately 100 times. At each single model training, the training dataset was randomly divided into two parts, 70% of the data was used for training and the remaining 30% was used for testing of that model.

3.2 Neural network model

In this approach, the system was modelled using a pure NN method (Fig. 7). For this aim, Kayri [30] has suggested using a Bayesian regularized artificial neural network (BRANN), because they limit overtraining and overfitting. The input vector of independent variables ui is linked to the target using the design represented in Fig. 8, with one hidden layer. Each single node is associated to those of the previous layer by compliant weights. In each neuron, inputs are multiplied by the corresponding weight and summed. Nevertheless, Alados et al. [31] propose to apply an activation function to the resulting sum, producing the neuron output, which is transferred to the next layer. After the feed forward step, the variance between the real output and predicted output of the network is defined as error. In the back-propagation phase, the error signal is transmitted from the output to the input layer via a layer-by-layer manner, adjusting the network weight. As Okut [32] explicates, the objective function used in BRANN has an additional term that castigates large weights: because of this contraction, the effective number of parameters attained by BRANN can be less than the total number of available parameters. In this way, a smoother mapping is achieved, with reduce overfitting and improved model generalization ability.

Fig. 7
figure 7

The architecture of an artificial neural network

Full size image
Fig. 8
figure 8

Neural network architecture

Full size image

3.2.1 Neural network-only model

The neural network model is defined via few hyperparameters, as the number of hidden layers and the number of neurons in each layer, etc. They must be selected before the training stage but there is no unique or predefined way of selecting them. In this study, a series of experiments has been done with different hyperparameters arrangement and it was observed that the best network performance was achieved with the parameters reported in the following. The performance of the networks is measured by the achieved minimum mean square error (MSE) and maximum correlation value R.

A network with one hidden layer has been considered since the number of effective parameters and overall performance of model in terms of its prediction precision did not change significantly by adding more hidden layers. The number of neurons in each hidden layer is selected accordingly to the number of input parameters (NI): 2 · NI − 1, according to the rule of thumb suggested by João [33]. As Kayri [30] mentioned, adding more neurons resulted in increasing computation time without performance improvements: the effective number of parameters is unchanged. During BRANN training, the less relevant weights are set to zero. In the hidden layer, a tangent hyperbolic activation function was chosen as suggested [34], since they reduce the number of training iterations and because the output of the system is a real number. On the other side, for the output layer, a “purelin” activation function is used.

MATLAB (2020a) Statistics and Machine Learning toolbox was employed for exploring the BR artificial neural network. In this study, as Reece [35] reported, the training process is halted if (a) it reaches the maximum number of iterations (2000); (b) the maximum amount of time is exceeded (no limit has been considered); (c) the estimation error is below the target (0.003); (d) the performance gradient drops below minimum gradient; or (d) the Marquardt adjustment parameter (μ) becomes larger than 1010.

To improve generalization, taking into account the small dataset used, Shaikhina [36] suggested to train multiple NNs, selecting a random training dataset (while preserving the initial 20% of the data for the final evaluation). Therefore, 100 neural networks, with the previously described architecture, were trained, with all seven independent parameters used in FP plus the dullness level of the grinding wheel. Then only top 10 models, based on their R value, were selected for final testing stage: the average output of these models was used for roundness predictions based on the 20% dataset kept as final test data. The resulting correlation between them and the actual roundness values for each test is represented in Fig. 9, with an R value around 0.7, i.e. a 52% increase over the FP model R value.

Fig. 9
figure 9

NN test regression plot

Full size image

3.2.2 Neural network-hybrid model

It is clear that both the FP and NN approaches have their advantages and drawbacks. But as Driscoll et al. [37] reported, generally physic models tend to have higher bias but lower variance. On the other hand, machine learning models tend to have a high variance and low bias. It is therefore suggested to combine both methods to deliver a further robust system. In the proposed hybrid model structure by Ahmad [38] g(z), the output ƒ(x) of the FP model, based on known parameters “x”, is exploited as an additional input for the NN model, together with the global inputs “z” to the process. Parameters “x” are a subset of “z”, as wheel dullness indicator (that is considered by the ML models) does not play any role in the adopted physical model:

$$ y=\mathrm{g}\left(\mathbf{z},\mathrm{f}\left(\mathbf{x}\right)\right) $$
(13)

For doing so, an NN model is considered as before, with one hidden layer and number of neurons selected, based on previously explained method. The input parameters of this new NN are the ones from NN in the previous section plus primary and secondary outputs from the FP (explained in Section 2.1.4.) such as expected roundness, detach index, expected number of lobes and stability parameter. As previously explained, inputs are normalized and a BRANN with the same activation functions was adopted. Then, 100 models were trained and tested as before and consequently, top 10 models were selected, to perform the final test.

The results obtained from the hybrid model (Fig. 10) illustrate that with this approach, in the test dataset, the average correlation value R between data and predicted value reaches 0.9, with an improvement of 28% with respect to the NN-only method with same architecture and an improvement of 89% with respect to the sole FP method.

Fig. 10
figure 10

NN hybrid test regression plot

Full size image

3.3 Support vector regression (SVR)

Support vector machine (SVM) analysis is a widespread machine learning tool for classification and regression, first proposed by Vapnik [39]. SVM regression is contemplated as a nonparametric technique because it depends on kernel functions. As Campbell [40] describes, SVMs have properties such as good generalization ability and a small number of free adjusting parameters, and unlike NN approach, it has no prerequisite for designing the architecture of the machine learning model. They were initially established for classification tasks, but they can be employed in regression problems as support vector regression (SVR) by including of a loss function based on a distance measure. SVR constructs a linear model after the input has been mapped into a higher dimensional feature space using some nonlinear mapping (usually by reproducing kernels). The estimation accuracy of SVR depends on three hyperparameters:

  • Kernel function, such as linear function, polynomial function, radial basis function and sigmoid function.

  • Box constraint: parameter that controls the maximum penalty imposed on margin-violating observations and aids in preventing overfitting (regularization). If the box constraint is increased, the SVM classifier assigns fewer support vectors. However, increasing the box constraint can lead to longer training times.

  • Insensitive loss function (ε): the value of ε influences the number of support vectors used to form the regression function. If ε increases, fewer support vectors are chosen, and the smoothness of the regression function increases too, explains [26].

For finding those parameters, an automatic hyperparameters optimization was conducted on the dataset: the best combination based on model MSE is reported in Table 3.

Table 3 SVR optimal SVR hyperparameters
Full size table

3.3.1 SVR model

Once SVR hyperparameters are selected, the SVR model is ready for the learning process. As explained in Section 2.2.1, two different SVR models were created: one using the seven input parameters from FP model and one using primary and secondary inputs, by the hybrid method.

As before, the top 10 models from each approach were selected and averaged, to perform the final test. Figure 11 shows average R values achieved with these two models: in the SVR only approach, the correlation between predicted and actual roundness was less than in the FP model, but, by the hybrid approach, the correlation value was doubled and performed even better than FP model with 73% improvement.

Fig. 11
figure 11

SVRs test regression plots: a SVR only, b SVR hybrid

Full size image

3.4 Gaussian process regression (GPR)

Gaussian process regression (GPR) models are nonparametric kernel-based probabilistic models, which make them powerful tools for Bayesian supervised learning. They have in common with support vector machines and regularization networks the theory of regularization via reproducing kernels that allow the straight specification of the smoothness properties of the class of functions under consideration. As Smola [41] stated, this makes them popular for regression of small datasets. Through a series of experiments and automatic hyperparameters optimization bringing the least MSE, a GPR model with customized parameters (Table 4) is selected for roundness prediction.

Table 4 GPR parameters
Full size table

Employing top 10 models from 100 trained and tested models and averaging results obtained from each of them for roundness prediction, the difference in terms of correlation between predicted and actual values is much more significant between two approaches. As shown in Fig. 12, the correlation value obtained by GPR hybrid method is raised by 100% with respect to FP model and 50% with respect to GPR only method.

Fig. 12
figure 12

GPRs test regression plots: a GPR only, b GPR hybrid

Full size image

4 Discussion

This paper presents results from attempting to combine first principle and machine learning techniques into hybrid models to forecast performance of a centreless grinding process in terms of workpiece final roundness. The FP model is established on theoretical calculations and assumptions that need prior understanding of the system under the study. The adopted FP model, while similar to models discussed in similar literature, exhibits an unsatisfactory accuracy, probably because of improperly treated phenomena, e.g. contact length dependency on local compliance, on contact force and on grinding wheel roughness; variability in material properties of the grinding wheel and workpiece; and progressive grinding wheel wear and dullness. On the contrary, NN, SVR and GPR models are established straight from experimental data, engaging a range of statistical techniques to identify suitable mathematical models. However, precise estimates are possible only if a large training set is available, with accurate data. Therefore, for obtaining the benefits of both methods, they have been combined into a hybrid modelling approach. From NN approach, it was observed that the hybrid model with one hidden layer leads to significant reduction in prediction error. It was also noticed that, using the SVR and GPR approaches, the improvement from normal model to the hybrid model was more significant. Comparing these seven models, the best test results was obtained by hybrid GPR model that, in addition, takes considerably less time for training with respect to an NN hybrid with a similar precision. Figure 13 presents a brief comparison between all seven models in terms of precision.

Fig. 13
figure 13

Precision comparison between models

Full size image

For understanding what causes this difference between pure machine learning (ML) models and hybrid models, a sensitivity analysis has been conducted by automatic relevance determination (ARD) based on GPR model, on both input datasets [42]. Figure 14 illustrates that in standard data-driven models, the roundness value is most sensitive to the Beta angle and then to WP diameter, infeed rate (Inf) and Gamma angle. However, by adding primary and secondary outputs of FP model as secondary input in ML models, new parameters are more interrelated with WP roundness: Fig. 15 shows that simulated roundness (SRN) and simulated number of the lobes (NLb), estimated by the FP model, do not help ML model as expected. The secondary outputs of the FP model, such as the detach index (DI) and the stability index (SI), have the highest correlation with WP roundness.

Fig. 14
figure 14

Primary model inputs sensitivity

Full size image
Fig. 15
figure 15

Primary and secondary model inputs sensitivity

Full size image

5 Conclusion

A hybrid approach has been suggested to improve roundness predicted by the numerical models based on first principles. Data-driven models, based on nominal process parameters augmented by additional outputs provided by a Physics-based model, deliver an optimal estimation that alleviates the effect of the unavoidable uncertainties and epistemic errors. The results presented in this paper indicate that even a first principal model with mediocre primary output performance includes other secondary outputs which are beneficial to enhance machine learning techniques, compared to black box approaches with the same techniques.

Future activities will be aimed at improving the first principle model. A larger campaign on a commercial centreless grinding machine will be used to examine more combination of parameters and further improve prediction accuracy.