Skip to main content
SpringerLink
Log in

A stability prediction method research for milling processes based on implicit multistep schemes

  • ORIGINAL ARTICLE
  • Published:
The International Journal of Advanced Manufacturing Technology Aims and scope Submit manuscript

Abstract

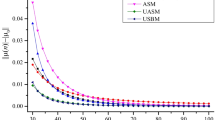
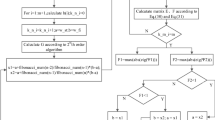
Chatter suppression during milling operations is of great significant for tool life, surface quality, and cutting efficiency. Based on the Hamming and Simpson methods, a Hamming–Simpson–based method is presented in this paper for accurately and efficiently determining the milling stability. The milling dynamic model with consideration of the regeneration effect is expressed by delay differential equations (DDEs) with time-periodic coefficients. After separating the tooth-passing period into two different phases, the two linear multistep methods are simultaneously adopted to estimate the state term by discretizing the forced vibration phase into time intervals of equal length. Subsequently, the state transition matrix can be determined over one period and the chatter-free borderline can be searched according to the Floquet theory. On this basis, the precision and efficiency of the Hamming–Simpson–based method are analyzed in detail through comparing with the three benchmark methods. Analysis results indicate that the Hamming method is required to convert variables which may affect the prediction accuracy. To overcome this shortcoming and promote the computational accuracy, a three-step implicit multistep exponential fitting method is applied to predict chatter stability; meanwhile, the Simpson method is responsible for the correction of the prediction. The effectiveness of the proposed method has been comparatively analyzed through two benchmark examples. Numerical simulations illustrate that the proposed method exhibits better prediction accuracy and computational efficiency.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

References

  1. Altintas Y (2012) Manufacturing automation: metal cutting, mechanics, machine tool vibrations, and CNC design. Cambridge University Press, New York

    Google Scholar 

  2. Siddhpura M, Paurobally R (2012) A review of chatter vibration research in turning. Int J Mach Tools Manuf 61(10):27–47

    Google Scholar 

  3. Altintas Y, Stepan G, Merdol D, Dombovari Z (2008) Chatter stability of milling in frequency and discrete time domain. CIRP J Manuf Sci Technol 1(1):35–44

    Google Scholar 

  4. Quintana G, Ciurana J (2011) Chatter in machining processes: a review. Int J Mach Tools Manuf 51(5):363–376

    Google Scholar 

  5. Wiercigroch M, Budak E (2001) Sources of nonlinearities, chatter generation and suppression in metal cutting. Philos Trans R Soc Lond A 359(1781):663–693

    MATH  Google Scholar 

  6. Faassen RPH, Van De Wouw N, Oosterling JAJ, Nijmeijer H (2003) Prediction of regenerative chatter by modeling and analysis of high-speed milling. Int J Mach Tools Manuf 43(14):1437–1446

    Google Scholar 

  7. Altintas Y, Weck M (2004) Chatter stability of metal cutting and grinding. CIRP Ann 53(2):619–642

    Google Scholar 

  8. Ding H, Ding Y, Zhu LM (2012) On time-domain methods for milling stability analysis. Chin Sci Bull 57(33):4336–4345

    Google Scholar 

  9. Altintas Y, Budak E (1995) Analytical prediction of stability lobes in milling. CIRP Ann 44(1):357–362

    Google Scholar 

  10. Budak E, Altintas Y (1998) Analytical prediction of chatter stability in milling—part II: application of the general formulation to common milling systems. ASME J Dyn Syst Meas Control 120(1):31–36

    Google Scholar 

  11. Merdol SD, Altintas Y (2004) Multi frequency solution of chatter stability for low immersion milling. J Manuf Sci Eng 126(3):459–466

    Google Scholar 

  12. Balachandran B (2001) Nonlinear dynamics of milling processes. Philos Trans R Soc A 359(1781):793–819

    MATH  Google Scholar 

  13. Balachandran B, Zhao MX (2000) A mechanics based model for study of dynamics of milling operations. Meccanica 35(2):89–109

    MATH  Google Scholar 

  14. Long X, Balachandran B (2007) Stability analysis for milling process. Nonlinear Dyn 49(3):349–359

    MATH  Google Scholar 

  15. Bayly PV, Halley JE, Mann BP, Davies MA (2003) Stability of interrupted cutting by temporal finite element analysis. J Manuf Sci Eng 125(2):220–225

    Google Scholar 

  16. Butcher EA, Bobrenkov OA, Bueler E, Nindujarla P (2009) Analysis of milling stability by the Chebyshev collocation method: algorithm and optimal stable immersion levels. J Comput Nonlinear Dyn 4(3):031003

    Google Scholar 

  17. Yan Z, Liu Z, Wang X, Liu B, Luo Z, Wang D (2016) Stability prediction of thin-walled workpiece made of Al7075 in milling based on shifted Chebyshev polynomials. Int J Adv Manuf Technol 1–10

  18. Insperger T, Stépán G (2004) Updated semi-discretization method for periodic delay-differential equations with discrete delay. Int J Numer Methods Biomed Eng 61(1):117–141

    MathSciNet  MATH  Google Scholar 

  19. Insperger T, Stépán G, Turi J (2008) On the higher-order semi-discretizations for periodic delayed systems. J Sound Vib 313(1–2):334–341

    Google Scholar 

  20. Insperger T (2010) Full-discretization and semi-discretization for milling stability prediction: some comments. Int J Mach Tools Manuf 50(7):658–662

    MathSciNet  Google Scholar 

  21. Jiang SL, Sun YW, Yuan XL, Liu WR (2017) A second-order semi-discretization method for the efficient and accurate stability prediction of milling process. Int J Adv Manuf Technol 92(1–4):583–595

    Google Scholar 

  22. Ding Y, Zhu LM, Zhang XJ, Ding H (2010a) A full-discretization method for prediction of milling stability. Int J Mach Tools Manuf 50(5):502–509

    Google Scholar 

  23. Ding Y, Zhu LM, Zhang XJ, Ding H (2010b) Second-order full discretization method for milling stability prediction. Int J Mach Tools Manuf 50(10):926–932

    Google Scholar 

  24. Quo Q, Sun YW, Jiang Y (2012) On the accurate calculation of milling stability limits using third-order full-discretization method. Int J Mach Tools Manuf 62:61–66

    Google Scholar 

  25. Ozoegwu CG, Omenyi SN, Ofochebe SM (2015) Hyper-third order full-discretization methods in milling stability prediction. Int J Mach Tools Manuf 92:1–9

    Google Scholar 

  26. Liu YL, Zhang DH, Wu BH (2012) An efficient full-discretization method for prediction of milling stability. Int J Mach Tools Manuf 63:44–48

    Google Scholar 

  27. Ji YJ, Wang XB, Liu ZB, Wang HJ, Yan ZH (2018) An updated full-discretization milling stability prediction method based on the higher-order Hermite-Newton interpolation polynomial. Int J Adv Manuf Technol 95(5–8):2227–2242

    Google Scholar 

  28. Tang X, Peng F, Yan R, Gong Y, Li Y, Jiang L (2017) Accurate and efficient prediction of milling stability with updated full discretization method. Int J Adv Manuf Technol 88(9–12):2357–2368

    Google Scholar 

  29. Yan Z, Wang X, Liu Z, Wang D, Jiao L, Ji Y (2017) Third-order updated full-discretization method for milling stability prediction. Int J Adv Manuf Technol 92(5–8):2299–2309

    Google Scholar 

  30. Li MZ, Zhang GJ, Huang Y (2013) Complete discretization scheme for milling stability prediction. Nonlinear Dyn 71:187–199

    MathSciNet  Google Scholar 

  31. Xie QZ (2016) Milling stability prediction using an improved complete discretization method. Int J Adv Manuf Technol 83(5–8):815–821

    Google Scholar 

  32. Li ZQ, Yang ZK, Peng YR, Zhu F, Ming XZ (2016) Prediction of chatter stability for milling process using Runge-Kutta-based complete discretization method. Int J Adv Manuf Technol 86(1–4):943–952

    Google Scholar 

  33. Niu JB, Ding Y, Zhu LM, Ding H (2014) Runge–Kutta methods for a semi-analytical prediction of milling stability. Nonlinear Dyn 76(1):289–304

    MathSciNet  MATH  Google Scholar 

  34. Dai Y, Li H, Xing X, Hao B (2018) Prediction of chatter stability for milling process using precise integration method. Precis Eng 52:152–157

    Google Scholar 

  35. Dai Y, Li H, Hao B (2018) An improved full-discretization method for chatter stability prediction. Int J Adv Manuf Technol 96(9–12):3503–3510

    Google Scholar 

  36. Li H, Dai Y, Fan Z (2019) Improved precise integration method for chatter stability prediction of two-DOF milling system. Int J Adv Manuf Technol 101(5–8):1235–1246

    Google Scholar 

  37. Ding Y, Zhu LM, Zhang XJ, Ding H (2011) Numerical integration method for prediction of milling stability. J Manuf Sci Eng 133(3):031005

    Google Scholar 

  38. Ding Y, Zhu LM, Zhang XJ, Ding H (2013) Stability analysis of milling via the differential quadrature method. J Manuf Sci Eng 135:044502

    Google Scholar 

  39. Zhang Z, Li HG, Meng G, Liu C (2015) A novel approach for the prediction of the milling stability based on the Simpson method. Int J Mach Tools Manuf 99:43–47

    Google Scholar 

  40. Zhang X, Xiong C, Ding Y, Ding H (2017) Prediction of chatter stability in high speed milling using the numerical differentiation method. Int J Adv Manuf Technol 89(9–12):2535–2544

    Google Scholar 

  41. Qin CJ, Tao JF, Li L, Liu CL (2017) An Adams-Moulton-based method for stability prediction of milling processes. Int J Adv Manuf Technol 89(9–12):3049–3058

    Google Scholar 

  42. Tao JF, Qin CJ, Liu CL (2017) Milling stability prediction with multiple delays via the extended Adams-Moulton-based method. Math Probl Eng 2017:1–15

    MathSciNet  Google Scholar 

  43. Qin CJ, Tao JF, Liu CL (2017) Stability analysis for milling operations using an Adams-Simpson-based method. Int J Adv Manuf Technol 92(1–4):969–979

    Google Scholar 

  44. Tang C, Yan HQ, Zhang H, Chen ZQ, Liu M, Zhang GM (2005) The arbitrary order implicit multistep schemes of exponential fitting and their applications. J Comput Appl Math 173(1):155–168

    MathSciNet  MATH  Google Scholar 

  45. Tang C, Wang WP, Yan HQ, Chen ZQ (2006) High-order predictor corrector of exponential fitting for the N-body problems. J Comput Phys 214(2):505–520

    MathSciNet  MATH  Google Scholar 

Download references

Funding

This work was partially supported by the Natural Science Foundation of Jiangsu Province Outstanding Youth Fund (Grant No. BK20160084) and the Fundamental Research Funds for the Central Universities (Grant No. NS2016056).

Author information

Authors and Affiliations

  1. College of Mechanical and Electrical Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing, 210016, China

    Yi Wu & Youpeng You

  2. School of Safety and Environment Engineering, Hunan Institute of Technology, Hengyang, 421001, China

    Jianjun Jiang

Authors
  1. Yi Wu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Youpeng You
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Jianjun Jiang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yi Wu.

Additional information

Publisher’s note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wu, Y., You, Y. & Jiang, J. A stability prediction method research for milling processes based on implicit multistep schemes. Int J Adv Manuf Technol 105, 3271–3288 (2019). https://doi.org/10.1007/s00170-019-04487-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00170-019-04487-3

Keywords

Search

Navigation