Defining an ‘Epidemiological Risk Index’ to analyse COVID-19 mortality across European regions

Abstract

The spread and severity of COVID-19 within the European regions have been highly heterogeneous, with significant differences in both the number of infected persons and mortality across regions. This paper improves the weak ability of welfare variables, such as the HDI, to explain COVID-19 mortality. We propose a novel ‘Epidemiological Risk Index’, including environmental quality, global interaction, health system infrastructure, and population characteristics, which provides a better explanation of pandemic mortality in European regions. We deal with spatial interdependence in COVID-19 mortality by using spatial lagged covariates and Geographical Weighted Regressions. The findings in this study call attention to the influence of epidemiological factors in addition to purely development factors in explaining the severity of COVID-19.

1 Introduction

The irruption of the COVID-19 pandemic has not only shown up human and social vulnerabilities but has also revealed the limited capacity of national and international authorities to effectively control the spread of a virus across the world. The consequences of the epidemic have reached all countries, affecting economic activities, modifying social patterns and people’s interactions, in addition to having serious impacts on life and health.

As new data about the severity of the virus propagation and mortality have become available, an asymmetric impact on countries and regions across the world has been identified, suggesting that geography plays a significant role in the repercussions of COVID-19. Some recent studies investigate territorial aspects of the pandemic, such as cross-country comparisons of mortality (Bilinski and Emanuel 2020; Sornette et al. 2020), the identification of the relationship between mortality and socio-economic variables (Pacheco-Barrios et al. 2020; Arbel et al. 2021), or the impact that testing practices have on number of deceases by country (Liang et al. 2020; Marziali et al. 2021). Therefore, delving into the underlying factors that explain the regional mortality, particularly that of the initial (and unexpected) wave, is of utmost importance to learn how to fight against possible new epidemics and how to preserve human lives.

This paper, which uses COVID-19 mortality data for 252 EU regions from Eurostat,¹ makes four main contributions to the existing literature. First, it identifies some of the main factors behind the regional mortality in Europe during the first wave of COVID-19.² These factors are associated with local socio-economic and sanitary characteristics that play a role in explaining the extent of coronavirus mortality and that have to be measured at a more spatial disaggregated level such as regions, in view that national and international heterogeneities may blur the way in which these factors operate (e.g. through social interactions). Second, it proposes a synthetic Epidemiological Risk Index (ERI) to analyse COVID-19 based on the existing underlying factors. Synthetic indicators help structure the information of the individual factors in an orderly and reasonable way, obtaining aggregate measures that allow a territorial arrangement. These have already been used to analyse, for instance, COVID-19 and tourism vulnerability (Duro et al. 2021), and to measure the relative capacity of economies to achieve sustainable growth through global trade and investment (as suggested by the Hinrich Foundation).³ Third, the proposed framework is used to clarify the role of the starting conditions in each European region and illustrate how such conditions drove local regional mortality across Europe during the first wave of the pandemic. And fourth, we control spatial interdependence across EU regions by using spatial lagged covariates in a count data model and a Geographical Weighted Regression (GWR). In particular, the empirical analysis contrasts regional mortality with a multi-dimensional set of territorial characteristics (i.e. welfare level, social structure, sanitary infrastructure, and economic structure) of each region. These multiple factors are integrated into two indexes, namely the traditional Human Development Index (HDI) and our proposal of the Epidemiological Risk Index (ERI), to capture regional specificities that ultimately help to determine the pandemic severity.

The research approach uses the HDI to synthesize the level of socio-economic development and the welfare standards in each region following earlier contributions by other researchers. This composite measurement, firstly proposed by the United Nations Development Program in 1990 (UNDP 1990), is useful in making cross-country (or cross-regional) comparisons. An advantage of the HDI is the extension of the development measurement to other variables than income (gross domestic product), as it includes three dimensions: knowledge, health, and income. From its first calculation in 1990, the United Nations has annually published the international ranking of the Index in its Human Development Report, illustrating huge disparities across countries. Indeed, the simple and multi-dimensional structure of the HDI offers a useful measure for comparatively evaluating human development. The Index is also available for comparing territorial units (such as regions or smaller areas) other than countries—the only restriction being information availability for the required variables.

In this paper, the analysis of COVID-19 mortality starts with a regional calculation of the HDI for the European NUTS-II, similar to that done recently. For instance, Liu et al. (2020) observed an (unexpected) positive correlation between the HDI and the risk of infections and COVID-19 deaths in Italy during the first wave of the pandemic. By adopting an international perspective, Shahbazi and Khazaei (2020) obtained a direct significant correlation between the incidence and mortality rate of COVID-19 and HDI at the global level. Martins et al. (2020) provided comparable results, but they consider not only the relation among the socio-economic conditions (i.e. the HDI index) with the daily COVID-19 cases during the first wave in the tropical and subtropical Brazilian states, but also atmospheric variables and other control variables. Other papers such us Marziali et al. (2021), Troumbis (2021), and Prasetyo et al. (2023) also focus on HDI, and although they found some relationship (sometimes only correlations) between HDI and COVID-19 deaths, it is reasonable to suspect that this is only part of the story in view of limitations of the extreme simplicity of HDI (Faiz 2020). In this regard, Rath (2021) questions the traditional definition of the HDI in the context of the coronavirus pandemic and proposes including some additional elements to capture sub-dimensional development indicators in the Index structure.

Over time, some weaknesses of the HDI have been identified that may limit its ability to reflect development levels across the world, since it heavily emphasizes economic aspects, which leads to the prioritization of economic growth at the expense of other dimensions of well-being. In particular, the literature has proposed modifications in the Index definition, which include the way of aggregating the three constituent components (Sagar and Najam 1998), the way of defining the components and the structure (Noorbakhsh 1998), or the inclusion of sustainability issues (Neumayer 2001). Analogously, the HDI has shown a limited ability to explain the consequences of the COVID-19 pandemic in view of puzzling results (Faiz, 2000). Although the HDI is useful to summarize human development and social welfare into a single numerical value, it shows little potential to explain the underlying factors that determine the severity of the pandemic. Indeed, the (development focused) HDI fails to include important aspects related to health and social performances such as sanitary, social, epidemiologic, and environmental risks. To overcome previous limitations, we propose the calculation of an Epidemiological Risk Index (ERI) that includes the following relevant areas of a sanitary emergency: (i) environmental quality, (ii) propagation issues, (iii) health system infrastructure, and (iv) population characteristics.

In comparison to the HDI, the proposed new index is more suitable for explaining mortality in the European regions as it includes dimensions affecting COVID-19 mortality that are not being covered by HDI, especially those concerning international exchanges implying social interactions by individuals of different geographical areas. Consequently, the ERI provides new insights about the pandemic mortality and its causes across the European regions and highlights determinant issues to consider in epidemiological and sanitary policies. In particular, and contrary to a generally accepted aprioristic idea, the socio-economic development level has hardly explained the mortality during the first wave in the European regions, as we show in our econometric analysis. To explain the determining factors behind mortality one must, therefore, consider variables other than purely development-focused indicators. These variables consist of the population characteristics, the health system dimension, international regional connections, and environmental quality. These epidemiological-related variables have ultimately determined the risk of the pandemic and its mortality consequences in the European regions. Therefore, the outcomes in this paper show a novel approach to conducting spatial analyses of the pandemic since the proposed index not only includes specific factors shaping the epidemiological risk of regions but it also provides a synthetic measurement for that risk that is simple, direct, and easily understandable by policymakers and citizens.⁴

As there has been a clear spatial clusterisation of this phenomenon, any empirical analysis of COVID-19 determinants must take into account important regional differences in terms of COVID-19 mortality. To do this, we use firstly a count data model that includes spatial lagged variables and, secondly, we estimate a Geographically Weighted Regression (GWR).

The remainder of the paper is organized as follows: Sect. 2 explains the methodology used for the calculation of the ERI and the other covariates and describes the econometric specification. Section 3 reviews empirical literature about COVID-19 mortality and discusses validity of HDI and ERI. Section 4 discusses the main results. Finally, Sect. 5 summarizes the main findings and policy implications.

2 Research approach

2.1 The dependent variable

The COVID-19 mortality in European regions during the year 2020 is analysed at NUTS-II level for 252 regions, which is the standard territorial level in this kind of analysis.⁵ However, one should note that measuring COVID-19 mortality is not an easy task as there are no reliable and homogeneous sources for all EU countries, there is no consensus among researchers (i.e. there are several approaches that have been considered by scholars) and there have been important asymmetries in the registration methods for COVID-19 deaths, especially during the first wave of the pandemic, as some countries allocated deaths not to COVID-19 but to specific diseases triggered by it.⁶ In this regard, as for the measure of mortality, one line of research considers raw deaths, as Ehlert (2021) in Germany, Bilinski and Emanuel (2020) in the US; other authors focus on excess deaths, which are attributed to COVID-19, as Bilinski and Emanuel (2020) in the US; other use data on relative deaths (e.g. number of deaths per million inhabitants), as Sornette et al. (2020) using worldwide data and Kapitsinis (2020) in EU regions; and others focus on data from confirmed COVID-19 deaths, as Pachecho-Barrios et al. (2020) using worldwide data and Florida and Mellander (2022) in Sweden.

According to these strategies and data availability, there are some proxies to COVID-19 that might be used for research purposes, such as the excess mortality in 2020 relative to previous years or the total number of deaths in 2020 relative to population. In line with similar papers dealing with socio-economic determinants of COVID-19 mortality (e.g. Rodriguez-Pose and Burlina, 2021), we have chosen excess deaths in 2020, and we have proxied it as the ratio between the difference of deaths in 2020 minus the average deaths in 2015–2019 over the average deaths in 2015–2019. This ratio is our dependent variable (Mortality). We sourced data for mortality in 2020 from Eurostat, (except for Slovenia and Ireland, for which it came from their respective national statistical offices). For all countries in our dataset, Eurostat also provided the data for average mortality during the period 2015–2019. Although using the “extra” deaths in 2020 has some potential problems as (i) not all additional deaths have been caused by COVID-19⁷ and (ii) in 2020 there was also a reduction in “normal” mortality due to lockdown policies in all countries, we consider that our measure proxies COVID-19 mortality in a reasonable way.

If we analyse spatial distribution of Mortality (see Fig. 1), it is easy to identify that it is not randomly distributed across European regions but, on the contrary, there are some areas where mortality figures are considerably higher than in previous years, such as regions like Lombardy (Northern Italy) and Madrid (Central Spain). In terms of spatial autocorrelation, Fig. 2 shows Moran’s I (Moran 1948) for Mortality and suggests the existence of a slight positive spatial autocorrelation (i.e. values of Moran’s I range from − 1 (dispersion) to 1 (autocorrelation), whilst values close to 0 indicate a random and non-spatial distribution), although only slightly so for the whole distribution of regions.⁸

Fig. 1

Source: Derived by the authors from Eurostat data

Excess deaths in 2020 (related to the period 2015–2019).

Fig. 2

Source: Calculated by the authors

Spatial autocorrelation of excess death rates in 2020 (related to the period 2015–2019).

Additionally, we investigated whether spatial autocorrelation corresponds to a general or a local phenomenon. In this sense, Fig. 3 corroborates findings from Fig. 1 and shows that there are two clusters of high-high spatial autocorrelation: one in the areas comprising Northern Italy and South–East France, and the other in Central Spain, while there are several low-low clusters in areas that include all Danish, Swedish and Finnish regions, and most Greek ones.

Fig. 3

Source: Calculated by the authors

Local Spatial autocorrelation (LISA) of excess deaths in 2020 (related to the period 2015–2019).

2.2 Econometric strategy

We estimate the excess mortality in a region as a function of the local specific characteristics described in next section:

$$Y_{i} = \beta X_{i} + \beta {{WX}}_{i} + \varepsilon_{i}$$

(1)

where ${Y}_{i}$ is the dependent variable (extra mortality in 2020 in region i), ${X}_{i}$ is a matrix containing all independent variables plus an intercept, ${{WX}}_{i}$ includes the spatially weighted average of neighbouring regions of some independent variables, and $\varepsilon$ is the error term. The fact that all variables (both dependent and independent) have some degree of spatial dependence renders the standard estimation methods inappropriate, since the assumption of non-dependence between cross-sectional observations is presumably not satisfied. Therefore, one needs spatial econometric methods and models to tackle these specifically spatial issues. This is one of the paper’s most significant contributions because most articles dealing with COVID-19 determinants have neglected such spatial econometric issues.⁹ Since we have shown the existence of several spatial dependence processes in previous sections, we explore different econometric strategies to control them. Starting from a standard count data (CD) model to which we add some spatial lagged variables, we then complete this analysis by using a Geographical Weighted Regression (GWR).

The CD family is quite large and, among the most used are, on one side, the Poisson (P), the Negative Binomial (NB) models and, on the other, the Zero Inflated Poisson (ZIP) and the Zero Inflated Negative Binomial (ZINB) models. Although Poisson models are the most popular specification of CDM, they suffer from two key limitations, as they assume that the mean and the variance are equal (this assumption is often violated, causing overdispersion), and they can manage phenomena in which the count variable includes some zeroes (the zero problem), but not when this number is excessive. As for the first issue, we explore whether there is overdispersion following the approach by Fávero et al. (2020) and we control for this potential limitation using robust errors. For the second issue, there is no zero inflation, since all values of the dependent variable are positive.

Geographically Weighted Regression (GWR), first implemented by Fotheringham et al. (2002), allows spatial heterogeneity and is specially recommended when using a large number of heterogeneous spatial units, such as EU regions. GWR estimates separate regression coefficients for each observation, rather than just looking at the mean, as in OLS methods. This procedure allows one to highlight whether the same covariates may have quite different effects on the dependent variable depending on the observation, given that close areas have stronger effects than distant ones.¹⁰ Regression parameters in a GWR approach have the following structure:

$$\hat{\beta }_{i} = \left( {X^{T} W_{i} X} \right)^{ - 1} X^{T} W_{i} Y$$

(2)

where ${\widehat{\beta }}_{i}$ is the vector of parameter estimates for region $i$, ${W}_{i}$ is the diagonal weights matrix for region $i$, $X$ is the matrix of the covariates, and $Y$ is the vector of the dependent variables.

As the volume of results is quite large, and as output includes separate $\beta$ coefficients and R² for each observation, typically one presents GWR coefficients using maps rather than tables. Similar applications of GWR on spatial factors influencing COVID-19 include analyses for Wuhan in China (Xu et al., 2022), Tehran in Iran (Lak et al. 2021; Nasiri et al. 2021) and Oman (Mansour et al. 2021).

3 Regional characteristics explaining excess mortality

There are several approaches that have been considered by scholars when dealing with the measure of urban/regional determinants with statistical significance on mortality. Among them we may highlight health and socio-economic determinants, such as elderly population (Florida and Mellander 2022; Buja et al. 2020; Ehlert 2021; Kapitsinis 2020; Sornette et al. 2020); population density and socio-economic characteristics (Florida and Mellander 2022; Arbel et al. 2021; Ehlert 2021; Marziali et al. 2021; McCann et al. 2021; Hantrais and Letablier 2021; Kapitsinis 2020); pollution (McCann et al. 2021; Kapitsinis 2020); infection tests and government measures such as quarantines or lockdowns (Hantrais and Letablier, 2021; Kapitsinis 2020; Liang et al. 2020); mobility (McCann et al. 2021) and public transport (Buja et al., 2020); employment (Buja et al., 2020); education (Florida and Mellander 2022); social interaction (Buja et al., 2020; Kapitsinis 2020; Kuebart and Stabler 2020); healthcare infrastructure such us physicians, nursing homes, childcare and hospital beds (Florida and Mellander 2022; Ehlert 2021; Kosfeld et al. 2021; McCann et al. 2021; Hantrais and Letablier, 2020; Kapitsinis 2020); migration movements (Florida and Mellander 2022; Ehlert 2021); regional institutional factors (McCann et al. 2021; Rodríguez-Pose and Burlina 2021); and agglomeration (Sridhar 2023; McCann et al. 2021; Kapitsinis 2020), among main factors. Unfortunately, these approaches usually lack a systematic strategy in terms of a broad view of what influences COVID-19 mortality and focus only in partial dimensions.

Since the epidemiologic consequences, such as the number of infections and the number of deaths, depend on aspects beyond the development-focused indicators, additional dimensions are required to complete the wide spectrum of issues influencing the pandemic spread and the pandemic severity. Accordingly, departing from recent literature targeting on HDI as one relevant determinant of COVID-19 mortality, in this paper we contribute by extending that index into a completer and more appropriated one, the Epidemiological Risk Index (ERI).

3.1 The human development index (HDI)

The annual Human Development Reports of the United Nations Development Program (UNDP 1990) first proposed the HDI in 1990 and it constituted a step forward in the measurement of development across the world. Given its simplicity and comparability, the Index became a useful statistical instrument for international welfare analyses and is extensively used to rank countries according to their development levels.

The HDI is a statistical indicator that, apart from income, contains a more comprehensive measure of human development. Specifically, the HDI combines information related to three dimensions of social development: life expectancy, education, and income per capita. For each dimension, the essential part is captured using a suitable variable able to cover the wide spectrum of the corresponding dimension. The value for each individual part is computed on a scale between 0 and 1, where 0 corresponds to the minimum value and 1 corresponds to the maximum value.

For each region ($\text{i}$ $=1, \ldots , 252$), life expectancy is calculated as the number of years of life expectancy at birth. The Life Expectancy Index (${\mathrm{LEI}}_{\text{i}}$) contrasts the life expectancy value (${\mathrm{LE}}_{\text{i}}$) with the assumed maximum (85) and minimum (20) values¹¹as follows:

$$ {\text{LEI}}_{\text{i}} = \frac{{{\text{LE}}_{\text{i}} - {\text{minimum}} \;{\text{LE}}}}{{{\text{maximum }}\;{\text{LE}} - {\text{minimum }}\;{\text{LE}}}} = \frac{{{\text{LE}}_{\text{i}} - 20}}{85 - 20}.$$

(3)

The education index for $i$ (${\mathrm{EI}}_{\text{i}}$) is calculated as the mean expected years of schooling (${\mathrm{ES}}_{\text{i}}$) and the mean years of schooling (${\mathrm{MS}}_{\text{i}}$), in the following manner:

$${\text{EI}}_{\text{i}} = \frac{1}{2}\left( {\frac{{{\text{ES}}_{\text{i}} }}{{{\text{maximum}} \;{\text{ES}}}}} \right) + \frac{1}{2}\left( {\frac{{{\text{MS}}_{\text{i}} }}{{{\text{maximum}}\;{\text{MS}}}}} \right) = \frac{1}{2}\left( {\frac{{{\text{ES}}_{\text{i}} }}{18} + \frac{{{\text{MS}}_{\text{i}} }}{15}} \right)$$

(4)

where the maximum values for ${\mathrm{ES}}_{\text{i}}$ and ${\mathrm{MS}}_{\text{i}}$ are assumed to be 18 and 15, respectively, and the minimum values are set equal to 0.

Finally, the Income Index (${\text{II}}_{\text{i}}$) is calculated as:

$${\text{II}}_{\text{i}} = \;\frac{{\ln \left( {{\text{GDP}}_{\text{pc}} } \right)_{\text{i}} - \ln \left( {{\text{minimum}} \;{\text{GDP}}} \right)}}{{\ln \left( {{\text{maximum}}\; {\text{GDP}}} \right) - \ln \left( {{\text{minimum}}\;{\text{GDP}}} \right)}} = \;\frac{{\ln \left( {{\text{GDP}}_{\text{pc}} } \right)_{\text{i}} - \ln \left( {100} \right) }}{{\ln \left( {75,000} \right) - \ln \left( {100} \right) }},$$

(5)

being ${\mathrm{GDP}{\text{pc}}}_{\text{i}}$ the Gross Domestic Product per capita, whose minimum and maximum values are 100 and 75,000, respectively, and being $ln$ the natural logarithm.

The arithmetic mean of the three indexes (Eqs. (3), (4), and (5)) gives the HDI of $i$ (${\mathrm{HDI}}_{\text{i}}$):

$${\text{HDI}}_{\text{i}} = \frac{1}{3}\left( {{\text{LEI}}_{\text{i}} + {\text{EI}}_{\text{i}} + {\text{II}}_{\text{i}} } \right),$$

(6)

which ranges between 0 (lowest value) and 1 (highest value). The larger (lower) the value of ${\mathrm{HDI}}_{\text{i}}$, the larger (lower) the development achievement of the corresponding economy.

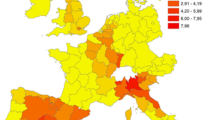
Figure 4 shows that the HDI is inhomogeneous across European regions. The highest levels are in Scandinavia, Finland, some regions of France, Belgium, the Netherlands, and most of Ireland, while lower levels are found in Estonia, Romania, Bulgaria, Portugal, and some German regions.

Fig. 4

Source: Calculated by the authors

Human Development Index (2018).

3.2 The Epidemiological Risk Index (ERI)

In view of the limitations of the HDI in explaining the pandemic consequences pointed out by the literature (e.g. Liu et al. 2020), in this paper we propose an alternative measure to evaluate the role of socio-economic characteristics of EU regions over COVID-19 mortality. The proposed new ERI allows us to cover the essence of a sanitary crisis and its consequences, since it includes relevant aspects of the sanitary emergency not captured by the HDI. We define a composite indicator that includes the environmental dimension, the regional interactions with foreign countries, the health system infrastructure, and population characteristics. All these aspects appear relevant for explaining the consequences of the COVID-19, and particularly in determining why some regions suffered greater mortality than others.

Each relevant dimension included in the ERI is computed as the average of the counterpart elements, and the maximum and minimum values used to obtain individual indexes are determined according to the maximum and minimum values observed in the database. Specifically, the individual elements in the new Index are obtained through the following calculation:

$${\text{Index}}_{\text{i}} = \frac{{\ln (x_{\text{i}} ) - \ln \left( {{\text{minimum}}\; x_{\text{i}} } \right)}}{{\ln \left( {{\text{maximum}} \;x_{\text{i}} } \right) - \ln \left( {{\text{minimum}} \;x_{\text{i}} } \right)}},$$

(7)

where ${x}_{\text{i}}$ refers to the various indicators used to capture the dimension included. For each region $i$, the ERI is calculated as the average mean of the four dimensions included, in the form:

$${\text{ERI}}_{\text{i}} = \frac{1}{4}\left( {{\text{EI}}_{\text{i}} + {\text{GI}}_{\text{i}} + {\text{HI}}_{\text{i}} + {\text{PI}}_{\text{i}} } \right),$$

(8)

the elements in Eq. 8 being equal to: (i) the environmental index (${\mathrm{EI}}_{\text{i}}$), including pollutant emissions¹²; (ii) the global interaction index (${\mathrm{GI}}_{\text{i}}$), including the maritime transport of passengers, the air transport of passengers and the arrivals at tourist accommodation establishments¹³; (iii) the health system index (${\mathrm{HI}}_{\text{i}}$), including the number of beds in hospitals per inhabitant, the number of doctors per inhabitant and the number of employees in the health and social activity sector in relation to the total population; and (iv) the population characteristics index (${\mathrm{PI}}_{\text{i}}$), that includes the median population age¹⁴ and the rate of population at risk of poverty. Overall, the ERI includes most of significant determinants of COVID-19 mortality identified by empirical literature, and adds some of them not covered by HDI concerning environmental issues and interactions across countries.¹⁵

Figure 5 shows the results of the ERI calculation. Not surprisingly, since the new Index focuses on the specifical epidemiological factors of territories, it produces different patterns than the ones from the HDI. Particularly, the spatial distribution of the ERI indicates higher risk levels for Southern and Eastern regions and lower levels for British and Irish regions and some Central and Northern regions.

Fig. 5

Source: Calculated by the authors

Epidemiological Risk Index (2019).

3.3 Other independent (Control) variables

In addition to the HDI and the ERI, we have computed other variables to control for some regional characteristics that may, potentially, influence mortality rates. These variables have a geographical dimension, a demographic dimension, a social and educational dimension, and an economic dimension.

Concretely, we include a dummy which measures insularity (ISLAND), as we assume that spatial isolation may prevent coronavirus transmission and, consequently, it may reduce mortality (Chiesa et al. 2021). Demography is captured by a variable controlling for total population of the region (POP) as recent empirical evidence indicates a positive relationship between size (e.g. number of inhabitants) and the spread of the disease (Arauzo-Carod et al. 2021) and number of inhabitants aged over 85 years old (AGE), as ageing is a clear determinant of COVID mortality (Sasson 2021). Recent education and training (TRAIN) cover the social dimension, as there is empirical evidence showing a positive relationship between educational levels and the availability of tools to prevent infection and mortality due to COVID-19 (Alobuia et al. 2020). Finally, the economic dimension is captured by the unemployment rate but, to avoid correlation with the GDP, we preferred the spatial lag (W_UNEM) to the variable measured in the same region (additionally, using this measure we capture the existence of unemployment situations in areas larger than single regions). This economic dimension is necessary although the results to be expected are uncertain for two reasons. On one hand, lower unemployment levels may proxy higher income (see Arauzo-Carod et al. 2021, for the case of Barcelona) and, therefore, less exposure to coronavirus (Baena-Díez et al. 2020; Burström and Tao 2020). However, on the other hand, lower unemployment levels also suggest less social interaction and, consequently, less exposure to coronavirus (Chiesa et al. 2021). Finally, in addition to the HDI, we compute its spatially lagged version (W_HDI), to take into control social development, not only in each region, but also in neighbouring ones.

4 Empirical results

The excess mortality caused by COVID-19 is explained in terms of the effects of covariates belonging to several dimensions (geographical, demographic, social and economic). In this sense, the baseline estimation shown in Table 1 follows a parsimonious strategy in which we depart from a simple estimation including only a few covariates by adding additional covariates for each model.¹⁶ As our variable of interest is the HDI, its effects are explored in all the estimations, although in none of them the coefficient is significant, which implies that, at least according to current definition of HDI, this indicator does not have a demonstrable effect in terms of lowering or increasing mortality linked to COVID-19. That suggests the need for alternative measures of human welfare.

Table 1 Baseline estimation (current HDI)

Apart from the HDI, the dimensions that have the strongest effects on COVID-19 mortality (both in a positive and a negative way) are the economic, the geographical, the social and, to some extent, the demographic. As for the economic ones, the spatial lag of unemployment (W_UNEM) reduces mortality, which suggests not only the clusterisation of both high and low unemployment rates, but also that lagged regions with high unemployment levels have lower social interaction that may reduce the spread of the pandemic. Similarly, being an island has no significant effect on mortality, which is quite surprising as one might expect geographical isolation to inhibit disease outbreaks. As for the demographic dimension, population (POP) has no significant effects (as in Rodriguez-Pose and Burlina, 2021) and ageing (AGE) is a clear booster of COVID mortality, which is logical from a medical point of view and has been largely demonstrated by previous empirical literature (see, for instance, Sasson 2021 and Le Couteur et al. 2020), especially during the early stages of COVID-19 outbreak (Arauzo-Carod et al. 2021). Finally, training inside the labour market (TRAIN) reduces mortality, which is reasonable if we assume that continuous training provides individuals with additional tools to protect themselves from the pandemic.

In any case, the results in Table 1 support our initial assumption regarding lack of suitability of the current HDI to precisely capture the influence that development standards have on mortality (at least according to the way these are traditionally measured), in line with the suggestions of Rath (2021) and Faiz (2020).¹⁷ Accordingly, we have re-estimated the same model but using the proposed ERI indicator instead of the traditional HDI (see Table 2).

Table 2 Extended estimation (ERI)

It is noteworthy that our results are robust to the introduction of the ERI (all covariates keep similar effects and significance levels) and it, contrary to the HDI, has a positive and significant effect on mortality in half of the models (although caution is required in view of one of the estimations only being significant only at the 10% level). Overall, this implies that our proposed measurement of epidemiological risk allows us to explain increases in mortality of the European regions due to COVID-19 in a manner that is clearly better than when using the HDI.¹⁸ This is a key result that suggests the non-relevance of a general indicator such as HDI when dealing with the determinants of the COVID-19 pandemic and the necessity of alternative (i.e. more specific) measures such as the ERI.

To explore whether there is any simultaneous effect when analysing the role of both indicators, Table 3 includes both HDI and ERI.¹⁹ In this case, the results are unchanged for both our covariates of interest and for the control variables, indicating their robustness. In this sense, income, education, and life expectancy do not provide appropriate insights for understanding why some areas suffer differently from the mortality arising from the pandemic. Accordingly, societal, health and environmental indicators as those provided by the dimensions included in the ERI (i.e. environment, transport, health system and population characteristics) are better predictors of that phenomenon and, then, should be introduced in standard analyses.²⁰

Table 3 Extended estimation (HDI and ERI)

Despite the previous econometric results, we wish to analyse whether the lack of significance of HDI is a common feature of the EU regions considered, or whether there are some noticeable spatial asymmetries.²¹ This is shown in Fig. 6, which contains GWR results for the HDI, both in terms of their coefficient (in colours) and significance (in stripes). Concretely, a higher influence of HDI over the COVID-19 mortality appears in the Southern regions, especially at the Iberian Peninsula and Central and Northern Italy, and significant effects of HDI over mortality also concentrate in the same area (as well as in Slovenia, some Austrian regions, Ireland, Scotland and Western England and Wales). Overall, stronger, and significant effects concentrate in the Iberian Peninsula, suggesting the existence of some social and lifestyle specificities that are captured by the HDI indicator (e.g. typologies of social interaction) and have real effects in terms of mortality. Nevertheless, if we consider the full range of EU regions, we must conclude that the HDI is not a powerful predictor of such COVID-19 related mortality, so alternative measures are needed.

Fig. 6

Source: Calculated by the authors

GWR results of Human Development Index.

Fig. 7

Source: Calculated by the authors

GWR results of Epidemiological Risk Index.

As for the ERI results, the index is significant in most of previous econometric specifications (see Tables 2 and 3), and at a regional level, the pattern is quite similar when looking at GWR results at Fig. 7 (except for some Scandinavian, French, Greek and other Eastern European regions). Additionally, the indicator has a clear core-periphery pattern in terms of the intensity of the effect on mortality, that being core around Switzerland (i.e. Lombardy, Piemonte, Baden-Württemberg, Franche-Comté, Rhône-Alpes, etc.), so that in these areas the components of the ERI have a stronger effect on mortality, while in geographically peripheral areas like most of the Iberian Peninsula (except Catalonia), Ireland, Scotland, Wales and Central and Northern England the socio-economic characteristics measured by the ERI have a lower effect on mortality.

Overall, our results indicate that COVID-19 mortality has a spatial dimension that crosses administrative borders and goes beyond specific national or regional characteristics; a dimension that health authorities must consider when designing anti-pandemic policies to increase their effectiveness. This dimension also applies to many other similar diseases (e.g. Monkeypox) that are triggered by social and economic interactions among regions.

5 Conclusions

This paper has provided insights into the role played by socio-economic characteristics on mortality caused by COVID-19. To do that, we go beyond traditional welfare measures such as the ‘Human Development Index’ and we propose an ‘Epidemiological Risk Index’ as a better alternative. Compared to previous analyses of the COVID-19 mortality, the index defined in this paper allows to synthesise a set of factors determining the epidemiological risk instead of using the common procedure of a large set of individual variables. As for the spatial dimension of our analysis, this paper has used data at regional level (mainly NUTS-II regions, but also NUTS-I in some cases) on the assumption that there are sufficiently homogeneous areas within regions in terms of potential mortality determinants.

This paper provides novel outcomes that could guide policymaking. In particular, the analysis identifies the role played by the socio-economic, environmental and health characteristics in explaining the excess mortality associated with COVID-19 during 2020 for 252 European regions. The research has evaluated the inability of the Human Development Index to explain mortality, and our conclusions regarding its inappropriateness to determine the negative impacts of the current pandemic should be borne in mind, since it highlights the fact that epidemiological impacts are not strictly related to the development levels of societies. In contrast, the proposed Epidemiological Risk Index, which includes demographic, public health, social and environmental characteristics, offers a more precise representation of the factors behind the pandemic mortality.

Specifically, the ability of the new (epidemiologically focused) index to explain excess mortality in the European regions should be taken into consideration when analysing the consequences of the pandemic. This evidence deserves special attention for several reasons. First, the new indicator overcomes the weakness of the HDI in analysing COVID-19, and particularly, in explaining pandemic mortality. Second, the outcomes in this paper offer new insights into the importance of other dimensions, not necessarily related to development. This suggests the need to monitor the various components in the new index by regional authorities, to help prevent future waves of the pandemic and insulate regions from the negative effects. Since the approach offers a new way of interpreting the pandemic issues and its negative consequences territorially, it may also improve decision-making in other (not strictly epidemiological) areas such as trade policy, global value chain issues, industrial policy, environmental measures, and inter-country and inter-regional economic planning. The Epidemiological Risk Index proposed in this paper identifies a set of influencing factors behind COVID-19 mortality, and therefore, it has an undoubted interest for policy measures to fight against pandemics, both from a global and a local (or regional) sanitary and health perspective.

Furthermore, although there are many recent papers dealing with determinants and effects of COVID-19 pandemic, few of them consider the spatial dimension of the disease. Our approach of using spatial econometric techniques and a Geographically Weighted Regression (GWR) estimation allows us to identify such dimensions and handle them correctly by introducing a much-needed spatial dimension to COVID-19 policies, something that has not been yet addressed by public authorities. This strategy allows us to show that geography matters for public health measures, and that public regional authorities should take into account the situation in neighbouring areas when designing policy responses for their own regions.

All the results are presented with the caveat that COVID-19 is a new phenomenon that needs additional research to fully understand its socio-economic implications and determinants. Also, using specific data about COVID-19 mortality instead of our excess mortality proxy will lead to more precise results. Finally, as the EU has suffered different COVID-19 mortality waves since March 2020, and their characteristics have changed due to the different variants of the virus in each wave, it is important to better identify core determinants of these processes using temporally disaggregated data. Addressing these limitations will guide future research in this area.

Appendix

See Table

Table 4 Definition of explanatory variables

4.