A new method to prioritize the QFDs’ engineering characteristics inspired by the Law of  Comparative Judgment

Abstract

The primary module of Quality Function Deployment (QFD) is the House of Quality (HoQ), which supports the design of new products and services by translating customer requirements (CRs) into engineering characteristics (ECs). Within the HoQ framework, the traditional technique for prioritizing ECs is the independent scoring method (ISM), which aggregates the weights of the CRs and the relationships between CRs and ECs (i.e., null, weak, medium, and high) through a weighted sum. However, ISM incorporates two questionable operations: (i) an arbitrary numerical conversion of the relationships between CRs and ECs, and (ii) the “promotion” of these relationships from ordinal to cardinal scale. To address these conceptual shortcomings, this paper introduces a novel procedure for prioritizing ECs, inspired by the Thurstone’s Law of Comparative Judgment (LCJ). This procedure offers a solution that is conceptually sound and practical, overcoming the conceptual shortcomings of ISM, while maintaining its simplicity, flexibility, and ease of implementation. The proposed approach is supported by a realistic application example illustrating its potential.

1 Introduction

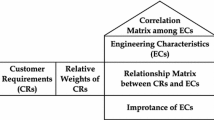
Quality Function Deployment (QFD) is a commonly used methodology for facilitating customer-oriented design of new products and services (Franceschini 2001). The initial module of QFD, known as the House of Quality (HoQ), aims to translate the customer requirements (CRs) of a new product/service into engineering characteristics (ECs), i.e., technical design features that directly impact the CRs (Zare Mehrjerdi 2010). Figure 1a exemplifies the HoQ’s relationship matrix with CRs and ECs indicated in rows and columns; the symbols in Fig. 1b represent the intensities of the relationships between ECs and CRs. Additionally, a weight (${w}_{{CR}_{i}}$) is assigned to each i-th CR, reflecting its importance from three complementary perspectives: final customer, corporate brand image, and improvement goals for the new product/service in relation to existing counterparts in the market (Akao 1994; Franceschini and Maisano 2018).

Fig. 1

a Relationship matrix and EC prioritization using the independence scoring method (ISM). b Intensity of the relationships between ECs and CRs, and conventional conversion into numerical coefficients (r_ij)

Several actors participate in the QFD construction. The leading role is played by the members of the QFD team, i.e., a working group consisting of experts from the company of interest, with complementary skills ranging from marketing, design, quality, production, maintenance, etc. Another important role is played by a sample of interviewed respondents—i.e., (potential) end users who contribute to the collection of the so-called voice of the customer (VoC)—from which the QFD team extrapolates the HoQ’s CRs (Akao 1994; Franceschini and Rossetto 1995). To effectively identify the VoC, which is foundational to the whole QFD process, it is needed to meticulously select interviewees. This selection should be based on both the quantity and the quality of participants, ensuring that they possess a comprehensive understanding of the product or service under consideration, even if not from a technical standpoint. Concurrently, the QFD team members are expected to bring their specialized technical knowledge to the table, facilitating collaborative decision-making throughout the design and development stages. This approach, as outlined by Akao (1994) and Huang et al. (2022), is integral to the traditional HoQ construction method, which aims to equitably distribute tasks among all involved parties. Thus, while there may be room for enhancing the traditional HoQ, it would be ill-advised to alter the fundamental (largely manual) methods of data gathering that are familiar to the above-mentioned groups. This stance, however, does not preclude the possibility of refining the data processing stage, provided that the initial data collection methods remain unchanged.

Returning to the traditional QFD construction method, ECs should be prioritized considering their impact on the final customer; in general, ECs that have relatively intense relationships with CRs characterized by relatively high ${w}_{{CR}_{i}}$ values deserve more attention during the design phase. The conventional approach for prioritizing ECs is the so-called independence scoring method (ISM), which is a weighted sum of the coefficients (r_ij) derived from the numerical conversion of the relationship matrix symbols (see Fig. 1b), utilizing the ${w}_{{CR}_{i}}$ values as weights (Akao 1994). The resulting EC weight can be determined by Eq. 1, as exemplified in the lower part of Fig. 1a:

$${w}_{{EC}_{j}}=\sum_{\forall i}\left({r}_{ij}\cdot {w}_{{CR}_{i}}\right)$$

(1)

However, the ISM method incorporates two conceptually questionable operations: (i) an inherently arbitrary conversion of the relationship intensities (defined on an ordinal scale: ∅ < $\Delta$ < $\bigcirc$ < ●) into conventional numerical coefficients (r_ij: ∅ → 0, $\Delta$→ 1, $\bigcirc$ → 3, ● → 9, cf. Figure 1b), and (ii) the aggregation of r_ij values through a weighted sum, which introduces an (undue) promotion to a cardinal scale with meaningful intervals (Franceschini et al. 2015). These questionable transformations can result in a distorted prioritization of ECs (Lyman 1990).

To address these conceptual shortcomings, this paper proposes a novel technique for prioritizing ECs based on Thurstone’s Law of Comparative Judgment (LCJ) (Thurstone 1927). Some advantages of the LCJ are that this technique is well-established, conceptually rigorous, effective and robust in practice (Maranell, 1974; Brown and Peterson 2009; Kelly et al. 2022). The integration of the LCJ into the new procedure and the integration of some “dummy” ECs (see Sect. 5) will enable the prioritization of ECs on a cardinal scale (Franceschini et al. 2022).

The remainder of this article is organized into five sections. Section 2 contains a brief review of the state-of-art techniques for prioritizing ECs that are alternative to ISM. Section 3 illustrates a case study that will accompany the description of the new procedure. Section 4 briefly recalls the LCJ, illustrating its underlying assumptions and practical application. Section 5 provides a step-by-step description of the proposed procedure, accompanied by an application example referring to the case study introduced in Sect. 3. The concluding section summarizes the major contributions of this research, its practical implications, limitations and insights for future development.

2 Literature review

Although ISM is the most widely used technique for EC prioritization, it has some shortcomings documented in a plurality of scientific contributions. In addition to (i) the arbitrary numerical conversion of the relationship matrix coefficients and (ii) the undue promotion of their ordinal scale into a cardinal one (cf. Figure 1b), there are other shortcomings, such as the fact that EC weights may not be consistent with CR weights. The latter shortcoming has inspired a corrective normalization (Lyman 1990) that, however, does not resolve the previous two.

The scientific literature includes multiple alternative techniques that aim to overcome the weaknesses of ISM and expand its scope. At the risk of oversimplifying, these techniques can be synthesized into three macro-categories (Franceschini et al. 2022).

• 1. Rule-based techniques. Practical techniques achieve a computationally simple, intuitive, and satisfactory prioritization of ECs, which is not necessarily the optimal one (assuming it exists). In some operational contexts, these techniques are classified as “heuristic” or “experience-based”. Let us recall, for example, Borda’s method or other techniques based on pairwise comparisons (Dym et al. 2002), and another technique (called ordinal prioritization method) based on the adaptation of a model proposed by Yager to the HoQ context (Franceschini et al. 2015; Galetto et al. 2018; Yager 2001).

• 2. Multi-criteria decision-making (MCDM) techniques. EC prioritization can be also seen as an MCDM problem involving conflicting CRs. Several MCDM techniques have been used in previous studies to improve the performance of QFD (Huang et al. 2022; Ping et al. 2020). Let us recall for example the application of the ELECTRE-II (ÉLimination Et Choix Traduisant la REalité) method (Liu and Ma 2021) or the EDAS approach (evaluation based on distance from average solution) (Ghorabaee et al. 2015; Mao et al. 2021).

• 3. Techniques based on fuzzy logic. These techniques, which could also be interpreted as advanced heuristics, take into account the inherent uncertainty in the formulation of CR-importance judgments (by interviewed respondents) or in the formulation of relationship matrix intensities (by QFD team members). For example, the techniques proposed by Li et al. (2019) and Shi et al. (2022) apply to the open design contest, in which the intensity of relationships between CRs and ECs and the prioritization of ECs are inferred on the basis of linguistic variables and text-format information, describing the subjective imprecision of human cognition.

Most of the aforementioned techniques require additional information beyond that collected in the traditional QFD process. For example, techniques to handle information related to linguistic variables require verbatim transposition of interviews that were conducted in open-ended form (Li et al. 2019); most of the techniques based on fuzzy logic require some technical expertise in setting working parameters, such as thresholds or weights. The procedure proposed in this paper—which can be referred to as “distribution-based” since it relies on statistical assumptions regarding the distribution of the QFD team preferences (Franceschini et al. 2022)—fits the information contained in the classic HoQ and can also be implemented and automated by non-experts (cf. Section 5).

3 Test case

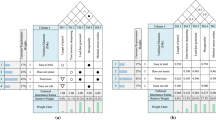
Referring to an application example adapted from the scientific literature (Franceschini et al. 2015), let us consider a company of mountain sports accessories that plans to design a new model of climbing safety harness through the QFD. Figure 2 illustrates the HoQ that was constructed by combining information obtained through interviews with a sample of respondents (i.e., potential end users) and from the technical examination of QFD team members (i.e., corporate staff with technical and design expertise). Eight CRs and eight ECs were identified.¹ The ${w}_{{CR}_{i}}$ values inherently may take into account information concerning the CR importance to final customers, corporate brand image, and improvement goals, combining them through a multiplicative aggregation model (Franceschini 2001; Franceschini and Maisano 2018). For simplicity, Fig. 2 shows only the ${w}_{{CR}_{i}}$ values, omitting the three CR-importance contributions mentioned above. Next, ECs are prioritized, determining the ${w}_{{EC}_{j}}$ values reported in the lower part of Fig. 2 through the ISM (cf. Equation 1). This HoQ will be used as a test case to illustrate the new EC prioritization procedure step-by-step (cf. Section 5). The concluding part compares the results of the new prioritization procedure with those derived from the traditional ISM.

Fig. 2

Relationship matrix referring to the design of a new climbing safety harness model, adapted from (Franceschini et al. 2015). The ${w}_{{EC}_{j}}$ values are determined by converting the relationship matrix symbols into numerical coefficients (r_ij, cf. Figure 1b), and applying the ISM (Eq. 1)

4 Basics of the law of comparative judgment

The very general problem in which Thurstone’s LCJ finds application is summarized as follows: a set of experts formulate their individual (subjective) judgments about a specific attribute of some objects and these judgments must be merged into a collective one (Maranell, 1974; Kelly et al. 2022). The attribute can be defined as “a specific feature of objects, which evokes a subjective response in each expert”. Consider, for example, the intensity of the aroma (attribute) of some alternative coffee blends (objects), which are assessed by a panel of experienced café customers (experts).

In this scenario, Thurstone (1927) postulated the existence of a psychological continuum, i.e., “an abstract and unknown unidimensional scale, in which the position of the objects is directly proportional to their degree of the attribute of interest”. Although the psychological continuum is a unidimensional imaginary scale, the LCJ can be used to approximate the position of the objects of interest on it. According to the so-called case V of Thurstone’s LCJ, the position of a generic j-th object (EC_j) is in fact postulated to be distributed normally: EC_j ~ N(${\mu }_{{EC}_{j}}$, ${\sigma }_{{EC}_{j}}^{2}$), where ${\mu }_{{EC}_{j}}$ and ${\sigma }_{{EC}_{j}}^{2}$ are the unknown mean value and variance of that object’s attribute.² Figure 3 represents the hypothetical distributions of the position of any two generic objects, ${EC}_{j}$ and ${EC}_{k}$. The distribution associated with a given object is characterized by a dispersion (or variance), which reflects the intrinsic expert-to-expert variability in positioning (albeit indirectly, as we will better understand below) that object on the psychological continuum. Let ${\mu }_{{EC}_{j}}$ and ${\mu }_{{EC}_{k}}$ correspond to the (unknown) expected values of the two objects and ${\sigma }_{{EC}_{j}}^{2}$ and ${\sigma }_{{EC}_{k}}^{2}$ the (unknown) variances. The difference $\left({EC}_{j}-{EC}_{k}\right)$ will follow a normal distribution with parameters:

$${\mu }_{\left({EC}_{j}-{EC}_{k}\right)}={\mu }_{{EC}_{j}}-{\mu }_{{EC}_{k}}\;{\rm{and}}\; {\sigma }_{\left({EC}_{j}-{EC}_{k}\right)}=\sqrt{{\sigma }_{{EC}_{j}}^{2}+{\sigma }_{{EC}_{k}}^{2}-2\cdot {\rho }_{{EC}_{j},{ EC}_{k}}\cdot {\sigma }_{{EC}_{j}}\cdot {\sigma }_{{EC}_{k}}}$$

(2)

where:

Fig. 3

Theoretical distributions of the position of two generic objects (i.e., ${EC}_{j}$ and ${EC}_{k}$) in the psychological continuum. b Graphical representation of the quantity (${{1} - {p}_{jk}}$), being ${p}_{jk}\; =\;P[{\left({{EC}_{j}} - {{EC}_{k}}\right)\geq{0}}]$

${\mu }_{{EC}_{j}}$ and ${\mu }_{{EC}_{k}}$ denote the (unknown) mean values of ${EC}_{j}$ and ${EC}_{k}$ in the psychological continuum;

${\sigma }_{{EC}_{j}}^{2}$ and ${\sigma }_{{EC}_{k}}^{2}$ denote the (unknown) variances of ${EC}_{j}$ and ${EC}_{k}$;

${\rho }_{{EC}_{j},{ EC}_{k}}$ denotes the (unknown) correlation between objects ${EC}_{j}$ and ${EC}_{k}$.

Considering the area subtended by the distribution of $\left({EC}_{j}-{EC}_{k}\right)$, let us draw a vertical line passing through the point with ${EC}_{j}-{EC}_{k}=0$ (see Fig. 3b). The area to the right of the line depicts the observed proportion of times (${p}_{jk}$) that ${EC}_{j}\ge {EC}_{k}$ or $\left({EC}_{j}-{EC}_{k}\right)\ge 0$. Of course, the area to the left depicts the complementary proportion $\left({1-p}_{jk}\right)$.

In addition, it is postulated that the variances of the objects are all equal (${\sigma }_{{EC}_{1}}^{2}={\sigma }_{{EC}_{2}}^{2}= \dots ={\sigma }^{2}$) and the intercorrelations (in the form of Pearson coefficients ${\rho }_{{EC}_{j}{, EC}_{k}}$) between pairs of objects (${EC}_{j}$, ${EC}_{k}$) are all equal too (${\rho }_{{EC}_{j}{, EC}_{k}}=\rho , \forall j,k$).

Having outlined this framework, let us now focus on the LCJ's application, which is based on the following four steps:

• 1. A set of experts (j₁, j₂, …) formulate their preferences for each object (EC_j) versus every other object (EC_k), considering all possible ${C}_{2}^{m}$= m∙(m – 1)/2 pairs, m being the total number of objects. In practice, the following question needs to be answered: “How do you judge the degree of the attribute of EC_j compared to that of EC_k, in relative terms?”. Judgments are expressed through relationships of strict preference (e.g., “EC₁ > EC₂” or “EC₁ < EC₂”) or indifference (e.g., “EC₁–EC₂”). Results are then aggregated into a proportion matrix (P). Precisely, for each possible paired comparison between two objects (EC_j and EC_k), the conventional portion of experts who prefer the first object to the second one is determined as:

  $$p_{{jk}} = 1 \cdot p_{{jk}}^{{^{{( > )}} }} + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2} \cdot p_{{jk}}^{{^{ (\sim) } }} + 0 \cdot p_{{jk}}^{{^{{( < )}} }} , \in \left[ {0,1} \right],$$

  (3)

  ${p}_{jk}^{(>)}$ being the portion of experts for whom EC_j > EC_k,

  ${p}_{jk}^{(\sim )}$ being the portion of experts for whom EC_j ~ EC_k,

  ${p}_{jk}^{(<)}$ being the portion of experts for whom EC_j < EC_k.

  It can be noted that ${p}_{jk}$ is the same quantity represented in Fig. 3b. The LCJ allows for its quantification on the basis of the (empirical) expert judgments.

  The coefficient “½” multiplying ${p}_{jk}^{(\sim )}$ conventionally weighs the indifference relationship as an intermediate coefficient between that related to the “favourable” (“EC_j > EC_k”) strict preference relation (with coefficient “1”) and that related to the “unfavourable” (“EC_j < EC_k”) strict preference relation (with coefficient “0”). Taking into account that ${p}_{jk}^{(\sim )}={p}_{kj}^{(\sim )}$, this type of weighting guarantees the complementarity relationship:

  $${p}_{jk}=1-{p}_{kj},$$

  (4)

  which can be demonstrated by combining Eq. 3 with the two following relationships:

  $${p}_{jk}^{\left(>\right)}+{p}_{jk}^{\left(\sim \right)} +{p}_{jk}^{\left(<\right)}=1,$$

  (5)

• 2. Next, p_jk values are transformed into z_jk values, through the relationship:

  $$z_{jk}\, = \,{\Phi }^{ - 1} \left( {1{ }{-}{ }p_{jk}} \right)$$

  (6)

• 3. Φ⁻¹(·) being the reverse of the cumulative distribution function (Φ) of the standard normal distribution. The element z_jk represents a unit normal deviate, which will be positive for all values of (1 – p_jk) over 0.50 and negative for all values of (1 – p_jk) under 0.50.

• 4. In general, objects are judged differently by experts. However, if all experts express the same preference for each outcome, the model is no more viable (p_jk values of 1.00 and 0.00 would correspond to z_jk values of $\pm \infty$). A simplified approach for tackling this problem is to associate those p_jk values ≤ 0.00135 with z_jk = Φ⁻¹(1–0.00135) = 3 and those p_jk values ≥ 0.99865 with z_jk = Φ⁻¹ (1 – 0.99865) = − 3. More sophisticated solutions to deal with this issue have been proposed (Franceschini et al. 2022).

Next, the z_jk values related to the possible paired comparisons are reported into a matrix Z. The element z_jk is reported in the j-th row and k-th column. The relationship z_kj = −z_jk holds, being unit normal deviates related to complementary cumulative probabilities (cf. Equation 4).

A scaling can be performed by (i) summing the values into each column of the matrix Z and (ii) dividing these sums by m. It can be demonstrated that the result obtained for each k-th column (x_k) corresponds to the unknown average value (${\mu }_{{EC}_{k}}$) of the k-th object’s attribute, up to a positive scale factor and an additive constant: ${x}_{k}={\sum }_{k}\left({z}_{jk}\right)/m={c}_{1}\cdot {\mu }_{{EC}_{k}}+{c}_{2}$. In other words, the LCJ results into an interval scaling, i.e., objects are defined on a scale (x) with arbitrary zero point and unit (Thurstone 1927; Franceschini et al. 2022).

5 Methodological approach

The LCJ can be adapted for prioritizing the ECs within the HoQ context. In this case, the focus is on the ECs (i.e., objects), which need to be prioritized according to the degree of intensity (i.e., attribute) of their relationships with each specific CR. Unlike the traditional application of LCJ, where individual experts formulate paired comparisons of objects, in this context paired comparisons emerge indirectly from the HoQ's relationship matrix. This approach represents a departure from the traditional LCJ method, since experts do not make individual judgements that are then aggregated. Instead, in the new procedure, several expert judgements—derived from the collective compilation of the relationship matrix by the QFD team members (Zare Mehrjerdi 2010)—are then aggregated through the LCJ. This point is clarified in the explanation below, which is structured in four steps (a, b, c and d).

(a) Transformation of relationship matrix into rankings Focusing on the i-th specific row of the relationship matrix, a ranking of ECs can be determined according to the degree of their relationships with the i-th CR. For example, with reference to the relationship matrix in Fig. 2 and to “CR₆—Lightweight”, the following ranking can be obtained: ∙

$$\left( {EC_{ \bullet } \sim EC_{2} } \right) > \left( {EC_{\bigcirc } \sim EC_{3} \sim EC_{6} } \right) > \left( {EC_{\vartriangle } \sim EC_{7} \sim EC_{8} } \right) > \left( {EC_{\emptyset } \sim EC_{1} \sim EC_{4} \sim EC_{5} } \right)$$

(7)

In addition to the “regular” ECs, i.e., EC₁ to EC₈, the above ranking also includes four “dummy” or “anchor” ECs, i.e., EC_●, ${{EC}}_{\bigcirc } ,{{EC}}_{\Delta } ,{{ and}}\;{{EC}}_{\emptyset }$, which represent the degree of intensity of the relationships expressed in the relationship matrix, espresso in absolute terms (“None” → $\varnothing$, “Low” → $\Delta$, “Medium” → $\bigcirc$, and “High” → ●; cf. Figure 1b). The introduction of these objects in the rankings, which by their nature are formulated in relative terms, is necessary in order not to lose part of the available information content: that is, the degree of intensity of the relationships in absolute terms. For example, referring to the new simplified relationship matrix in Fig. 4 (which is different from that in the test case in Fig. 2), the relationships of the three ECs (EC₁, EC₂ and EC₃) with CR₁ (i.e., ${EC}_{1}\to ,{EC}_{2}\to \varnothing ,{EC}_{3}\to \varnothing$) result into the ranking ${EC}_{1}>\left({EC}_{2}\sim {EC}_{3}\right),$ which would be identical to that obtained by considering the relationships of the same ECs with CR₂ (i.e., $EC_{1} \to \bigcirc ,EC_{2} \to {\Delta } ,EC_{3} \to \Delta$). In this case, the transformation into relative rankings leads to losing information about the absolute degree of intensity of individual relationships, which distinguishes the two configurations.

Fig. 4

Transformation of a relationship matrix into EC rankings, with or without dummy ECs (i.e., EC_●, ${{EC}}_{\bigcirc } ,{{EC}}_{\vartriangle } ,{{ and}}\;{{EC}}_{\emptyset }$)

Referring to the LCJ framework, similarly to regular ECs, dummy ECs are assumed to project a normal distribution on the psychological continuum, with unknown mean value and unknown variance, equal to that of the other objects (cf. Section 4) (Franceschini and Maisano 2019). The dummy objects are also used to perform the so-called “anchoring” of the scaling resulting from the LCJ, as described below.

(b) Transformation of rankings into paired comparison relationships. Each ranking can be uniquely translated into paired comparisons. Figure 5 exemplifies this process for each CR in the relationship matrix. Since the test case includes twelve total ECs—i.e., eight regular (EC₁ to EC₈) and four dummy ones (EC_●${{EC}}_{\bigcirc } ,{{EC}}_{\Delta } ,{{ and}}\;{{EC}}_{\emptyset }$)—the total paired comparisons are ${C}_{2}^{12}=\left(\begin{array}{c}12\\ 2\end{array}\right)=\frac{12\cdot 11}{2}=66.$

Fig. 5

Transformation of the relationship matrix in (a) into EC rankings (b) and paired comparison relationships (c)

(c) LCJ application. Next, a proportion (p_jk) must be associated with each jk-th paired comparison. In the traditional LCJ (cf. Section 4), p_jk reflects the portion of expert population that expressed a preference of object EC_j over object EC_k⁽³⁾. Although experts do not directly express their preferences between pairs of ECs, for each CR in the relationship matrix (which was collectively constructed by the QFD team members), an EC ranking can be determined as illustrated in Fig. 4; then, this ranking can be decomposed into paired comparisons between ECs.

Additionally, each CR in the HoQ corresponds to a certain percentage weight (i.e., ${w}_{{CR}_{i}}$, being $\sum_{\forall i}{w}_{{CR}_{i}}=1$), which describes its importance from different points of view (cf. Section 3). This weight can also be associated with the relative EC ranking and the paired comparison relationships resulting from it. For a given (jk-th) comparison between pairs of ECs, there are therefore as many paired comparison relationships as the number of CRs (with their associated weights). Figure 5 exemplifies the process of constructing paired comparison relationships from the relationship matrix in Fig. 2.

Adapting the LCJ (cf. Section 4), the p_jk proportions can be determined by aggregating the preceding comparisons by means of a weighted sum; before showing this aggregation, for the sake of clarity, it is appropriate to take a step back.

With reference to each i-th CR and each jk-th paired comparison (i.e., EC_j versus EC_k), the following three binary coefficients are defined:

$$ \begin{aligned}{c}_{i,jk}^{\left(>;\right)}\;\text{being equal to}\; 1\;\text{ if }{EC_{j}}>{EC_{k}} \left(\text{otherwise }\;0\right), \\ {c}_{i,jk}^{\left(\sim\right)}\;\text{being equal to}\; 1\;\text{ if }{EC_{j}}>{EC_{k}} \left(\text{otherwise }\;0\right), \\ {c}_{i,jk}^{\left(<\right)}\;\text{being equal to}\; 1\;\text{ if }{EC_{j}}>{EC_{k}} \left(\text{otherwise }\;0\right),\end{aligned}$$

(8)

It can be seen that these coefficients are mutually exclusive and the complementarity relationship holds: ${c}_{i,jk}^{\left(>\right)}+{c}_{i,jk}^{\left(\sim \right)} +{c}_{i,jk}^{\left(<\right)}=1$. A general coefficient expressing the degree of preference of EC_j over EC_k from the perspective of the i-th CR can be defined as:

$$c_{{i,jk}} = 1 \cdot c_{{i,jk}}^{ (>) } + {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}} \cdot c_{{i,jk}}^{ (\sim) } + 0 \cdot c_{{i,jk}}^{ (<) } \in \left\{ {0,{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}},1} \right\}$$

(9)

Note the similarity between Eqs. 3 and 9; by construction, it results that: ${c}_{i,jk}=1-{c}_{i,kj}$. Figure 6 exemplifies the calculation of the binary coefficients and the corresponding ${c}_{i,jk}$ values, for the paired comparison relationships in Fig. 5c.

Fig. 6

Calculation of the ${c}_{i,jk}$ values (bolded) by combining the binary coefficients ${{c}_{i,jk}^{\left(>;\right)}}, {{c}_{i,jk}^{\left(\sim\right)}}, {{c}_{i,jk}^{\left(<;\right)}}$ obtained from the paired comparison relationships in Fig. 4, through Eq. 9. The relevant p_jk values (in the last column) are calculated by applying Eq. 10

Finally, the coefficients ${c}_{i,jk}$ are aggregated in the following weighted sum, which determines the p_jk value:

$${p}_{jk}=\sum_{\forall i}\left({c}_{i,jk}\cdot {w}_{{CR}_{i}}\right), \in \left[\mathrm{0,1}\right]$$

(10)

This value expresses the weighted fraction of CR for which the j-th EC has a greater influence than the k-th one. For example, the paired comparison “EC₁, EC₂” (at the top of Fig. 6) would result in:

$${p}_{12}=0.5\cdot 7\mathrm{\%}+0.5\cdot 20\mathrm{\%}+0.5\cdot 3\mathrm{\%}+0.5\cdot12\mathrm{\%}+0\cdot 27\mathrm{\%}+0\cdot 10\mathrm{\%}+1\cdot 14\mathrm{\%}+0\cdot 7\mathrm{\%}=0.350$$

(11)

The p_jk values can be aggregated into a P matrix of proportions, which—consistently with the LCJ—is made up of elements that are symmetrical with respect to the main diagonal and complementary to each other with respect to the unit⁴. Figure 7a contains the P matrix that results from the paired comparison relationships in Fig. 5c. Henceforth, the traditional LCJ (cf. Section 4) is applied, determining the Z matrix (see Fig. 7b) and, subsequently, the interval scaling (x) of the ECs (see Fig. 7c).

Fig. 7

a P matrix, b Z matrix, and c scaling resulting from the application of the proposed procedure to the test case. Items marked with “*” in the matrix P are associated with values of ± 3 in the matrix Z (cf. Section 4). $\sum_{k}$ is the summation of the values reported in the k-th column of the matrix Z; the xk values concern the interval scaling resulting from the LCJ; the yk values concern the ratio scaling downstream of the anchoring in Eq. 12

(d) Scale anchoring. Taking inspiration from the methodology developed in (Franceschini and Maisano 2019), the interval scaling resulting from the LCJ can be “anchored” with respect to the (unknown) psychological continuum, using two of the previously introduced dummy objects: EC_∅, i.e., an anchor object corresponding to the absence of relationship, and EC_●, i.e., an anchor object corresponding to the maximum possible degree of intensity of the relationship with the CR of interest. Therefore, the (interval) scale (x) is transformed into a new one (y), defined in the conventional range [0, 10], through the following linear transformation:

$$\frac{{y_{k} - 0}}{10 - 0} = \frac{{x_{k} - x_{\emptyset } }}{{x_{ \bullet } - x_{\emptyset } }}\; \to y_{k} = 10 \cdot \frac{{x_{k} - x_{\emptyset } }}{{x_{ \bullet } - x_{\emptyset } }},$$

(12)

where.

x_∅ and x_● are the scale values of EC_∅ and EC_● respectively, resulting from the LCJ;

x_k is the scale value of a generic k-th EC, resulting from the LCJ;

y_k is the relevant transformed scale value in the conventional range [0, 10].

The new scale (y) has a conventional unit and a zero point (which corresponds to the absence of the attribute); it can therefore be considered as a ratio scale.

Although the mathematical operations required to implement the LCJ might seem complex, they are in fact computationally straightforward and can be entirely automated using a basic spreadsheets such as MS Excel (Brown and Peterson 2009; Franceschini and Maisano 2019).

6 Concluding remarks

This paper introduced a new procedure for prioritizing the HoQ’s ECs, based on Thurstone’s LCJ. Besides being conceptually more rigorous and overcoming some shortcomings of the traditional ISM, the new procedure offers several other advantages. First, it can be integrated into the traditional procedure for constructing the HoQ without requiring additional or extra works from participants. This means that interviewees providing the VoC and the QFD team members responsible for creating the relationship matrix do not have to change their traditional work, as the mathematical implementation of the LCJ is fully automatable with a simple spreadsheet. Second, it prioritizes the ECs in the form of a ratio scaling, anchoring the LCJ solution through several dummy ECs. In addition, it is easy to implement, flexible, and adaptable to other response modes than the traditional one (e.g., those in which judgments are inherently uncertain or incomplete). The effectiveness and the robustness of the new EC prioritization are ensured by the LCJ itself, which is a well-established technique that has been used and tested in multiple contexts (Franceschini et al. 2022).

With reference to the exemplified test case, it is interesting to note that the proposed procedure produces results quite in line with those of the ISM, as shown in Fig. 8. This diagram denotes a relatively high correlation (i.e., Pearson correlation coefficient R² ≈ 0.8602) between the two approaches, which produce two very similar final rankings of ECs (only a rank reversal between EC₁ and EC₈ is observed):

$$\begin{gathered} {\text{ISM}}: EC_{{6}} > EC_{{7}} > EC_{{2}} > EC_{{5}} > EC_{{3}} > EC_{{1}} > EC_{{8}} > EC_{{4}} \hfill \\ {\text{New}}\;{\text{procedure}}: EC_{{6}} > EC_{{7}} > EC_{{2}} > EC_{{5}} > EC_{{3}} > EC_{{8}} > EC_{{1}} > EC_{{4}} . \hfill \\ \end{gathered}$$

(13)

Fig. 8

Comparison between the results of the new prioritization procedure (y-scaling) and the traditional one (ISM), with reference to the test case in Sect. 3. Note that the ISM results have been previously calculated in Fig. 2, while the y-scaling has been previously determined in Fig. 7c

Other tests have confirmed some agreement between the proposed procedure and the ISM although there are specific situations in which the two approaches may produce different results. Precisely for these situations, the authors claim the superiority of the new procedure, as it avoids questionable and potentially distorting operations. This aspect will be further investigated in future studies.

In conclusion, the new procedure represents an additional tool in the QFD-team's toolbox, to expand the perspective of analysis. The limitations of the proposed procedure are those inherent in the LCJ, namely some postulates concerning the (normal) distribution of judgments in the psychological continuum (cf. Section 4).

Regarding the future, possible adaptations of the proposed procedure to problems characterized by uncertain and/or incomplete formulation of relationships between ECs and CRs will be investigated. Additionally, a structured comparison will be made between the results of the new procedure and those of other alternative procedures to ISM, which are already present in the scientific literature.