Skip to main content
SpringerLink
Log in

Enhancement of shock-capturing methods via machine learning

  • Original Article
  • Published:
Theoretical and Computational Fluid Dynamics Aims and scope Submit manuscript

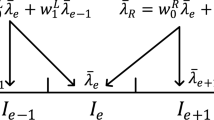
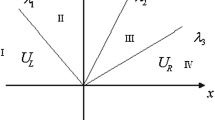
Abstract

In recent years, machine learning has been used to create data-driven solutions to problems for which an algorithmic solution is intractable, as well as fine-tuning existing algorithms. This research applies machine learning to the development of an improved finite-volume method for simulating PDEs with discontinuous solutions. Shock-capturing methods make use of nonlinear switching functions that are not guaranteed to be optimal. Because data can be used to learn nonlinear relationships, we train a neural network to improve the results of a fifth-order WENO method. We post-process the outputs of the neural network to guarantee that the method is consistent. The training data consist of the exact mapping between cell averages and interpolated values for a set of integrable functions that represent waveforms we would expect to see while simulating a PDE. We demonstrate our method on linear advection of a discontinuous function, the inviscid Burgers’ equation, and the 1-D Euler equations. For the latter, we examine the Shu–Osher model problem for turbulence–shock wave interactions. We find that our method outperforms WENO in simulations where the numerical solution becomes overly diffused due to numerical viscosity.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

Notes

  1. Note that the error oscillates between two different values because in the exact solution the discontinuity switches between being on the edge of a cell and 1/3 of a cell width away from either the left or right of a cell edge since the CFL number is 2/3. To get a smooth curve, we apply a filter to the error and plot \(E(i) = \frac{e(i)+e(i-1)+e(i-2)}{3}\).

References

  1. Bar-Sinai, Y., et al.: Learning data-driven discretizations for partial differential equations. Proc. Natl. Acad. Sci. 116(31), 15344–15349 (2019)

    MathSciNet  MATH  Google Scholar 

  2. Borges, R., et al.: An improved weighted essentially non-oscillatory scheme for hyperbolic conservation laws. J. Comput. Phys. 227(6), 3191–3211 (2008)

    MathSciNet  MATH  Google Scholar 

  3. Castro, M., Costa, B., Don, W.S.: High order weighted essentially non-oscillatory WENO-Z schemes for hyperbolic conservation laws. J. Comput. Phys. 230(5), 1766–1792 (2011)

    MathSciNet  MATH  Google Scholar 

  4. Chollet, F. et al.: Keras. https://keras.io (2015)

  5. Chu, C.K.: Numerical methods in fluid dynamics. In: Advances in Applied Mechanics, vol. 18. Elsevier, Amsterdam, pp. 285–331 (1979)

  6. Dissanayake, M.W.M.G., Phan-Thien, N.: Neural-network-based approximations for solving partial differential equations. Commun. Numer. Methods Eng. 10(3), 195–201 (1994)

    MATH  Google Scholar 

  7. Fang, J., Li, Z., Lu, L.: An optimized low-dissipation monotonicitypreserving scheme for numerical simulations of high-speed turbulent flows. J. Sci. Comput. 56(1), 67–95 (2013)

    MathSciNet  MATH  Google Scholar 

  8. Gottlieb, S., Shu, C.W.: Total variation diminishing Runge–Kutta schemes. Math. Comput. Am. Math. Soc. 67(221), 73–85 (1998)

    MathSciNet  MATH  Google Scholar 

  9. Ha, Y., et al.: An improved weighted essentially non-oscillatory scheme with a new smoothness indicator. J. Comput. Phys. 232(1), 68–86 (2013)

    MathSciNet  MATH  Google Scholar 

  10. Harten, A.: High resolution schemes for hyperbolic conservation laws. J. Comput. Phys. 49(3), 357–393 (1983)

    MathSciNet  MATH  Google Scholar 

  11. Harten, A. et al.: Uniformly high order accurate essentially non-oscillatory schemes, III. In: Upwind and High-Resolution Schemes. Springer, Berlin, pp. 218–290 (1987)

  12. Hsieh, J.T. et al.: Learning neural PDE solvers with convergence guarantees. In: arXiv preprint arXiv:1906.01200 (2019)

  13. Jiang, G.S., Shu, C.W.: Efficient implementation of weighted ENO schemes. J. Comput. Phys. 126(1), 202–228 (1996)

    MathSciNet  MATH  Google Scholar 

  14. Kim, C.H., Ha, Y., Yoon, J.: Modified non-linear weights for fifth-order weighted essentially non-oscillatory schemes. J. Sci. Comput. 67(1), 299–323 (2016)

    MathSciNet  MATH  Google Scholar 

  15. Kim, J.W., Lee, D.J.: Optimized compact finite difference schemes with maximum resolution. AIAA J. 34(5), 887–893 (1996)

    MATH  Google Scholar 

  16. Kingma, D.P., Ba, J.: Adam: a method for stochastic optimization. In: arXiv preprint arXiv:1412.6980 (2014)

  17. Lagaris, I.E., Likas, A., Fotiadis, D.I.: Artificial neural networks for solving ordinary and partial differential equations. IEEE Trans. Neural Netw. 9(5), 987–1000 (1998)

    Google Scholar 

  18. Lele, S.K.: Compact finite difference schemes with spectral-like resolution. J. Comput. Phys. 103(1), 16–42 (1992)

    MathSciNet  MATH  Google Scholar 

  19. LeVeque, R.J., et al.: Finite Volume Methods For Hyperbolic Problems, vol. 31. Cambridge University Press, Cambridge (2002)

    MATH  Google Scholar 

  20. Li, G., Qiu, J.: Hybrid weighted essentially non-oscillatory schemes with different indicators. J. Comput. Phys. 229(21), 8105–8129 (2010)

    MathSciNet  MATH  Google Scholar 

  21. Liu, Y.: Globally optimal finite-difference schemes based on least squares. Geophysics 78(4), T113–T132 (2013)

    Google Scholar 

  22. Peer, A., Dauhoo, M.Z., Bhuruth, M.: A method for improving the performance of the WENO5 scheme near discontinuities. Appl. Math. Lett. 22(11), 1730–1733 (2009)

    MathSciNet  MATH  Google Scholar 

  23. Pfau, D. et al.: Spectral inference networks: unifying deep and spectral learning. In: arXiv preprint arXiv:1806.02215 (2018)

  24. Rathan, S., Raju, G.N.: A modified fifth-order WENO scheme for hyperbolic conservation laws. Comput. Math. Appl. 75(5), 1531–1549 (2018)

    MathSciNet  MATH  Google Scholar 

  25. Rathan, S., Raju, G.N.: Improved weighted ENO scheme based on parameters involved in nonlinear weights. Appl. Math. Comput. 331, 120–129 (2018)

    MathSciNet  MATH  Google Scholar 

  26. Shu, C.W.: Essentially non-oscillatory and weighted essentially nonoscillatory schemes for hyperbolic conservation laws. In: Advanced numerical approximation of nonlinear hyperbolic equations. Springer, Berlin, pp. 325–432 (1998)

  27. Shu, C.W.: High-order finite difference and finite volume WENO schemes and discontinuous Galerkin methods for CFD. Int. J. Comput. Fluid Dyn. 17(2), 107–118 (2003)

    MathSciNet  MATH  Google Scholar 

  28. Tam, C.K., Webb, J.C.: Dispersion-relation-preserving finite difference schemes for computational acoustics. J. Comput. Phys. 107(2), 262–281 (1993)

    MathSciNet  MATH  Google Scholar 

  29. Wang, Z.J., Chen, R.F.: Optimized weighted essentially nonoscillatory schemes for linear waves with discontinuity. J. Comput. Phys. 174(1), 381–404 (2001)

    MATH  Google Scholar 

  30. Yu, J., Hesthaven, J.S., Yan, C.: A data-driven shock capturing approach for discontinuous Galerkin methods. Tech. rep. (2018)

  31. Zhang, J.H., Yao, Z.X.: Optimized explicit finite-difference schemes for spatial derivatives using maximum norm. J. Comput. Phys. 250, 511–526 (2013)

    MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical and Civil Engineering, California Institute of Technology, Pasadena, CA, 91125, USA

    Ben Stevens & Tim Colonius

Authors
  1. Ben Stevens
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Tim Colonius
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ben Stevens.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Communicated by Steven L. Brunton.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

This material is based upon work supported by the National Science Foundation Graduate Research Fellowship under Grant No. 1745301.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Stevens, B., Colonius, T. Enhancement of shock-capturing methods via machine learning. Theor. Comput. Fluid Dyn. 34, 483–496 (2020). https://doi.org/10.1007/s00162-020-00531-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00162-020-00531-1

Keywords

Search

Navigation