Electrostatic body forces in cracked dielectrics and their implication on Maxwell stress tensors

Abstract

In solid mechanics, Maxwell stresses are known to be induced if a body is exposed to magnetic and, in the case of dielectrics, electric fields. Acting as tractions at outer or inner surfaces as well as volume forces, they are superimposed with tractions and stresses due to mechanical loads and provide a more or less significant contribution, depending on loading, material properties and geometric aspects. The Maxwell stress tensor, constituting the physical and mathematical basis, however, is controversially discussed to date. Several formulations are known, most of them having been suggested more than 100 years ago. Being equivalent in vacuum, they differ qualitatively just as quantitatively in solid or fluidic matter. In particular, the dissimilar effect of body forces, emanating from a choice of established Maxwell stress tensor approaches, on crack tip loading in dielectric solids is investigated theoretically in this paper. Due to the singularity of fields involved, their impact is basically non-negligible compared to external mechanical loading. The findings obtained indicate that fracture mechanics could be the basis of an experimental validation of Maxwell stress tensors.

1 Introduction

The coupling of electrical or magnetic quantities, on the one hand side, and mechanical stress or strain on the other is probably among the most investigated so-called multiphysical problems in deformable matter nowadays. In this context, piezoelectricity, electro- and magnetostriction and flexoelectricity are commonly explored effects, in particular in the engineering and solid-state mechanics community. Especially in soft materials, electro- or magnetostatically induced stresses, known as Maxwell stresses, are exploited for actuation purposes in, e.g., artificial muscles [1,2,3] or soft robots [4, 5]. Being physically related to the well-known Lorentz force acting on free charges in vacuum [6,7,8], they are essentially disregarded in stiff materials such as ceramics, metals or many polymers, where constitutive effects listed above usually dominate. An exception is found in fracture mechanics of dielectric solids, mostly with piezoelectric coupling, under electromechanical loading. In some works [9,10,11,12,13,14], Maxwell stresses are taken into account in the form of electric field-induced tractions on the crack faces, which effectuate a relief of the crack tip loading. The effect of Maxwell stresses acting as body forces has, to our best knowledge, never been investigated in this context. Both effects coexist in a cracked dielectric and can be investigated separately due to the principle of linear superposition.

Most of the solid mechanics papers that address this subject are based on the Maxwell stress tensor introduced by Minkowski [15]. However, different approaches have been published around the same time, e.g., by Einstein and Laub [16], Abraham [17] and Lorentz [18]. While all these approaches yield identical global forces acting on bodies embedded in vacuum, they produce dissimilar local tractions and stresses even in a vacuum environment and cause different resulting forces in fluidic or solid surrounding matter. Besides quantitative discrepancies there are qualitative differences, in so far as the Maxwell stress tensor according to Einstein and Laub is the only of the aforementioned that provides non-vanishing body forces in the case of an isotropic homogeneous medium. Furthermore, the approaches differ in respect of tensor symmetry, where an asymmetric Maxwell stress tensor correlates with local body couples.

It should be noted that constitutive effects, such as piezoelectricity or electrostriction, must be clearly distinguished from electric body forces and surface tractions stemming from the Maxwell stress tensor, since their physical origin is totally different, see e.g., [19]. For example in [20,21,22], a total stress is introduced that is composed additively of Cauchy and Maxwell stresses, and which is finally calculated based on balance equations and a tailored thermodynamic potential. While displacements emerging from boundary value problems may thereupon become identical for different formulations of Maxwell stress tensors, the Cauchy stresses and energies involved are dissimilar. Considering the Cauchy stress to be relevant for mechanical fracture, the prediction of structural failure necessarily requires the explicit knowledge of an appropriate Maxwell stress tensor.

To investigate forces arising in an electric field, an experiment has been made with an oil droplet immersed in an oil bath [23]. While the densities of the two fluids are sufficiently similar to inhibit buoyancy, the dielectric permittivity differs by a factor of 2.25. The observed shape change of the droplet was later taken as a basis to validate the Maxwell stress approaches in connection with numerical calculations [24, 25]. In [24], solely two of the four above-mentioned models were considered, and effects of body forces due to Maxwell stress and electrostriction have been disregarded; thus, the results of the study are not fully conclusive. In [25] the evaluation of the oil droplet experiment was improved by numerically calculating the time-dependent deformation of the interface accounting for surface tension and viscous stresses. The Lorentz model finally provided plausible results in light of correctly predicting an oblate shape of the droplet in steady state. Moreover, the total force on a magnet immersed in a ferrofluid was measured, which also provided indications of the possible validity of the Lorentz model; however, the low magnetic susceptibility of the ferrofluid resulting in minor deviations between the models’ predictions leads the author to deem the experiment inconclusive.

Consequently, an experiment is sought providing conditions that allow for the greatest possible effect of Maxwell stresses on easily accessable quantities. Large gradients of the electric field are favorable in this context, just as interfaces exhibiting a pronounced jump of dielectric permittivity. A crack in a brittle dielectric solid exposed to a perpendicular electric field is supposed to provide these conditions in the vicinity of the crack tip, where electric and mechanical fields are known to theoretically exhibit a singular behavior approaching infinity. The induced electrostatic body forces are complemented by the well-known tractions on the crack faces coming along with a jump of the Maxwell stress tensor. Although the induced displacement field will be too small to be exploited for evaluation, the effect of Maxwell stresses might have an essential influence on the crack tip loading and thus on the effective crack growth resistance.

The goal of this paper is to calculate and investigate Maxwell stresses in front of the tip of a crack in electrically loaded isotropic and anisotropic dielectric materials, exemplarily based on the approaches of Einstein–Laub and Abraham. The induced stresses are superimposed with those emanating from a mechanical load with an intensity typically effectuating critical crack growth in ceramics. Implications with regard to fracture mechanics and the potential of such experiments in terms of validation of the theory of Maxwell stresses will be critically discussed.

2 Theoretical framework

In the following, electrostatic as well as mechanically quasistatic problems will be considered. Additionally, owing to the inherent brittleness of the dielectrics of interest, infinitesimal strain theory is adopted. While the former allows to dispense with magnetic quantities and to introduce an electric potential $\varphi$, whose negative gradient provides the electric field

$$\begin{aligned} E_i = - \varphi _{,i}, \end{aligned}$$

(1)

the latter introduces the Cauchy strain tensor $\varepsilon _{ij}$ with the suitable strain–displacement relation in terms of

$$\begin{aligned} \varepsilon _{ij} = \frac{1}{2}(u_{i,j} + u_{j,i})\,. \end{aligned}$$

(2)

Electric Maxwell stresses act in two ways. On the one hand they occur as surface traction $t_{i}^\textrm{el}$ at every bi-material interface in dielectric bodies. This traction vector is linked to the jump of the Maxwell stress tensor $T_{ij}$ via the unit normal $n_{j}$ of the interface [24]

$$\begin{aligned} t_{i}^\textrm{el}= \Big ( T_{ij}^\mathrm {+} - T_{ij}^\mathrm {-}\Big )n_{j}^\mathrm {+}. \end{aligned}$$

(3)

The superscripts $\mathrm {+}$ and ${-}$ denote the two sides of the interface and may, e. g., represent the interior and exterior, respectively, of a crack slit, where $n_{j}^{+}$ points from ${-}$ to ${+}$. These tractions have been taken into account in some publications in the context of piezoelectric fracture mechanics [9,10,11,12,13]. For example, calculations in [14, 26] showed a reduction in crack tip loading of up to 40% due to Maxwell stresses on the faces of a Griffith crack. The effect of the electric body forces $f_i^\textrm{el}$, on the other hand, has not been taken into account yet. They are derived from the Maxwell stress tensor according to

$$\begin{aligned} f_i^\textrm{el}= T_{ij,j}. \end{aligned}$$

(4)

While there is widespread agreement on the definition of the Maxwell stress tensor in vacuum, its formulation in matter is part of a century-long controversy [24, 27, 28], starting with the publications of [15, 17]. Some of the most famous contributions to this controversy are collected in Table 1, where zero free volume charges are assumed.

Table 1 Established formulations of the Maxwell stress tensor and related body forces; $D_{i}$: electric displacement, $\kappa _{0}$: vacuum permittivity

It is worth noting that the Lorentz tensor [18] coincides with the vacuum Maxwell stress tensor, which all models pass into in case of vanishing polarization and whose divergence yields the electrostatic part of the well-known Lorentz force exerted on free charges. When looking at the third column of Table 1, it becomes clear that the models according to Lorentz, Abraham and Minkowski provide vanishing body forces in isotropic homogeneous media, since in this case the electric displacement is simply replaced by $D_i = \kappa _\textrm{B} E_i$ with the dielectric permittivity $\kappa _{\textrm{B}}$. Furthermore, the Maxwell stress tensors by Minkowski and Einstein and Laub are generally not symmetric which results in the existence of body couples and local torsional moments, respectively, and thus in an asymmetry of the Cauchy stress tensor [8, 19].

In the following, only models with symmetric stress tensors are considered. In the case of an isotropic dielectric, this applies to the model of Einstein and Laub ($\textrm{EL}$), whereas the other three Maxwell stress tensors, despite their symmetry, are unsuitable, not producing any body forces in an isotropic homogeneous medium. The investigations in a transversely isotropic dielectric are eventually based on the model according to Abraham ($\textrm{A}$). Due to these choices, all investigations are feasible within the framework of nonpolar continuum mechanics. It should not remain unmentioned that the Minkowski tensor is commonly applied evaluating surface tractions, e. g., in piezoelectric fracture mechanics [26, 29], whereupon the attracting forces at opposite crack faces in the limiting case of $\kappa _{\textrm{B}}\rightarrow {\mathcal {1}}$ are consistent with those known from capacitor plates.

In order to calculate the stresses caused by the body forces, the balance equations

$$\begin{aligned} D_{i,i} = 0 \end{aligned}$$

(5)

and

$$\begin{aligned} \sigma _{ij,j} = -f_{i}^\textrm{el} \end{aligned}$$

(6)

have to be solved first. Equations (5) and (6) generally constitute a nonlinear and bilaterally coupled system of equations if the medium has piezoelectric properties, introducing the Cauchy stress according to

$$\begin{aligned} \sigma _{ij} = c_{ijkl}\epsilon _{kl} - e_{kij}E_{k}, \end{aligned}$$

(7)

and the electric displacement

$$\begin{aligned} D_{i} = e_{ikl}\epsilon _{kl} + \kappa _{ij}E_{j}. \end{aligned}$$

(8)

Electric field and strain are introduced here as independent variables Eqs. (5) and (6) have to be solved for. Elastic, piezoelectric and dielectric properties are represented by the tensors $c_{ijkl}$, $e_{kij}$ and $\kappa _{ij}$. Two interacting electromechanical coupling mechanisms due to piezoelectricity and Maxwell stress are considered in this model, while real materials exhibit further coupling mechanisms owing to, e.g., electrostriction or flexoelectricity. Although electromechanical problems frequently target piezoelectric materials, dielectrics without piezoelectric properties are considered in the following, avoiding the effort in solving a coupled system of nonlinear partial differential equations. Thus, Eq. (5) is first solved independently for the electric field, accounting for Eq. (8) with $e_{ikl}=0$. The body forces are then calculated and inserted into Eq. (6). Because of the unilateral decoupling of the equations, the body forces represent dead loads in the mechanical sense. Based on the principle of the minimum of the total potential energy, the balance equations are transformed into the weak form

$$\begin{aligned} \begin{aligned}&\int \limits _\Omega (\sigma _{ij} \delta u_{i,j} - f_{i}^\textrm{el}\delta u_{i}) \,\textrm{d}V- \int \limits _{\partial \Omega } t_i^\textrm{ext} \delta u_{i}\,\textrm{d}A- \int \limits _\Gamma t_{i}^\textrm{el}\delta u_{i}\,\textrm{d}A = 0\,,\\&\int \limits _\Omega D_{i} \delta \varphi _{,i}\,\textrm{d}V- \int \limits _{\partial \Omega } \omega ^{\textrm{ext}}\delta \varphi \,\textrm{d}A= 0\,, \end{aligned} \end{aligned}$$

(9)

which will be solved in the further course with the help of the finite element (FE) method. Here, $\Omega$ and $\partial \Omega$ are the domain occupied by the dielectric body and its boundary, respectively, while $\Gamma \subseteq \partial \Omega$ is the union of all interfaces on which Maxwell tractions act according to Eq. (3), and quantities with the superscript “ext” represent externally controlled mechanical and electrical boundary conditions. Furthermore, the surface charge density

$$\begin{aligned} \omega = -n_{i}D_{i} \end{aligned}$$

(10)

has been introduced. Since the influence of the body forces is the focus of the investigations, electrically induced surface tractions $t_i^\textrm{el}$ will not be considered further on. Although they generally cannot be neglected in fracture mechanics of dielectrics, their impact on crack tip loading can simply be taken into account by linear superposition.

2.1 Einstein–Laub model in an isotropic dielectric

First of all, an isotropic homogeneous dielectric with permittivity $\kappa _\textrm{B}$ under static electrical load will be considered. The only model from Table 1 providing nonzero body forces in this case is the one by Einstein and Laub [16], i.e.,

$$\begin{aligned} f_i^\textrm{el}= f_i^\textrm{EL}= (\kappa _\textrm{B}- \kappa _0) E_j E_{i,j}. \end{aligned}$$

(11)

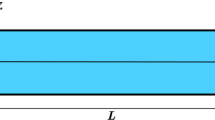
Emanating from the microscopic Lorentz force acting on dipoles, the general formulation according to Table 1, which is often referred to as Kelvin force density in the literature, represents the macroscopic force on a polarized material point due to graded electric fields [30]. To investigate the effect of these body forces on crack problems numerically, the two-dimensional model depicted in Fig. 1 is used in combination with the FE package FEniCS [31, 32].

Fig. 1

Square plate with center crack of length 2a and electrical load $D_{2}^{\textrm{ext}}$

It is loaded purely electrically via the electric displacement $D_2^\textrm{ext}$ at the upper and lower boundaries, and the crack is assumed impermeable for electric fields and traction free, i. e., $\omega ^\textrm{ext}, t_{i}^{\textrm{ext}} = 0$. Furthermore, a generalized state of plane strain is assumed, implying $\varepsilon _{33} = 0$ and $E_{3}, D_{3} = 0$. Due to symmetry and the small ratio of crack length to body dimension, the model approximates a Griffith crack in an infinite plate, allowing for reasonable comparison with analytical solutions. For the linear-elastic isotropic material of the plate Young’s modulus $E = 210\,\textrm{GPa}$, Poisson’s ratio $\nu = 0.3$ and an electric permittivity $\kappa _\textrm{B}=10 \kappa _0$ are assumed. The weak formulation of the problem at hand is obtained from Eq. (9) according to

$$\begin{aligned} \int \limits _\Omega \kappa _\textrm{B}\varphi _{,i}\delta \varphi _{,i}\,\textrm{d}V- \int \limits _{\partial \Omega }D_i^\textrm{ext} n_i \delta \varphi \,\textrm{d}A= 0 \end{aligned}$$

(12)

and

$$\begin{aligned} \int \limits _\Omega \left( c_{ijkl}\epsilon _{ij}\delta \epsilon _{kl} - f_i^\textrm{EL}\delta u_i\right) \,\textrm{d}V= 0, \end{aligned}$$

(13)

so that the electric field is obtained independently from Eq. (12) due to the unilateral coupling. The body force vector $f_i^\textrm{EL}$ is subsequently calculated via Eq. (11) at every node of the FE mesh illustrated in Fig. 2 and finally plugged into Eq. (13) which is eventually solved.

Fig. 2

Finite element mesh of the problem given in Fig. 1 with detailed excerpt of the crack tip. The crack faces are highlighted in red

The unit vectors of the body force, emanating from this procedure, are depicted in Fig. 3. Apparently, the vector field has two axes of symmetry. Of particular interest is the magnified area around the crack tip. There, all vectors are directed radially to the crack tip because of the singularity of the electric field at this point and the gradient $E_{i,j}$ in Eq. (11). The symmetry around the $x_1$-axis in this region indicates that the body forces result in a compressive stress on the ligament, i.e., on a straight line in front of the crack tip, where the polar angle $\theta = 0$, see Fig. 1.

Fig. 3

Unit vectors of body forces resulting from the model of [16] with detailed excerpt of the crack tip ($D_{2}^{\textrm{ext}} = 0.01\,\hbox {C}/\hbox {m}^2$)

For an assessment in the context of fracture mechanics, the stresses $\sigma _{12}$ and $\sigma _{22}$ on the ligament near the crack tip ($r/a\ll 1$) are of particular interest and are thus depicted in Fig. 4 for an electric load $D_{2}^{\textrm{ext}} = 0.01\,\textrm{C}/\textrm{m}^{2}$. Due to the absence of external mechanical loading or piezoelectric coupling, any mechanical stress is induced electrically by Maxwell body forces. While there are no shear stresses $\sigma _{12}$ of relevant magnitude, a compressive stress $\sigma _{22}<0$ is obtained which seems to be singular at $r \rightarrow 0$. It should be noted that this singularity cannot be proven rigorously on the basis of a numerical solution and

Fig. 4

Numerically calculated shear and normal stresses on the ligament ($\theta =0$) caused by the body forces with unit vectors plotted in Fig. 3

will be characterized in the following. The basic hypothesis is that the compressive stresses on the ligament are approximated well by an approach of the form

$$\begin{aligned} \sigma _{22}^\textrm{EL}(r, \theta =0) = L_\textrm{EL}r^\eta \end{aligned}$$

(14)

for $r / a\ll 1$. The factor $L_\textrm{EL}$, depending on loading, the dielectric constant and geometry, plays the same role as the stress intensity factors (SIF) of Linear Elastic Fracture Mechanics (LEFM) and $\eta$ represents the type of singularity. To determine the latter, it is useful to introduce the natural logarithm of the absolute value of the numerically calculated compressive stresses, so that Eq. (14) can be transformed to

$$\begin{aligned} \ln \left( |\sigma _{22}^\textrm{EL}|/\textrm{MPa}\right) = \ln \left( |L_\textrm{EL}|/(\textrm{MPa}\,\textrm{m}^{-\eta })\right) + \eta \zeta \end{aligned}$$

(15)

with the substitution $\zeta = \ln (r/\textrm{m})$. Since Eq. (15) is a linear equation with $\zeta$ being the independent variable, the exponent $\eta$ can be approximated by linear regression according to [33]

$$\begin{aligned} \eta \approx \frac{\textstyle { \sum _{i=1}^{n}\left( \zeta _i - {\overline{\zeta }}\right) \left( \ln (|\sigma _{22}^\textrm{EL}(\zeta _i)|/\textrm{MPa}) - \overline{\ln (|\sigma _{22}^\textrm{EL}(\zeta _i)|/\textrm{MPa})}\right) }}{\textstyle {\sum _{i=1}^{n} \left( \zeta _i - {\overline{\zeta }}\right) ^2}}, \end{aligned}$$

(16)

where $i\in \{1,\ldots ,n\}$ numbers the discrete values involved and quantities with an overbar are arithmetic averages. The result of the regression depends on the range $r_\textrm{min}<r<r_\textrm{max}$ in which Eq. (16) is evaluated. The dependence on the upper limit is illustrated in Fig. 5, where $\eta$ is plotted vs. $r_{\textrm{max}}/a$, while the edge length ${r_\textrm{min}}/{a} = 10^{-5}$ of the first finite element in front of the crack tip is chosen as the lower limit in all cases. The results for the exponent vary essentially

Fig. 5

Approximated values of the exponent $\eta$ depending on the upper limit of the evaluation range $r_{\textrm{max}}/{a}$ of the linear regression

by $\pm 2\%$ around $\eta =-1$. The stress $\sigma _{22}^\textrm{EL}$ consequently appears to exhibit an $r^{-1}$-singularity which dominates over the $r^{-\frac{1}{2}}$-singularity of LEFM associated with the well-known mode-I relation [34]

$$\begin{aligned} \sigma _{22}^\textrm{mech}(r, \theta = 0) = \frac{\textstyle {K_I}}{\textstyle {\sqrt{2\pi }}} r^{-\frac{1}{2}} + {\mathcal {O}}\left( r^{\frac{1}{2}}\right) ,\quad r\rightarrow 0, \end{aligned}$$

(17)

where $K_{I}$ is the corresponding stress intensity factor (SIF). More detailed knowledge of the factor $L_\textrm{EL}$ is needed to investigate the relation between the two singular behaviors. By means of parameter studies and dimensional analysis it was found that the compressive stress in the vicinity of the crack tip is well approximated employing

$$\begin{aligned} L_\textrm{EL}= - \frac{\textstyle {1}}{\textstyle {2}} \left( D_2^\textrm{ext}\right) ^2 \left( \frac{\textstyle {1}}{\textstyle {\kappa _\textrm{B}}} - \frac{\textstyle {\kappa _0}}{\textstyle {\kappa _\textrm{B}^2}}\right) a, \end{aligned}$$

(18)

whereupon the relation

$$\begin{aligned} \sigma _{22}^\textrm{EL}(r, \theta =0) = - \frac{\textstyle {a}}{\textstyle {2}} \left( D_2^\textrm{ext}\right) ^2 \left( \frac{\textstyle {1}}{\textstyle {\kappa _\textrm{B}}} - \frac{\textstyle {\kappa _0}}{\textstyle {\kappa _\textrm{B}^2}}\right) r^{-1} \end{aligned}$$

(19)

finally holds. The factor 1/2 was identified by comparison with the numerical data.

The strong singularity leads to an infinite energy in any domain enclosing a crack tip. This fact is just as unphysical as any kind of singularity itself, being attributed to the unrealistic model of a sharp crack tip. Akin to classical LEFM, where the problem of infinite stresses is circumvented by considering their asymptotic behavior in the crack tip near field rather than their magnitudes, a SIF complemented by an “L-factor,” according to Eq. (18), might constitute a suitable fracture law for brittle dielectrics. In this context, the size of the L-dominated compared to the K-dominated zone is crucial and will thus be investigated below.

Some results of numerical parameter studies are summarized in Fig. 6. The first plot shows the compressive stress $\sigma _{22}^\textrm{EL}$ caused by the body forces at a fixed location ${r}/{a}=10^{-4}$ in front of the crack tip as a function of the electrical load $D_2^\textrm{ext}$. All other parameters and boundary conditions are constant. A parabolic curve matching Eq. (19) is obvious. The maximum absolute value of 5 GPa at $D_2^\textrm{ext}=0.01\,\mathrm {{C}/{m^2}}$, corresponding to an electric field $E_2^\textrm{ext} = D_2^\textrm{ext}/\kappa _\textrm{B}\approx 8.8\cdot 10^{6}\,\mathrm {{V}/{m}}$, constitutes an enormous compressive stress at the selected position. The second plot shows the compressive stress at the same location as a function of the permittivity ratio ${\kappa _\textrm{B}}/{\kappa _0}$ at a constant electrical load $D_2^\textrm{ext}=0.01\,\mathrm {{C}/{m^2}}$. According to the bracketed part of Eq. (19) it has a minimum at ${\kappa _\textrm{B}}/{\kappa _0}=2$ and approaches zero for ${\kappa _\textrm{B}}/{\kappa _0}\rightarrow \infty$. The linear relationship between stress at a fixed location $r/a=10^{-4}$ and the half crack length a is confirmed in the third plot.

Fig. 6

Parameter studies of the induced stress on the ligament based on Eq. (19)

A comparison of the numerical results and the approach given in Eq. (19) is shown in Fig. 7.

Fig. 7

Comparison of the numerically calculated compressive stress from the Einstein–Laub model and the approximation according to Eq. (19)

If the above-described crack is additionally loaded with a tensile stress $\sigma _{22}^\textrm{ext}$, the total stress on the ligament in the crack tip near field is well approximated by

$$\begin{aligned} \sigma _{22}(r, \theta =0) = \sigma _{22}^\textrm{mech}(r, \theta =0) + \sigma _{22}^\textrm{EL}(r, \theta =0) = \frac{\textstyle {K_{I}\left( \sigma _{22}^\textrm{ext}\right) }}{\textstyle {\sqrt{2\pi r}}} + \frac{\textstyle {L_\textrm{EL}\left( D_2^\textrm{ext}\right) }}{\textstyle {r}} \end{aligned}$$

(20)

applying linear superposition. The first term exhibits the classical $1/\sqrt{r}$ -singularity with the approximate SIF $K_I\approx \sigma _{22}^\textrm{ext}\sqrt{\pi a}$, and the second term is adopted from Eq. (14) where all location-invariant terms are collected in $L_\textrm{EL}$. The opposing signs of $L_\textrm{EL}$ and $K_I$ together with the different types of singularities lead to a stress distribution on the ligament which has got two characteristic points. The first one is a maximal stress

$$\begin{aligned} \sigma ^\textrm{max} = -\frac{1}{4\pi } \frac{K_I^2}{L_\textrm{EL}} =\Big (\frac{\textstyle {\sigma _{22}^\textrm{ext}}}{\textstyle {D_2^\textrm{ext}}}\Big )^2 \frac{\textstyle {1}}{\textstyle {4\Big (\frac{\textstyle {1}}{\textstyle {\kappa _\textrm{B}}} - \frac{\textstyle {\kappa _0}}{\textstyle {\kappa _\textrm{B}^2}}\Big )}} \end{aligned}$$

(21)

at the distance

$$\begin{aligned} r^\textrm{max} = 8\pi \Big ( \frac{L_\textrm{EL}}{K_I}\Big )^2 = 8 \frac{\textstyle {\big (D_2^\textrm{ext}\big )^4}}{\textstyle {\big (\sigma _{22}^\textrm{ext}\big )^2}} \Big (\frac{\textstyle {1}}{\textstyle {\kappa _\textrm{B}}} - \frac{\textstyle {\kappa _0}}{\textstyle {\kappa _\textrm{B}^2}}\Big )^2 a \end{aligned}$$

(22)

to the crack tip which is indicated by a triangle in Fig. 8. The second characteristic point is a root of Eq. (20), providing a radial distance to the crack tip

$$\begin{aligned} r^\textrm{com} =\frac{\textstyle {1}}{\textstyle {4}}r^\textrm{max} \end{aligned}$$

(23)

below which the stress is compressive and which is indicated by a filled circle in Fig. 8. To get an estimate for these radii,

Fig. 8

Mechanically induced (dashed), electrically induced (dash-dotted) and combined (solid) stresses on the ligament in the vicinity of a crack tip

Figure 9 shows the ratio of the electrically and mechanically induced stress for various electric loads $E_2^\textrm{ext} = D_2^\textrm{ext}/\kappa _\textrm{B}$ plotted versus the normalized radial coordinate. As largest electric load $E_2^\textrm{ext} = 10^7\,\mathrm {V/m}$ is chosen, since most dielectric bulk materials break down electrically at this load [35]. In order to provide an upper limit of the effect of the body forces, a comparatively small mechanical load $K_I = 1\,\textrm{MPa}\sqrt{\textrm{m}}$, corresponding to the fracture toughness of ceramics in order of magnitude, a typical permittivity of non-piezoelectric dielectrics $\kappa _\textrm{B}=10\kappa _0$ [35, 36] and a large crack length $a=100\,\textrm{mm}$ are employed. For the chosen parameters and upper bound of $D_2^\textrm{ext}$, it follows from Eq. (18) that the factor $L_\textrm{EL}$ is in the range of $[-400\,\textrm{Pam},0]$, where zero represents the load-free case. Additionally, a typical radius of atoms $r_\textrm{atom}\approx 10^{-10}\,\textrm{m}$ is indicated in Fig. 9 by a vertical dashed line for the sake of comparison. Since the point of changeover from compressive to tensile stress $r^\textrm{com}$ comes along with a ratio $\sigma _{22}^\textrm{EL}/\sigma _{22}^\textrm{mech}= -1$, marked as circles in Fig. 9, it becomes clear that, for $E_2^{\textrm{ext}}\le 10^6\,\textrm{V}/\textrm{m}$, the distances to the crack tip where the electrostatic body forces cause a compressive total stress are smaller than atom radii and thus violate the continuum hypothesis which LEFM and Maxwell stresses are based on. On the other hand, the K-concept of LEFM is only applicable if the $1/\sqrt{r}$-dominated zone according to Eq. (17) is sufficiently larger than the domain at the crack tip deviating from this course. While classically the focus in this context is on small scale yielding or phase transformation, Fig. 8 illustrates that body forces can take on this role equally. Defining the zone in which the body forces have a significant impact on the $1/\sqrt{r}$-singularity as $\vert \sigma _{22}^\textrm{EL}/ \sigma _{22}^\textrm{mech}\vert \ge 0.05$, this area is limited by $r = 5\cdot 10^{-8}\,\textrm{m}$ in the case of $E_{2}^{\textrm{ext}} = 10^{6}$ V/m and thus substantially larger than atom radii.

Fig. 9

Ratio of electrically and mechanically induced stresses in the vicinity of the crack tip for a range of electric loads and a constant mechanical load corresponding to $K_I = 1\,\textrm{MPa}\sqrt{\textrm{m}}$. The radii of maximal stress according to Eq. (22) are marked with triangles and those of compressive stress from Eq. (23) as circles. The electric permittivity is $\kappa _\textrm{B}= 10 \kappa _0$, and the crack length is $a=100\,\textrm{mm}$

Since electric fields beyond those depicted in Fig. 9 are hardly bearable for most bulk materials and much smaller mechanical loads are irrelevant in terms of fracture mechanics, the radii $r^{\textrm{com}}$ and $r^{\textrm{max}}$, being proportional to $a$ (compare Eq. (22)), could only increase in the case of longer cracks or for a larger dielectric constant. Similar considerations can be made for the maximal stress from Eq. (21), which is included as triangles in Fig. 9 and plotted double-logarithmically versus the electric load in Fig. 10. Even for an electric load $E_{2}^{\textrm{ext}} = 10^{7}$ V/m and $\kappa _{\textrm{B}} = 10\kappa _{0}$, there is still a maximal tensile stress of about $10^2\,\textrm{MPa}$, which increases by two orders of magnitude if the electric load is decreased by one, independent of the crack length $a$, see Eq. (21). So, there is always a large tensile stress in the vicinity of the crack tip, however, being far below corresponding magnitudes of pure mechanical loading. Directly at the crack tip there could be compressive stress which might inhibit crack growth even under critical mechanical loading.

Fig. 10

Maximum stress from Eq. (21) at constant mechanical load $K_I =1 \,\textrm{MPa}\sqrt{\textrm{m}}$ with $\kappa _\textrm{B}=10\kappa _0$ and $\kappa _\textrm{B}=10^3\kappa _0$. The crack length is in both cases $a=100\,\textrm{mm}$

An exception to the dielectrics considered so far with a permittivity of $\kappa _\textrm{B}= 10\kappa _0$ is ferroelectric ceramics such as barium titanate (BT) or lead zirconate titanate (PZT). Their permittivity is typically $\kappa _\textrm{B}\approx 10^3\kappa _0$, which leads to an increase of the radii $r^\textrm{max}$ and $r^\textrm{com}$ by four orders of magnitude as a comparison of Figs. 9 and 11 shows.

Fig. 11

Ratio of electrically and mechanically induced stresses versus radial distance from crack tip on the ligament in the style of Fig. 9 with $\kappa _\textrm{B}=10^3 \kappa _0$

The size of the region in which the electrostatic body forces have a relevant influence is thus several orders of magnitude above atomic radii at an electric field strength of $E_2^{\textrm{ext}}\ge 10^5 \,\textrm{V}/\textrm{m}$ and thus definitely ranges within the scope of continuum theories. As shown in Fig. 10, the maximum tensile stress decreases by two orders of magnitude if the permittivity is increased. However, ferroelectric ceramics exhibit piezoelectric coupling properties so that Eqs. (5) and (6) form a bilaterally coupled system of nonlinear differential equations, requiring further research for the sake of quantitative findings.

2.2 Abraham model in a transversely isotropic dielectric

In the following, the influence of the body force

$$\begin{aligned} f_i^\textrm{A}= \frac{\textstyle {1}}{\textstyle {2}} (D_{j} E_{j,i} - E_j D_{j,i}) + \frac{\textstyle {1}}{\textstyle {2}} (D_{i} E_{j} - D_j E_{i})_{,j}, \end{aligned}$$

(24)

resulting from the Maxwell stress model according to Abraham, on a crack of the geometry as the one in Fig. 1 will be investigated. Since the body force vector $f_i^\textrm{A}$ in the case of electrostatics vanishes in isotropic homogeneous dielectrics, a transversely isotropic material is considered in this section. For this purpose, the stiffness and permittivity tensors $c_{pq}$ and $\kappa _{ij}$ of single-crystal BT are employed, the former of which is depicted in Voigt notation. Although the Maxwell stress tensor of Einstein and Laub is non-symmetric in anisotropic media, the associated body force

$$\begin{aligned} f_i^\textrm{EL}= ( D_{j} - \kappa _0 E_{j})E_{j,i} \end{aligned}$$

(25)

is also considered in this section for the purpose of comparison. Since an influence of the orientation of the transverse isotropy is to be expected, the material tensors are introduced both for $x_1$- as well as $x_2$-poling-directions, resulting in the matrix representations shown in Table 2 with the coefficients from Table 3. Although these coefficients have been determined in experiments with an intrinsic constitutive coupling, keeping strain and electric field, respectively, constant, they may readily be adopted here for the sake of gaining fundamental insights. It should further be noted that the ratio of anisotropy $(\kappa _{11} - \kappa _{22})/\kappa _{11}$ of just roughly 12% is responsible for the electrostatic body force according to the Abraham model. As before, an electric displacement of $D_2^\textrm{ext} = 0.01\,\mathrm {{C}/{m^2}}$ is applied as electrical boundary condition.

Table 2 Material tensors of transversely isotropic elastic dielectric for different poling orientations

Table 3 Elastic and dielectric constants of single-crystal barium titanate in generalized plane strain condition [37]

The body force unit vectors calculated for the two transversal orientations and Maxwell stress models are shown in Fig. 12. Accordingly, the vectors $e_i^\textrm{A}$ of the Abraham model rotate by $180^\circ$ if the orientation of the transverse isotropy is changed, while the vectors $e_i^\textrm{EL}$ remain virtually unaffected.

Fig. 12

Unit vectors of the body forces derived from the Maxwell stress tensors according to [17] (top row) and [16] (bottom row) near the crack tip in a transversely isotropic medium with two different orientations of the transversal axis given in Table 2

The direction of the vectors $e_i^\textrm{A}$ in Fig. 12 indicates that there is tensile stress in case of a $x_1$-orientation and compressive stress in the case of $x_2$-orientation of the transversal axis. The directions of the vectors $e_i^\textrm{EL}$ result, as in the isotropic case, in compressive stresses independent of the anisotropy orientation. This issue is shown in more detail in Fig. 13 in terms of the shear stresses $\sigma _{12}^\textrm{A}(r, \theta =0)$, $\sigma _{12}^\textrm{EL}(r, \theta =0)$ and tensile stresses $\sigma _{22}^\textrm{A}(r, \theta =0)$, $\sigma _{22}^\textrm{EL}(r, \theta =0)$ in front of the crack tip. As the shear stresses are many orders of magnitude smaller than the normal stresses, they are negligible as in the isotropic case. As expected, the normal stress $\sigma _{22}^\textrm{A}(r, \theta =0)$ changes its sign if the orientation of the transversal axis is rotated by $90^\circ$ and apparently exhibits a singularity at the crack tip, while $\sigma _{22}^\textrm{EL}(r, \theta =0)$ is negative in both cases. Given that stresses in the crack tip near field are still well approximated by approaches of the shape

$$\begin{aligned} \begin{aligned} \sigma _{22}^\textrm{A}(r, \theta =0)&= L_\textrm{A}r^{\eta _\textrm{A}}\,,\\ \sigma _{22}^\textrm{EL}(r, \theta =0)&= L_\textrm{EL}r^{\eta _\textrm{EL}}\,, \end{aligned} \end{aligned}$$

(26)

Fig. 13

a Shear and b normal stresses on the ligament near a crack tip caused by the body forces of the Abraham and Einstein–Laub Maxwell stress models in a transversely isotropic material, according to Tables 2 and 3, with different orientations of the transversal axis

the types of the singularities being expressed by the exponents $\eta _\textrm{A}$ and $\eta _\textrm{EL}$ are estimated in the same way as in the previous section applying Eq. (16). The result of this evaluation is presented in Fig. 14. While the $\eta _\textrm{EL}$ are symmetrically distributed around $\eta _\textrm{EL}=-1$ with a maximal deviation of $\pm 4\%$, the values $\eta _\textrm{A}$ are comparatively wide spread in a range of $-1.72\le {\eta }_\textrm{A}\le -1.31$. However, one can conclude by comparison of the plots a) and b) that $\vert \eta _\textrm{EL}\vert < \vert \eta _\textrm{A}\vert$. Since no specific value could be identified for $\eta _\textrm{A}$, a unique derivation of $L_\textrm{A}$, as it was done for the Einstein and Laub model in the previous section, cannot be performed. However, linear regression is applied to calculate approximations according to [33]

$$\begin{aligned} \left( \begin{array}{c} |L_{\textrm{A}}|(\textrm{m}^{(2+\eta _{\textrm{A}})}/\textrm{N}) \\ |L_{\textrm{EL}}|(\textrm{m}/\textrm{N}) \end{array}\right) = \textrm{exp}\biggl ({\overline{\ln (|\sigma _{22}^{\textrm{A}/ \textrm{EL}}(\zeta _i)|/\textrm{MPa})} - \eta _{\textrm{A}/ \textrm{EL}} {\overline{\zeta }}}\biggr ). \end{aligned}$$

(27)

The results of both models are depicted in Fig. 15. Obviously, $L_\textrm{A}$ is several orders of magnitudes smaller than $L_\textrm{EL}$. After all, it is concluded that the radius of significant influence of $\sigma _{22}^\textrm{A}$ is much smaller than the one of $\sigma _{22}^\textrm{EL}$, whereupon the continuum hypothesis is probably violated. Consequently, experimental observations on crack closure might support either Einstein and Laub’s or Abraham’s theory of Maxwell stress.

Fig. 14

Exponents ${\eta }_\textrm{A}$ and ${\eta }_\textrm{EL}$, according to Eq. (26), of the singularities depicted in Fig.  13 for the a Einstein–Laub and b Abraham models calculated via Eq. (16) and illustrated in the style of Fig. 5. Results with $x_1$-orientation are marked as circles and those with $x_2$-orientation as triangles

Fig. 15

Intensity factors ${L}_\textrm{A}$ and ${L}_\textrm{EL}$ of the singularities in Fig. 13 for the a Einstein–Laub and b Abraham models calculated via Eq. (27). Results with $x_1$-orientation are marked as circles and those with $x_2$-orientation as triangles

3 Conclusion

Electrostatically induced body forces based on Maxwell stress tensors introduced by Einstein and Laub on the one hand and Abraham on the other have been investigated numerically with regard to implications on fracture mechanics of brittle dielectrics. While the model of Einstein and Laub yields nonzero body forces in the case of isotropic homogeneous media, Abraham’s theory requires anisotropy, just as other established theories, e.g., by Minkowski or Lorentz. Furthermore, the above models differ in terms of symmetry of the Maxwell stress tensor and quantitative predictions. Experimental validations of the approaches have scarcely been informative to date, inter alia due to the lack of samples in which the investigated effect is sufficiently pronounced compared to other ones, although recent numerical simulations of the deformation of a droplet support Lorentz’s model. A brittle cracked specimen might be an appropriate means in this context, since the crack tip gives rise to a distinctive field concentration, exhibiting even a singularity in its initial configuration and for infinitely small deformations, respectively. Due to this aspect, the body forces induced by an electric field have a larger impact on the mechanical behavior than for any other kind of sample. It could be shown at the example of the two chosen Maxwell stress models that stresses in front of the crack tip of an electromechanically loaded specimen are noticeably, however, differently influenced by the electric field, depending on the model. Remarkable are compressive stresses predicted close to the crack tip and a higher-order singularity, certainly requiring a modification of the classical K-concept of conventional linear elastic fracture mechanics for the assessment of crack growth initiation. The occurrence of the predicted strong singularity raises the fundamental question of whether the model of a sharp crack is really the “philosopher’s stone,” or if an approach accounting for a finite crack opening displacement, thus dispensing with any kind of crack tip singularity, is the way to go. The parameter range in terms of crack length, ratio of electrical and mechanical loads and dielectric permittivity has to be chosen carefully in view of length scales involved in the continuum approach. It could be shown that an appropriate choice is within the scope of technical feasibility of an experiment, predominantly with piezoelectric ceramics. To evaluate the plausibility of different Maxwell stress models, easily measurable critical loads of crack growth initiation will serve as an indicator instead of whole displacement fields as in previous experiments. However, a meaningful evaluation of experiments necessarily requires the consideration of additional effects in the model, in particular electrostriction and piezoelectricity which are theoretically well-established.