Skip to main content
SpringerLink
Log in

A three-dimensional continuum model for the mechanics of an elastic medium reinforced with fibrous materials in finite elastostatics

  • Original Article
  • Published:
Continuum Mechanics and Thermodynamics Aims and scope Submit manuscript

Abstract

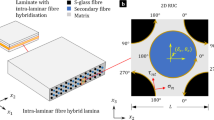
A three-dimensional model for the mechanics of elastic/hyperelastic materials reinforced with bidirectional fibers is presented in finite elastostatics. This includes the constitutive formulation of matrix–fiber composite system and the derivation of the corresponding Euler equilibrium equation. The responses of the matrix material and reinforcing fibers are characterized, respectively, via the Neo-Hookean model and quadratic strain energy potential of the Green–Lagrange type. These are further refined by the Mooney–Rivlin strain energy model and the high-order polynomial energy potential of fibers to incorporate the nonlinear behaviors of the matrix material and fibers. Within the framework of differential geometry and strain-gradient elasticity, the general kinematics of bidirectional fibers, including the three-dimensional bending of a fiber and twist between the two adjoining fibers, are formulated, and subsequently integrated into the model of continuum deformation. The admissible boundary conditions are also derived by virtue of variational principles and virtual work statement. In particular, a dimension reduction process is applied to the resulting three-dimensional model through which a compatible two-dimensional model describing both the in-plane and out-of-plane deformations of thin elastic films reinforced with fiber mesh is obtained. To this end, model implementation and comparison with the experimental results are performed, indicating that the proposed model successfully predicts key design considerations of fiber mesh reinforced composite films including stress–strain responses, deformation profiles, shear strain distributions and local structure (a unit fiber mesh) deformations. The proposed model is unique in that it is formulated within the framework of differential geometry of surface to accommodate the three-dimensional kinematics of the composite, yet the resulting equations are reframed in the orthonormal basis for enhanced practical unitality and mathematical tractability. Hence, the resulting model may also serve as an alternative Cosserat theory of plates and shells arising in two-dimensional nonlinear elasticity.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21

Similar content being viewed by others

References

  1. Voigt, W.: Theoretical studies on the elasticity relationships of crystals. Abh. Königlichen Ges. Wiss. Gött. 34, 3–52 (1892)

    Google Scholar 

  2. Monecke, J.: Microstructure dependence of material properties of composites. Phys. Status Solidi B 154, 805–813 (1989)

    Article  ADS  Google Scholar 

  3. Hahm, S.W., Khang, D.Y.: Crystallization and microstructure-dependent elastic moduli of ferroelectric P(VDF-TrFE) thin films. Soft Matter 6, 5802–5806 (2010)

    Article  ADS  Google Scholar 

  4. Moravec, F., Holecek, M.: Microstructure-dependent nonlinear viscoelasticity due to extracellular flow within cellular structures. Int. J. Solids Struct. 47, 1876–1887 (2010)

    Article  Google Scholar 

  5. Martinez, R.V., Branch, J.L., Fish, C.R., Jin, L., Shepherd, R.F., Nunes, R.M., Suo, Z., Whitesides, G.M.: Robotic tentacles with three-dimensional mobility based on flexible elastomers. Adv. Mater. 25(2), 205–12 (2013)

    Article  Google Scholar 

  6. Wang, Y., Gregory, C., Minor, M.A.: Improving mechanical properties of molded silicone rubber for soft robotics through fabric compositing. Soft Robot. 5(3), 272–290 (2018)

    Article  Google Scholar 

  7. Pritts, M.B., Rahn, C.D.: Design of an artificial muscle continuum robot. In: Proceedings of IEEE International Conference on Robotics and Automation, vol. 5, pp. 4742–4746 (2004)

  8. Yan, B., Huang, J., Han, L., Gong, L., Li, L., Israelachvili, J.N., Zeng, H.: Duplicating dynamic strain-stiffening behavior and nanomechanics of biological tissues in a synthetic self-healing flexible network hydrogel. ACS Nano 11(11), 11074–11081 (2017)

    Article  Google Scholar 

  9. Toupin, R.A.: Theories of elasticity with couple stress. Arch. Ration. Mech. Anal. 17, 85–112 (1964)

    Article  MathSciNet  Google Scholar 

  10. Mindlin, R.D., Tiersten, H.F.: Effects of couple-stresses in linear elasticity. Arch. Ration. Mech. Anal. 11, 415–448 (1962)

    Article  MathSciNet  Google Scholar 

  11. Truesdell, C., Noll, W.: The non-linear field theories of mechanics. In: Flugge, S. (ed.) Handbuch der Physik, vol. 3. Springer, Berlin (1965)

    Google Scholar 

  12. Landau, L.D., Lifshitz, E.M.: Theory of Elasticity, 3rd edn. Pergamon Press, Oxford (1986)

    Google Scholar 

  13. Dill, E.H.: Kirchhoff’s theory of rods. Arch. Hist. Exact Sci. 44, 1–23 (1992)

    Article  MathSciNet  Google Scholar 

  14. Antman, S.S.: Nonlinear Problems of Elasticity. Springer, Berlin (2005)

    Google Scholar 

  15. Spencer, A.J.M., Soldatos, K.P.: Finite deformations of fibre-reinforced elastic solids with fibre bending stiffness. Int. J. Non-Linear Mech. 42, 355–368 (2007)

    Article  ADS  Google Scholar 

  16. Steigmann, D.J.: Theory of elastic solids reinforced with fibers resistant to extension, flexure and twist. Int. J. Non-Linear Mech. 47, 734–742 (2012)

    Article  ADS  Google Scholar 

  17. Steigmann, D.J., Dell’Isola, F.: Mechanical response of fabric sheets to three-dimensional bending, twisting, and stretching. Acta Mech. Sin. 31(3), 373–382 (2015)

    Article  ADS  MathSciNet  Google Scholar 

  18. Kim, C., Zeidi, M.: Gradient elasticity theory for fiber composites with fibers resistant to extension and flexure. Int. J. Eng. Sci. 131, 80–99 (2018)

    Article  MathSciNet  Google Scholar 

  19. Zeidi, M., Kim, C.: Mechanics of an elastic solid reinforced with bidirectional fiber in finite plane elastostatics: complete analysis. Contin. Mech. Thermodyn. 30, 573–592 (2018)

    Article  ADS  MathSciNet  Google Scholar 

  20. Zeidi, M., Kim, C.: Mechanics of fiber composites with fibers resistant to extension and flexure. Math. Mech. Solids 24(1), 3–17 (2017)

    Article  MathSciNet  Google Scholar 

  21. Dell’Isola, F., Giorgio, I., Pawlikowski, M., Rizzi, N.L.: Large deformations of planar extensible beams and pantographic lattices: heuristic homogenization, experimental and numerical examples of equilibrium. Proc. R. Soc. A 472(2185), 20150790 (2016)

    Article  ADS  Google Scholar 

  22. Dell’Isola, F., Cuomo, M., Greco, L., Della Corte, A.: Bias extension test for pantographic sheets: numerical simulations based on second gradient shear energies. J. Eng. Math. 103(1), 127–157 (2017)

    Article  MathSciNet  Google Scholar 

  23. Dell’Isola, F., Della Corte, A., Greco, L., Luongo, A.: Plane bias extension test for a continuum with two inextensible families of fibers: a variational treatment with Lagrange multipliers and a perturbation solution. Int. J. Solids Struct. 81, 1–12 (2016)

    Article  Google Scholar 

  24. Javili, A., dell’Isola, F., Steinmann, P.: Geometrically nonlinear higher-gradient elasticity with energetic boundaries. J. Mech. Phys. Solids 61(12), 2381–2401 (2013)

    Article  ADS  MathSciNet  Google Scholar 

  25. dell’Isola, F., Seppecher, P., Madeo, A.: How contact interactions may depend on the shape of Cauchy cuts in Nth gradient continua: approach a la D’Alembert. Z. Angew. Math. Phys. 63, 1119–1141 (2012)

    Article  MathSciNet  Google Scholar 

  26. Dell’Isola, F., Corte, A.D., Giorgio, I.: Higher-gradient continua: the legacy of Piola, Mindlin, Sedov and Toupin and some future research perspectives. Math. Mech. Solids 22(4), 852–872 (2016)

    Article  MathSciNet  Google Scholar 

  27. Bolouri, S.E.S., Kim, C.: A model for the second strain gradient continua reinforced with extensible fibers in plane elastostatics. Contin. Mech. Thermodyn. 33(5), 2141–2165 (2021)

    Article  ADS  MathSciNet  Google Scholar 

  28. Bolouri, S.E.S., Kim, C., Yang, S.: Linear theory for the mechanics of third-gradient continua reinforced with fibers resistance to flexure. Math. Mech. Solids 25(4), 937–960 (2020)

    Article  MathSciNet  Google Scholar 

  29. Kim, C., Islam, S.: Mechanics of third-gradient continua reinforced with fibers resistant to flexure in finite plane elastostatics. Contin. Mech. Thermodyn. 32, 1595–1617 (2020)

    Article  ADS  MathSciNet  Google Scholar 

  30. Islam, S., Zhalmuratova, D., Chung, H.J., Kim, C.: A model for hyperelastic materials reinforced with fibers resistance to extension and flexure. Int. J. Solids Struct. 193, 418–433 (2020)

    Article  Google Scholar 

  31. Mihai, L.A., Goriely, A.: How to characterize a nonlinear elastic material A review on nonlinear constitutive parameters in isotropic finite elasticity. Proc. R. Soc. A 473(2207), 20170607 (2017)

    Article  ADS  MathSciNet  Google Scholar 

  32. Islam, S., Bolouri, S.E.S., Kim, C.: Mechanics of hyperelastic composites reinforced with nonlinear elastic fibrous materials in finite plane elastostatics. Int. J. Eng. Sci. 165, 103491 (2021)

    Article  MathSciNet  Google Scholar 

  33. Naghdi, P.M.: The theory of shells and plates. In: Truesdell, C. (ed.) Linear Theories of Elasticity and Thermoelasticity. Springer, Berlin (1973). https://doi.org/10.1007/978-3-662-39776-3_5

    Chapter  Google Scholar 

  34. Steigmann, D.J.: Tension-field theory. Proc. R. Soc. Lond. A 429(1876), 141–173 (1990)

    Article  ADS  MathSciNet  Google Scholar 

  35. Zeidi, M., Kim, C.I.: Finite plane deformations of elastic solids reinforced with fibers resistant to flexure: complete solution. Arch. Appl. Mech. 88(5), 819–835 (2017)

    Article  Google Scholar 

  36. Kim, C.I.: Strain-gradient elasticity theory for the mechanics of fiber composites subjected to finite plane deformations: comprehensive analysis. Multiscale Sci. Eng. 1(2), 150–160 (2019)

    Article  ADS  Google Scholar 

  37. Ogden, R.W.: Non-linear Elastic Deformations. Ellis Horwood Ltd., Chichester (1984)

    Google Scholar 

  38. Steigmann, D.J.: Finite Elasticity Theory. Oxford University Press, Oxford (2017)

    Book  Google Scholar 

  39. Koiter, W.T.: Couple-stresses in the theory of elasticity. Proc. K. Ned. Akad. Wet. 67, 17–44 (1964)

    MathSciNet  Google Scholar 

  40. Germain, P.: The method of virtual power in continuum mechanics, Part 2: microstructure. SIAM J. Appl. Math. 25(3), 556–575 (1973)

    Article  Google Scholar 

  41. Spencer, A.J.M.: Deformations of Fibre-Reinforced Materials. Oxford University Press, London (1972)

    Google Scholar 

  42. Spencer, A.J.M.: Continuum theory of the mechanics of fibre reinforced Composites. In: CISM Courses and Lectures No. 282. Springer (1984)

  43. Rivlin, R.S.: Constitutive equations for a fiber-reinforced lamina. In: Parker, D.F., England, A.H. (eds.) IUTAM Symposium on Anisotropy, Inhomogeneity and Nonlinearity in Solid Mechanics, pp. 379–384. Kluwer Academic Publishers, Dordrecht (1995)

  44. Holzapfel, G.A., Ogden, R.W.: Mechanics of Biological Tissue. Springer, Heidelberg (2006)

    Book  Google Scholar 

  45. Dorfmann, L., Ogden, R.W.: Nonlinear mechanics of soft fibrous materials. In: CISM International Centre for Mechanical Sciences, vol. 559 (2015). https://doi.org/10.1007/978-3-7091-1838-2

  46. Reissner, E.: A further note on finite-strain force and moment stress elasticity. Z. Angew. Math. Phys. 38, 665–673 (1987)

    Article  Google Scholar 

  47. Myung, D., Koh, W., Ko, J., Hu, Y., Carrasco, M., Noolandi, J., Ta, C.N., Frank, C.W.: Biomimetic strain hardening in interpenetrating polymer network hydrogels. Polymer 48, 5376–5387 (2007)

    Article  Google Scholar 

  48. Shadwick, R.E.: Mechanical design in arteries. J. Exp. Biol. 202(23), 3305–3313 (1999)

    Article  Google Scholar 

  49. Steigmann, D.J.: Invariants of the stretch tensors and their application to finite elasticity theory. Math. Mech. Solids 7(4), 393–404 (2002)

    Article  MathSciNet  Google Scholar 

  50. Yeo, J.C., Yu, J., Koh, Z.M., Wang, Z., Lim, C.T.: Wearable tactile sensor based on flexible microfluidics. Lab Chip 16(17), 3244–3250 (2016)

    Article  Google Scholar 

  51. Elsayed, Y., Vincensi, A., Lekakou, C., Geng, T., Saaj, C.M., Ranzani, T., Cianchetti, M., Menciassi, A.: Finite element analysis and design optimization of a pneumatically actuating silicone module for robotic surgery applications. Soft Robot. 1(4), 255–262 (2014)

    Article  Google Scholar 

  52. Sparks, J.L., Vavalle, N.A., Kasting, K.E., Long, B., Tanaka, M.L., Sanger, P.A., Schnell, K., Conner-Kerr, T.A.: Use of silicone materials to simulate tissue biomechanics as related to deep tissue injury. Adv. Skin Wound Care 28(2), 59–68 (2015)

    Article  Google Scholar 

  53. Trivedi, A.R., Siviour, C.R.: A simple rate-temperature dependent hyperelastic model applied to neoprene rubber. J. Dyn. Behav. Mater. 6(3), 336–347 (2020)

    Article  Google Scholar 

  54. Bai, Y., Liu, C., Huang, G., Li, W., Feng, S.: A hyper-viscoelastic constitutive model for polyurea under uniaxial compressive loading. Polymers 8(4), 133 (2016)

    Article  Google Scholar 

  55. Siviour, C., Jordan, J.: High strain rate mechanics of polymers: a review. J. Dyn. Behav. Mater. 2(1), 15–32 (2016)

    Article  Google Scholar 

  56. Zheng, B., Gao, X., Li, M., Deng, T., Huang, Z., Zhou, H., Li, D.: Formability and failure mechanisms of woven CF/PEEK composite sheet in solid-state thermoforming. Polymers 11(6), 966 (2019)

    Article  Google Scholar 

  57. Fazita, N., Jayaraman, K., Bhattacharyya, D.: Formability analysis of bamboo fabric reinforced poly(lactic) acid composites. Materials 9(7), 539 (2016)

    Article  ADS  Google Scholar 

  58. Zheng, B., Wang, H., Huang, Z., Zhang, Yi., Zhou, H., Li, D.: Experimental investigation and constitutive modeling of the deformation behavior of Poly-Ether-Ether-Ketone at elevated temperatures. Polymer Test. 63, 349–359 (2017)

    Article  Google Scholar 

  59. Dworak, M., Rudawski, A., Markowski, J., Blazewicz, S.: Dynamic mechanical properties of carbon fibre-reinforced PEEK composites in simulated body-fluid. Compos. Struct. 161, 428–434 (2017)

    Article  Google Scholar 

  60. Boudeau, N., Liksonov, D., Barriere, T., Maslovc, L., Gelin, J.C.: Composite based on polyetheretherketone reinforced with carbon fibres, an alternative to conventional materials for femoral implant: Manufacturing process and resulting structural behaviour. Mater. Des. 40, 148–156 (2012)

    Article  Google Scholar 

  61. Vaidya, U.K., Chawla, K.K.: Processing of fibre reinforced thermoplastic composites. Int. Mater. Rev. 53(4), 185–218 (2013)

    Article  Google Scholar 

  62. Morales, A.P., Güemes, A., Fernandez-Lopez, A., Valero, V.C., Llano, S.D.L.R.: Bamboo-polylactic acid (PLA) composite material for structural applications. Materials 10(11), 1286 (2017)

    Article  ADS  Google Scholar 

  63. Abilash, N., Sivapragash, M.: Optimizing the delamination failure in bamboo fiber reinforced polyester composite. J. King Saud Univ. Eng. Sci. 28(1), 92–102 (2016)

    Google Scholar 

  64. Takuda, H., Enami, T., Kubota, K., Hatta, T.: The formability of a thin sheet of Mg–8.5Li–1Zn alloy. J. Mater. Process. Technol. 101(3), 281–286 (2000)

    Article  Google Scholar 

  65. Deng, T., Zhang, W., Jiang, W., Zhou, H., Huang, Z., Peng, X., Zhou, H., Li, D.: A hybrid lamination model for simulation of woven fabric reinforced thermoplastic composites solid-state thermo-stamping. Mater. Des. 200, 109419 (2021)

    Article  Google Scholar 

  66. Biswas, S., Ahsan, Q., Cenna, A., Hasan, M., Hassan, A.: Physical and mechanical properties of jute, bamboo and coir natural fiber. Fibers Polymers 14, 1762–1767 (2013)

    Article  Google Scholar 

  67. Wei, X., Zhou, H., Chen, F., Wang, G.: Bending flexibility of moso bamboo (Phyllostachys edulis) with functionally graded structure. Materials 12(12), 2007 (2019)

    Article  ADS  Google Scholar 

  68. Mirkhalaf, S.M., Fagerström, M.: The mechanical behavior of polylactic acid (PLA) films: fabrication, experiments and modelling. Mech. Time-Depend. Mater. 25, 119–131 (2019)

    Article  ADS  Google Scholar 

  69. Bai, J., Chen, D., Xiong, J., Shenoi, R.A.: Folding analysis for thin-walled deployable composite boom. Acta Astronaut. 159, 622–636 (2019)

    Article  ADS  Google Scholar 

  70. Huanga, H., Guan, F., Pan, L., Xu, Y.: Design and deploying study of a new petal-type deployable solid surface antenna. Acta Astronaut. 148, 99–110 (2018)

    Article  ADS  Google Scholar 

  71. Chu, Z., Deng, Z., Qi, X., Li, B.: Modeling and analysis of a large deployable antenna structure. Acta Astronaut. 95, 51–60 (2014)

    Article  ADS  Google Scholar 

  72. Block, J., Straubel, M., Wiedemann, M.: Ultralight deployable booms for solar sails and other large gossamer structures in space. Acta Astronaut. 68, 7–8 (2011)

    Article  Google Scholar 

  73. Pankow, M., White., C.: Design and testing of bi-stable booms for space applications. In: 20th International Conference on Composite Materials, vol. 3405, No. 4 (2015)

  74. Wang, S., Schenk, M., Jiang, S., Viquerat, A.: Blossoming analysis of composite deployable booms. Thin Walled Struct. 157, 107098 (2020)

    Article  Google Scholar 

  75. Mallikarachchi, H.Y.C.: Thin-walled composite deployable booms with tape-spring hinges. Doctoral Thesis. University of Cambridge (2011). https://doi.org/10.17863/CAM.14004

  76. Lüders, C.: Nonlinear-elastic orthotropic material modeling of an epoxy-based polymer for predicting the material behavior of transversely loaded fiber-reinforced composites. J. Compos. Sci. 4(2), 46 (2020)

    Article  Google Scholar 

  77. Giorgio, I., Dell’Isola, F., Steigmann, D.J.: Edge effects in Hypar nets. C. R. Méc. 347, 114–123 (2019)

    Article  ADS  Google Scholar 

  78. Carpi, F., Frediani, G., Turco, S., Rossi, D.D.: Bioinspired tunable lens with muscle-like electroactive elastomers. Adv. Funct. Mater. 21, 4152–4158 (2011)

    Article  Google Scholar 

Download references

Acknowledgements

This work was supported by the Natural Sciences and Engineering Research Council of Canada via Grant #RGPIN-2022-03613 and the Chung-Ang University Research Grants in 2022. Kim would like to thank Dr. David Steigmann for stimulating his interest in this subject and for discussions concerning the underlying theory.

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, University of Alberta, Edmonton, AB, T6G 1H9, Canada

    Chun I. L. Kim & Suprabha Islam

  2. School of Energy Systems Engineering, Chung-Ang University, Seoul, South Korea

    Seunghwa Yang

Authors
  1. Chun I. L. Kim
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Suprabha Islam
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Seunghwa Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Chun I. L. Kim.

Additional information

Communicated by Andreas Öchsner.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix: Finite element analysis of the fourth-order coupled PDE

Appendix: Finite element analysis of the fourth-order coupled PDE

The systems of PDEs in Eqs. (92)–(93) are fourth-order differential equations with coupled nonlinear terms. The case of such less regular PDEs deserves delicate mathematical treatment and is of particular practical interest. Hence, it is not trivial to demonstrate the associated numerical analysis procedures. For preprocessing, Eq. (92) may be recast as

For \(i=1\):

$$\begin{aligned} 0= & {} \mu (Q+\chi _{1,22})+\kappa (Q+E_{,2})(CC+EE+DD+FF+MM+NN)-\kappa (Q+C_{,2}+E_{,1}+E_{,2}) \\{} & {} (CC+CD+DD+DF+MM+MN+EC+EE+FD+FF+NM+NN)+\kappa (C+E) \\{} & {} (2QC+2E_{,1}E+2C_{,2}C+2UE-QC-QE-E_{,2}C-E_{,2}E-CQ-CE_{,1}-EC_{,2}-EE_{,2} \\{} & {} +2F_{,1}F+2D_{,2}D+2F_{,2}F-RD-RF-F_{,2}D-F_{,2}F+DR-DF_{,1}-FD_{,2}-FF_{,2} \\{} & {} +2N_{,1}N+2M_{,2}M+2N_{,2}N-M_{,1}M-M_{,1}N-N_{,2}M-N_{,2}N+MM_{,1}-MN_{,1}-NM_{,2} \\{} & {} -MM_{,2})+\Bigg [\frac{E_{11}}{4}(2QCCC+2QCDD+2QCMM+2RDCC+2RDDD+2RDMM \\{} & {} +2M_{,1}MCC+2M_{,1}MDD+2M_{,1}MMM+2CCQC+2CCRD+2CCM_{,1}M+2DDQC \\{} & {} +2DDRD+2DDM_{,1}M+2MMQC+2MMD_{,1}D+2MMM_{,1}M)+(E_{12}-E_{11})(QC \\{} & {} +RD+M_{,1}M)\Bigg ]C+\Bigg [\frac{E_{11}}{4}(CC+DD+MM)^{2}+\frac{(E_{12}-E_{11})}{2} (CC+DD+MM) \\{} & {} +\frac{(E_{11}-2E_{12})}{4}\Bigg ]Q+\Bigg [\frac{E_{21}}{4} (2E_{,2}DDD+2E_{,2}DFF+2E_{,2}ENN+2F_{,2}FEE+2F_{,2}FFF \\{} & {} +2F_{,2}FNN+2SNEE+2SNFF+2SNNN+2EEE_{,2}E+2EEF_{,2}F+2EESN+2FFE_{,2}E \\{} & {} +2FFF_{,2}F+2FFSN+2NNE_{,2}E+2NNF_{,2}F+2NNSN)(E_{22}-E_{21})(E_{,2}E+F_{,2}F \\{} & {} +SN)\Bigg ] E+\Bigg [\frac{E_{21}}{4}(EE+FF+NN)^{2}+\frac{(E_{22}-E_{21})}{2}(EE+FF+NN)+ \frac{(E_{21}-2E_{22})}{4}\Bigg ]Q \\{} & {} \mathbf {-}C_{1}Q_{,11}\mathbf {-}C_{2}U_{,22}-\tau U_{,11}-\tau Q_{,22}, \end{aligned}$$

and similarly for \(i=2\) and 3, where

$$\begin{aligned} 0= & {} Q-\chi _{1,11},\text { }0=R-\chi _{2,11},\ 0=C-\chi _{1,1},\ 0=D-\chi _{2,1}, \nonumber \\ 0= & {} E-\chi _{1,2},\ 0=F-\chi _{2,2},\ 0=A-\mu (Q+\chi _{1,22})-cQ_{,11}, \nonumber \\ 0= & {} B-\mu (R+\chi _{2,22})-cR_{,11},0=M-\chi _{3,1},0=N-\chi _{3,2}, \nonumber \\ 0= & {} U-\chi _{1,22},0=V-\chi _{2,22},\text { }0=T-\chi _{3,11},\text { } 0=S-\chi _{3,22}, \end{aligned}$$
(109)

where \(Q=\chi _{1,11},\ R=\chi _{2,11},\) \(T=\chi _{3,11},~C=\chi _{1,1},\) \(D=\chi _{2,1},M=\chi _{3,1},~E=\chi _{1,2},~F=\chi _{2,2},\) \(N=\chi _{3,2},\) \(U=\chi _{1,22,}\) \(V=\chi _{2,22}\) and \(S=\chi _{3,22}\). Hence, the order of differential equations is reduced from the three coupled equations of the fourth order to seventeen coupled equations of the2nd order. Especially, the nonlinear terms in the above equations (e.g., \(A\chi _{2,2},B\chi _{2,1}\) etc...) can be systematically treated via the Picard iterative procedure and/or Newton method;

$$\begin{aligned} -A^{initial}\chi _{2,2}^{initial}+B^{initial}\chi _{2,1}^{initial}&\implies&-A_{0}\chi _{2,2}^{0}+B_{0}\chi _{2,1}^{0} \nonumber \\ A^{initial}\chi _{1,2}^{initial}-B^{initial}\chi _{1,1}^{initial}&\Longrightarrow&A_{0}\chi _{1,2}^{0}-B_{0}\chi _{1,1}^{0}, \end{aligned}$$
(110)

where the estimated values of A, B continue to be updated based on their previous estimations (e.g., \(A_{1}\) and \(B_{1}\) are refreshed by their previous estimations of \(A_{o}\) and \(B_{o}\)) as iteration progresses and similarly for the rest of nonlinear terms.

Also, the weight forms of Eq. (109) can be found as

$$\begin{aligned} 0= & {} \int _{\Omega }w_{1}\Bigg \{\mu (Q+\chi _{1,22})+\kappa (Q+E_{,2})(CC+EE+DD+FF+MM+NN)-\kappa (Q+C_{,2}+E_{,1}+E_{,2}) \\{} & {} (CC+CD+DD+DF+MM+MN+EC+EE+FD+FF+NM+NN)+\kappa (C+E) \\{} & {} (2QC+2E_{,1}E+2C_{,2}C+2UE-QC-QE-E_{,2}C-E_{,2}E-CQ-CE_{,1}-EC_{,2}-EE_{,2} \\{} & {} +2F_{,1}F+2D_{,2}D+2F_{,2}F-RD-RF-F_{,2}D-F_{,2}F+DR-DF_{,1}-FD_{,2}-FF_{,2} \\{} & {} +2N_{,1}N+2M_{,2}M+2N_{,2}N-M_{,1}M-M_{,1}N-N_{,2}M-N_{,2}N+MM_{,1}-MN_{,1}-NM_{,2} \\{} & {} -MM_{,2})+\Bigg [\frac{E_{11}}{4}(2QCCC+2QCDD+2QCMM+2RDCC+2RDDD+2RDMM \\{} & {} +2M_{,1}MCC+2M_{,1}MDD+2M_{,1}MMM+2CCQC+2CCRD+2CCM_{,1}M+2DDQC \\{} & {} +2DDRD+2DDM_{,1}M+2MMQC+2MMD_{,1}D+2MMM_{,1}M)+(E_{12}-E_{11})(QC \\{} & {} +RD+M_{,1}M)\Bigg ]C+\Bigg [\frac{E_{11}}{4}(CC+DD+MM)^{2}+\frac{(E_{12}-E_{11})}{2} (CC+DD+MM) \\{} & {} +\frac{(E_{11}-2E_{12})}{4}\Bigg ]Q+\Bigg [\frac{E_{21}}{4} (2E_{,2}DDD+2E_{,2}DFF+2E_{,2}ENN+2F_{,2}FEE+2F_{,2}FFF \\{} & {} +2F_{,2}FNN+2SNEE+2SNFF+2SNNN+2EEE_{,2}E+2EEF_{,2}F+2EESN+2FFE_{,2}E \\{} & {} +2FFF_{,2}F+2FFSN+2NNE_{,2}E+2NNF_{,2}F+2NNSN)(E_{22}-E_{21})(E_{,2}E+F_{,2}F \\{} & {} +SN)\Bigg ]E+\Bigg [\frac{E_{21}}{4}(EE+FF+NN)^{2}+\frac{(E_{22}-E_{21})}{2}(EE+FF+NN)+ \frac{(E_{21}-2E_{22})}{4}\Bigg ]Q \\{} & {} \mathbf {-}C_{1}Q_{,11}\mathbf {-}C_{2}U_{,22}-\tau U_{,11}-\tau Q_{,22}\Bigg \}d\Omega , \end{aligned}$$
$$\begin{aligned} 0= & {} \int _{\Omega }w_{4}(Q-\chi _{1,11})d\Omega ,\ 0=\int _{\Omega }w_{5}(R-\chi _{2,11})d\Omega ,\ 0=\int _{\Omega }w_{6}(T-\chi _{3,11})d\Omega , \nonumber \\ 0= & {} \int _{\Omega }w_{7}(C-\chi _{1,1})d\Omega ,\ 0=\int _{\Omega }w_{8}(D-\chi _{2,1})d\Omega ,\ 0=\int _{\Omega }w_{9}(M-\chi _{3,1})d\Omega , \nonumber \\ 0= & {} \int _{\Omega }w_{10}(E-\chi _{1,2})d\Omega ,\ 0=\int _{\Omega }w_{11}(F-\chi _{2,2})d\Omega ,\ 0=\int _{\Omega }w_{12}(N-\chi _{3,2})d\Omega , \nonumber \\ 0= & {} \int _{\Omega }w_{13}(U-\chi _{1,22})d\Omega ,\ 0=\int _{\Omega }w_{14}(V-\chi _{2,22})d\Omega ,\ 0=\int _{\Omega }w_{15}(S-\chi _{3,22})d\Omega , \nonumber \\ 0= & {} \int _{\Omega }w_{16}(A-\mu (Q+\chi _{1,22})-C_{1}Q_{,11}-C_{2}U_{,22})d\Omega ,\ \nonumber \\ 0= & {} \int _{\Omega }w_{17}(B-\mu (R+\chi _{2,22})-C_{1}R_{,11}-C_{2}V_{,22})d\Omega . \end{aligned}$$
(111)

Thus, we apply integration by part and the Green–Stokes’ theorem, (e.g. \(\mu \int _{\Omega ^{e}}w_{1}\chi _{1,22}d\Omega =-\mu \int _{\Omega ^{e}}w_{1,2}\chi _{1,2}d\Omega +\mu \int _{\partial \Gamma }w_{1}\chi _{1,2}Nd\Gamma \)) and thereby obtain the following weak forms of Eq. (111)

$$\begin{aligned} 0= & {} \int _{\Omega }\{\mu w_{1}Q-\mu w_{1,2}\chi _{1,2}+w_{1}\kappa (Q+E_{,2})(CC+EE+DD+FF+MM+NN)-w_{1}\kappa (Q+C_{,2} \\{} & {} +E_{,1}+E_{,2})(CC+CD+DD+DF+MM+MN+EC+EE+FD+FF+NM+NN) \\{} & {} +w_{1}\kappa (C+E)(2QC+2E_{,1}E+2C_{,2}C+2UE-QC-QE-E_{,2}C-E_{,2}E-CQ-CE_{,1} \\{} & {} -EC_{,2}-EE_{,2}+2F_{,1}F+2D_{,2}D+2F_{,2}F-RD-RF-F_{,2}D-F_{,2}F+DR-DF_{,1} \\{} & {} -FD_{,2}-FF_{,2}+2N_{,1}N+2M_{,2}M+2N_{,2}N-M_{,1}M-M_{,1}N-N_{,2}M-N_{,2}N+MM_{,1} \\{} & {} -MN_{,1}-NM_{,2}-MM_{,2})+w_{1}\Bigg [\frac{E_{11}}{4}(2QCCC+2QCDD+2QCMM+2RDCC \\{} & {} +2RDDD+2RDMM+2M_{,1}MCC+2M_{,1}MDD+2M_{,1}MMM+2CCQC+2CCRD \\{} & {} +2CCM_{,1}M+2DDQC+2DDRD+2DDM_{,1}M+2MMQC+2MMD_{,1}D+2MMM_{,1}M) \\{} & {} +(E_{12}-E_{11})(QC+RD+M_{,1}M)\Bigg ]C+w_{1}\Bigg [\frac{E_{11}}{4}(CC+DD+MM)^{2}+ \frac{(E_{12}-E_{11})}{2}(CC \\{} & {} +DD+MM)+\frac{(E_{11}-2E_{12})}{4}\Bigg ]Q+w_{1}\Bigg [\frac{E_{21}}{4} (2E_{,2}DDD+2E_{,2}DFF+2E_{,2}ENN+2F_{,2}FEE \\{} & {} +2F_{,2}FFF+2F_{,2}FNN+2SNEE+2SNFF+2SNNN+2EEE_{,2}E+2EEF_{,2}F+2EESN \\{} & {} +2FFE_{,2}E+2FFF_{,2}F+2FFSN+2NNE_{,2}E+2NNF_{,2}F+2NNSN)(E_{22}-E_{21})(E_{,2}E \\{} & {} +F_{,2}F+SN)\Bigg ]E+w_{1}\Bigg [\frac{E_{21}}{4}(EE+FF+NN)^{2}+\frac{(E_{22}-E_{21})}{ 2}(EE+FF+NN) \\{} & {} +\frac{(E_{21}-2E_{22})}{4}\Bigg ]Q\mathbf {+}w_{1,1}C_{1}Q_{,1}\mathbf {+} w_{1,2}C_{2}U_{,2}\mathbf {+}w_{1,1}\tau U_{,1}\mathbf {+}w_{1,2}\tau Q_{,2}\}d\Omega +\mu \int _{\partial \Gamma }w_{1}\chi _{1,2}Nd\Gamma \\{} & {} -C_{1}\int _{\partial \Gamma }w_{1}Q_{,1}Nd\Gamma -C_{2}\int _{\partial \Gamma }w_{1}U_{,2}Nd\Gamma -\tau \int _{\partial \Gamma }w_{1}U_{,1}Nd\Gamma -\tau \int _{\partial \Gamma }w_{1}Q_{,2}Nd\Gamma , \end{aligned}$$
$$\begin{aligned} 0= & {} \int _{\Omega }(w_{4}Q+w_{3,1}\chi _{1,1})d\Omega -\int _{\partial \Gamma }w_{4}\chi _{1,1}Nd\Gamma ,\text { } \nonumber \\ 0= & {} \int _{\Omega }(w_{5}R+w_{5,1}\chi _{2,1})d\Omega -\int _{\partial \Gamma }w_{5}\chi _{2,1}Nd\Gamma ,\ \nonumber \\ 0= & {} \int _{\Omega }(w_{6}T+w_{6,1}\chi _{3,1})d\Omega -\int _{\partial \Gamma }w_{6}\chi _{3,1}Nd\Gamma ,\text { } \nonumber \\ 0= & {} \int _{\Omega }(w_{7}C-w_{7}\chi _{1,1})d\Omega ,\ 0=\int _{\Omega }w_{8}(D-\chi _{2,1})d\Omega ,\ 0=\int _{\Omega }w_{9}(M-\chi _{3,1})d\Omega , \nonumber \\ 0= & {} \int _{\Omega }w_{10}(E-\chi _{1,2})d\Omega ,\ 0=\int _{\Omega }w_{11}(F-\chi _{2,2})d\Omega ,\text { }0=\int _{\Omega }w_{12}(N-\chi _{3,2})d\Omega , \nonumber \\ 0= & {} \int _{\Omega }(w_{13}U+w_{13,2}\chi _{1,2})d\Omega -\int _{\partial \Gamma }w_{13}\chi _{1,2}Nd\Gamma ,\text { }\ \nonumber \\ 0= & {} \int _{\Omega }(w_{14}V+w_{14,2}\chi _{2,2})d\Omega -\int _{\partial \Gamma }w_{14}\chi _{2,2}Nd\Gamma , \nonumber \\ \ 0= & {} \int _{\Omega }(w_{15}S+w_{15,2}\chi _{3,2})d\Omega -\int _{\partial \Gamma }w_{15}\chi _{3,2}Nd\Gamma , \nonumber \\ 0= & {} \int _{\Omega }(w_{16}A-\mu w_{16}Q+\mu w_{16,2}\chi _{1,2}+C_{1}w_{16,1}Q_{,1}+C_{2}w_{16,2}U_{,2})d\Omega \nonumber \\{} & {} -\int _{\partial \Gamma }\mu w_{16}\chi _{1,2}Nd\Gamma -\int _{\partial \Gamma }C_{1}w_{16}Q_{,1}Nd\Gamma -\int _{\partial \Gamma }C_{2}w_{16}U_{,2}Nd\Gamma , \nonumber \\ 0= & {} \int _{\Omega }(w_{17}B-\mu w_{17}R+\mu w_{17,2}\chi _{2,2}+C_{1}w_{17,1}R_{,1}+C_{2}w_{17,2}V_{,2})d\Omega \nonumber \\{} & {} -\int _{\partial \Gamma }\mu w_{17}\chi _{2,2}Nd\Gamma -\int _{\partial \Gamma }C_{1}w_{17}R_{,1}Nd\Gamma -\int _{\partial \Gamma }C_{2}w_{17}V_{,2}Nd\Gamma , \end{aligned}$$
(112)

where \(\Omega \), \(\partial \Gamma \) and \(N\ \) are, respectively, the domain of interest, the associated boundary and the rightward unit normal to the boundary \(\partial \Gamma \) in the sense of the Green–Stokes’ theorem. The unknown potentials of \(\chi _{1},\) \(\chi _{2},\chi _{3},\ Q,\ R,C,D,E,F,T,S,U,V,M,N,\ A\) and B can be expressed in the form of Lagrangian polynomial that

$$\begin{aligned} (*)=\sum _{j=1}^{n=4}[(*)_{j}\Psi _{j}(x,y)]. \end{aligned}$$
(113)

Accordingly, the test function w is found to be

$$\begin{aligned} w_{m}=\sum _{i=1}^{n=4}w_{m}^{i}\Psi _{i}(x,y);\text { }i=1,2,3,4,\text { and } m=1,2,3,4,\ldots 10, \end{aligned}$$
(114)

where \(w_{i}\) is the weight of the test function and \(\Psi _{i}(x,y)\) are the associated shape functions; \(\Psi _{1}=\frac{ (x-2)(y-1)}{2},\) \(\Psi _{2}=\frac{x(y-1)}{-2},~\Psi _{3}=\frac{xy}{2} \) and \(\Psi _{4}=\frac{y(x-2)}{-2}\). Invoking Eqs. (113), (112) can be recast in terms of Lagrangian polynomial representation as

$$\begin{aligned} 0= & {} \sum _{i,j=1}^{n=4}\Bigg [\int _{\Omega ^{e}}\Bigg \{\mu \Psi _{i}\Psi _{j}Q_{j}-\mu \Psi _{i,2}\Psi _{j,2}\chi _{1j}+\kappa (\Psi _{i}\Psi _{j}Q+\Psi _{i}\Psi _{j,2}E_{j})(CC+EE+DD+FF+MM+NN) \\{} & {} -\kappa (\Psi _{i}\Psi _{j}Q+\Psi _{i}\Psi _{j,2}C_{j}+\Psi _{i}\Psi _{j,1}E_{j}+\Psi _{i}\Psi _{j,2}E_{j})(CC+CD+DD+DF+MM+MN+EC \\{} & {} +EE+FD+FF+NM+NN)+\kappa (\Psi _{i}\Psi _{j}C_{j}+\Psi _{i}\Psi _{j}E_{j})(2QC+2E_{,1}E+2C_{,2}C+2UE-QC \\{} & {} -QE-E_{,2}C-E_{,2}E-CQ-CE_{,1}-EC_{,2}-EE_{,2}+2F_{,1}F+2D_{,2}D+2F_{,2}F-RD-RF-F_{,2}D \\{} & {} -F_{,2}F+DR-DF_{,1}-FD_{,2}-FF_{,2}+2N_{,1}N+2M_{,2}M+2N_{,2}N-M_{,1}M-M_{,1}N-N_{,2}M-N_{,2}N \\{} & {} +MM_{,1}-MN_{,1}-NM_{,2}-MM_{,2})+\Bigg [\frac{E_{11}}{4}(2QCCC+2QCDD+2QCMM+2RDCC \\{} & {} +2RDDD+2RDMM+2M_{,1}MCC+2M_{,1}MDD+2M_{,1}MMM+2CCQC+2CCRD \\{} & {} +2CCM_{,1}M+2DDQC+2DDRD+2DDM_{,1}M+2MMQC+2MMD_{,1}D+2MMM_{,1}M) \\{} & {} +(E_{12}-E_{11})(QC+RD+M_{,1}M)\Bigg ]\Psi _{i}\Psi _{j}C_{j}+\Bigg [\frac{E_{11}}{4} (CC+DD+MM)^{2}+\frac{(E_{12}-E_{11})}{2}(CC \\{} & {} +DD+MM)+\frac{(E_{11}-2E_{12})}{4}\Bigg ]\Psi _{i}\Psi _{j}Q_{j}+\Bigg [\frac{E_{21}}{4 }(2E_{,2}DDD+2E_{,2}DFF+2E_{,2}ENN+2F_{,2}FEE \\{} & {} +2F_{,2}FFF+2F_{,2}FNN+2SNEE+2SNFF+2SNNN+2EEE_{,2}E+2EEF_{,2}F+2EESN \\{} & {} +2FFE_{,2}E+2FFF_{,2}F+2FFSN+2NNE_{,2}E+2NNF_{,2}F+2NNSN)(E_{22}-E_{21})(E_{,2}E \\{} & {} +F_{,2}F+SN)\Bigg ]\Psi _{i}\Psi _{j}E_{j}+\Bigg [\frac{E_{21}}{4}(EE+FF+NN)^{2}+\frac{ (E_{22}-E_{21})}{2}(EE+FF+NN) \\{} & {} +\frac{(E_{21}-2E_{22})}{4}\Bigg ]\Psi _{i}\Psi _{j}Q_{j}\mathbf {+}\Psi _{i,1}\Psi _{j,1}C_{1}Q_{j}\mathbf {+}\Psi _{i,2}\Psi _{j,2}C_{2}U_{j}\mathbf { +}\Psi _{i,1}\Psi _{j,1}\tau U_{j}\mathbf {+}\Psi _{i,2}\Psi _{j,2}\tau Q_{j}\Bigg \}d\Omega \Bigg ] \\{} & {} +\sum _{i=1}^{n=4}\Bigg \{\mu \int _{\partial \Gamma ^{e}}\Psi _{i}\chi _{1,2}Nd\Gamma -C_{1}\int _{\partial \Gamma ^{e}}\Psi _{i}Q_{,1}Nd\Gamma -C_{2}\int _{\partial \Gamma ^{e}}\Psi _{i}U_{,2}Nd\Gamma -\tau \int _{\partial \Gamma ^{e}}\Psi _{i}U_{,1}Nd\Gamma \\{} & {} -\tau \int _{\partial \Gamma ^{e}}\Psi _{i}Q_{,2}Nd\Gamma \Bigg \}, \end{aligned}$$
$$\begin{aligned} 0= & {} \sum _{i,j=1}^{n=4}(\Psi _{i}\Psi _{j}Q+\Psi _{i,1}\Psi _{j,1}\chi _{1j})d\Omega -\sum _{i=1}^{n=4}\left\{ \int _{\partial \Gamma ^{e}}\Psi _{i}\chi _{1,1}Nd\Gamma \right\} ,\text { } \nonumber \\ 0= & {} \sum _{i,j=1}^{n=4}[(\Psi _{i}\Psi _{j}R_{j}+\Psi _{i}\Psi _{j,1}\chi _{2j})d\Omega -\sum _{i=1}^{n=4}\left\{ \int _{\partial \Gamma ^{e}}\Psi _{i}\chi _{2,1}Nd\Gamma \right\} ,\ \nonumber \\ 0= & {} \sum _{i,j=1}^{n=4}[(\Psi _{i}\Psi _{j}T_{j}+\Psi _{i}\Psi _{j,1}\chi _{3j})d\Omega -\sum _{i=1}^{n=4}\left\{ \int _{\partial \Gamma ^{e}}\Psi _{i}\chi _{3,1}Nd\Gamma \right\} ,\text { } \nonumber \\ 0= & {} \sum _{i,j=1}^{n=4}[(\Psi _{i}\Psi _{j}C_{j}-\Psi _{i}\Psi _{j,1}\chi _{1j})d\Omega ,\ 0=\sum _{i,j=1}^{n=4}(\Psi _{i}\Psi _{j}D-\Psi _{i}\Psi _{j,1}\chi _{2j})d\Omega ,\ \nonumber \\ 0= & {} \sum _{i,j=1}^{n=4}(\Psi _{i}\Psi _{j}M_{j}-\Psi _{i}\Psi _{j,1}\chi _{3j})d\Omega , \nonumber \\ 0= & {} \sum _{i,j=1}^{n=4}(\Psi _{i}\Psi _{j}E_{j}-\Psi _{i}\Psi _{j,2}\chi _{1j})d\Omega ,\ 0=\sum _{i,j=1}^{n=4}(\Psi _{i}\Psi _{j}F_{j}-\Psi _{i}\Psi _{j,2}\chi _{2j})d\Omega ,\text { }\nonumber \\ 0= & {} \sum _{i,j=1}^{n=4}(\Psi _{i}\Psi _{j}N_{j}-\Psi _{i}\Psi _{j,2}\chi _{3j})d\Omega , \nonumber \\ 0= & {} \sum _{i,j=1}^{n=4}[(\Psi _{i}\Psi _{j}U_{j}+\Psi _{i}\Psi _{j,2}\chi _{1j})d\Omega -\sum _{i=1}^{n=4}\left\{ \int _{\partial \Gamma ^{e}}\Psi _{i}\chi _{1,2}Nd\Gamma \right\} , \nonumber \\ 0= & {} \sum _{i,j=1}^{n=4}[(\Psi _{i}\Psi _{j}V_{j}+\Psi _{i}\Psi _{j,2}\chi _{2j})d\Omega -\sum _{i=1}^{n=4}\left\{ \int _{\partial \Gamma ^{e}}\Psi _{i}\chi _{2,2}Nd\Gamma \right\} , \nonumber \\ \ 0= & {} \sum _{i,j=1}^{n=4}[(\Psi _{i}\Psi _{j}S_{j}+\Psi _{i}\Psi _{j,2}\chi _{3j})d\Omega -\sum _{i=1}^{n=4}\left\{ \int _{\partial \Gamma ^{e}}\Psi _{i}\chi _{3,2}Nd\Gamma \right\} , \nonumber \\ 0= & {} \sum _{i,j=1}^{n=4}[(\Psi _{i}\Psi _{j}A_{j}-\mu \Psi _{i}\Psi _{j}Q_{j}+\mu \Psi _{i,2}\Psi _{j,2}\chi _{1j}+C_{1}\Psi _{i,1}\Psi _{j,1}Q_{j}+C_{2}\Psi _{i,2}\Psi _{j,2}U_{j})d\Omega \nonumber \\{} & {} -\sum _{i=1}^{n=4}\left\{ \int _{\partial \Gamma ^{e}}\mu \Psi _{i}\chi _{1,2}Nd\Gamma -\int _{\partial \Gamma ^{e}}C_{1}\Psi _{i}Q_{,1}Nd\Gamma -\int _{\partial \Gamma ^{e}}C_{2}\Psi _{i}U_{,2}Nd\Gamma \right\} , \nonumber \\ 0= & {} \sum _{i,j=1}^{n=4}[(\Psi _{i}\Psi _{j}B_{j}-\mu \Psi _{i}\Psi _{j}R_{j}+\mu \Psi _{i,2}\Psi _{j,2}\chi _{2j}+C_{1}\Psi _{i,1}\Psi _{j,1}R_{j}+C_{2}\Psi _{i,2}\Psi _{j,2}V_{j})d\Omega \nonumber \\{} & {} -\sum _{i=1}^{n=4}\left\{ \int _{\partial \Gamma ^{e}}\mu w_{17}\chi _{2,2}Nd\Gamma -\int _{\partial \Gamma ^{e}}C_{1}w_{17}R_{,1}Nd\Gamma -\int _{\partial \Gamma ^{e}}C_{2}\Psi _{i}V_{,2}Nd\Gamma \right\} , \end{aligned}$$
(115)

Now, for the local stiffness matrices and forcing vectors for each elements, we find

$$\begin{aligned} \left[ \begin{array}{cccc} K_{11}^{11} &{} K_{12}^{11} &{} K_{13}^{11} &{} K_{14}^{11} \\ K_{21}^{11} &{} K_{22}^{11} &{} K_{23}^{11} &{} K_{24}^{11} \\ K_{31}^{11} &{} K_{32}^{11} &{} K_{33}^{11} &{} K_{34}^{11} \\ K_{41}^{11} &{} K_{42}^{11} &{} K_{43}^{11} &{} K_{44}^{11} \end{array} \right] _{Local}\left[ \begin{array}{c} \chi _{1}^{1} \\ \chi _{1}^{2} \\ \chi _{1}^{3} \\ \chi _{1}^{4} \end{array} \right] _{Local}=\left[ \begin{array}{c} F_{1}^{1} \\ F_{2}^{1} \\ F_{3}^{1} \\ F_{4}^{1} \end{array} \right] _{Local}, \end{aligned}$$
(116)

where

$$\begin{aligned} \left[ K_{ij}^{11}\right] =\int _{\Omega }(-\mu \Psi _{i,2}\Psi _{j,2})d\Omega , \end{aligned}$$
(117)

and

$$\begin{aligned} \{F_{i}^{1}\}{} & {} =\mu \int _{\partial \Gamma ^{e}}\Psi _{i}\chi _{1,2}Nd\Gamma -C_{1}\int _{\partial \Gamma ^{e}}\Psi _{i}Q_{,1}Nd\Gamma -C_{2}\int _{\partial \Gamma ^{e}}\Psi _{i}U_{,2}Nd\Gamma -\tau \nonumber \\{} & {} \quad \int _{\partial \Gamma ^{e}}\Psi _{i}U_{,1}Nd\Gamma -\tau \int _{\partial \Gamma ^{e}}\Psi _{i}Q_{,2}Nd\Gamma \end{aligned}$$
(118)

Thus, the unknown potentials (i.e., \(Q,\ R,C,D,E,F,T,S,U,V,M,N,\ A\) and B) can be expressed as

$$\begin{aligned} Q_{i}=\{\chi _{1}^{i}\}_{,11},\text { }R_{i}=\{\chi _{2}^{i}\}_{,11}\text { etc...,} \end{aligned}$$
(119)

and similarly for the rest of unknowns.

In the simulation, we employed the following convergence criteria

$$\begin{aligned} \left| A_{n+1}-A_{n}\right| =e_{1}\le \varepsilon ,\text { } \left| B_{n+1}-B_{n}\right| =e_{2}\le \varepsilon \text {, where } \varepsilon =\text {maximum error}=10^{-10}, \end{aligned}$$
(120)

which demonstrates fast convergence within 12 iterations using FEniCS nonlinear solver (see, Table. 1).

Table 1 Maximum numerical errors with respect to the number of iterations
Full size table

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kim, C.I.L., Islam, S. & Yang, S. A three-dimensional continuum model for the mechanics of an elastic medium reinforced with fibrous materials in finite elastostatics. Continuum Mech. Thermodyn. 36, 119–153 (2024). https://doi.org/10.1007/s00161-023-01266-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00161-023-01266-0

Keywords

Search

Navigation