1 Introduction

Internal ballistics is the part of mechanics that study the processes determining the movement of the projectile in the gun tube under the influence of the conversion of the gas-powder mixture (GPM) into gaseous products of gunpowder combustion (GCP) and, in the case of rocket engines, determining the pressure development as a function of time in the combustion chamber as well as determining the thrust force reaction of the rocket [1,2,3,4,5,6,7,8,9,10].

In classic gun tube weapons, propellant systems are treated as heat machines, in which the kinetic energy of the propelled projectile is obtained by burning the propellant charge through the combustion products, which are powder gases. The internal ballistics of classic gun tube weapons is divided into phases:

  • pyrostatic,

  • pyrodynamic- active,

  • pyrodynamic- adiabatic expansion of muzzle gases.

The main purpose of pyrostatics is to determine the burning properties of gunpowder as a propellant. To determine these properties, a closed vessel (chamber) is used, which allows you to measure the pressure of GCP in a constant volume. Thanks to the obtained measurements, the thermodynamic properties of the GCP, such as the covolume and total impulse, and the ballistic properties of the gun powder, such as the force of the powder and the proper burning rate, are determined. These results are then processed and used in ballistic calculations. The research methods of pyrostatics allow to study the increase of pressure in the closed cartridge chambers of the barrels from the moment of ignition of the propellant charge to the moment of the beginning of the projectile’s movement.

The role of pyrodynamics is to study the processes of energy changes and, consequently, the pressure in the space between the bottom of the chamber and the bottom of the projectile in the gun tube, which affect the motion of the projectile. The basic result of these (pyrodynamic) tests are graphs of:

  • pressure distribution of the gas-powder mixture in the space behind the bottom of the projectile as a function of time,

  • projectile velocity as a function of time,

  • path of the bottom of the projectile as a function of time,

  • pressure as a function of the path of the bottom of the projectile,

  • velocity as a function of the path of the bottom of the projectile.

The graphs obtained in this way are called ballistic curves, and the algorithm of calculations aimed at obtaining such graphs is referred to as the solution to the main problem of internal ballistics. The design of the propellant system determines to a large extent the mathematical description and solution method. To solve the main problem of internal ballistics, various methods are used, e.g. analytical, numerical, tables. Most often, theoretical methods are finally verified by experimental research and corrected if necessary.

The pyrodynamic period finish when the projectile leaves the gun tube, but the powder gases still act on the projectile. The impact of the GCP after leaving the barrel through the bottom of the projectile increases its velocity and the range of the weapon’s recoil. Transitional ballistics studies support the design of muzzle elements (reducing or increasing recoil) and allow you to limit the light and acoustic effects of the shot (silencers). Over the years, the approach to solving the main problem of internal ballistics has evolved significantly [11,12,13,14]. Nowadays, most design processes are computer-aided, but in the case of internal ballistics they are not generally common available. The analytical solution of the system of nonlinear differential equations describing the phases of the phenomenon of a shot in a gun barrel does not exist. Therefore, in order to obtain more accurate solutions to the system of equations, it is worth using numerical methods. On the basis of the adopted physical model, a mathematical model is created, which should take into account the specific features of a given problem. Firstly, the constitutive differential equations of internal ballistics were identified [15,16,17].

2 Constitutive differential equations of internal ballistics

As a fundamental for burning phenomenon of the gun powder the analysis has been started from equation of the rate of increase in the thickness of the burnt layer of gunpowder (2.1) and then, in the appropriate order, have been described the values resulting from the previous ones.

Constitutive differential equation of the rate of increase in the thickness of the burnt layer of gunpowder

The burning rate of powder grains is determined by a linear relationship directly proportional to the static pressure between the bottom of the chamber and the bottom of the projectile, with a constant proportionality factor equal to the burn rate factor \(u_{1}\):

$$\begin{aligned} \frac{de_{s}\left( t \right) }{dt}=u_{1}p_{s}\left( x,t \right) \left[ \frac{m}{s} \right] \end{aligned}$$
(2.1)

where:

\(u_{1}\left[ \frac{m}{sPa} \right] \)—burn rate factor,

\(p_{s}\left( x,t \right) \)—static pressure depends of x from the range \(0\le x\le L\left( t \right) \) at the given t,

\(e_{s}\)—the thickness of the burnt layer of powder grains depends on time (Fig. 1).

Knowing that the static pressure of GCP in the space behind the bottom of the projectile at a given time t depends on the position x between the bottom of the chamber and the bottom of the projectile (Fig. 1), the average static pressure in the space behind the projectile should be used:

$$\begin{aligned} {<p_{s}\left( x,t \right) >}_{L\left( t \right) }=p\left( t \right) -\frac{\rho _{m}\left( t \right) }{2}\left( v\left( t \right) \right) ^{2} \end{aligned}$$
(2.2)

where:

\(\rho _{m}\)—bulk density of GPM,

\(L\left( t \right) =l_{0}+l\left( t \right) =\frac{W_{0}}{s}+l\left( t \right) \),

\(l_{0} \)—length of the cartridge chamber,

\(l\left( t \right) \)—change the path of the bottom of the bullet in the barrel,

\(W_{0}\)—volume of the cartridge chamber.

s—cross-sectional area,

v(t)—velocity.

Fig. 1
figure 1

Drawings of the: a ballistic propellant system during the shot (m—weight of the projectile), b gun powder grain structure [18]

Full size image

Finally, the constitutive equation for the rate of increase in the thickness of the burned powder layer will be written in the form presented below:

$$\begin{aligned} \frac{de_{s}\left( t \right) }{dt}=\dot{e}_{s}(t)=u_{1}{<p_{s}\left( x,t \right) >}_{L\left( t \right) }\left[ \frac{m}{s}\right] \end{aligned}$$
(2.3)

where:

\(e_{s}\left( t \right) \left[ m \right] \)—the thickness of the burnt powder grain layer depends on time (Fig. 1),

\(\dot{e}_{s}(t)\) [m/s]— rate of increase in the thickness of the burned powder layer on time.

Constitutive differential equation of the rate of volume creation after burning powder charge grains

The equation for the rate of volume creation after the burnt particles of the powder charge is described by the relationship:

$$\begin{aligned} \frac{d\mathrm {\Lambda }_{\textrm{s}}\left( t \right) }{dt}=\dot{\Lambda }_{s}(t)=S(e)\frac{de_{s}\left( t \right) }{dt}\left[ \frac{m^{3}}{s}\right] \end{aligned}$$
(2.4)

where:

\(S\left( e \right) \left[ m^{2} \right] \)—function of the combustion surface of powder grains (Fig. 1).

Constitutive differential equation of the relative mass creation rate of gaseous products of gunpowder combustion

The relative rate of formation of GCP is described by the relationship:

$$\begin{aligned} \frac{d\psi \left( t \right) }{dt}=\dot{\psi }\left( t \right) =\frac{S_{1}}{\mathrm {\Lambda }_{\textrm{1}}}\delta \dot{e}_{s}\left( t \right) \, \left[ \frac{1}{s} \right] \end{aligned}$$
(2.5)

where accordingly \(S_{1}\left[ m^{2} \right] \) and \(\mathrm {\Lambda }_{\textrm{1}}\, \left[ m^{3} \right] \)—the surface area and the initial volume of the powder grain, \(\delta \)—bulk powder mass density. Using the function of the relative combustion area of the powder grains:

$$\begin{aligned} \sigma =\frac{S\left( e \right) }{S_{1}} \end{aligned}$$
(2.6)

the rate of formation of gaseous combustion products (GCP) will take the form:

$$\begin{aligned} \frac{d\psi \left( t \right) }{dt}=\dot{\psi }(t)=\frac{S\left( e \right) }{S_{1}}\frac{de_{s}\left( t \right) }{dt}\left[ \frac{1}{s}\right] \end{aligned}$$
(2.7)

Taking into account that the volume of powder grains before combustion \(\mathrm {\Lambda }_{\textrm{1}}\) is equal:

$$\begin{aligned} \mathrm {\Lambda }_{\textrm{1}}=\frac{\omega }{\delta }\, \left[ m^{3} \right] \end{aligned}$$
(2.8)

where:

\(\omega \)—weight of the powder charge,

\(\delta \)—bulk powder mass density.

The rate of formation of gaseous combustion products (GCP) will eventually take the form:

$$\begin{aligned} \frac{d\psi \left( t \right) }{dt}=\dot{\psi }\left( t \right) =\frac{\delta }{\omega }S\left( e \right) \frac{de_{s}\left( t \right) }{dt}=\frac{\delta }{\omega }\dot{\Lambda }_{s}\left( t \right) \left[ \frac{1}{s} \right] \end{aligned}$$
(2.9)

Constitutive equation for the rate of formation of the relative mass of gaseous combustion products of the igniter

Using experimental information such as igniter weight \(\omega _{z}\left[ kg \right] \) and time \(t_{z_{k}}\left[ s \right] \) of its decomposition into gaseous combustion products, it is possible to determine the average mass flow of gaseous combustion products of the igniter:

$$\begin{aligned} G_{Z}=\frac{\omega _{z}}{t_{z_{k}}}=const\, \left[ \frac{kg}{s} \right] \end{aligned}$$
(2.10)

Knowing that the relative mass of the igniter burnt \(\Psi _{z}\) is determined by the quotient of the current mass resource of the burnt igniter \(\omega _{sz}(t)\) by the mass of the igniter charge \(\omega _{z}\):

$$\begin{aligned} \psi _{Z}\left( t \right) =\frac{\omega _{s_{z}}\left( t \right) }{\omega _{z}} \end{aligned}$$
(2.11)

and also, that the current mass resource of the burnt igniter is determined by the relationship:

$$\begin{aligned} \omega _{s_{z}}\left( t \right) =G_{Z}\cdot t \end{aligned}$$
(2.12)

it is possible to represent the relative mass of the igniter burnt as:

$$\begin{aligned} \psi _{Z}\left( t \right) =\frac{G_{Z}t}{\omega _{z}} \end{aligned}$$
(2.13)

which leads to the equation for the rate of creation of the relative mass of gaseous combustion products of the igniter:

  • for a moment of time \(t\le t_{z}\)

    $$\begin{aligned} \frac{d\psi _{z}\left( t \right) }{dt}=\dot{\psi }_{z}\left( t \right) =\frac{G_{z}}{\omega _{z}}\, \left[ \frac{1}{s} \right] \end{aligned}$$
    (2.14)

  • for a moment of time \(t>t_{z_{k}}\)

$$\begin{aligned} \dot{\psi _{z}}=0 \end{aligned}$$
(2.15)

From the Eqs. (2.12–2.14) result that the average mass flow of gaseous combustion products of the igniter is linear in time which corresponds to the design assumptions of the igniters [18].

Balance differential equation of mass production rate of gaseous combustion products

The balance equation for the mass production rate of gaseous combustion products is the sum of the constitutive equations for the rate of creation of relative masses of gaseous combustion products of the propellant and igniter:

$$\begin{aligned} \frac{dN\left( t \right) }{dt}=\dot{N}\left( t \right) =\dot{\psi _{z}}{\left( t \right) \omega }_{z}+\dot{\psi }\left( t \right) \omega \, \left[ \frac{kg}{s} \right] \end{aligned}$$
(2.16)

Depending on the instant of time t, particular terms of the equation are used. The first part concerns the combustion of the igniter, the second—the combustion of powder charge grains.

Balance differential equation of the rate of increase of the velocity of the projectile in the gun tube

Using the projectile momentum balance equation, it is possible to determine the acceleration of the projectile in the gun tube. Using Newton’s second law, it can be written that the change in velocity of the fictitious mass of the projectile is equal to the impulse of the force acting on the bottom of the projectile:

$$\begin{aligned} \varphi mdv\left( t \right) =sp_{s}\left( t \right) dt \end{aligned}$$
(2.17)

where:

\(\varphi \)—projectile mass fictitiousness coefficient,

m—mass of the gas-powder mixture,

\(v\left( t \right) \)—velocity of the projectile,

\(p_{s}\left( t \right) \)—static pressure,

s—cross-sectional area of the barrel.

Transforming the above relationship, and taking into account the fact that the force acting on the bottom of the projectile is the product of the static pressure at the bottom \(p_{s}\left( L,t \right) \) and the cross section of the gun tube s, the equation of the rate of increase of the velocity of the projectile in the gun tube was obtained:

$$\begin{aligned} \frac{dv\left( t \right) }{dt}=\dot{v}\left( t \right) =\frac{Sp_{s}\left( L,t \right) }{\varphi m} \end{aligned}$$
(2.18)

Balance differential equation of the rate of increase of the path of the bottom of the bullet in the barrel

According to the classical principles of mechanics, the way-increase rate equation is given by the relation of the projectile way derivative l by time t:

$$\begin{aligned} \frac{dl\left( t \right) }{dt}=\dot{l}\left( t \right) =v \end{aligned}$$
(2.19)

Balance differential equation of the rate of changes in the temperature of gaseous combustion products

Using the ballistic total energy balance equation shown below:

$$\begin{aligned} \frac{\rho _{m}}{k-1}\frac{d\varepsilon _{I_{p}}}{dt}-\frac{p_{s}\left( L,t \right) }{\rho _{m}\left( t \right) }\frac{d\rho _{m}\left( t \right) }{dt}-\rho _{m}\left( t \right) \left( q_{\vartheta }\frac{d\psi \left( t \right) }{dt}+q_{z}\frac{d\psi _{z}\left( t \right) }{dt} \right) =0 \end{aligned}$$
(2.20)

and whereas, according to the definition, the current strength of gaseous combustion products is determined by the relationship:

$$\begin{aligned} \varepsilon _{I_{p}}=RT \end{aligned}$$
(2.21)

where:

R—gas constant,

T—temperature.

\(q_{\vartheta }\)—explosion heat of the propellant,

\(q_{z}\)—explosion heat of the igniter.

The equation of the rate of changes in the temperature of gaseous combustion products after transformations will take the form:

$$\begin{aligned} \frac{dT}{dt}=\dot{T}=\frac{k-1}{R}\left( \frac{p_{s}\left( L,t \right) }{{{(\rho }_{m}\left( t \right) )}^{2}}\frac{d\rho _{m}\left( t \right) }{dt}+q_{\vartheta }\frac{d\psi \left( t \right) }{dt}+q_{z}\frac{d\psi _{z}\left( t \right) }{dt} \right) \end{aligned}$$
(2.22)

Constitutive equation for the volumetric mass density of the gas-powder mixture

Taking into account the definition of the volumetric density of the mass stock and referring it to the considered issue, the equation of the volumetric mass stock density of the gas-powder mixture was obtained:

$$\begin{aligned} \rho _{m}\left( t \right) =\frac{\omega ^{*}}{W\left( t \right) }=\frac{\omega ^{*}}{sL\left( t \right) } \end{aligned}$$
(2.23)

where: \(\omega ^{*}=\omega +\omega _{z}\) and \(L\left( t \right) =l_{o}+l\).

Constitutive free volume equation

The free volume between the bottom of the chamber and the bottom of the projectile is given by the following equation:

$$\begin{aligned} W_{s}\left( t \right) =W_{o}+sl\left( t \right) -\left( \frac{\omega }{\mathrm {\delta }}-\frac{\omega _{s}\left( t \right) }{\mathrm {\delta }} \right) -\alpha \left( \omega _{s}\left( t \right) +\omega _{s_{z}}\left( t \right) \right) \end{aligned}$$
(2.24)

where:

\(\alpha \)—covolume of the GCP [m\(^{3}\)/kg],

By transforming the above equation, it can be presented in the form:

$$\begin{aligned} W_{s}\left( t \right) =W_{o}+sl\left( t \right) -\frac{\omega }{\mathrm {\delta }}\left( 1-\frac{\omega _{s}\left( t \right) }{\omega } \right) -\alpha \omega \frac{\omega _{s}\left( t \right) }{\omega }-\alpha \omega _{z}\frac{\omega _{sz}\left( t \right) }{\omega _{z}} \end{aligned}$$
(2.25)

By definition, the relative mass of the burnt gunpowder is equal to:

$$\begin{aligned} \psi =\frac{\omega _{s}\left( t \right) }{\omega } \end{aligned}$$
(2.26)

and the relative mass of the igniter is determined by the relationship:

$$\begin{aligned} \psi _{z}=\frac{\omega _{sz}\left( t \right) }{\omega _{z}} \end{aligned}$$
(2.27)

the constitutive free volume equation will eventually take the form:

$$\begin{aligned} W_{s}\left( t \right) =W_{o}+sl\left( t \right) -\frac{\omega }{\mathrm {\delta }}\left( 1-\psi \left( t \right) \right) -\alpha \omega \psi \left( t \right) -\alpha \omega _{z}\psi _{z}\left( t \right) \end{aligned}$$
(2.28)

Constitutive equation of the total pressure of gaseous combustion products (GCP)

Based on the van der Waals real gas equation of state, it is possible to determine changes in the total pressure of gaseous combustion products. Taking into account that high pressures occur in barreled weapons, the effect of cohesive pressure has been omitted in this equation. Total pressure \(p\left( t \right) \) is determined for a solid system in which changes in the gas parameters of combustion products occur in thermodynamic equilibrium, and thus enforcing the non-gradient nature of intensive quantities, such as the determined pressure. Therefore, the real gas van der Waals equation can be expressed as an expression:

$$\begin{aligned} p\left( t \right) =R\frac{N\left( t \right) T\left( t \right) }{W_{s}\left( t \right) } \end{aligned}$$
(2.29)

Constitutive equation for the volume mass density of gaseous combustion products (GCP)

The volumetric mass density of gaseous combustion products is described by the following equation:

$$\begin{aligned} \rho \left( t \right) =\frac{\omega _{s}^{*}}{W_{s}\left( t \right) } \end{aligned}$$
(2.30)

where: \(\, \omega _{s}^{*}=\omega _{s}\left( t \right) +\omega _{s_{z}}\left( t \right) \).

Balance equation of the dynamic pressure of the gas-powder mixture at the bottom of the projectile

The equation of the dynamic pressure of the gas-powder mixture at the bottom of the projectile is determined according to the relation:

$$\begin{aligned} p_{d}=p(t)=\frac{\rho _{m}\left( v\left( t \right) \right) ^{2}}{2} \end{aligned}$$
(2.31)

Balance equation of static pressure at the bottom of the projectile

The static pressure of the gas-powder mixture at the bottom of the projectile is determined by the relationship:

$$\begin{aligned} p_{s}\left( L,t \right) =p\left( t \right) -\frac{\rho _{m}\left( v\left( t \right) \right) ^{2}}{2} \end{aligned}$$
(2.32)

Balance equation of the average static pressure of gaseous combustion products in the space between the bottom of the chamber and the bottom of the projectile

The equation of the average static pressure of gaseous combustion products is defined as:

$$\begin{aligned} {<p_{s}\left( x,t \right) >}_{L\left( t \right) }=p\left( t \right) -\frac{\rho _{m}\left( t \right) }{2}\left( v\left( t \right) \right) ^{2} \end{aligned}$$
(2.33)

3 Physical model

The solution to the main problem of the internal ballistics of barrel weapons for the adopted physical model consists in determining the following parameters:

  • total pressure,

  • dynamic pressure,

  • static pressure,

  • average static pressure,

  • temperature of gaseous products of gunpowder combustion (GCP),

  • velocity of the projectile inside the gun tube,

  • displacement of the projectile inside the gun tube.

The shot phenomenon for the adopted physical model has been divided into five phases, each of which is characterized by its own assumptions and is different from the others. The individual phases are listed below in the order in which they occur.

3.1 Preliminary phase

The preliminary phase is based on pyrostatics. It starts from the time then the firing pin hits the primer until the gaseous combustion products of the igniter obtain pressure equal to the ignition pressure of the powder charge \(p_{Z}\). The stream of gaseous combustion products of the igniter is constant. It flows through the firing channels of the primer reaching the cartridge chamber with a constant free volume determined in accordance with the relationship:

$$\begin{aligned} W_{s}=W_{o}-\frac{\omega }{\delta } \end{aligned}$$
(3.1)

where: \(W_{s}\)—volume of free space behind the bottom of the projectile, \(W_{0}\)—volume of the cartridge chamber, \(\omega \)—gunpowder mass, \(\delta \)—gunpowder density.

The igniter operation time \(t_{z_{k}}\) is determined by the relation:

$$\begin{aligned} t_{z_{k}}=\frac{\omega _{z}}{G_{z}} \end{aligned}$$
(3.2)

Due to the above relations, the preliminary phase lasts in the pressure range:

$$\begin{aligned} p_{a}\le p\left( t \right) \le p_{z} \end{aligned}$$
(3.3)

and time interval:

$$\begin{aligned} 0\le t\le t_{z} \end{aligned}$$
(3.4)

where: \(p_{a}\)—ambient pressure, \(p_{z}\)—ignition pressure of the propellant charge, \(t_{z}\)—time of ignition of the propellant charge.

Preliminary phase values: \(t=t_{z}\) oraz \(p=p_{z}\) define the initial values of the initial phase \(p=p_{z},\, \, v=0,\, \, l=0,\, \, \psi =0,\, \, \sigma =1,\, \, T=T\left( t_{z} \right) \).

Where: v—velocity of the projectile, l—displacement of the projectile, \(\sigma \)—the relative area of the burnt gunpowder, \(\, \psi \)—relative part of burnt gunpowder, T—temperature of the GCP.

3.2 Initial phase

Like the preliminary phase, the initial phase is also based on pyrostatics. the beginning of the phase occurs for \(t_{z}\) which determines the achievement of the ignition pressure by the gaseous combustion products of the igniter \(p_{z}\). Based on the geometric law of combustion, it was assumed that the ignition of the propellant charge is instantaneous over the entire surface of the powder grains (see Fig. 1—S(e)). The projectile does not change position due to the frictional resistance posed by the surface of the transition cone of the cartridge chamber.

As the pressure of gaseous products of gunpowder combustion (GCP) increases, the jacket of the projectile enters the gun tube rifling. After reaching the forcing pressure \(p=p_{0}\), whose value is necessary to overcome the resistance of pressing the projectiles jacket into the thread of the gun tube, the initial phase is completed. The pressure range in this phase is:

$$\begin{aligned} p_{z}\le p\le p_{0} \end{aligned}$$
(3.5)

and an equivalent time interval:

$$\begin{aligned} t_{z}\le t\le t_{0} \end{aligned}$$
(3.6)

The final values of the initial phase such \(p=p_{0}\) and \(t=t_{0}\) etermine the initial values of the next phase, in this case the pyrodynamic phase: \(p=p_{0},\, \, v=0,\, \, l=0,\, e_{s}=e_{s}\left( t_{0} \right) ,\, \psi =\, \psi \left( t_{0} \right) ,\, \, \sigma =\sigma \left( \psi _{0} \right) ,\, \, T=T\left( t_{0} \right) \),

Where: \(e_{s}\)—the thickness of the burnt layer of gunpowder grain.

The ignition pressure generated by the gaseous combustion products of the igniter (\(p_{z})\) is taken in the range of \({2\le p}_{z}\le 10\) MPa, while the value of the forcing pressure is in the range \({20\le p}_{0}\le 50\) MPa [18]. In the initial phase, no external work is performed by gaseous products of gunpowder combustion (GCP), while the combustion of the powder charge takes place in the structural volume of the cartridge chamber \(W_{0}\).

3.3 Pyrodynamic phase

In the primary pyrodynamic phase, projectile propulsion is possible due to the mechanical work done by gaseous combustion products. The force acting on the bottom of the projectile, related to the pressure of gaseous products of gunpowder combustion (GCP), causes the projectile to move with accelerated motion, which increases its velocity and displacement. The temperature of the GCP begins to decrease from the value of the isochoric combustion temperature\(T_{\vartheta }\), which makes its current value smaller \(\left( T<T_{\vartheta } \right) \). As a result of the rapid production of the mass of GCP and the energy obtained from the combustion of the propellant charge, the pressure p in the area behind the bottom of the projectile in the gun tube very quickly reaches the maximum value \(p_{m}\), then it decreases less dynamically. This is due to the fact that in the first period the rate of production of GCP and the related rate of heat production have a decisive influence on the rapid increase of pressure behind the bottom of the projectile.

In the second phase, the situation changes, thanks to the increase in the velocity of the projectile, the production of the gaseous products of gunpowder combustion (GCP) and heat energy has a smaller impact on the pressure than the increase in the volume behind the bottom of the projectile and its kinetic energy, which results in reaching a maximum value of the pressure. The end of the pyrodynamic phase occurs in time \(t=t_{k}\) which corresponds to the moment of complete combustion of the powder charge. This phase can therefore be defined by the thickness range of the burnt grain:

$$\begin{aligned} e_{s}\left( t_{0} \right) \le e_{s}\le e_{1} \end{aligned}$$
(3.7)

and the time period associated with it:

$$\begin{aligned} t_{0}\le t\le t_{k} \end{aligned}$$
(3.8)

Final values of pyrodynamic phase such \(e_{s}=e_{1}\) and \(t=t_{k}\) lead to the initial conditions of the adiabatic phase: \(p=p_{k},\, \, v=v_{k},\, \, l=l_{k},\, \, T=T\left( t_{k} \right) \),

Were: \(e_{1}\)—gunpowder grain thickness, the index k denotes the moment of end of burning of the propellant charge.

3.4 Adiabatic phase

The adiabatic phase, also called the expansion phase of the GCP, starts from a moment of time \(t=t_{k}\) defined in the previous phase to the time \(t=t_{w}\) (the index w denotes the moment when the bottom of the projectile has reached the muzzle of the gun tube). According to the definition of the solid system, the mass of GCP in the space behind bottom of the projectile is constant and corresponds to the mass \(\omega \) of the burnt powder charge. The thermal energy of the GCP causes the movement of the projectile. The lack of heat energy production and the work of the GCP on the propulsion of the projectile causes a further drop in the pressure of the GCP from \(p_{k}\) to \(p_{w}\) value as well as temperature from \(T_{k}\) to \(T_{w}\) value. At the same time the velocity of the projectile increases from \(v_{k}\) to v and displacement from \(l_{k}\) to \(l_{w}\). The adiabatic phase is finished for time \(t=t_{w}\), pressure of GCP is about tens of MPa and GCP temperature reaches limits 1000–2000 K [18]. The final values of the adiabatic phase are the initial values of the post-muzzle phase.

3.5 Post-muzzle phase

The post-muzzle phase begins with the time \(t=t_{w}\), when the bottom of the projectile has reached the muzzle of the gun tube. The mass of GCP at a temperature \(T_{w}\) and pressure \(p_{w}\) as a large amount of thermal energy. After the bottom of the projectile leaves the gun tube (\(t>t_{w})\) GCP flows to the environment through the end of the gun tube reducing the temperature. The pressure drops approaching the value of the ambient pressure at this time. With the outflow of gases from the gun tube, a shock wave appears, as well as sound (noise) and light effects (flash), as well as a muzzle flame. In the early part of the post-muzzle phase, i.e. when the projectile is still near the muzzle of the gun, the GCP affect it, slightly increasing its velocity (maximum 1–2% of its muzzle velocity [18]). The impact of post-muzzle combustion products on the gun seems to be more important for the recoil of the weapon and the drive of the mechanisms.

The ballistic phases presented above are described by differential equations and analytical equations. Below are sets of equations for individual phases, which together build a mathematical model for the problem of solving the main problem of internal ballistics.

4 Mathematical model

4.1 Preliminary phase

Preliminary phase that lasts in the pressure region:

$$\begin{aligned} p_{a}\le p\left( t \right) \le p_{z} \end{aligned}$$

and the corresponding time interval:

$$\begin{aligned} 0\le t\le t_{zap} \end{aligned}$$

is described by the following set of equations:

$$\begin{aligned}{} & {} \frac{de_{s}\left( t \right) }{dt}=\dot{e}_{s}\left( t \right) =0 \end{aligned}$$
(4.1)
$$\begin{aligned}{} & {} \frac{d\mathrm {\Lambda }_{\textrm{s}}\left( t \right) }{dt}=\dot{\Lambda }_{s}\left( t \right) =0 \end{aligned}$$
(4.2)
$$\begin{aligned}{} & {} \frac{d\psi \left( t \right) }{dt}=\dot{\psi }\left( t \right) =0\, \end{aligned}$$
(4.3)
$$\begin{aligned}{} & {} \frac{d\psi _{z}\left( t \right) }{dt}=\dot{\psi }_{z}\left( t \right) =\frac{G_{z}}{\omega _{z}}\, \end{aligned}$$
(4.4)
$$\begin{aligned}{} & {} \frac{dN\left( t \right) }{dt}=\dot{N}\left( t \right) =\dot{\psi _{z}}{\left( t \right) \omega }_{z} \end{aligned}$$
(4.5)
$$\begin{aligned}{} & {} \frac{dv\left( t \right) }{dt}=\dot{v}\left( t \right) =0\, \, \end{aligned}$$
(4.6)
$$\begin{aligned}{} & {} \frac{dl\left( t \right) }{dt}=\dot{l}\left( t \right) =0\, \, \, \, \, \, \end{aligned}$$
(4.7)
$$\begin{aligned}{} & {} \frac{dT}{dt}=\dot{T}=\frac{k-1}{R}\left( \frac{p_{s}\left( L,t \right) }{{{(\rho }_{m}\left( t \right) )}^{2}}\frac{d\rho _{m}\left( t \right) }{dt}+q_{\vartheta }\frac{d\psi \left( t \right) }{dt}+q_{z}\frac{d\psi _{z}\left( t \right) }{dt} \right) \end{aligned}$$
(4.8)
$$\begin{aligned}{} & {} \rho _{m}\left( t \right) =0 \end{aligned}$$
(4.9)
$$\begin{aligned}{} & {} W_{s}\left( t \right) =W_{o}-\alpha \omega _{z}\psi _{z}\left( t \right) \end{aligned}$$
(4.10)
$$\begin{aligned}{} & {} p\left( t \right) =R\frac{N\left( t \right) T\left( t \right) }{W_{s}\left( t \right) } \end{aligned}$$
(4.11)
$$\begin{aligned}{} & {} \rho \left( t \right) =\frac{\omega _{s}^{*}}{W_{s}\left( t \right) } \end{aligned}$$
(4.12)
$$\begin{aligned}{} & {} p_{d}=\frac{\rho _{m}\left( v\left( t \right) \right) ^{2}}{2} \end{aligned}$$
(4.13)
$$\begin{aligned}{} & {} p_{s}\left( L,t \right) =p\left( t \right) -\frac{\rho _{m}\left( v\left( t \right) \right) ^{2}}{2} \end{aligned}$$
(4.14)
$$\begin{aligned}{} & {} {<p_{s}\left( x,t \right) >}_{L\left( t \right) }=p\left( t \right) -\frac{\rho _{m}\left( t \right) }{2}\left( v\left( t \right) \right) ^{2} \end{aligned}$$
(4.15)

where: \(\mathrm {\Lambda }_{\textrm{s}}\)—initial powder charge volume, R—gas constant of GCP, \(\omega ^{*}=\omega +\omega _{z}\), \(L\left( t \right) =l_{o}+l\)

4.2 Initial phase

Initial phase that lasts in the pressure region:

$$\begin{aligned} p_{z}\le p\le p_{0} \end{aligned}$$

and the corresponding time interval:

$$\begin{aligned} t_{z}\le t\le t_{0} \end{aligned}$$

is described by the following set of equations:

$$\begin{aligned}{} & {} \frac{de_{s}\left( t \right) }{dt}=\dot{e}_{s}\left( t \right) =u_{1}p\left( t \right) \end{aligned}$$
(4.16)
$$\begin{aligned}{} & {} \frac{d\mathrm {\Lambda }_{\textrm{s}}\left( t \right) }{dt}=\dot{\Lambda }_{s}(t)=S(e)\frac{de_{s}\left( t \right) }{dt}\left[ \frac{m^{3}}{s}\right] \end{aligned}$$
(4.17)
$$\begin{aligned}{} & {} \frac{d\psi \left( t \right) }{dt}=\dot{\psi }\left( t \right) =\frac{\delta }{\omega }S\left( e \right) \frac{de_{s}\left( t \right) }{dt}=\frac{\delta }{\omega }\dot{\Lambda }_{s}\left( t \right) \end{aligned}$$
(4.18)
$$\begin{aligned}{} & {} \frac{d\psi _{z}\left( t \right) }{dt}=\dot{\psi }_{z}\left( t \right) =\frac{G_{z}}{\omega _{z}}\, \left[ \frac{1}{s} \right] \end{aligned}$$
(4.19)
$$\begin{aligned}{} & {} \frac{dN\left( t \right) }{dt}=\dot{N}\left( t \right) =\dot{\psi _{z}}{\left( t \right) \omega }_{z}+\dot{\psi }\left( t \right) \omega \, \end{aligned}$$
(4.20)
$$\begin{aligned}{} & {} \frac{dv\left( t \right) }{dt}=\dot{v}\left( t \right) =0 \end{aligned}$$
(4.21)
$$\begin{aligned}{} & {} \frac{dl\left( t \right) }{dt}=\dot{l}\left( t \right) =0 \end{aligned}$$
(4.22)
$$\begin{aligned}{} & {} \frac{dT}{dt}=\dot{T}=\frac{k-1}{R}\left( \frac{p_{s}\left( L,t \right) }{{{(\rho }_{m}\left( t \right) )}^{2}}\frac{d\rho _{m}\left( t \right) }{dt}+q_{\vartheta }\frac{d\psi \left( t \right) }{dt}+q_{z}\frac{d\psi _{z}\left( t \right) }{dt} \right) \end{aligned}$$
(4.23)
$$\begin{aligned}{} & {} \rho _{m}\left( t \right) =0 \end{aligned}$$
(4.24)
$$\begin{aligned}{} & {} W_{s}\left( t \right) =W_{o}-\frac{\omega }{\mathrm {\delta }}\left( 1-\psi \left( t \right) \right) -\alpha \omega \psi \left( t \right) -\alpha \omega _{z}\psi _{z}\left( t \right) \end{aligned}$$
(4.25)
$$\begin{aligned}{} & {} p\left( t \right) =R\frac{N\left( t \right) T\left( t \right) }{W_{s}\left( t \right) } \end{aligned}$$
(4.26)
$$\begin{aligned}{} & {} \rho \left( t \right) =\frac{\omega _{s}^{*}}{W_{s}\left( t \right) } \end{aligned}$$
(4.27)
$$\begin{aligned}{} & {} p_{d}=\frac{\rho _{m}\left( v\left( t \right) \right) ^{2}}{2} \end{aligned}$$
(4.28)
$$\begin{aligned}{} & {} p_{s}\left( L,t \right) =p\left( t \right) -\frac{\rho _{m}\left( v\left( t \right) \right) ^{2}}{2} \end{aligned}$$
(4.29)
$$\begin{aligned}{} & {} {<p_{s}\left( x,t \right) >}_{L\left( t \right) }=p\left( t \right) -\frac{\rho _{m}\left( t \right) }{2}\left( v\left( t \right) \right) ^{2} \end{aligned}$$
(4.30)

and after reaching \(t_{z_{k}}\):

$$\begin{aligned}{} & {} \frac{de_{s}\left( t \right) }{dt}=\dot{e}_{s}\left( t \right) =u_{1}p\left( t \right) \end{aligned}$$
(4.31)
$$\begin{aligned}{} & {} \frac{d\mathrm {\Lambda }_{\textrm{s}}\left( t \right) }{dt}=\dot{\Lambda }_{s}(t)=S(e)\frac{de_{s}\left( t \right) }{dt} \end{aligned}$$
(4.32)
$$\begin{aligned}{} & {} \frac{d\psi \left( t \right) }{dt}=\dot{\psi }\left( t \right) =\frac{\delta }{\omega }S\left( e \right) \frac{de_{s}\left( t \right) }{dt}=\frac{\delta }{\omega }\dot{\Lambda }_{s}\left( t \right) \end{aligned}$$
(4.33)
$$\begin{aligned}{} & {} \frac{d\psi _{z}\left( t \right) }{dt}=\dot{\psi }_{z}\left( t \right) =0 \end{aligned}$$
(4.34)
$$\begin{aligned}{} & {} \frac{dN\left( t \right) }{dt}=\dot{N}\left( t \right) =\dot{\psi _{z}}{\left( t \right) \omega }_{z}+\dot{\psi }\left( t \right) \omega \, \end{aligned}$$
(4.35)
$$\begin{aligned}{} & {} \frac{dv\left( t \right) }{dt}=\dot{v}\left( t \right) =0 \end{aligned}$$
(4.36)
$$\begin{aligned}{} & {} \frac{dl\left( t \right) }{dt}=\dot{l}\left( t \right) =0 \end{aligned}$$
(4.37)
$$\begin{aligned}{} & {} \frac{dT}{dt}=\dot{T}=\frac{k-1}{R}\left( \frac{p_{s}\left( L,t \right) }{{{(\rho }_{m}\left( t \right) )}^{2}}\frac{d\rho _{m}\left( t \right) }{dt}+q_{\vartheta }\frac{d\psi \left( t \right) }{dt}+q_{z}\frac{d\psi _{z}\left( t \right) }{dt} \right) \end{aligned}$$
(4.38)
$$\begin{aligned}{} & {} \rho _{m}\left( t \right) =0 \end{aligned}$$
(4.39)
$$\begin{aligned}{} & {} W_{s}\left( t \right) =W_{o}+sl\left( t \right) -\frac{\omega }{\mathrm {\delta }}\left( 1-\psi \left( t \right) \right) -\alpha \omega \psi \left( t \right) -\alpha \omega _{z}\psi _{z}\left( t \right) \end{aligned}$$
(4.40)
$$\begin{aligned}{} & {} p\left( t \right) =R\frac{N\left( t \right) T\left( t \right) }{W_{s}\left( t \right) } \end{aligned}$$
(4.41)
$$\begin{aligned}{} & {} \rho \left( t \right) =\frac{\omega _{s}^{*}}{W_{s}\left( t \right) } \end{aligned}$$
(4.42)
$$\begin{aligned}{} & {} p_{d}=\frac{\rho _{m}\left( v\left( t \right) \right) ^{2}}{2} \end{aligned}$$
(4.43)
$$\begin{aligned}{} & {} p_{s}\left( L,t \right) =p\left( t \right) -\frac{\rho _{m}\left( v\left( t \right) \right) ^{2}}{2} \end{aligned}$$
(4.44)
$$\begin{aligned}{} & {} {<p_{s}\left( x,t \right) >}_{L\left( t \right) }=p\left( t \right) -\frac{\rho _{m}\left( t \right) }{2}\left( v\left( t \right) \right) ^{2} \end{aligned}$$
(4.45)

4.3 Pyrodynamic phase

Pyrodynamic phase is described by the range of the layer thickness of the burnt powder grain at time \(t_{o}\) (i.e. the time when the gaseous combustion products-GCP reach the forcing pressure), and the thickness of the burnt grain layer at time \(t_{k}\) (the time when the grain burn finish):

$$\begin{aligned} e_{s}\left( t_{o} \right) \le e_{s}\left( t \right) \le e_{s}\left( t_{k} \right) \end{aligned}$$

The system of equations for this phase will take the form:

$$\begin{aligned}{} & {} \frac{de_{s}\left( t \right) }{dt}=\dot{e}_{s}(t)=u_{1}{<p_{s}\left( x,t \right) >}_{L\left( t \right) } \end{aligned}$$
(4.46)
$$\begin{aligned}{} & {} \frac{d\mathrm {\Lambda }_{\textrm{s}}\left( t \right) }{dt}=\dot{\Lambda }_{s}(t)=S(e)\frac{de_{s}\left( t \right) }{dt}\left[ \frac{m^{3}}{s}\right] \end{aligned}$$
(4.47)
$$\begin{aligned}{} & {} \frac{d\psi \left( t \right) }{dt}=\dot{\psi }\left( t \right) =\frac{\delta }{\omega }S\left( e \right) \frac{de_{s}\left( t \right) }{dt}=\frac{\delta }{\omega }\dot{\Lambda }_{s}\left( t \right) \end{aligned}$$
(4.48)
$$\begin{aligned}{} & {} \frac{d\psi _{z}\left( t \right) }{dt}=\dot{\psi }_{z}\left( t \right) =0 \end{aligned}$$
(4.49)
$$\begin{aligned}{} & {} \frac{dN\left( t \right) }{dt}=\dot{N}\left( t \right) =\dot{\psi _{z}}{\left( t \right) \omega }_{z}+\dot{\psi }\left( t \right) \omega \, \end{aligned}$$
(4.50)
$$\begin{aligned}{} & {} \frac{dv\left( t \right) }{dt}=\dot{v}\left( t \right) =\frac{Sp_{s}\left( L,t \right) }{\varphi m} \end{aligned}$$
(4.51)
$$\begin{aligned}{} & {} \frac{dl\left( t \right) }{dt}=\dot{l}\left( t \right) =v\left( t \right) \end{aligned}$$
(4.52)
$$\begin{aligned}{} & {} \frac{dT}{dt}=\dot{T}=\frac{k-1}{R}\left( \frac{p_{s}\left( L,t \right) }{{{(\rho }_{m}\left( t \right) )}^{2}}\frac{d\rho _{m}\left( t \right) }{dt}+q_{\vartheta }\frac{d\psi \left( t \right) }{dt}+q_{z}\frac{d\psi _{z}\left( t \right) }{dt} \right) \end{aligned}$$
(4.53)
$$\begin{aligned}{} & {} \rho _{m}\left( t \right) =\frac{\omega ^{*}}{W\left( t \right) }=\frac{\omega ^{*}}{sL\left( t \right) } \end{aligned}$$
(4.54)
$$\begin{aligned}{} & {} W_{s}\left( t \right) =W_{o}+sl\left( t \right) -\frac{\omega }{\mathrm {\delta }}\left( 1-\psi \left( t \right) \right) -\alpha \omega \psi \left( t \right) -\alpha \omega _{z}\psi _{z}\left( t \right) \end{aligned}$$
(4.55)
$$\begin{aligned}{} & {} p\left( t \right) =R\frac{N\left( t \right) T\left( t \right) }{W_{s}\left( t \right) } \end{aligned}$$
(4.56)
$$\begin{aligned}{} & {} \rho \left( t \right) =\frac{\omega _{s}^{*}}{W_{s}\left( t \right) } \end{aligned}$$
(4.57)
$$\begin{aligned}{} & {} p_{d}=\frac{\rho _{m}\left( v\left( t \right) \right) ^{2}}{2} \end{aligned}$$
(4.58)
$$\begin{aligned}{} & {} p_{s}\left( L,t \right) =p\left( t \right) -\frac{\rho _{m}\left( v\left( t \right) \right) ^{2}}{2} \end{aligned}$$
(4.59)
$$\begin{aligned}{} & {} {<p_{s}\left( x,t \right) >}_{L\left( t \right) } =p\left( t \right) -\frac{\rho _{m}\left( t \right) }{2}\left( v\left( t \right) \right) ^{2} \end{aligned}$$
(4.60)

4.4 Adiabatic phase

Adiabatic phase is limited by the variability of the projectile displacement in the gun tube:

$$\begin{aligned} l\left( t_{k} \right) \le l\left( t \right) \le \, l_{w} \end{aligned}$$

where: \(l\left( t_{k} \right) \)—location of the projectiles bottom at the time of the end of burning the powder grains \(t_{k}\), \(l_{w}\)—gun tube length.

The system of equations for this phase will take the form:

$$\begin{aligned}{} & {} \frac{de_{s}\left( t \right) }{dt}=\dot{e}_{s}\left( t \right) =0 \end{aligned}$$
(4.61)
$$\begin{aligned}{} & {} \frac{d\mathrm {\Lambda }_{\textrm{s}}\left( t \right) }{dt}=\dot{\Lambda }_{s}\left( t \right) =0 \end{aligned}$$
(4.62)
$$\begin{aligned}{} & {} \frac{d\psi \left( t \right) }{dt}=\dot{\psi }\left( t \right) =0 \end{aligned}$$
(4.63)
$$\begin{aligned}{} & {} \frac{d\psi _{z}\left( t \right) }{dt}=\dot{\psi }_{z}\left( t \right) =0 \end{aligned}$$
(4.64)
$$\begin{aligned}{} & {} \frac{dN\left( t \right) }{dt}=\dot{N}\left( t \right) =0 \end{aligned}$$
(4.65)
$$\begin{aligned}{} & {} \frac{dv\left( t \right) }{dt}=\dot{v}\left( t \right) =\frac{Sp_{s}\left( L,t \right) }{\varphi m} \end{aligned}$$
(4.66)
$$\begin{aligned}{} & {} \frac{dl\left( t \right) }{dt}=\dot{l}\left( t \right) =v\left( t \right) \end{aligned}$$
(4.67)
$$\begin{aligned}{} & {} \frac{dT}{dt}=\dot{T}=\frac{k-1}{R}\left( \frac{p_{s}\left( L,t \right) }{{{(\rho }_{m}\left( t \right) )}^{2}}\frac{d\rho _{m}\left( t \right) }{dt}+q_{\vartheta }\frac{d\psi \left( t \right) }{dt}+q_{z}\frac{d\psi _{z}\left( t \right) }{dt} \right) \end{aligned}$$
(4.68)
$$\begin{aligned}{} & {} \rho _{m}\left( t \right) =\frac{\omega ^{*}}{W\left( t \right) }=\frac{\omega ^{*}}{sL\left( t \right) } \end{aligned}$$
(4.69)
$$\begin{aligned}{} & {} W_{s}\left( t \right) =W_{o}+sl\left( t \right) -\frac{\omega }{\mathrm {\delta }}\left( 1-\psi \left( t \right) \right) -\alpha \omega \psi \left( t \right) -\alpha \omega _{z}\psi _{z}\left( t \right) \end{aligned}$$
(4.70)
$$\begin{aligned}{} & {} p\left( t \right) =R\frac{N\left( t \right) T\left( t \right) }{W_{s}\left( t \right) } \end{aligned}$$
(4.71)
$$\begin{aligned}{} & {} \rho \left( t \right) =\frac{\omega _{s}^{*}}{W_{s}\left( t \right) } \end{aligned}$$
(4.72)
$$\begin{aligned}{} & {} p_{d}=\frac{\rho _{m}\left( v\left( t \right) \right) ^{2}}{2} \end{aligned}$$
(4.73)
$$\begin{aligned}{} & {} p_{s}\left( L,t \right) =p\left( t \right) -\frac{\rho _{m}\left( v\left( t \right) \right) ^{2}}{2} \end{aligned}$$
(4.74)
$$\begin{aligned}{} & {} {<p_{s}\left( x,t \right) >}_{L\left( t \right) }=p\left( t \right) -\frac{\rho _{m}\left( t \right) }{2}\left( v\left( t \right) \right) ^{2} \end{aligned}$$
(4.75)

5 Program for numerical solution of internal ballistics

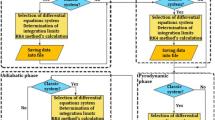
Using the equations formulated in the previous section describing the solution to the main problem of internal ballistics in Lagrange coordinates and using the Delphi 7 programming environment, the “Ball-Lagr” numerical program was designed to enable numerical simulation of the internal ballistics of classic gun tube weapons. Delphi is a universal programming language and software that uses the Delphi dialect of the Object Pascal programming language and provides an integrated development environment. Analytic equations have been defined as functions that are executed in each iteration of program execution [19]. The differential equations, on the other hand, are divided into functions in individual ballistic phases and only during a given phase is the part of the equations corresponding to it performed. The Ball-Lagr program is based on the following block diagram Fig. 2.

Fig. 2
figure 2

Block diagram of the general algorithm of the Ball-Lagr program

Full size image

Classic system of barrel weapons is characterized by the fact that during the shot, the entire mass of the gas-powder mixture, i.e., unburnt powder and gaseous combustion products, remain in the barrel until the projectile leaves the barrel.

This tool allows you to generate the graphs of each of the 15 equations, in particular the pressure versus time course and the projectile velocity versus time. Eight differential equations are stored in the state vector, while the remaining equations are solved using procedures that perform calculations up to date while generating solutions to differential equations.

Numerical simulations determine changes in values over time of the following ballistic parameters such as:

  • burnt grain layer density \(e_{s}\),

  • volume of burned grains \(\mathrm {\Lambda }_{\textrm{s}}\),

  • the relative mass of burnt powder grains \(\psi \) and igniter \(\psi _{z}\),

  • mass GCP \(\omega _{s}\),

  • velocity v and displacement l of the projectiles bottom in the gun tube,

  • volumetric density \(\rho _{m}\) GPM and \(\rho \) GCP,

  • free volume \(W_{s}\) behind the bottom of the projectile and the volume of burnt grains \(\mathrm {\Lambda }_{\textrm{s}}\),

  • temperature T of the GCP,

  • total pressure at the bottom of the cartridge chamber p,

  • dynamic pressure \(p_{d}\) GPM at the bottom of the projectile and the displacement l of the projectiles bottom in the gun tube,

  • static pressure \(p_{s}\) GPM on the projectiles bottom and projectile velocity v,

  • average static pressure \(p_{s}\) of GCP behind projectiles bottom.

6 Numerical simulation of the internal ballistics for a sample small arms cartridge

The purpose of the simulation was to evaluate the operation of the developed program for simulating the solution to the internal ballistics problem in Lagrange coordinates for an example small-caliber weapon cartridge.

The analytic equations have been defined as functions that are executed in each iteration of program execution. Differential equations, on the other hand, are divided into functions in individual ballistic phases and only during a given phase is the part of the equations corresponding to it performed.

Launching the Ball-Lagr program requires specifying the parameters controlling the program and the initial values for 8 differential equations, which are specified in the “Oblicz” (Calculate) table, as well as data on the physico-chemical and ballistic parameters of the propellants (BMP), shown in the Figs. 3 and 4.

Fig. 3
figure 3

Ball-Lagr user window for entering control parameters and initial values

Full size image
Fig. 4
figure 4

Ball-Lagr user window for entering powder data

Full size image

Where:

\(e_{1}\)—the thickness of the combustible layer of powder,

\(l_{w}\)—the path traveled by the bottom of the projectile in the gun tube,

eps, eps1, eps2—a variable for the precision function, whose role was to compact the step in a certain area,

skok—step for the RK4 (Runge–Kutta methods) calculation procedure between successive iterations of the program,

\(p_{z}\)—ignition pressure value,

\(t_{zap}\)—time to reach ignition pressure,

a1—variable for selecting the combustion surface (grain shape). Takes values from the range \(<0\div 3>\). For the variable value \(a_{1}:=\) the “PowSpal” function calculates the burning area of spherical powder grains. For \(a_{1}:=1\) cylinder-shaped combustion surface of grains. Dla \(a_{1}:=2\) tube-shaped combustion surface. For \(a_{1}:=3\) or powder grains in the shape of cuboids,

wek.x—vector of initial conditions for differential equations.

Fig. 5
figure 5

Graph of changes in the thickness of the burnt grain layer e\(_{\textbf{s}}\) versus time

Full size image
Fig. 6
figure 6

Graph of burnt grain volume \(\lambda _{\textbf{s}}\) versus time

Full size image
Fig. 7
figure 7

Graph of the relative mass of burnt grains of gunpowder \(\Psi \) and igniter \(\Psi \) \(_{\textbf{z}}\) versus time

Full size image
Fig. 8
figure 8

Graph of the mass of gaseous products of combustion Nversus time

Full size image
Fig. 9
figure 9

Graph of the path traveled by the bottom of the projectile l and the velocity of the projectile in the barrel v versus time

Full size image
Fig. 10
figure 10

Graph of the GPM mass density \(\rho _{\textbf{0m}}\) and GCP mass density \(\rho _{\textbf{0}}\) versus time

Full size image
Fig. 11
figure 11

Graph of and burnt grain volume \(\lambda _{\textbf{s}}\) and free volume behind the bottom of the projectile W\(_{\textbf{s}}\) versus time

Full size image
Fig. 12
figure 12

Graph ot the GCP temperatureT versus time

Full size image
Fig. 13
figure 13

Graph of the GCP total pressure p at the bottom of the chamber and GCP mass density \(\rho _{\textbf{0}}\) versus time

Full size image
Fig. 14
figure 14

Graph of GPM dynamic pressure at the bottom of the projectile p\(_{\textbf{d}}\) and the path traveled by the bottom of the projectile l versus time

Full size image
Fig. 15
figure 15

Graph of GPM static pressure at the bottom of the projectile p\(_{\textbf{s}}\) the velocity of the projectile in the barrel v versus time

Full size image
Fig. 16
figure 16

Graph of GCP static pressure \(<p_{\textbf{s}}>\) behind the bottom of the projectile versus time

Full size image

Where:

\(G_{z}\)—average mass flow of gaseous combustion products of the igniter

\(\alpha \)—covolume,

k—isentropic exponent,

\(q_{z}\quad -\)heat associated with the igniter,

R—gas constant,

\(p_{0}\)—forcing pressure,

\(T_{o}\)—ambient temperature,

\(u_{1}\)—proper burn rate,

\(\varphi \)—secondary work factor, factor of the fictitious mass of the projectile,

\({\delta }\)—bulk powder mass density,

\(m_{p}\)—mass of projectile,

d—caliber,

\(p_{a}\)—ambient pressure,

\(q_{p}\)—heat associated with the powder,

\(\omega \)—mass of the powder.

Parameters related to grain dimensions (data downloaded depending on the adopted value of the a\(_{1}\) variable from the calculations tab):

\(D_{z}\)—grain diameter (in the case of the spherical-shape grain variant),

\(d_{w}\)—cylindrical diameter (in the case of tube-shaped grain variant),

\(l_{ziar}\)—grain length,

a, b, c—cuboid dimensions (in the case of cuboid-shaped grain variant).

\(\omega _{z}\)—mass of igniter,

\(l_{o}\)—chamber length.

Having the ballistic parameters of the selected type of powder, as well as the tool which is the designed Ball-Lagr program, it was possible to carry out a simulation for the selected powder weight and the selected type of weapon, which allowed to obtain internal ballistics solution diagrams. The tool provides a wide range of possibilities for analyzing the entered data, which is shown in the graphs of the selected parameters in Figs. 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15 and 16.

On the basis of the sample charts from the Ball-Lagr program obtained above, it is possible to conduct e.g. in-depth analysis of the identification of factors significantly affecting the shot phenomenon, and in particular the extreme values of pressure, temperature and projectile velocity, which are the most important parameters in the process of designing weapons and ammunition.

Moreover, such a wide package of results, including the courses of variables as a function of distance and time, makes it possible to properly configure the measurement base required for experimental verification of the results of numerical simulations.

7 Conclusions

Conclusions that can be drawn on the basis of performed numerical analyses are as follows:

  1. 1.

    The mathematical model of internal ballistics was developed, consisting of 15 mathematical equations, in which 8 equations are differential equations, while the remaining equations are analytical equations.

  2. 2.

    Based on the presented model, a digital tool was created to solve the main problem of internal ballistics, which was designed in the Delphi 7 development environment.

  3. 3.

    The designed Ball-Lagr program gives a wide range of possibilities to analyze the entered data related to the parameters of weapons and propellants.

  4. 4.

    As a continuation of the issues raised in this work, experimental tests should be carried out, the purpose of compare the results of numerical simulations using the Bal-Lagr program with the results of shooting tests for a specific small arms cartridge.

Using the possibilities of modern science and technology, it can be said that the presented mathematical model has been formulated without significant simplifications, and its (numerical) solution itself will be performed with high accuracy. Due to this fact, it can be concluded that the accuracy of solving the main problem of internal ballistics will be determined each time by the input data, and especially the reliably obtained values of the energy and ballistic characteristics of the propellants.

A possible further development of the program is to implement other models to solve the main problem of internal ballistics, so that the end user (designer) can choose different models and check which model works best in his conditions or investigate shock waves propagation [20,21,22,23,24,25]. In addition, using the field of optimization techniques, an attempt can be made to implement algorithms that would be able to search for example, the smallest powder weight value at specific powder parameters and a given maximum pressure and projectile muzzle velocity. Moreover, it is possible to extend the model in order to analyze shock wave phenomena occurring in the space between the bottom of the bullet and the bottom of the cartridge chamber.