Microscale investigation of phase transformation and plasticity in multi-crystalline shape memory alloy using discrete dislocation–transformation method

Abstract

Martensitic phase transformation and plasticity are two primary mechanisms of deformation in shape memory alloys (SMAs) and the interaction between them influences the behaviour of SMA during cyclic loading, specifically the pseudoelasticity behaviour and the shape memory effect. This interaction, which occurs in microscale, affects the reversibility and eventually the actuation capacity of SMAs. In order to capture this interaction in microscale, a discrete dislocation–transformation model was developed in Sakhaei et al. (Mech Mater 97:1–18, 2016) and was applied to simulate the single-crystalline NiTi samples under thermo-mechanical loads. In this study, the microscale coupling between phase transformation and plasticity as well as grain size and orientation effects is investigated in multi-crystalline shape memory alloys under thermal and mechanical loading by using the discrete dislocation–transformation framework through the representative numerical simulations. The results illustrated the dependency of dislocation slip and martensitic transformation to crystalline orientations as well as grain size and grain boundary densities in the multi-crystalline SMAs.

1 Introduction

Shape memory alloys (SMAs) have the ability to recover the original structure after experiencing a macroscopic inelastic deformation upon applying desirable thermo-mechanical cyclic loading. This performance is called the “shape memory effect” or “pseudoelasticity”, depending on the loading type. Furthermore, SMAs could consume and dissipate energy by illustrating hysteric behaviour under cyclic loads. These specific behaviours are due to martensitic phase transformation that makes SMAs an attractive material for actuation scenarios in various industrial applications [2]. The martensitic transformation is a diffusionless and solid–solid phase transformation between two different crystalline structures. The phase with higher symmetry is named austenite, whereas the phase with lower symmetry in atomistic structure is called martensite.

Martensitic phase transformation which generates the recoverable strain has the main contribution to the inelastic deformation of a sample made of SMA. However, the plasticity mechanism could also provoke irrecoverable strain in SMAs that influences the reversibility behaviour of this material under thermal and/or mechanical cyclic loadings [3,4,5]. Ezaz et al. [6] illustrated that the slip planes in body-centred cubic structure (BCC) of austenitic NiTi are active, and therefore, the transformation and plasticity mechanisms could interact each other as well as the total thermo-mechanical response of SMA. This phenomenon is explored in several types of metallic alloys and is generally called as transformation-induced plasticity (TRIP) in the literature. These phenomena have been investigated in microscale in various studies in the literature. For example, Xu et al. have developed a three-dimensional phase field model for single-crystalline NiTi shape memory alloys which has integrated the austenite and martensite plasticity mechanisms [7]. They have also observed that during cyclic deformation the reverse transformation is affected by plastic deformation, and therefore, the residual martensitic phase would be remained through cyclic loading. Furthermore, the effect of grain boundaries on shape memory effect and pseudoelasticity of polycrystalline NiTi SMA has been studied using the two-dimensional phase field model in [8], where the grain size dependency of martensitic transformation and plasticity in polycrystalline SMAs have been revealed.

The nature of transformation-induced strains in NITI SMAs during austenite to martensite phase transformation has been also studied in nanoscale level using molecular dynamics (MD) simulations [9,10,11]. For example, Wang et al. have observed that the transformation-induced plasticity and phase transformation have been generated in martensitic phases and near the martensitic variants interfaces in monocrystalline NiTi SMA using MD simulations [10]. Furthermore, they have shown that the transformation ratcheting generated under isothermal pseudoelastic behaviour of NiTi is due to the occurrence of plastic deformation at grain boundaries as well as the accumulation of residual martensitic phases in the microstructure [11].

At the macroscopic level, the effect of transformation-induced plasticity in SMAs has been considered in different phenomenological models (e.g. see [12,13,14,15]). It is assumed that the local stress fields associated with the martensitic transformation may activate the plasticity although the external stresses are lower than the yield stress of the material [16, 17]. Therefore, they come up with a phenomenological continuum models that are able to consider the interaction between plasticity and phase transformation in the macroscopic simulations. Furthermore, Yu et al. have developed a constitutive model for anisotropic pseudoelasticity of single-crystalline NiTi shape memory alloys considering experimental studies [18]. Similar to [1], they have also considered the martensitic phases as ellipsoidal inclusion inside austenitic phase to accommodate the effect of internal stresses and transformation-induced plasticity in their model. The model was then used for the investigation of anisotropic behaviour under multi-axial loading scenarios through comparison with experiments.

At the microscopic length scale, plasticity phenomenon is interpreted by kinetic of dislocations along slip planes and the martensitic phase transformation occurs through the creation of plate-like regions. Therefore, the influence of plastic deformation on phase transformation might be studied by looking at the effect of dislocations on the nucleation and growth of the martensitic regions. Similarly, the impact of martensitic inclusions on the generation and movement of dislocations represents the effect of phase transformation on plasticity. Although it is not yet proved whether the dislocation plasticity assists the martensitic phase transformation or resists against the movement of martensite–austenite interface, some studies have attempted to provide an answer based on microscale simulation [1, 19, 20]. Discrete dislocation dynamic method facilitates to model the microstructure of plastic deformation by considering the nucleation, motion, and annihilation of dislocations [21]. Shi et al. [19] used the discrete dislocation dynamic method for modelling plasticity and combined it with the proposed discrete transformation model to simulate the phase transformation in multi-phase TRIP steel. However, their framework was unable to model the reversible martensitic transformation in SMAs and simulate the response of material under thermal loading. Furthermore, [1, 4] presented a modified discrete dislocation–transformation model for SMAs to study the interaction between plasticity and martensitic transformation under cyclic thermal and mechanical loading for single-crystal samples of SMA.

In the current work, we aim to apply the discrete dislocation–transformation framework presented in our earlier work [1] for multi-grain SMA structure. The goal is to study the effect of grain boundaries and Hall–Petch effects in addition to the interaction between plasticity and phase transformation under cyclic mechanical loading in the multi-grain NiTi SMA.

The polycrystalline structure is composed of numerous grains with different sizes and orientations. These grains are connected to each other via grain boundaries across which the orientation of the crystals changes. The material behaviour of single- and polycrystalline SMAs are different with each other as in single crystals, the behaviour is highly dependent on the direction of loading and crystal orientation, whereas the polycrystalline SMA shows less anisotropic behaviour. Furthermore, the grain boundaries have a resistance role on the dislocation slip and the growth of transformation regions. Shi et al. [22] studied the interaction of martensitic phase transformation of dislocation plasticity in polycrystalline multi-phase TRIP steel. They also investigated the Hall–Petch effect and orientation effect in their study. However, they did not model the two-way phase transformation which occurs in SMAs. Moreover, their model was unable to incorporate temperature effects and thermal cycling as important factors that affect the response of SMAs. Therefore, the current study aims to cover these gaps and investigate the interaction between plasticity and martensitic transformation in the presence of grain boundaries by using the authors’ earlier proposed discrete dislocation–transformation model in [1].

The structure of this paper is as follows: in Sect. 2, a summary of the discrete dislocation–transformation method as well as the numerical implementations for modelling the microscale behaviour of multi-crystalline shape memory alloys is presented. In Sect. 3, the interaction between plasticity and phase transformation in the presence of grain boundaries is analysed. Moreover, the orientation effect, grain size effects, and the interaction of grain boundaries on dislocation dynamic and martensitic transformation are investigated in this section. Finally, concluding remarks are provided in Sect. 4.

2 Thermo-mechanical discrete dislocation–transformation model

The discrete dislocation–transformation framework used in this study for simulation the behaviour of multi-crystalline SMAs has been presented completely in the authors’ previously published article in [1]. Therefore, we only summarized the important aspect of this model here and the readers should refer to [1] for comprehensive explanation.

2.1 Discrete dislocation–transformation model

As it is described in [1], two-dimensional discrete dislocation–transformation model is developed by incorporating the two-dimensional discrete dislocation method presented by [21] and the representation of martensitic transformation in the microstructure. To model the phase transformation, the martensitic regions are speculated to generate and grow as elliptically shaped inclusions during a thermo-mechanical loading process. Therefore, the migration and evolution of dislocation cores and martensitic regions in austenite domain characterize the plastic deformation and martensitic transformation, respectively. In the current model, it is essential to determine the stress, strain, and displacement fields due to the existence of dislocation cores, martensitic regions, and boundary conditions in the domain before updating the configuration of them for the next time step using kinematic relations.

If the material domain is occupied $\Omega$ with boundary $\partial \Omega$, the stress, strain, and displacement field of the configuration under prescribed boundary conditions are determined with the decomposition method presented in [1, 19, 21] as

$$\begin{aligned} {\left\{ \begin{array}{ll} \varvec{\sigma } = \varvec{\sigma }^\text {d} + \varvec{\sigma }^\text {m} + \varvec{\sigma }^\text {c} , \\ \varvec{\varepsilon } = \varvec{\varepsilon }^\text {d}+\varvec{\varepsilon }^\text {m}+\varvec{\varepsilon }^\text {c} , \\ \varvec{u} = \varvec{u}^\text {d}+\varvec{u}^\text {m}+\varvec{u}^\text {c} , \end{array}\right. } \end{aligned}$$

(1)

where all the quantities with d, m, and c superscripts correspond to fields associated with the dislocations, martensitic plates, and the complementary problem, respectively. Figure 1 illustrates the above decomposition schematically.

Fig. 1

Dividing the problem into three sub-problems: interacting dislocations in infinite region, martensitic inclusions in infinite medium, and complementary problem

At any time t, we define $N^\text {d} = N^\text {d}(t)$ the total number of edge dislocation cores and by $N^\text {m} = N^\text {m}(t)$ the total number of martensitic regions inside $\Omega$. Therefore, the terms in Eq. (1) are calculated as a summation of states from each individual dislocation and martensitic region as

$$\begin{aligned} {\left\{ \begin{array}{ll} \varvec{\sigma }^\text {d}=\sum \limits _{i=1}^{N^\text {d}} \varvec{\sigma }^\text {d}_{i} , \\ \varvec{\varepsilon }^\text {d}=\sum \limits _{i=1}^{N^\text {d}} \varvec{\varepsilon }^\text {d}_{i} , \\ \varvec{u}^\text {d}=\sum \limits _{i=1}^{N^\text {d}} \varvec{u}^\text {d}_{i} , \end{array}\right. }\quad {\left\{ \begin{array}{ll} \varvec{\sigma }^\text {m}=\sum \limits _{j=1}^{N^\text {m}} \varvec{\sigma }^\text {m}_{j} ,\\ \varvec{\varepsilon }^\text {m}=\sum \limits _{j=1}^{N^\text {m}} \varvec{\varepsilon }^\text {m}_{j} ,\\ \varvec{u}^\text {m}=\sum \limits _{j=1}^{N^\text {m}} \varvec{u}^\text {m}_{j} , \end{array}\right. } \end{aligned}$$

(2)

where the subscripts i and j determine the individual dislocations and martensitic inclusion, respectively. The calculation related to dislocations and martensitic inclusions is performed analytically in an infinite medium, and the complementary field is applied to assure the actual boundary conditions in the original finite domain.

The displacement and stress fields of any arbitrary point in the domain because of the existence of dislocation cores depend only on location of dislocations $i = 1, \ldots , N^\text {d}$ and Burgers vector $\varvec{b}^{i}$ of the ith dislocation core and elastic properties of the domain. By defining a local coordinate system as shown in Fig. 2-a, the stress and displacement fields at each point $\varvec{x}$ in the plane due to the dislocation i are determined as

$$\begin{aligned} \begin{aligned} \varvec{u}^\text {d}_{i}(\varvec{x}) = \frac{b^{i}}{2\pi (1-\nu ^{p})} \left[ \left( \frac{1}{2}\frac{x_b x_n}{r^{2}} - (1-\nu ^{p})\tan ^{-1} \frac{x_b}{x_n} \right) \varvec{e}_b + \left( \frac{1}{2}\frac{x_n^{2}}{r^{2}} - \frac{1}{4}(1-2\nu ^{p})\ln \frac{r^{2}}{(b^{i})^{2}}\right) \varvec{n} \right] \end{aligned} \end{aligned}$$

(3)

and

$$\begin{aligned} \left( \sigma ^\text {d}_{i}\right) _{bb}&= - c_i \frac{x_n(3 x_b^2 + x_n^2)}{r^2} ,\qquad \left( \sigma ^\text {d}_{i}\right) _{nn} = c_i \frac{x_n (x_b^2 - x_n^2) }{r^2} , \nonumber \\ \left( \sigma ^\text {d}_{i}\right) _{bn}&= c_i \frac{x_b(x_b^2 - x_n^2) }{r^2} \ , \qquad \text {with}\quad c_i := \frac{\mu ^{p} b^{i}}{2\pi (1-\nu ^{p})} \ , \end{aligned}$$

(4)

where $b^{i} = \Vert \varvec{b}^{i}\Vert$, $r := \Vert \varvec{x}-\varvec{x}^{i}\Vert$, $x_b := (\varvec{x}-\varvec{x}^{i}) \cdot \varvec{e}_b$, $x_n := (\varvec{x}-\varvec{x}^{i}) \cdot \varvec{n}$, and $\nu ^{p} = \left( 3 \kappa ^{p} - 2 \mu ^{p} \right) / \left( 2 \left( 3 \kappa ^{p} + \mu ^{p} \right) \right)$ refers to the Poisson’s ratio of the medium where the dislocation core is embedded, with $p = \text {a}, \text {m}$ for the austenitic and martensitic phases, respectively.

Fig. 2

a Displacement field at an arbitrary point $\varvec{x}$ due to a dislocation i at point $\varvec{x}^{i}$, b Schematic diagram of an elliptical martensitic region embedded in an austenitic grain

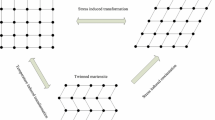
Regarding the fields due to the martensitic transformation, it is possible to characterize the transformation at the continuum level by a pair of vectors $\varvec{a}$ and $\varvec{n}$, where $\varvec{a}$ is the transformation strain vector and $\varvec{n}$ is the normal vector to the habit plane. According to experiments conducted in [23] and the assumptions made in [1, 19], it is considered here that each martensitic region has an elliptical shape as shown in Fig. 2-b. Furthermore, the nominal habit plane normal $\varvec{m}_j$ is considered as the major semi-axis of the elliptical plate and the transformation strain of the jth martensitic inclusion is calculated as

$$\begin{aligned} \varvec{\varepsilon }^\text {tr}_j := \frac{1}{2}\gamma (\varvec{m}_j^{\perp }\otimes \varvec{m}_j+\varvec{m}_j\otimes \varvec{m}_j^{\perp })+\delta (\varvec{m}_j\otimes \varvec{m}_j) , \end{aligned}$$

(5)

where $\delta = \varvec{a}_j \cdot \varvec{m}_j$ and $\gamma = \varvec{a}_j \cdot \varvec{m}_j^{\perp }$ are dilation and shape strain terms during transformation, respectively. $\varvec{m}_j^{\perp }$ is a unit vector perpendicular to $\varvec{m}_j$ and in the loading plane as presented in Fig. 2b.

The stress field $\varvec{\sigma }^\text {m}_j$ inside and outside of elliptical martensitic plate could be determined based on the Eshelby solution of elliptical region using the eigen-strain of inclusion $\varvec{\varepsilon }^\text {m}_j$ [24]. The eigen-strain in our problem is because of the difference between elastic behaviour of martensitic and austenitic phases and the transformation strain. For the points inside of the jth martensitic plate, the strain and stress fields are determined by

$$\begin{aligned} \varvec{\varepsilon }^\text {m}_j&= \mathbb {S}[(\mathbb {C}^\text {m}-\mathbb {C}^\text {a})\mathbb {S}+\mathbb {C}^\text {a}]^{-1}\mathbb {C}^\text {m}\varvec{\varepsilon }^\text {tr}_j&\quad \text {in} \quad \Omega ^\text {m}_j , \nonumber \\ \varvec{\sigma }^\text {m}_j&= \mathbb {C}^\text {a}(\mathbb {S}-\mathbb {I})[(\mathbb {C}^\text {m}-\mathbb {C}^\text {a})\mathbb {S}+\mathbb {C}^\text {a}]^{-1}\mathbb {C}^\text {m}\varvec{\varepsilon }^\text {tr}_j&\quad \text {in} \quad \Omega ^\text {m}_j , \end{aligned}$$

(6)

where $\mathbb {S}$ is the fourth-order Eshelby’s tensor for interior points [24]. Furthermore, the stress fields of the points outside of martensitic elliptical inclusion are determined by Muskhelishvili decomposition as it is presented in [19].

Finally to satisfy the original boundary condition of the problem as illustrated in Fig. 1, we need to solve and add a complementary field to the decomposition problem presented in Eq. (1). Therefore, assuming the original boundary condition as

$$\begin{aligned} \varvec{u}_{0}=\varvec{u}_{0}(\varvec{x},t)&\quad \text {on} \quad \partial \Omega _{u} , \nonumber \\ \varvec{t}_{0}=\varvec{t}_{0}(\varvec{x},t)&\quad \text {on} \quad \partial \Omega _{t} , \end{aligned}$$

(7)

the boundary conditions for the complementary problem are given by

$$\begin{aligned} \varvec{u}^\text {c}&:=\varvec{u}_0 - \varvec{u}^\text {d} -\varvec{u}^\text {m} \qquad&\text {on} \quad \partial \Omega _u , \nonumber \\ \varvec{t}^\text {c}&:=\varvec{t}_0 - \varvec{t}^\text {d} -\varvec{t}^\text {m} \qquad&\text {on} \quad \partial \Omega _t , \end{aligned}$$

(8)

where $\partial \Omega _{u}$ and $\partial \Omega _{t}$ indicate the area that the displacement and traction boundary condition are prescribed, respectively. Furthermore, $\varvec{t}^\text {c}=\varvec{\sigma }^\text {c}\varvec{n}$, $\varvec{t}^\text {d}=\varvec{\sigma }^\text {d}\varvec{n}$, and $\varvec{t}^\text {m}=\varvec{\sigma }^\text {m}\varvec{n}$ where $\varvec{n}$ is the outward unit vector normal to $\partial \Omega$. The elastic boundary value problem is then solved by finite element method at each time step to compute the complementary terms in Eq. (1).

2.2 Two-dimensional dislocation dynamics

The discrete dislocation method correlates the plastic deformation in crystalline structures with nucleation, motion and annihilation of dislocations. In this study, we follow the discrete dislocation model which is specified for two-dimensional plane strain problems in [21] and is presented comprehensively in [1].

As indicated in [21], the nucleation of new dislocations and the glide of existing ones are determined by Peach–Koehler force, $f_i^d$ which is the work conjugate to the dislocation displacement. The Peach–Koehler force is determined as the product of the total stress at the ith dislocation position and the strain tensor due to a glide of the dislocation on the slip system ${\varvec{b}_i,\varvec{n}_i}$ as

$$\begin{aligned} f_i^\text {d} := (\varvec{\sigma }-\varvec{\sigma }_i^\text {d})\cdot (\varvec{b}_i\otimes \varvec{n}_i). \end{aligned}$$

(9)

When the magnitude of this force at the ith source point overreaches a critical value ($f_i^\text {cr}$), a pair of dislocations with different signed Burgers vector are set up. This is formulated in [1, 19] as

$$\begin{aligned} \frac{1}{t_\text {nuc}}\int _{t}^{t+t_\text {nuc}}|f_i^\text {d}| \text {d}t \ge f_i^\text {cr} \quad \Rightarrow \quad \text {Nucleation of dislocation dipole.} \end{aligned}$$

(10)

Furthermore, the kinetic formulation for gliding of the ith dislocation is represented as

$$\begin{aligned} v_i^\text {d} = {\left\{ \begin{array}{ll} f_i^\text {d} / B_\text {d} &{} \qquad \text {if} \qquad 0\le \left| f_i^\text {d}/B_\text {d} \right| \le v_\text {max}^\text {d} , \\ \text {sign}(f_i^\text {d}) v_\text {max}^\text {d} &{} \qquad \text {if} \qquad \left| f_i^\text {d}/B_\text {d} \right| > v_\text {max}^\text {d} , \end{array}\right. } \end{aligned}$$

(11)

where $B_\text {d}$ is a drag constant, $v_i^\text {d}$ is the velocity of ith dislocation on a slip plane i, and $v_\text {max}^\text {d}$ is the limit for maximum velocity of dislocations.

It is worth mentioning that the interface between martensite and austenite phases and grain boundaries in the microstructures work as the obstacle against the migration of dislocations in the slip systems and changing the thickness of grain boundaries is not the scope of this study. Furthermore, two dislocations with opposite Burgers vectors will be annihilated from the domain if the distance between them is less than a material-dependent parameter $L_{\text {e}}$ which is considered as $L_{\text {e}}=6 b_i$ based on [21].

2.3 Martensitic transformation kinetics

Transformation kinetics means updating the martensitic region configuration from time t to $t+\Delta t$ that includes the roles for nucleation and annihilation as well as growth and shrinkage of elliptical martensitic inclusions during forward and backward transformation in SMAs [1].

Similar to Peach–Koehler force in dislocation dynamics, it is possible to determine the local driving force acting on the interface between austenite and martensite domains $S_j^\text {m}$ according to [1, 25] as

$$\begin{aligned} f_j^\text {tr}= \varvec{\sigma }^{+}\varvec{n}\cdot \varvec{\varepsilon }_j^\text {tr}\varvec{n}+\frac{1}{2}\mathbb {D}^\text {a}\varvec{\sigma }^{+}\cdot \varvec{\sigma }^{+}-\frac{1}{2}\mathbb {D}^\text {m}\varvec{\sigma }^{-}\cdot \varvec{\sigma }^{-} - \frac{\rho \lambda }{\theta _T}(\theta -\theta _T) , \end{aligned}$$

(12)

where $\varvec{\sigma }^+$ and $\varvec{\sigma }^-$ are the local stress tensor across the interface, $\mathbb {D}^\text {a}=(\mathbb {C}^\text {a})^{-1}$ and $\mathbb {D}^\text {m}=(\mathbb {C}^\text {m})^{-1}$ are the compliance tensors for austenitic and martensitic phases, $\varvec{n}$ is the habit plane normal vector, and $\varvec{\varepsilon _j^\text {tr}}$ is the transformation strain. Moreover, $\rho$ is the mass density, $\lambda$ is transformation latent heat, $\theta$ is temperature, and $\theta _T$ is called transformation temperature of shape memory alloys which is the average of austenite and martensite start temperatures.

Similar to nucleation rule of dislocations, a new martensitic embryo is generated when the transformation driving force exceeds a critical value ($f_j^{cr}$) at jth randomly distributed transformation source point. Due to the fact that there is no austenite/martensite interface at transformation source point, the nucleation transformation driving force could be calculated as $f_j^\text {nuc} := \varvec{\sigma } \cdot \varvec{\varepsilon }_j^\text {tr} - \frac{\rho \lambda }{\theta _T}(\theta -\theta _T)$ according to Eq. (12). At this point, an elliptical embryo with semi-axes $c_0$ and $d_0$ is created and the transformation source j would be deleted.

The kinetic rules for growth and shrinkage of the elliptical martensitic regions are presented in [1] by determining the velocity of ellipse tips as

$$\begin{aligned} v^{(q)}_\text {tip} = {\left\{ \begin{array}{ll} \left( \pi e c / B \right) \bar{f}^{(q)} &{} \ \text {if} \quad 0\le \left| \left( \pi e c / B \right) \bar{f}^{(q)} \right| \le v_\text {max} , \\ \text {sign}( \bar{f}^{(q)}) v_\text {max} &{} \ \text {if} \quad \left| \left( \pi e c / B \right) \bar{f}^{(q)} \right| > v_\text {max} \ , \end{array}\right. } \end{aligned}$$

(13)

where $v^{(1)}_\text {tip}$ and $v^{(2)}_\text {tip}$ are the velocities of tips 1 and 2 when the opposite one is kept fixed, c is the major semi-axis of elliptical region, B is a viscosity-like constant, and $v_\text {max}$ is the cut-off value for tip velocity which is physically related to the sound speed in the material. Furthermore, $\bar{f}^{(q)}$ is the effective driving force at tip (q) where $q=1,2$ and it is determined according to [1] by integrating the local driving force acting on martensitic interface as

$$\begin{aligned} \bar{f}^{(q)} := \frac{1}{\pi e c} \int _{S_j} f^\text {tr}_j w^{(q)} \text {d}s \ , \end{aligned}$$

(14)

where $f^\text {tr}_j$ is the local driving force calculated in Eq. (12) for any points on the austenite/martensite interface, and $w^{(1)}$ and $w^{(2)}$ are weighting functions independent of $v^{(1)}_\text {tip}$ (please refer to [1] for more details).

Finally, during the backward phase transformation, the shrinkage of each elliptical martensitic region is continued until the size of that region goes less than the embryonic dimensions ($d_0$ and $c_0$). At this point, the martensitic inclusion is eliminated from the microstructure completely.

3 Thermo-mechanical loading of multi-crystalline SMA

In this section, the mechanical behaviour of un-textured multi-crystalline shape memory alloy samples is investigated under thermo-mechanical loads using the 2D discrete dislocation–transformation model which is described in Sect. 2. To interpret the results, we have defined the dislocation density as $\rho ^\text {d} = \rho ^\text {d}(t) := \frac{N^\text {d}}{\left| \Omega \right| }$ and the total martensitic volume fraction, $\zeta ^\text {m} = \zeta ^\text {m}(t) := \frac{\left| \Omega ^\text {m} \right| }{\left| \Omega \right| }$ at a given time t, where $\left| \Omega ^\text {m} \right|$ is the total area occupied by the martensitic phase. It is worth mentioning that the un-textured multi-crystalline structure consists of randomly oriented grains.

3.1 Problem assumptions and material parameters

The assumptions related to computational framework (i.e. discrete dislocation–transformation method) are same as reported in [1]. The material in all the simulations are considered under plane strain conditions in the $(\bar{1} \ 0 \ 1)$ plane which is named as loading plane in Fig. 3. Then, $(1 \ 2 \ 1)$ $[1 \ \bar{1} \ 1]$, $(\bar{1} \ 2 \ \bar{1})$ $[\bar{1} \ \bar{1} \ \bar{1}]$, and $(1 \ 0 \ 1)$ $[0 \ 1 \ 0]$ are considered as active slip systems for dislocation slips in BCC structure. Furthermore, to study the martensitic phase transformation in two-dimensional state, two groups of transformation systems are chosen in a way that the habit plane normal $\varvec{m}$ and the strain vector $\varvec{a}$ are lied in the loading plane.

Fig. 3

Schematic of slip planes and plane–strain loading plane for BCC crystal

In the multi-crystalline model, different grains are attached together across grain boundaries. This leads to another assumption regarding the grain boundaries. It is considered that the dislocations and martensitic areas which are nucleated and grown inside a grain cannot pass the grain boundaries. A multi-crystalline sample including of four grains as well as the pinning of dislocations and martensitic regions in grain boundaries are illustrated schematically in Fig. 4.

Fig. 4

Schematic of multi-crystal problem including dislocations and martensitic regions pinning at grain boundaries

In this study, the multi-crystalline specimens are assumed to be initially in the austenitic phase under a stress-free and dislocation-free configuration. Furthermore, the dislocation sources are randomly scattered in the domain on the slip planes. The strength $\tau ^\text {cr}$ of each dislocation source is randomly generated from a Gaussian distribution. The locations and strengths $f^\text {cr}$ of the transformation sources are determined in a similar way, with consideration of habit planes instead of slip planes. Table 1 summarizes the material parameters which are used in the simulations which are collected from [21, 26, 27]. Moreover, in this study, each multi-crystalline structure is composed of grains of the same size and square shape and the orientation of each grain is assigned randomly. Due to the computational limitations, the maximum number of grains are bounded 16 grains.

Table 1 Material parameters used in the simulations

The multi-crystalline NiTi specimens in this study is subjected to plane strain uniaxial loading when the temperature is constant and above $A_\text {f}$. The boundary conditions according to Fig. 4 are defined as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} u_1(x_1=0 , t)= 0, &{} \qquad t_2(x_1=0 , t)=0 ,\\ u_1(x_1=L , t)= L\dot{\bar{\varepsilon }}t, &{} \qquad t_2(x_1=L , t)=0 ,\\ t_1(x_2=0 , t)= 0, &{} \qquad t_2(x_2=0 , t)=0 ,\\ t_1(x_2=H , t)= 0, &{} \qquad t_2(x_2=H , t)=0 , \end{array}\right. } \end{aligned}$$

(15)

where $\dot{\bar{\varepsilon }}$ is the applied strain rate. In order to improve computational efficiency, it is suggested to impose a relatively high strain rate. In this study, it is assumed to be equal to $5 \times 10^{3} \text {s}^{-1}$. Furthermore, the values of dislocation source and transformation sources densities used in the simulations are $\rho ^{\text {d}}_{\text {source}} = 30\,\upmu \text {m}^{-2} and \ \rho ^{\text {m}}_{\text {source}} = 8\,\upmu \text {m}^{-2}$.

3.2 Discrete dislocation–transformation method and grain orientation effects

Although the macroscopic behaviour of polycrystalline materials is considered to be isotropic and homogeneous, the microstructure of polycrystalline materials is anisotropic and it is combined from numerous crystals with different orientations. The grain orientations would induce a non-uniform local stress in the microstructures that affects the plastic deformation and strength of metals [28], the direction of crack propagation [29], and the propensity for twinning [30]. Therefore, at this part of the study, we illustrate the potential of our proposed discrete dislocation–transformation framework (as a tool for microscale modelling of the interaction between dislocations and martensitic transformation in the microstructure), in capturing the effect of grain orientations on local stress as well as the martensitic transformation and dislocation plasticity mechanism in the microstructure.

As schematically depicted in Fig. 5, the mechanical responses of four bi-crystal cases are studied under isothermal mechanical loading. Each case is combined from two grains which the orientation of the first grain of each case is kept the same while the orientation of the second grain is defined by rotating the first orientation by zero, 15, 30, and 45 degrees and are named as cases 1 to 4, respectively.

Fig. 5

Schematic of grain orientation problem

The specimens are loaded at a rate $\dot{\bar{\varepsilon }} >0$, as described above, up to an average axial strain of $\bar{\varepsilon } = 0.01$. The results of these simulations are presented in Fig. 6 in terms of (a) the stress–strain curve (averaged over the whole sample), (b) the evolution of the dislocation density, and (c) the evolution of martensitic volume fraction as a function of the average axial strain $\bar{\varepsilon }_{11}$. Furthermore, to demonstrate the contribution of plasticity to the irreversible strain after a complete cycle involving the forward and reverse martensite transformation processes of shape memory alloy, the full pseudoelastic behaviour of the material during loading and unloading condition is provided in Appendix section in Fig. 12

Figure 6a illustrates the pseudo-elastic behaviour of the above-mentioned bi-crystal samples. As it was expected, Fig. 6a shows the different mechanical response for the four cases due to different orientation of grains. However, it is not clear yet that this variation of results is due to the difference of dislocation slip directions or transformation systems or both of them. To find out the answer of this question, the change of dislocation density and martensitic volume fraction along the loading are compared for the above four cases in Fig. 6b and c, respectively.

Fig. 6

Effect of grain orientation on pseudoelasticity behaviour of bi-crystal samples by comparing a the stress–strain response, b the dislocation density, and c the martensitic volume fraction

As shown in Fig. 6b, the evolution of dislocations varies from a bi-crystalline sample to another. This is in agreement with the physical fact that the plastic deformation behaviour of a crystalline grain is orientation dependent. Furthermore, the above result confirms that the discrete dislocation–transformation framework proposed in this study is able to capture the effect of slip system orientations in microscale simulations.

To investigate the effect of transformation system orientations on the mechanical response of the SMA, the change of the martensitic volume fraction for specimens 1 to 4 under isothermal mechanical loading is compared in Fig. 6c. The value of martensitic volume fraction ($\zeta$) for four different bi-crystalline samples explains how much the martensitic regions grow in each of the cases. Therefore, it can be concluded that the grain orientation has clear effect on the nucleation and growth of the martensitic phase and more importantly our discrete dislocation–transformation framework is able to capture the effect of grain orientations on the transformation mechanism in microscale modelling of the structure.

3.3 Discrete dislocation–transformation method and grain size effect (Hall–Petch effect)

The grain size is another important factor related to the polycrystalline metals. The effect of grain size on the mechanical behaviour of metals was first proposed by Hall and Petch; therefore, the grain size effect is also called “Hall–Petch effect”. There are a lot of studies that investigate the grain size effect in polycrystalline structure experimentally and computationally [31]. Shi et al. [22] studied the effect of grain size on the transformation-induced plasticity in TRIP steels by discrete dislocation–transformation model. It was observed that the grain boundaries play an obstacle role against the dislocation motion. It is clear that the smaller grain size means higher grain boundary density and more resistance against dislocation motions. Therefore, the finer grain size materials exhibit higher strength behaviour in comparison with coarse grain polycrystalline structure.

To investigate microstructurally the effect of grain size on the mechanical behaviour of multi-crystalline domain, three multi-crystalline samples are studied with discrete dislocation–transformation method under isothermal mechanical loading. These specimens are combined from 4, 9, and 16 square-shaped grains, respectively. Furthermore, the orientation of each grain in multi-crystalline structure is assigned randomly. The schematic of the multi-crystalline samples is depicted in Fig. 7.

Fig. 7

Schematic of models to study grain size effect

In Fig. 8, the mechanical responses of the three multi-crystalline domains with different grain sizes under isothermal mechanical loading are compared together. As it is shown in the figure, the specimens with finer grains show more hardening mechanical behaviour. The small grain sample has higher grain boundary densities; therefore, it causes more resistance against dislocation motion and phase transformation. To have a better understanding about the effect of grain boundaries on the dislocation dynamic and transformation growth, the evolution of dislocation density and martensitic volume fraction is compared for simulations with different grain sizes. These are illustrated in Fig. 8b and c, respectively.

Fundamentally, work hardening is quantified by increasing the number of dislocations in microstructure of crystalline metals. As shown in Fig. 8b, the size of the grains affects the dislocation density in the domain. As the smaller grain specimens have more grain boundary densities in their microstructures, the likelihood of dislocations reaching the grains and having pinned to the boundaries would be increased. Therefore, the sample with higher dislocation density in Fig. 8b shows more hardening response in Fig. 8a.

Fig. 8

Grain size effect on pseudoelasticity behaviour of multi-crystalline samples by comparing a the stress–strain response, b the dislocation density, and c the martensitic volume fraction

Figure 8c shows the particular effect of grain boundaries on the phase transformation in multi-crystalline NiTi. As it is illustrated in the figure, the samples with finer grains show less martensitic transformation. This result is in accordance with the assumption which is considered in the beginning of this section. Based on this assumption, the martensitic regions stop growing by reaching the grain boundaries. Therefore, the resistance against martensitic growth increases in multi-crystalline samples with smaller grains.

To provide more detailed insight into the effect of grain boundaries on mechanical behaviour of samples including plasticity and martensitic transformation, the distribution of the local axial stress $\sigma _{11}$ inside the samples and the corresponding microstructure are shown in Fig. 9 for the three aforementioned cases (four grains, nine grains, and sixteen grains). The figures include a contour plot at the end of the loading step, when the average axial strain is $\bar{\varepsilon }_{11} = 0.01$. In Fig. 9, dislocation cores are indicated with the symbol “+” while the martensitic regions are represented through their external (elliptical) shapes and the grain boundaries are highlighted with red colour.

Figure 9 presents a typical plastic deformation with dislocation pile-ups at the grain boundaries, which generate the hardening observed in Fig. 8a. It is illustrated that there is more dislocation pinning in the boundaries in Fig. 9c in comparison with Fig. 9a and b due to the higher density of grain boundaries. Therefore, more resistance against dislocation motion in Fig. 9 causes higher dislocation densities and more hardening behaviour that are shown in Fig. 8a and b, respectively.

Furthermore, Fig. 9 illustrates the local stress concentration at grain boundaries in the microstructure. As a result, the specimens with smaller grains (higher density of grain boundary) represent more local regions with concentrated local stresses in the microstructure (the light yellow area in Fig. 9). Therefore, predicting the non-uniform stress distribution as illustrated in Fig. 9 is one of the potentials of the current discrete dislocation–transformation framework presented in this study. This could be applied for calculating the local stress concentration in microstructure that affects other deformation mechanisms such as twinning, fracture, and failure.

Fig. 9

Distribution of axial stress, dislocations, and martensitic regions at an average strain of 0.01 for the following cases: a four grains, b nine grains, and c sixteen grains

3.4 Grain size effect under thermal cyclic loading of multi-crystal NiTi

This section studies the mechanical behaviour of multi-crystalline SMA under thermal cyclic loading and constant external stresses. These simulations are performed to observe the shape memory effect in multi-crystalline NiTi and the effect of grain sizes on this behaviour. Here, the same samples presented in Fig. 7 are cooled from austenite to martensitic phase and then heated back to the initial temperature when they are under constant uniaxial stress.

The grain size effect on thermal cyclic loading of multi-crystalline NiTi is illustrated in Fig 10a–c. As shown in Fig. 10a, the specimen with larger grain size experiences larger transformation strain than specimens with smaller grain sizes along cooling and heating. Furthermore, to study the grain size effect on both transformation and plasticity mechanisms, the evolution of martensitic volume fraction and dislocation density is compared for different grain sizes in Fig. 10b and c, respectively.

Fig. 10

Grain size effect on the shape memory behaviour of multi-crystalline NiTi under temperature cyclic loading

Figure 10b presents that the material transformed less in finer grain samples. It is because of the fact that by reducing the size of grains, the density of grain boundaries increased and each grain boundary acts as a resistance wall against the growth of transformation interface. Moreover, Fig. 10c illustrates that the amount of dislocation density and, as a result, plastic strain is higher in specimens with larger grain size. At a glance, it is against the fact that grain boundaries cause the increase of dislocations and hence work hardening. However, by looking deeply at Fig. 10c it is notable that dislocation generation is induced by phase transformation around the temperature of $70^\circ C$, and before martensitic transformation, there is no dislocation dynamics. It means that the plastic mechanism is activated by the local stress field generated by martensitic regions. Therefore, the sample with higher transformation growth (grain size = 2 $\upmu \textrm{m}$ in Fig. 10b) shows higher dislocation density in Fig. 10c.

3.5 Effect of applied stress in thermal cyclic loading of multi-crystal NiTi

Finally, two-way shape memory effect behaviour of a multi-crystalline SMA sample made from nine grains is studied under temperature cycling and two different uniaxial stresses equal to 50 and 300 MPA. The results are presented in Fig. 11. As shown in Fig. 11b and d, for both samples, the martensitic regions transformed back completely by heating to the initial temperature in austenite phase. This means there is no residual strain due to the remaining martensitic phase after thermal cyclic loading. However, Fig. 11a and c illustrates some non-reversible strain after thermal cycling in both sample. This remaining strain is due to the dislocation plasticity which is induced mainly by the martensitic transformation (as the uniaxial applied stress is much lower than yield stress in NiTi material). It is observed that the plastic strain for the sample under 300 MPa external stress is higher than that of the sample under 50 MPa applied stress. It is due to the fact that the Peach–Koehler force (driving force for dislocation generation and motion) is computed by local stress field which is a combination of stress field of martensitic regions (which is similar for both sample) and the external stresses.

Fig. 11

Two-way shape memory effect of multi-crystalline NiTi under thermal cyclic loading with an externally applied uniaxial stress of a, b 50 MPa, and c, d 300 MPa

4 Conclusions

In this study, the interaction between dislocation slip plasticity and martensitic phase transformation was investigated. This interaction included the effects of martensitic transformation on dislocation plasticity (i.e. transformation-induced plasticity) and effects of dislocations on the generation and growth of martensitic regions. These phenomena were modelled by a discrete dislocation–transformation method at the sub-micron length scale.

The two-dimensional bi-crystalline samples of NiTi shape memory alloy were simulated by the discrete dislocation–transformation framework. The results illustrated the effect of different structural orientations on the thermo-mechanical response of the SMAs. It was explained that both dislocation slip and martensitic transformation are orientation dependent. Therefore, changing the orientation of one grain in a bi-crystalline sample led the mechanical response of the specimen during loading to change.

Furthermore, the effects of grain size and grain boundary densities on the two-way shape memory effect and pseudoelasticity behaviour were studied. The grain boundaries act as an obstacle against the dislocation motion and martensitic growth. Therefore, the smaller grain specimens caused more dislocation pinning and less martensitic growth, and as a result, it showed more hardening responses. These results also confirm that our discrete dislocation–transformation framework has the ability to simulate the Hall–Petch effect in polycrystalline structures.

Finally, despite the limitations of a two-dimensional discrete dislocation–transformation model, it still provides useful validated information about the interaction between plasticity and martensitic phase transformation. The model could describe the grain orientations and grain size effects in shape memory alloys at the length scales that are somewhat sophisticated to resolve experimentally, particularly when the loading conditions change. This could be therefore a robust computational tool for further investigation on coexistence of plasticity and phase transformation in SMAs and other alloys. Furthermore, the proposed computational method would benefit the data-driven and machine learning modelling approaches by providing further data from the microstructure of SMAs and accelerates the data sampling methodologies.

A Full pseudoelasticity response

In this appendix, the full stress–strain curve of pseudoelasticity behaviour of polycrystalline NiTi during loading and unloading is provided in Fig. 12. This graph demonstrates the irreversibility in the super-elasticity response and the contribution of plasticity to the irreversible strain after a complete cycle involving the forward and reverse martensite transformation processes of shape memory alloy. Figure 12 is particularly related to the four polycrystalline case with four different grain orientations described in Figs. 5 and 6 in Sect. 3.2.

Fig. 12

Grain size effect on the shape memory behaviour of multi-crystalline NiTi under temperature cyclic loading