Mathematical modelling of thermoelasticity problems for thin biperiodic cylindrical shells

Abstract

The objects of consideration are thin linearly thermoelastic Kirchhoff-Love-type circular cylindrical shells having a periodically microheterogeneous structure in circumferential and axial directions (biperiodic shells). The aim of this contribution is to formulate and discuss two new averaged mathematical models for the analysis of selected dynamic thermoelasticity problems for the shells under consideration: the non-asymptotic tolerance and the consistent asymptotic models. The starting equations are the well-known governing equations of linear Kirchhoff-Love theory of thin elastic cylindrical shells combined with Duhamel–Neumann thermoelastic constitutive relations and coupled with the known linearized Fourier heat conduction equation in which the heat sources are neglected. For the microperiodic shells under consideration, the starting equations mentioned above have highly oscillating, non-continuous and periodic coefficients. The tolerance model is derived applying the tolerance averaging technique and a certain extension of the known stationary action principle. It has constant coefficients depending also on a cell size. Hence, this model makes it possible to study the effect of a microstructure size on the global shell thermoelasticity (the length-scale effect). The consistent asymptotic model is obtained using the consistent asymptotic approach. It has constant coefficients being independent of the period lengths. Moreover, the comparison between the tolerance model for biperiodic shells proposed here and the known tolerance model for cylindrical shells with a periodic structure in the circumferential direction only (uniperiodic shells) is presented.

1 Introduction

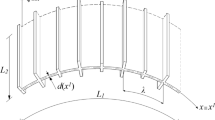
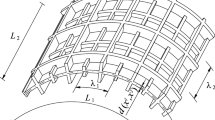
Thin linearly thermoelastic Kirchhoff-Love-type circular cylindrical shells with a periodically microinhomogeneous structure in circumferential and axial directions are objects of consideration. Shells of this kind are termed biperiodic. By periodic inhomogeneity we shall mean periodically varying thickness and/or periodically varying inertial, elastic and thermal properties of the shell material. We restrict our consideration to those biperiodic cylindrical shells, which are composed of a large number of identical elements. Moreover, every such element, called a periodicity cell, can be treated as a thin shell. Typical examples of such shells are presented in Figs. 1 (stiffened shell) and 2 (a shell composed of two kinds of periodically distributed materials).

Thermoelastic problems of periodic structures (shells, plates, beams) are described by partial differential equations with periodic, highly oscillating and discontinuous coefficients. Thus, these equations are too complicated to constitute the basis for investigations of most of the engineering problems. To obtain averaged equations with constant coefficients, many different approximate modelling methods for structures of this kind have been formulated. Periodic cylindrical shells (plates) are usually described using homogenized models derived by applying asymptotic methods. These asymptotic models represent certain equivalent structures with constant or slowly varying rigidities and averaged mass densities. Unfortunately, the asymptotic procedures are usually restricted to the first approximation, which leads to homogenized models neglecting the effect of a periodicity cell size (called the length-scale effect) on the overall shell behaviour. The mathematical foundations of this modelling technique can be found in Bensoussan et al. [1], Jikov et al. [2]. Applications of the asymptotic homogenization procedure to modelling of stationary and non-stationary phenomena for microheterogeneous shells (plates) are presented in a large number of contributions. From the extensive list on this subject we can mention paper by Lutoborski [3] and monographs by Lewiński and Telega [4], Andrianov et al. [5].

The length-scale effect can be taken into account using the non-asymptotic tolerance averaging technique. This technique is based on the concept of the tolerance relations related to the accuracy of the performed measurements and calculations. The mathematical foundations of this modelling technique can be found in Woźniak and Wierzbicki [6], Woźniak et al. [7, 8], Ostrowski [9]. A certain extended version of the tolerance modelling technique has been proposed by Tomczyk and Woźniak in [10]. For periodic structures, governing equations of the tolerance models have constant coefficients dependent also on a cell size. Some applications of this averaging method to the modelling of mechanical and thermomechanical problems for various periodic structures are shown in many works. We can mention here monograph by Tomczyk [11] and papers by Tomczyk and Litawska [12,13,14], Tomczyk et al. [15,16,17], where the length-scale effect in mechanics of periodic cylindrical shells is investigated; papers by Baron [18], where dynamic problems of medium thickness periodic plates are studied and by Marczak and Jędrysiak [19], Marczak [20, 21], where dynamics of periodic sandwich plates is analysed; papers by Jędrysiak [22,23,24], which deal with stability of thin periodic plates; papers by Łaciński and Woźniak [25], Rychlewska et al. [26], Ostrowski and Jędrysiak [27], Kubacka and Ostrowski [28], where problems of heat conduction in conductors with periodic structure are analysed. Let us also mention papers by Bagdasaryan et al. [29], Tomczyk and Gołąbczak [30], which deal with coupled thermoelasticity problems, respectively, for multicomponent, multi-layered periodic composites and for thin cylindrical shells with microperiodic structure in circumferential direction (uniperiodic shells). The extended list of references on this subject can be found in [6,7,8,9, 11].

Fig. 1

Fragment of the shell reinforced by two families of biperiodically spaced ribs

Fig. 2

Fragment of the shell composed of two different materials periodically and densely distributed in circumferential and axial directions

The tolerance averaging technique was also adopted to formulate mathematical models for analysis of various mechanical and thermomechanical problems for functionally graded solids, e.g. for heat conduction in longitudinally graded hollow cylinder by Ostrowski and Michalak [31, 32], for thermoelasticity of transversally graded laminates by Pazera and Jędrysiak [33], Pazera et al. [34], for dynamics for functionally graded annular plates by Wirowski and Rabenda [35], for dynamics or stability of functionally graded thin cylindrical shells by Tomczyk and Szczerba [36,37,38,39].

The main aim of this contribution is to formulate and discuss a new mathematical averaged tolerance model for the analysis of selected dynamic thermoelasticity problems for the biperiodic cylindrical shells under consideration. Contrary to the starting exact equations of the shell thermoelasticity with periodic, highly oscillating and discontinuous coefficients, governing equations of the proposed averaged model have constant coefficients depending also on a characteristic cell length dimension. Hence, this model allows us to describe the influence of a length scale on the thermoelastic shell behaviour. In order to derive this model we shall apply a certain new variational approach to the tolerance modelling of microheterogeneous media given by Woźniak in [8]. This approach is based on the tolerance averaging of integral functionals describing behaviour of the microinhomogeneous structures. Then, by using a certain extension of the known stationary action principle to the resulting averaged functionals we arrive at the tolerance model equations. Moreover, it will be proved that the result obtained by using the variational approach mentioned above coincides with that derived by means of an orthogonalization approach. The orthogonalization method is based on the tolerance averaging of the partial differential equations describing thermoelasticity behaviour of microinhomogeneous structures combined with certain orthogonality conditions [6, 9, 10]. The proposed here tolerance model of thermoelasticity problems for the thin biperiodic cylindrical shells will be compared with the tolerance model for thin cylindrical shells having a microperiodic structure along the circumferential direction only (uniperiodic shells). This uniperiodic shell model was formulated by Tomczyk and Gołąbczak in [30]. The main differences and similarities between both models will be discussed.

The second aim is to derive a new averaged consistent asymptotic model for the analysis of selected dynamic thermoelasticity problems for the biperiodic cylindrical shells under consideration. The model will be derived applying a certain new approach to the asymptotic modelling of microheterogeneous media proposed by Woźniak in [8]. This approach is based on the consistent asymptotic averaging of integral functionals describing behaviour of the microheterogeneous structures and on using the extended stationary action principle. The asymptotic model equations have constant coefficients being independent of a period lengths. The main advantage of this asymptotic approach is that the effective elastic and thermal moduli of the microperiodic shells under consideration can be obtained without specification of the periodic cell problem.

2 Formulation of the problem: starting equations

We assume that $x^{1}$ and $x^{2}$ are coordinates parametrizing the shell midsurface M in circumferential and axial directions, respectively. We denote ${\mathbf{x}}\equiv (x^{1},x^{2})\in \Omega \equiv (0,L_{1} )\times (0,L_{2} )$, where $L_{1} ,L_{2}$ are length dimensions of M, cf. Figs. 1 and 2. Let $O\,\bar{{x}}^{1}\bar{{x}}^{2}\bar{{x}}^{3}$ stand for a Cartesian orthogonal coordinate system in the physical space $E^{3}$ and denote ${{\bar{{\mathbf{x}}}}}\equiv (\bar{{x}}^{1},\bar{{x}}^{2},\bar{{x}}^{3})$. Let us introduce the orthonormal parametric representation of the underformed cylindrical shell midsurface M by means of $M\equiv \left\{ {\,{{\bar{{\mathbf{x}}}}}\in E^{3}:{{\bar{{\mathbf{x}}}}}={{\bar{{\mathbf{r}}}}}\left( {x^{1}\,,x^{2}} \right) ,\,\left( {\,x^{1},x^{2}} \right) \in \Omega \,} \right\}$, where ${{\bar{{\mathbf{r}}}}}(\cdot )$ is the smooth invertible function such that $\partial \,{{\bar{{\mathbf{r}}}}}\text{/ }\partial x^{1}\cdot \partial \,{{\bar{{\mathbf{r}}}}}\text{/ }\partial x^{2}=0$, $\partial \,{{\bar{{\mathbf{r}}}}}\text{/ }\partial x^{1}\cdot \partial \,{{\bar{{\mathbf{r}}}}}\text{/ }\partial x^{1}=1$, $\partial \,{{\bar{{\mathbf{r}}}}}\text{/ }\partial x^{2}\cdot \partial \,{{\bar{{\mathbf{r}}}}}\text{/ }\partial x^{2}=1$. Note that derivative $\partial \,{{\bar{{\mathbf{r}}}}}\text{/ }\partial x^{\upalpha }$, $\upalpha =1,2$, should be understood as differentiation of each component of $\,{{\bar{{\mathbf{r}}}}}\in E^{3}$, i.e. $\partial \,{{\bar{{\mathbf{r}}}}}\text{/ }\partial x^{\upalpha }=[\partial \bar{{r}}^{1}/\partial x^{\upalpha },\partial \bar{{r}}^{2}/\partial x^{\upalpha },\partial \bar{{r}}^{3}/\partial x^{\upalpha }]$.

Let $d({\mathbf{x}})$, r stand for the shell thickness and the midsurface curvature radius, respectively.

Throughout the paper, indices $\upalpha ,\upbeta ,$…run over 1,2 and are related to midsurface parameters $x^{1}, x^{2}$, summation convention holds. Partial differentiation related to $x^{\upalpha }$ is represented by $\partial _{\upalpha }$, $\partial _{\upalpha } =\partial /\partial x^{\upalpha }$. Moreover, it is denoted $\partial _{\upalpha ...\delta } \equiv \partial _{\upalpha } ...\partial _{\delta }$. Let $a_{\upalpha \upbeta }$ and $a^{\upalpha \upbeta }$ stand for the covariant and contravariant midsurface first metric tensors, respectively. Denote by $b_{\upalpha \upbeta }$ the covariant midsurface second metric tensor. Under orthonormal parametrization introduced on M, $a_{\upalpha \upbeta } =a^{\upalpha \upbeta }$ are unit tensors and components of tensor $b_{\upalpha \upbeta }$ are: $b_{22} =b_{12} =b_{21} =0$, $b_{11} =-r^{-1}$. We denote $t\in \mathrm{I}=[t_{0} ,t_{1} ]$ as the time coordinate.

The basic cell $\Delta$ and an arbitrary cell $\Delta ({\mathbf{x}})$ with the centre at point ${\mathbf{x}}\in \Omega _{\Delta }$ are defined by means of: $\Delta \equiv [-\lambda _{1} /2,\;\lambda _{1} /2]\times [-\lambda _{2} /2,\;\lambda _{2} /2]$, $\Delta ({\mathbf{x}})\equiv {\mathbf{x}}+\Delta \,$, $\Omega _{\Delta } \equiv \{{\mathbf{x}}\in \Omega :\Delta ({\mathbf{x}})\subset \Omega \}$, where $\lambda _{1}$and $\lambda _{2}$ are the period lengths of the shell structure, respectively, in $x^{1}$- and $x^{2}$-directions. The diameter $\lambda \equiv \sqrt{(\lambda _{1} )^{2}+(\lambda _{2} )^{2}}$ of $\Delta$, called the microstructure length parameter,    is assumed to satisfy conditions:    $\lambda /\mathop {\sup }\limits _{{\mathbf{x}}\in \Omega } d({\mathbf{x}})>>1$, $\lambda /r<<1$ and $\lambda /\min (L_{1} ,L_{2} )<<1$.

Setting ${\mathbf{z}}\equiv (z^{1},z^{2})\in [-\lambda _{1} /2,\;\lambda _{1} /2]\times [-\lambda _{2} /2,\;\lambda _{2} /2]$, we assume that the cell $\Delta$ has two symmetry axes: for $z^{1}=0$ and $z^{2}=0$. It is also assumed that inside the cell not only the geometrical but also elastic, inertial and thermal properties of the shell are described by symmetric (i.e. even) functions of ${\mathbf{z}}$.

Denote by $u_{\upalpha } =u_{\upalpha } ({\mathbf{x}},t)$, $w=w({\mathbf{x}},t)$, ${\mathbf{x}}\in \Omega$, $t\in \mathrm{I}$, the shell displacements in directions tangent and normal to M, respectively. Elastic properties of the shell are described by shell stiffness tensors $D^{\upalpha \upbeta \gamma \delta }({\mathbf{x}})$, $B^{\upalpha \upbeta \gamma \delta }({\mathbf{x}})$. Let $\mu ({\mathbf{x}})$ stand for a shell mass density per midsurface unit area. Let $f^{\upalpha }({\mathbf{x}},t)$, $f({\mathbf{x}},t)$ be the external forces per midsurface unit area, respectively, tangent and normal to M.

Denote by $\theta ({\mathbf{x}},t)$ the temperature field treated as the temperature increment from a certain constant reference temperature $T_{0}$ (by reference temperature we shall mean the zero stress temperature). It is assumed that $\theta /T_{0}<<1$. Let $\bar{{d}}^{\upalpha \upbeta }({\mathbf{x}})$ stand for the membrane thermal stiffness tensor (tensor of thermoelastic moduli: $\bar{{d}}^{\upalpha \upbeta }=D^{\upalpha \upbeta \gamma \delta }\upalpha _{\gamma \delta }$, where $\upalpha _{\gamma \delta }$ are coefficients of thermal expansion). Denote by $K^{\upalpha \upbeta }({\mathbf{x}})$ and $c({\mathbf{x}})$ the tensor of heat conductivity and the specific heat, respectively. The heat sources will be neglected. For biperiodic shells, $D^{\upalpha \upbeta \gamma \delta }({\mathbf{x}})$, $B^{\upalpha \upbeta \gamma \delta }({\mathbf{x}})$, $\mu ({\mathbf{x}})$, $\bar{{d}}^{\upalpha \upbeta }({\mathbf{x}})$, $K^{\upalpha \upbeta }({\mathbf{x}})$, $c({\mathbf{x}})$ are periodic, highly oscillating and non-continuous functions with respect to argument x.

It is assumed that the temperature along the shell thickness is constant. From this restriction it follows that only the coupling between temperature field $\theta$ and membrane stresses occurs (describing by tensor $\bar{{d}}^{\upalpha \upbeta }({\mathbf{x}}))$, while the coupling of temperature and bending stresses is absent.

The starting equations are the well-known governing equations of linear Kirchhoff-Love theory of thin elastic cylindrical shells combined with Duhamel–Neumann thermoelastic constitutive relations and coupled with the known linearized Fourier heat conduction equation in which the heat sources are neglected [40,41,42,43,44]. Thus, the starting equations consist of

(a) the Duhamel–Neumann stress–strain–temperature relations

$$\begin{aligned} n^{\upalpha \upbeta }({\mathbf{x}},t)= & {} D^{\upalpha \upbeta \gamma \delta }({\mathbf{x}})\varepsilon _{\gamma \delta } ({\mathbf{x}},t)-\bar{{d}}^{\upalpha \upbeta }({\mathbf{x}})\theta ({\mathbf{x}},t), \nonumber \\ m^{\upalpha \upbeta }({\mathbf{x}},t)= & {} B^{\upalpha \upbeta \gamma \delta }({\mathbf{x}})\kappa _{\gamma \delta } ({\mathbf{x}},t),\quad ({\mathbf{x}},t)\in \Omega \times \mathbf{I}, \end{aligned}$$

(1)

where

$$\begin{aligned} \varepsilon _{\upalpha \upbeta } =\frac{1}{2}(\partial _{\upbeta } u_{\upalpha } +\partial _{\upalpha } u_{\upbeta } )-b_{\upalpha \upbeta } w,\quad \kappa _{\upalpha \upbeta } =-\partial _{\upalpha \upbeta } w, \end{aligned}$$

(2)

(b) the dynamic equilibrium equations

$$\begin{aligned} \partial _{\upbeta } n^{\upalpha \upbeta }-\mu a^{\upalpha \upbeta }\ddot{{u}}_{\upbeta } +f^{\upalpha }=0,\quad \partial _{\upalpha \upbeta } m^{\upalpha \upbeta }+b_{\upalpha \upbeta } n^{\upalpha \upbeta }-\mu \ddot{{w}}+f=0, \end{aligned}$$

(3)

which after combining with (1) and (2) are expressed in displacement fields $u_{\upalpha }, w$ and temperature field $\theta$

$$\begin{aligned}&\partial _{\upbeta } (D^{\upalpha \upbeta \gamma \delta }\partial _{\delta } u_{\gamma } )+r^{-1}\partial _{\upbeta } (D^{\upalpha \upbeta 11}w)-\partial _{\upbeta } (\bar{{d}}^{\upalpha \upbeta }\theta )-\mu a^{\upalpha \upbeta }\ddot{{u}}_{\upbeta } +f^{\upalpha }=0, \nonumber \\&r^{-1}D^{\upalpha \upbeta 11}\partial _{\upbeta } u_{\upalpha } +\partial _{\upalpha \upbeta } (B^{\upalpha \upbeta \gamma \delta }\partial _{\gamma \delta } w)-r^{-1}\bar{{d}}^{11}\theta +r^{-2}D^{1111}w+\mu \ddot{{w}}-f=0, \end{aligned}$$

(4)

(c) the linearized heat conduction equation based on the Fourier law coupled with (4)

$$\begin{aligned} \partial _{\upalpha } (K^{\upalpha \upbeta }\partial _{\upbeta } \theta )-c\dot{{\theta }}=T_{0} (\bar{{d}}^{\upalpha \upbeta }\partial _{\upalpha } \dot{{u}}_{\upbeta } +r^{-1}\bar{{d}}^{11}\dot{{w}}). \end{aligned}$$

(5)

We recall that $b_{\upalpha \upbeta }$ in (2), (3) is the second metric tensor of the shell midsurface; under orthonormal parametrization introduced on M, components of tensor $b_{\upalpha \upbeta }$ are: $b_{22} =b_{12} =b_{21} =0$, $b_{11} =-r^{-1}$.

Equations (4) and (5) describe the dynamic thermoelasticity problems for the shells under consideration. Coefficients of these equations are periodic, highly oscillating and non-continuous functions in x.

Now, we are to show that Eqs. (4) and (5) can be also derived from the extended principle of stationary action proposed in [8]. These equations cannot be obtained from the principle of stationary action in its classical form because heat conduction Eq. (5) involves the odd derivatives of unknown functions $\theta ({\mathbf{x}},t)$, $u_{\upalpha } =u_{\upalpha } ({\mathbf{x}},t)$, $w=w({\mathbf{x}},t)$, $({\mathbf{x}},t)\in \Omega \times \mathrm{I}$, with respect to argument t.

We assume that the thermoelastic problems of thin shells considered here are described by the following action functional

$$\begin{aligned} A(u_{\upalpha } ,w,p^{\upalpha \upbeta },\mathop {r}\limits ^{\frown } )=\int \limits _0^{L_{1} } {\int \limits _0^{L_{2} } {\int \limits _{t_{0} }^{t_{1} } {L({\mathbf{x}},t,\partial _{\upbeta } u_{\upalpha } ,u_{\upalpha } ,\dot{{u}}_{\upalpha } ,\partial _{\upalpha \upbeta } w,w,\dot{{w}},p^{\upalpha \upbeta },\mathop {r}\limits ^{\frown } )\mathrm{d}t\mathrm{d}x^{2}\mathrm{d}x^{1}} } }, \end{aligned}$$

(6)

where Lagrangian L, being a highly oscillating function with respect to x, is determined by

$$\begin{aligned}&L=-\;\frac{1}{2}(D^{\upalpha \upbeta \gamma \delta }\partial _{\upbeta } u_{\upalpha } \partial _{\delta } u_{\gamma } +\frac{2}{r}D^{\upalpha \upbeta 11}w\partial _{\upbeta } u_{\upalpha } +\frac{1}{r^{2}}D^{1111}ww \nonumber \\&\qquad +B^{\upalpha \upbeta \gamma \delta }\partial _{\upalpha \upbeta } w\partial _{\gamma \delta } w-K^{\upalpha \upbeta }\partial _{\upalpha } \theta \partial _{\upbeta } \theta -\mu a^{\upalpha \upbeta }\dot{{u}}_{\upalpha } \dot{{u}}_{\upbeta } -\mu \dot{{w}}^{2})+f^{\upalpha }u_{\upalpha } +fw \nonumber \\&\qquad +p^{\upalpha \upbeta }\partial _{\upbeta } u_{\upalpha } +\frac{1}{r}p^{11}w+\mathop {r}\limits ^{\frown } \theta , \end{aligned}$$

(7)

and where functions $p^{\upalpha \upbeta }({\mathbf{x}},t)$, $\mathop {r}\limits ^{\frown } ({\mathbf{x}},t)$ are highly oscillating with respect to x and determined by independent equations

$$\begin{aligned} p^{\upalpha \upbeta }= & {} \bar{{d}}^{\upalpha \upbeta }\theta , \nonumber \\ \mathop {r}\limits ^{\frown }= & {} c\dot{{\theta }}+T_{0} (\bar{{d}}^{\upalpha \upbeta }\partial _{\upalpha } \dot{{u}}_{\upbeta } +r^{-1}\bar{{d}}^{11}\dot{{w}}). \end{aligned}$$

(8)

Equation (8) is called the constitutive equations for functions $p^{\upalpha \upbeta }({\mathbf{x}},t)$, $\mathop {r}\limits ^{\frown } ({\mathbf{x}},t)$. It has to be emphasized that functions $p^{\upalpha \upbeta }$, $\mathop {r}\limits ^{\frown }$ are not arguments of Lagrangian (7); they play the role of non-variational parameters.

Under assumption that $\partial L/\partial (\partial _{\upbeta } u_{\upalpha } )$, $\partial L/\partial (\partial _{\upalpha \upbeta } w)$ and $\partial L/\partial (\partial _{\upbeta } \theta )$ are continuous, from the extended principle of stationary action applied to $A(u_{\upalpha } ,w,p^{\upalpha \upbeta },\mathop {r}\limits ^{\frown } )$, we obtain the following system of Euler-Lagrange equations

$$\begin{aligned}&\partial _{\upbeta } \frac{\partial L}{\partial (\partial _{\upbeta } u_{\upalpha } )}-\frac{\partial L}{\partial u_{\upalpha } }+\frac{\partial }{\partial t}\frac{\partial L}{\partial \dot{{u}}_{\upalpha } }=0, \nonumber \\&\quad -\partial _{\upalpha \upbeta } \frac{\partial L}{\partial (\partial _{\upalpha \upbeta } w)}-\frac{\partial L}{\partial w}+\frac{\partial }{\partial t}\frac{\partial L}{\partial \dot{{w}}}=0, \nonumber \\&\partial _{\upbeta } \frac{\partial L}{\partial (\partial _{\upbeta } \theta )}-\frac{\partial L}{\partial \theta }=0. \end{aligned}$$

(9)

Combining (9) with (7) and (8) we arrive finally at the explicit form of the fundamental equations of the thermoelasticity shell theory under consideration. These equations coincide with well-known Eqs. (4), (5).

The passage from action functional (6) to Euler-Lagrange Eq. (9) in which $p^{\upalpha \upbeta }$, $\mathop {r}\limits ^{\frown }$ are given by constitutive Eq. (8) represents the extended principle of stationary action or the principle of stationary action extended by constitutive equations.

Applying the tolerance averaging technique [8, 9] to Lagrange function (7) and independently to constitutive Eq. (8) and then using the extended stationary action principle we obtain the tolerance model equations describing thermoelastic phenomena in the biperiodic shells being object of considerations in this paper. All coefficients in the governing equations of the tolerance model are constant in contrast to those from direct description (4), (5), and some of them depend on a microstructure size.

It will be shown that the result obtained by using the variational approach mentioned above coincides with that derived by means of an orthogonalization approach based on the tolerance averaging of thermoelasticity Eqs. (4), (5) and then on using the residual orthogonality conditions [6, 9, 10].

Moreover, applying the consistent asymptotic procedure [8, 9] to Lagrange function (7) and independently to constitutive Eq. (8) and then using the extended stationary action principle we derive the asymptotic model equations describing thermoelastic behaviour of the periodic shells under consideration. The governing equations of the asymptotic model have constant coefficients but independent of period lengths.

To make this paper self-consisted, in the subsequent section we shall outline the main concepts and the fundamental assumptions of the tolerance modelling procedure and of the consistent asymptotic approach,    which in the general form are given in monographs [6,7,8,9,10].

3 Concepts and assumptions of tolerance and asymptotic modelling techniques

3.1 Main concepts and modelling assumptions of the tolerance averaging procedure

The fundamental concepts of the tolerance modelling procedure under consideration are those of two tolerance relations between points and real numbers determined by tolerance parameters, slowly varying functions, tolerance-periodic functions, fluctuation shape functions and the averaging operation.

Below, the mentioned above concepts and assumptions will be specified with respect to two-dimensional region $\Omega =(0,L_{1} )\times (0,L_{2} )$ defined in this paper.

Let $\lambda$ be a positive real number. Points ${\mathbf{x}},{\mathbf{y}}$ belonging to $\Omega =(0,L_{1} )\times (0,L_{2} )$ are said to be in tolerance determined by $\lambda$, if and only if the distance between points ${\mathbf{x}},{\mathbf{y}}$ does not exceed $\lambda$, i.e. $\left| {{\mathbf{x}}-{\mathbf{y}}} \right| \le \lambda$.

Let $\tilde{{\delta }}$ be a positive real number. Real numbers $\mu ,\;\nu$ are said to be in tolerance determined by $\tilde{{\delta }}$, if and only if $\left| {\mu -\nu } \right| \le \tilde{{\delta }}$.

The above relations are denoted by: $\mathbf{x}\mathop {\approx }\limits ^{\lambda } \mathbf{y}$, $\mu \mathop {\approx }\limits ^{\tilde{{\delta }}} \nu$. Positive parameters $\lambda ,\tilde{{\delta }}$ are called tolerance parameters.

Let F be a function defined in $\bar{{\Omega }}=[0,L_{1} ]\times [0,L_{2} ]$, which is continuous, bounded and differentiable in $\bar{{\Omega }}$ together with its derivatives up to the $R-$th order. It can be observed that function F is said to be differentiable in closed set $\bar{{\Omega }}$; however, we do not specify how derivatives are defined on its fringe $\partial \Omega$ because differentiation may look differently for any particular problem. Non-negative integer R is assumed to be specified in every problem under consideration. Note that function F can also depend on time coordinate t as parameter. Let $\delta \equiv (\lambda ,\delta _{0} ,\delta _{1} ,..,\delta _{R} )$ be the set of tolerance parameters. The first of them represents the distances between points in $\bar{{\Omega }}$. The second one and the $k-$th one, $k=1,..,R$, are related, respectively, to the absolute differences between the values of function F and its gradient $\partial ^{k}F(\cdot )$ in points ${\mathbf{x}},{\mathbf{y}}$ belonging to $\bar{{\Omega }}$ such that $\left| {{\mathbf{x}}-{\mathbf{y}}} \right| \le \lambda$. A function F is said to be slowly varying of the R-th kind with respect to cell $\Delta$ and tolerance parameters $\delta$, $F\in SV_{\delta }^{R} (\Omega ,\Delta )$, if and only if the following conditions are fulfilled

$$\begin{aligned}&(\forall ({\mathbf{x}},{\mathbf{y}})\in \Omega ^{2})[({\mathbf{x}}\mathop {\approx }\limits ^{\lambda } {\mathbf{y}})\Rightarrow F({\mathbf{x}})\mathop {\approx }\limits ^{\delta _{0} } F({\mathbf{y}})\;\;\mathrm{and}\;\;\partial ^{k}F({\mathbf{x}})\mathop {\approx }\limits ^{\delta _{k} } \partial ^{k}F({\mathbf{y}}),\;\;\;k=1,2,\ldots ,R]\,, \end{aligned}$$

(10)

$$\begin{aligned}&(\forall {\mathbf{x}}\in \Omega )\;\left[ {\lambda \,\left| {\partial ^{k}F({\mathbf{x}})} \right| \mathop {\approx }\limits ^{\delta _{k} } \;0,\quad \;k=1,2,\ldots ,R} \right] \,. \end{aligned}$$

(11)

Roughly speaking, the slowly varying function can be treated (together with its gradients up to the R-th order) as constant on an arbitrary cell. Moreover, the products of derivatives of slowly varying functions and microstructure length parameter $\lambda$ are negligibly small.

It is worth to known that tolerance parameter $\lambda$ in every problem under consideration is known a priori as a characteristic cell length dimension, whereas values of tolerance parameters $\delta _{0} ,\delta _{1} ,\ldots ,\delta _{R}$ can be determined only a posteriori, i.e. after obtaining unique solution to the considered initial-boundary value problem.

An essentially bounded and weakly differentiable function $\varphi$ defined in $\bar{{\Omega }}=[0,L_{1} ]\times [0,L_{2} ]$, which can also depend on time coordinate t as parameter, is called tolerance-periodic in reference to cell $\Delta$ and tolerance parameters $\delta \equiv (\lambda ,\delta _{0} )$, if for every ${\mathbf{x}}\in \Omega _{\Delta }$ there exist $\Delta$-periodic function $\tilde{{\varphi }}(\cdot )$ defined in $E^{2}$ such that $\varphi \left| {\Delta ({\mathbf{x}})\cap Dom\,\varphi } \right.$ and $\tilde{{\varphi }}\left| {\Delta ({\mathbf{x}})\cap Dom\,\tilde{{\varphi }}} \right.$ are indiscernible in tolerance determined by $\delta \equiv (\lambda ,\delta _{0} )$. Function $\tilde{{\varphi }}$ is a $\Delta$-periodic approximation of f in $\Delta ({\mathbf{x}})$. For function $\varphi (\cdot )$ being tolerance-periodic together with its derivatives up to the R-th order, we shall write $\varphi \in TP_{\delta }^{R} (\Omega ,\Delta )$, $\delta \equiv (\lambda ,\delta _{0} ,\delta _{1} ,..,\delta _{R} )$.

Let f be a function defined in $\bar{{\Omega }}=[0,L_{1} ]\times [0,L_{2} ]$, which is integrable and bounded in every cell $\Delta ({\mathbf{x}})$, ${\mathbf{x}}\in \Omega _{\Delta }$. The averaging operation of $f(\cdot )$ is defined by

$$\begin{aligned} <f>({\mathbf{x}})\equiv \frac{1}{\left| \Delta \right| }\;\int \limits _{\Delta ({\mathbf{x}})} {f({\mathbf{z}})\mathrm{d}{\mathbf{z}},} \quad \quad {\mathbf{x}}\in \Omega _{\Delta }. \end{aligned}$$

(12)

It can be observed that if f is $\Delta$-periodic, then $<f>$ is constant, but if f is a tolerance-periodic function, then $<f>({\mathbf{x}})$ is a slowly varying function with respect to ${\mathbf{x}}$.

Let h be a continuous, highly oscillating, $\lambda$-periodic function defined in $\bar{{\Omega }}=[0,L_{1} ]\times [0,L_{2} ]$, which has continuous gradients $\partial ^{k}h,\;\,k=1,\ldots ,R-1,$ and either continuous or piecewise continuous bounded gradient $\partial ^{R}h$. Function h will be called the fluctuation shape function of the R-th kind, $h\in FS^{R}(\Omega ,\Delta )$, if it satisfies conditions: $h\in O(\lambda ^{R}),\;\;\;\partial ^{k}h\in O(\lambda ^{R-k}),\;\;\;k=1,2,\ldots ,R,\;<\upmu h>=0$, where $\upmu (\cdot )$ is a certain positive-valued $\lambda$-periodic function defined in $\bar{{\Omega }}$.

The tolerance modelling under consideration is based on three assumptions. The first of them is termed the tolerance averaging approximation. The second one is called the micro–macrodecomposition. The third one is termed the residual orthogonality assumption.

For an integrable periodic function f defined in $\bar{{\Omega }}\equiv [0,L_{1} ]\times [0,L_{2} ]$ and for slowly varying function $F\in SV_{\delta }^{R} (\Omega ,\Delta )$ and fluctuation shape function $h\in FS^{R}(\Omega ,\Delta )$, the following tolerance relations, called the tolerance averaging approximation, hold for every ${\mathbf{x}}\in \Omega$

$$\begin{aligned}&<f\partial ^{k}F>({\mathbf{x}})=<f>\partial ^{k}F({\mathbf{x}})+O(\delta ),\quad k=0,1\ldots ,R\,\;,\quad \;\;\;\;\partial ^{0}F\equiv F. \nonumber \\&<f\,\partial ^{r}(hF)>({\mathbf{x}})=<f\,\partial ^{r}h>F({\mathbf{x}})+O(\delta ),\quad \;r=1,2,\ldots ,R. \end{aligned}$$

(13)

In the course of modelling, terms $O(\delta )$ in (13) are neglected.

In the problem discussed in this contribution, R is equal either 1 or 2.

The second fundamental assumption, called the micro–macrodecomposition,    states that the displacement and temperature fields occurring in the starting Lagrangian under consideration can be decomposed into macroscopic and microscopic parts. The macroscopic part is represented by unknown averaged displacements and temperature being slowly varying functions in periodicity directions. The microscopic part is described by the known highly oscillating periodic fluctuation shape functions multiplied by unknown temperature fluctuation amplitudes and displacement fluctuation amplitudes being slowly varying in x.

Micro–macrodecomposition introduced in the thermoelastic problem discussed in this paper is presented in Sect. 4.1.

The third fundamental assumption, called the residual orthogonality assumption, states that for micro–macrodecomposition mentioned above, the governing equations of the exact shell theory under consideration do not hold, i.e. there exist residual fields which have to satisfy certain orthogonality conditions. Obviously, this assumption occurs in the orthogonalization approach only. In the thermoelastic problem studied here, the orthogonality conditions are presented in Sect. 4.2.

3.2 Basic concepts and assumptions of the asymptotic modelling procedure

The basic notions of the consistent asymptotic procedure [8, 9] are those of the fluctuation shape functions and the averaging operation. These concepts are explained in Sect. 3.1. The consistent asymptotic modelling does not require notions of tolerance-periodic and slowly varying functions.

The consistent asymptotic decomposition is the basic assumption imposed on the starting Lagrangian under consideration. It states that the displacement and temperature fields occurring in the Lagrangian must be replaced by families of fields depending on parameter $\upvarepsilon \in (0,1]$ and defined in an arbitrary cell. These families of displacements and temperature are decomposed into averaged part independent of $\upvarepsilon$ and highly oscillating part depending on $\upvarepsilon$.

Consistent asymptotic decomposition introduced in the thermoelastic problem discussed in this paper is presented in Sect. 5.1.

4 Tolerance modelling

4.1 Governing equations of the tolerance model; variational approach

The tolerance modelling procedure for Euler-Lagrange Eq. (9) is realized in two steps.

The first step is based on the tolerance averaging of Lagrangian (7) under micro–macrodecomposition of displacements $u_{\upalpha } ({\mathbf{x}},t)$, $u_{\upalpha } \in TP_{\delta }^{1} (\Omega ,\Delta )$, $w({\mathbf{x}},t)$, $w\in TP_{\delta }^{2} (\Omega ,\Delta )$ and temperature field $\theta ({\mathbf{x}},t)$, $\theta \in TP_{\delta }^{1} (\Omega ,\Delta )$, $({\mathbf{x}},t)\in \Omega \times I$, which in the problem analysed here is assumed in the form

$$\begin{aligned} u_{\upalpha } ({\mathbf{x}},t)= & {} u_{\upalpha }^{0} ({\mathbf{x}},t)+h({\mathbf{x}})U_{\upalpha } ({\mathbf{x}},t), \nonumber \\ w({\mathbf{x}},t)= & {} w^{0}({\mathbf{x}},t)+g({\mathbf{x}})W({\mathbf{x}},t), \nonumber \\ \theta ({\mathbf{x}},t)= & {} \theta ^{0}({\mathbf{x}},t)+b({\mathbf{x}})\Theta ({\mathbf{x}},t), \end{aligned}$$

(14)

where

$$\begin{aligned}&u_{\upalpha }^{0} (\cdot ,t),\;U_{\upalpha } (\cdot ,t),\,\theta ^{0}(\cdot ,t),\,\Theta (\cdot ,t)\in SV_{\delta }^{1} (\Omega ,\Delta ),\quad \delta \equiv (\lambda ,\delta _{0} ,\delta _{1} )\,, \nonumber \\&w^{0}(\cdot ,t)\,,\;W(\cdot ,t)\in SV_{\delta }^{2} (\Omega ,\Delta )\,,\quad \delta \equiv (\lambda ,\delta _{0} ,\delta _{1} ,\delta _{2} )\; \end{aligned}$$

(15)

for any $t\in \mathbf{I}$.

Macrodisplacements $u_{\upalpha }^{0} ,w^{0}$ and macrotemperature $\theta ^{0}$ as well as displacement fluctuation amplitudes $U_{\upalpha } ,W$ and temperature fluctuation amplitude $\Theta$ are the new unknowns, which must satisfy conditions (15).

Fluctuation shape functions for displacements $h\in FS^{1}(\Omega ,\Delta )$, $g\in FS^{2}(\Omega ,\Delta )$ and fluctuation shape function for temperature $b\in FS^{1}(\Omega ,\Delta )$ are the known, $\lambda$-periodic, continuous and highly oscillating    functions. They have to satisfy conditions: $h\in O(\lambda )$, $\lambda \partial _{\upalpha } h\in O(\lambda )$, $g\in O(\lambda ^{2})$, $\lambda \partial _{\upalpha } g\in O(\lambda ^{2}), \quad \lambda ^{2}\partial _{\upalpha \upbeta } g\in O(\lambda ^{2})$, $b\in O(\lambda )$, $\lambda \partial _{\upalpha } b\in O(\lambda )$, $<\upmu \,h>=<\upmu \,g>=<cb>0$. Functions $h,\,g,\,b$ from the qualitative point of view describe the expected character of micro-oscillations of displacement or temperature. These micro-oscillations are caused by a periodically heterogeneous structure of the shell. It means that the choice of the fluctuation shape functions depends on the shape of microdisturbances, which can be expected during every process under consideration. These functions can be obtained as exact or approximate solutions to periodic eigenvalue cell problems, cf. e.g. [11, 22,23,24]. For example, in dynamic processes the fluctuation shape functions are exact or approximate solutions to the periodic eigenvalue problems describing free vibrations of the cell. In this case, they represent either the principal modes of free periodic cell vibrations or physically reasonable approximation of these modes. They can also be derived from the periodic finite element method discretization of the cell. The choice of these functions can be also based on the experience or intuition of the researcher.

We substitute the right-hand sides of (14) into starting Lagrangian (7) and constitutive Eq. (8) for functions $p^{\upalpha \upbeta }({\mathbf{x}},t)$, $\mathop {r}\limits ^{\frown } ({\mathbf{x}},t)$. Then, we average the results over cell applying formula (12) and tolerance averaging approximation (13). As a result we obtain function $<L_{hgb}>$ being the averaged form of Lagrangian (7) in $\Delta (x)$. Under the additional approximation $1+\lambda /r\approx 1$ (i.e. after neglecting terms of an order of $\lambda /r)$ the final result has the form

$$\begin{aligned}&<L_{hgb}>(\partial _{\upbeta } u_{\upalpha }^{0} ,u_{\upalpha }^{0} ,U_{\upalpha } ,\dot{{u}}_{\upalpha }^{0} ,\dot{{U}}_{\upalpha } ,\partial _{\upalpha \upbeta } w^{0},w^{0},W,\dot{{w}}^{0},\dot{{W}}, \partial _{\upalpha } \theta ^{0},\theta ^{0},\Theta ,p^{\upalpha \upbeta },\mathop {r}\limits ^{\frown } ) \nonumber \\&=-\,\,\frac{1}{2}[<D^{\upalpha \upbeta \gamma \delta }>\partial _{\upbeta } u_{\upalpha }^{0} \partial _{\delta } u_{\gamma }^{0} +2<D^{\upalpha \upbeta \gamma \delta }\partial _{\delta } h>\partial _{\upbeta } u_{\upalpha }^{0} U_{\gamma } +\,<\partial _{\upbeta } h\,D^{\upalpha \upbeta \gamma \delta }\partial _{\delta } h>U_{\gamma } U_{\upalpha } \nonumber \\&\quad +2r^{-1}(<D^{\upalpha \upbeta 11}>\partial _{\upbeta } u_{\upalpha }^{0} w^{0}+<D^{\upalpha \upbeta 11}\partial _{\upbeta } h>w^{0}U_{\upalpha } ) \nonumber \\&\quad +r^{-2}<D^{1111}>(w^{0})^{2}+<B^{\upalpha \upbeta \gamma \delta }>\partial _{\upalpha \upbeta } w^{0}\partial _{\gamma \delta } w^{0} \nonumber \\&\quad +2<B^{\upalpha \upbeta \gamma \delta }\partial _{\gamma \delta } g>\partial _{\upalpha \upbeta } w^{0}W+<\partial _{\upalpha \upbeta } g\,B^{\upalpha \upbeta \gamma \delta }\partial _{\gamma \delta } g>W^{2}+ \nonumber \\&\quad -<K^{\upalpha \upbeta }>\partial _{\upalpha } \theta ^{0}\partial _{\upbeta } \theta ^{0}-2<K^{\upalpha \upbeta }\partial _{\upalpha } b>\partial _{\upbeta } \theta ^{0}\Theta -<\partial _{\upalpha } b\,K^{\upalpha \upbeta }\partial _{\upbeta } b>\Theta ^{2}+ \nonumber \\&\quad -<\mu>a^{\upalpha \upbeta }\dot{{u}}_{\upalpha }^{0} \dot{{u}}_{\upbeta }^{0} -<\mu>(\dot{{w}}^{0})^{2}-\underline{<\mu (h)^{2}>}\underline{\,}a^{\upalpha \upbeta }\dot{{U}}_{\upalpha } \dot{{U}}_{\upbeta } -\underline{<\mu (g)^{2}>}\,(\dot{{W}})^{2}]\, \nonumber \\&\quad +<f^{\upalpha }>u_{\upalpha }^{0} +\underline{<f^{\upalpha }h>}\,U_{\upalpha } +<f>w^{0}+\underline{<fg>}\,W\; \nonumber \\&\quad +<p^{\upalpha \upbeta }>\partial _{\upbeta } u_{\upalpha }^{0} +<p^{\upalpha \upbeta }\partial _{\upbeta } h>U_{\upalpha } +r^{-1}<p^{11}>w^{0}+<\mathop {r}\limits ^{\frown }>\theta ^{0}+\underline{<\mathop {r}\limits ^{\frown } b>}\Theta , \end{aligned}$$

(16)

with averaged constitutive equations given by

$$\begin{aligned}&<p^{\upalpha \upbeta }>=<\bar{{d}}^{\upalpha \upbeta }>\theta ^{0}+\underline{<\bar{{d}}^{\upalpha \upbeta }b>}\,\Theta , \nonumber \\&<p^{\upalpha \upbeta }\partial _{\upbeta } h>=<\bar{{d}}^{\upalpha \upbeta }\partial _{\upbeta } h>\theta ^{0}+\underline{<\bar{{d}}^{\upalpha \upbeta }b\partial _{\upbeta } h>}\,\Theta , \nonumber \\&<\mathop {r}\limits ^{\frown }>=<c>\dot{{\theta }}^{0}+T_{0} [<\bar{{d}}^{\upalpha \upbeta }>\partial _{\upalpha } \dot{{u}}_{\upbeta }^{0} +<\bar{{d}}^{\upalpha \upbeta }\partial _{\upalpha } h>\dot{{U}}_{\upbeta } +r^{-1}<\bar{{d}}^{11}>\dot{{w}}^{0}], \nonumber \\&<\mathop {r}\limits ^{\frown } b>=\underline{<c\,b^{2}>}\,\dot{{\Theta }}+T_{0} [\underline{<b\,\bar{{d}}^{\upalpha \upbeta }>}\,\partial _{\upalpha } \dot{{u}}_{\upbeta }^{0} +\underline{<b\,\bar{{d}}^{\upalpha \upbeta }\partial _{\upalpha } h>}\,\dot{{U}}_{\upbeta } ]. \end{aligned}$$

(17)

The underlined terms in (16), (17) depend on a period length $\lambda$.

Action functional

$$\begin{aligned} A_{hgb} (u_{\upalpha }^{0} ,U_{\upalpha } ,w^{0},W,p^{\upalpha \upbeta },\mathop {r}\limits ^{\frown } )=\int \limits _0^{L_{1} } {\int \limits _0^{L_{2} } {\int \limits _{t_{0} }^{t_{1} } {<L_{hgb} >} } } \mathrm{d}t\mathrm{d}x^{2}\mathrm{d}x^{1}, \end{aligned}$$

(18)

with $<L_{hgb}>$ given by (16) and with averaged constitutive equations for functions $p^{\upalpha \upbeta },\,\mathop {r}\limits ^{\frown }$ expressed by (17), is called the tolerance averaging of starting action functional $A(u_{\upalpha } ,w,\,p^{\upalpha \upbeta },\,\mathop {r}\limits ^{\frown } )$, cf. formula (6), under decomposition (14).

In the second step, we apply the extended principle of stationary action to averaged Lagrange function (16). In this step, expressions (17) are treated as non-variational parameters.

Under assumption that $\partial <L_{hgb} >/\partial (\partial _{\upbeta } u_{\upalpha }^{0} )$, $\partial <L_{hgb} >/\partial (\partial _{\upalpha \upbeta } w^{0})$, $\partial <L_{hgb} >/\partial (\partial _{\upbeta } \theta ^{0})$, $\partial <L_{hgb} >/\partial U_{\upalpha }$, $\partial <L_{hgb} >/\partial W$, $\partial <L_{hgb} >/\partial \Theta$ are continuous, from the extended principle of stationary action applied to (18) we obtain the following system of Euler-Lagrange equations for $u_{\upalpha }^{0} ,w^{0},U_{\upalpha } ,W,\theta ^{0},\Theta$ as the basic unknowns

$$\begin{aligned}&\partial _{\upbeta } \frac{\partial<L_{hgb}>}{\partial (\partial _{\upbeta } u_{\upalpha }^{0} )}-\frac{\partial<L_{hgb}>}{\partial u_{\upalpha }^{0} }+\frac{\partial }{\partial t}\frac{\partial<L_{hgb}>}{\partial \dot{{u}}_{\upalpha }^{0} }=0, \nonumber \\&\quad -\partial _{\upalpha \upbeta } \frac{\partial<L_{hgb}>}{\partial (\partial _{\upalpha \upbeta } w^{0})}-\frac{\partial<L_{hgb}>}{\partial w^{0}}+\frac{\partial }{\partial t}\frac{\partial<L_{hgb}>}{\partial \dot{{w}}^{0}}=0, \nonumber \\&\frac{\partial }{\partial t}\frac{\partial<L_{hgb}>}{\partial \dot{{U}}_{\upalpha } }-\frac{\partial<L_{hgb}>}{\partial U_{\upalpha } }=0,\quad \frac{\partial }{\partial t}\frac{\partial<L_{hgb}>}{\partial \dot{{W}}}-\frac{\partial<L_{hgb}>}{\partial W}=0, \nonumber \\&\partial _{\upbeta } \frac{\partial<L_{hgb}>}{\partial (\partial _{\upbeta } \theta ^{0})}-\frac{\partial<L_{hgb}>}{\partial \theta ^{0}}=0,\quad \frac{\partial <L_{hgb} >}{\partial \Theta }=0. \end{aligned}$$

(19)

Combining (19) with (16) and (17) we obtain finally the explicit form of the tolerance model equations. These equations can be written in the form of

• the stress–strain–temperature relations

  $$\begin{aligned}&N^{\upalpha \upbeta }=<D^{\upalpha \upbeta \gamma \delta }>\partial _{\delta } u_{\gamma }^{0} +r^{-1}<D^{\upalpha \upbeta 11}>w^{0}+<D^{\upalpha \upbeta \gamma \delta }\partial _{\delta } h>U_{\gamma } \;+ \nonumber \\&\quad -<\bar{{d}}^{\upalpha \upbeta }>\theta ^{0}-\underline{<\bar{{d}}^{\upalpha \upbeta }b>}\,\Theta , \nonumber \\&M^{\upalpha \upbeta }=<B^{\upalpha \upbeta \gamma \delta }>\partial _{\gamma \delta } w^{0}+<B^{\upalpha \upbeta \gamma \delta }\partial _{\gamma \delta \,} g>W, \nonumber \\&H^{\upbeta }=<\partial _{\upalpha } hD^{\upalpha \upbeta \gamma \delta }>\partial _{\delta } u_{\gamma }^{0} +<\partial _{\upalpha } hD^{\upalpha \upbeta \gamma \delta }\partial _{\delta } h>U_{\gamma } \nonumber \\&\quad +r^{-1}<\partial _{\upalpha } hD^{\upalpha \upbeta 11}>w^{0}\;-<\partial _{\upalpha } h\,\bar{{d}}^{\upalpha \upbeta }>\theta ^{0}-\underline{<\bar{{d}}^{\upalpha \upbeta }\partial _{\upalpha } h\,b>}\,\Theta , \nonumber \\&G=<\partial _{\upalpha \upbeta } g\,B^{\upalpha \upbeta \gamma \delta }>\;\partial _{\gamma \delta } w^{0}+<\partial _{\upalpha \upbeta } g\,B^{\upalpha \upbeta \gamma \delta }\partial _{\gamma \delta } g>W, \end{aligned}$$

  (20)

• the dynamic equilibrium equations

  $$\begin{aligned}&\partial _{\upalpha } N^{\upalpha \upbeta }-<\mu>a^{\upalpha \upbeta }\ddot{{u}}_{\upalpha }^{0} +<f^{\upbeta }>=0, \nonumber \\&\partial _{\upalpha \upbeta } M^{\upalpha \upbeta }+r^{-1}N^{11}+<\mu>\ddot{{w}}^{0}-<f>=0, \nonumber \\&\quad \underline{<\upmu \;(h)^{2}>}\,a^{\upalpha \upbeta }\,\ddot{{U}}_{\upalpha } +H^{\upbeta }-\underline{<f^{\upbeta }h>}=0, \nonumber \\&\quad \underline{<\upmu \;(g)^{2}\;>}\,\ddot{{W}}+G-\underline{<fg>}=0, \end{aligned}$$

  (21)

• coupled with the heat conduction equations

  $$\begin{aligned}&<K^{\upalpha \upbeta }>\partial _{\upalpha \upbeta } \theta ^{0}+<K^{\upalpha \upbeta }\partial _{\upalpha } b>\partial _{\upbeta } \Theta -<c>\dot{{\theta }}^{0} \nonumber \\&=T^{0}[<\,\bar{{d}}^{\upalpha \upbeta }>\partial _{\upalpha } \dot{{u}}_{\upbeta }^{0} +<\,\bar{{d}}^{\upalpha \upbeta }\partial _{\upalpha } h>\dot{{U}}_{\upbeta } +r^{-1}<\,\bar{{d}}^{11}>\dot{{w}}^{0}], \nonumber \\&<K^{\upalpha \upbeta }\partial _{\upalpha } b>\partial _{\upbeta } \theta ^{0}-<K^{\upalpha \upbeta }\partial _{\upalpha } b\,\partial _{\upbeta } b>\Theta + \nonumber \\&\quad -\underline{<c(b)^{2}>}\,\dot{{\Theta }}=T^{0}[\underline{<\,b\,\bar{{d}}^{\upalpha \upbeta }>\,}\partial _{\upalpha } \dot{{u}}_{\upbeta }^{0} +\underline{<\,\bar{{d}}^{\upalpha \upbeta }b\,\partial _{\upalpha } h>}\,\dot{{U}}_{\upbeta } ]. \end{aligned}$$

  (22)

  Equations (20)–(22) together with micro–macrodecomposition (14) and physical reliability conditions (15) constitute the tolerance model for the analysis of selected dynamic thermoelasticity problems for biperiodic shells under consideration. Coefficients of the derived model equations are constant, and some of them involve microstructure length parameter $\lambda$ (underlined terms).

4.2 Discussion of results

The important features of the tolerance model proposed here are listed below.

• In contrast to exact thermoelasticity shell Eqs. (4), (5) with periodic, discontinuous and highly oscillating coefficients, tolerance model Eqs. (20)–(22) proposed here have constant coefficients. Moreover, some of them depend on a period length $\lambda$ (underlined terms). Hence, the tolerance model makes it possible to describe the effect of a microstructure size on the global thermoelastic shell behaviour. Moreover, we can analyse the length-scale effect not only in non-stationary but also in stationary problems for the biperiodic shells considered here.

• The number and form of boundary conditions for macrodisplacements $u_{\upalpha }^{0} ,w^{0}$ and macrotemperature $\theta ^{0}$ are the same as in the classical shell theory governed by thermoelasticity Eqs. (4), (5). Kinematic fluctuation amplitudes $U_{\upalpha } ,\;W$ and thermal fluctuation amplitudes $\Theta$ are governed by differential Eq. (21)${}_{3,4}$ and (22)${}_{2}$, respectively. These equations do not involve spatial derivatives of $U_{\upalpha } ,\;W$, $\Theta$. Therefore, there are no extra boundary conditions for these functions, and that is why they play the role of kinematic and thermal internal variables.

• Decomposition (14) and hence also governing Eqs. (20)–(22) of the tolerance model are uniquely determined by the given a priori highly oscillating    periodic fluctuations shape functions for displacements $h\in FS^{1}(\Omega ,\Delta )$, $h\in O(\lambda )$, $g\in FS^{2}(\Omega ,\Delta )$, $g\in O(\lambda ^{2})$, and fluctuations shape function for temperature $b\in FS^{1}(\Omega ,\Delta )$, $b\in O(\lambda )$, which represent micro-oscillations of displacement and temperature fields inside a cell. These functions can be obtained as exact or approximate solutions to periodic eigenvalue cell problems, cf. e.g. [11, 22,23,24]. They can also be regarded as the shape functions resulting from the periodic discretization of the cell using, for example, the finite element method. The choice of these functions can be also based on the experience or intuition of the researcher.

• It has to be emphasized that solutions to selected initial/boundary value problems formulated in the framework of the tolerance model have a physical sense only if conditions (15) hold for the pertinent tolerance parameters $\delta$, i.e. if unknowns $u_{\upalpha }^{0} ,w^{0},\,\theta ^{0}$, $U_{\upalpha } ,W,\,\Theta$ of the tolerance model equations are slowly varying functions in periodicity directions. These conditions can be also used for the a posteriori evaluation of tolerance parameters $\delta$ and, hence, for the verification of the physical reliability of the obtained solutions.

• For a homogeneous shell with a constant thickness, $D^{\upalpha \upbeta \gamma \delta }({\mathbf{x}})$, $B^{\upalpha \upbeta \gamma \delta }({\mathbf{x}})$, $\upmu ({\mathbf{x}})$, $\bar{{d}}^{\upalpha \upbeta }({\mathbf{x}})$, $K^{\upalpha \upbeta }({\mathbf{x}})$, $c({\mathbf{x}})$, ${\mathbf{x}}\in \Omega$, are constant and because $<\upmu h>=<\upmu g>=<cb>=0$, we obtain $<h>=<g>=<b>=0$, and hence $<\partial _{\upalpha } h>=<\partial _{\upalpha } g>=<\partial _{\upalpha \upbeta } g>=<\partial _{\upalpha } b>=0$. In this case Eq. (21)${}_{1,2}$ and (22)${}_{1}$ reduce to the well-known shell equations of motion (4), (5) for averaged displacements $u_{\upalpha }^{0} ({\mathbf{x}},t),\;w^{0}({\mathbf{x}},t)$, ${\mathbf{x}}\in \Omega \times \mathbf{I}$, and to heat conduction Eq. (6) for averaged temperature $\theta ^{0}({\mathbf{x}},t)$. Independently, for fluctuation amplitudes $U_{\upalpha } ({\mathbf{x}},t),\;W({\mathbf{x}},t),\;\Theta ({\mathbf{x}},t)$ we arrive at the system of equations, which under condition $<f^{\upbeta }h>=<fg>=0$ and under homogeneous initial conditions for $U_{\upalpha }$, W and $\Theta$ has only trivial solution $U_{\upalpha } =W=\Theta =0$. Hence, from decomposition (14) it follows that $u_{\upalpha } =u_{\upalpha }^{0} ,\;w=w^{0}\,,\;\theta =\theta ^{0}$. It means that Eqs. (20)–(22) generated by tolerance averaged Lagrange function (16) reduce to starting Eq. (4), (5) generated by Lagrange function (7).

4.3 Governing equations of the tolerance model; orthogonalization approach

In this subsection, it will be shown that results (20)–(22) obtained by using the variational approach to the modelling of dynamic thermoelasticity problems for the shells under consideration based on the tolerance averaging of action functional (6) and on applying the extended stationary action principle coincide with the results derived by means of an orthogonalization approach based on the tolerance averaging of Eqs. (4), (5) combined with certain orthogonality conditions [6, 9, 10].

The micro–macrodecomposition of displacements $u_{\upalpha } ({\mathbf{x}},t)$, $u_{\upalpha } \in TP_{\delta }^{1} (\Omega ,\Delta )$, $w({\mathbf{x}},t)$, $w\in TP_{\delta }^{2} (\Omega ,\Delta )$ and temperature field $\theta ({\mathrm{x}},t)$, $\theta \in TP_{\delta }^{1} (\Omega ,\Delta )$, $({\mathbf{x}},t)\in \Omega \times \mathbf{I}$, is assumed in form (14).

We substitute the right-hand sides of (14) into starting Eqs. (4), (5). For decomposition (14), governing Eqs. (4), (5) do not hold, i.e. there exist residual fields defined by

$$\begin{aligned} p^{\upalpha }\equiv & {} \partial _{\upbeta } (D^{\upalpha \upbeta \gamma \delta }\partial _{\delta } (u_{\gamma }^{0} +hU_{\gamma } ))+r^{-1}\partial _{\upbeta } (D^{\upalpha \upbeta 11}(w^{0}+gW))+ \nonumber \\&-\partial _{\upbeta } (\bar{{d}}^{\upalpha \upbeta }(\theta ^{0}+b\Theta ))-\mu a^{\upalpha \upbeta }(\ddot{{u}}_{\upbeta }^{0} +h\ddot{{U}}_{\upbeta } )+f^{\upalpha }, \nonumber \\ \bar{{p}}\equiv & {} r^{-1}D^{\upalpha \upbeta 11}\partial _{\upbeta } (u_{\upalpha }^{0} +hU_{\upalpha } )+\partial _{\upalpha \upbeta } (B^{\upalpha \upbeta \gamma \delta }\partial _{\gamma \delta } (w^{0}+gW))+ \nonumber \\&-r^{-1}\bar{{d}}^{11}(\theta ^{0}+b\Theta )+r^{-2}D^{1111}(w^{0}+gW)+\mu (\ddot{{w}}^{0}+g\ddot{{W}})-f, \nonumber \\ s\equiv & {} \partial _{\upalpha } (K^{\upalpha \upbeta }\partial _{\upbeta } (\theta ^{0}+b\Theta ))-c(\dot{{\theta }}^{0}+b\dot{{\Theta }})+ \nonumber \\&-T_{0} (\bar{{d}}^{\upalpha \upbeta }\partial _{\upalpha } (\dot{{u}}_{\upbeta }^{0} +h\dot{{U}}_{\upbeta } )+r^{-1}\bar{{d}}^{11}(\dot{{w}}^{0}+g\dot{{W}})).\; \end{aligned}$$

(23)

Following [6, 9, 10], we introduce the residual orthogonality assumption which states that residual fields (23) have to satisfy the following orthogonality conditions

$$\begin{aligned}<p^{\upalpha }>=0,\;<p^{\upalpha }h>=0,\;<\bar{{p}}>=0,\;<\bar{{p}}g>=0,\;<s>=0,\;<sb>=0, \end{aligned}$$

(24)

for almost every ${\mathbf{x}}\in \Omega$ and every $t\in \mathbf{I}$. Averaging operation $<\cdot>$ on cell $\Delta$ is defined by (12).

Conditions (24), on the basis of tolerance averaging approximation (13), lead to the system of averaged equations for unknowns $u_{\upalpha }^{0} ,w^{0},U_{\upalpha } ,W,\theta ^{0},\Theta$ being slowly varying functions in periodicity directions. Under extra approximation $1+\lambda /r\approx 1$, this system coincides with that obtained in Sect. 4.1 and can be written in the form of stress–strain–temperature relations (20) and dynamic equilibrium equations (21) coupled with heat conduction equations (22). Note that in monograph [9], the variational and orthogonalization approaches lead to two different systems, but this result was obtained under assumption that the definition of slowly varying functions in the variational approach was different from the definition of these functions in the orthogonalization method.

4.4 Comparison of tolerance models for biperiodic and uniperiodic shells

Let us compare the formulated here tolerance model for the thin biperiodic cylindrical shells under consideration governed by Eqs. (20)–(22) together with micro–macrodecomposition (14) and physical reliability conditions (15), with the corresponding tolerance model for the thin cylindrical shells with a periodic structure in circumferential direction only (uniperiodic shells) proposed by Tomczyk and Gołąbczak in [30]. An example of such a shell is presented in Fig. 3.

Fig. 3

Example of an uniperiodic shell

For the uniperiodic shells under consideration, elastic stiffness tensors $D^{\upalpha \upbeta \gamma \delta }(x^{1})$, $B^{\upalpha \upbeta \gamma \delta }(x^{1})$, the shell mass density $\upmu (x^{1})$, membrane thermal stiffness tensor $\bar{{d}}^{\upalpha \upbeta }(x^{1})$, tensor of heat conductivity $K^{\upalpha \upbeta }(x^{1})$ and specific heat $c(x^{1})$ are periodic, highly oscillating and non-continuous functions only with respect to argument $x^{1}\in (0,L_{1} )$ and they are independent of argument $x^{2}\in (0,L_{2} )$.

Following [30], the tolerance model equations for the analysis of dynamic thermoelasticity problems for the uniperiodic shells under consideration are represented by

• the stress–strain–temperature relations

  $$\begin{aligned}&N^{\upalpha \upbeta }=<D^{\upalpha \upbeta \gamma \delta }>\partial _{\delta } u_{\gamma }^{0} +r^{-1}<D^{\upalpha \upbeta 11}>w^{0}+<D^{\upalpha \upbeta \gamma 1}\partial _{1} h>U_{\gamma } \; \nonumber \\&\quad +\underline{\underline{<D^{\upalpha \upbeta \gamma 2}h>}}\,\partial _{2} U_{\gamma } -<\bar{{d}}^{\upalpha \upbeta }>\theta ^{0}-\underline{<\bar{{d}}^{\upalpha \upbeta }b>}\,\Theta , \nonumber \\&M^{\upalpha \upbeta }=<B^{\upalpha \upbeta \gamma \delta }>\partial _{\gamma \delta } w^{0}+<B^{\upalpha \upbeta 11}\partial _{11} g>W \nonumber \\&\quad +2\underline{\underline{<B^{\upalpha \upbeta 12}\partial _{1} g>}}\,\partial _{2} W+\underline{\underline{<B^{\upalpha \upbeta 22}g>}}\,\partial _{22} W, \end{aligned}$$

  (25)
  $$\begin{aligned}&H^{\upbeta }=<\partial _{1} hD^{\upbeta 1\gamma \delta }>\partial _{\delta } u_{\gamma }^{0} -\underline{\underline{<hD^{\upbeta 2\gamma \delta }>}}\,\partial _{2\delta } u_{\gamma }^{0} \nonumber \\&\quad +<D^{\upbeta 11\gamma }(\partial _{1} h)^{2}>U_{\gamma } -\underline{\underline{<D^{\upbeta 22\gamma }(h)^{2}>}} \partial _{22} U_{\gamma } \nonumber \\&\quad +r^{-1}<\partial _{1} h\,D^{\upbeta 111}>w^{0}\;-<\partial _{1} h\,\bar{{d}}^{\upbeta 1}>\theta ^{0}+\underline{\underline{<\bar{{d}}^{\upbeta 2}h>}}\,\partial _{2} \theta ^{0}+ \nonumber \\&\quad -\underline{<\bar{{d}}^{\upbeta 1}\partial _{1} h\,b>}\,\Theta +\underline{\underline{<\bar{{d}}^{\upbeta 2}bh>}}\,\partial _{2} \Theta , \nonumber \\&G=<\partial _{11} gB^{11\upalpha \upbeta }>\;\partial _{\upalpha \upbeta } w^{0}-2\underline{\underline{<\partial _{1} gB^{\upalpha \upbeta 12}>}}\,\partial _{\upalpha \upbeta 2} w^{0} \nonumber \\&\quad +\underline{<g\,B^{\upalpha \upbeta 22}>}\;\partial _{\upalpha \upbeta 22} w^{0}\,+<(\partial _{11} g)^{2}B^{1111}>W+(\underline{2\underline{<\partial _{11} gB^{1122}g>}}+ \nonumber \\&\quad -4\underline{\underline{<(\partial _{1} g)^{2}B^{1212}>}})\;\partial _{22} W+\underline{\underline{<(g)^{2}B^{2222}\,>}}\;\partial _{2222} W, \end{aligned}$$

  (26)

• the dynamic equilibrium equations

  $$\begin{aligned}&\partial _{\upalpha } N^{\upalpha \upbeta }-<\upmu>a^{\upalpha \upbeta }\ddot{{u}}_{\upalpha }^{0} +<f^{\upbeta }>=0, \nonumber \\&\partial _{\upalpha \upbeta } M^{\upalpha \upbeta }+r^{-1}N^{11}+<\upmu>\ddot{{w}}^{0}-<f>=0, \nonumber \\&\quad \underline{<\upmu \;(h)^{2}>}\,a^{\upalpha \upbeta }\,\ddot{{U}}_{\upalpha } +H^{\upbeta }-\underline{<f^{\upbeta }h>}=0, \nonumber \\&\quad \underline{<\upmu \;(g)^{2}\;>}\,\ddot{{W}}+G-\underline{<fg>}=0, \end{aligned}$$

  (27)

• the heat conduction equations

  $$\begin{aligned}&<K^{\upalpha \upbeta }>\partial _{\upalpha \upbeta } \theta ^{0}+<K^{1\upbeta }\partial _{1} b>\partial _{\upbeta } \Theta +\underline{\underline{<K^{2\upbeta }b>}}\,\partial _{2\upbeta } \Theta -<c>\dot{{\theta }}^{0} \nonumber \\&=T_{0} [<\,\bar{{d}}^{\upalpha \upbeta }>\partial _{\upalpha } \dot{{u}}_{\upbeta }^{0} +<\,\bar{{d}}^{1\upbeta }\partial _{1} h>\dot{{U}}_{\upbeta } +\underline{\underline{<\,\bar{{d}}^{2\upbeta }h>}}\,\partial _{2} \dot{{U}}_{\upbeta } +r^{-1}<\,\bar{{d}}^{11}>\dot{{w}}^{0}], \nonumber \\&\underline{\underline{<K^{2\upbeta }b>}}\;\partial _{2\upbeta } \theta ^{0}+<K^{1\upbeta }\partial _{1} b>\partial _{\upbeta } \theta ^{0}+\underline{\underline{<K^{22}(b)^{2}>}}\partial _{22} \Theta -<K^{11}(\partial _{1} b)^{2}>\Theta + \nonumber \\&\quad -\underline{<c(b)^{2}>}\,\dot{{\Theta }}=T_{0} [\underline{<\,b\,\bar{{d}}^{\upalpha \upbeta }>\,}\partial _{\upalpha } \dot{{u}}_{\upbeta }^{0} +\underline{<\,\bar{{d}}^{1\upbeta }b\,\partial _{1} h>}\,\dot{{U}}_{\upbeta } +\underline{\underline{<\,\bar{{d}}^{2\upbeta }b\,h>}}\,\partial _{2} \dot{{U}}_{\upbeta } ], \end{aligned}$$

  (28)

  where the basic unknowns $u_{\upalpha }^{0} ,w^{0},U_{\upalpha } ,W,\theta ^{0},\Theta$ are slowly varying functions in the argument $x^{1}$ only, and also fluctuation shape functions $h,\,g,b$ are periodic functions in $x^{1}$. Equations (25)–(28) together with micro–macrodecomposition (14) and physical reliability conditions (15) constitute the tolerance model for the analysis of selected dynamic thermoelasticity problems for uniperiodic shells under consideration. Obviously, the functions in (14) and (15) which are tolerance-periodic, slowly varying or periodic in $x^{1}$ and $x^{2}$ must be replaced by corresponding functions tolerance-periodic, slowly varying or periodic in $x^{1}$ only. Moreover, the basic cell $\Delta$ and the region $\Omega$ are now defined as follows: $\Delta \equiv [-\lambda /2,\;\lambda /2]$, $\Omega \equiv (0,L_{1} )$, where $\lambda \equiv \lambda _{1}$, cf. Fig. 3. Equations (25)–(28) have constant coefficients. Doubly and singly underlined terms in (25)–(28) depend on the microstructure length parameter. The main differences and similarities between both models are:

• Model Eqs. (25)–(28) for the uniperiodic shells are more complicated that those (20)–(22) for biperiodic shells and contain a lot of length-scale terms (doubly underlined terms) which do not have counterparts in the equations for biperiodic shells. The occurrence of these terms is strictly related to the fact that physical reliability conditions for uniperiodic shells of form (15), but with functions slowly varying in one direction only (i.e. with respect to $x^{1}$ midsurface parameter, $x^{1}\in (0,L_{1} ))$, are less restrictive than conditions (15) for biperiodic shells with functions slowly varying in the two circumferential and axial directions (i.e. with respect to $x^{1},x^{2}$ midsurface parameters, $x^{1}\in (0,L_{1} )$, $x^{1}\in (0,L_{1} ))$.

• In the framework of the uniperiodic shell model, unknown kinematic fluctuation amplitudes $U_{\upalpha } ,\;W$ and thermal fluctuation amplitude $\Theta$ are governed by partial differential equations (27)${}_{3,4}$ and (28)${}_{2}$, respectively, whereas within the biperiodic shell model these unknowns are governed by ordinary differential equations (21)${}_{3,4}$ and (22)${}_{2}$, respectively, involving only time derivatives. Hence, there are no extra boundary conditions for unknowns $U_{\upalpha } ,\;W,\,\Theta$ of the biperiodic shell model and that is why they play the role of kinematic or thermal internal variables. On the other hand, the boundary conditions for unknown $U_{\upalpha } ,\;W,\,\Theta$ of the uniperiodic shell model should be defined only on boundaries $x^{2}=0,\;x^{2}=L_{2}$.

• Both of these models are uniquely determined by the postulated a priori $\lambda -$periodic fluctuations shape functions for displacements $h\in O(\lambda )$, $g\in O(\lambda ^{2})$ and for temperature $b\in O(\lambda )$. In the uniperiodic shell model we deal with fluctuation shape functions which are periodic in one direction only (i.e. with respect to argument $x^{1}$, $x^{1}\in (0,L_{1} ))$, whereas in the other one these functions are periodic in two directions (i.e. with respect to arguments $x^{1},x^{2}$, $x^{1}\in (0,L_{1} )$, $x^{2}\in (0,L_{2} ))$.

• In contrast to starting Eqs. (4), (5) with discontinuous, highly oscillating and periodic coefficients, both tolerance models have constant coefficients. Moreover, a lot of them depend on microstructure length parameter $\lambda$ (underlined terms). Hence, both tolerance models considered here make it possible to describe the effect of length scale on the global shell behaviour.

• The solutions to selected initial/boundary value problems formulated within the uniperiodic or biperiodic shell models have a physical sense only if the basic unknowns are slowly varying functions either in argument $x^{1}$ (uniperiodic shells) or in arguments $x^{1},x^{2}$ (biperiodic shells).

5 Consistent asymptotic modelling

The asymptotic model equations can be obtained directly from tolerance model Eqs. (20)–(22) by the formal limit passage $\lambda \rightarrow 0$. However, the same results can be obtained independently of the tolerance model by applying the consistent asymptotic procedure (variational approach) proposed in [8] and discussed in detail in [9]. In this approach the concepts of tolerance-periodic and slowly varying functions are not introduced. On passing from the tolerance to asymptotic modelling, we retain only the concepts of fluctuation shape function and averaged operation. Below, asymptotic model equations will be derived by applying the consistent asymptotic modelling.

5.1 Governing equations of the asymptotic model

Asymptotic modelling procedure for Euler-Lagrange Eq. (9) is realized in two steps.

The first step is based on consistent asymptotic averaging of Lagrangian (7) and independently on the consistent asymptotic averaging of constitutive equations (8) for functions $p^{\upalpha \upbeta }({\mathbf{x}},t)$, $\mathop {r}\limits ^{\frown } ({\mathbf{x}},t)$ being the non-variational parameters of Lagrange function (7).

In order to do it, we shall restrict considerations to displacement fields $u_{\upalpha } =u_{\upalpha } ({\mathbf{z}},t)$, $w=w({\mathbf{z}},t)$ and temperature field $\theta ({\mathbf{z}},t)$ defined in $\Delta ({\mathbf{x}})\times \mathbf{I}$, ${\mathbf{z}}\in \Delta ({\mathbf{x}})$, ${\mathbf{x}}\in \Omega _{\Delta }$, $t\in \mathbf{I}$. Then, we replace $u_{\upalpha } ({\mathbf{z}},t)$, $w({\mathbf{z}},t)$ and $\theta ({\mathbf{z}},t)$ by families of displacements $u_{\upvarepsilon \upalpha } ({\mathbf{z}},t)\equiv u_{\upalpha } ({\mathbf{z}}/\upvarepsilon ,t)$, $w_{\upvarepsilon } ({\mathbf{z}},t)\equiv w({\mathbf{z}}/\upvarepsilon ,t)$ and family of temperature field $\theta _{\upvarepsilon } ({\mathbf{z}},t)\equiv \theta ({\mathbf{z}}/\upvarepsilon ,t)$ where $0<\upvarepsilon<<1$, ${\mathbf{z}}\in \Delta _{\upvarepsilon } ({\mathbf{x}}),$ $\Delta _{\upvarepsilon } \equiv (-\upvarepsilon \lambda _{1} /2,\upvarepsilon \lambda _{1} /2)\times (-\upvarepsilon \lambda _{2} /2,\upvarepsilon \lambda _{2} /2)$ (scaled cell), $\Delta _{\upvarepsilon } ({\mathbf{x}})\equiv {\mathbf{x}}+\Delta _{\upvarepsilon } \,,\;\,{\mathbf{x}}\in \Omega _{\Delta _{\upvarepsilon } }$ (scaled cell with a centre at ${\mathbf{x}}\in \Omega _{\Delta _{\upvarepsilon } } )$.

We introduce the consistent asymptotic decomposition of displacement and temperature families $u_{\upvarepsilon \upalpha } ({\mathbf{z}},t)$, $w_{\upvarepsilon } ({\mathbf{z}},t)$, $\theta _{\upvarepsilon } ({\mathbf{z}},t)$, $({\mathbf{z}},t)\in \Delta _{\upvarepsilon } \times \mathbf{I}$ in the area of every $\upvarepsilon$-scaled cell

$$\begin{aligned} u_{\upvarepsilon \upalpha } ({\mathbf{z}},t)\equiv u_{\upalpha } ({\mathbf{z}}/\upvarepsilon ,t)= & {} u_{\upalpha }^{0} ({\mathbf{z}},t)+\upvarepsilon h_{\upvarepsilon } ({\mathbf{z}})U_{\upalpha } ({\mathbf{z}},t), \nonumber \\ w_{\upvarepsilon } ({\mathbf{z}},t)\equiv w({\mathbf{z}}/\upvarepsilon ,t)= & {} w^{0}({\mathbf{z}},t)+\upvarepsilon ^{2}g_{\upvarepsilon } ({\mathbf{z}})W({\mathbf{z}},t), \nonumber \\ \theta _{\upvarepsilon } ({\mathbf{z}},t)\equiv \theta ({\mathbf{z}}/\upvarepsilon ,t)= & {} \theta ^{0}({\mathbf{z}},t)+\upvarepsilon b_{\upvarepsilon } ({\mathbf{z}})\Theta ({\mathbf{z}},t). \end{aligned}$$

(29)

As in the tolerance approach, functions $u_{\upalpha }^{0} ,w^{0}$and $U_{\upalpha } ,W$ are termed macrodisplacements and displacement fluctuation amplitudes, respectively; functions $\theta ^{0},\,\Theta$ are called macrotemperature and temperature fluctuation amplitude. Unknowns $u_{\upalpha }^{0} ,U_{\upalpha } ,\theta ^{0},\Theta$ are assumed to be continuous and bounded in $\bar{{\Omega }}$ together with their first derivatives. Unknowns $w^{0},W$ are assumed to be continuous and bounded in $\bar{{\Omega }}$ together with their derivatives up to the second order. Moreover, all unknowns mentioned above are independent of $\varepsilon$. We recall that they are not referred to the slowly varying functions introduced in the tolerance averaging.

Fluctuation shape functions for displacements $h_{\upvarepsilon } ({\mathbf{z}})\equiv h({\mathbf{z}}/\upvarepsilon )$, $h_{\upvarepsilon } \in FS^{1}(\Omega ,\Delta _{\upvarepsilon } )$, $g_{\upvarepsilon } ({\mathbf{z}})\equiv g({\mathbf{z}}/\upvarepsilon )$, $g_{\upvarepsilon } \in FS^{2}(\Omega ,\Delta _{\upvarepsilon } )$, and fluctuation shape function for temperature $b_{\upvarepsilon } ({\mathbf{z}})\equiv b({\mathbf{z}}/\upvarepsilon )$, $b_{\upvarepsilon } \in FS^{1}(\Omega ,\Delta _{\upvarepsilon } )$, in (29) are highly oscillating and $\Delta _{\upvarepsilon }$-periodic. They have to be known in every problem under consideration. They depend on $\upvarepsilon \lambda$ as a parameter and have to satisfy conditions: $h_{\upvarepsilon } \in O(\upvarepsilon \lambda )$, $\upvarepsilon \lambda \partial _{\upalpha } h_{\upvarepsilon } \in O(\upvarepsilon \lambda )$, $g_{\upvarepsilon } \in O((\upvarepsilon \lambda )^{2})$, $\upvarepsilon \lambda \partial _{\upalpha } g_{\upvarepsilon } \in O((\upvarepsilon \lambda )^{2}),$ $(\upvarepsilon \lambda )^{2}\partial _{\upalpha \upbeta } g_{\upvarepsilon } \in O((\upvarepsilon \lambda )^{2})$, $b_{\upvarepsilon } \in O(\upvarepsilon \lambda )$, $\upvarepsilon \lambda \partial _{\upalpha } b_{\upvarepsilon } \in O(\upvarepsilon \lambda )$, $<\mu \,h_{\upvarepsilon }>=<\mu \,g_{\upvarepsilon }>=<cb_{\upvarepsilon } >0$. It has to be emphasized that $\partial _{\upalpha } h_{\upvarepsilon } ({\mathbf{z}})\equiv \frac{1}{\upvarepsilon }\bar{{\partial }}_{\upalpha } h({\mathbf{z}}/\upvarepsilon ), \quad \partial _{\upalpha } g_{\upvarepsilon } ({\mathbf{z}})\equiv \frac{1}{\upvarepsilon }\bar{{\partial }}_{\upalpha } g({\mathbf{z}}/\upvarepsilon ), \quad \partial _{\upalpha \upbeta } g_{\upvarepsilon } ({\mathbf{z}})\equiv \frac{1}{\upvarepsilon ^{2}}\bar{{\partial }}_{\upalpha \upbeta } g({\mathbf{z}}/\upvarepsilon )$, $\partial _{\upalpha } b_{\upvarepsilon } ({\mathbf{z}})\equiv \frac{1}{\upvarepsilon }\bar{{\partial }}_{\upalpha } b({\mathbf{z}}/\upvarepsilon )$, where differential operator $\bar{{\partial }}_{\upalpha }$ means differentiation over $z_{\upalpha } /\upvarepsilon$.

Because of Lagrangian L defined by (7) is highly oscillating with respect to ${\mathbf{x}}$ and essentially bounded in its domain, then there exists Lagrangian $\tilde{{L}}({\mathbf{z}},t,\partial _{\upbeta } u_{\upalpha } ,u_{\upalpha } ,\dot{{u}}_{\upalpha } ,\partial _{\upalpha \upbeta } w,w,\dot{{w}},p^{\upalpha \upbeta },\mathop {r}\limits ^{\frown } )$ being the periodic approximation of Lagrangian L in $\Delta ({\mathbf{x}})$, $z\in \Delta ({\mathbf{x}})$, ${\mathbf{x}}\in \Omega _{\Delta }$. Let $\tilde{{L}}_{{}\upvarepsilon }$ be a family of functions given by

$$\begin{aligned} \tilde{{L}}_{{}\varepsilon }= & {} \tilde{{L}}({\mathbf{z}}/\varepsilon ,t,\partial _{\upbeta } u_{\varepsilon \upalpha } ,u_{\varepsilon \upalpha } ,\dot{{u}}_{\varepsilon \upalpha } ,\partial _{\upalpha \upbeta } w_{\varepsilon } ,w_{\varepsilon } ,\dot{{w}}_{\varepsilon } ,\partial _{\upbeta } \theta _{\varepsilon } ,\theta _{\varepsilon } ,p_{\varepsilon }^{\upalpha \upbeta } ,\mathop {r}\limits ^{\frown } _{\varepsilon } ) \nonumber \\= & {} -\,\,\frac{1}{2}[D^{\upalpha \upbeta \gamma \delta }\partial _{\upbeta } u_{\varepsilon \upalpha } \partial _{\delta } u_{\varepsilon \gamma } +2r^{-1}D^{\upalpha \upbeta 11}w_{\varepsilon } \partial _{\upbeta } u_{\varepsilon \upalpha } \nonumber \\&+r^{-2}D^{1111}w_{\varepsilon } w_{\varepsilon } +B^{\upalpha \upbeta \gamma \delta }\partial _{\upalpha \upbeta } w_{\varepsilon } \partial _{\gamma \delta } w_{\varepsilon } + \nonumber \\&-K^{\upalpha \upbeta }\partial _{\upalpha } \theta _{\varepsilon } \partial _{\upbeta } \theta _{\varepsilon } -\mu a^{\upalpha \upbeta }\dot{{u}}_{\varepsilon \upalpha } \dot{{u}}_{\varepsilon \upbeta } -\mu (\dot{{w}}_{\varepsilon } )^{2}]\; \nonumber \\&+f^{\upalpha }u_{\varepsilon \upalpha } +f\,w_{\varepsilon } +p_{\varepsilon }^{\upalpha \upbeta } \partial _{\upbeta } u_{\varepsilon }^{\upalpha } +r^{-1}p_{\varepsilon }^{11} w_{\varepsilon } +\mathop {r}\limits ^{\frown } _{\varepsilon } \theta _{\varepsilon }, \end{aligned}$$

(30)

where $p_{\varepsilon }^{\upalpha \upbeta } ,\;\mathop {r}\limits ^{\frown }_{\varepsilon }$ play the role of invariational parameters and are given by independent equations

$$\begin{aligned} p_{\varepsilon }^{\upalpha \upbeta }= & {} \bar{{d}}^{\upalpha \upbeta }\theta _{\varepsilon } , \nonumber \\ \mathop {r}\limits ^{\frown } _{\varepsilon }= & {} c\dot{{\theta }}_{\varepsilon } +T_{0} (\bar{{d}}^{\upalpha \upbeta }\partial _{\upalpha } \dot{{u}}_{\varepsilon \upbeta } +r^{-1}\bar{{d}}^{11}\dot{{w}}_{\varepsilon } ). \end{aligned}$$

(31)

We substitute the right-hand sides of (29) into (30) and independently into (31). Then, we take into account that under limit passage $\varepsilon \rightarrow 0$, terms depending on $\varepsilon$ can be neglected and every continuous and bounded function of argument ${\mathbf{z}}\in \Delta _{\varepsilon } ({\mathbf{x}}),$ tends to function of argument ${\mathbf{x}}\in \bar{{\Omega }}$. Moreover, if $\varepsilon \rightarrow 0$ then, by means of a property of the mean value, cf. Jikov et al. [2], the obtained result tends weakly to function $L^{0}$ being the averaged form of starting Lagrangian (7) under consistent asymptotic decomposition (29). Introducing the extra approximation $1+\lambda /r\approx 1$, this result has the form

$$\begin{aligned}&L_{0} (\partial _{\upbeta } u_{\upalpha }^{0} ,u_{\upalpha }^{0} ,U_{\upalpha } ,\dot{{u}}_{\upalpha }^{0} ,\partial _{\upalpha \upbeta } w^{0},w^{0},W,\dot{{w}}^{0},\partial _{\upbeta } \theta ^{0},\theta ^{0},\Theta ,p^{\upalpha \upbeta },\mathop {r}\limits ^{\frown } ) \nonumber \\&\quad =-\,\frac{1}{2}[<D^{\upalpha \upbeta \gamma \delta }>\partial _{\upbeta } u_{\upalpha }^{0} \partial _{\delta } u_{\gamma }^{0} +2<D^{\upalpha \upbeta \gamma \delta }\partial _{\delta } h>\partial _{\upbeta } u_{\upalpha }^{0} U_{\gamma } \nonumber \\&\qquad +<\partial _{\upbeta } h\,D^{\upalpha \upbeta \gamma \delta }\partial _{\delta } h>U_{\gamma } \,U_{\upalpha } +2r^{-1}(<D^{\upalpha \upbeta 11}>\partial _{\upbeta } u_{\upalpha }^{0} w^{0} \nonumber \\&\qquad +<D^{\upalpha \upbeta 11}\partial _{\upbeta } h>w^{0}U_{\upalpha } )+r^{-2}<D^{1111}>(w^{0})^{2} \nonumber \\&\qquad +<B^{\upalpha \upbeta \gamma \delta }>\partial _{\upalpha \upbeta } w^{0}\partial _{\gamma \delta } w^{0}+2<B^{\upalpha \upbeta \gamma \delta }\partial _{\gamma \delta } g>\partial _{\upalpha \upbeta } w^{0}W \nonumber \\&\qquad +<\partial _{\upalpha \upbeta } g\,B^{\upalpha \upbeta \gamma \delta }\partial _{\gamma \delta } g>(W)^{2}+ \nonumber \\&\qquad -<K^{\upalpha \upbeta }>\partial _{\upalpha } \theta ^{0}\partial _{\upbeta } \theta ^{0}-2<K^{\upalpha \upbeta }\partial _{\upalpha } b>\partial _{\upbeta } \theta ^{0}\Theta + \nonumber \\&\qquad -<\partial _{\upalpha } b\,K^{\upalpha \upbeta }\partial _{\upbeta } b>(\Theta )^{2}+ \nonumber \\&\qquad -<\mu>a^{\upalpha \upbeta }\dot{{u}}_{\upalpha }^{0} \dot{{u}}_{\upbeta }^{0} -<\mu>(\dot{{w}}^{0})^{2}]+<f^{\upalpha }>u_{\upalpha }^{0} \;+<f>w^{0} \nonumber \\&\qquad +<p^{\upalpha \upbeta }>\partial _{\upbeta } u_{\upalpha }^{0} +<p^{\upalpha \upbeta }\partial _{\upbeta } h>U_{\upalpha } +r^{-1}<p^{11}>w^{0}+<\mathop {r}\limits ^{\frown } >\Theta , \end{aligned}$$

(32)

where averaged constitutive equations for functions $<p^{\upalpha \upbeta }>$, $<\mathop {r}\limits ^{\frown }>$ are given by

$$\begin{aligned}&<p^{\upalpha \upbeta }>=<\bar{{d}}^{\upalpha \upbeta }>\theta ^{0},\quad<p^{\upalpha \upbeta }\partial _{\upbeta } h>=<\bar{{d}}^{\upalpha \upbeta }\partial _{\upbeta } h>\theta ^{0}, \nonumber \\&<\mathop {r}\limits ^{\frown }>=<c>\dot{{\theta }}^{0}+T_{0} [<\bar{{d}}^{\upalpha \upbeta }>\partial _{\upalpha } \dot{{u}}_{\upbeta }^{0} +<\bar{{d}}^{\upalpha \upbeta }\partial _{\upalpha } h>\dot{{U}}_{\upbeta } +r^{-1}<\bar{{d}}^{11}>\dot{{w}}^{0}]. \end{aligned}$$

(33)

In the framework of consistent asymptotic procedure we introduce the consistent asymptotic action functional

$$\begin{aligned} A_{hgb}^{0} (u_{\upalpha }^{0} ,U_{\upalpha } ,w^{0},W,p^{\upalpha \upbeta },\mathop {r}\limits ^{\frown } )=\int \limits _0^{L_{1} } {\int \limits _0^{L_{2} } {\int \limits _{t_{0} }^{t_{1} } {L_{0} } } } \mathrm{d}t\mathrm{d}x^{2}\mathrm{d}x^{1}, \end{aligned}$$

(34)

where $L_{0}$ is given by (32).

The second step in the asymptotic modelling of Euler-Lagrange Eq. (9) is to apply the extended principle of stationary action to averaged Lagrange function (32). In this step, expressions (33) are treated as non-variational parameters.

Under assumption that $\partial L_{0} /\partial (\partial _{\upbeta } u_{\upalpha }^{0} )$, $\partial L_{0} /\partial (\partial _{\upalpha \upbeta } w^{0})$, $\partial L_{0} /\partial (\partial _{\upbeta } \theta ^{0})$, $\partial <L_{hgb} >/\partial U_{\upalpha }$, $\partial <L_{hgb} >/\partial W$, $\partial <L_{hgb} >/\partial \Theta$ are continuous, from the extended principle of stationary action applied to (34) we obtain the following system of Euler-Lagrange equations for $u_{\upalpha }^{0} ,w^{0},U_{\upalpha } ,W,\theta ^{0},\Theta$ as the basic unknowns

$$\begin{aligned}&\partial _{\upbeta } \frac{\partial L_{0} }{\partial (\partial _{\upbeta } u_{\upalpha }^{0} )}-\frac{\partial L_{0} }{\partial u_{\upalpha }^{0} }+\frac{\partial }{\partial t}\frac{\partial L_{0} }{\partial \dot{{u}}_{\upalpha }^{0} }=0, \nonumber \\&\quad -\partial _{\upalpha \upbeta } \frac{\partial L_{0} }{\partial (\partial _{\upalpha \upbeta } w^{0})}-\frac{\partial L_{0} }{\partial w^{0}}+\frac{\partial }{\partial t}\frac{\partial L_{0} }{\partial \dot{{w}}^{0}}=0, \nonumber \\&\frac{\partial L_{0} }{\partial U_{\upalpha } }=0,\quad \quad \quad \quad \quad \frac{\partial L_{0} }{\partial W}=0, \nonumber \\&\partial _{\upbeta } \frac{\partial L_{0} }{\partial (\partial _{\upbeta } \theta ^{0})}-\frac{\partial L_{0} }{\partial \theta ^{0}}=0,\quad \quad \frac{\partial L_{0} }{\partial \Theta }=0. \end{aligned}$$

(35)

Combining (35) with (32) and (33) we arrive at the explicit form of the consistent asymptotic model equations for $u_{\upalpha }^{0} ({\mathbf{x}},t),w^{0}({\mathbf{x}},t)$, $U_{\upalpha } ({\mathbf{x}},t),W({\mathbf{x}},t)$, $\theta ^{0}({\mathbf{x}},t),\Theta ({\mathbf{x}},t)$, $({\mathbf{x}},t)\in \Omega \times I$

$$\begin{aligned}&<D^{\upalpha \upbeta \gamma \delta }>\partial _{\upbeta \delta } u_{\gamma }^{0} +r^{-1}<D^{\upalpha \upbeta 11}>\partial _{\upbeta } w^{0}+<D^{\upalpha \upbeta \gamma \delta }\partial _{\delta } h>\partial _{\upbeta } U_{\gamma } -<\bar{{d}}^{\upalpha \upbeta }>\partial _{\upbeta } \theta ^{0}+ \nonumber \\&\quad -<\mu>a^{\upalpha \upbeta }\ddot{{u}}_{\upbeta }^{0} +<f^{\upalpha }>=0, \nonumber \\&<B^{\upalpha \upbeta \gamma \delta }>\partial _{\upalpha \upbeta \gamma \delta } w^{0}+<D^{\upalpha \upbeta \gamma \delta }\partial _{\gamma \delta } g>\partial _{\upalpha \upbeta } W+r^{-1}(<D^{11\gamma \delta }>\partial _{\delta } u_{\gamma }^{0} \nonumber \\&\quad +r^{-1}<D^{1111}>w^{0}+r^{-1}<D^{11\gamma \delta }\partial _{\gamma } h>U_{\delta } -<\bar{{d}}^{11}>\theta ^{0}) \nonumber \\&\quad +<\mu>\ddot{{w}}^{0}-<f>=0, \nonumber \\&<\partial _{\upalpha } h\,D^{\upalpha \upbeta \gamma \delta }\partial _{\delta } h>U_{\gamma } =-<\partial _{\upalpha } h\,D^{\upalpha \upbeta \gamma \delta }>\;\partial _{\delta } u_{\gamma }^{0} -r^{-1}<\partial _{\upalpha } hD^{\upalpha \upbeta 11}>w^{0}+<\partial _{\upalpha } h\,\bar{{d}}^{\upalpha \upbeta }>\theta ^{0}, \nonumber \\&<\partial _{\upalpha \upbeta } g\,B^{\upalpha \upbeta \gamma \delta }\partial _{\gamma \delta } g>W=-<\partial _{\upalpha \upbeta } gB^{\upalpha \upbeta \gamma \delta }>\partial _{\gamma \delta } w^{0}, \nonumber \\&<K^{\upalpha \upbeta }>\partial _{\upalpha \upbeta } \theta ^{0}+<K^{\upalpha \upbeta }\partial _{\upalpha } b>\partial _{\upbeta } \Theta -<c>\dot{{\Theta }}^{0} \nonumber \\&=T_{0} [<\bar{{d}}^{\upalpha \upbeta }>\partial _{\upalpha } \dot{{u}}_{\upbeta }^{0} +<\bar{{d}}^{\upalpha \upbeta }\partial _{\upalpha } h>\dot{{U}}_{\upbeta } +r^{-1}<\bar{{d}}^{11}>\dot{{w}}^{0}], \nonumber \\&<\partial _{\upalpha } b\,K^{\upalpha \upbeta }\partial _{\upbeta } b>\Theta =-<K^{\upalpha \upbeta }\partial _{\upalpha } b>\partial _{\upbeta } \theta ^{0}. \end{aligned}$$

(36)

Averages $<\cdot>$ occurring in (36) are constant and calculated by means of (12).

Equation (36) consists of partial differential equations for macrodisplacements $u_{\upalpha }^{0} ,\,w^{0}$ and macrotemperature $\theta ^{0}$ coupled with linear algebraic equations for kinematic fluctuation amplitudes $U_{\upalpha } ,\,W$ and thermal fluctuation amplitude $\Theta$. After eliminating fluctuation amplitudes from the governing equations by means of

$$\begin{aligned} U_{\gamma }= & {} -G_{\gamma \eta }^{-1} \,\;[<\partial _{\upbeta } hD^{\upbeta \eta \mu \vartheta }>\;\partial _{\vartheta } u_{\mu }^{0} +r^{-1}<\partial _{\upbeta } hD^{\upbeta \eta 11}>w^{0}-<\partial _{\upbeta } h\,\bar{{d}}^{\upbeta \eta }>\theta ^{0}], \nonumber \\ W= & {} -E^{-1}<\partial _{\upalpha \upbeta } gB^{\upalpha \upbeta \gamma \delta }>\partial _{\gamma \delta } w^{0}\,, \nonumber \\ \Theta= & {} -C^{-1}<K^{\upalpha \upbeta }\partial _{\upalpha } b>\partial _{\upbeta } \theta ^{0}, \end{aligned}$$

(37)

where $G_{\upalpha \gamma } =<\partial _{\upbeta } h\,D^{\upalpha \upbeta \gamma \delta }\partial _{\delta } h>$, $E=<\partial _{\upalpha \upbeta } g\,B^{\upalpha \upbeta \gamma \delta }\partial _{\gamma \delta } g>$, $C=<\partial _{\upalpha } b\,K^{\upalpha \upbeta }\partial _{\upbeta } b>$, $G_{\upalpha \gamma } G_{\gamma \eta }^{-1} =\delta _{\upalpha \eta }$ ($\delta _{\upalpha \eta }$ is an unit tensor) we arrive finally at the asymptotic model equations expressed only in macrodisplacements $u_{\upalpha }^{0} ,\,w^{0}$ and macrotemperature $\theta ^{0}$

$$\begin{aligned}&D_{h}^{\upalpha \upbeta \gamma \delta } \partial _{\upbeta \delta } u_{\gamma }^{0} +r^{-1}D_{h}^{\upalpha \upbeta 11} \partial _{\upbeta } w^{0}-\bar{{D}}_{b}^{\upalpha \upbeta } \partial _{\upbeta } \theta ^{0}-<\mu>a^{\upalpha \upbeta }\ddot{{u}}_{\upbeta }^{0} +<f^{\upalpha }>=0, \nonumber \\&B_{g}^{\upalpha \upbeta \gamma \delta } \partial _{\upalpha \upbeta \gamma \delta } w^{0}+r^{-1}D_{h}^{11\gamma \delta } \partial _{\delta } u_{\gamma }^{0} +r^{-2}D_{h}^{1111} w^{0}-r^{-1}\bar{{D}}_{h}^{11} \theta ^{0} \nonumber \\&\qquad +<\mu>\ddot{{w}}^{0}-<f>=0, \nonumber \\&\bar{{K}}_{b}^{\upalpha \upbeta } \partial _{\upalpha \upbeta } \theta ^{0}-[<c>+T_{0}<\bar{{d}}^{\upalpha \upbeta }\partial _{\upalpha } h>G_{\upbeta \eta }^{-1} <\partial _{\upalpha } h\,\bar{{d}}^{\upalpha \eta }>]\dot{{\theta }}^{0} \nonumber \\&\quad =T_{0} [\bar{{D}}_{h}^{\upalpha \upbeta } \partial _{\upalpha } \dot{{u}}_{\upbeta }^{0} +r^{-1}\bar{{D}}_{h}^{11} \dot{{w}}^{0}], \end{aligned}$$

(38)

where

$$\begin{aligned}&D_{h}^{\upalpha \upbeta \gamma \delta } \equiv<D^{\upalpha \upbeta \gamma \delta }>-<D^{\upalpha \upbeta \eta \chi }\;\partial _{\chi } h>G_{\eta \xi }^{-1}<\partial _{\chi } hD^{\chi \xi \gamma \delta }>, \nonumber \\&B_{g}^{\upalpha \upbeta \gamma \delta } \equiv<B^{\upalpha \upbeta \gamma \delta }>-<B^{\upalpha \upbeta \mu \zeta }\partial _{\mu \zeta } g>E^{-1}\;<\partial _{\mu \zeta } gB^{\mu \zeta \gamma \delta }>\,, \nonumber \\&\bar{{D}}_{h}^{\upalpha \upbeta } \equiv<\bar{{d}}^{\upalpha \upbeta }>-<D^{\upalpha \upbeta \gamma \delta }\partial _{\delta } h>G_{\gamma \eta }^{-1}<\partial _{\delta } h\,\bar{{d}}^{\delta \eta }>, \nonumber \\&\bar{{K}}_{b}^{\upalpha \upbeta } \equiv<K^{\upalpha \upbeta }>-<K^{\upalpha \zeta }\partial _{\zeta } b>C^{-1}<K^{\upbeta \zeta }\partial _{\zeta } b>. \end{aligned}$$

(39)

Tensors $D_{h}^{\upalpha \upbeta \gamma \delta }$, $B_{g}^{\upalpha \upbeta \gamma \delta }$ are tensors of effective elastic moduli for biperiodic shells considered here.

Tensor $\bar{{D}}_{h}^{\upalpha \upbeta }$ is a tensor of effective elastic–thermal moduli.

Tensor $\bar{{K}}_{b}^{\upalpha \upbeta }$ is a tensor of effective thermal moduli.

Because of functions $u_{\upalpha } ({\mathbf{x}},t),w({\mathbf{x}},t)$, $\theta ({\mathbf{x}},t)$ have to be uniquely defined in $\Omega \times \mathrm{I}$, we conclude that $u_{\upalpha } ({\mathbf{x}},t),w({\mathbf{x}},t)$, $\theta ({\mathbf{x}},t)$ must take the form of (14) with $U_{\upalpha } ,W,\Theta$ given by (37). Obviously, now unknowns $u_{\upalpha }^{0} ,w^{0},U_{\upalpha } ,W,\,\theta ^{0},\Theta$ in (14) are not assumed to be slowly varying in the sense given by (10), (11). In the asymptotic approach, they are assumed to be bounded and continuous in $\bar{{\Omega }}$ together with their appropriate derivatives.

Equation (38) together with decomposition (14) in which $U_{\upalpha } ,W,\Theta$ are given by (37) represents the consistent asymptotic model of selected dynamic thermoelasticity problems for the thin biperiodic cylindrical shells under consideration.

5.2 Discussion of results

The important features of the derived consistent asymptotic model are listed below.

• Contrary to starting Eqs. (4), (5) with periodic, highly oscillating and discontinuous coefficients, asymptotic model Eq. (38) formulated here has constant coefficients but independent of a period length. It means that this model is not able to describe the influence of a cell size on the global shell thermoelasticity.

• Unknown functions $u_{\upalpha }^{0} ,U_{\upalpha }$, $w^{0},W$ and $\theta ^{0},\,\Theta$ of the asymptotic model are demanded to be bounded and continuous in $\bar{{\Omega }}$ together with their appropriate derivatives. These unknowns are assumed to be independent of parameter $\varepsilon \in (0,1]$. This is the main difference between the asymptotic approach under consideration and approach which is used in the known homogenization theory, cf. Bensoussan et al. [1]; Jikov et al. [2].

• Within the asymptotic model we formulate boundary conditions only for the macrodisplacements $u_{\upalpha }^{0} ,w^{0}$ and macrotemperature $\theta ^{0}$. The number and form of these conditions are the same as in the classical shell theory governed by starting Eqs. (4), (5).

• The extra unknown functions $U_{\upalpha } ,W,\,\Theta$ called fluctuation amplitudes are governed by a system of linear algebraic Eq. (36)${}_{3-5}$ and can be always eliminated from the governing equations by means of (37). Hence, the unknowns of final asymptotic model Eq. (38) are only macrodisplacements $u_{\upalpha }^{0} ,w^{0}$ and macrotemperature $\theta ^{0}$.

• Resulting asymptotic model Eq. (38) are uniquely determined by the postulated a priori periodic fluctuations shape functions, $h\in FS^{1}(\Omega ,\Delta )$, $h\in O(\lambda )$, $g\in FS^{2}(\Omega ,\Delta )$, $g\in O(\lambda ^{2})$, $b\in FS^{1}(\Omega ,\Delta )$, $b\in O(\lambda )$ representing oscillations of displacement and temperature fields inside a cell. As in the tolerance approach, these functions can be obtained as exact or approximate solutions to periodic eigenvalue cell problems, cf. [11, 22,23,24]. They can also be regarded as the shape functions resulting from the periodic discretization of the cell using, for example, the finite element method. The choice of these functions can be also based on the experience or intuition of the researcher. If the fluctuation shape functions are not derived as solutions to certain periodic eigenvalue problems, then effective moduli (39) of the shell are obtained without specification of the periodic cell problems. It is a very important advantage of the asymptotic model proposed here because in most cases obtaining the solutions to the cell problems is not easy and cannot be realized in the analytical form. This situation is different from that occurring in the known asymptotic homogenization approach, cf. e.g. Bensoussan et al. [1], where only solutions to the periodic cell problems make it possible to define the effective moduli of the structure under consideration.

• Taking into account that for a homogeneous shell with a constant thickness, $D^{\upalpha \upbeta \gamma \delta }({\mathbf{x}})$, $B^{\upalpha \upbeta \gamma \delta }({\mathbf{x}})$, $\mu ({\mathbf{x}})$, $\bar{{d}}^{\upalpha \upbeta }({\mathbf{x}})$, $K^{\upalpha \upbeta }({\mathbf{x}})$, $c({\mathbf{x}})$, ${\mathbf{x}}\in \Omega$, are constant and bearing in mind that $<\partial _{\upalpha } h>=<\partial _{\upalpha } g>=<\partial _{\upalpha \upbeta } g>=<\partial _{\upalpha } b>=0$ we obtained from (37) that $U_{\upalpha } =W=\theta =0$ and from (39) that $D_{h}^{\upalpha \upbeta \gamma \delta } \equiv D^{\upalpha \upbeta \gamma \delta }$, $B_{g}^{\upalpha \upbeta \gamma \delta } \equiv B^{\upalpha \upbeta \gamma \delta }$, $\bar{{D}}_{h}^{\upalpha \upbeta } =\bar{{d}}^{\upalpha \upbeta }$, $\bar{{K}}_{b}^{\upalpha \upbeta } =K^{\upalpha \upbeta }$. Hence, from decomposition (14) it follows that $u_{\upalpha } =u_{\upalpha }^{0} ,\;w=w^{0}$, $\theta =\theta ^{0}$. It means that Eq. (38) generated by asymptotically averaged Lagrange function (32) together with asymptotically averaged constitutive Eq. (33) reduces to starting Eqs. (4), (5) generated by Lagrange function (7) together with constitutive Eq. (8) for invariational parameters occurring in (7). Let us recall that in the consistent asymptotic approach, unknowns $u_{\upalpha }^{0} ,w^{0},U_{\upalpha } ,W,\,\theta ^{0},\Theta$ in (14) are not referred to the slowly varying functions introduced in the tolerance averaging and defined by means of (10), (11), but they must be continuous and bounded in $\bar{{\Omega }}$ together with their appropriate derivatives.

6 Remarks and conclusions

The objects of analysis are thin linearly thermoelastic Kirchhoff-Love-type circular cylindrical shells having a periodically microheterogeneous structure in circumferential and axial directions (biperiodic shells), cf. Figs. 1 and  2.

Considerations are based on the known Kirchhoff-Love theory of elasticity combined with Duhamel–Neumann thermoelastic constitutive relations and on Fourier’s theory of heat conduction, cf. [40,41,42,43,44]. Exact shell Eqs. (4) and (5) describing the dynamic thermoelastic problems for the shells considered in this contribution have highly oscillating, non-continuous and periodic coefficients.

The main aim of this paper is to formulate and discuss a new mathematical non-asymptotic averaged model of thermoelastic problems for the biperiodic shells under consideration. In order to do it, the tolerance modelling technique [8, 9] and a certain extension of the known stationary action principle [8, 9] are applied. Note that the classical stationary action principle cannot be used because the heat conduction is described with the odd order partial differential equations with respect to the time coordinate. The tolerance model derived here is represented by stress–strain–temperature relations (20) and dynamic equilibrium Eq. (21) coupled with heat conduction Eq. (22). The tolerance model equations have constant coefficients depending also on a cell size. Hence, this model makes it possible to analyse the effect of period lengths on the global thermodynamic shell behaviour (the length-scale effect). Solutions to the initial-boundary value problems have the physical sense only if the basic kinematic and thermal unknowns of the tolerance model are slowly varying functions in periodicity directions. This requirement can be verified only a posteriori, and it determines the range of the physical applicability of the model.

The second aim is to formulate a certain asymptotic model of dynamic thermoelasticity problems for the shells under consideration. As a tool of modelling we shall apply the consistent asymptotic approach [8, 9] and extended stationary action principle. Governing Eq. (38) of the asymptotic model has constant coefficients being independent of a microstructure size.

Both the tolerance and asymptotic models are uniquely determined by the periodic, highly oscillating fluctuation shape functions representing disturbances of temperature and displacement fields inside a cell. These functions must be known in every considered problem.

It was shown that the final averaged tolerance equations can be derived using two different methods. The first of them (variational approach) is based on the tolerance averaging of integral action functional (6) defined by the known Lagrange function (7) describing thermoelasticity behaviour of the biperiodic shells under consideration and then applying the extended principle of stationary action to tolerantly averaged action functional (18) determined by means of averaged Lagrangian (16) with non-variational parameters (17). The second of them (orthogonalization approach) is based on the tolerance averaging of starting thermoelasticity Eqs. (4), (5) and then using residual orthogonality assumption (24), cf. [6, 9, 10].

Comparing the derived here tolerance model Eqs. (20)–(22) of thermoelasticity problems for thin biperiodic cylindrical shells and corresponding known tolerance model Eqs. (25)–(28) for thin uniperiodic cylindrical shells (i.e. shells with a periodic structure in circumferential direction only) proposed by Tomczyk and Gołąbczak in [30], it is seen that the equations for uniperiodic shells are more complicated that those (20)–(22) for biperiodic shells and contain a lot of length-scale terms (doubly underlined terms) which do not have counterparts in the equations for biperiodic shells. The occurrence of these terms is strictly related to the fact that physical reliability conditions for uniperiodic shells of form (15), but with functions slowly varying in one direction only, i.e. in the circumferential direction, are less restrictive than conditions (15) for biperiodic shells with functions slowly varying in the two circumferential and axial directions. In the framework of the uniperiodic shell model, unknown kinematic $U_{\upalpha } ,\;W$ and thermal $\Theta$ fluctuation amplitudes are governed by partial differential equations (27)${}_{3,4}$ and (28)${}_{2}$, respectively, whereas within the biperiodic shell model these unknowns are governed by ordinary differential equations (21)${}_{3,4}$ and (22)${}_{2}$, respectively, involving only time derivatives. Hence, there are no extra boundary conditions for unknowns $U_{\upalpha } ,\;W,\,\Theta$ of the biperiodic shell model and that is why they play the role of kinematic or thermal internal variables.

Some applications of tolerance model Eqs. (20)–(22) and asymptotic model Eq. (38) to the analysis of various dynamical thermoelasticity problems for the thin biperiodic cylindrical shells under consideration are reserved for the forthcoming papers.