Skip to main content
SpringerLink
Log in

Double porosity in fluid-saturated elastic media: deriving effective parameters by hierarchical homogenization of static problem

  • Original Article
  • Published:
Continuum Mechanics and Thermodynamics Aims and scope Submit manuscript

Abstract

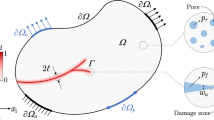
We propose a model of complex poroelastic media with periodic or locally periodic structures observed at microscopic and mesoscopic scales. Using a two-level homogenization procedure, we derive a model coherent with the Biot continuum, describing effective properties of such a hierarchically structured poroelastic medium. The effective material coefficients can be computed using characteristic responses of the micro- and mesostructures which are solutions of local problems imposed in representative volume elements describing the poroelastic medium at the two levels of heterogeneity. In the paper, we discus various combinations of the interface between the micro- and mesoscopic porosities, influence of the fluid compressibility, or solid incompressibility. Gradient of porosity is accounted for when dealing with locally periodic structures. Derived formulae for computing the poroelastic material coefficients characterize not only the steady-state responses with static fluid, but are relevant also for quasistatic problems. The model is applicable in geology, or in tissue biomechanics, in particular for modeling canalicular-lacunar porosity of bone which can be characterized at several levels.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Allaire G.: Homogenization and two-scale convergence. SIAM J. Math. Anal. 23, 1482–1518 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  2. Arbogast T., Douglas J., Hornung U.: Derivation of the double porosity model of single phase flow via homogenization theory. SIAM J. Math. Anal. 21, 823–836 (1990)

    Article  MathSciNet  MATH  Google Scholar 

  3. Auriault J., Boutin C.: Deformable porous media with double porosity. Quasi-static. I: Coupling effects. Transp. Porous Media 7, 63–82 (1992)

    Article  Google Scholar 

  4. Auriault J., Boutin C.: Deformable porous media with double porosity. Quasi-static. II: Memory effects. Transp. Porous Media 10, 153–169 (1993)

    Article  Google Scholar 

  5. Auriault J.L., Sanchez-Palencia E.: Etude du comportment macroscopique d’un milieu poreux saturé déformable. J. de Mécanique 16(4), 575–603 (1977)

    MathSciNet  MATH  Google Scholar 

  6. Ba, J., Zhang, L., Sun, W., Hao, Z.: Velocity field of wave-induced local fluid flow in double-porosity media. Sci. China Phys. Mech. Astron. 57(6), 1020–1030 (2014)

  7. Bader K., Hofstetter K., Hellmich C., Eberhardsteiner J.: The poroelastic role of water in cell walls of the hierarchical composite “softwood”. Acta Mech. 217, 75–100 (2011)

    Article  MATH  Google Scholar 

  8. Baffico L., Grandmont C., Maday Y., Osses A.: Homogenization of elastic media with gaseous inclusions. Multiscale Model. Simul. (SIAM) 7(1), 432–465 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  9. Barenblatt G.I.: On certain boundary value problems for the equations of seepage of liquid in fissured rocks. PMM 27(52), 348–350 (1963)

    MathSciNet  MATH  Google Scholar 

  10. Barenblatt G.I., Zheltov I.P., Kochina I.N.: Basic concepts in the theory of seepage of homogeneous liquids in fissured rocks. PMM 24(5), 852–864 (1960)

    MATH  Google Scholar 

  11. Bensoussan A., Lions J., Papanicolaou G.: Asymptotic Methods in Periodic Media. North-Holland, Amsterdam (1978)

    MATH  Google Scholar 

  12. Berryman J.G.: Poroelastic response of fractured porous media. Transp. Porous Med. 93, 293–307 (2012)

    Article  Google Scholar 

  13. Berryman, J.G., Pride, S.R.: Models for computing geomechanical constants of double-porosity materials from the constituents’ properties. J. Geophys. Res. Solid Earth 107(B3), ECV 2-1–ECV 2-14 (2002)

  14. Biot M.A.: General theory of three-dimensional consolidation. J. Appl. Phys. 12, 155–164 (1941)

    Article  ADS  MATH  Google Scholar 

  15. Biot M.A.: Theory of elasticity and consolidation for a porous anisotropic solid. J. Appl. Phys. 26(2), 182–185 (1955)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  16. Biot M.A., Willis D.G.: The elastic coefficients of the theory of consolidation. J. Appl. Mech. 79, 594–601 (1957)

    MathSciNet  Google Scholar 

  17. Brezis H.: Functional Analysis, Sobolev Spaces and Partial Differential Equations. Springer, New York (2010)

    Book  Google Scholar 

  18. Brezzi, F., Fortin, M.: Mixed and Hybrid Finite Element Methods. Computational Mathematics. Vol. 15, Springer, Berlin (1991)

  19. Brown D., Popov P., Efendiev Y.: On homogenization of stokes flow in slowly varying media with applications to fluid–structure interaction. Int. J. Geomath. 2(2), 281–305 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  20. Brown D., Popov P., Efendiev Y.: Effective equations for fluid–structure interaction with applications to poroelasticity. Appl. Anal. 93(4), 771–790 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  21. Cardoso L., Fritton S.P., Gailani G., Benalla M., Cowin S.C.: Advances in assessment of bone porosity, permeability and interstitial fluid flow. J. Biomech. 46, 253–265 (2013)

    Article  Google Scholar 

  22. Chen Z.X.: Transient flow of slightly compressible fluids through double-porosity, double-permeability systems: a state-of-art review. Trans. Porous Media 4, 147–184 (1989)

    Article  Google Scholar 

  23. Cioranescu D., Damlamian A., Griso G.: The periodic unfolding method in homogenization. J. Math. Anal. (SIAM) 40(4), 1585–1620 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  24. Cioranescu, D., Donato, P.: An Introduction to Homogenization. No. 17 in Oxford Lecture Series in Mathematics and its Applications. Oxford University Press, Oxford (1999)

  25. Cowin, S., Cardoso, L.: Blood and interstitial flow in the hierarchical pore space architecture of bone tissue. J. Biomech. (2015). doi:10.1016/j.jbiomech.2014.12.013

  26. Cowin S.C.: Bone poroelasticity. J. Biomech. 32, 217–238 (1999)

    Article  Google Scholar 

  27. Daly, K.R., Roose, T.: Multiscale modelling of hydraulic conductivity in vuggy porous media. Proc. R. Soc. A 470, 20130383 (2014)

  28. Ene I., Saint Jean Paulin J.: Homogenization and two-scale convergence for a Stokes or Navier-Stokes flow in an elastic thin porous medium. Math. Models Methods Appl. Sci. 6(7), 941–955 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  29. Ersahin, M., Ozgun, H., Dereli, R., Ozturk, I., Roest, K., van Lier, J.: A review on dynamic membrane filtration: materials, applications and future perspectives. Biores. Technol. 122, 196–206 (2012)

  30. Gailani G., Cowin S.: Ramp loading in the Russian doll poroelasticity. J. Mech. Phys. Solids 59, 103–120 (2011)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  31. Li Y., Fu Z.Y., Su B.L.: Hierarchically structured porous materials for energy conversion and storage. Adv. Funct. Mater. 22, 4634–4667 (2012)

    Article  Google Scholar 

  32. Mehrabian A., Abousleiman Y.N.: Generalized Biot’s theory and Mandel’s problem of multiple-porosity and multiple-permeability poroelasticity. J. Geophys. Res. Solid Earth 119, 2745–2763 (2014)

    Article  ADS  Google Scholar 

  33. Rohan E., Cimrman R.: Multiscale FE simulation of diffusion-deformation processes in homogenized dual-porous media. Math. Comput. Simul. 82, 1744–1772 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  34. Rohan, E., Lukeš, V.: Modeling nonlinear phenomena in deforming fluid-saturated porous media using homogenization and sensitivity analysis concepts. Appl. Math. Comput. doi:10.1016/j.amc.2015.01.054(2015)

  35. Rohan E., Naili S., Cimrman R., Lemaire T.: Hierarchical homogenization of fluid saturated porous solid with multiple porosity scales. Comptes Rendus Mec. 340, 688–694 (2012)

    Article  ADS  Google Scholar 

  36. Rohan E., Naili S., Cimrman R., Lemaire T.: Multiscale modeling of a fluid saturated medium with double porosity: relevance to the compact bone. J. Mech. Phys. Solids 60, 857–881 (2012)

    Article  ADS  MathSciNet  Google Scholar 

  37. Rohan, E., Naili, S., Turjanicová, J., Lemaire, T.: Models of poroelastic double porous structures based on hierarchical homogenization—application to compact bone. In: Proceedings of the fifth biot conference on poromechanics, vol. 5, pp. 1152–1159. American Society of Civil Engineers, Wien (2013)

  38. Rohan E., Shaw S., Whiteman J.: Poro-viscoelasticity modelling based on upscaling quasistatic fluid-saturated solids. Comput. Geosci. 18, 883–895 (2014)

    Article  MathSciNet  Google Scholar 

  39. Royer P., Auriault J.L., Boutin C.: Macroscopic modeling of double-porosity reservoirs. J. Pet. Sci. Eng. 16(4), 187–202 (1996)

    Article  Google Scholar 

  40. Royer P., Auriault J.L., Strzelecki T.: Macroscopic behavior of gas flow with adsorption through a fractured porous medium. Mech. Res. Commun. 23(1), 67–73 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  41. Sanchez-Palencia, E.: Non-homogeneous media and vibration theory. No. 127 in Lecture Notes in Physics. Springer, Berlin (1980)

  42. Shen, W., Lanoye, E., Dormieux, L., Kondo, D.: Homogenization of saturated double porous media with Eshelby-like velocity field. Acta Geophys. 62(5), 1142–1162 (2014)

  43. Warren, J., Root, P.: The behavior of naturally fractured reservoirs. Soc. Pet. Eng. J. 3(3), 245–255 (1963) (1963)

Download references

Author information

Authors and Affiliations

  1. NTIS New Technologies for Information Society, European Centre of Excellence, Faculty of Applied Sciences, University of West Bohemia in Pilsen, Univerzitní 22, 30614, Plzeň, Czech Republic

    Eduard Rohan

  2. Laboratoire Modélisation et Simulation Multi Echelle, MSME UMR 8208 CNRS, Université Paris-Est, 61, Avenue du Général de Gaulle, 94010, Créteil Cedex, France

    Salah Naili & Thibault Lemaire

Authors
  1. Eduard Rohan
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Salah Naili
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Thibault Lemaire
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Salah Naili.

Additional information

Communicated by Andreas Öchsner.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Rohan, E., Naili, S. & Lemaire, T. Double porosity in fluid-saturated elastic media: deriving effective parameters by hierarchical homogenization of static problem. Continuum Mech. Thermodyn. 28, 1263–1293 (2016). https://doi.org/10.1007/s00161-015-0475-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00161-015-0475-9

Keywords

Search

Navigation