Skip to main content
SpringerLink
Log in

An innovative adaptive Kriging-based parallel system reliability method under error stopping criterion for efficiently analyzing the global reliability sensitivity index

  • Research
  • Published:
Structural and Multidisciplinary Optimization Aims and scope Submit manuscript

Abstract

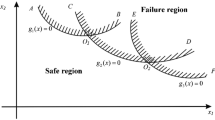
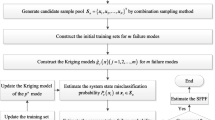
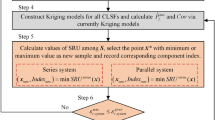
Global reliability sensitivity index measures the effect of uncertainty of model input on model failure probability, which is critical for simplifying analysis model and the reliability-based design optimization model. For efficiently estimating the global reliability sensitivity index of each model input, this paper transforms it into estimating an unconditional failure probability and a two failure modes-based parallel system failure probability from the perspective of single-loop estimation method. Furthermore, the relationship of computational accuracy among the global reliability sensitivity index, the unconditional failure probability, and the two failure modes-based system failure probability is constructed, on which the error stopping criterion-based sequentially adaptive Kriging model approach is developed to significantly decrease the number of calls to the actual limit state functions and the corresponding computational time under the sufficient accuracy. Results of three case studies covering explicit and implicit limit state functions demonstrate the accuracy and efficiency of the proposed method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  • Assaf SA, Zirkle LD (1976) Approximate analysis of non-linear stochastic systems. Int J Control 23(4):477–492

    Article  Google Scholar 

  • Barabesi L, Fattorini L (2002) Kernel estimators of probability density functions by ranked-set sampling. Commun Stat-Theory Methods 31(4):597–610

    Article  MathSciNet  Google Scholar 

  • Bichon BJ, Eldred MS, Swiler LP et al (2008) Efficient global reliability analysis for nonlinear implicit performance function. AIAA J 46:2459–2568

    Article  Google Scholar 

  • Bierig C, Chernov A (2016) Approximation of probability density functions by the multilevel Monte Carlo maximum entropy method. J Comput Phys 314:661–681

    Article  MathSciNet  Google Scholar 

  • China Aeronautical Materials Handbook (2001) The second edition, Beijing, Standards Press of China

  • Echard B, Gayton N, Lemaire M (2011) AK-MCS: An active learning reliability method combining Kriging and Monte Carlo Simulation. Struct Saf 33:145–154

    Article  Google Scholar 

  • Echard B, Gayton N, Lemaire M et al (2013) A combined importance sampling and Kriging reliability method for small failure probabilities with time-demanding numerical models. Reliab Eng Syst Saf 111:232–240

    Article  Google Scholar 

  • Feng KX, Lu ZZ, Chen ZB et al (2023) An innovative Bayesian updating method for laminated composite structures under evidence uncertainty. Compos Struct 304:116429

    Article  Google Scholar 

  • Gao HF, Zio E, Wang AJ et al (2020) Probabilistic-based combined high and low cycle fatigue assessment for turbine blades using a substructure-based Kriging surrogate model. Aerosp Sci Technol 104:105957

    Article  Google Scholar 

  • He LL, Lu ZZ, Feng KX (2019) A novel estimation method for failure-probability-based sensitivity by conditional probability theorem. Struct Multidisc Optim 61:1589–1602

    Article  MathSciNet  Google Scholar 

  • Hristov PO, Diazdelao FA (2023) Subset simulation for probabilistic computer models. Appl Math Model 120:769–785

    Article  MathSciNet  Google Scholar 

  • Hu Z, Mahadevan S (2016) A single-loop Kriging surrogate modeling for time-dependent reliability analysis. J Mech Des 138:061406

    Article  Google Scholar 

  • Keshtegar B, Meng Z (2017) A hybrid relaxed first-order reliability method for efficient structural reliability analysis. Struct Saf 66:84–93

    Article  Google Scholar 

  • Li LY, Lu ZZ, Feng J et al (2012) Moment-independent importance measure of basic variable and its state dependent parameter solution. Struct Saf 38:40–47

    Article  Google Scholar 

  • Li G, He WX, Zeng Y (2019a) An improved maximum entropy method vis fractional moments with Laplace transform for reliability analysis. Struct Multidisc Optim 59(4):1301–1320

    Article  Google Scholar 

  • Li LY, Papaioannou I, Straub D (2019b) Global reliability sensitivity estimation based on failure samples. Struct Saf 81:101871

    Article  Google Scholar 

  • Liu JS. Monte Carlo strategies in scientific computing, New York, 2001.

  • Lu ZH, Hu DZ, Zhang YG (2017) Second-order fourth moment method for structural reliability. J Eng Mech 143:06016010

    Article  Google Scholar 

  • Rosario ZD, Iaccarino G, Fenrich RW (2019) Fast precision margin with the first-order reliability method. AIAA J 57(11):5042–5053

    Article  Google Scholar 

  • Saludheen A, Firaz MZ, Ankith M et al (2021) Carbon fibre composite development for in-ground UAV’s with NACA0012 aerofoil wing. Mater Today: Proc 47:6839–6848

    Google Scholar 

  • Sobol IM (1998) On quasi-Monte Carlo integrations. Math Comput Simul 47:103–112

    Article  MathSciNet  Google Scholar 

  • Wang ZY, Shafieezadeh A (2019) ESC: an efficient error-based stopping criterion for Kriging-based reliability analysis methods. Struct Multidiscip Optim 59:1621–1637

    Article  Google Scholar 

  • Wang YP, Xiao SN, Lu ZZ (2018) A new efficient simulation method based on Bayes’ theorem and importance sampling Markov chain simulation to estimate the failure-probability-based global sensitivity measure. Aerosp Sci Technol 79:364–372

    Article  Google Scholar 

  • Wang YP, Xiao SN, Lu ZZ (2019) An efficient method based on Bayes’ theorem to estimate the failure-probability-based sensitivity measure. Mech Syst Signal Process 115:607–620

    Article  Google Scholar 

  • Wang JQ, Lu ZZ, Wang L (2023) An efficient method for estimating failure probability bounds under random-interval mixed uncertainties by combining line sampling with adaptive Kriging. Int J Numer Meth Eng 124(2):308–333

    Article  MathSciNet  Google Scholar 

  • Wei PF, Lu ZZ, Hao WR et al (2012) Efficient sampling methods for global reliability sensitivity analysis. Comput Phys Commun 183:1728–1743

    Article  MathSciNet  Google Scholar 

  • Xiang ZL, He XH, Zou YF et al (2023) An importance sampling method for structural reliability analysis based on interpretable deep generative network. Eng Comput. https://doi.org/10.1007/s00363-023-01790-2

    Article  Google Scholar 

  • Yun WY, Lu ZZ, Jiang X (2019a) An efficient method for moment-independent global sensitivity analysis by dimensional reduction technique and principle of maximum entropy. Reliab Eng Syst Saf 187:174–182

    Article  Google Scholar 

  • Yun WY, Lu ZZ, Zhou YC et al (2019b) AK-SYSi: an improved adaptive Kriging model for system reliability analysis with multiple failure modes by a refined U learning function. Struct Multidiscip Optim 59:263–278

    Article  MathSciNet  Google Scholar 

  • Zhang XF, Pandey MD (2013) Structural reliability analysis based on the concepts of entropy, fractional moment and dimensional reduction method. Struct Saf 43:28–40

    Article  Google Scholar 

  • Zhang XD, Quek ST (2022) Efficient subset simulation with active learning Kriging model for low failure probability prediction. Probab Eng Mech 68:103256

    Article  Google Scholar 

Download references

Acknowledgements

This work was supported by the Aeronautical Science Foundation of China (Grant No. 20220009053001), Young Talent Fund of Association for Science and Technology in Shaanxi of China (Grant No. 20230446), Natural Science Foundation of Chongqing (Grant No. CSTB2022NSCQ-MSX0861), Guangdong Basic and Applied Basic Research Foundation (Grant No. 2022A1515011515), and the National Natural Science Foundation of China (Grant No. 12002237, 12302154).

Author information

Authors and Affiliations

  1. School of Aeronautics, Northwestern Polytechnical University, Xi’an, 710072, Shaanxi, China

    Wanying Yun, Shutong Zhang & Fengyuan Li

  2. National Key Laboratory of Strength and Structural Integrity, Aircraft Strength Research Institute of China, Xi’an, 710065, China

    Xiangming Chen & Zhe Wang

  3. Innovation Center NPU Chongqing, Northwestern Polytechnical University, Chongqing, 400000, China

    Wanying Yun

  4. Research & Development Institute of Northwestern Polytechnical University in Shenzhen, Shenzhen, 518057, Guangdong, China

    Wanying Yun

  5. Chinese Flight Test Establishment, Aircraft, Flight Test Technology Institute, Xi’an, 710089, Shaanxi, China

    Wanying Yun

  6. School of Aerospace Engineering and Applied Mechanics, Tongji University, Shanghai, 200092, China

    Kaixuan Feng

Authors
  1. Wanying Yun
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Shutong Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Fengyuan Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Xiangming Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Zhe Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Kaixuan Feng
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

WY: conceptualization, methodology, writing-original draft, funding acquisition. SZ: methodology, writing-review. FL: methodology, writing-review. XC: writing-review & editing, resources, software. ZW: methodology, formal analysis. KF: writing-review & editing.

Corresponding author

Correspondence to Wanying Yun.

Ethics declarations

Conflict of interest

We declare that we do not have any commercial or associative interest that represents a conflict of interest in connection with the work submitted.

Replication of results

The original codes of the case study I in Sect. 4.1 are available in the Supplementary materials.

Additional information

Responsible Editor: Chao Hu

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary Information

Below is the link to the electronic supplementary material.

Supplementary file1 (ZIP 4 KB)

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yun, W., Zhang, S., Li, F. et al. An innovative adaptive Kriging-based parallel system reliability method under error stopping criterion for efficiently analyzing the global reliability sensitivity index. Struct Multidisc Optim 67, 51 (2024). https://doi.org/10.1007/s00158-024-03752-8

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s00158-024-03752-8

Keywords

Search

Navigation