A novel multi-fidelity cokriging model assisted by multiple non-hierarchical low-fidelity datasets

Abstract

Multi-fidelity (MF) surrogate models for incorporating multiple non-hierarchical low-fidelity (LF) datasets, whose rank of fidelity level is unknown, have attracted much attention in engineering problems. However, most of existing approaches either need to build extra surrogate models for LF datasets in the fitting process or ignore the cross-correlations among these LF datasets, resulting in accuracy deterioration of an MF model. To address this, a novel multi-fidelity cokriging model is proposed in this article, termed as MCOK, which can incorporate arbitrary number of non-hierarchical LF datasets without building extra LF surrogate models. A self-contained derivation of MCOK predictor and its mean square error are presented. It puts all the covariances between any two MF datasets into a single matrix and introduces additional parameters “gamma” to account for their cross-correlations. A novel method for tuning these additional parameters in a latent space is developed to deal with the problem associated with non-positive definite correlation matrix. The proposed MCOK method is then validated against a set of numerical test cases and further demonstrated via an engineering example of aerodynamic data fusion for FDL-5A flight vehicle. Results from current test cases show that MCOK outperforms existing non-hierarchical cokriging, linear regression MF surrogate model, and latent-map Gaussian processes model, with more accurate and robust predictions, which makes it more practical for engineering modeling problems.

1 Introduction

Surrogate model has been widely applied to different areas of aerospace science and engineering due to its capability of yielding usable approximations of the quantity of interest and simultaneously featuring real-time-capable evaluations (Forrester and Keane 2009; Simpson et al. 2001; Viana et al. 2014; Bertram et al. 2018). Particularly, they are built through a small number of samples and used to replace high-fidelity (HF) but time-consuming physical tests or simulations so that the design efficiency could be greatly improved (Sacks et al. 1989). With the integration of GPU technology, the efficiency could be further accelerated (Gardner et al. 2018). However, in many real-world engineering design, building a sufficiently accurate surrogate model still needs large number of expensive experimental tests or HF simulations, which makes the cost easily become prohibitive (Giselle Fernández-Godino et al. 2019; Park et al. 2017). To tackle this problem, multi-fidelity (MF) surrogate models have gained popularity as they use a set of low-fidelity (LF) models to provide information about variation trend and assist in predicting the quantity of interest, while reducing the number of expensive tests or HF simulations (Han and Görtz 2012). It is a very promising way and strikes a balance between the high cost and prediction accuracy by fusing the HF and LF datasets (Cheng et al. 2021; Han et al. 2020; Liu et al. 2018; Zhou et al. 2020a).

Currently, the existing MF modeling approaches can be divided into three categories according to diverse means of data fusion (Zhou et al. 2017, 2020b). The first category is a correction-based method using a bridge or scaling function to capture the differences and ratios between the LF and HF models. The correction can be multiplicative (Haftka 1991; Alexandrov et al. 2001), additive (Choi et al. 2009; Song et al. 2019), or hybrid (Gano et al. 2005; Han et al. 2013). As these methods are easy to understand with relatively simple forms, they are the most extensive approaches for MF surrogate models (Zhou et al. 2020a). The second category is space mapping (Bandler et al. 1994; Robinson et al. 2008; Jiang et al. 2018), which attempts to establish an appropriate mapping relation between the HF and LF design space. The third category is variable-fidelity kriging, such as cokriging. Cokriging was originally proposed in geostatistical community (Journel and Huijbregts 1978) and then extended to deterministic computer experiments via introducing automatic regression parameters by Kennedy and O’Hagan (2000), also termed as KOH autoregressive model. Later, Qian and Wu (2008) used a Gaussian process model instead of a constant term as the multiplicative factor to account for the nonlinear scaling change, resulting in a dramatic improvement in prediction performance. Le Gratiet and Garnier (2014) proposed a recursive cokriging model, which significantly reduced the computational complexity of the original cokriging model. Ulaganathan et al. (2015) extended this method by incorporating MF gradient information during the model construction. Zaytsev (2016) also used a recursive way to implement a cokriging model incorporating MF data with more than two levels. Perdikaris et al. (2017) developed a nonlinear autoregressive cokriging model to learn the complex nonlinear relations between multiple LF and HF models. Guo et al. (2018) and Park et al. (2018) discussed the properties of different terms in the likelihood function to find a proper scale factor before the LF model. Bu et al. (2022) proposed an alternative way to choose the scale factor by minimizing the posterior variance of the discrepancy function. Han et al. (2012) developed a new cokriging model by redefining the cokriging weights and by a novel approach to constructing the cokriging correlation matrix. He also put forward an extension cokriging method, termed as hierarchical Kriging (HK) model (Han and Görtz 2012), which is as accurate as KOH autoregressive model but provides a more reasonable estimate of the mean-squared error (MSE). Besides, he extended the original HK with two-level fidelities to multi-level HK model (MHK), which can fuse different datasets with arbitrary levels of fidelity (Han et al. 2020). Zimmermann and Han (2010) developed a simplified cross-correlation estimation approach based on Han’s method (Han et al. 2012), which makes the new cokriging model more robust. Courrier et al. (2016) compared these two cokriging models and found that Zimmermann’s method was more efficient and accurate in some engineering modeling cases. Zhou et al. (2020a) proposed a generalized cokriging model which can integrate both nested and non-nested MF sampling data. Due to the remarkable performance, cokriging has gained popularity in various fields (Liu et al. 2018), such as aerospace field (Hebbal et al. 2021; Shi et al. 2020), intelligent manufacturing (Krishnan and Ganguli 2021), and marine industry (Liu et al. 2022).

Although many MF modeling methods mentioned above have already been extended to incorporate multiple LF datasets with three or more fidelities (Han et al. 2020; Le Gratiet and Garnier 2014; Ulaganathan et al. 2015; Zaytsev 2016; Perdikaris et al. 2017), they assume that these LF datasets used for building an MF surrogate model are hierarchical. In other words, the fidelity levels of all LF datasets are determined or ranked in advance. However, in many cases, the fidelity levels of the LF models are not hierarchical and cannot be pre-determined. This can lead to situations where the data fusion process fails to deliver accurate results. Such non-hierarchical LF datasets are commonly encountered but often overlooked, as they are generated in different ways to simplify the HF model. For example, it could be hard to distinguish the fidelity level between the datasets obtained by solving Euler equations on a fine computational grid and those obtained by solving Navier–Stokes equations on a coarse grid. To address this issue, many new MF methods for incorporating non-hierarchical LF datasets have been proposed recently. Yamazaki and Mavriplis (2013) developed a three-level cokriging model based on Han’s work (Han et al. 2012) to handle with non-hierarchical LF datasets and applied it to aerodynamic data fusion. Chen et al. (2016) proposed three different non-hierarchical multi-model fusion approaches based on spatial random processes, with different assumptions and structures to capture the relationships between the simulation models and the HF observations. Zhang et al. (2018) proposed a simple and yet powerful MF surrogate model based on single linear regression, termed as linear regression multi-fidelity surrogate (LR-MFS), especially for fitting HF data with noise. Xiao et al. (2018) developed an extended cokriging model (ECK) by attributing various weights to LF models of different fidelities. Cheng et al. (2021) proposed an MF surrogate modeling method based on variance-weighted sum to flexibly handle multiple non-hierarchical LF data. Eweis-Labolle et al. (2022) used a latent-map Gaussian Processes (LMGP) model to convert data fusion into a latent space learning problem where the relations among different non-hierarchical datasets can be automatically learned. Zhang et al. (2022) improved Xiao’s method by minimizing the second derivative of the prediction values of the discrepancy model to obtain optimal scale factors for the LF surrogate models, and developed a non-hierarchical cokriging modeling method, termed as NHLF-COK, which was comparable to LR-MFS and ECK models. Besides, Yousefpour et al. (2023) developed an open-source library for kernel-based learning via Gaussian Processes (GPs) called GP+, which contains powerful MF modeling methods and shows several unique advantages over other GP modeling libraries.

However, most of these MF models for incorporating multiple non-hierarchical LF datasets have two major limitations: (1) Most approaches, such as LR-MFS and NHLF-COK, require the construction of additional surrogate models for LF datasets as a preliminary step in the fitting process, which makes the MF model predictor largely depend on the accuracy of these LF surrogate models. In other words, if LF surrogate models are built inaccurately or even provide incorrect model variation trends, the final prediction accuracy of the MF model will not be as good as expected. (2) They only consider the covariances between HF and LF datasets while ignoring the effects of cross-covariances among LF models, which may lead to a reduction in model accuracy. Under these circumstances, further improvements in accuracy are still required before they can be widely used in real-world engineering modeling problems, which motivates the study of this article.

The objective of this article is to develop a novel and engineeringly practical surrogate model, termed as multi-fidelity cokriging (MCOK), capable of incorporating non-hierarchical LF datasets with arbitrary levels of fidelity, without building additional surrogate models for LF datasets, and fully considering the effects of cross-covariances among different LF models. Its core idea is to put all the covariances between any two datasets of different fidelities together into a single cokriging correlation matrix and introduce additional parameters in the matrix to account for the cross-correlations between different MF datasets. This is of great benefit to explore underlying factors and improve the prediction accuracy. In fact, our method is an extension of the two-level cokriging model by Zimmermann and Han (2010) to a model that can incorporate data with arbitrary levels of fidelities. Note that such extension is not straightforward since the correlation matrix could easily become non-positive definite, which is fatal for hyperparameter tuning using maximum likelihood estimation (MLE). To deal with this problem, we develop a novel method for tuning the additional parameters by replacing them with the distances between latent points in a two-dimensional latent space, allowing for quantifying the correlations among different datasets. These latent points can move freely to avoid matrix singularity when changing positions during MLE, which makes the proposed MCOK model efficient and robust. Additionally, while our proposed MCOK model and the LMGP model exhibit similarities in optimizing model parameters and both models can consider the cross-covariances among LF models without building extra LF surrogate models during the fitting process, they still differ in the basic assumption regarding the regression function served as the model variation trend. More specifically, in an LMGP model, the authors assume that the random functions for MF data all have stationary and the same mean, while in an MCOK model, we assume that they have stationary but different means. This assumption, indeed, benefits the fusion of multiple MF datasets with systematic biases, such as aerodynamic data obtained from different physical models, making the MCOK model more accurate. A detailed discussion of this will be presented in the next section.

The remainder of this article is organized as follows. Section 2 introduces the formulation of MCOK model, including its predictor and MSE, the choice of correlation function and the hyperparameter tuning strategy, along with a novel method for tuning the additional parameters to overcome correlation matrix singularity. Section 3 presents a set of numerical test cases to validate the proposed method and employs an aerodynamic data fusion example involving the FDL-5A hypersonic flight vehicle to further demonstrate our approach. Three other representative MF surrogate models NHLF-COK, LR-MFS, and LMGP are also built for comparison. At last, general conclusions and future work beyond the present scope are presented.

2 Multi-fidelity cokriging model formulation

Cokriging model is a statistical interpolation method for the enhanced prediction of a less intensively sampled primary variable of interest with assistance of intensively sampled auxiliary variables (Han et al. 2012). Compared with the conventional KOH autoregressive model, Han’s cokriging model might be more practical and can reduce the notational complexity of cokriging correlation matrix (Han et al. 2012). Additionally, a scale factor ${{\sigma_{1} } \mathord{\left/ {\vphantom {{\sigma_{1} } {\sigma_{2} }}} \right. \kern-0pt} {\sigma_{2} }}$ ($\sigma_{1} ,\sigma_{2}$ are the process variances of HF and LF model, respectively) is introduced in the cokriging predictor to account for the influence of the LF model on the prediction of the HF model. However, the optimal value of ${{\sigma_{1} } \mathord{\left/ {\vphantom {{\sigma_{1} } {\sigma_{2} }}} \right. \kern-0pt} {\sigma_{2} }}$ is hard to estimate, resulting in Han’s cokriging model being less robust (Courrier et al. 2016). To avoid this problem, Zimmermann and Han (2010) presented a simplified cross-correlation estimation by introducing additional model parameters before cross-correlation terms in the cokriging correlation matrix. Results show that compared to Han’s method, though Zimmerman’s method is considerably simpler, it performed in all given examples comparable or, arguably, even better (Zimmermann and Han 2010). Herein, our work is based on Zimmermann’s method and a detailed derivation is presented in the following subsections.

2.1 General descriptions and assumptions

For an m-dimensional modeling problem, suppose we are concerned with the prediction of an expensive-to-evaluate HF model $y_{0} ({\mathbf{x}}),$ with assistance of L cheaper-to-evaluate LF models $y_{k} = f_{k} ({\mathbf{x}}), \, k = 1,2, \ldots ,L,$ whose fidelity levels are not determined or ranked in advance. This assumption is quite different from that of building an MHK model (Han et al. 2020), which argues that the fidelity levels of LF models can be clearly ranked and applies a hierarchical treatment. In other words, the knowledge of the relative accuracies of all the LF models, $y_{1} ({\mathbf{x}}),y_{2} ({\mathbf{x}}), \ldots ,y_{L} ({\mathbf{x}})$, with respect to the highest fidelity model $y_{0} ({\mathbf{x}})$ is not provided here in an MCOK model.

Assume that the high- and all lower-fidelity models are sampled at $n_{0} ,n_{1} ,n_{2} , \ldots ,n_{L}$ sampling sites, respectively. The HF dataset is denoted as ${\varvec{S}}_{0} {\kern 1pt} = {\kern 1pt} {\kern 1pt} \left[ {{\varvec{x}}_{0}^{(1)} ,{\varvec{x}}_{0}^{(2)} ,...,{\varvec{x}}_{0}^{{(n_{0} )}} } \right]^{{\text{T}}} \in {\mathbb{R}}^{{n_{0} \times m}}$ and the kth LF dataset is denoted as ${\varvec{S}}_{k} {\kern 1pt} = {\kern 1pt} {\kern 1pt} \left[ {{\varvec{x}}_{k}^{(1)} ,{\varvec{x}}_{k}^{(2)} ,...,{\varvec{x}}_{k}^{{(n_{k} )}} } \right]^{{\text{T}}} \in {\mathbb{R}}^{{n_{k} \times m}}$. The corresponding function values are ${\varvec{y}}_{S,0} = \left[ {y_{0}^{(1)} ,y_{0}^{(2)} ,...,y_{0}^{{(n_{0} )}} } \right]^{{\text{T}}} \in {\mathbb{R}}^{{n_{0} }}$ and ${\varvec{y}}_{S,k} = \left[ {y_{k}^{(1)} ,y_{k}^{(2)} ,...,y_{k}^{{(n_{k} )}} } \right]^{{\text{T}}} \in {\mathbb{R}}^{{n_{k} }}$, respectively. Thus, the pairs $({\varvec{S}}_{0} ,{\varvec{y}}_{S,0} )$ and $({\varvec{S}}_{k} ,{\varvec{y}}_{S,k} )$ denote the measured input–output dataset of HF and the kth LF level in the vector space, respectively.

As in the case of a kriging, the output of a deterministic computer experiment is treated as a realization of a stationary random process. Hence, we assume that the HF model and the kth LF model are realizations of dependent random functions:

$$\begin{gathered} Y_{0} ({\mathbf{x}}) = {\mathbf{f}}_{0} {{\varvec{\upbeta}}}_{0} + Z_{0} ({\mathbf{x}}) = \sum\limits_{j = 1}^{h} {f_{0}^{(j)} } ({\mathbf{x}})\beta_{0}^{(j)} + Z_{0} ({\mathbf{x}}), \hfill \\ Y_{k} ({\mathbf{x}}) = {\mathbf{f}}_{k} {{\varvec{\upbeta}}}_{k} + Z_{k} ({\mathbf{x}}) = \sum\limits_{j = 1}^{h} {f_{k}^{(j)} } ({\mathbf{x}})\beta_{k}^{(j)} + Z_{k} ({\mathbf{x}}), \, k = 1,2, \ldots ,L, \hfill \\ \end{gathered}$$

(1)

where ${\mathbf{f}}_{0} = \left[ {f_{0}^{(1)} ({\mathbf{x}}),f_{0}^{(2)} ({\mathbf{x}}), \ldots ,f_{0}^{(h)} ({\mathbf{x}})} \right] \in {\mathbb{R}}^{1 \times h} ,$ ${\mathbf{f}}_{k} = \left[ {f_{k}^{(1)} ({\mathbf{x}}),f_{k}^{(2)} ({\mathbf{x}}), \ldots ,f_{k}^{(h)} ({\mathbf{x}})} \right] \in {\mathbb{R}}^{1 \times h} ,$ are a set of $h$ pre-determined regression or basis functions and ${{\varvec{\upbeta}}}_{0} = \left[ {\beta_{0}^{(1)} ,\beta_{0}^{(2)} , \ldots ,\beta_{0}^{(h)} } \right]^{{\text{T}}} \in {\mathbb{R}}^{h \times 1} ,$ ${{\varvec{\upbeta}}}_{k} = \left[ {\beta_{k}^{(1)} ,\beta_{k}^{(2)} , \ldots ,\beta_{k}^{(h)} } \right]^{{\text{T}}} \in {\mathbb{R}}^{h \times 1}$ are the unknown constant coefficients, serving as the model variation trend. Note that here we assume that the random functions have stationary but different means, namely, $E\left[ {Y_{0} ({\mathbf{x}})} \right] = {\mathbf{f}}_{0} {{\varvec{\upbeta}}}_{0} \ne E\left[ {Y_{1} ({\mathbf{x}})} \right] = {\mathbf{f}}_{1} {{\varvec{\upbeta}}}_{1} \ne \cdots \ne E\left[ {Y_{L} ({\mathbf{x}})} \right] = {\mathbf{f}}_{L} {{\varvec{\upbeta}}}_{L}$. Besides, the stationary random processes $Z_{0} ( \cdot )$ and $Z_{k} ( \cdot )$ have zero mean and a covariance of

$$\begin{gathered} Cov\left[ {Z_{0} \left( {{\mathbf{x}}_{0} } \right),Z_{0} \left( {{\mathbf{x^{\prime}}}_{0} } \right)} \right] = \sigma_{0}^{2} R^{(00)} \left( {{\mathbf{x}}_{0} ,{\mathbf{x^{\prime}}}_{0} } \right), \hfill \\ Cov\left[ {Z_{k} \left( {{\mathbf{x}}_{k} } \right),Z_{k} \left( {{\mathbf{x^{\prime}}}_{k} } \right)} \right] = \sigma_{k}^{2} R^{{{(}kk{)}}} \left( {{\mathbf{x}}_{k} ,{\mathbf{x^{\prime}}}_{k} } \right), \, k = 1,2, \ldots ,L, \hfill \\ \end{gathered}$$

(2)

for any two different sampling sites ${\mathbf{x}}_{0} ,{\mathbf{x^{\prime}}}_{0}$ from the HF dataset $({\varvec{S}}_{0} ,{\varvec{y}}_{S,0} )$, and ${\mathbf{x}}_{k} ,{\mathbf{x^{\prime}}}_{k}$ from the kth LF dataset $({\varvec{S}}_{k} ,{\varvec{y}}_{S,k} )$. Here, $\sigma_{0}^{2} ,\sigma_{k}^{2}$ are the process variances of $Z_{0} ( \cdot ),Z_{k} ( \cdot )$ respectively, and $R^{{{(}00{)}}} ,R^{{{(}kk{)}}}$ are spatial correlation functions only corresponding to the HF data and the data of kth low-fidelity, respectively. Then, the cross-covariances between the HF dataset and the kth LF dataset are given by

$$Cov\left[ {Z_{0} \left( {{\mathbf{x}}_{0} } \right),Z_{k} \left( {{\mathbf{x^{\prime}}}_{k} } \right)} \right] = \sigma_{0} \sigma_{k} R^{(0k)} \left( {{\mathbf{x}}_{0} ,{\mathbf{x^{\prime}}}_{k} } \right), \, k = 1,2, \ldots ,L.$$

(3)

Besides, the MCOK model not only considers the cross-covariances between the HF dataset and LF datasets, but also takes the cross-covariance between any two of LF datasets into account. In other words, for each two LF datasets of different fidelities, their underlying correlation can also be learned automatically when tuning MCOK model parameters. Therefore, the cross-covariance corresponding to the kth LF dataset and another different jth LF dataset is given by

$$Cov\left[ {Z_{j} \left( {{\mathbf{x}}_{j} } \right),Z_{k} \left( {{\mathbf{x^{\prime}}}_{k} } \right)} \right] = \sigma_{j} \sigma_{k} R^{(jk)} \left( {{\mathbf{x}}_{j} ,{\mathbf{x^{\prime}}}_{k} } \right), \, j,k = 1,2, \ldots ,L, \, k \ne j,$$

(4)

where $R^{(jk)}$ is the cross-correlation function.

2.2 Multi-fidelity cokriging predictor and mean-squared error

Assuming that the response of the HF model $y_{0}$ can also be approximated by a linear combination of all the observed datasets with varying fidelity levels (Journel and Huijbregts 1978), the MCOK predictor of $y_{0} ({\mathbf{x}})$ at an untried HF sampling site ${\mathbf{x}}$ is formally defined as

$$\hat{y}_{0} ({\mathbf{x}}) = {\mathbf{w}}_{0}^{{\text{T}}} {\mathbf{y}}_{S,0} + {\mathbf{w}}_{1}^{{\text{T}}} {\mathbf{y}}_{S,1} + \cdots + {\mathbf{w}}_{L}^{{\text{T}}} {\mathbf{y}}_{S,L} ,$$

(5)

where ${\mathbf{w}}_{0}^{{\text{T}}} ,{\mathbf{w}}_{k}^{{\text{T}}} { (}k = 1,2, \ldots ,L)$ are the vectors of weight coefficients for the HF dataset and the kth LF dataset, respectively. Note that we do not need to build a surrogate model for each LF dataset, which avoids the accuracy loss caused by inaccurate LF surrogate predictor. We replace ${\mathbf{y}}_{S,0} ,{\mathbf{y}}_{S,k}$ with the corresponding random quantities ${\mathbf{Y}}_{0} ,{\mathbf{Y}}_{k}$, treat $\hat{y}_{0} ({\mathbf{x}})$ as random, and try to minimize its MSE:

$$MSE\left[ {\hat{y}_{0} {(}{\mathbf{x}}{)}} \right] = E\left[ {{(}{\mathbf{w}}_{0}^{{\text{T}}} {\mathbf{Y}}_{0} + {\mathbf{w}}_{1}^{{\text{T}}} {\mathbf{Y}}_{1} + \cdots + {\mathbf{w}}_{L}^{{\text{T}}} {\mathbf{Y}}_{L} - Y_{0} {)}^{2} } \right],$$

(6)

subject to the unbiasedness constraint:

$$E\left[ {{\mathbf{w}}_{0}^{{\text{T}}} {\mathbf{Y}}_{0} + {\mathbf{w}}_{1}^{{\text{T}}} {\mathbf{Y}}_{1} + \cdots + {\mathbf{w}}_{L}^{{\text{T}}} {\mathbf{Y}}_{L} } \right] = E\left[ {Y_{0} } \right].$$

(7)

Substituting Eq. (1) into Eq. (7), then the unbiasedness constraint reads

$${\mathbf{w}}_{0}^{{\text{T}}} {\mathbf{F}}_{0} {{\varvec{\upbeta}}}_{0} + \cdots + {\mathbf{w}}_{L}^{{\text{T}}} {\mathbf{F}}_{L} {{\varvec{\upbeta}}}_{L} + {\mathbf{w}}_{0}^{{\text{T}}} \underbrace {{E\left[ {{\mathbf{Z}}_{0} } \right]}}_{ = 0} + \cdots + {\mathbf{w}}_{L}^{{\text{T}}} \underbrace {{E\left[ {{\mathbf{Z}}_{L} } \right]}}_{ = 0} - {\mathbf{f}}_{0} {{\varvec{\upbeta}}}_{0} - \underbrace {{E\left[ {Z_{0} } \right]}}_{ = 0} = 0,$$

(8)

and therefore

$$\left( {{\mathbf{w}}_{0}^{{\text{T}}} {\mathbf{F}}_{0} - {\mathbf{f}}_{0} } \right){{\varvec{\upbeta}}}_{0} + \cdots + {\mathbf{w}}_{L}^{{\text{T}}} {\mathbf{F}}_{L} {{\varvec{\upbeta}}}_{L} = 0.$$

(9)

In order to fulfill the unbiasedness constraint independent of the choice of the regression parameters ${{\varvec{\upbeta}}}_{0} ,{{\varvec{\upbeta}}}_{k}$, the following stronger unbiasedness conditions must be imposed:

$${\mathbf{w}}_{0}^{{\text{T}}} {\mathbf{F}}_{0} - {\mathbf{f}}_{0} = 0, \, {\mathbf{w}}_{k}^{{\text{T}}} {\mathbf{F}}_{k} = 0, \, k = 1,2, \ldots ,L$$

(10)

where ${\mathbf{F}}_{0} ,{\mathbf{F}}_{k} {, }k = 1,2, \cdots ,L,$ are basis functions and denoted as the regression matrices:

$$\begin{gathered} {\mathbf{F}}_{0} = \left[ {\begin{array}{*{20}c} {f_{0}^{(1)} \left( {{\varvec{x}}_{0}^{(1)} } \right)} & {f_{0}^{(2)} \left( {{\varvec{x}}_{0}^{(1)} } \right)} & \cdots & {f_{0}^{(h)} \left( {{\varvec{x}}_{0}^{(1)} } \right)} \\ {f_{0}^{(1)} \left( {{\varvec{x}}_{0}^{(2)} } \right)} & {f_{0}^{(2)} \left( {{\varvec{x}}_{0}^{(2)} } \right)} & \cdots & {f_{0}^{(h)} \left( {{\varvec{x}}_{0}^{(2)} } \right)} \\ \vdots & \vdots & \ddots & \vdots \\ {f_{0}^{(1)} \left( {{\varvec{x}}_{0}^{{(n_{0} )}} } \right)} & {f_{0}^{(2)} \left( {{\varvec{x}}_{0}^{{(n_{0} )}} } \right)} & \cdots & {f_{0}^{(h)} \left( {{\varvec{x}}_{0}^{{(n_{0} )}} } \right)} \\ \end{array} } \right] \in {\mathbb{R}}^{{n_{0} \times h}} , \hfill \\ {\mathbf{F}}_{k} = \left[ {\begin{array}{*{20}c} {f_{k}^{(1)} \left( {{\varvec{x}}_{k}^{(1)} } \right)} & {f_{k}^{(2)} \left( {{\varvec{x}}_{k}^{(1)} } \right)} & \cdots & {f_{k}^{(h)} \left( {{\varvec{x}}_{k}^{(1)} } \right)} \\ {f_{k}^{(1)} \left( {{\varvec{x}}_{k}^{(2)} } \right)} & {f_{k}^{(2)} \left( {{\varvec{x}}_{k}^{(2)} } \right)} & \cdots & {f_{k}^{(h)} \left( {{\varvec{x}}_{k}^{(2)} } \right)} \\ \vdots & \vdots & \ddots & \vdots \\ {f_{k}^{(1)} \left( {{\varvec{x}}_{k}^{{(n_{k} )}} } \right)} & {f_{k}^{(2)} \left( {{\varvec{x}}_{k}^{{(n_{k} )}} } \right)} & \cdots & {f_{k}^{(h)} \left( {{\varvec{x}}_{k}^{{(n_{k} )}} } \right)} \\ \end{array} } \right] \in {\mathbb{R}}^{{n_{k} \times h}} . \hfill \\ \end{gathered}$$

(11)

In this article, we consider an ordinary MCOK model, thus $h = 1$, and ${\mathbf{F}}_{0} ,{\mathbf{F}}_{k}$ can be written as

$${\mathbf{F}}_{0}= [\underbrace{1,1, \ldots ,1}_{n_0}]^\text{T}, {\mathbf{F}}_{k} = [\underbrace{1,1, \ldots ,1}_{n_k}]^\text{T}, \quad k = 1,2, \ldots ,L.$$

(12)

Solving the above constrained minimization problem by Lagrange multiplier method, the weights of MCOK in Eq. (5) can be found by the following system of linear equations:

$$\left[ \begin{gathered} \begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {{\mathbf{C}}^{{{\text{(00)}}}} } & {{\mathbf{C}}^{{{\text{(01)}}}} } \\ \end{array} } & \cdots \\ \end{array} } & {{\mathbf{C}}^{{{\text{(0}}L{\text{)}}}} } \\ \end{array} } & {{\mathbf{F}}_{0} } \\ \end{array} } & {\mathbf{0}} \\ \end{array} } & \cdots \\ \end{array} } & {\mathbf{0}} \\ \end{array} \hfill \\ \begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {{\mathbf{C}}^{{{\text{(10)}}}} } & {{\mathbf{C}}^{{{\text{(11)}}}} } \\ \end{array} } & \cdots \\ \end{array} } & {{\mathbf{C}}^{{{\text{(1}}L{\text{)}}}} } \\ \end{array} } & {\mathbf{0}} \\ \end{array} } & {{\mathbf{F}}_{1} } \\ \end{array} } & \cdots \\ \end{array} } & {\mathbf{0}} \\ \end{array} \hfill \\ \begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {{\text{ }}\begin{array}{*{20}c} \vdots & {{\text{ }} \vdots } \\ \end{array} } & {{\text{ }} \ddots } \\ \end{array} } & {{\text{ }} \vdots } \\ \end{array} } & {{\text{ }} \vdots } \\ \end{array} } & {{\text{ }} \vdots } \\ \end{array} } & \ddots \\ \end{array} } & \vdots \\ \end{array} \hfill \\ \begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {{\mathbf{C}}^{{{\text{(}}L{\text{0)}}}} } & {{\mathbf{C}}^{{{\text{(}}L1{\text{)}}}} } \\ \end{array} } & \cdots \\ \end{array} } & {{\mathbf{C}}^{{{\text{(}}LL{\text{)}}}} } \\ \end{array} } & {\mathbf{0}} \\ \end{array} } & {\mathbf{0}} \\ \end{array} } & \cdots \\ \end{array} } & {{\mathbf{F}}_{L} } \\ \end{array} \hfill \\ \begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {{\mathbf{F}}_{0} ^{{\text{T}}} } & {{\text{ }}{\mathbf{0}}^{{\text{T}}} } \\ \end{array} } & {{\text{ }} \cdots } \\ \end{array} } & {{\mathbf{0}}^{{\text{T}}} } \\ \end{array} } & {{\text{ }}{\mathbf{0}}} \\ \end{array} } & {\mathbf{0}} \\ \end{array} } & \cdots \\ \end{array} } & {\mathbf{0}} \\ \end{array} \hfill \\ \begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {{\mathbf{0}}^{{\text{T}}} } & {{\text{ }}{\mathbf{F}}_{1} ^{{\text{T}}} } \\ \end{array} } & {{\text{ }} \cdots } \\ \end{array} } & {{\mathbf{0}}^{{\text{T}}} } \\ \end{array} } & {{\text{ }}{\mathbf{0}}} \\ \end{array} } & {\mathbf{0}} \\ \end{array} } & \cdots \\ \end{array} } & {\mathbf{0}} \\ \end{array} \hfill \\ \begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {{\text{ }}\begin{array}{*{20}c} \vdots & {{\text{ }} \vdots } \\ \end{array} } & {{\text{ }} \ddots } \\ \end{array} } & \vdots \\ \end{array} } & {{\text{ }} \vdots } \\ \end{array} } & {{\text{ }} \vdots } \\ \end{array} } & \ddots \\ \end{array} } & \vdots \\ \end{array} \hfill \\ \begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {{\mathbf{0}}^{{\text{T}}} } & {{\text{ }}{\mathbf{0}}^{{\text{T}}} } \\ \end{array} } & {{\text{ }} \cdots } \\ \end{array} } & {{\mathbf{F}}_{L} ^{{\text{T}}} } \\ \end{array} } & {{\text{ }}{\mathbf{0}}} \\ \end{array} } & {\mathbf{0}} \\ \end{array} } & \cdots \\ \end{array} } & {\mathbf{0}} \\ \end{array} \hfill \\ \end{gathered} \right]\left[ \begin{gathered} {\text{ }}{\mathbf{w}}_{0} \hfill \\ {\text{ }}{\mathbf{w}}_{1} \hfill \\ {\text{ }} \vdots \hfill \\ {\text{ }}{\mathbf{w}}_{L} \hfill \\ \mu _{0} /2 \hfill \\ \mu _{1} /2 \hfill \\ {\text{ }} \vdots \hfill \\ \mu _{L} /2 \hfill \\ \end{gathered} \right] = \left[ \begin{gathered} {\mathbf{c}}_{0} ({\mathbf{x}}) \hfill \\ {\mathbf{c}}_{1} ({\mathbf{x}}) \hfill \\ {\text{ }} \vdots \hfill \\ {\mathbf{c}}_{L} ({\mathbf{x}}) \hfill \\ {\mathbf{f}}_{{\text{0}}}^{{\text{T}}} ({\mathbf{x}}) \hfill \\ {\text{ }}{\mathbf{0}} \hfill \\ {\text{ }} \vdots \hfill \\ {\text{ }}{\mathbf{0}} \hfill \\ \end{gathered} \right],$$

(13)

where ${{\varvec{\upmu}}} = \left[ {\mu_{0} ,\mu_{1} , \ldots ,\mu_{L} } \right]^{{\text{T}}}$ are the vectors of Lagrange multipliers, and

$$\begin{gathered} {\mathbf{C}}^{{{(}00{)}}} : = \left[ {\sigma_{0}^{2} R^{(00)} \left( {{\mathbf{x}}_{0}^{(p)} ,{\mathbf{x}}_{0}^{(q)} } \right)} \right]_{p,q} \in {\mathbb{R}}^{{n_{0} \times n_{0} }} , \, p,q = 1,2, \ldots ,n_{0} , \hfill \\ {\mathbf{C}}^{{{(}0k{)}}} : = \left[ {\sigma_{0} \sigma_{k} R^{(0k)} \left( {{\mathbf{x}}_{0}^{(p)} ,{\mathbf{x}}_{k}^{(q)} } \right)} \right]_{p,q} = \left( {{\mathbf{C}}^{(k0)} } \right)^{{\text{T}}} \in {\mathbb{R}}^{{n_{0} \times n_{k} }} , \, k = 1,2, \ldots ,L; \, p = 1,2, \ldots ,n_{0} , \, q = 1,2, \ldots ,n_{k} , \hfill \\ {\mathbf{C}}^{{{(}jk{)}}} : = \left[ {\sigma_{j} \sigma_{k} R^{(jk)} \left( {{\mathbf{x}}_{j}^{(p)} ,{\mathbf{x}}_{k}^{(q)} } \right)} \right]_{p,q} = \left( {{\mathbf{C}}^{{{(}kj)}} } \right)^{{\text{T}}} \in {\mathbb{R}}^{{n_{j} \times n_{k} }} , \, j,k = 1,2, \ldots ,L; \, p = 1,2, \ldots ,n_{j} , \, q = 1,2, \ldots ,n_{k} , \hfill \\ {\mathbf{c}}_{0} : = \left[ {\sigma_{0}^{2} R^{(00)} \left( {{\mathbf{x}}_{0}^{{{(}p{)}}} ,{\mathbf{x}}} \right)} \right]_{p} \in {\mathbb{R}}^{{n_{0} \times 1}} , \, p = 1,2, \ldots ,n_{0} , \hfill \\ {\mathbf{c}}_{k} : = \left[ {\sigma_{0} \sigma_{k} R^{(0k)} \left( {{\mathbf{x}}_{k}^{{{(}p{)}}} ,{\mathbf{x}}} \right)} \right]_{p} \in {\mathbb{R}}^{{n_{k} \times 1}} , \, k = 1,2, \ldots ,L; \, p = 1,2, \ldots ,n_{k} . \hfill \\ \end{gathered}$$

(14)

Here, ${\mathbf{C}}^{{{(}00{)}}}$ denotes the covariance matrix modeling the correlation between any two observed HF samples ${\mathbf{x}}_{0}^{(p)}$ and ${\mathbf{x}}_{0}^{(q)}$; ${\mathbf{C}}^{{{(}0k{)}}}$ or ${\mathbf{C}}^{{{(}k0{)}}}$ denotes the covariance matrix modeling the cross-correlation between an observed HF sample ${\mathbf{x}}_{0}^{(p)}$ and an observed LF sample ${\mathbf{x}}_{k}^{(q)}$ of kth LF level; ${\mathbf{C}}^{{{(}jk{)}}}$ or ${\mathbf{C}}^{{{(}kj{)}}}$ denotes the covariance matrix modeling the cross-correlation between an observed LF sample ${\mathbf{x}}_{j}^{(p)}$ of jth LF level and an observed LF sample ${\mathbf{x}}_{k}^{(q)}$ of kth LF level. ${\mathbf{c}}_{0} ({\mathbf{x}})$ denotes the covariance vector modeling the correlation between an observed HF samples ${\mathbf{x}}_{0}^{(p)}$ and an unknown sample ${\mathbf{x}}$; ${\mathbf{c}}_{k} ({\mathbf{x}})$ denotes the covariance vector modeling the cross-correlation between an observed LF samples ${\mathbf{x}}_{k}^{{{(}p{)}}}$ of kth LF level and an unknown sample ${\mathbf{x}}$. Note that it is essential that all the blocks comprising the covariance matrix must be positive definite to ensure the covariance matrix is invertible (Bertram and Zimmermann 2018). However, the covariance matrix could be ill-conditioned if two HF or LF samples are very close to each other, and it may also lose its diagonal dominance and become non-positive definite if there is a large difference in hyperparameters for auto- and cross-correlation functions (Han et al. 2010). Besides, searching for the optimal values of these various process variances in Eq. (14) could also incur additional cost during the model training process (Bertram and Zimmermann 2018; Yamazaki and Mavriplis 2013).

In order to make the MCOK predictor more robust and simplify covariance data fitting, we do not follow Han’s (Han et al. 2010) or Yamazaki’s methods (Yamazaki and Mavriplis 2013) but refer to Zimmermann’s simplification method (Zimmermann and Han 2010), and assume that all the Gaussian processes feature the same spatial inter-correlations, more specifically,

$$Cov\left[ {Z_{0} ({\mathbf{x}}),Z_{0} ({\mathbf{x^{\prime}}}_{{}} )} \right] = Cov\left[ {Z_{1} ({\mathbf{x}}),Z_{1} ({\mathbf{x^{\prime}}}_{{}} )} \right] = \cdots = Cov\left[ {Z_{L} ({\mathbf{x}}),Z_{L} ({\mathbf{x^{\prime}}}_{{}} )} \right], \, \forall {\mathbf{x}},{\mathbf{x^{\prime}}}.$$

(15)

As a direct consequence,

$$\begin{gathered} \sigma_{0}^{2} = \sigma_{1}^{2} = \sigma_{2}^{2} = \cdots = \sigma_{L}^{2} = :\sigma^{2} , \hfill \\ R^{(00)} \left( {{\mathbf{x}},{\mathbf{x^{\prime}}}} \right) = R^{(11)} \left( {{\mathbf{x}},{\mathbf{x^{\prime}}}} \right) = R^{(22)} \left( {{\mathbf{x}},{\mathbf{x^{\prime}}}} \right) = \cdots = R^{(LL)} \left( {{\mathbf{x}},{\mathbf{x^{\prime}}}} \right) = :R\left( {{\mathbf{x}},{\mathbf{x^{\prime}}}} \right), \hfill \\ \end{gathered}$$

(16)

This simplification is reasonable because the basic premise assumes that both HF and multiple LF data describe the same phenomenon, although with varying levels of accuracy. It is well suited for the case when the LF data are sufficiently correlated with HF data or have the similar variation trend. But when the correlation is relatively small, the fusion accuracy will be limited, and we get less benefit from this simplification.

To account for the cross-correlations between any two datasets of different fidelities, an additional parameter vector “${{\varvec{\upgamma}}}$” is then introduced:

$$\begin{gathered} R^{(0k)} \left( {{\mathbf{x}},{\mathbf{x^{\prime}}}} \right) = R^{(k0)} \left( {{\mathbf{x}},{\mathbf{x^{\prime}}}} \right) = \gamma^{(0k)} R\left( {{\mathbf{x}},{\mathbf{x^{\prime}}}} \right), \, k = 1,2, \ldots ,L, \, \hfill \\ R^{(jk)} \left( {{\mathbf{x}},{\mathbf{x^{\prime}}}} \right) = R^{(kj)} \left( {{\mathbf{x}},{\mathbf{x^{\prime}}}} \right) = \gamma^{(jk)} R\left( {{\mathbf{x}},{\mathbf{x^{\prime}}}} \right), \, j,k = 1,2, \ldots ,L. \hfill \\ \end{gathered}$$

(17)

Here, $\gamma \in (0,1)$ and after optimization, the value of $\gamma$ is a measure of how strongly the two datasets of different fidelities are correlated (Zimmermann and Han 2010). For $\gamma$ close to 0, the two datasets are weakly correlated or uncorrelated, while for $\gamma$ close to 1, they are fully correlated and have a strong connection. Since there exist “L” LF datasets, the total number of additional parameters to be introduced is ${{L(L + 1)} \mathord{\left/ {\vphantom {{L(L + 1)} 2}} \right. \kern-0pt} 2}$. For example, when $L = 2$, there are two different LF datasets along with a HF dataset, and it needs three parameters $\gamma^{(01)} ,\gamma^{(02)}$, and $\gamma^{(12)}$ to learn the correlations between the HF dataset (level 0) and the first LF (level 1) dataset, the HF dataset (level 0) and the second LF (level 2) dataset, and the first LF (level 1) dataset and the second LF (level 2) dataset, respectively.

By utilizing the above hypothesis and substituting Eq. (11), Eq. (13) can be rewritten as

$$\left[ \begin{gathered} \begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {{\text{ }}{\mathbf{R}}^{{{\text{(00)}}}} } & {{\text{ }}\gamma ^{{(01)}} {\mathbf{R}}^{{{\text{(01)}}}} } \\ \end{array} } & \cdots \\ \end{array} } & {\gamma ^{{(0L)}} {\mathbf{R}}^{{{\text{(0}}L{\text{)}}}} } \\ \end{array} } & {{\mathbf{F}}_{0} } \\ \end{array} } & {\mathbf{0}} \\ \end{array} } & \cdots \\ \end{array} } & {\mathbf{0}} \\ \end{array} \hfill \\ \begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\gamma ^{{(01)}} {\mathbf{R}}^{{{\text{(10)}}}} } & {{\text{ }}{\mathbf{R}}^{{{\text{(11)}}}} } \\ \end{array} } & {{\text{ }} \cdots } \\ \end{array} } & {\gamma ^{{(1L)}} {\mathbf{R}}^{{{\text{(1}}L{\text{)}}}} } \\ \end{array} } & {\mathbf{0}} \\ \end{array} } & {{\mathbf{F}}_{1} } \\ \end{array} } & \cdots \\ \end{array} } & {\mathbf{0}} \\ \end{array} \hfill \\ \begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {{\text{ }}\begin{array}{*{20}c} \vdots & {{\text{ }} \vdots } \\ \end{array} } & {{\text{ }} \ddots } \\ \end{array} } & {{\text{ }} \vdots } \\ \end{array} } & {{\text{ }} \vdots } \\ \end{array} } & {{\text{ }} \vdots } \\ \end{array} } & \ddots \\ \end{array} } & \vdots \\ \end{array} \hfill \\ \begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\gamma ^{{(0L)}} {\mathbf{R}}^{{{\text{(}}L{\text{0)}}}} } & {\gamma ^{{(1L)}} {\mathbf{R}}^{{{\text{(}}L1{\text{)}}}} } \\ \end{array} } & \cdots \\ \end{array} } & {{\text{ }}{\mathbf{R}}^{{{\text{(}}LL{\text{)}}}} } \\ \end{array} } & {{\text{ }}{\mathbf{0}}} \\ \end{array} } & {\mathbf{0}} \\ \end{array} } & \cdots \\ \end{array} } & {{\mathbf{F}}_{L} } \\ \end{array} \hfill \\ \begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {{\text{ }}{\mathbf{F}}_{0}^{{\text{T}}} } & {{\text{ }}{\mathbf{0}}^{{\text{T}}} } \\ \end{array} } & {{\text{ }} \cdots } \\ \end{array} } & {{\text{ }}{\mathbf{0}}^{{\text{T}}} } \\ \end{array} } & {{\text{ }}{\mathbf{0}}} \\ \end{array} } & {\mathbf{0}} \\ \end{array} } & \cdots \\ \end{array} } & {\mathbf{0}} \\ \end{array} \hfill \\ \begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {{\text{ }}{\mathbf{0}}^{{\text{T}}} } & {{\text{ }}{\mathbf{F}}_{1} ^{{\text{T}}} } \\ \end{array} } & {{\text{ }} \cdots } \\ \end{array} } & {{\text{ }}{\mathbf{0}}^{{\text{T}}} } \\ \end{array} } & {{\text{ }}{\mathbf{0}}} \\ \end{array} } & {\mathbf{0}} \\ \end{array} } & \cdots \\ \end{array} } & {\mathbf{0}} \\ \end{array} \hfill \\ \begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {{\text{ }} \vdots } & {{\text{ }} \vdots } \\ \end{array} } & {{\text{ }} \ddots } \\ \end{array} } & {{\text{ }} \vdots } \\ \end{array} } & {{\text{ }} \vdots } \\ \end{array} } & {{\text{ }} \vdots } \\ \end{array} } & \ddots \\ \end{array} } & \vdots \\ \end{array} \hfill \\ \begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {{\text{ }}{\mathbf{0}}^{{\text{T}}} } & {{\text{ }}{\mathbf{0}}^{{\text{T}}} } \\ \end{array} } & {{\text{ }} \cdots } \\ \end{array} } & {{\text{ }}{\mathbf{F}}_{L} ^{{\text{T}}} } \\ \end{array} } & {{\text{ }}{\mathbf{0}}} \\ \end{array} } & {\mathbf{0}} \\ \end{array} } & \cdots \\ \end{array} } & {\mathbf{0}} \\ \end{array} \hfill \\ \end{gathered} \right]\left[ \begin{gathered} {\text{ }}{\mathbf{w}}_{0} \hfill \\ {\text{ }}{\mathbf{w}}_{1} \hfill \\ {\text{ }} \vdots \hfill \\ {\text{ }}{\mathbf{w}}_{L} \hfill \\ {{\mu _{0} } \mathord{\left/ {\vphantom {{\mu _{0} } {2\sigma ^{2} }}} \right. \kern-\nulldelimiterspace} {2\sigma ^{2} }} \hfill \\ {{\mu _{1} } \mathord{\left/ {\vphantom {{\mu _{1} } {2\sigma ^{2} }}} \right. \kern-\nulldelimiterspace} {2\sigma ^{2} }} \hfill \\ {\text{ }} \vdots \hfill \\ {{\mu _{L} } \mathord{\left/ {\vphantom {{\mu _{L} } {2\sigma ^{2} }}} \right. \kern-\nulldelimiterspace} {2\sigma ^{2} }} \hfill \\ \end{gathered} \right] = \left[ \begin{gathered} {\text{ }}{\mathbf{r}}_{0} ({\mathbf{x}}) \hfill \\ \gamma ^{{(01)}} {\mathbf{r}}_{1} ({\mathbf{x}}) \hfill \\ {\text{ }} \vdots \hfill \\ \gamma ^{{(0L)}} {\mathbf{r}}_{L} ({\mathbf{x}}) \hfill \\ {\text{ }}{\mathbf{f}}_{{\text{0}}}^{{\text{T}}} ({\mathbf{x}}) \hfill \\ {\text{ }}{\mathbf{0}} \hfill \\ {\text{ }} \vdots \hfill \\ {\text{ }}{\mathbf{0}} \hfill \\ \end{gathered} \right],$$

(18)

where

$$\begin{gathered} {\mathbf{R}}^{{{(}00{)}}} : = \left[ {R\left( {{\mathbf{x}}_{0}^{(p)} ,{\mathbf{x}}_{0}^{(q)} } \right)} \right]_{p,q} \in {\mathbb{R}}^{{n_{0} \times n_{0} }} , \, p,q = 1,2, \ldots ,n_{0} , \hfill \\ {\mathbf{R}}^{{{(}0k{)}}} : = \left[ {R\left( {{\mathbf{x}}_{0}^{(p)} ,{\mathbf{x}}_{k}^{(q)} } \right)} \right]_{p,q} = \left( {{\mathbf{R}}^{{{(}k{0)}}} } \right)^{{\text{T}}} \in {\mathbb{R}}^{{n_{0} \times n_{k} }} , \, k = 1,2, \ldots ,L; \, p = 1,2, \ldots ,n_{0} , \, q = 1,2, \ldots ,n_{k} , \hfill \\ {\mathbf{R}}^{{{(}jk{)}}} : = \left[ {R\left( {{\mathbf{x}}_{j}^{(p)} ,{\mathbf{x}}_{k}^{(q)} } \right)} \right]_{p,q} = \left( {{\mathbf{R}}^{{{(}kj{)}}} } \right)^{{\text{T}}} \in {\mathbb{R}}^{{n_{j} \times n_{k} }} , \, k,j = 1,2, \ldots ,L; \, p = 1,2, \ldots ,n_{j} , \, q = 1,2, \ldots ,n_{k} , \hfill \\ {\mathbf{r}}_{0} : = \left[ {R\left( {{\mathbf{x}}_{0}^{{{(}p{)}}} ,{\mathbf{x}}} \right)} \right]_{p} \in {\mathbb{R}}^{{n_{0} \times 1}} , \, p = 1,2, \ldots ,n_{0} , \hfill \\ {\mathbf{r}}_{k} : = \left[ {R\left( {{\mathbf{x}}_{k}^{{{(}p{)}}} ,{\mathbf{x}}} \right)} \right]_{p} \in {\mathbb{R}}^{{n_{k} \times 1}} , \, k = 1,2, \ldots ,L; \, p = 1,2, \ldots ,n_{k} . \hfill \\ \end{gathered}$$

(19)

Note that only the computations of correlation vector ${\mathbf{r}}_{0}$ and ${\mathbf{r}}_{k}$ involve the unknown sample ${\mathbf{x}}$. After solving for the new weights ${\mathbf{w}}_{0}^{{\text{T}}}$ and ${\mathbf{w}}_{k}^{{\text{T}}}$, the MCOK predictor can be written as follows, which is very similar to a kriging predictor:

$$\begin{gathered} \hat{y}_{0} \left( {\mathbf{x}} \right) = {\mathbf{w}}_{0}^{{\text{T}}} {\mathbf{y}}_{S,0} + {\mathbf{w}}_{1}^{{\text{T}}} {\mathbf{y}}_{S,1} + \ldots + {\mathbf{w}}_{L}^{{\text{T}}} {\mathbf{y}}_{S,L} = \left[ \begin{gathered} {\tilde{\mathbf{r}}}({\mathbf{x}}) \hfill \\ \, {\tilde{\mathbf{\varphi }}} \hfill \\ \end{gathered} \right]^{{\text{T}}} \left[ {\begin{array}{*{20}c} {{\tilde{\mathbf{R}}}} & {{\tilde{\mathbf{F}}}} \\ {{\tilde{\mathbf{F}}}^{{\text{T}}} } & {\mathbf{0}} \\ \end{array} } \right]^{ - 1} \left[ \begin{gathered} {\tilde{\mathbf{y}}}_{S} \hfill \\ {\mathbf{0}} \hfill \\ \end{gathered} \right] \hfill \\ \,\,\,\, \quad \quad = {\tilde{\mathbf{\varphi }}}^{{\text{T}}} {\tilde{\mathbf{\beta }}} + {\tilde{\mathbf{r}}}^{{\text{T}}} ({\mathbf{x}})\underbrace {{{\tilde{\mathbf{R}}}^{ - 1} \left( {{\tilde{\mathbf{y}}}_{S} - {\mathbf{\tilde{F}\tilde{\beta }}}} \right)}}_{{: = {\mathbf{V}}_{MCoK} }}, \hfill \\ \end{gathered}$$

(20)

where

$$\begin{gathered} {\tilde{\mathbf{R}}} = \left[ \begin{gathered} \begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} { \, {\mathbf{R}}^{{(00)}} } & { \, \gamma^{(01)} {\mathbf{R}}^{{(01)}} } \\ \end{array} } & \cdots \\ \end{array} } & {\gamma^{(0L)} {\mathbf{R}}^{{{(0}L{)}}} } \\ \end{array} \hfill \\ \begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\gamma^{(01)} {\mathbf{R}}^{{(10)}} } & { \, {\mathbf{R}}^{{(11)}} } \\ \end{array} } & { \, \cdots } \\ \end{array} } & {\gamma^{(1L)} {\mathbf{R}}^{{{(1}L{)}}} } \\ \end{array} \hfill \\ \begin{array}{*{20}c} {\begin{array}{*{20}c} { \, \begin{array}{*{20}c} \vdots & { \, \vdots } \\ \end{array} } & { \, \ddots } \\ \end{array} } & { \, \vdots } \\ \end{array} \hfill \\ \begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\gamma^{(0L)} {\mathbf{R}}^{{{(}L{0)}}} } & {\gamma^{(1L)} {\mathbf{R}}^{{{(}L1{)}}} } \\ \end{array} } & \cdots \\ \end{array} } & { \, {\mathbf{R}}^{{{(}LL{)}}} } \\ \end{array} \hfill \\ \end{gathered} \right] \in {\mathbb{R}}^{{\left( {n_{0} + \sum\limits_{k = 1}^{L} {n_{k} } } \right) \times \left( {n_{0} + \sum\limits_{k = 1}^{L} {n_{k} } } \right)}} , \hfill \\ {\tilde{\mathbf{r}}}({\mathbf{x}}) = \left[ \begin{gathered} \, {\mathbf{r}}_{0} ({\mathbf{x}}) \hfill \\ \gamma^{(01)} {\mathbf{r}}_{1} ({\mathbf{x}}) \hfill \\ \, \vdots \hfill \\ \gamma^{(0L)} {\mathbf{r}}_{L} ({\mathbf{x}}) \hfill \\ \end{gathered} \right] \in {\mathbb{R}}^{{\left( {n_{0} + \sum\limits_{k = 1}^{L} {n_{k} } } \right) \times 1}} , \, {\tilde{\mathbf{y}}}_{S} = \left[ \begin{gathered} {\mathbf{y}}_{S,0} \hfill \\ {\mathbf{y}}_{S,1} \hfill \\ \, \vdots \hfill \\ {\mathbf{y}}_{S,L} \hfill \\ \end{gathered} \right] \in {\mathbb{R}}^{{\left( {n_{0} + \sum\limits_{k = 1}^{L} {n_{k} } } \right) \times 1}} , \hfill \\ {\tilde{\mathbf{F}}} = \left[ {\begin{array}{*{20}c} {{\mathbf{F}}_{0}^{{}} } & {\mathbf{0}} & \cdots & {\mathbf{0}} \\ {\mathbf{0}} & {{\mathbf{F}}_{1}^{{}} } & \cdots & {\mathbf{0}} \\ \vdots & \vdots & \ddots & \vdots \\ {\mathbf{0}} & {\mathbf{0}} & \cdots & {{\mathbf{F}}_{L}^{{}} } \\ \end{array} } \right] \in {\mathbb{R}}^{{\left( {n_{0} + \sum\limits_{k = 1}^{L} {n_{k} } } \right) \times \left( {L + 1} \right)h,}} \, \hfill \\ {\tilde{\mathbf{\varphi }}} = \left[ {\begin{array}{*{20}c} {{\mathbf{f}}_{{0}}^{{\text{T}}} ({\mathbf{x}})} \\ {\mathbf{0}} \\ \vdots \\ {\mathbf{0}} \\ \end{array} } \right] \in {\mathbb{R}}^{{\left( {L + 1} \right)h \times 1}} , \, {\tilde{\mathbf{\beta }}} = \left[ {\begin{array}{*{20}c} {{{\varvec{\upbeta}}}_{0} } \\ {{{\varvec{\upbeta}}}_{1} } \\ \vdots \\ {{{\varvec{\upbeta}}}_{L} } \\ \end{array} } \right] \in {\mathbb{R}}^{{\left( {L + 1} \right)h \times 1}} = \left( {{\tilde{\mathbf{F}}}^{{\text{T}}} {\tilde{\mathbf{R}}}^{ - 1} {\tilde{\mathbf{F}}}} \right)^{ - 1} {\tilde{\mathbf{F}}}^{{\text{T}}} {\tilde{\mathbf{R}}}^{ - 1} {\tilde{\mathbf{y}}}_{S} . \hfill \\ \end{gathered}$$

(21)

and for an ordinary MCOK model, we have

$$\begin{gathered} {\tilde{\mathbf{F}}} = \left[ {\begin{array}{*{20}c} {\mathbf{1}} & {\mathbf{0}} & \cdots & {\mathbf{0}} \\ {\mathbf{0}} & {\mathbf{1}} & \cdots & {\mathbf{0}} \\ \vdots & \vdots & \ddots & \vdots \\ {\mathbf{0}} & {\mathbf{0}} & \cdots & {\mathbf{1}} \\ \end{array} } \right] \in {\mathbb{R}}^{{\left( {n_{0} + \sum\limits_{k = 1}^{L} {n_{k} } } \right) \times \left( {L + 1} \right)}} , \, \hfill \\ {\tilde{\mathbf{\varphi }}} = \left[ {\begin{array}{*{20}c} 1 \\ 0 \\ \vdots \\ 0 \\ \end{array} } \right] \in {\mathbb{R}}^{{\left( {L + 1} \right) \times 1}} , \, {\tilde{\mathbf{\beta }}} = \left[ {\begin{array}{*{20}c} {\beta_{0} } \\ {\beta_{1} } \\ \vdots \\ {\beta_{L} } \\ \end{array} } \right] \in {\mathbb{R}}^{{\left( {L + 1} \right) \times 1}} = \left( {{\tilde{\mathbf{F}}}^{{\text{T}}} {\tilde{\mathbf{R}}}^{ - 1} {\tilde{\mathbf{F}}}} \right)^{ - 1} {\tilde{\mathbf{F}}}^{{\text{T}}} {\tilde{\mathbf{R}}}^{ - 1} {\tilde{\mathbf{y}}}_{S} . \hfill \\ \end{gathered}$$

(22)

Here, $\, {\tilde{\mathbf{\beta }}}$ is a constant vector and its derivation will be introduced in the Sect. 2.4. Note that the vector ${\mathbf{V}}_{MCOK}$ defined in Eq. (20) only depends on the observed HF and LF datasets, and it can be calculated during the model fitting stage of MCOK. Besides, ${\tilde{\mathbf{\varphi }}}^{{\text{T}}}$ is already known and ${\tilde{\mathbf{\beta }}}$ is also calculated by the observed HF and LF datasets. Once the MCOK is built, ${\mathbf{V}}_{MCOK}$,${\tilde{\mathbf{\varphi }}}^{{\text{T}}}$ and ${\tilde{\mathbf{\beta }}}$ are all obtained and can be stored. Hence, the prediction of the unknown $y_{0}$ at an unknown sample ${\mathbf{x}}$ only requires recalculating ${\tilde{\mathbf{r}}}^{{\text{T}}} \left( {\mathbf{x}} \right)$.

Then, the MSE of the MCOK prediction can be derived as follows:

$$MSE\left[ {\hat{y}_{0} ({\mathbf{x}})} \right] = \sigma^{2} \left\{ {1 - \left[ \begin{gathered} {\tilde{\mathbf{r}}}({\mathbf{x}}) \hfill \\ \, {\tilde{\mathbf{\varphi }}} \hfill \\ \end{gathered} \right]^{{\text{T}}} \left[ {\begin{array}{*{20}c} {{\tilde{\mathbf{R}}}} & {{\tilde{\mathbf{F}}}} \\ {{\tilde{\mathbf{F}}}^{{\text{T}}} } & {\mathbf{0}} \\ \end{array} } \right]^{ - 1} \left[ \begin{gathered} {\tilde{\mathbf{r}}}({\mathbf{x}}) \hfill \\ \, {\tilde{\mathbf{\varphi }}} \hfill \\ \end{gathered} \right]} \right\} = \sigma^{2} \left[ {1 - {\tilde{\mathbf{r}}}^{{\text{T}}} ({\mathbf{x}}){\tilde{\mathbf{R}}}^{ - 1} {\tilde{\mathbf{r}}}({\mathbf{x}}) + \frac{{\left( {{\tilde{\mathbf{\varphi }}} - {\tilde{\mathbf{F}}}^{{\text{T}}} {\tilde{\mathbf{R}}}^{ - 1} {\tilde{\mathbf{r}}}} \right)^{2} }}{{{\tilde{\mathbf{F}}}^{{\text{T}}} {\mathbf{R}}^{ - 1} {\tilde{\mathbf{F}}}}}} \right].$$

(23)

2.3 Correlation function

As presented in Eqs. (19) and (21), the construction of correlation matrix ${\tilde{\mathbf{R}}}$ and correlation vector ${\tilde{\mathbf{r}}}$ for MCOK requires the calculation of correlation function $R$, which only depends on the Euclidean distance between two different sampling sites, ${\mathbf{x}}$ and ${\mathbf{x^{\prime}}}$, and is often expressed as the form

$$R\left( {{\mathbf{x}},{\mathbf{x^{\prime}}}} \right) = \prod\limits_{i = 1}^{m} {R\left( {\theta_{i} ,x_{i}^{{}} - x^{\prime}_{i} } \right)} , \, \forall \theta_{i} \in {\mathbb{R}}^{ + } ,$$

(24)

where $\theta_{i}$ is a hyperparameter that scales the influence of the ith input variable on the functional response and can be tuned by a specific optimization strategy. Note that the same hyperparameters ${{\varvec{\uptheta}}} = \left[ {\theta_{1} ,\theta_{2} , \ldots ,\theta_{m} } \right]^{{\text{T}}}$ are used in all auto- and cross-correlation functions to reduce the degrees of freedom.

There are various spatial correlation functions such as Gaussian (squared) exponential, cubic splines, and Matérn functions, of which the Gaussian squared exponential function is arguably the one used most widely in engineering cases because of its simplicity, flexibility, and infinite differentiability, it being formulated as

$$R\left( {{\mathbf{x}},{\mathbf{x^{\prime}}}} \right) = \exp \left( { - \sum\limits_{i = 1}^{m} {\theta_{i} \left| {x_{i}^{{}} - x^{\prime}_{i} } \right|^{2} } } \right).$$

(25)

It is frequently shown in practical applications that the Gaussian squared exponential function can result in a more accurate global prediction (Palar et al. 2020; Zhou et al. 2020a).

2.4 Hyperparameter tuning by maximum likelihood estimation

After the correlation function is determined, we will focus on the method of tuning the hyperparameters ${{\varvec{\uptheta}}}$ and additional parameters ${{\varvec{\upgamma}}}$ hereafter.

Assuming that the sampled data are distributed according to a Gaussian process, the responses at sampling sites are considered to be correlated random functions with the corresponding likelihood function given by

$$L\left( {{\tilde{\mathbf{\beta }}},\sigma^{2} ,{{\varvec{\uptheta}}},{{\varvec{\upgamma}}}} \right) = \frac{1}{{\sqrt {\left( {2\pi \sigma^{2} } \right)^{{n_{0} + \sum\limits_{k = 1}^{L} {n_{k} } }} \left| {{\tilde{\mathbf{R}}}\left( {{{\varvec{\uptheta}}},{{\varvec{\upgamma}}}} \right)} \right|} }}\exp \left( { - \frac{1}{2}\frac{{({\tilde{\mathbf{y}}}_{S} - {\mathbf{\tilde{F}\tilde{\beta }}})^{{\text{T}}} {\tilde{\mathbf{R}}}\left( {{{\varvec{\uptheta}}},{{\varvec{\upgamma}}}} \right)^{ - 1} ({\tilde{\mathbf{y}}}_{S} - {\mathbf{\tilde{F}\tilde{\beta }}})}}{{\sigma^{2} }}} \right).$$

(26)

Taking logarithm and derivatives with respect to the parameters to be estimated, we can analytically obtain closed-form solutions for the optimum values of ${\tilde{\mathbf{\beta }}},\sigma^{2}$ as follows:

$$\left\{ \begin{gathered} {\tilde{\mathbf{\beta }}} = \left( {{\tilde{\mathbf{F}}}^{{\text{T}}} {\tilde{\mathbf{R}}}^{ - 1} {\tilde{\mathbf{F}}}} \right)^{ - 1} {\tilde{\mathbf{F}}}^{{\text{T}}} {\tilde{\mathbf{R}}}^{ - 1} {\tilde{\mathbf{y}}}_{S} , \hfill \\ \sigma^{2} = \frac{{\left( {{\tilde{\mathbf{y}}}_{S} - {\mathbf{\tilde{F}\tilde{\beta }}}} \right)^{{\text{T}}} {\tilde{\mathbf{R}}}^{ - 1} \left( {{\tilde{\mathbf{y}}}_{S} - {\mathbf{\tilde{F}\tilde{\beta }}}} \right)}}{{n_{0} + n_{1} + \cdots + n_{L} }}. \hfill \\ \end{gathered} \right.$$

(27)

Substituting it into the associated Eq. (26), we are left with maximizing the concentrated ln likelihood function (neglecting constant terms), which is of the form

$$\ln \left[ {L({{\varvec{\uptheta}}},{{\varvec{\upgamma}}})} \right] = - \left( {n_{0} + n_{1} + \cdots + n_{L} } \right)\ln \left[ {\sigma^{2} ({{\varvec{\uptheta}}},{{\varvec{\upgamma}}})} \right] - \ln \left| {{\tilde{\mathbf{R}}}({{\varvec{\uptheta}}},{{\varvec{\upgamma}}})} \right|.$$

(28)

Herein, we use an improved version of the Hooke-Jeeves pattern search method (by using multi-start search and a trust-region method) to solve the preceding optimization problem. Besides, we normalize the input variables ${\mathbf{x}}$ to the range $[0.0, \, 1.0]^{m}$ and limit the searching of ${{\varvec{\uptheta}}}$ to the range $[10^{ - 6} ,10^{2} ]^{m}$ and ${{\varvec{\upgamma}}}$ to the range $(0, \, 1)^{{{{L(L + 1)} \mathord{\left/ {\vphantom {{L(L + 1)} 2}} \right. \kern-0pt} 2}}}$.

However, according to our numerical experiments, we found that the correlation matrix ${\tilde{\mathbf{R}}}$ could easily become non-positive definite during the optimization process, which might lead to the failure of matrix decomposition and model construction. Hence, we develop a novel method for tuning the additional parameters to avoid non-positive definite correlation matrix.

2.5 A novel parameter tuning method to avoid non-positive definite correlation matrix

A mandatory requirement for the success of cokriging model is the positive definiteness of the associated cokriging correlation matrix (Bertram and Zimmermann 2018). As spatial correlations are usually modeled by positive definite correlation functions, such as Gaussian squared exponential function, the corresponding correlation matrices for mutually distinct samples are supposed to be positive definite. However, for an MCOK model, we observe that the introduction of additional parameters brings instability and complexity to obtaining a positive definite cokriging correlation matrix since we do not consider the underlying relationship among additional parameters, and they can be any value in the interval $(0,1)$ without any limits.

For example, there exist two LF datasets along with a HF dataset, and $\gamma^{(01)} = 0.98,\gamma^{(02)} = 0.04,\gamma^{(12)} = 0.95$ in a certain iteration of hyperparameter tuning, which means the HF dataset is strongly correlated to the first LF dataset and they share similar characteristics, while the HF dataset is weakly correlated to the second LF dataset as $\gamma^{(02)}$ is much smaller than $\gamma^{(01)}$ and close to 0. In this event, we believe that the cross-correlation between the first and the second LF datasets should also be small, that is, $\gamma^{(12)}$ is supposed to be close to 0 as well. However, $\gamma^{(12)}$ is equal to 0.95 in fact. It is evident that this situation is unreasonable but could happen if we do not set constraints for optimizing the additional parameters, resulting in the non-positive definite correlation matrix. To address this, we propose to optimize the latent positions ${\mathbf{z}}$ instead of optimizing original additional parameters ${{\varvec{\upgamma}}}$ directly.

Inspired by the latent space used in the fitting of an LMGP model from Oune and Bostanabad (2021) and Eweis-Labolle et al. (2022), we treat each level of fidelity as a point in a latent space. With this latent representation, the distance between any two different latent points can be recognized as the correlation between these two fidelities. Here, a latent space refers to a low-dimensional manifold encoding underlying factors which distinguish different datasets (Oune and Bostanabad 2021). Figure 1 shows the sketch of a 1D, 2D, and 3D latent space for three different fidelities. The latent points A, B, and C represent HF level, LF1 level, and LF2 level, respectively. Then, the values of three distances, $d_{AB} ,d_{AC} ,d_{BC}$, represent the cross-correlations between HF and LF1, HF and LF2, LF1 and LF2, respectively, and are calculated by their coordinates $d_{AB} = \left\| {{\mathbf{z}}(A) - {\mathbf{z}}(B)} \right\|_{2} ,d_{AC} = \left\| {{\mathbf{z}}(A) - {\mathbf{z}}(C)} \right\|_{2} ,d_{BC} = \left\| {{\mathbf{z}}(B) - {\mathbf{z}}(C)} \right\|_{2}$. In order to limit the value of cross-correlation to the range $(0,1)$, we use the following conversion formula to calculate an additional parameter $\gamma$ from its corresponding Euclidean distance d:

$$\gamma = \exp ( - d_{{}}^{2} ).$$

(29)

Fig. 1

Sketch of varying dimensional latent space for three different fidelities

Therefore, we can obtain the values of original additional parameters ${{\varvec{\upgamma}}}$ when existing three levels of fidelities by $\gamma^{(01)} = \exp ( - d_{AB}^{2} )$, $\gamma^{(02)} = \exp ( - d_{AC}^{2} )$, $\gamma^{(12)} = \exp ( - d_{BC}^{2} )$. Hence, if two latent points are far away from each other, their distance will be quite long and the corresponding $\gamma$ will be close to 0; if two latent points are close to each other, their distance will be short and $\gamma$ will be close to 1. Certainly, if any two points coincide, their distance d is equal to 0 and $\gamma$ is equal to 1, which means the corresponding datasets they represent are fully correlated. However, although the probability of encountering the special scenario where all points coincide is very low, it can still lead to the correlation matrix being ill-conditioned when the HF and LF samples are nested, i.e., the HF sampling set is a subset of the LF one. Hence, when all the ${{\varvec{\upgamma}}}$ are optimized to 1, we reassign their values to 0.9999 to ensure that ${{\varvec{\upgamma}}} \in (0, \, 1)^{{{{L(L + 1)} \mathord{\left/ {\vphantom {{L(L + 1)} 2}} \right. \kern-0pt} 2}}}$ and avoid matrix singularity. In this way, the direct optimization of ${{\varvec{\upgamma}}}$ is substituted with the optimization of the coordinate z of points in a latent space.

It is recommended by Zhang et al. (2020) to use a 2D latent space for each level of fidelity. The reason is that in a 1D latent space, the mappings cannot represent three equally correlated levels. In other words, the situation that $d_{AB} = d_{AC} = d_{BC}$ will not happen. In a 3D latent space, each point has three coordinates to be optimized, which brings a heavy burden for MLE search. Thus, we choose to use a 2D latent space where each point only has two coordinates to be optimized and all points can move freely to avoid covariance singularity when exchanging positions during the MLE optimization (Zhang et al. 2020). Besides, in order to reduce the computational cost as much as possible, two constraints are employed to ensure translation and rotation invariances: (1) The first latent position of HF level is located at the origin, namely, $z_{1} (A) = z_{2} \left( A \right) = 0$; (2) The second latent position of LF1 has $z_{1} (B) \ge 0,z_{2} \left( B \right) = 0$. Thus, fitting an MCOK model with L levels of LF datasets involves estimating $m + 2 \times (L - 1) + 1$ parameters in total. Note that the number of coordinates ${\mathbf{z}}$ to be optimized, $2 \times (L - 1) + 1$, is not larger than that of original additional parameters ${{\varvec{\upgamma}}}$, $L \times (L + 1)/2$, which is helpful to save the computational cost of MLE. In Table 1, we have provided the numbers of the original additional model parameters ${{\varvec{\upgamma}}}$ and the new additional model parameters ${\mathbf{z}}$ that represent the coordinates of latent positions, respectively. It can be observed that, regardless of the value of $L$, the number of new model parameters never exceeds the number of original model parameters. Moreover, when $L$ is large than three, the required number of new model parameters is even fewer.

Table 1 Comparison of original and new additional model parameters

Now, recall the case we mentioned in the first paragraph of this section, we use a 2D latent space to represent it here, as sketched in Fig. 2. According to Eq. (29), we can find that $d_{AB} = 0.14, \, d_{AC} = 1.73, \, d_{BC} = 0.23$ and these three sides cannot form a triangle, which causes correlation matrix singularity. Note that this can be prevented by using the parameter tunning approach mentioned above. Thus, to avoid non-positive definite correlation matrix, we can optimize the coordinates of latent points representing fidelity levels in a 2D latent space instead.

Fig. 2

Sketch of a certain case of three fidelities with $\gamma^{(01)} = 0.98,\gamma^{(02)} = 0.04,\gamma^{(12)} = 0.95$

In general, for maximizing Eq. (28), one objective function evaluation at $({{\varvec{\uptheta}}}_{*} ,{\mathbf{z}}_{*} )$ consists of the following steps:

• (1) Compute ${\mathbf{d}}_{*}$ with respect to ${\mathbf{z}}_{*}$ and obtain ${{\varvec{\upgamma}}}_{*}$ according to Eq. (29);

• (2) Compute ${\tilde{\mathbf{R}}}({{\varvec{\uptheta}}}_{*} ,{{\varvec{\upgamma}}}_{*} )$ according to Eq. (21);

• (3) Compute ${\tilde{\mathbf{\beta }}}({{\varvec{\uptheta}}}_{*} ,{{\varvec{\upgamma}}}_{*} )$ and $\sigma^{2} ({{\varvec{\uptheta}}}_{*} ,{{\varvec{\upgamma}}}_{*} )$ by solving Eq. (27);

• (4) Evaluate Eq. (28).

2.6 The difference between MCOK and LMGP models

The LMGP model is a state-of-the-art surrogate model that was originally proposed to handle the single-fidelity modeling of mixed data, which includes both quantitative and qualitative inputs (Oune and Bostanabad 2021). It has since been extended for MF data fusion (Eweis-Labolle et al. 2022) and Bayesian optimization (Foumani et al. 2023), showcasing its advanced capabilities. In an LMGP model, it is assumed that all the random functions $Y_{0} ({\mathbf{x}}),Y_{k} ({\mathbf{x}})$ have stationary and the same mean, namely, $E\left[ {Y_{0} ({\mathbf{x}})} \right] = {\mathbf{f}}_{0} {{\varvec{\upbeta}}}_{0} = E\left[ {Y_{1} ({\mathbf{x}})} \right] = {\mathbf{f}}_{1} {{\varvec{\upbeta}}}_{1} \cdots = E\left[ {Y_{L} ({\mathbf{x}})} \right] = {\mathbf{f}}_{L} {{\varvec{\upbeta}}}_{L} .$ In other words, ${{\varvec{\upbeta}}}_{0} = {{\varvec{\upbeta}}}_{1} = \cdots = {{\varvec{\upbeta}}}_{L}$, and we set them all equal to ${{\varvec{\upbeta}}}$ for convenience. Then, the unbiasedness constraint reads

$${\mathbf{w}}_{0}^{{\text{T}}} {\mathbf{F}}_{0} {{\varvec{\upbeta}}} + \cdots + {\mathbf{w}}_{L}^{{\text{T}}} {\mathbf{F}}_{L} {{\varvec{\upbeta}}} + {\mathbf{w}}_{0}^{{\text{T}}} \underbrace {{E\left[ {{\mathbf{Z}}_{0} } \right]}}_{ = 0} + \cdots + {\mathbf{w}}_{L}^{{\text{T}}} \underbrace {{E\left[ {{\mathbf{Z}}_{L} } \right]}}_{ = 0} - {\mathbf{f}}_{0} {{\varvec{\upbeta}}} - \underbrace {{E\left[ {Z_{0} } \right]}}_{ = 0} = 0,$$

(30)

and therefore,

$$\left( {\sum\limits_{k = 0}^{L} {{\mathbf{w}}_{k}^{{\text{T}}} } {\mathbf{F}}_{k} - {\mathbf{f}}_{0} } \right){{\varvec{\upbeta}}} = 0 \, \Rightarrow \, \sum\limits_{k = 0}^{L} {{\mathbf{w}}_{k}^{{\text{T}}} } {\mathbf{F}}_{k} - {\mathbf{f}}_{0} = 0.$$

(31)

Note that only one single unbiasedness condition is required in an LMGP model. Then, the LMGP predictor can be written in matrix form as

$$\begin{gathered} \hat{y}_{0} \left( {\mathbf{x}} \right) = {\mathbf{w}}_{0}^{{\text{T}}} {\mathbf{y}}_{S,0} + {\mathbf{w}}_{1}^{{\text{T}}} {\mathbf{y}}_{S,1} + \cdots + {\mathbf{w}}_{L}^{{\text{T}}} {\mathbf{y}}_{S,L} \hfill \\ \, = \left[ \begin{gathered} \, {\mathbf{r}}_{0} ({\mathbf{x}}) \hfill \\ \gamma^{(01)} {\mathbf{r}}_{1} ({\mathbf{x}}) \hfill \\ \, \vdots \hfill \\ \gamma^{(0L)} {\mathbf{r}}_{L} ({\mathbf{x}}) \hfill \\ \, {\mathbf{f}}_{{0}}^{{\text{T}}} ({\mathbf{x}}) \hfill \\ \end{gathered} \right]^{{\text{T}}} \left[ {\begin{array}{*{20}c} {{\mathbf{R}}^{{(00)}} } & {\gamma^{(01)} {\mathbf{R}}^{{(01)}} } & \cdots & {\gamma^{(0L)} {\mathbf{R}}^{{{(0}L{)}}} } & {{\mathbf{F}}_{0} } \\ {\gamma^{(01)} {\mathbf{R}}^{{(10)}} } & {{\mathbf{R}}^{{(11)}} } & \cdots & {\gamma^{(1L)} {\mathbf{R}}^{{{(1}L{)}}} } & {{\mathbf{F}}_{1} } \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ {\gamma^{(0L)} {\mathbf{R}}^{{{(}L{0)}}} } & {\gamma^{(1L)} {\mathbf{R}}^{{{(}L1{)}}} } & \cdots & {{\mathbf{R}}^{{{(}LL{)}}} } & {{\mathbf{F}}_{L} } \\ {{\mathbf{F}}_{0}^{{\text{T}}} } & {{\mathbf{F}}_{1}^{{\text{T}}} } & \cdots & {{\mathbf{F}}_{L}^{{\text{T}}} } & {\mathbf{0}} \\ \end{array} } \right]^{ - 1} \left[ \begin{gathered} {\mathbf{y}}_{S,0} \hfill \\ {\mathbf{y}}_{S,1} \hfill \\ \, \vdots \hfill \\ {\mathbf{y}}_{S,L} \hfill \\ \, {\mathbf{0}} \hfill \\ \end{gathered} \right] \hfill \\ \, = \, {\mathbf{f}}_{0} ({\mathbf{x}}){{\varvec{\upbeta}}} + {\tilde{\mathbf{r}}}^{{\text{T}}} ({\mathbf{x}})\underbrace {{{\tilde{\mathbf{R}}}^{ - 1} \left( {{\tilde{\mathbf{y}}}_{S} - {\mathbf{\tilde{F}\beta }}} \right)}}_{{: = {\mathbf{V}}_{LMGP} }}, \hfill \\ \end{gathered}$$

(32)

where

$$\begin{gathered} {\tilde{\mathbf{R}}} = \left[ \begin{gathered} \begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} { \, {\mathbf{R}}^{{(00)}} } & { \, \gamma^{(01)} {\mathbf{R}}^{{(01)}} } \\ \end{array} } & \cdots \\ \end{array} } & {\gamma^{(0L)} {\mathbf{R}}^{{{(0}L{)}}} } \\ \end{array} \hfill \\ \begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\gamma^{(01)} {\mathbf{R}}^{{(10)}} } & { \, {\mathbf{R}}^{{(11)}} } \\ \end{array} } & { \, \cdots } \\ \end{array} } & {\gamma^{(1L)} {\mathbf{R}}^{{{(1}L{)}}} } \\ \end{array} \hfill \\ \begin{array}{*{20}c} {\begin{array}{*{20}c} { \, \begin{array}{*{20}c} \vdots & { \, \vdots } \\ \end{array} } & { \, \ddots } \\ \end{array} } & { \, \vdots } \\ \end{array} \hfill \\ \begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\gamma^{(0L)} {\mathbf{R}}^{{{(}L{0)}}} } & {\gamma^{(1L)} {\mathbf{R}}^{{{(}L1{)}}} } \\ \end{array} } & \cdots \\ \end{array} } & { \, {\mathbf{R}}^{{{(}LL{)}}} } \\ \end{array} \hfill \\ \end{gathered} \right] \in {\mathbb{R}}^{{\left( {n_{0} + \sum\limits_{k = 1}^{L} {n_{k} } } \right) \times \left( {n_{0} + \sum\limits_{k = 1}^{L} {n_{k} } } \right)}} , \hfill \\ {\tilde{\mathbf{r}}}({\mathbf{x}}) = \left[ \begin{gathered} \, {\mathbf{r}}_{0} ({\mathbf{x}}) \hfill \\ \gamma^{(01)} {\mathbf{r}}_{1} ({\mathbf{x}}) \hfill \\ \, \vdots \hfill \\ \gamma^{(0L)} {\mathbf{r}}_{L} ({\mathbf{x}}) \hfill \\ \end{gathered} \right] \in {\mathbb{R}}^{{\left( {n_{0} + \sum\limits_{k = 1}^{L} {n_{k} } } \right) \times 1}} , \, {\tilde{\mathbf{y}}}_{S} = \left[ \begin{gathered} {\mathbf{y}}_{S,0} \hfill \\ {\mathbf{y}}_{S,1} \hfill \\ \, \vdots \hfill \\ {\mathbf{y}}_{S,L} \hfill \\ \end{gathered} \right] \in {\mathbb{R}}^{{\left( {n_{0} + \sum\limits_{k = 1}^{L} {n_{k} } } \right) \times 1}} , \hfill \\ {\tilde{\mathbf{F}}} = \left[ {\begin{array}{*{20}c} {{\mathbf{F}}_{0} } \\ {{\mathbf{F}}_{1} } \\ \vdots \\ {{\mathbf{F}}_{L} } \\ \end{array} } \right] \in {\mathbb{R}}^{{\left( {n_{0} + \sum\limits_{k = 1}^{L} {n_{k} } } \right) \times h}} , \, {{\varvec{\upbeta}}} = \left[ {\begin{array}{*{20}c} {\beta_{1} } \\ {\beta_{2} } \\ \vdots \\ {\beta_{h} } \\ \end{array} } \right] \in {\mathbb{R}}^{h \times 1} = \left( {{\tilde{\mathbf{F}}}^{{\text{T}}} {\tilde{\mathbf{R}}}^{ - 1} {\tilde{\mathbf{F}}}} \right)^{ - 1} {\tilde{\mathbf{F}}}^{{\text{T}}} {\tilde{\mathbf{R}}}^{ - 1} {\tilde{\mathbf{y}}}_{S} . \hfill \\ \end{gathered}$$

(33)

For an ordinary LMGP model, ${\tilde{\mathbf{F}}} = \left[ {1,1, \ldots ,1} \right]{}^{{\text{T}}} \in {\mathbb{R}}^{{\left( {n_{0} + \sum\limits_{k = 1}^{L} {n_{k} } } \right)}}$ and $\beta$ is a constant scalar. Note that in the experimental study section, the ordinary LMGP model is adopted for the purpose of fair comparison with the ordinary MCOK model.

From the above derivation process, it can be observed that due to the assumption of different means for random functions in MCOK, it is able to effectively eliminate the differences when dealing with MF data fusion with systematic biases. However, the LMGP model does not perform well in this regard because it assumes that all random functions of the MF data have the same mean. In the context of aerodynamic data fusion, there usually exists a systematic bias between MF aerodynamic data obtained from different physical models. For example, the aerodynamic coefficients calculated using the Euler equations and Reynolds-averaged Navier–Stokes (RANS) equations always have a systematic deviation because the Euler equations cannot account for the viscosity of the fluid. Hence, in such a scenario, it is evident that we cannot assume the two aerodynamic datasets of different fidelities to have the same mean and choosing the MCOK model is more appropriate.

2.7 Discussion about the advantages of present MCOK model

Here, we summarize the advantages of the proposed MCOK model as follows:

• (1) Different from MHK or other hierarchical MF surrogate models, the proposed MCOK model can incorporate arbitrary number of non-hierarchical LF datasets whose rank of fidelity level or underlying correlations are not known in advance.

• (2) It puts all the covariances and cross-covariances between HF and LF sample points into a single matrix and avoids fitting extra surrogate models for LF datasets, which can not only reduce the model complexity but also lower the risk of accuracy loss due to inaccurate LF surrogate models.

• (3) It introduces parameter vector “${{\varvec{\upgamma}}}$” to account for cross-correlations between datasets of different fidelities and the difficulty associated with modeling cross-covariance is avoided. In addition, the problem associated with non-positive definite correlation matrix is successfully solved by using a novel parameter tuning strategy for ${{\varvec{\upgamma}}}$, which makes the resulting MCOK method efficient and robust for engineering applications.

• (4) It is well suited for fusing MF aerodynamic data with systematic biases since it assumes that the random functions of MF data have stationary but different means. These means are served as model variation trends and can eliminate the systematic bias when fusing MF data. This basic assumption makes the MCOK model more general and accurate compared to the LMGP model.

• (5) The formulation and implementation of the MCOK model are as simple as that of a conventional kriging model, as presented in Eq. (20), despite requiring slightly increased computational effort. Few modifications are required if one wants to implement an MCOK code with an ordinary kriging code in hand, which makes it more practical for real-world engineering applications.

3 Experimental study

In this section, two numerical cases are firstly employed to demonstrate our proposed MCOK model. Then another six numerical test cases of different dimensions and an aerodynamic data fusion example are used to further validate its merits and effectiveness by comparing it with another three representative MF surrogate models, NHLF-COK, LR-MFS (see Appendix 1 for detailed derivation), and LMGP, that can also incorporate multiple non-hierarchical LF datasets.

To measure the prediction accuracy of the built surrogates, the coefficient of determination $R^{2}$, the root-mean-square error (RMSE), and the maximum absolute error (MAE) are calculated:

$$\begin{gathered} R^{2} = 1 - \frac{{\sum\limits_{i = 1}^{N} {\left( {y_{i} - \hat{y}_{i} } \right)^{2} } }}{{\sum\limits_{i = 1}^{N} {\left( {y_{i} - \overline{y}_{i} } \right)^{2} } }}, \, R^{2} \in \left( { - \infty ,1} \right] \hfill \\ RMSE = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^{N} {\left( {y_{i} - \hat{y}_{i} } \right)^{2} } } , \hfill \\ MAE = \max \left| {y_{i} - \hat{y}_{i} } \right|, \hfill \\ \end{gathered}$$

(34)

where $N$ is the number of validation samples, and $y_{i}$,$\hat{y}_{i}$ are the true response and predicted value, respectively, of the ith validation sample. The values of $R^{2}$ and RMSE reflect the global accuracy of the model, and that of MAE reflects the local predictive performance: the closer $R^{2}$ is to 1 and the smaller the values of RMSE and MAE, the more accurate the model is.

3.1 One-dimensional test case

We are concerned with the modeling of a one-dimensional HF model of interest from Forrester and Keane (2009):

$${\text{HF}}: y_{0} (x) = (6x - 2)^{2} \sin (12x - 4),$$

(35)

with assistance of two non-hierarchical LF models:

$$\begin{gathered} {\text{LF1: }}y_{1} (x) = y_{0} (x) - 1.5[(6x - 2)^{2} - 6x], \hfill \\ {\text{LF2: }}y_{2} (x) = 0.6y_{0} (x) + 1.8\sin (9x - 3) - 3, \hfill \\ x \in \left[ {0,1} \right]. \hfill \\ \end{gathered}$$

(36)

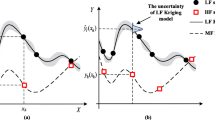
Figure 3a shows the true responses of three models above and the observed samples of each model. It is shown that $y_{2} (x)$ appears to be more accurate than $y_{1} (x)$ with respect to $y_{0} (x)$ as it shares a similar variation trend with $y_{0} (x)$. Note that we do not use this knowledge of relative accuracy during MF modeling via MCOK. In this case, the HF and LF samples are ${\mathbf{S}}_{0} = [0.0,0.4,0.8,1.0]^{{\text{T}}}$ and ${\mathbf{S}}_{1,2} = [0.0,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1.0]^{{\text{T}}}$, respectively. Note that in this case, two LF models share the same low-fidelity sampling sites for convenience. To calculate the error metrics given by Eq. (34), another 100 validation samples are generated by the Latin hypercube sampling (LHS) method. Based on the HF and LF datasets, four MF models are constructed, as sketched in Fig. 3b. The detailed comparison results are summarized in Table 2.

Fig. 3

The true model and different MF surrogate models for a one-dimensional test case

Table 2 Comparison of different MF surrogate models for a one-dimensional test case

It is shown in Fig. 3b that, the MCOK model precisely features the observed functional values at all sampling sites, which verifies the correctness of our proposed method. Compared with NHLF-COK, LR-MFS, and LMGP models, MCOK provides the most accurate prediction and is closer to the exact analytical function, especially in the areas $x \in \left[ {0.0,0.8} \right]$. Besides, a kriging model built based on the HF samples only is also plotted in Fig. 3b and it has the worst prediction without the assistance of LF samples. In the following cases, we will no longer focus on building a single-fidelity kriging model, but instead, emphasize the comparison of four MF surrogate models. In Table 2, one can also see that the RMSE and MAE of MCOK model is the smallest, and the R² is closer to 1, which means our proposed method has the highest local and global accuracy. Table 2 also gives the tuned values of additional parameters, which are calculated by the optimized coordinates of latent points. It can be found that, for both LMGP and MCOK models, their additional parameter $\gamma^{(02)}$ is close to 1 and is larger than $\gamma^{(01)}$, showing that $y_{2} (x)$ is more correlated with $y_{0} (x)$, while $y_{1} (x)$ has little correlation with $y_{0} (x)$. This observation matches with our knowledge of the relative accuracies of $y_{2} (x)$ and $y_{1} (x)$ with respect to $y_{0} (x)$. Certainly, for both NHLF-COK and LR-MFS models, their model parameter $\rho_{1}$ is smaller than $\rho_{2}$, which also reflects the relative accuracies of LF models with respect to the HF model. Besides, both LMGP and MCOK models additionally provide a parameter $\gamma^{(12)}$ to quantify the correlation between the two LF models, $y_{1} (x)$ and $y_{2} (x)$, which is benefit to improve model accuracy but not available in the other two MF surrogate models.

To further demonstrate the advantages of our MCOK model, particularly in comparison with the LMGP model, we have translated the two original LF models downward by a certain distance and obtain:

$$\begin{gathered} {\text{LF1: }}y_{1} (x) = y_{0} (x) - 1.5[(6x - 2)^{2} - 6x] - 8, \hfill \\ {\text{LF2: }}y_{2} (x) = 0.6y_{0} (x) + 1.8\sin (9x - 3) - 24, \hfill \\ x \in \left[ {0,1} \right]. \hfill \\ \end{gathered}$$

(37)

Figure 4a shows the true responses of translated LF models above and the observed samples of each model. It can be observed that the translated LF models are far away from each other and also far away from the HF model. Figure 4b shows that the prediction accuracy of the LMGP model significantly decreases, while the predicted curves of the other three MF surrogate models have not shown any noticeable changes when there exist systematic biases among MF datasets. This is because the NHLF-COK and LR-MFS models have separately built LF surrogate models for each LF dataset, so each model has different means, and the discrepancy model in their fitting process can also help to eliminate systematic biases. Therefore, the systematic biases in translated MF datasets do not significantly affect the fusion results of NHLF-COK, LR-MFS, and MCOK models. In Table 3, one can also see that all the error metrics for the LMGP model show a degradation, while the error metrics for NHLF-COK and LR-MFS exhibit slight improvements. It is worth noting that the error metrics for the MCOK model remain unchanged for both the original LF datasets and the translated LF datasets. This can be explained by the model parameters provided in Table 4. It can be found that the change in $\beta_{1}$ is exactly equal to the translation of the LF1 model, and the change in $\beta_{2}$ is exactly equal to the translation of the LF2 model. Thus, the optimized $\theta$ and ${{\varvec{\upgamma}}}$ remain almost unchanged and the fusion result of MCOK also remains unchanged accordingly. For the LMGP model, its model parameters $\theta$ and ${{\varvec{\upgamma}}}$ vary greatly, leading to significant differences in the final fusion results.

Fig. 4

The translated LF datasets and different MF surrogate models for a one-dimensional test case

Table 3 Comparison of different MF surrogate models with translated LF datasets

Table 4 Detailed comparison of model parameters of LMGP and MCOK models for different LF datasets

3.2 Two-dimensional test case

A two-dimensional analytical function with two sets of non-hierarchical LF data modified from Han et al. (2020) is employed here and the HF model is given by

$${\text{HF: }}y_{0} ({\mathbf{x}}) = \left( {4 - 2.1x_{1}^{2} + \frac{{x_{1}^{4} }}{3}} \right)x_{1}^{2} + x_{1} x_{2} + ( - 4 + 4x_{2}^{2} )x_{2}^{2} ,$$

(38)

with the two modified LF models given by

$$\begin{gathered} {\text{LF1: }}y_{1} ({\mathbf{x}}) = 1.2y_{1} (x_{1} + 0.1,x_{2} - 0.1) - 0.5x_{1} x_{2} - 0.5, \hfill \\ {\text{LF2: }}y_{2} ({\mathbf{x}}) = 1.5y_{1} (x_{1} + 0.2,x_{2} - 0.2) - x_{1} x_{2} - 10, \hfill \\ x_{1} \in \left[ { - 2,2} \right],x_{2} \in \left[ { - 1,1} \right]. \hfill \\ \end{gathered}$$

(39)

Note that the LF2 model exhibits a larger translation relative to the HF model compared to the L1 model. Figure 5 shows the actual contour plot of the HF model, along with the 15 HF sample points selected by a LHS plan and marked with white circles. We also randomly choose 30 LF samples by LHS for $y_{1} ({\mathbf{x}})$ and $y_{2} ({\mathbf{x}})$, respectively. To calculate the error metrics, 1000 validation samples are also generated by LHS method.

Fig. 5

The true HF model and sampling sites for a two-dimensional test case

Then, NHLF-COK, LR-MFS, LMGP, and MCOK models are built based on the same HF and LF datasets, and the comparison results are listed in Table 5. It is shown that our proposed MCOK model is the most accurate one among the four MF surrogate models since it has the best error metrics. Additional model parameters ${{\varvec{\upgamma}}}$ of MCOK and LMGP models suggest that $y_{1} ({\mathbf{x}})$ appears to be more accurate than $y_{2} ({\mathbf{x}})$ with respect to $y_{0} ({\mathbf{x}})$ as $\gamma^{(01)}$ is larger than $\gamma^{(02)}$. This is consistent with the tuned model parameters ${{\varvec{\uprho}}}$ of the other two MF surrogate models, which shows that MCOK and LMGP models have accurately determined the correlations between the HF model and LF models. Note that the additional model parameter $\gamma^{(02)}$ of the LMGP model is smaller than that of the MCOK model, which indicates that the LF2 model’s translation reduces its correlation with the HF model. However, for the MCOK model, translation does not have any impact on the learning of their correlation. The predicted contour plots of the four MF surrogate models are sketched in Fig. 6a–d, respectively. Compared with the true HF model, the predicted contour by our proposed MCOK model shares a more accurate variation trend than the other MF models and can correctly identify the locations of local and global optimal domains.

Table 5 Comparison of different MF surrogate models for a two-dimensional test case

Fig. 6

The true model and different MF surrogate models for a two-dimensional test case

3.3 Additional numerical test cases

In this subsection, six additional numerical test cases of different dimensions and numbers of LF models are tested to further demonstrate the effectiveness of the MCOK model. The features of the six numerical test cases are summarized in Table 6, including problem dimension, number of LF models, and sampling configurations for the HF model and each LF model. These cases are all chosen or modified from Cheng et al. (2021) and Zhang et al. (2022), and their detailed mathematical expressions are listed in Appendix 2. For the fairness of model comparison, we no longer intentionally translate the LF models in these numerical test cases.

Table 6 Features of six numerical test cases

For each test case, the initial HF and LF samples are randomly and uniformly generated by LHS method. Note that the selection of the number of sample points for HF data and LF data is obtained from Cheng et al. (2021), which suggests that the number of HF samples is about 5–20 times the problem dimension and the number of LF samples for each model is about 4–6 times that of HF samples. To alleviate the influence of the distribution of initial sample points on the modeling accuracy, each case is duplicated 20 times. We also generate 2000 validate sample points randomly by LHS for each test case to calculate the values of three error metrics.

The average values of three error metrics are summarized in Table 7 and the best values of these metrics for different MF surrogate models are marked in bold. It can be seen that the results of our proposed MCOK model have the largest values of R² and the smallest values of both RMSE and MAE in the six numerical test cases, except for Case No.4, where the local accuracy of the MCOK model is slightly worse than that of the LMGP model. Overall, the MCOK model shows the best prediction performance in both global and local accuracy. The boxplots of R², RMSE, and MAE for different MF surrogate models are shown in Fig. 7. It is shown that although there exist some outliers of the proposed MCOK model in some cases, it still performs the best among the four MF surrogate models. In general, our proposed MCOK modeling method can be promising and effective in most function problems.

Table 7 Average values of three error metrics by different MF surrogate models for six test cases

Fig. 7

The boxplots of three error metrics results of different MF surrogate models for six test cases

3.4 Engineering test example: aerodynamic data fusion for a hypersonic flight vehicle

To further demonstrate the performance of our proposed MCOK model for engineering problems, we apply it to aerodynamic data fusion for the FDL-5A hypersonic flight vehicle developed by the US Air Force Flight Dynamics Laboratory (Ehrlich 2008), whose baseline configuration is shown in Fig. 8.

Fig. 8

Baseline configuration of FDL-5A hypersonic flight vehicle (Ehrlich 2008)

To fuse the aerodynamic force coefficients of the FDL-5A under different configurations and flight conditions, we first parameterize its geometric shape with 22 design variables, i.e., five geometric parameters for the planar shape of its body, six parameters for the middle control section defined by the class-shape transformation (CST) method, three thickness parameters, and eight shape parameters of the vertical fin and elevons, as shown in Fig. 9. We also consider four quantities defining the flight conditions as input variables, giving a total of 26 input variables for building the MF surrogate model; their detailed descriptions and their variation ranges are given in Table 8. Here, the ranges of some of the geometric shape variables are restricted to avoid generating abnormal configurations and causing difficulties in aerodynamic computation.

Fig. 9

Parameterized geometry of FDL-5A hypersonic flight vehicle

Table 8 Nomenclature of input variables for aerodynamic data fusion for FDL-5A flight vehicle

In this experiment, both RANS and Euler solvers are used for simulating hypersonic flows over changed configurations to establish different datasets with varying fidelities for aerodynamic data fusion. Note that for demonstrating our method and for simplicity, real-gas effects are not considered in the simulations. In order to determine the HF and LF models, the grid convergence for the baseline configuration by RANS and Euler solvers is carried out, with the flow condition being $Ma = 7.98, \, H = 24.5\;{\text{km}}, \, \alpha = 10^{ \circ }$. The results are shown in Fig. 10 and the zero-grid spacing lift, drag, and pitching moment (Lyu et al. 2015), which were obtained using Richardson’s extrapolation based on RANS results, are also plotted in Fig. 10a. It can be seen that the variation of each aerodynamic coefficient is nearly constant for each grid level, and we finally decide to use the L₀ grid and L₁ grid with 2 million and 0.5 million cells, respectively, for RANS computations, and the L2 grid and L3 grid with 2 million and 1 million cells, respectively, for Euler computations. These computations grids are sketched in Fig. 11. Table 9 shows the comparison of aerodynamic coefficients computed by different fidelity models and wind tunnel experimental data for baseline configuration, with the relative errors given in the brackets. It can be seen that the RANS results using the L₀ Grid have the smallest relative error among the four different fidelity models and hence it is supposed to be the HF CFD model. However, the relative accuracies of the remaining three CFD models are difficult to be assigned as they behave differently for each aerodynamic coefficient. Our proposed MCOK model can handle such non-hierarchical LF datasets without assigning fidelity levels for them, as long as the HF model has been determined. Besides, the zero-grid spacing values by RANS solver are the closest to the experimental data, which also means that using higher fidelity physical model on finer computational grid is more accurate.

Fig. 10

Variation of aerodynamic coefficients with respect to grid size ($Ma = 7.98, \, H = 24.5\;{\text{km}}, \, \alpha = 10^{ \circ }$)

Fig. 11

Computational grids for the RANS and Euler computations

Table 9 Comparison of aerodynamic coefficients computed by different fidelity models and experimental data for FDL-5A baseline configuration ($Ma = 7.98, \, H = 24.5km, \, \alpha = 10^{^\circ }$)

We randomly but uniformly generate 150 samples for the HF model and 600 samples for each LF model using LHS method in the aforementioned design space, and establish a training dataset with 1950 samples in total. Then, we additionally generate 450 HF samples for testing the model accuracy. Also, to avoid the influence of initial samples on the modeling accuracy, this experiment is repeated 5 times and each experiment has a different MF dataset of training and testing samples.

The average results of the error metrics for the four MF approaches for this experiment are shown in Table 10 and it can be seen that the proposed MCOK model outperforms the other MF models in terms of both local and global accuracy, with the largest R² value and the smallest RMSE, MAE values. The LMGP model performs slightly worse than the MCOK model in predicting lift and drag coefficients, but the fusion results for the moment coefficient are comparatively poor. Besides, the results of the other two MF models are significantly worse than that of LMGP and MCOK models. Figure 12 shows the boxplots of three error metrics, which also presents that MCOK model is much more accurate and robust than the other three MF models, with a smaller interquartile range. Figure 13 plots heatmaps of the correlation matrix for CFD models of different fidelities. It can be found that the CFD models applying the same governing equations on different grids are essentially very close to each other and strongly correlated, while the CFD models using different governing equations are dramatically different and are weakly correlated. Hence, our modeling method can construct a more accurate MF model by learning the relationships or correlations among different datasets of various fidelities.

Table 10 Average values of three error metrics by different MF surrogate models for FDL-5A hypersonic flight vehicle aerodynamic data fusion example

Fig. 12

The boxplots of three error metrics results of different MF surrogate models for FDL-5A hypersonic flight vehicle aerodynamic data fusion example

Fig. 13

The heatmaps of the correlation matrix for CFD models with different fidelities

4 Conclusions

In this article, a novel multi-fidelity cokriging model, termed as MCOK, is proposed to incorporate multiple non-hierarchical LF datasets with unknown rank of fidelity level or underlying correlations. It can not only avoid fitting surrogate models for every LF dataset, reducing the risk of accuracy loss due to inaccurate LF predictor, but also fully take the effects of cross-covariance among LF models into account, resulting in significant improvement of model accuracy. The proposed MCOK model is validated against a set of numerical test cases of varying dimensions and further demonstrated via an engineering problem of aerodynamic data fusion for FDL-5A hypersonic flight vehicle. Some conclusions can be drawn as follows.

• (1) The core idea of MCOK model is to put the covariance and cross-covariance between any two MF sample points into a single matrix, which is simplified by introducing parameter vector “${{\varvec{\upgamma}}}$” to account for the cross-correlations between different MF datasets. The parameter vector ${{\varvec{\upgamma}}}$ can be tuned through maximum likelihood estimation, which also provides a promising way for fidelity identification and correlation analysis in some engineering problems.

• (2) It is observed that the correlation matrix can be non-positive definite if we directly tune the parameter vector “${{\varvec{\upgamma}}}$” and a novel method is proposed to deal with it. The parameters are transformed to the distances between latent points and optimized to quantify the cross-correlations between different datasets. This is crucial for the success of an MCOK model as non-positive definite matrix will lead to the failure of matrix decomposition and hyperparameter tuning.

• (3) Compared to the LMGP model, which can also consider the cross-covariances among LF models without building extra surrogate models, our proposed MCOK model is able to handle with multiple MF datasets with large systematic biases, such as aerodynamic data obtained by different physical models. This is because the LMGP model assumes that all random functions for each MF dataset have stationary and the same mean, while our approach assumes that they have stationary but different means, and thus the systematic bias can be eliminated through model training.

• (4) The implementation of the proposed MCOK model is as simple as that of a conventional kriging model, such as an ordinary kriging, despite requiring slightly increased computational effort for decomposing a larger correlation matrix. Few modifications are required to turn an ordinary kriging code into an MCOK code.

• (5) From current test cases presented herein, it is shown that MCOK model outperforms existing MF surrogate models, such as NHLF-COK, LR-MFS, and LMGP models, with smaller error metrics and standard deviations in the repeated experiments, which makes it more promising for engineering modeling and data fusion problems.

Beyond the scope of this research, we will apply MCOK model to higher-dimensional modeling problems with more input variables to further examine its performance. Besides, the influence of decomposing large correlation matrix of an MCOK model on the modeling efficiency should also be investigated.

Appendices

Appendix 1: Details of the comparative methods

1.1 Non-hierarchical co-kriging (NHLF-COK)

The formulation of the NHLF-COK model, which incorporates the data from an HF model and “$L$” LF models, can be written as

$$\hat{y}_{0} ({\mathbf{x}}) = \sum\limits_{k = 1}^{L} {\rho_{k} } \hat{y}_{k} ({\mathbf{x}}) + \hat{y}_{d} ({\mathbf{x}}),$$

(40)

where $\rho_{k} \, (k = 1,2, \ldots ,L)$ is the multiplicative scale factor corresponding to the LF model prediction $\hat{y}_{k} ({\mathbf{x}})$, and $\hat{y}_{d} ({\mathbf{x}})$ denotes the prediction of a discrepancy model between the HF model and the ensembled L LF models. Note that we continue to use the same nomenclature as that of our MCOK model defined in Nomenclature for consistency.

Then, the covariance matrix that expresses the correlations between the HF and LF datasets can be formally defined as

$${\mathbf{C}} = \left[ {\begin{array}{*{20}c} {\sigma_{1}^{2} {\mathbf{R}}_{1} ({\mathbf{S}}_{1} ,{\mathbf{S}}_{1} )} & 0 & \cdots & {\rho_{1} \sigma_{1}^{2} {\mathbf{R}}_{1} ({\mathbf{S}}_{1} ,{\mathbf{S}}_{0} )} \\ 0 & {\sigma_{2}^{2} {\mathbf{R}}_{2} ({\mathbf{S}}_{2} ,{\mathbf{S}}_{2} )} & \cdots & {\rho_{2} \sigma_{2}^{2} {\mathbf{R}}_{2} ({\mathbf{S}}_{2} ,{\mathbf{S}}_{0} )} \\ \vdots & \vdots & \ddots & \vdots \\ {\rho_{1} \sigma_{1}^{2} {\mathbf{R}}_{1} ({\mathbf{S}}_{0} ,{\mathbf{S}}_{1} )} & {\rho_{2} \sigma_{2}^{2} {\mathbf{R}}_{2} ({\mathbf{S}}_{0} ,{\mathbf{S}}_{2} )} & \cdots & {\sum\nolimits_{k = 1}^{L} {\rho_{k}^{2} \sigma_{k}^{2} {\mathbf{R}}_{k} ({\mathbf{S}}_{0} ,{\mathbf{S}}_{0} )} + \sigma_{d}^{2} {\mathbf{R}}_{d} ({\mathbf{S}}_{0} ,{\mathbf{S}}_{0} )} \\ \end{array} } \right],$$

(41)

where $\sigma_{( \cdot )}^{2}$ denotes the process variance of the LF model and discrepancy model, the notion ${\mathbf{R}}_{k} ({\mathbf{S}}_{i} ,{\mathbf{S}}_{j} )$ represents a matrix of correlations of the form ${\mathbf{R}}_{k}$ between the datasets ${\mathbf{S}}_{i}$ and ${\mathbf{S}}_{j}$, and ${\mathbf{R}}_{d} ({\mathbf{S}}_{0} ,{\mathbf{S}}_{0} )$ represents a matrix of the form ${\mathbf{R}}_{d}$ between the data ${\mathbf{S}}_{0}$ and ${\mathbf{S}}_{0}$. The Gaussian squared exponential function mentioned in Sect. 2.3 can still be chosen as the correlation function here.

In the construction of an NHLF-COK model, there are more model hyperparameters to estimate: ${{\varvec{\uptheta}}}_{d} ,{{\varvec{\uptheta}}}_{k} \, (k = 1,2, \ldots ,L)$ and $L$ scale factors $\rho_{k} (k = 1,2, \ldots ,L)$. Here, the hyperparameters ${{\varvec{\uptheta}}}$ of all L LF surrogate models and discrepancy model can be tuned by MLE, while the optimal scale factors ${{\varvec{\uprho}}}$ are obtained by solving a suboptimization problem, whose objective is to minimize the mean second derivative of the prediction value of the discrepancy model, with the following expression:

$$\begin{gathered} \min . \, G_{2} = \frac{1}{N}\sum\limits_{t = 1}^{N} {\sum\limits_{i = 1}^{m} {\left( {\frac{{\partial^{2} \hat{y}_{d} ({\mathbf{x}}^{(t)} )}}{{\partial (x_{i}^{(t)} )^{2} }}} \right)} }^{2} , \hfill \\ {\text{w}}{\text{.r}}{\text{.t}}{. }{{\varvec{\uprho}}} = \left[ {\rho_{1} , \ldots ,\rho_{L} } \right], \hfill \\ \end{gathered}$$

(42)

where $N$ is the number of validation samples. The interior-point method is adopted here to search for the optimal scale factors.

To obtain the NHLF-COK predictor for any untried ${\mathbf{x}}$, the covariance vector is defined as

$${\mathbf{c}}({\mathbf{x}}) = \left[ {\rho_{1} \sigma_{1}^{2} {\mathbf{R}}_{1} ({\mathbf{S}}_{0} ,{\mathbf{x}}), \ldots ,\rho_{L} \sigma_{L}^{2} {\mathbf{R}}_{L} ({\mathbf{S}}_{0} ,{\mathbf{x}}),\sum\nolimits_{k = 1}^{L} {\rho_{k}^{2} \sigma_{k}^{2} {\mathbf{R}}_{k} ({\mathbf{S}}_{0} ,{\mathbf{x}})} + \sigma_{d}^{2} {\mathbf{R}}_{d} ({\mathbf{S}}_{0} ,{\mathbf{x}})} \right]^{{\text{T}}} .$$

(43)

Then, the prediction response $\hat{y}_{0} ({\mathbf{x}})$ can be formulated as

$$\hat{y}_{0} ({\mathbf{x}}) = {{\varvec{\upbeta}}} + {\mathbf{c}}^{{\text{T}}} {\mathbf{C}}^{ - 1} \left( {{\mathbf{y}}_{S} - {\mathbf{1\beta }}} \right),$$

(44)

where

$$\begin{gathered} {\mathbf{y}}_{S} = \left[ {{\varvec{y}}_{S,1} ,{\varvec{y}}_{S,2} , \ldots ,{\varvec{y}}_{S,L} ,{\varvec{y}}_{S,0} } \right]^{{\text{T}}} , \hfill \\ {{\varvec{\upbeta}}} = \frac{{{\mathbf{1}}^{{\text{T}}} {\mathbf{C}}^{ - 1} {\mathbf{y}}_{S} }}{{{\mathbf{1}}^{{\text{T}}} {\mathbf{C}}^{ - 1} {\mathbf{1}}}}. \hfill \\ \end{gathered}$$

(45)

By using the standard stochastic-process approach, the MSE of this predictor is given by

$$s_{0}^{2} ({\mathbf{x}}) = \sum\limits_{k = 1}^{L} {\rho_{k}^{2} \sigma_{k}^{2} } + \sigma_{d}^{2} - {\mathbf{c}}^{{\text{T}}} {\mathbf{C}}^{ - 1} {\mathbf{c}} + \frac{{\left( {{\mathbf{1}} - {\mathbf{1}}^{{\text{T}}} {\mathbf{C}}^{ - 1} {\mathbf{c}}} \right)^{2} }}{{{\mathbf{1}}^{{\text{T}}} {\mathbf{C}}^{ - 1} {\mathbf{1}}}}.$$

(46)

1.2 Linear regression multi-fidelity surrogate (LR-MFS)

LR-MFS model shares a similar formulation with the NHLF-COK, but has a different discrepancy model. The basic formulation of LR-MFS is expressed as

$$\hat{y}_{0} ({\mathbf{x}}) = \sum\limits_{k = 1}^{L} {\rho_{k} } \hat{y}_{k} ({\mathbf{x}}) + \hat{y}_{d} ({\mathbf{x}}),$$

(47)

where $\hat{y}_{d} ({\mathbf{x}})$ denotes the discrepancy model that is presented in the form of polynomial response surface (PRS) as

$$\hat{y}_{d} ({\mathbf{x}}) = \sum\limits_{j = 1}^{p} {\xi_{j} ({\mathbf{x}})b_{j} } ,$$

(48)

where $\xi_{j} ({\mathbf{x}})$ denotes the jth monomial basis, and $b_{j}$ is the unknown coefficient of $\xi_{j} ({\mathbf{x}})$. A const or low-order polynomials is often used for approximating the discrepancy model due to the limited HF samples. Hence, the LR-MFS predictor is given by

$$\hat{y}_{0} ({\mathbf{x}}) = \sum\limits_{k = 1}^{L} {\rho_{k} } \hat{y}_{k} ({\mathbf{x}}) + \sum\limits_{j = 1}^{p} {\xi_{j} ({\mathbf{x}})b_{j} } .$$

(49)

Written in matrix form, Eq. (49) is given by

$$\hat{y}_{0} ({\mathbf{x}}) = {\mathbf{XB}},$$

(50)

where

$$\begin{gathered} {\mathbf{X}} = \left[ \begin{gathered} \begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\hat{y}_{1} ({\mathbf{x}}_{0}^{(1)} )} & \cdots \\ \end{array} } & { \, \hat{y}_{L} ({\mathbf{x}}_{0}^{(1)} )} \\ \end{array} } & { \, \xi_{1} ({\mathbf{x}}_{0}^{(1)} )} & \cdots & {\xi_{p} ({\mathbf{x}}_{0}^{(1)} )} \\ \end{array} \hfill \\ \begin{array}{*{20}c} {\begin{array}{*{20}c} { \, \vdots } & { \, \ddots } & { \, \vdots } \\ \end{array} } & { \, \vdots } & { \, \ddots } & { \, \vdots } \\ \end{array} \hfill \\ \begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\hat{y}_{1} ({\mathbf{x}}_{0}^{{(n_{0} )}} )} & \cdots & {\hat{y}_{L} ({\mathbf{x}}_{0}^{{(n_{0} )}} )} \\ \end{array} } & {\xi_{1} ({\mathbf{x}}_{0}^{{(n_{0} )}} )} & \cdots \\ \end{array} } & {\xi_{p} ({\mathbf{x}}_{0}^{{(n_{0} )}} )} \\ \end{array} \hfill \\ \end{gathered} \right], \hfill \\ {\mathbf{B}} = \left[ {\rho_{1} ,\rho_{2} , \cdots ,\rho_{L} ,b_{1} ,b_{2} , \cdots b_{p} } \right]^{{\text{T}}} . \hfill \\ \end{gathered}$$

(51)

Note that $n_{0}$ is the number of HF samples, X is the augmented design matrix, and B is the unknown coefficient vector, which can be obtained by the square sum of errors as

$$\mathop {\min .}\limits_{{\mathbf{B}}} \, \left( {{\mathbf{y}}_{S,0} - {\mathbf{XB}}} \right)^{{\text{T}}} \left( {{\mathbf{y}}_{S,0} - {\mathbf{XB}}} \right),$$

(52)

where ${\varvec{y}}_{S,0} = \left[ {y_{0} ({\mathbf{x}}^{(1)} ),y_{0} ({\mathbf{x}}^{(2)} ), \ldots ,y_{0} ({\mathbf{x}}^{{(n_{0} )}} )} \right]^{{\text{T}}}$ and the standard regression technique can yield the following form of unknown coefficients:

$${\mathbf{B}} = ({\mathbf{X}}^{{\text{T}}} {\mathbf{X}})^{ - 1} {\mathbf{X}}^{{\text{T}}} {\mathbf{y}}_{S,0} .$$

(53)

In this article, a second-order fully expanded polynomial is taken as the discrepancy model.

Appendix 2: Expression about six numerical cases

The expressions of another six numerical test cases used in Sect. 3.2 are listed below.

Case 1

$$\begin{gathered} y_{0} = 2\sin ({{\pi x} \mathord{\left/ {\vphantom {{\pi x} 5}} \right. \kern-0pt} 5}), \hfill \\ y_{1} = {{x(x - 5)(x - 12)} \mathord{\left/ {\vphantom {{x(x - 5)(x - 12)} {30}}} \right. \kern-0pt} {30}}, \hfill \\ y_{2} = {{(x + 2)(x - 5)(x - 10)} \mathord{\left/ {\vphantom {{(x + 2)(x - 5)(x - 10)} {30}}} \right. \kern-0pt} {30}}, \hfill \\ x \in \left[ {0,10} \right] \hfill \\ \end{gathered}$$

(54)

Case 2

$$\begin{gathered} y_{0} = - \sin x_{1} - e^{{{{x_{1} } \mathord{\left/ {\vphantom {{x_{1} } {100}}} \right. \kern-0pt} {100}}}} + 10 + {{x_{2}^{2} } \mathord{\left/ {\vphantom {{x_{2}^{2} } {10}}} \right. \kern-0pt} {10}}, \hfill \\ y_{1} = - \sin x_{1} - e^{{{{x_{1} } \mathord{\left/ {\vphantom {{x_{1} } {100}}} \right. \kern-0pt} {100}}}} + 10.3 + 0.03(x_{1} - 0.3)^{2} + {{(x_{2} - 1)^{2} } \mathord{\left/ {\vphantom {{(x_{2} - 1)^{2} } {10}}} \right. \kern-0pt} {10}}, \hfill \\ y_{2} = - \sin (0.9x_{1} ) - e^{{{{0.9x_{1} } \mathord{\left/ {\vphantom {{0.9x_{1} } {100}}} \right. \kern-0pt} {100}}}} + 10 + {{0.64x_{2}^{2} } \mathord{\left/ {\vphantom {{0.64x_{2}^{2} } {10}}} \right. \kern-0pt} {10}}, \hfill \\ x_{1} ,x_{2} \in \left[ {0,1} \right] \hfill \\ \end{gathered}$$

(55)

Case 3

$$\begin{gathered} y_{0} = \left( {x_{1} - 1} \right)^{2} + 2\left( {2x_{2}^{2} - x_{1} } \right)^{2} + 3\left( {3x_{3}^{2} - x_{2} } \right)^{2} + 4\left( {4x_{4}^{2} - x_{3} } \right)^{2} , \hfill \\ y_{1} = \left( {x_{1} - 1} \right)^{2} + 2\left( {2x_{2}^{2} - 0.75x_{1} } \right)^{2} + 3\left( {3x_{3}^{2} - 0.75x_{2} } \right)^{2} + 4\left( {4x_{4}^{2} - 0.75x_{3} } \right)^{2} , \hfill \\ y_{2} = \left( {x_{1} - 1} \right)^{2} + 2\left( {2x_{2}^{2} - 1.25x_{1} } \right)^{2} + 3\left( {3x_{3}^{2} - 1.25x_{2} } \right)^{2} + 4\left( {4x_{4}^{2} - 1.25x_{3} } \right)^{2} , \hfill \\ y_{3} = \left( {x_{1} - 1} \right)^{2} + 2\left( {2.25x_{2}^{2} - x_{1} } \right)^{2} + 3\left( {3.25x_{3}^{2} - x_{2} } \right)^{2} + 4\left( {4.25x_{4}^{2} - x_{3} } \right)^{2} , \hfill \\ x_{1} ,x_{2} ,x_{3} ,x_{4} \in \left[ { - 2,2} \right] \hfill \\ \end{gathered}$$

(56)

Case 4

$$\begin{gathered} y_{0} = \frac{{x_{1} }}{2}\left[ {\sqrt {1 + \left( {x_{2} + x_{3}^{2} } \right)\frac{{x_{4} }}{{x_{1}^{20} }}} - 1} \right] + \left( {x_{1} + 3x_{4} } \right)e^{{\left( {1 + \sin x_{3} } \right)}} , \hfill \\ y_{1} = 0.79\left( {1 + \frac{{\sin x_{1} }}{10}} \right)y_{1} - 2x_{1} + x_{2}^{2} + x_{3}^{2} + 0.5, \hfill \\ y_{2} = y_{1} + e^{{{{x_{3} } \mathord{\left/ {\vphantom {{x_{3} } 2}} \right. \kern-0pt} 2}}} - \frac{{x_{1} }}{100}, \hfill \\ x_{1} ,x_{2} ,x_{3} ,x_{4} \in \left[ {0.5,1} \right] \hfill \\ \end{gathered}$$

(57)

Case 5

$$\begin{gathered} y_{0} = \left[ {100\left( {x_{2} - x_{1}^{2} } \right)^{2} + \left( {x_{1} - 1} \right)^{2} + 100\left( {x_{3} - x_{2}^{2} } \right)^{2} + \left( {x_{2} - 1} \right)^{2} + 100\left( {x_{4} - x_{3}^{2} } \right)^{2} } \right. \hfill \\ \, {{\left. {{ + }\left( {x_{3} - 1} \right)^{2} + 100\left( {x_{5} - x_{4}^{2} } \right)^{2} + \left( {x_{4} - 1} \right)^{2} + 100\left( {x_{6} - x_{5}^{2} } \right)^{2} + \left( {x_{5} - 1} \right)^{2} } \right]} \mathord{\left/ {\vphantom {{\left. {{ + }\left( {x_{3} - 1} \right)^{2} + 100\left( {x_{5} - x_{4}^{2} } \right)^{2} + \left( {x_{4} - 1} \right)^{2} + 100\left( {x_{6} - x_{5}^{2} } \right)^{2} + \left( {x_{5} - 1} \right)^{2} } \right]} {100000}}} \right. \kern-0pt} {100000}}, \hfill \\ y_{1} = \left[ {100\left( {x_{2} - x_{1}^{2} } \right)^{2} + 4\left( {x_{1} - 1} \right)^{2} + 100\left( {x_{3} - x_{2}^{2} } \right)^{2} + 4\left( {x_{2} - 1} \right)^{2} + 100\left( {x_{4} - x_{3}^{2} } \right)^{2} } \right. \hfill \\ \, {{\left. {{ + 4}\left( {x_{3} - 1} \right)^{2} + 100\left( {x_{5} - x_{4}^{2} } \right)^{2} + 4\left( {x_{4} - 1} \right)^{2} + 100\left( {x_{6} - x_{5}^{2} } \right)^{2} + 4\left( {x_{5} - 1} \right)^{2} } \right]} \mathord{\left/ {\vphantom {{\left. {{ + 4}\left( {x_{3} - 1} \right)^{2} + 100\left( {x_{5} - x_{4}^{2} } \right)^{2} + 4\left( {x_{4} - 1} \right)^{2} + 100\left( {x_{6} - x_{5}^{2} } \right)^{2} + 4\left( {x_{5} - 1} \right)^{2} } \right]} {100000}}} \right. \kern-0pt} {100000}}, \hfill \\ y_{2} = \left[ {80\left( {x_{2} - x_{1}^{2} } \right)^{2} + \left( {x_{1} - 1} \right)^{2} + 80\left( {x_{3} - x_{2}^{2} } \right)^{2} + \left( {x_{2} - 1} \right)^{2} + 80\left( {x_{4} - x_{3}^{2} } \right)^{2} } \right. \hfill \\ \, {{\left. {{ + }\left( {x_{3} - 1} \right)^{2} + 80\left( {x_{5} - x_{4}^{2} } \right)^{2} + \left( {x_{4} - 1} \right)^{2} + 80\left( {x_{6} - x_{5}^{2} } \right)^{2} + \left( {x_{5} - 1} \right)^{2} } \right]} \mathord{\left/ {\vphantom {{\left. {{ + }\left( {x_{3} - 1} \right)^{2} + 80\left( {x_{5} - x_{4}^{2} } \right)^{2} + \left( {x_{4} - 1} \right)^{2} + 80\left( {x_{6} - x_{5}^{2} } \right)^{2} + \left( {x_{5} - 1} \right)^{2} } \right]} {100000}}} \right. \kern-0pt} {100000}}, \hfill \\ y_{3} = \left[ {100\left( {x_{2} - x_{1}^{2} } \right)^{2} + 100\left( {x_{3} - x_{2}^{2} } \right)^{2} + 100\left( {x_{4} - x_{3}^{2} } \right)^{2} } \right.{ + }100\left( {x_{5} - x_{4}^{2} } \right)^{2} \hfill \\ \, {{\left. { + 100\left( {x_{6} - x_{5}^{2} } \right)^{2} } \right]} \mathord{\left/ {\vphantom {{\left. { + 100\left( {x_{6} - x_{5}^{2} } \right)^{2} } \right]} {100000}}} \right. \kern-0pt} {100000}}, \hfill \\ x_{1} ,x_{2} ,x_{3} ,x_{4} ,x_{5} ,x_{6} \in \left[ { - 5,10} \right] \hfill \\ \end{gathered}$$

(58)

Case 6

$$\begin{gathered} y_{0} = \frac{{2\pi x_{3} \left( {x_{4} - x_{6} } \right)}}{{\ln \left( {{{x_{2} } \mathord{\left/ {\vphantom {{x_{2} } {x_{1} }}} \right. \kern-0pt} {x_{1} }}} \right)\left[ {1 + {{2x_{7} x_{4} } \mathord{\left/ {\vphantom {{2x_{7} x_{4} } {\left( {\ln \left( {{{x_{2} } \mathord{\left/ {\vphantom {{x_{2} } {x_{1} }}} \right. \kern-0pt} {x_{1} }}} \right)x_{1}^{2} x_{8} } \right) + {{x_{3} } \mathord{\left/ {\vphantom {{x_{3} } {x_{5} }}} \right. \kern-0pt} {x_{5} }}}}} \right. \kern-0pt} {\left( {\ln \left( {{{x_{2} } \mathord{\left/ {\vphantom {{x_{2} } {x_{1} }}} \right. \kern-0pt} {x_{1} }}} \right)x_{1}^{2} x_{8} } \right) + {{x_{3} } \mathord{\left/ {\vphantom {{x_{3} } {x_{5} }}} \right. \kern-0pt} {x_{5} }}}}} \right]}}, \hfill \\ y_{1} = 0.4y_{1} + x_{1}^{2} x_{8} + {{x_{1} x_{7} } \mathord{\left/ {\vphantom {{x_{1} x_{7} } {x_{3} }}} \right. \kern-0pt} {x_{3} }} + {{x_{1} x_{6} } \mathord{\left/ {\vphantom {{x_{1} x_{6} } {x_{2} }}} \right. \kern-0pt} {x_{2} }} + x_{1}^{2} x_{4} , \hfill \\ y_{2} = 0.6y_{1} + 10{{x_{1} x_{5} } \mathord{\left/ {\vphantom {{x_{1} x_{5} } {x_{2} }}} \right. \kern-0pt} {x_{2} }} + {{x_{1} x_{8} } \mathord{\left/ {\vphantom {{x_{1} x_{8} } {x_{4} }}} \right. \kern-0pt} {x_{4} }} + x_{1}^{3} x_{7} , \hfill \\ x_{1} \in \left[ {0.05,0.15} \right],x_{2} \in \left[ {100,50000} \right],x_{3} \in \left[ {63070,115600} \right], \hfill \\ x_{4} \in \left[ {990,1110} \right],x_{5} \in \left[ {63.1,116} \right],x_{6} \in \left[ {700,820} \right], \hfill \\ x_{7} \in \left[ {1120,1680} \right],x_{8} \in \left[ {9855,12045} \right] \hfill \\ \end{gathered}$$

(59)