IGA-based topology optimization in the design of stress-constrained compliant mechanisms

Abstract

Topology design of compliant mechanisms has gained wide popularity among the scientific community, and their use in the mechanical engineering field is being of upmost importance. In this paper, an isogeometric analysis (IGA) formulation is used to solve the topology optimization problem of compliant mechanisms. Stress constraints are introduced in the problem to guarantee the attainment of realistic solutions. For this purpose, an overweight constraint is considered for the design process, replacing the use of local stress constraints. The material distribution in the domain is modeled with quadratic B-splines and with a uniform relative density within each element of the mesh. These strategies to define the material layout are used to compare the IGA-based formulation with the finite element (FEM) formulation. The IGA formulation provides several advantages with respect to the classical FEM-based approaches that are shown and analyzed with an input-parameters sensitivity analysis. The sensitivity analysis and the assessment of the importance of introducing of stress constraints in the problem are developed by solving two benchmark problems. Regarding the sensitivity analysis of input parameters, the results show that the ratio between the material and the springs stiffnesses is the parameter with the largest influence on the solutions of the problem. Moreover, the advantages of the IGA formulations over FEM formulations are related with the computational time, the smoothness of the structural borders, and the non-appearance of the checkerboard patterns. With respect to the stress constraints, the results show that they have to be considered in order to avoid instability and structural integrity problems.

1 Introduction

A compliant mechanism is a structure that can transfer or transmit motion, force, or energy through the elastic deformation of its composing material. Due to some external perturbation (force, pressure, displacement, electrical or thermal excitation) applied on a specified boundary (input port), it is capable of generating a movement in a desired direction (output port). Compliant mechanisms differ from conventional rigid-link mechanisms since those do not contain rigid links or joints, being intentionally designed to be flexible. The most important advantages of compliant mechanisms are their easier manufacturing process since they require a reduced number of parts and need of lubrication due to their lower wear, noise, friction, and backlash. Finally, they have built-in restoring forces. There are two kinds of compliant mechanisms: lumped and distributed. While the flexibility of the lumped compliant mechanisms is mainly derived from the localized areas, the flexibility of the distributed ones is provided by the whole mechanism.

Three different methods have already been used for the design of compliant mechanisms. The first one designs the compliant mechanisms from a kinematic point of view. In this method, a known rigid-link mechanism is chosen as an initial solution of the problem and it is converted to a compliant mechanism (Murphy et al. 1993; Howell and Midha 1993; Mettlach and Midha 1996; Pei et al. 2010; Yu et al. 2012; Ling et al. 2018; Zhang et al. 2019c). The second one, known as building blocks approach, is based on the idea that a mechanism should be composed of a certain number of sub-mechanisms (Kim et al. 2008; Hoetmer et al. 2010; Krishnan et al. 2010; Lamers et al. 2015).

The one addressed in this paper designs the compliant mechanism from a structural point of view. For this purpose, topology optimization is used since it does not require a rigid-link mechanism configuration as an initial solution and makes possible the design of single-piece fully compliant mechanisms (Sigmund 1997; Nishiwaki et al. 1998; Bruns and Tortorelli 2001; Kogiso et al. 2008; Li et al. 2011; De Leon et al. 2015; Tran et al. 2017; Zhu et al. 2020). Since compliant mechanisms are intentionally flexible, the topology optimization methods developed for the stiffest structure design cannot be directly applied to their design. This intentional flexibility allows the structure to work as a mechanism in contrast to the solution of the maximum stiffness topology optimization problem. The use of topology optimization in the design of compliant mechanisms allows changing the topology during the optimization process. Moreover, topology optimization is able to deal with the precise elastic behavior of complex geometries. However, the use of topology optimization in the design of compliant mechanisms has two main difficulties: a balance between stiffness and flexibility, and the control of the stress level. The combination of stiffness and flexibility is required by compliant mechanisms since these have to be stiff enough to support all the external solicitations and, at the same time, flexible enough to satisfy their functional requirements. Despite these drawbacks, the topology design of compliant mechanisms has become more popular and increasingly used to solve real-life industrial problems due to the advent of additive manufacturing technologies. As a result, two categories of methods to deal with topology optimization problems of compliant mechanisms have already been developed. The first one consists on maximizing some mechanical measurements, including mechanical advantage (Sigmund 1997), geometrical advantage (Zhu and Zhang 2012), mechanical efficiency (Luo et al. 2008), and output displacements (De Leon et al. 2015). The second category of methods consists in a multi-objective topology optimization problem based on both the stiffness and the flexibility (Frecker et al. 1997; Saxena and Ananthasuresh 1998; Zhu et al. 2014; Tran et al. 2020; Nguyen et al. 2022).

Different strategies have been used to incorporate the local stress constraints in the formulation of the topology optimization problem of compliant mechanisms. The introduction of stress constraints in the topology optimization problem of compliant mechanisms (De Leon et al. 2015; Chu et al. 2017; Emmendoerfer et al. 2020; Assis da Silva et al. 2020a; Reinisch et al. 2021; Emmendoerfer et al. 2022; Stankiewicz et al. 2022) is required to control the stress level and to attain realistic solutions. These constraints guarantee that structures, mechanisms, or elements are capable of performing the function they were designed for. In other words, the non-introduction of stress constraints in the design problem can lead to non-realistic results, albeit, with a better performance with respect to the objective function. Different ways to formulate the stress constraints in the topology optimization problem have been used. Among the available strategies, the Local Stress Constraint approach (Cheng and Jiang 1992; Duysinx and Bendsøe 1998; Navarrina et al. 2005; Le et al. 2010; Emmendoerfer and Fancello 2014; Assis da Silva and Beck 2017; Senhora et al. 2020; Assis da Silva et al. 2020b; Senhora et al. 2023) establishes one constraint for each local stress considered. In this approach, the number of constraints is equal to the number of local stresses analyzed. This number is related with the number of design variables used in the definition of the optimization problem. As many local stress constraints as design variables have to be formulated to ensure that some issues (as checkerboard patterns) are avoided. Second, the Global Stress Constraint approach (Le et al. 2010; París et al. 2009; Yang et al. 2018; Liu et al. 2018; Fan et al. 2019; Xu et al. 2021; Han et al. 2021) formulates only one constraint to consider all local stress constraints, regardless the number of design variables used in the definition of the problem. Finally, the Block Aggregation of Stress Constraints approach (Le et al. 2010; París et al. 2007, 2010a, b; Zhang et al. 2019b; Wang et al. 2021) formulates a certain number of constraints to take into account all the local stress constraints. This approach is an intermediate situation between the previous approaches since the number of constraints is higher than 1 but considerably lower than the number of design variables. The Global Stress Constraint and the Block Aggregation of Stress Constraints approaches can be formulated by considering two different strategies, using aggregation functions or creating an alternative model. Aggregation functions are used to estimate the maximum value of a certain set of values, in this case, the maximum value of all the local stress constraints. Several functions have been used as aggregation functions: the Kreisselmeier-Steinhauser (KS) function (Assis da Silva et al. 2020a; Zhang et al. 2019b; Kreisselmeier and Steinhauser 1979, 1983; Verbart et al. 2017), the p-norm approach (Xu et al. 2021; Duysinx and Sigmund 1998; Lee et al. 2016; Chen et al. 2022) and, finally, the induced constraint aggregation functions (Kennedy and Hicken 2015; Lambe et al. 2016). By contrast, the creation of an alternative model consists on modifying one of the characteristics of the original structural model in this alternative model when the local stresses are higher than its maximum allowable value, i.e., the imposed constraints are violated. Two alternative approaches have been developed in this field, the damage approach (Verbart et al. 2016) and the overweight approach (Villalba et al. 2022).

Different ways of defining the material layout in the domain have been used in the formulation of the topology optimization problem. However, only three of them have been extensively used in the design of compliant mechanisms. First, the solid isotropic material with penalty (SIMP) approach (Xu et al. 2021; Eschenauer and Olhoff 2001; Allaire et al. 2004; Zhao et al. 2010; Zhang et al. 2014; Zuo and Saitou 2017; Groen and Sigmund 2018; Wang et al. 2022; Zuo et al. 2022) defines the material layout with the use of design variables. The structural domain has to be meshed, and the number of the design variables used is equal to the number of elements of the mesh. Each design variable defines the relative density at each element of the mesh and as a result the relative density in the entire element takes a constant value. By contrast, the level set method (LSM) (Emmendoerfer et al. 2020; Emmendoerfer and Fancello 2014; Wang et al. 2003; Amstutz and Adrä 2006; Dijk et al. 2013; Picelli et al. 2018; Wang and Kang 2018; Liu et al. 2019; Bai and Zuo 2022) uses an auxiliary function to determine the amount of material at each point of the domain. The most common auxiliary function is the Heaviside function. This auxiliary function has the same role as the design variables of the SIMP approach. Although the use of a function in the definition of the material layout avoids the mesh dependence phenomena, the solution of the problem tends to be in general more complex. Finally, the isogeometric analysis (IGA) (Liu et al. 2018; Hassani et al. 2012; Qian 2013; Gao et al. 2020, 2022, 2023; Ghasemi et al. 2020; Hamdia et al. 2022) is also used in the definition of the material layout in the domain. The first work in the topology optimization field with the use of the isogeometric formulation was developed in Seo et al. (2010a). Since then, the isogeometric topology optimization problem has been implemented by using different approaches. The trimmed spline surfaces (Seo et al. 2010b; Kang and Youn 2016; Wang and Benson 2016a) uses spline surfaces and trimming curves to represent the outer and the inner boundaries of the geometric design models. For this purpose, the coordinates of control points of both elements are used as design variables. The density-based methods (Liu et al. 2018; Hassani et al. 2012; Qian 2013; Kumar and Parthasarathy 2011; Kazemi et al. 2016; Gao et al. 2019; Qiu et al. 2022; Zhuang et al. 2022; Wang et al. 2023) consider the same ideas that the topology optimization with the classical finite element formulations. In a similar way that the SIMP approach, a set of design variables are used to define the relative density in the domain. These design variables establish the value of the relative density in the control points of the mesh. NURBS, B-splines, or T-splines that define the influence of each control point in the domain are used to compute the value of the relative density at each point of the domain. The level set-based methods (Shojaee et al. 2012; Wang and Benson 2016b; Jahangiry and Tavakkoli 2017; Xu et al. 2019; Wu et al. 2020; Song et al. 2020) initially used the isogeometric analysis for the computation of the structural analysis. The parametrization of the level set function was made with the radial basis functions (RBF). However, it was later demonstrated that the isogeometric analysis can be also used to parametrize the level set functions. Finally, the moving morphable components (MMC) or moving morphable voids (MMV) methods (Hou et al. 2017; Xie et al. 2018, 2019, 2021; Gai et al. 2020; Zhang et al. 2019a) use the isogeometric analysis to construct the patches to represent the geometries of the structural components or the structural holes, respectively. In this paper, the topology optimization problem of compliant mechanisms consists in maximizing the output displacement, and the stress constraints approach in the problem is the overweight approach. The goal of this study is to introduce an IGA analysis and an overweight constraint in the design of compliant mechanism using topology optimization. This approach for the compliant mechanism problem is new and brings new insights to the scientific community.

The remainder of this paper is structured as follows. Section 2 describes the topology optimization problem with all its components used in the mechanisms design. Section 3 discusses the most important aspects of the numerical implementation. In Sect. 4, the topology optimization problem is applied to different numerical examples, a sensitivity analysis of the problem parameters is developed and the influence of the stress constraints is analyzed. Finally, conclusions are established in Section 5.

2 Mechanisms design

The topology optimization of compliant mechanisms (Sigmund 1997; Nishiwaki et al. 1998; Bruns and Tortorelli 2001; Kogiso et al. 2008; Li et al. 2011; De Leon et al. 2015; Tran et al. 2017; Zhu et al. 2020) is widely studied problems in the mechanical engineering field. Its objective is to design mechanisms that transfer an input solicitation to a desired mechanical output in an efficient way. On the one hand, the inputs to the compliant mechanisms tend to be prescribed forces, displacements, temperature changes, or electrical signals. In this case, only prescribed forces are considered. On the other hand, the outputs of the compliant mechanisms tend to be structural displacements. At the beginning of the design process, the specifications of the available design domain, the supports, the input and the output ports and their forces and kinematics, the strength requirements, and the manufacturing constraints, which may include length scales and manufacturing issues, have to be defined. As previously commented, the compliant mechanisms topology optimization problem stated in this paper consists in maximizing the structural displacements in the place where the output port is placed. Finally, although the design of non-linear compliant mechanisms is more interesting from an engineering point of view, in this paper, only linear compliant mechanisms are designed, for the safe of validating and assessing the quality of the proposed approaches.

2.1 Problem formulation

The conventional topology optimization problem of compliant mechanisms is formulated with only a volume constraint. An overweight constraint is introduced in this paper to control the stress level of the obtained solutions. The design problem is solved with and without the overweight constraint to analyze its influence on the solutions.

First, the conventional topology optimization problem of compliant mechanisms with the overweight constraint can be stated as

$$\begin{aligned} \begin{aligned} \underset{\varvec{\rho }}{\text {max}} \hspace{1 cm}&T(\varvec{\rho })=u_\text{out}(\varvec{\rho }) \\ \text {s.t.} \hspace{1.15 cm}&\textbf{K}(\varvec{\rho })\textbf{u}=\textbf{f} \\&V = V_{0} \\&g(\varvec{\rho }) \le \zeta \\&0 < \rho _\text{min} \le \rho \le 1 \, , \end{aligned} \end{aligned}$$

(1)

where $u_\text{out}$ is the displacement at the output port, $\textbf{K}$ is the structural stiffness matrix, $\textbf{u}$ is the structural displacement vector, $\textbf{f}$ is the applied load vector, V is the structural volume, $V_{0}$ is the objective structural volume, $g(\varvec{\rho })$ is the overweight constraint, $\zeta$ is the relaxation parameter of the overweight constraint, and $\rho _\text{min}$ is the minimum value that the relative density can take in the domain to avoid numerical issues related with the singularity of the structural stiffness matrix.

2.2 Material layout

Different methodologies have been used to define the material layout in the structural domain. Among them, two methodologies are considered to define the material distribution since they have been previously used by the authors for the same purpose. The methodologies considered are a uniform relative density per element based on finite element method (FEM) formulations and a material distribution defined with quadratic B-splines, based on isogeometric analysis (IGA) formulations.

First, a uniform relative density per element formulation has been used to define the material layout in the domain. This methodology has been widely used in the literature because of its simplicity since only one design variable is required for each element of the mesh. The relative density can be defined in any point of the domain as

$$\begin{aligned} \rho (\textbf{x}) = \rho _{e} \hspace{0.3 cm} \forall \textbf{x} \in \Upomega _{e} \hspace{0.3 cm} \text {where} \hspace{0.3 cm} e = 1, \ldots, N_{\text {el}} \, , \end{aligned}$$

(2)

where $\rho$ is the relative density of the domain, $\rho _{e}$ is the relative density at element e, $N_{\text {el}}$ is the number of elements of the finite element mesh, and $\textbf{x}$ is the point coordinates vector of the domain where the relative density is computed. In this case, the design variables of the problem are the values of the relative density at each element of the finite element mesh. The structural analysis is computed using quadratic finite elements to mitigate the appearance of checkerboard patterns in the solutions.

On the other hand, a material distribution defined with B-splines has also been used to define the material layout in the domain. In contrast to the previous methodology, the use of B-splines implies the use of the same B-splines in the computation of the structural analysis. The relative density can be defined in any point of the domain as

$$\begin{aligned} \rho (\textbf{x}) = \sum _{i=1}^{N_\text{CP}} \rho _{i} B_{i}(\textbf{x}) \, , \end{aligned}$$

(3)

where $\rho$ is the relative density of the domain, $\rho _{i}$ is the relative density in the control point i, $B_{i}$ is the B-spline that defines the influence of the control point i at each point, $N_\text{CP}$ is the number of control points considered to define the relative density in the domain, and $\textbf{x}$ is the point coordinates vector of the domain where the relative density is computed. In this case, the design variables of the problem are the value of the relative density at the control points. Quadratic B-splines have been considered in the definition of the material layout and in the computation of the structural analysis for IGA. Its formulation can be seen in the Appendix of this paper.

2.3 Volume constraint

An equality volume constraint has been considered in the formulation of the problem to establish the quantity of material that has to be used. This means that the structural volume is maintained constant during all the optimization processes. The structural volume can be computed as

$$\begin{aligned} V = \int _{\Upomega } \rho (\textbf{x}) \hspace{0.1cm} \text {d}\Upomega \, . \end{aligned}$$

(4)

This equation can be simplified for the different strategies of distributing the material in the domain. First, in the uniform relative density per element formulation, the relative density takes a constant value in each element of the mesh. This means that the structural volume can be computed as

$$\begin{aligned} V = \sum _{e=1}^{N_{\text {el}}} \rho _{e} V_{e} \, , \end{aligned}$$

(5)

where $V_{e}$ is the volume of element e. On the other hand, the structural volume for the material distribution defined with quadratic B-splines can be defined as

$$\begin{aligned} V = \sum _{i=1}^{N_\text{CP}} \rho _{i} \int _{\Upomega } B_{i}(\textbf{x}) \hspace{0.1cm} \text {d}\Upomega \, , \end{aligned}$$

(6)

where $B_{i} (x)$ is the B-spline that defines the influence of the control point i at each point of the domain.

2.4 Overweight approach

The overweight approach is an alternative method to the classical stress constraints aggregation functions used to formulate a global stress constraint and the Damage Approach. All these methods combine the effect of a certain number of local stress constraints in only one global stress constraint. Regarding the overweight approach, the violation of the local stress constraints is penalized through a material overweight in the parts of the domain where the stresses are higher than their maximum value. The overweight approach has been recently developed in Villalba et al. (2022) and, in this paper, it is used in the topology optimization problem to force the structural stresses to be under their maximum allowable value. As it was established in Villalba et al. (2022), the overweight constraint can be stated as

$$\begin{aligned} g(\varvec{\rho })=\frac{\tilde{W}}{W} - 1 \le \zeta \, , \end{aligned}$$

(7)

where $\tilde{W}$ is the structural weight of the overweight model and W is the structural weight of the original one. As stated before, $\zeta$ is a relaxation parameter of the overweight constraint to avoid having an equality constraint that would be active during all the optimization process. The structural weight of both models can be stated as

$$\begin{aligned} W=\int _{\Upomega } \rho \text {d} \Upomega \, , \hspace{0.3 cm} \text {and} \hspace{0.3 cm} \tilde{W}=\int _{\Upomega } \tilde{\rho } \text {d} \Upomega \, , \end{aligned}$$

(8)

where $\rho$ is the relative density of the original model and $\tilde{\rho }$ is the relative density of the overweight one. The relative density of the overweight model can be computed as

$$\begin{aligned} \tilde{\rho } = \rho _\text{min} + \beta (\rho - \rho _\text{min}) \, , \end{aligned}$$

(9)

where $\beta$ is the overweight function and $\rho _\text{min}$ is the minimum value that the relative density can take. The next step is to formulate the overweight function $\beta$ with a detailed explanation being found in Villalba et al. (2022). Therefore, the overweight function is formulated as

$$\begin{aligned} \beta = \left\{ \begin{array}{l} 1 \hspace{2.25 cm} \text {if} \hspace{0.2 cm} \frac{\sigma }{\sigma _\text{max}} \le (1 - \psi ) \, ; \\ e^{\frac{\delta \tau ^{2}}{\psi ^{2\psi /\tau }}(h+\psi )^{\frac{2\psi }{\tau }}} \hspace{0.3 cm} \text {if} \hspace{0.2 cm} (1-\psi )< \frac{\sigma }{\sigma _\text{max}} < 1 \, ; \\ e^{\delta (h+\tau )^{2}} \hspace{1.25 cm} \text {if} \hspace{0.2 cm} \frac{\sigma }{\sigma _\text{max}} \ge 1 \, , \end{array} \right. \end{aligned}$$

(10)

where $\delta$ is the exponential degradation coefficient, $\tau$ is the magnitude of the overweight function movement to the left, $\psi$ is the size of the definition range of the transition function and $h(\sigma ,\sigma _\text{max})$ is the local stress constraint. Finally, the local stress constraint that has to be introduced in the overweight function can be stated as

$$\begin{aligned} h(\sigma ,\sigma _\text{max}) = \frac{\sigma _\text{VM}}{\sigma _\text{max} \varphi } - 1 \le 0 \, , \end{aligned}$$

(11)

where $\sigma _\text{VM}$ is the equivalent von Mises stress, $\sigma _\text{max}$ is the maximum allowable stress and $\varphi$ is the stress relaxation coefficient that increases the value of the maximum allowable stress for intermediate values of the relative density. This stress relaxation coefficient depends on the value of the relative density as

$$\begin{aligned} \varphi = 1 - \varepsilon + \frac{\varepsilon }{\rho } \, , \end{aligned}$$

(12)

where $\varepsilon$ is the stress relaxation parameter. At this point, it is important to remark that an initial stress relaxation is not advisable to avoid removing parts of the structure that may appear again later if necessary.

2.5 Sensitivity analysis

The sensitivity analysis of all the terms of the topology optimization problem of compliant mechanisms introduced previously is developed below.

2.5.1 Objective function

The objective function does not directly depend on the design variables. In this case, it is necessary to compute as many structural analysis as structural displacements are used to define the objective function. The derivative of the objective function can be computed as

$$\begin{aligned} \frac{\partial T}{\partial \rho _{e}} = \frac{\partial u_\text{out}}{\partial \rho _{e}} \, , \end{aligned}$$

(13)

where the derivative of the output displacement $u_\text{out}$ with respect to the design variables can be computed as

$$\begin{aligned} \frac{\partial u_\text{out}}{\partial \rho _{e}} = -p \rho _{e}^{p-1} \varvec{\gamma }_{e}^{\text {T}} \textbf{k}_{e}^{0} \textbf{u}_{e} \, , \end{aligned}$$

(14)

where p is the penalty coefficient for intermediate values of relative density, and $\textbf{k}_{e}^{0}$ and $\textbf{u}_{e}$ are the stiffness matrix and the displacement vector, respectively, associated with element e. Finally, the multiplier $\varvec{\gamma }$ can be computed by solving the adjoint problem,

$$\begin{aligned} \textbf{K}(\varvec{\rho }) \varvec{\gamma } = {\textbf {G}}_\text{out} \, , \end{aligned}$$

(15)

where the load vector ${\textbf {G}}_\text{out}$ consists in a vector with a unitary value at the output degrees of freedom and zeros in the remaining ones.

2.5.2 Material distribution

The relative density function directly depends on the design variables. For this reason, it is possible to obtain the analytical expression of its derivatives. First, the derivative of the relative density with respect to the design variables in the uniform relative density per element formulation can be computed as

$$\begin{aligned} \left\{ \begin{aligned} \frac{\partial \rho (\textbf{x})}{\partial \rho _{e}}&= 1 \hspace{0.3 cm} \forall \textbf{x} \in \Upomega _{e} \, , \hspace{0.3 cm} \text {where} \hspace{0.3 cm} e = 1, \ldots, N_{\text {el}} \\ \frac{\partial \rho (\textbf{x})}{\partial \rho _{e}}&= 0 \hspace{0.3 cm} \forall \textbf{x} \notin \Upomega _{e} \, . \end{aligned} \right. \end{aligned}$$

(16)

On the other hand, the derivative of the relative density with respect to the design variables in the material distribution defined with quadratic B-splines formulation can be computed as

$$\begin{aligned} \frac{\partial \rho (\textbf{x})}{\partial \rho _{i}} = B_{i}(\textbf{x}) \, . \end{aligned}$$

(17)

2.5.3 Volume constraint

The structural volume also directly depends on the design variables and, in a similar way to the relative density, it is possible to attain the analytical expression of its sensitivities. First, the derivative of the structural volume with respect to the design variables in the uniform relative density per element formulation can be computed as

$$\begin{aligned} \frac{\partial V}{\partial \rho _{e}} = V_{e} \, . \end{aligned}$$

(18)

On the other hand, the derivative of the structural volume with respect to the design variables in the material layout defined with quadratic B-splines can be stated as

$$\begin{aligned} \frac{\partial V}{\partial \rho _{i}} = \int _{\Upomega } B_{i}(\textbf{x}) \text {d}\Upomega \, . \end{aligned}$$

(19)

2.5.4 Overweight constraint

The entire sensitivity analysis of the overweight constraint has been developed in Villalba et al. (2022). For this reason, only the sensitivity analysis of the formulas introduced in this paper is shown below. The sensitivity analysis of the overweight constraint has been also computed applying the Adjoint Variable Approach. It depends directly on the design variables and indirectly through the structural stresses used to state the local stress constraints. Therefore, the sensitivity analysis of the overweight constraint can be computed as

$$\begin{aligned} \frac{\text {d}g}{\text {d}\rho _{i}} = \varvec{\lambda }^{\text {T}} \left( \frac{\text {d}\textbf{f}}{\text {d}\rho _{i}} - \frac{\text {d}\textbf{K}}{\text {d}\rho _{i}} \varvec{\alpha } \right) + \frac{\partial g}{\partial \rho _{i}} \, , \end{aligned}$$

(20)

where $\varvec{\lambda }$ is the adjoint variable, $\textbf{K}$ is the structural stiffness matrix, $\textbf{f}$ is the vector of applied loads, and $\varvec{\alpha }$ is the nodal displacement vector. The adjoint variable can be computed as

$$\begin{aligned} \textbf{K}^{\text {T}} \varvec{\lambda } = \left( \frac{\partial g}{\partial \sigma _\text{VM}} \frac{\text {d}\sigma _\text{VM}}{\text {d}\varvec{\sigma }} \frac{\text {d}\varvec{\sigma }}{\text {d}\varvec{\alpha }} \right) ^{\text {T}} \, . \end{aligned}$$

(21)

Finally, the terms $\frac{\partial g}{\partial \sigma _\text{VM}}$ and $\frac{\partial g}{\partial \rho _{i}}$ can be computed using the chain rule as

$$\begin{aligned} \frac{\partial g}{\partial \sigma _\text{VM}} = \frac{\partial g}{\partial \tilde{W}} \frac{\partial \tilde{W}}{\partial \tilde{\rho _{i}}} \frac{\partial \tilde{\rho _{i}}}{\partial \beta _{s}} \frac{\partial \beta _{s}}{\partial \sigma _\text{VM}} \, , \end{aligned}$$

(22)

and

$$\begin{aligned} \frac{\partial g}{\partial \rho _{i}} = \frac{\partial g}{\partial W} \frac{\partial W}{\partial \rho _{i}} + \frac{\partial g}{\partial \tilde{W}} \frac{\partial \tilde{W}}{\partial \tilde{\rho _{i}}} \frac{\partial \tilde{\rho _{i}}}{\partial \rho _{i}} \, . \end{aligned}$$

(23)

3 Implementation

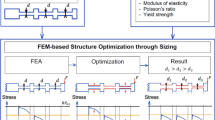
Figure 1 shows the flowchart of the algorithm developed. The numerical implementation has been made in Fortran and the topology optimization problem is solved with a gradient-based method, the Sequential Linear Programming (SLP). The optimization algorithm used by the SLP approach to solve the topology optimization problem is the Simplex algorithm. This algorithm is complemented with two gradient-based algorithms. The first one is used when the overweight constraint is not active and only considers the gradient of the objective function to compute the modifications of the design. By contrast, the second one is considered when the overweight constraint is strongly violated and only uses the gradient of the overweight constraint to compute the modification of the design. The main objective of this algorithm is to attain a feasible design. At this point, the values of all parameters introduced in the formulation are established in Table 1. Due to the high non-linearity of the problem, the convergence criteria considered in this paper consist in comparing the obtained solution during a certain number of iterations. When this solution does not experience important changes, the optimum has been attained.

Fig. 1

Algorithm flowchart

Table 1 Definition of parameters introduced in the formulation

4 Results

The formulation proposed in this paper is validated by studying two mechanism problems frequently analyzed in the topology optimization field. A sensitivity analysis of all the parameters related to the problem formulation is developed. The influence of the introduction of stress constraints is also analyzed. Both examples are two-dimensional mechanisms in plane stress. The initial design of all the examples consists in a uniform material distribution. The starting value of the relative density is equal to the volume constraint, satisfying the volume constraint. This initial design has been chosen since both approaches (FEM and IGA) can represent it properly by taking all the design variables a constant value. The initial design only has influence in the number of iterations required to solve the problem. All the examples have been computed on a Gen Intel(R) Core(TM) i9-12900K processor of 3.20 GHz with 64 GB of RAM. Any filtering technique, either in sensitivity or in density, has not been used in the attainment of the solutions of the problem. This decision was taken to avoid altering the results obtained with both approaches (FEM and IGA) in order to be able to make a more realistic comparison of these results.

4.1 Inverter mechanism

The first example corresponds to an inverter mechanism with null displacements in the upper and lower parts of the left edge (Sigmund 1997; Kogiso et al. 2008; De Leon et al. 2015). A horizontal force is applied on the input port (A) to maximize the horizontal displacement on the output port (B). Figure 2 shows the dimensions of the domain in mm and the position of the input and output ports. The domain of the structure is discretized with a regular mesh of $160 \times 80$ eight-node quadrilateral elements (or knot spans) in the finite element (and isogeometric analysis) formulations, respectively. The structural thickness is 0.1 mm and a point load (2 N) is applied on the input port. The properties of the material are: Young’s modulus $E = 100$ MPa, Poisson’s ratio $\nu = 0.3$ and limit yield stress $\hat{\sigma }_\text{lim} = 100$ MPa, to impede break. Finally, a volume constraint of $25\%$ of the total volume of the domain has been considered.

Fig. 2

Inverter mechanism: domain configuration and dimensions [mm]

Figures 3 and 4 show the optimal solution of the problem. Noting that only half of the structure has been computed due to the symmetry of the problem. The solution obtained with both material distributions have the same topology and both are similar to the solutions attained in the literature for the same topology optimization problem (Sigmund 1997; Kogiso et al. 2008; De Leon et al. 2015). However, the solution attained with the IGA formulation (Fig. 4) has more intermediate densities than the solution attained with the FEM formulation (Fig. 3). This circumstance is due to continuous way in the definition of the material layout when the IGA formulation is used, in contrast with the discontinuous way attained with the FEM formulation. On the one hand, the FEM formulations define the relative density in an elemental way since the design variables define the value of the relative density at each element of the mesh. This formulation allows the appearance of sharp transitions between adjacent elements with the minimum and the maximum value of the relative density, without the appearance of intermediate densities. By contrast, the IGA formulation defines the relative density in a nodal way as the design variables define the value of the relative density in a set of control points. The relative density at each point of the domain is computed by multiplying the design variables by the B-splines that define its influence. This strategy to define the material layout provides solutions with smooth transitions between the maximum and the minimum values of the relative density. Consequently, the intermediate densities appear in the areas placed between control points with the maximum and the minimum value of the relative density. Table 2 shows the value of the most important parameters of the problem: number of design variables, $n_\text{DV}$, maximum modification of the design variables between two consecutive iterations at the first iteration, ${\varDelta \rho _{i,0}}_\text{max}$, factor of reduction of this maximum modification, $F_\text{Red}$, and number of iterations computed for the same maximum modification of the design variables, $N_\text{It,Red}$. Table 3 shows the results obtained with the solution of the topology optimization problem. It has been required 1000 iterations to guarantee the convergence to the optimal solution with both material distributions. The output displacement obtained with both solutions is quite similar. However, the CPU time required by the IGA formulation is $58\%$ of the CPU time required by the FEM formulation to solve the same problem. Finally, Table 4 shows the distribution of the computing time per algorithm of an average iteration. The structural analysis is the critical part in terms of CPU time in case of the finite element formulation, since it uses $77\%$ of the total CPU time used to solve the problem. This circumstance is related with the number of nodes required to compute the structural analysis. Considering that the finite element analysis uses three times as many nodes as the isogeometric analysis. By contrast, the critical part of the isogeometric formulation is the sensitivity analysis. However, it only uses $50\%$ of the CPU time required by the solution of the topology optimization problem and, in this case, the structural analysis uses $32\%$ of the CPU time. This circumstance is related with the number of design variables that influence in the value of the relative density at each knot span. In both material distributions, the structural analysis and the sensitivity analysis use at least $80\%$ of the required total CPU time.

Fig. 3

Inverter mechanism: optimal solution for the finite element method approach

Fig. 4

Inverter mechanism: optimal solution for the isogeometric analysis approach

Table 2 Inverter mechanism: general parameters of the problem for both FEM and IGA discretization

Table 3 Inverter mechanism: results

Table 4 Inverter mechanism: distribution of CPU time per iteration

4.2 Gripper mechanism

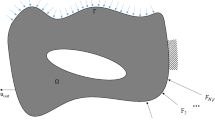
The second example corresponds to a gripper mechanism with null displacements on the upper and the lower parts of the left edge (Sigmund 1997; Kogiso et al. 2008; De Leon et al. 2015). A horizontal force is applied on the input port to maximize the vertical displacements on the output ports. Figure 5 shows the geometry and the dimensions of the domain and the position of the input and output ports. The domain of the structure is discretized with a regular mesh of 10,752 eight-node quadrilateral elements or knot spans for the finite element and isogeometric analysis formulations, respectively. The structural thickness is 1.5 mm and a point load (100 N) is applied in the input port. The properties of the material considered in the solution of the problem are as follows: Young’s modulus $E = 73$ GPa, Poisson’s ratio $\nu = 0.35$ , and yield stress $\hat{\sigma }_\text{max} = 140$ MPa. Finally, a volume constraint of $30\%$ of the total volume of the domain has been considered for the topology optimization problem.

Fig. 5

Gripper mechanism: domain dimensions [mm]

Figures 6 and 7 show the optimal solution for the problem (only one half of the structure has to be computed due to the symmetry of the problem). The solutions obtained with both material distributions are topologically equivalents and similar to the solutions attained in the literature (Sigmund 1997; Kogiso et al. 2008; De Leon et al. 2015). The results with both approaches (FEM and IGA) are affected by the mesh dependency phenomena, as both formulations require to divide the domain in a certain number of elements in case of FEM-approach or knot spans in case of IGA-approach. The solutions obtained with the IGA formulations presents two advantages with respect to the solutions attained with the FEM formulations. On the one hand, the structural borders defined in the IGA solutions are not limited to the borders of the knot spans and they can be easily replaced by straight line segments. By contrast, the structural borders defined in the FEM solutions in a full-void approach are limited to the borders of the elements of the mesh. This means that the structural borders are zigzag in both examples since regular meshes has been considered to discretize the domain. On the other hand, the IGA formulations avoid the appearance of checkerboard patterns in the solutions attained because of the continuity in the definition of the relative density that depends on several design variables in the entire domain in contrast with the FEM formulations where the relative density only depends on one design variable at each element of the mesh. Table 5 shows the values of the most important parameters of the problem. Table 6 shows the results obtained. 1000 iterations were required to guarantee the convergence to the optimal solution with both material distributions. The output displacement obtained with both solutions is quite similar. However, the CPU time required by the IGA formulation is $46\%$ of the CPU time required by the FEM formulation to solve the same problem. Table 7 shows the distribution of the computing time per algorithm of an average iteration. The structural analysis is the critical part in terms of CPU time in case of the finite element formulation, since it uses $84\%$ of the CPU time required to solve the problem. By contrast, the critical part with the isogeometric formulation is the sensitivity analysis using $44\%$ of the CPU time required by the solution of the topology optimization problem. Moreover, in this case, the structural analysis uses $38\%$ of the CPU time.

Fig. 6

Gripper mechanism: optimal solution for finite element method approach

Fig. 7

Gripper mechanism: optimal solution for isogeometric analysis approach

Table 5 Gripper mechanism: general parameters of the problem

Table 6 Gripper mechanism: results

Table 7 Gripper mechanism: distribution of CPU time per iteration

4.3 Sensitivity analysis

A sensitivity analysis for the parameters defined in the formulation of the problem is developed in this section. For this purpose, an individual modification of each parameter is established. The parameters considered in this sensitivity analysis are as follows: structural load, volume fraction, penalization factor, Poisson’s coefficient, Young’s modulus, input spring stiffness, output spring stiffness, and both spring stiffnesses simultaneously. The overweight constraint is not activated since the structural stresses could influence the obtained results.

• Structural load Figure 8 shows that the topology of the solutions obtained when the structural load value is modified does not change. This circumstance is due to the fact that the overweight constraint has not been considered in this sensitivity analysis. However, the value of the output displacement, as it can be seen in Table 8, changes in the same way and in the same magnitude that the value of the structural load.

• Volume constraint Figure 9 shows that the base topology of the solutions obtained when the volume constraint value is modified does not change. The difference among all the solutions is the thickness of the structural bars. However, the value of the output displacement, as it can be seen in Table 9, is modified in the same way than the value of the volume constraint.

• Penalization coefficient Figure 10 shows that the general topology of the solutions obtained when the penalization coefficient of intermediate values of relative density value is modified only changes when there is no penalization, i.e., when the coefficient is equal to 1. In this case, an important part of the structural domain takes intermediate values of the relative density. The value of the output displacement, as seen in Table 10, does not importantly change when the penalization coefficient value is modified.

• Poisson’s coefficient Figure 11 shows that the topology of the solutions obtained when the Poisson’s coefficient value is modified does not change. In the same way that with the penalization coefficient, the value of the output displacement, as it can be seen in Table 11, is not importantly modified when the Poisson’s coefficient value is changed.

• Young’s modulus Figure 12 shows that the topology of the solutions obtained when the Young’s modulus value is modified experiments important changes as its value is increased. This circumstance is related to the ratio between the Young’s modulus and the spring stiffnesses. When both parameters are unbalanced, the material tends to concentrate in the central part of the domain and to disappear from the proximity of the supports and the input and output ports. Regarding the value of the output displacement, as it can be seen in Table 12, there are important differences in its value when the structural topology does not experiment changes, but, when the structural topology is modified, due to the unbalance between the material and spring stiffnesses the value of the output displacement tends to be stable.

• Input spring stiffness Figure 13 shows that the solutions obtained when the input spring stiffness value is modified show important topology changes as its value is reduced. Since only the input spring stiffness has been modified, the material tends to disappear from the proximity of the input port. Regarding the value of the output displacement, as it can be seen in Table 13, it is modified in the opposite way that the value of the input spring stiffness.

• Output spring stiffness Figure 14 shows that the topology of the solutions obtained when the output spring stiffness value is modified experiments important changes as the its value is reduced. As only the output spring stiffness has been modified the material tends to disappear from the proximity of the output port. Regarding the value of the output displacement, as it can be seen in Table 14, it is modified in the opposite way that the value of the output spring stiffness.

• Both springs stiffnesses Figure 15 shows that the topology of the solutions obtained when the both spring stiffness values are modified experiments important changes as their value is reduced. Since both spring stiffnesses are modified, the material tends to concentrate in the central part of the domain and to disappear from the proximity of the structural support and the input and output ports. Regarding the value of the output displacement, as it can be seen in Table 15, it is modified in the opposite way that the value of both spring stiffnesses.

Fig. 8

Sensitivity analysis of the structural load

Table 8 Sensitivity analysis of the structural load

Fig. 9

Sensitivity analysis of the volume constraint

Table 9 Sensitivity analysis of the volume constraint

Fig. 10

Sensitivity analysis of the penalization coefficient

Table 10 Sensitivity analysis of the penalization coefficient

Fig. 11

Sensitivity analysis of Poisson’s coefficient

Table 11 Sensitivity analysis of Poisson’s coefficient

Fig. 12

Sensitivity analysis of the Young’s modulus

Table 12 Sensitivity analysis of the Young’s modulus

Fig. 13

Sensitivity analysis of input spring stiffness

Table 13 Sensitivity analysis of input spring stiffness

Fig. 14

Sensitivity analysis of output spring stiffness

Table 14 Sensitivity analysis of output spring stiffness

Fig. 15

Sensitivity analysis of both spring stiffnesses

Table 15 Sensitivity analysis of both spring stiffnesses

Fig. 16

A dimensional comparison of the sensitivity analysis for the involved parameters

Figure 16 shows the general behavior of the objective function with respect to the parameters analyzed previously in the sensitivity analysis. Numerical values of both axes have been omitted, since these depend on the example solved and are different for each parameter. The penalization coefficient and the Poisson’s coefficient do not have influence over the value of the output displacement and the relationship between the structural load and the output displacement is linear. The volume constraint has a little influence over the value of the output displacement. The value of the output displacement tends to be constant for high values of the Young’s modulus, this coincides with the modification of the structural topology. However, when the structural topology does not change, the influence of the Young’s modulus over the output displacement value is important. Finally, and in the same way that the Young’s modulus, the input spring stiffness, the output spring stiffness and both spring stiffness have little influence over the value of the output displacement when these take values considerably higher. In this case, the limit situation is equivalent to a fixed support, i.e., null displacements. However, in all these cases, when the value of the spring stiffness is reduced, the influence over the output displacement is considerably important, since the limit situation in this case means the absence of springs. These analyses can be corroborated by the sensitivity equations (13, 14 and 15).

4.4 Stress constraints analysis

In this section, the influence of stress constraints in the topology optimization problem of compliant mechanisms is analyzed. Firstly, it is important to remark that the attainment of realistic solutions can be guaranteed if stress constraints are considered in the formulation of the problem. Otherwise, the attained solutions can suffer issues related to stability or integrity due to excessive stresses. The analysis of stress constraints in the topology optimization problem should be done similarly to the previous analysis modifying the maximum allowable stress. This has been possible since a linear structural analysis has been considered in the formulation of the problem. The reason to choose the maximum allowable stress instead of the structural load is the variation of the value of the output displacement, the objective function, when the structural load is modified as it can be seen in Table 8. Figure 17 shows the variation of the optimal solution obtained for different values of the maximum starting stress. The distribution of the material tends to be more diffuse as the value of the maximum initial stress is increased. This circumstance is related with the violation of the overweight constraint and tends to be more relevant in the isogeometric solutions due to the continuous definition of the relative density. However, the global topology of all solutions tends to be quite similar despite of this diffusivity. The two/three first figures at the top, depending on the case, are the same since the overweight constraint is not active in any moment of the optimization process. However, the rest of the figures are affected by the activation of the overweight constraint which produces in some cases the attainment of infeasible solutions in terms of manufacture. Table 16 shows the value of the output displacement of each optimal solution represented in Fig. 17. In Table 16, it is possible to confirm that some of the solutions, as it was previously commented, are not influenced by the overweight constraint as the value of the output displacement is the same. Moreover, it is possible to see in Table 16 that the value of the output displacement is reduced in the same way that the value of the maximum starting stress is increased. This circumstance is important since better performances of the mechanism are obtained when the stresses are not near to their maximum allowable value.

Figures 18 and 19 show the evolution of the objective function and the overweight constraint during the optimization process for both problems, inverter and gripper mechanisms. Regarding the objective function, it is possible to observe, in the left part of all the figures that its value coincides until the overweight constraint is active for the first time. On the other hand, and with respect to the overweight constraint, dramatic variations of its value appear in the first iterations of the optimization process. These dramatic variations are related with the high non-linearity of the overweight constraint, the maximum modification of the design variables between two consecutive iterations, and the use of a gradient-based method as optimization algorithm. However, it is possible to observe in all the figures that the structural stresses are controlled since its value in the right part of all the figures tends to be constant. Finally, it is possible to observe that the value of the objective function is increased or maintained constant when the overweight constraint is violated. When the structural stresses are under their maximum allowable value or when the overweight constraint is active, but not violated, the value of the objective function is reduced.

To conclude, it has been demonstrated the importance of including stress constraints in the formulation of the topology optimization problem of compliant mechanisms. There are two main reasons: (i) to guarantee that the mechanisms are able to do its task without suffering from stability or integrity problems and (ii) to guarantee that the designed mechanism is making its best performance. The latter means that the stress constraints are not active in any moment of the optimization process since the simple activation of only one local stress constraint reduces the magnitude of the objective function.

Fig. 17

Stress constraints analysis

Table 16 Stress constraints analysis

Fig. 18

Inverter mechanism. Stress constraint analysis

Fig. 19

Gripper mechanism. Stress constraint analysis

5 Conclusions

This paper introduces an isogeometric formulation together with an overweight constraint in the solution of the topology optimization problem of compliant mechanisms. The isogeometric formulation uses quadratic B-splines to define the material layout and to compute the structural analysis. The overweight constraint is used to introduce stress constraints in the topology optimization problem in an efficient way. However, a classical finite element formulation with serendipity quadratic finite elements is also used to define the material layout and to solve the structural analysis in order to check the effectiveness of the overweight constraint separately. Moreover, a sensitivity analysis of all the parameters used to define the topology optimization problem and an analysis of the influence that the introduction of stress constraints has in the obtained solutions are included in this paper. The use of the isogeometric formulation in the solution of the conventional topology optimization problem of compliant mechanisms has been demonstrated to be a valid alternative to the classical finite element formulations. Firstly, the solutions obtained for both problems were equivalent in terms of topology. One of the advantages of the isogeometric formulation with quadratic B-splines is the CPU time required to solve the problem since it means a reduction of the 40–60% of the CPU time required to solve the same problem with serendipity quadratic finite elements. This reduction of CPU time with the isogeometric formulation is related with the size of global stiffness matrix used to solve the structural analysis, i.e., with the number of points required to compute the structural analysis. However, the isogeometric formulation provides other advantages with respect to the finite element formulations. These advantages are related with the smoothness of the structural borders and the non-appearance of checkerboard patterns in the solutions. Both advantages are consequence of the continuity in the definition of the relative density that depends on several design variables in the entire domain in contrast with the FEM formulations where the relative density only depends on one design variable at each element of the mesh.

Regarding the sensitivity analysis, the parameters can be classified in three categories. Firstly, there are parameters as the penalization coefficient used to attain full/void solutions and the Poisson’s coefficient of the chosen material that do not have any influence in the solutions obtained, neither in the value of the objective function nor in the topology of the solution. Secondly, there are parameters as the structural load and the volume constraint that only have influence in the value of the objective function. In case of the former the solution obtained is the same as well as the topology of the solutions obtained with the latter, in which the only difference is the bars thickness. Finally, the parameters with the biggest influence in the solutions obtained are the Young’s modulus of the material and the spring stiffness as a set or individually. However, it has been demonstrated that the variations in the structural topology and the value of the objective function is related with the ratio between the Young’s modulus and the springs stiffnesses.

It has also been demonstrated that stress constraints have to be considered in the topology optimization problem of compliant mechanisms to guarantee that the solutions obtained are realistic. Although the main objective of the stress constraints is to guarantee that the mechanisms are able to develop its task without suffering from integrity or stability problems derived from excessive structural stresses, it has been also demonstrated that the best performance of the mechanisms in terms of the objective function (output displacement) is obtained when the stress constraints are not active in any case during the optimization process. For this reason, the introduction of stress constraints in the topology optimization problem of compliant mechanisms is not only used as a way to guarantee that the stresses are lower than their maximum, but also to guarantee that the mechanism is performing at its best performance.

In conclusion, the use of the isogeometric formulation proposed in this paper reports important benefits from a computation point of view in the topology optimization problem of compliant mechanisms. The CPU time required to obtain the solution of the problem has been reduced at least a 40% with respect to the CPU time required for the classical quadratic finite element formulation. This reduction of CPU time makes possible to attain solutions with high spatial definition since a large number of design variables can be used. Moreover, the isogeometric formulation provides solutions with smoother structural borders and without checkerboard patterns. On the other hand, the introduction of stress constraints in the topology optimization problem of compliant mechanisms has an important role not only to guarantee that the structural stresses are lower than their maximum allowable value but also to ensure that the obtained mechanism is attaining its best performance in terms of the objective function. The latter can be guaranteed if the stress constraints are not active in all the optimization process; otherwise, a change of the material considered in the optimization problem is required to attain it.

Appendix: isogeometric formulation

The isogeometric formulation considered in this paper to define the material layout and to compute the structural analysis makes use of quadratic B-splines. The use of B-splines makes necessary to divide the structural domain into rectangular or square regions that are known as patches. Each patch is divided in a set of knot spans in a similar way that in the definition of a regular mesh of FEM. On the other hand, it is required a certain compatibility between two adjacent patches. The edge of contact between two adjacent patches has to be defined by an entire edge of each patch. This edge of contact has to be divided in the same number of knot spans in both patches. The quadratic B-splines used in the formulation of this paper to solve two-dimensional problems can be stated as

$$\begin{aligned} B_{i}(\textbf{x}) = B_{i_{x}}(x) B_{i_{y}}(y) \end{aligned}$$

(24)

where $B_{i_{x}}$ and $B_{i_{y}}$ are the quadratic B-splines in the directions x and y of the control point i whose relative position in the patch is defined by $i_{x}$ and $i_{y}$. The quadratic B-splines in any direction are defined as

• B-spline 1

  • Knot Span 1

    $$\begin{aligned} B_{1}(x) = n^{2} \left( \frac{1}{n} - \frac{x}{l_{x}} \right) ^{2} \end{aligned}$$

    (25)

  • Rest of Knot Spans

    $$\begin{aligned} B_{1}(x) = 0 \end{aligned}$$

    (26)

• B-spline 2

  • Knot Span 1

    $$\begin{aligned} B_{2}(x) = \frac{n^{2}}{2} \left( \frac{4 x}{n l_{x}} - \frac{3 x^{2}}{l_{x}^{2}} \right) \end{aligned}$$

    (27)

  • Knot Span 2

    $$\begin{aligned} B_{2}(x) = \frac{n^{2}}{2} \left( \frac{2}{n} - \frac{x}{l_{x}} \right) ^{2} \end{aligned}$$

    (28)

  • Rest of Knot Spans

    $$\begin{aligned} B_{2}(x) = 0 \end{aligned}$$

    (29)

• B-spline i (i = 3,..., n)

  • Knot Span i − 2

    $$\begin{aligned} B_{i}(x)= \frac{n^{2}}{2} \left( \frac{x}{l_{x}} - \frac{i-3}{n} \right) ^{2} \end{aligned}$$

    (30)

  • Knot Span i − 1

    $$\begin{aligned} B_{i}(x)= \frac{n^{2}}{2} \left( -\frac{2x^{2}}{l_{x}^{2}} + \frac{x(4i - 6)}{n l_{x}} - \frac{2 i^{2} - 6i + 3}{n^{2}} \right) \end{aligned}$$

    (31)

  • Knot Span i

    $$\begin{aligned} B_{i}(x)= \frac{n^{2}}{2} \left( \frac{i}{n} - \frac{x}{l_{x}} \right) ^{2} \end{aligned}$$

    (32)

  • Rest of Knot Spans

    $$\begin{aligned} B_{i}(x) = 0 \end{aligned}$$

    (33)

• B-spline n $+$ 1

  • Knot Span n − 1

    $$\begin{aligned} B_{n+1}(x) = \frac{n^{2}}{2} \left( \frac{x}{l_{x}} - \frac{n-2}{n}\right) ^{2} \end{aligned}$$

    (34)

  • Knot Span n

    $$\begin{aligned} B_{n+1}(x) = \frac{n^{2}}{2} \left( \frac{4}{n} - 3 + \frac{x}{l_{x}} \left( 6 - \frac{4}{n} \right) - \frac{3 x^{2}}{l_{x}^{2}}\right) \end{aligned}$$

    (35)

  • Rest of Knot Spans

    $$\begin{aligned} B_{n+1}(x) = 0 \end{aligned}$$

    (36)

• B-spline n $+$ 2

  • Knot Span n

    $$\begin{aligned} B_{n+2}(x) = n^{2} \left( \frac{x}{l_{x}} - \frac{n-1}{n} \right) ^{2} \end{aligned}$$

    (37)

  • Rest of Knot Spans

    $$\begin{aligned} B_{n+2}(x) = 0 \end{aligned}$$

    (38)

Fig. 20

Quadratic B-splines

where n is the number of knot spans in this direction, x is the local coordinate of the point considered in this direction, and $l_{x}$ is the dimension of the patch in this direction. A graphic representation of these quadratic B-splines can be seen in Figure 20. More details about the basis of the isogeometric analysis considered in this paper can be found in Villalba (2021).