Skip to main content
SpringerLink
Log in

An uncertainty propagation method for multimodal distributions through unimodal decomposition strategy

  • Research Paper
  • Published:
Structural and Multidisciplinary Optimization Aims and scope Submit manuscript

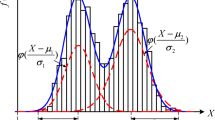
Abstract

In practical engineering problems, random variables may follow a multimodal distribution. Traditional uncertainty propagation methods may yield poor effectiveness for multimodal distribution problems. In this paper, an uncertainty propagation method is proposed for multimodal distributions via a unimodal decomposition strategy. First, a Gaussian mixture model is used to build the probability density function of multimodal random variables. Second, a set of unimodal elements is constructed based on the decomposed multimodal random variables. In this way, it avoids computing higher-order statistical moments and the first 4th-order statistical moments can satisfy the accuracy requirements. Third, the probability density function of the response function in each element is computed using an arbitrary polynomial chaos expansion and the maximum entropy method. Finally, the probability density function of the response function in the complete probability space can be obtained by accumulating the probability density functions of the response functions in the elements. Three examples are investigated to validate the effectiveness of the proposed method.

Graphical abstract

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18

Similar content being viewed by others

References

  • Ahlfeld R, Belkouchi B, Montomoli F (2016) SAMBA: sparse approximation of moment-based arbitrary polynomial chaos. J Comput Phys 320:1–16

    MathSciNet  MATH  Google Scholar 

  • Asquith WH (2007) L-moments and TL-moments of the generalized lambda distribution. Comput Stat Data Anal 51(9):4484–4496

    MathSciNet  MATH  Google Scholar 

  • Au S-K, Beck JL (2001) Estimation of small failure probabilities in high dimensions by subset simulation. Probab Eng Mech 16(4):263–277

    Google Scholar 

  • Bai S, Kang Z (2021) Robust topology optimization for structures under bounded random loads and material uncertainties. Comput Struct 252:106569

    Google Scholar 

  • Bhattacharyya B (2020) Global sensitivity analysis: a Bayesian learning based polynomial chaos approach. J Comput Phys 415:109539

    MathSciNet  MATH  Google Scholar 

  • Bhattacharyya B (2022) Uncertainty quantification and reliability analysis by an adaptive sparse Bayesian inference based PCE model. Eng Comput 38(2):1437–1458

    Google Scholar 

  • Bhattacharyya B (2023) On the use of sparse Bayesian learning-based polynomial chaos expansion for global reliability sensitivity analysis. J Comput Appl Math 420:114819

    MathSciNet  MATH  Google Scholar 

  • Bourinet JM, Deheeger F, Lemaire M (2011) Assessing small failure probabilities by combined subset simulation and support vector machines. Struct Saf 33(6):343–353

    Google Scholar 

  • Breitung K (1984) Asymptotic approximations for multinormal integrals. J Eng Mech 110(3):357–366

    MATH  Google Scholar 

  • Castillo-Barnes D, Martinez-Murcia FJ, Ramírez J (2020) Expectation-maximization algorithm for finite mixture of α-stable distributions. Neurocomputing 413:210–216

    Google Scholar 

  • Du X (2007) Saddlepoint approximation for sequential optimization and reliability analysis. J Mechan Design. https://doi.org/10.1115/1.2717225

    Article  Google Scholar 

  • Fan W, Wei J, Ang AHS (2016) Adaptive estimation of statistical moments of the responses of random systems. Probab Eng Mech 43:50–67

    Google Scholar 

  • Figueiredo MAT, Jain AK (2002) Unsupervised learning of finite mixture models. IEEE Trans Pattern Anal Mach Intell 24(3):381–396

    Google Scholar 

  • Grigoriu M, Probabilistic methods in structural engineering. In: G Augusti, A Baratta and F Casciati, Chapman and Hall - Methuen Inc., New York, 1984, pp. 556. Structural Safety. 4(3) (1987) 251–252.

  • Guo L, Liu Y, Zhou T (2019) Data-driven polynomial chaos expansions: a weighted least-square approximation. J Comput Phys 381:129–145

    MathSciNet  MATH  Google Scholar 

  • Hu Z, Du X (2018) Reliability Methods for Bimodal Distribution With First-Order Approximation1. ASCE-ASME J Risk and Uncert in Engrg Sys Part B Mech Engrg. https://doi.org/10.1115/1.4040000

    Article  Google Scholar 

  • Hu ZL, Mansour R, Olsson M (2021) Second-order reliability methods: a review and comparative study. Struct Multidisc Optim 64(6):3233–3263

    MathSciNet  Google Scholar 

  • Huang ZL, Jiang C, Zhou YS (2016) An incremental shifting vector approach for reliability-based design optimization. Struct Multidisc Optim 53(3):523–543

    MathSciNet  Google Scholar 

  • Jacquelin E, Baldanzini N, Bhattacharyya B (2019) Random dynamical system in time domain: a POD-PC model. Mech Syst Signal Process 133:106251

    Google Scholar 

  • Li L, Chen G, Fang M (2021) Reliability analysis of structures with multimodal distributions based on direct probability integral method. Reliab Eng Syst Saf 215:107885

    Google Scholar 

  • Liu Y, Zhao J, Qu Z (2021a) Structural reliability assessment based on subjective uncertainty. Int J Comput Methods 18(10):2150046

    MathSciNet  MATH  Google Scholar 

  • Liu Z, Yang M, Cheng J (2021b) A new stochastic isogeometric analysis method based on reduced basis vectors for engineering structures with random field uncertainties. Appl Math Model 89:966–990

    MathSciNet  MATH  Google Scholar 

  • Livesey AK, Brochon JC (1987) Analyzing the distribution of decay constants in pulse-fluorimetry using the maximum entropy method. Biophys J 52(5):693–706

    Google Scholar 

  • Marseguerra M, Zio E, Devooght J (1998) A concept paper on dynamic reliability via Monte Carlo simulation. Math Comput Simul 47(2):371–382

    Google Scholar 

  • Mori Y, Kato T (2003) Multinormal integrals by importance sampling for series system reliability. Struct Saf 25(4):363–378

    Google Scholar 

  • Ni YQ, Ye XW, Ko JM (2010) Monitoring-based fatigue reliability assessment of steel bridges: analytical model and application. J Struct Eng 136(12):1563–1573

    Google Scholar 

  • Nobile F, Tempone R, Webster CG (2008) A sparse grid stochastic collocation method for partial differential equations with random input data. SIAM J Numer Anal 46(5):2309–2345

    MathSciNet  MATH  Google Scholar 

  • Nouy A (2010) Identification of multi-modal random variables through mixtures of polynomial chaos expansions. CR Mec 338(12):698–703

    MATH  Google Scholar 

  • Oladyshkin S, Nowak W (2012) Data-driven uncertainty quantification using the arbitrary polynomial chaos expansion. Reliab Eng Syst Saf 106:179–190

    Google Scholar 

  • Pearson K, IX. Mathematical contributions to the theory of evolution.—XIX. Second supplement to a memoir on skew variation. Philosophical Transactions of the Royal Society of London. Series A, Containing Papers of a Mathematical or Physical Character. 216(538–548) (1916) 429–457.

  • Qiao X, Wang B, Fang X (2021) Non-probabilistic reliability bounds for series structural systems. Int J Comput Methods 18(09):2150038

    MathSciNet  MATH  Google Scholar 

  • Rahman S, Xu H (2004) A univariate dimension-reduction method for multi-dimensional integration in stochastic mechanics. Probab Eng Mech 19(4):393–408

    Google Scholar 

  • Sachdeva SK, Nair PB, Keane AJ (2006) Hybridization of stochastic reduced basis methods with polynomial chaos expansions. Probab Eng Mech 21(2):182–192

    Google Scholar 

  • Shao Q, Younes A, Fahs M (2017) Bayesian sparse polynomial chaos expansion for global sensitivity analysis. Comput Methods Appl Mech Eng 318:474–496

    MathSciNet  MATH  Google Scholar 

  • Smolyak SA (1963) Quadrature and interpolation formulas for tensor products of certain classes of functions. Soviet Math Dokl 4:240–243

    MATH  Google Scholar 

  • Sobczyk K, Trcebicki J (1999) Approximate probability distributions for stochastic systems: maximum entropy method. Comput Methods Appl Mech Eng 168(1):91–111

    MathSciNet  MATH  Google Scholar 

  • Tang JC, Fu CM, Mi CJ (2022) An interval sequential linear programming for nonlinear robust optimization problems. Appl Math Model 107:256–274

    MathSciNet  MATH  Google Scholar 

  • Tian WY, Chen WW, Wang ZH (2022) An extended SORA method for hybrid reliability-based design optimization. Int J Comput Methods. https://doi.org/10.1142/S0219876221500742

    Article  MathSciNet  MATH  Google Scholar 

  • Trenkler G (1994) Continuous univariate distributions: N.L. Johnson, S. Kotz and N. Balakrishnan (2nd ed., Vol. 1). New York: John Wiley. Computational statistics & data analysis. 21(1) (1996) 119

  • Valverde G, Saric AT, Terzija V (2012) Probabilistic load flow with non-Gaussian correlated random variables using Gaussian mixture models. IET Gener Transm Distrib 6(7):701–709

    Google Scholar 

  • Wang R, Luo Y (2019) Efficient strategy for reliability-based optimization design of multidisciplinary coupled system with interval parameters. Appl Math Model 75:349–370

    Google Scholar 

  • Wu SQ, Law SS (2012) Statistical moving load identification including uncertainty. Probab Eng Mech 29:70–78

    Google Scholar 

  • Wu J, Zhang D, Jiang C (2021) On reliability analysis method through rotational sparse grid nodes. Mech Syst Signal Process 147:107106

    Google Scholar 

  • Xu H, Rahman S (2004) A generalized dimension-reduction method for multidimensional integration in stochastic mechanics. Int J Numer Meth Eng 61(12):1992–2019

    MATH  Google Scholar 

  • Yang M, Zhang D, Cheng C (2021) Reliability-based design optimization for RV reducer with experimental constraint. Struct Multidisc Optim 63(4):2047–2064

    MathSciNet  Google Scholar 

  • Zeng YC, Song DL, Zhang WH (2020) Stochastic failure process of railway vehicle dampers and the effects on suspension and vehicle dynamics. Vehicle Syst Dyn. https://doi.org/10.1080/00423114.2019.1711136

    Article  Google Scholar 

  • Zhang Z, Jiang C, Han X (2019) A high-precision probabilistic uncertainty propagation method for problems involving multimodal distributions. Mech Syst Signal Process 126:21–41

    Google Scholar 

  • Zhao Q, Guo J, Hong J (2019) Closed-form error space calculation for parallel/hybrid manipulators considering joint clearance, input uncertainty, and manufacturing imperfection. Mech Mach Theory 142:103608

    Google Scholar 

Download references

Acknowledgements

The research presented in this paper was conducted with the support of The National Natural Science Foundation of China (Grant No. 52235005), Fundamental Research Program of China (JCKY2020110C105), The National Science Fund for Distinguished Young Scholars (Grant No. 51725502), and The National Natural Science Foundation of China (Grant No. 52105253).

Author information

Authors and Affiliations

  1. State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body, College of Mechanical and Vehicle Engineering, Hunan University, Changsha, China

    Boqun Xie, Chao Jiang, Zhe Zhang, Jing Zheng & Jinwu Li

Authors
  1. Boqun Xie
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Chao Jiang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Zhe Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Jing Zheng
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Jinwu Li
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Chao Jiang.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Replication of Results

The results reported in this research were performed in MATLAB. The authors will help interested researchers reproduce the results given in the article. Interested readers can contact the corresponding author for basic codes of this research with reasonable requests.

Additional information

Responsible Editor: Yoojeong Noh

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Xie, B., Jiang, C., Zhang, Z. et al. An uncertainty propagation method for multimodal distributions through unimodal decomposition strategy. Struct Multidisc Optim 66, 141 (2023). https://doi.org/10.1007/s00158-023-03591-z

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s00158-023-03591-z

Keywords

Search

Navigation