Robust optimal design of strain-gauge-based force sensors using moving morphable components method: enhanced sensitivity and reduced cross-interference

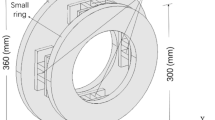
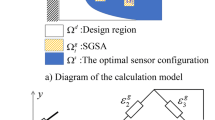
Abstract

Designing force sensors with superior performance is always a challenging topic in the industry as well as in academia. This paper employs the moving morphable components method in order to design strain-gauge-based force sensors with high sensitivity and low cross-interference. The function of the Wheatstone bridge (half-bridge) is taken into account in the automatic design implementation to make it practically more feasible. Compared with our previous study on sensor design with only the high-sensitivity constraint, the further consideration of low cross-interference leads to a strict situation where the numerical iteration is hard to converge. To overcome this difficulty, three strategies are proposed, including a new description of the sensing areas, the modification of strain-gauge output constraints, and the iterative scheme with gradually shrinking bounds. Numerical examples demonstrate that these strategies perform very well and can ensure a robust iteration. Furthermore, the developed robust implementation is quite generic, which may be adopted in optimization problems with complex and strict constraints.

Appendices

Appendix 1. Effects of initial parameters on optimization

Four different adjacent-bridge cases (with R^dt = 0.02) are considered here to show the effects of the initial parameters. Case A is the same as that shown in Fig. 8a, with an initially symmetric distribution of the SAs with respect to y = 0.5. Case B has a different initial location pattern of the SAs. The indexes of Case A and Case B show that the current calculation framework is very robust when handling the different initial locations of SAs. Case C and Case D compare the results for different numbers of the moving morphable components. Case C has 3 × 3 × 2 components while Case D has 5 × 5 × 2 components. The indexes of Case C and Case D agree well with those of Case A, which again clarifies the robustness of the proposed calculation framework.

However, the local structures around the SAs are totally different for different cases. The reason is that the formulation prefers to have the stress concentration regions around the SAs to enhance the sensitivity. Due to the rapidly decaying characteristic of stress concentration, only a small number of elements within the SAs are endowed with a high compliance and the increase of the compliance in those elements does not lead to a sharp increase in the global compliance. Thus, although the local structures are different, the constraints can be satisfied quite well with little difference in the value of the objective function. In this regard, there might exist many local optima near the global optimum which cannot be distinguished clearly by the current optimization algorithm. It is noted that a small number of components might be insufficient to construct the local structure (see the optimal configuration in Case C) since the SAs will be the main load-bearing structures, which can make the optimal configuration unusable. Hence, it is necessary to assume a large number of components in the initial state in practice.

Fig. 15

Effect of initial parameters

Appendix 2. Effect of the bridges

The introduction of bridges around the SAs is one of the main modifications adopted in the present TDF for the SAs, as compared to our previous work (Hu et al. 2020). Here, we investigate the effectiveness of the modified scheme by comparing the numerical results between the cases with and without bridges. For this purpose, Case C in Appendix 1 is considered. Figure 16 displays the corresponding iteration paths and the optimal configurations for the two cases (with and without bridges). It is seen that the absence of bridges leads to a weak connection between the SAs and the main structure, which obviously aggravates the instability of the iteration procedure.

Fig. 16

Iteration paths and optimal configurations of the case without bridges and the case with bridges. a Iteration paths of the two cases. b Optimal configuration of the case with bridges. c Optimal configuration of the case without bridges

Appendix 3. MMA coefficients

The MMA parameters ${u}_j^{(h)}$ and ${l}_j^{(h)}$ are controlled through their upper and lower bounds in the following way

$$ {\displaystyle \begin{array}{c}{l}_{\mathrm{min}}^{(h)}={D}_j^{(h)}-{C}_1^{ma}\left({\overline{D}}_j-{\underset{\_}{D}}_j\right);{l}_{\mathrm{max}}^{(h)}={D}_j^{(h)}-{C}_2^{ma}\left({\overline{D}}_j-{\underset{\_}{D}}_j\right);\\ {}{u}_{\mathrm{min}}^{(h)}={D}_j^{(h)}-{C}_2^{ma}\left({\overline{D}}_j-{\underset{\_}{D}}_j\right);{u}_{\mathrm{max}}^{(h)}={D}_j^{(h)}-{C}_1^{ma}\left({\overline{D}}_j-{\underset{\_}{D}}_j\right);\end{array}} $$

(41)

where $\left\{{l}_{\mathrm{min}}^{(h)},{l}_{\mathrm{max}}^{(h)},{u}_{\mathrm{min}}^{(h)},{u}_{\mathrm{max}}^{(h)}\right\}$ are the bounds of the MMA parameters at the h‐th step of iteration and ${D}_j^{(h)}$ is the current value of the design variable at the h‐th step of iteration with its upper and lower bounds ${\overline{D}}_j$ and ${\underline{D}}_j$. For details of the asymptotic expansion, the reader is referred to the paper of Svanberg (1987). Empirically, small values of the two coefficients ${C}_1^{ma}$ and ${C}_2^{ma}$ lead to a stable iteration procedure. If the iteration path cannot approach the current bounds within N_m steps, these two coefficients will be reduced by half. On the contrary, they will be increased by 50% when the bounds are updated in this study. In our calculations, the initial values of these two coefficients are set as ${C}_1^{ma}=10$ and ${C}_2^{ma}=1$.