Functionally graded optimisation of adsorption systems with phase change materials

Abstract

Adsorption phenomena are encountered in several engineering applications. One of its uses is in the storage and transport of gas in the form of adsorption tanks. The exothermic nature of the adsorption process decreases adsorption capacity presenting an impetus to understand the thermal characteristics of the gas storage process. Studies using mixtures of phase change materials and adsorbents in adsorption tanks demonstrate potential improvements in the adsorption capacity of the tanks. They also show that the distribution of phase change materials and adsorbent are important. Thus, this work presents two approaches for optimising the adsorbent domain. The first is to use a semi-analytic model to determine the best homogeneous material concentration for the adsorbent and phase change material for the vessel composition. The other is to use a 2D axisymmetric model to perform FGM optimisation to distribute material in the tank. Results for both models are presented and discussed for different conditions. The study shows that, for the cylindrical geometry, FGM optimisation is always, at least, marginally better than the homogeneous distribution from the semi-analytic model. However, FGM optimisation demands more computing time increases the complexity of implementation and results assembling. The semi-analytic approach is a possible alternative for optimising adsorption systems with phase change material mixed with adsorbents.

1 Introduction

Compressed natural gas (CNG) and liquefied natural gas (LNG) require high pressures or low temperatures (cryogenic), respectively. They are commonly used methods used for the storage and transport of gas (Hirata et al. 2009). An alternative means of storing and transporting gas is the use of the adsorbed natural gas (ANG), which makes it possible to store gas under lower pressures (35 to 50 atmospheres) and ambient temperature, when compared to CNG and LNG respectively, thereby, demanding less energy (Hirata et al. 2009). However, ANG storage density, which is lower than CNG, and the difficulty to retrieve the stored gas from an adsorption system, are challenges that ANG technology presents.

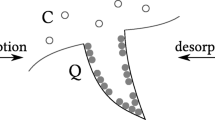
Gas adsorption is exploited in many industrial applications; examples include gas transport and storage (adsorbed natural gas), in the industrial separation process (Cavalcante 2000), in the CCS process (Leung et al. 2014) and in cooling application (Askalany et al. 2012). Adsorption consists of the adhesion of molecules from a fluid phase to the adsorbent surfaces. When the fluid reaches the adsorbed state, it becomes denser and sticks to the adsorbent surface, which is why adsorption may be used to store gas; as the process is exothermic, it releases heat. In contrast, desorption is an endothermic process and takes heat from the system. Figure 1 shows an schematic of this process. ANG technology uses the natural gas adsorption in porous materials to store and transport gas (Ayawei et al. 2017), thereby bringing benefits such as operating in relatively low pressures, which can result in lower operating costs and low energy consumption (Ayawei et al. 2017).

Fig. 1

Adsorption and desorption phenomena sketch. Adsorption liberates heat when the adsorbed state is reached, and desorption takes heat to reach gaseous state

Two important characteristics of the adsorption systems that are related to the performance of the equipment are the cycle time required to complete its charging and discharging cycles and the amount of residual gas left inside the vessel after a full cycle. These two characteristics are affected by the thermal behaviour of the system. Adsorption phenomena liberate heat; however, when the adsorbent material temperature increases, its adsorption capacity decreases. The opposite is the case for desorption, as temperature drops, so does the desorption capacity. The Dubinin-Astakov relation (Sahoo et al. 2010) describes the influence of the temperature in the saturation state. Consequently, thermal management has a significant influence on an adsorbent system as it impacts the adsorption and desorption capacity. The impact varies according to system ability to dissipate heat via thermal conduction and convection. The reduction of temperature changes during the cycles allows the same system to retain the same amount of gas for a shorter cycle time or store more gas during the same cycle time. In this work, phase change materials are used as a mean of passive thermal management.

Phase change materials (PCMs) are substances which have a high phase change enthalpy and, therefore, are considered suitable for storing energy in their internal energy (Sharma et al. 2009). Their elevated phase change enthalpy permits the material to absorb significant amounts of heat at a constant temperature; as a consequence, PCMs are a potential means of passively decreasing the temperature difference between the adsorption and desorption cycles of an ANG vessel.

The literature presents models for the adsorption phenomena, most of which involve carbon as adsorbent (Hirata et al. 2009; Goetz and Biloé 2005; Rahman et al. 2010; Sahoo et al. 2011; Sahoo et al. 2010; Mota et al. 2004; Mota 1999; Mota et al. 1997; Sahoo and Ramgopal 2014; Rahimi et al. 2015; Vo et al. 2016; Gautam 2020). The adsorbed gas stored inside the vessel is usually represented by the portion of pores occupied by the gas in the adsorbed phase. The Navier-Stokes equations may be used to solve the fluid problem (Wenger et al. 2008; Sahoo et al. 2010; Vasiliev et al. 2012); however, in gas adsorption problems, and for the porosity range presented in this study, the result from Darcy’s law equation provides a good correlation to the volume-averaged Navier-Stokes equation due to the decrease of the inertial and viscous terms (Sahoo et al. 2011). Additionally, Darcy’s law eliminates approximation problems regarding the LBB conditions (Polak 1983; Biloé et al. 2002; Song et al. 2010). There are 0D approaches known to present acceptable results for adsorption problems (Sahoo et al. 2014). Similarly to adsorption, there has been a range of models of the application, modelling and simulations involving phase change materials (Sharma et al. 2009; Zhang et al. 2007; Farid et al. 2004; Tyagi and Buddhi 2007; Mondal 2008; Fořt et al. 2017; Riahi et al. 2016; Kozak and Ziskind 2012).

The literature contains experimental results related to phase change materials improving adsorbent vessels. Studies involve the placement of PCM inside various adsorbent systems including for methane storage (Li and Li 2015), CO₂ storage (Toledo et al. 2013) and gas filtering (Zimmermann and Keller 2006). The means of positioning and geometry of the PCM varies from spheres (Toledo et al. 2013), copper tubes (Li and Li 2015). In all reported cases, PCM addition brings improvements related to higher storage/filtering capacity due to the decrease of the thermal amplitude during the operating cycles. The study shows that the phase change material amount and position inside the domain affect the results (Toledo et al. 2013). This suggests a distribution problem that arises from the fact that adding PCM reduces the area available to absorb. When the PCM amount and position are correct, it brings some improvements, and it is verified that in a filtering system, a mixture presenting 25% of PCM increased 17% the amount of gas filtered by the equipment (Zimmermann and Keller 2006). In this work, the employment of a Functionally Graded Material (FGM) distribution is expected to increase the capacity of the store and deliver gas by the adsorption storage systems evaluated.

FGM is related to the concept of topology optimisation (Paulino and Silva 2005). In this work, the topology optimisation method is employed to generate a graded solution for the adsorption domain with PCM. Topology optimisation algorithms are versatile tools applied in many fields and allow the optimised distribution of materials to be determined. Heat transfer problems are one of them, and topology optimisation algorithms have been developed to act in such systems; for instance, the optimisation of two-dimensional heat conduction problems (Gersborg-Hansen et al. 2005; Zhuang et al. 2007; Yoon 2010; Turteltaub 2001), multi-physics thermo-fluid problems (Koga et al. 2013; Matsumori et al. 2013), three-dimensional heat conduction problems (Burger et al. 2013), and transient heat transfer problems (Zhuang et al. 2013). In adsorption systems, it is verified that topology optimisation presented improvements when distributing different materials inside the system (Amigo et al. 2018). The reliability of the obtained solutions was also verified experimentally (Sá et al. 2018).

The system studied in this paper is a cylindrical adsorption vessel with a mixture of adsorbent and phase change material mixed in its interior. This type of continuous mixture of PCM and adsorbent is possible as both may be particulate (Hawlader et al. 2003; Su et al. 2017). Figure 2 shows a cylindrical vessel filled with adsorbent and PCM spheres. These spheres are mixed in the interior and adsorbent stores gas while PCM spheres keep the temperature low. The external walls have contact with the ambient air and lose heat via convection.

Fig. 2

Sketch of an adsorption system studied in this paper. It presents a mixture of adsorbent and phase change material inside its domains

An adsorption vessel performance may be improved, by changing its external surrounding, boundary conditions, and geometry (Prado et al. 2018). Such vessels may also be enhanced internally by changing material distribution, composition, and any apparatus that aids in thermal management inside the domain. This study focuses on the internal approach, the employment of a (i) 0D semi-analytic and a (ii) 2D functionally graded distribution will present a homogeneous solution and a graded solution, respectively, both of which aim to increase the capacity to store and deliver gas. Here, a 0D semi-analytic model for an adsorption system with an adsorbent-PCM mixture in its interior is developed. For the 2D and semi-analytic model, the phase change is modelled using the apparent specific heat capacity method for PCM phase change phenomena. The optimisation of the semi-analytic model is performed by a full factorial sweep varying the ambient temperature, and the phase change temperature. In contrast, the optimisation of the 2D model is performed via FGM. Results from both models are compared. Figure 3 shows the sketch of the 0D homogeneous solution and a graded solution for this system. The graded solution considers the effects caused by boundaries and heat transfer transport mechanisms, whereas the homogeneous solution neglects them. The grey zones determine the portion of phase change material mixed with the adsorbent.

Fig. 3

The sketch of homogeneous distribution and an FGM distribution inside an adsorption system

The 2D approach employs a single variable to describe the portion of PCM at each finite element to simulate the PCM behaviour inside the vessel, resulting in the modelling of a porous domain, composed of both PCM and adsorbent. This variable is responsible for adjusting the terms of the governing equations linearly between PCM and adsorbent. The adsorption tank described in Sahoo et al. (2011) is modelled to validate the implemented physics and be optimised. The implementation for PCM is validated using the Stefan problem analytical solution.

The optimised PCM distribution is expected to improve the adsorption vessel capacity to store and deliver gas. Results will determine the optimised PCM ratio in a mixture that reduces the thermal amplitude during the operating cycles and maximise the mass of stored and delivered gas. Additionally, the FG optimisation will show how different an optimised homogeneous PCM distribution is from an optimised FG PCM distribution. This information may be useful when deciding whether it is convenient to develop technology to build such vessels.

This paper conducts the study as follows. Section 2 describes the formulation and assumptions adopted. Furthermore, Section 3 presents the optimisation problem regarding the phase change material distribution inside an adsorption system. Section 4 illustrates the details about the implementation and the variational formulation employed for finite element method solving. Section 5 discusses the results obtained for the proposed cases. Finally, Section 6 concludes the work and presents the research highlights.

2 Mathematical model

This section describes the physics of the considered problem. Section 2.1 presents the basis assumptions for the model. Section 2.2 presents the governing equations for the adsorption phenomenon isolated for the 2D model. Section 2.3 describes the phase change phenomenon. Section 2.4 combines the equations for adsorption and PCM showing the governing equations for the 2D system with a mixture of adsorbent and PCM inside the domain. Section 2.5 presents the semi-analytic model equations derived by removing the space integral from the 2D model equations.

2.1 Assumptions

In order to build mathematical relations for this problem, the following assumptions are made:

• 1. Adsorbent constant specific heat capacity: the range of temperature fluctuation is expected to be around 100 K for the full carbon vessel and about 10 K for the vessel with PCM; consequently, it is suitable to consider the specific heat constant for an optimisation (Amigo et al. 2018). Additionally, there is a good correlation between experiment and simulation results when the specific heat is constant (Sahoo et al. 2011, 2014).

• 2. Local thermal equilibrium: it is assumed that the gas, the adsorbent material, and the PCM are in local thermal equilibrium (Mota et al. 2004). For a given position inside the domain, the gas, PCM, and adsorbent can be described by a single temperature.

• 3. Ideal gases: gases are assumed to exhibit their ideal thermodynamic behaviour (Sahoo et al. 2011); consequently, the equation that expresses density is:

  $$ \rho_{g} = \frac{M_{g} P}{R_{g} T} $$

  (1)

  where M_g is the molecular gas mass, R_g is the universal gas constant, P is the gas pressure, and T is the gas temperature.

• 4. Linear Driving Force (LDF) adsorption model: the Linear Driving Force model is chosen to represent the film diffusion, which is the dominant effect in the adsorption phenomena studied in this work (Mota et al. 1997).

• 5. Constant adsorption enthalpy ΔH: is assumed to be a constant due to the temperature and pressure ranges as confirmed by Sahoo et al. (2011).

• 6. Thermal conductivity: the Maxwell-Eucken relation is adopted to describe the thermal conductivity (k_eff(ε_t)) as a porous domain (Smith et al. 2013):

  $$ k_{eff}(\varepsilon_{t}) = k_{s} \frac{k_{g} + 2 k_{s} + 2 \varepsilon_{t} (k_{g}-k_{s})}{k_{g} + 2 k_{s} - \varepsilon_{t} (k_{g}-k_{s})} $$

  (2)

  where k_s and k_g are the thermal conductivity for the solid and gas, respectively, and ε_t is the material total porosity.

• 7. Gas velocity: the gas velocity, u_g, can be approximated by the Darcy law due to the low velocity within in the porous media as in Sahoo et al. (2014); therefore, it can be expressed by:

  $$ \mathbf{u_{g}} = - \frac{K_{f}}{\mu_{g}} \nabla P $$

  (3)

  where μ_g is the gas viscosity and K_f is the medium permeability. Inertial and viscous forces are assumed to be negligible.

• 8. Encapsulated PCM: As the PCM is encapsulated, there is no mass exchange between the PCM and the adsorbent (Hassabou 2011). The shell is assumed to be soft; consequently, the pressure inside the spheres is equal to the adsorption domain internal pressure. This assumption also implies that the enclosure can accommodate the density variation between one phase and the other with no pressure increases due to the expansion resistance imposed by the shell, thereby undergoing a phase change at constant pressure.

• 9. Constant properties for PCM: the specific heat, thermal conduction, density, and phase change enthalpy are considered constant for the phase change material in this work (Hassabou 2011). As observed in the performed analysis, the temperature variation during the simulations is narrow. Additionally, as the system is expected to transition between solid to liquid, the pressure variation will not cause considerable variation in the phase change temperature and thermophysical properties as explained in chapter 6 in Sandlel et al. (2006). Therefore, PCM properties are assumed to be constant during the process.

These general assumptions are used to assemble the basis for the 2D model and the semi-analytic model. However, as the semi-analytic model is obtained by removing the spatial derivatives from the 2D model, the assumptions that concern the spatial gradients such as thermal conduction are not applied to the semi-analytic model. The semi-analytic model considers the domain to have uniform characteristic properties. Table 1 illustrates for which model each assumption is made. Most of them are applied to both models; the exceptions are thermal conductivity and gas velocity. These find no meaning in the semi-analytic model because it does not use the spatial derivatives.

Table 1 Assumption table

2.2 Physics formulation for adsorption in the 2D model

This subsection presents the transport equations for the porous adsorbent material used in the 2D model. The state variables for the governing equations as P (pressure), T (temperature), and Q (adsorbed gas mass ratio). The mass equation transport may be written as Sahoo et al. (2014):

$$ \frac{\partial (\varepsilon_{t_{(ads)}} \rho_{g} + \rho_{b} Q)}{\partial t} + \nabla \cdot (\rho_{g} \mathbf{u_{g}}) = 0 $$

(4)

where $\varepsilon _{t_{(ads)}} = \varepsilon _{b_{(ads)}} + (1-\varepsilon _{b_{(ads)}})\varepsilon _{p_{(ads)}}$ is the porosity accessible to the gas phase, composed of the microporosity $\varepsilon _{b_{(ads)}}$ and the macroporosity $\varepsilon _{p_{(ads)}}$, u_g is the gas velocity, ρ_g is the gas density, $\rho _{b} = (1-\varepsilon _{t_{(ads)}})\rho _{s}$ is the bed density, ρ_s is the adsorbent density, and Q is the ratio of adsorbed gas mass to adsorbent mass ($\frac {kg}{kg}$). The first term describes the gas present in the macropores and the adsorbed gas in the micropores while the second term describes the gas flow in the location. Figure 4 shows the physical representation of macro and microporosity. Macroporosity is related to the spaces between the spheres while microporosity is related to the micropores in the particles.

The energy balance can be written as Sahoo et al. (2014):

$$ \begin{array}{@{}rcl@{}} C_{eff_{(ads)}}\frac{\partial T}{\partial t} - \nabla \cdot (k_{eff_{(ads)}} \nabla T) + \rho_{g} C_{pg} \mathbf{u_{g}}\cdot \nabla T \notag\\ - \rho_{b} \frac{\Delta H_{a}}{M_{g}}\frac{\partial Q}{\partial t} - \varepsilon_{t_{(ads)}} \frac{\partial P} {\partial t} = 0 \end{array} $$

(5)

where C_pg is the specific heat of gas, and C_eff(ads) is the effective specific heat for the adsorbent. C_eff(ads) is written as Sahoo et al. (2014):

$$ C_{eff(ads)} = (\varepsilon_{t_{(ads)}} \rho_{g} + \rho_{b} Q)C_{pg} + (1 - \varepsilon_{t_{(ads)}})\rho_{s} C_{p_{(ads)}} $$

(6)

Fig. 4

The grey areas show the macro and micro porosity influence regions

The LDF model (Mota et al. 1997), which describes the adsorption rate, $\frac {\partial Q}{\partial t}$ can be written as:

$$ \frac{\partial Q}{\partial t} = G (Q_{eq} - Q ) $$

(7)

where Q_eq is the equilibrium density of the adsorbed gas, given by the Dubinin-Astakhov (DA) equation (Sahoo et al. 2011):

$$ Q_{eq} = \rho_{adg} W_{f} exp \left( - \left( \frac{A}{\beta E_{0}} \right)^{n_{f}} \right) $$

(8)

where E₀ is the characteristic energy of adsorption, β is an affinity coefficient, and n_f is an equation parameter related to the micropore dispersion.

G is given by (Vasiliev et al. 2012):

$$ G = D e^{\left( \frac{-E_{[a,d]}}{R_{g} T} \right)} $$

(9)

where D is the intra-particle diffusion time constant. E_[a,d] is either the adsorption activation energy (subscript ‘a’) or the desorption activation energy (subscript ‘d’) and depends on whether there is local adsorption or desorption taking place. If δQt >= 0 then E_[a,d] = E_a and E_[a,d] = E_d otherwise.

The adsorbed gas density, ρ_adg, is given by Sahoo et al. (2011):

$$ \rho_{adg} = \frac{\rho_{boil}}{e^{(\alpha_{e} (T-T_{boil}) )}} $$

(10)

where α_e is the mean value of the thermal expansion of liquified gases and ρ_boil is the gas density at boiling point temperature (T_boil).

The effective volume of micro-pores, W_f, is given by:

$$ W_{f} = \rho_{f} w_{f} $$

(11)

where ρ_f is the adsorbent density and w_f is the specific volume of micropores.

The adsorption potential, A, is given by Sahoo et al. (2011):

$$ A = R_{g} T ln \left( \frac{P_{sat}}{P} \right) $$

(12)

where the saturated pressure P_sat is given by Sahoo et al. (2011):

$$ P_{sat} = P_{cr} \left( \frac{T}{T_{cr}} \right)^{2} $$

(13)

where P_cr is the critical pressure and T_cr is the critical temperature of the gas.

2.3 Formulation of phase change phenomenon in the 2D model

This section presents the phase change material model for the 2D axisymmetric model. The method for modelling the phase change phenomena for this application is based on the apparent heat capacity (Civan and Sliepcevich 1987). Although there are two other methods (enthalpy-based and temperature-based), however, the apparent heat method is chosen because the primary variable, which is the temperature, can be obtained directly from the solution of the finite element problem, and the semi-analytic problem. Furthermore, it does not require the separate solution of single-phase equations for each of the phases. The limitation of this method is the singularity that arises when the phase change interval is set to zero, and a range is not admissible (Civan and Sliepcevich 1987). Therefore, this method is characterised by a small temperature range where the phase change phenomenon occurs, Hassabou (2011), which is 3K in this work.

The energy equation, for a pure substance undergoing a phase change, as shown in image 32, may be written as Civan and Sliepcevich (1987):

$$ \begin{array}{@{}rcl@{}} \left\{\frac{\partial (\rho_{2} h_{2})}{\partial T} {+} \left[\frac{ \partial(\rho_{1} h_{1})}{\partial T} - \frac{\partial (\rho_{2} h_{2})}{\partial T} \right]\phi_{1} {+} (\rho_{1} h_{1} - \rho_{2} h_{2}) \frac{d \phi_{1}}{dT} \right\} \frac{\partial T}{\partial t} \notag\\ {+} \nabla \cdot \{(\rho_{1} h_{1} V_{1} {-} \rho_{2} h_{2} V_{2}) {-} [k_{2} {+} (k_{1} {-} k_{2})\phi_{1}] \cdot \nabla T\} {-} \frac{\partial P}{\partial t}{=} 0 \end{array} $$

(14)

where the subscripts 1 and 2 refer to phase 1 and 2 respectively, ρ is density, h is enthalpy, and ϕ₁ is the volume fraction (volume of one phase divided by the volume occupied by both phases).

Equation (14) may be simplified by applying the PCM constant properties assumption. Thus, (14) may be rewritten as (Civan and Sliepcevich 1987):

$$ \rho C_{papp} \frac{\partial T}{\partial t} - \nabla \cdot (k_{pcm} \nabla T) -\frac{\partial P}{\partial t}= 0 $$

(15)

where:

$$ C_{papp} = C_{p2} + (C_{p1} - C_{p2})\phi_{1} + {\Delta} L_{pc} \frac{\partial \phi_{1}}{\partial T} $$

(16)

$$ k_{pcm} = k_{2} + (k_{1} - k_{2}) \phi_{1} $$

(17)

where the subscript designates each phases properties, one refers to phase 1 and 2 to phase 2, L_pc is the phase change enthalpy. The ϕ₁ is similar to a Heaviside function, and it assumes value 1 when the temperature is above phase change temperature and value 0 otherwise. In this work, a hyperbolic tangent function is chosen to ensure a continuous behaviour for the phase change physics. Therefore, ϕ₁ becomes:

$$ \phi_{1} = \frac{\tanh(\gamma_{pcm} \cdot (T - T_{m}))+1.0}{2.0} $$

(18)

where γ_pcm is a factor which adjust the curve behaviour, here assuming the value 1.4.

The chosen method to model phase change assumes the phenomenon takes place in a small temperature range. The derivative of ϕ₁ may be written as:

$$ \frac{\partial \phi_{1}}{\partial T} = \frac{\gamma_{pcm} \cdot \text{sech}^{2}(\gamma_{pcm} \cdot (T-T_{m}))}{2.0} $$

(19)

Figure 5 presents the plots for ϕ and $\frac {\partial \phi }{\partial T}$.

Fig. 5

Plots for ϕ and $\frac {\partial \phi }{\partial T}$. T_m is set to 310.65 K. The upper border is T_m+ 1.5 and the lower border is T_m− 1.5

In this work, the phase change material is modelled as a porous body composed of many spheres. The same porous medium approach, which is applied for the adsorbent, is applied for the PCM. The gas may not be adsorbed by phase change material; however, it may flow through the spaces between spheres; therefore, the mass balance for the PCM becomes:

$$ \frac{\partial (\varepsilon_{t_{(pcm)}} \rho_{g})}{\partial t} + \nabla \cdot (\rho_{g} \mathbf{u_{g}}) = 0 $$

(20)

where $\varepsilon _{t_{(pcm)}} = \varepsilon _{bpcm} + (1-\varepsilon _{b{(pcm)}})\varepsilon _{p_{(pcm)}}$ and describes the total porosity brought by the spaces between the PCM spheres, ρ_g is the gas density, and u_g is the gas velocity. The first term represents the air between the spheres and the second term represents the gas stream that travels through these spaces.

Equation (15) also can be written as the energy balance of this porous medium.

$$ \begin{array}{@{}rcl@{}} C_{eff_{(pcm)}}\frac{\partial T}{\partial t} - \nabla \cdot (k_{eff_{(pcm)}} \nabla T) \notag\\ + \rho_{g} C_{pg} \mathbf{u_{g}}\cdot \nabla T - \varepsilon_{t_{(pcm)}} \frac{\partial P}{\partial t} = 0 \end{array} $$

(21)

where C_eff(pcm) is written as:

$$ C_{eff_{(pcm)}} = \varepsilon_{t_{(pcm)}} \rho_{g} C_{pg} + (1 - \varepsilon_{t_{(pcm)}})\rho_{pcm} C_{papp} $$

(22)

where $k_{eff_{(pcm)}}$ is (2) applied to PCM properties.

2.4 Formulation of the mixed adsorbent-PCM domain in the 2D model

In this subsection, the adsorption model and the PCM model are coupled using the design variable ε_pcm. The design variable defines the element composition; it assumes value 0 when no PCM is present and 1 when the element is composed 100% of PCM. The equations terms are adjusted according to the design variable. Figure 6 illustrates the role of the design variable in determining the tank.

Fig. 6

Mixture composition inside the adsorption vessel according to the ε_pcm

Summing (4) and (20), the mass equation for the domain becomes:

$$ \begin{array}{@{}rcl@{}} \left[ \left( \frac{\partial (\varepsilon_{t_{(ads)}} \rho_{g} + \rho_{b} q)}{\partial t} \right) + \nabla \cdot (\rho_{g} \mathbf{u_{g}}) \right]_{ads} \cdot \left( 1-\varepsilon_{pcm}\right) \notag\\ + \left[ \left( \frac{\partial (\varepsilon_{t_{(pcm)}} \rho_{g})}{\partial t} \right) + \nabla \cdot (\rho_{g} \mathbf{u_{g}}) \right]_{pcm} \cdot \left( \varepsilon_{pcm}\right) = 0 \end{array} $$

(23)

For the energy equation, (5) and (21) are summed, resulting in:

$$ \begin{array}{@{}rcl@{}} \left[ \left( C_{eff_{(ads)}}\frac{\partial T}{\partial t} \right) - \nabla \cdot (k_{eff_{(ads)}} \nabla T) + \rho_{g} C_{pg} \mathbf{u_{g}}\cdot \nabla T \right. \notag\\ \left. - \rho_{b} \frac{\Delta H_{a}}{M_{g}}\frac{\partial Q}{\partial t} - \varepsilon_{t_{(ads)}} \frac{\partial P}{\partial t} \right]_{ads} \cdot \left( 1-\varepsilon_{pcm} \right) \notag\\ + \left[ \left( C_{eff_{(pcm)}}\frac{\partial T}{\partial t} \right) - \nabla \cdot (k_{eff_{(pcm)}} \nabla T) + \rho_{g} C_{pg} \mathbf{u_{g}}\cdot \nabla T \right. \notag\\ \left. - \varepsilon_{t_{(pcm)}} \frac{\partial P}{\partial t} \right]_{pcm} \cdot \left( \varepsilon_{pcm} \right) = 0 \end{array} $$

(24)

The LDF model remains the same, and no adjustments are made.

2.5 Semi-analytic model

The semi-analytic model is obtained from (23) and (24) with spatial derivatives set to zero. It considers the whole system as a control volume and neglects local phenomena such as thermal conduction, internal convection, and pressure gradients, thereby removing spatial derivatives.

The spatial derivatives are replaced by their respective full domain integral resulting in the additional terms for the tank volume (V_Ω) and the inlet area (A_Γ) being introduced. For the semi-analytic model the mass equation becomes:

$$ \begin{array}{@{}rcl@{}} \left[ \left( \frac{\partial (\varepsilon_{t_{(ads)}} \rho_{g} + \rho_{b} q)}{\partial t} \right) \cdot \left( 1-\varepsilon_{pcm}\right) \cdot V_{\Omega} \right]_{ads}\notag\\ + \left[ \left( \frac{\partial (\varepsilon_{t_{(pcm)}} \rho_{g})}{\partial t} \right) \cdot \left( \varepsilon_{pcm}\right) \cdot V_{\Omega} \right]_{pcm}\notag\\ + \left[ \rho_{g} \cdot \mathbf{u_{g}} \cdot A_{\Gamma} \cdot \left( 1-\varepsilon_{pcm}\right) \right]_{ads}\notag\\ + \left[ \rho_{g} \cdot \mathbf{u_{g}} \cdot A_{\Gamma} \cdot \left( \varepsilon_{pcm}\right) \right]_{pcm} = 0 \end{array} $$

(25)

where V_Ω is the system volume and A_Γ is the inlet area.

Similarly, the energy balance suffers more changes as the thermal conduction terms are removed. The spatial derivatives are also replaced by the vessel volume and the inlet area by setting ∇ = 0 and integrating over V_Ω + A_Γ. Equation (24) becomes:

$$ \begin{array}{@{}rcl@{}} \left[ \left( C_{eff_{(ads)}}\frac{\partial T}{\partial t} \right) \cdot \left( 1-\varepsilon_{pcm} \right) \cdot V_{\Omega} \right]_{ads}\notag\\ + \left[ \left( C_{eff_{(pcm)}}\frac{\partial T}{\partial t} \right) \cdot \left( \varepsilon_{pcm} \right) \cdot V_{\Omega} \right]_{pcm} \notag\\ + \left[ \rho_{g} C_{pg} \mathbf{u_{g}} \cdot \left( 1-\varepsilon_{pcm} \right) \cdot A_{\Gamma}\right]_{ads}\notag\\ + \left[ \rho_{g} C_{pg} \mathbf{u_{g}} \cdot \left( \varepsilon_{pcm} \right) \cdot A_{\Gamma}\right]_{pcm} \notag\\ - \left[ (1-\varepsilon_{pcm}) \cdot \varepsilon_{t_{(ads)}} \frac{\partial P}{\partial t}\right]_{ads} \notag\\ - \left[ (\varepsilon_{pcm}) \cdot \varepsilon_{t_{(pcm)}} \frac{\partial P}{\partial t}\right]_{pcm} \notag\\ - \left[\rho_{b} \frac{\Delta H_{a}}{M_{g}}\frac{\partial Q}{\partial t} \cdot \left( 1-\varepsilon_{pcm} \right) \cdot V_{\Omega} \right]_{ads} = 0 \end{array} $$

(26)

The LDF model, from (7) is unchanged.

3 Optimisation

It is often desirable to reduce cycle time. This study employs the FGM approach to systematically distribute phase change material inside the adsorption storage medium in a manner that improves the thermal behaviour of such vessels, thus, improving their capacity for storing and delivering gas. Such a method implies a trade-off between the available region for adsorption and the amount of PCM to improve the vessel temperature. The adsorbent material replaced by phase change material must imply a temperature amplitude reduction that is enough to improve the adsorption capacity and compensate for the loss of adsorption area.

3.1 Optimisation of an ANG storage medium

The goal for optimally distributing phase change material inside of ANG storage media is to increase its capacity for storing and delivering gas. In this work, this goal is reached by maximising the amount of adsorbed gas inside the vessel. The semi-analytic model assumes a homogeneous solution, whereas the FGM optimisation method tackles the problem of generating a material distribution. The design variable, ε_pcm, denotes the phase change material (PCM) distribution. The proposed problem considers a system in which phase change material and adsorbent composition can vary continuously in the range of ε_pcm = 0 to 1. Here, the FGM optimisation methodology is employed to produce a graded distribution inside the domain.

The goal for the optimisation in this study is to maximise the mass of gas inside the vessel by the end of the adsorption cycle, which results in the optimisation problem written in (27):

$$ \begin{array}{@{}rcl@{}} \mathrm{Maximise:} & J_{a} = \left[{{\int}_{\Omega} \left( C_{1}(\varepsilon_{pcm}) \cdot Q(\varepsilon_{pcm}) \right)} dx \right]_{t_{ini}}^{t_{fin}} \notag\\ \mathrm{ \varepsilon_{pcm}}\notag\\ \mathrm{subject to:} & 0 \leq \varepsilon_{pcm} \leq 1 \notag\\ & Eq. (23) - \text{Continuity} \notag\\ & Eq. (24) - \text{Energy Balance} \notag\\ & Eq. (7) - \text{Adsorption Kinetics} \notag\\ & Eq. (38) - \text{Helmholtz Filtering} \end{array} $$

(27)

where C₁ is:

$$ C_{1}(\varepsilon_{pcm}) = (2 \pi r) \cdot \frac{\rho_{ads}V_{m}}{M_{g}} (1-\varepsilon_{t_{(ads)}}) (1-\varepsilon_{pcm}) $$

(28)

where r is the radial spatial coordinate and V_m is the molar volume of gases in STP conditions.

4 Numerical implementation

This section describes the numerical implementation of the physics governing equations. First, the 2D model is explained in the first four subsections. Finally, the semi-analytic model presented in the last subsection.

4.1 2D model

In this work, the finite element method (FEM) approximates the solution for pressure and temperature in the domain by solving the governing equations, and numerical integration is employed to solve the adsorption kinetics. Figure 7 shows the triangular element and the order of interpolation for each variable. Pressure, temperature, and adsorption ratio use first-order continuous Lagrange interpolation while ε_pcm uses discrete Lagrange of 0 degree. This strategy is possible because adsorption kinetics does not have second-order derivatives, and it is attractive because it provides a faster solution. FEM and sensitivities are implemented using Python programming language alongside with the FEniCS (Logg 2007) and Dolfin-Adjoint (Farrell et al. 2013) open-source software.

Fig. 7

The order for each field in a triangular element

Figure 8 summarises the whole process for obtaining the adjoint problem. Unified form language (UFL) handles the forward equations; then, Libadjoint creates the discrete adjoint equations; finally, FEniCS Form Compiler (FFC) package creates the adjoint code. Dolfin interface orchestrates all of these packages and tools.

Fig. 8

Method for obtaining adjoint problem

The optimisation sequence follows the diagram presented in Fig. 9. Initially, a PCM distribution is defined. Then, the governing equations are solved, and Dolfin-adjoint transforms the physical problem solution into linear subproblems. Then, the adjoint problem is generated to make possible the evaluation of sensitivities. The optimiser chosen for this application is the augmented Lagrangian method from ROL (Rapid Optimisation Library) (Rapid Optimization Library 2020). The new solution is determined by quasi-Newton line search method. The second-order derivatives are obtained via the L-BFGS-B method. The optimiser receives the gradients and returns a new distribution of pseudo-porosity’s (PCM distribution).

Fig. 9

Optimisation of virtual vessel scheme

L-BFGS-B algorithm is used because it is able to handle box constraints, which are encountered in the proposed optimisation problem.

4.2 Weak formulation

In this section, the weak form of equations will be presented. The mass and energy balance equations weak form are described in Section 4.2.1. In Section 4.2.2, the numerical integration regarding adsorption kinetics is presented.

4.2.1 Variational equation—fluid and thermal problem

The weak form of the smooth function $\mathbb {L}(u)$ is defined by:

$$ < \mathbb{L}(u),v > = {\int}_{\Omega} \mathbb{L}(u)\cdot v dx \forall u, v \in H^{1}({\Omega}) $$

(29)

Also, any Neumann boundary condition inside ∂Ω can be determined by:

$$ < \mathbb{L}(u),v >_{{\Gamma}_{W}} = \oint_{{\Gamma}_{W}} \mathbb{L}(u)\textbf{n} \cdot v ds \forall u, v \in H^{1}({\Omega}) $$

(30)

The Dirichlet boundary condition for the problem can be expressed as:

$$ u = \phi\ on\ {\Gamma}_{I}, u \in H^{1}({\Omega}):<\mathbb{L}(u),v> = 0\ \forall\ v \in {H^{1}_{0}}({\Omega}) $$

(31)

where Γ_I ⊂ ∂Ω, also $\phi \in H^{\frac {1}{2}}({\Gamma }_{I})$ and ${H^{1}_{0}}({\Omega })$ is the set of all functions in H¹(Ω) such that u = 0 on ∂Ω. From (4), and (5), the weak forms for the mass and energy balance can be written as:

$$ \begin{array}{@{}rcl@{}} \mathbb{M} = < \frac{(1-\varepsilon_{pcm}) \cdot \varepsilon_{t_{(ads)}} \cdot M_{g}}{R_{g}}\frac{\partial (P \cdot T^{-1})}{\partial t} , v_{M} >_{ads} \notag\\ +< \frac{(\varepsilon_{pcm}) \cdot \varepsilon_{t_{(pcm)}} \cdot M_{g}}{R_{g}}\frac{\partial (P \cdot T^{-1})}{\partial t} , v_{M} >_{pcm}\notag\\ +< (1-\varepsilon_{pcm}) \cdot (1-\varepsilon_{t_{(ads)}}) \cdot \rho_{s} \frac{\partial Q}{\partial t} , v_{M} >_{ads}\notag\\ + < \frac{(\varepsilon_{pcm}) M_{g} K_{f}}{R_{g} \mu_{g}} \frac{P}{T} \nabla P , \nabla v_{M} >_{pcm} \notag\\ + < \frac{(1-\varepsilon_{pcm}) M_{g} K_{f}}{R_{g} \mu_{g}} \frac{P}{T} \nabla P , \nabla v_{M} >_{ads} = 0 , \notag\\ \forall v_{M} \in H^{1}({\Omega}) \end{array} $$

(32)

$$ \begin{array}{@{}rcl@{}} \mathbb{E} = < (1-\varepsilon_{pcm}) \cdot C_{eff_{(ads)}} \cdot \frac{\partial T}{\partial t}, v_{E} >_{ads}\notag\\ + < \varepsilon_{pcm} \cdot C_{eff_{(pcm)}} \cdot \frac{\partial T}{\partial t}, v_{E} >_{pcm} \notag\\ + < (1-\varepsilon_{pcm}) \cdot k_{eff_{(ads)}} \nabla T , \nabla v_{E} >_{ads} \notag\\ + < \varepsilon_{pcm} \cdot k_{eff_{(pcm)}} \nabla T , \nabla v_{E} >_{pcm}\notag\\ - < (1-\varepsilon_{pcm}) \cdot \frac{\Delta H}{M_{g}} \cdot (1-\varepsilon_{t_{(ads)}}) \cdot \rho_{s} \frac{\partial Q}{\partial t} , v_{E} >_{ads}\notag\\ + < \varepsilon_{pcm} \cdot \frac{Cp_{g} M_{g} K_{f}}{R_{g} \mu_{g}} \frac{P}{T} \nabla P \cdot \nabla T ,v_{E} >_{pcm} \notag\\ + < (1-\varepsilon_{pcm}) \cdot \frac{ Cp_{g} M_{g} K_{f}}{R_{g} \mu_{g}} \frac{P}{T} \nabla P \cdot \nabla T ,v_{E} >_{ads} \notag\\ + < \varepsilon_{pcm} \cdot \varepsilon_{t_{(pcm)}} \cdot \frac{\partial P}{\partial t}, v_{E} >_{pcm} \notag\\ + < (1-\varepsilon_{pcm}) \cdot \varepsilon_{t_{(ads)}} \cdot \frac{\partial P}{\partial t}, v_{E} >_{ads} \notag\\ + < h_{c} \cdot (T-T_{ini}),v_{M}>_{{\Gamma}_{1}} = 0 , \notag\\ \forall v_{E} \in H^{1}({\Omega}) \end{array} $$

(33)

where ads, pcm, and both refer to the adsorbent process, phase change material process, and both processes.

Finally, the solution for the problem can be obtained by solving:

$$ \mathbb{M} + \mathbb{E} = 0 $$

(34)

4.2.2 Numerical integration

This study treats the adsorption physics separately of the fluid and thermal problem, which variational equations solve. Sorption problem is solved by approximating the time derivative numerically using the backward Euler method. Therefore, first, differential equations will handle the mass and energy balance equation, thereby, updating the pressure and temperature state variables. After that, the numeric differentiation in time will tackle the adsorption problem and solve it for the new set of pressure and temperature, updating the adsorption portion for the next time step.

After the numerical differential is applied, (7) becomes:

$$ Q_{1} = {\Delta} t \cdot G \cdot Q_{eq} - ({\Delta} t \cdot G + 1)\cdot Q_{0} $$

(35)

where Q₁ is the new adsorption density, whereas Q₀ is the adsorption density of the last time step. The Δt is the time step.

The derivatives for P and T may be written as:

$$ \frac{\partial P}{\partial t} = \frac{P1-P0}{\Delta t} $$

(36)

$$ \frac{\partial T}{\partial t} = \frac{T1-T0}{\Delta t} $$

(37)

where the subscripts 0 and 1 are the anterior state and the new state, respectively.

4.2.3 Helmholtz filter

The Helmholtz filter (Remacle et al. 2012) is applied to aid numerical convergence and reduce mesh dependency and checkerboard. The filter updates each design variable according to the local values, thereby acting as an averaging tool. The filter length determines the considered area during the update process. This tool is implemented by solving the following PDE (Remacle et al. 2012):

$$ -z^{2} \nabla^{2} \varepsilon_{pcm} + \varepsilon_{pcm} = \check{\varepsilon}_{pcm} $$

(38)

where z is the filter length and $\check {\varepsilon }_{pcm}$ is the function receiving the filter effect (smoothing).

The implementation of the Helmholtz filter consists of the solution of a PDE to smooth the design variable. The weak form of the (38) (Amigo et al. 2018):

$$ \begin{array}{@{}rcl@{}} \mathbb{H} = < \varepsilon_{pcm}, v_{H} > + < z^{2} \nabla \varepsilon_{pcm},\nabla v_{H} > = < \check{\varepsilon}_{pcm}, v_{H} > \notag\\ \forall v_{H} \in H^{1}({\Omega}) \end{array} $$

(39)

4.3 Semi-analytic model

For the semi-analytic model, no PDEs are solved as only time derivatives are solved. Figure 10 shows the schematic of the semi-analytic model solving sequence. After material properties, pressure input and initial conditions are set, the mass balance equation calculates the velocity at which gas flows.

Fig. 10

Semi-analytic model analysis scheme

5 Results and discussion

This section presents the correlation and the results obtained by both models. In Section 5.1, the validation for both models is presented. The optimisation based on the adsorption 2D model is compared with the literature and results are presented in Section 5.1.1. In Section 5.1.2, the phase change material model is validated with the analytic solution of the Stefan problem. The semi-analytic model is compared with the 2D model in Section 5.1.3. In Section 5.2, the optimisation results are presented. In Section 5.2.1, the optimisation based on the semi-analytic model is presented. In Section 5.2.2, the optimised material distributions are presented and compared with the homogeneous solution.

5.1 Model validation

This subsection presents the validation of the two models employed in this work. It will demonstrate the validated adsorption model, show the phase change material numeric model validation with a closed problem analytical solution, and then present the semi-analytic model validation.

5.1.1 Adsorption

In order to validate the adsorption model, it is compared to the experiment presented in Sahoo et al. (2011). The $30 \frac {L}{min}$ case is used for the comparison. This scenario was simulated by assuming ε_pcm = 0.0.

For a convection coefficient of $h=700 \frac {W}{m^{2}K}$ is assumed, and considering the thermal conductivity of copper ($k=385.0 \frac {W}{mK}$), and the vessel external wall thickness as 2 mm, (w_t = 0.002m), it is possible to calculate the Biot number (about 0.0036 for the cylinder shape). This Biot value indicates negligible thermal resistance for the tank external walls. Therefore, the role of tank wall thickness is neglected in the simulation.

For all charging cycle analysis, the initial conditions for the adsorbent domain are as follows:

• P(z,r) = P_i = 101325Pa for all charging designs

• T(z,r) = T_i = 300K for all charging designs

• Q = Q_eq(P_i,T_i)

The results are compared with those found in the literature with a prescribed volumetric rate of 30 L/min (Sahoo et al. 2011). The vessel geometry, boundary conditions, dimensions, and the mesh employed in the simulation are shown in Fig. 11. The boundary condition for this specific analysis is set to prescribed volumetric flow at Γ_I, given by:

$$ V_{in} = {{\int}_{{\Gamma}_{I}} \frac{\rho_{g} V_{m}}{M_{g}}} \mathbf{n} \cdot \mathbf{u}_{g} d{\Gamma}_{I} \text{on} {\Gamma}_{I} $$

(40)

where n is the unit outward on the surfaces.

Fig. 11

Bed geometry, finite element mesh, and cycle details

The temperature in the inlet (Γ_I) is equal to the ambient temperature, which determines the convective heat transfer on the walls. Temperature boundary conditions are:

$$ \begin{array}{@{}rcl@{}} T = T_{inlet} & \text{on} & {\Gamma}_{I} \notag\\ -\mathbf{n} \cdot k_{f} \nabla T = h_{W} (T-T_{0}) & \text{on} & {\Gamma}_{W} \end{array} $$

(41)

Figure 12 shows the comparison between this work and (Sahoo et al. 2011). In Fig. 12a, the pressure evolution is presented. The current model shows a good correlation with the literature, presenting a difference of 8% pressure in the final steps. In Fig. 12b, the temperature at the centre of the bed shows good agreement with the experimental and numerical data found in the literature (Sahoo et al. 2011). Comparison reliability improves when the gas flow is verified. Figure 13 shows the total gas volume inside the vessel. The 30 L/min observed in literature (Sahoo et al. 2011) is also verified in the virtual analysis.

Fig. 12

Comparison of the virtual analysis with the literature (Sahoo et al. 2011). a Pressure comparison. b Temperature comparison

Fig. 13

Comparison of the virtual analysis with the literature (Sahoo et al. 2011). Virtual analysis shows a steady gas flow of 30 L/min (0.5 L/s) as in literature

Figure 14 shows the temperature profile of the adsorption vessel at 3 min during the charging cycle. It matches the profiles found in the literature (Sahoo et al. 2011). The temperature profile, pressure, and temperature curves are in agreement with the data found in the literature.

Fig. 14

Temperature at 3 min of the charging cycle

5.1.2 Phase change model

The phase change material model is compared to the analytical solution of the second problem described in Stefan (1891), also known as the Stefan problem. The Stefan problem describes a situation in which a phase change phenomenon takes place in a homogeneous domain, and its analytical solution may be used to verify numerical models describing phase change (Ogoh and Groulx 2010). This scenario was simulated by assuming ε_pcm = 1.0 and ε_t(pcm) = 0.0. Figure 15 illustrates the boundary condition for the proposed problem and the domain. The wall temperature Tw is set to 350 K, whereas the domain temperature receives the value of 300 K. The phase change material properties are described in Appendix D. Phase change temperature is 313 K. The analysis simulates the transient heating phenomenon for 16 h. For all simulations, γ_pcm = 1.8, and it is assumed that the phase change phenomenon takes place in a 3 K temperature interval. This scenario simulates the same conditions of the Stefan problem; which is a one-dimensional problem wherein a melting front moves from one side to another due to the melting process caused by a hot wall in one of the extremities.

Fig. 15

Mesh, domain, and boundary conditions for the PCM model validation

An analytic model for the phase change phenomena is available in the literature in the form of a Laplace transform of the thermal energy balance equation. Appendix ?? describes the analytical equation for the Stefan problem. The Stefan problem explores a condition where a full PCM domain starts at the phase change temperature and with a heat source in one of its walls. The heat source allows the domain to undergo the phase change, and a temperature profile is created inside the domain. An analytic equation describes this temperature profile; it serves as a comparative to verify if the value chosen for γ_pcm is capable of returning reliable results.

Figure 16 shows the temperature profile at a range of times. Results show a good correlation between data. Although the temperature inside the line is slightly colder than it should be in 3 h of analysis, the phase change wall position is correct. In later periods, the phase change barrier advances faster than it is expected. Nevertheless, for all the adsorption analysis considered in this study, a period shorter than 3 h will be considered; thereby making the designed parameters suitable for these purposes.

Fig. 16

Temperature according to length

This validation is relevant because it adjusts the phase change material capacity. If unsuitable parameters are employed, the material will present altered phase-change enthalpy, then, behaving unrealistically.

5.1.3 Semi-analytic model verification

The semi-analytic model must be compared to the 2D model analysis to verify its reliability and quantify how much natural convection influences the results. All initial and boundary conditions are the same as those applied for the 2D model and are accordingly shown in Fig. 11, except for the convection coefficient. For the semi-analytic model, this coefficient is set to 0 (convection neglected).

The thermal conductivity for the adsorbent is decreased due to the porosity; therefore, the only regions affected by the convection are those close enough to the border. Figure 14 depicts the temperature gradient presented in the operating cycle.

Figure 17 shows that the semi-analytic model can predict the behaviour of the vessel in the experimented condition for a full carbon vessel well. The deviation in the temperature is caused by natural convection, which is present in the 2D model. When the amount of adsorbed gas is taken into account, it becomes clear that, for this condition, natural convection plays a minor role in the total amount of adsorbed gas. Therefore, the semi-analytic model is aligned not only with the 2D model but also with the literature.

Fig. 17

Comparison between the 2D model and the semi-analytic model built in Wolfram Mathematica for a full-carbon vessel

Figure 18 shows the same charts of Fig. 17 but for a 10% PCM scenario. It is possible to see the temperature plateau caused by phase change and the temperature deviation due to the convection. As expected, the 2D model has lower temperatures by the end of the analysis. Both models show good agreement in temperature and adsorbed gas.

Fig. 18

Comparison between the 2D model and the semi-analytic model built in Wolfram Mathematica for a 10% PCM mixture inside the tank

5.2 ANG optimisation

A cylindrical adsorption vessel with adsorbent and PCM mixture in its interior is optimised in this section. The model is axisymmetric; a radial section is modelled, and it represents an adsorbent bed subject to heat exchange with the exterior through natural convection. As thermal resistance in the vessel wall is very low, the thermal influence of this component is neglected as in Sahoo et al. (2011). The phase change material employed for the study is the eicosane (Kahwaji et al. 2018). The properties regarding these materials are listed in Appendix D.

Three conditions are analysed in this work:

• Case1—Charging only: the vessel is exposed to a single charging cycle. The pressure rises from the initial state to the final state following a given function;

• Case2—Charging followed by discharging: The vessel charges in the same fashion as in case 1, but there is a discharge sequence after that. The main characteristic that is present in this scenario is that the discharging process starts at the same pressure level that the charging process finishes and desorption also benefits from the heat generated by adsorption, which remains in the material internal energy or temperature;

• Case3—Charging followed by discharging after thermal equilibrium is reached: This case is particularly curious because it may be associated with a transport situation. The vessel is filled like in case 1; however, after this process ends, it is assumed that it remains at ambient temperature until it reaches thermal equilibrium and, then, it performs the discharging cycle. In this situation, the gas that remained in the gaseous form inside the tank during the charging cycle would be adsorbed due to the temperature drop, thereby decreasing the pressure. For this case, the initial pressure for the discharging cycle is obtained by maintaining constant the total gas mass inside the vessel and setting the internal temperature to the same value as the external temperature. The value for the initial pressure of the discharging cycle is defined by solving (42):

  $$ \begin{array}{@{}rcl@{}} (\varepsilon_{t_{(ads)}} \rho_{g}(P_{f},T_{f}) + \rho_{b} Q)\varepsilon_{pcm} \notag\\ + (\varepsilon_{t_{(pcm)}} \rho_{g}(P_{f},T_{f}))(1-\varepsilon_{pcm}) = \notag\\ (\varepsilon_{t_{(ads)}} \rho_{g}(P_{i},T_{amb}) + \rho_{b} Q_{eq}(P_{i},T_{amb}))\varepsilon_{pcm} \notag\\ + (\varepsilon_{t_{(pcm)}} \rho_{g}(P_{f},T_{f}))(1-\varepsilon_{pcm}) \end{array} $$

  (42)

  where T_f and P_f are, respectively, the final temperature of the charging cycle and the final pressure of the charging cycle, T_amb is the ambient temperature, and P_i is the initial pressure for the discharging cycle. Finally, the discharging cycle takes place at a different pressure than the end of the charging cycle, and desorption no longer benefits from the heat generated by adsorption.

The pressure input for each case is defined by a time-dependant function, as presented in Fig. 19. The time period considered in the analysis was from 0 to 240. For case 2, as indicated in Fig. 19, the considered charging cycle starts in 0 s and ends in 300 s; after that, discharging occurs from that time until 3600 s. For case 3, the time period adopted for charging cycle was from 0 to 360 s and for the discharging cycle from 0 to 3600 s. For all cases, the number of time steps used in the simulation is 1200.

Fig. 19

Pressure input for each analysed case. All functions are time dependant

5.2.1 Semi-analytic model full factorial sweep

Solving the semi-analytic model has a low computational cost. Therefore, it is possible to perform a sweep in a range of variable values of interest to visualise the behaviour of merit function of (27). In this study, the swept variables are the phase change temperature for the PCM and its concentration. The sweep was performed for ambient temperatures of 290.0 K, 302.5 K, 315.0 K, and 327.5 K. This procedure was applied in all cases.

The total number of analysis for each case is 28,684. The PCM concentration was tested from 0.0 to 0.5 in steps of 0.005, whereas the phase change temperature was tested from 290 until 340 K in steps of 0.704 K. The total number of steps for each variable are, respectively, 101, 71, and 4.

If the phase change temperature and the ambient temperatures are fixed in 310.65 K and 300.0 K, just the PCM portion may be adjusted. Figure 20 shows how the adsorbed volume and the energy consumed in the phase change phenomenon behave. The optimised PCM portion is, in this case, unique and well defined. The adsorbed volume decreases with increasing PCM ratio beyond the optimised PCM ratio. The problem lies in finding the point where the energy consumed by PCM stops increasing linearly with the increase of PCM ratio. The energy rises, initially, with the increasing of the design variable. Its rising trend declines after the optimised point because the heat generated by the remaining adsorbent is not enough to saturate the PCM. Consequently, going beyond the optimised point would remove the adsorbent area without significantly increasing the energy stored in PCM, which causes the vessel performance to decline. In this case, the optimised PCM ratio is 14.0%, and the improvement is about 21% when compared to the full carbon vessel.

Fig. 20

Total amount of adsorbed gas and energy consumed by the phase change according to the phase change material portion

Figure 21 presents the contour plot for the improvement in terms of adsorbed gas for all inlet temperature verified. The black regions indicate conditions where inserting PCM in the domain brings no benefit to the system. The improvement increases as the phase change temperature approach the ambient temperature. Because adsorption is the main phenomena, the phase change temperature must be higher than the initial temperature.

Fig. 21

Solution space for case 1. Improvement in function of the phase change temperature and PCM portion. The inlet temperature verified are a 290.0 K, b 302.5 K, c 315.0 K, and d 327.5 K

Case 1 reached a 23.2% improvement at 329.29 K of phase change temperature for an ambient temperature of 327.5 K. For all ambient temperatures, the improvement behaves similarly, and the optimised amount of PCM for this case is around 16%. Nevertheless, if more PCM is inserted in the domain beyond the optimised, the system loses adsorption capacity due to the trade-off between the adsorption area and temperature. The chart shows a small decrease in gain if phase change temperature decreases from optimal because PCM would start the analysis partially melted. Results suggest that the higher the ambient temperature is, the more beneficial the addition of PCM becomes. The full-carbon vessel can adsorb more gas at a lower ambient temperature than the same system at higher ambient temperatures. The change in the mass of adsorbed gas is shown in Fig. 22 for two different external temperatures, 327.5 K and 290.0 K and the full carbon vessel and a vessel with optimised PCM mixture. The internal temperature variation is presented in Fig. 23 while Table 2 shows the temperature variation during the filling cycle for two ambient temperatures, considering full carbon and optimised PCM mixture configurations. For both ambient temperatures, PCM causes a similar temperature amplitude reduction. Consequently, the total volume of adsorbed gas increase between the external ambient temperatures is similar, as presented in Table 3. However, as adsorption systems adsorb less gas at high ambient temperature, the increase is proportionally higher, which explains the larger gas increase with PCM with an increase of ambient temperature.

Fig. 22

Case 1 adsorbed gas volume evolution during the filling cycle for full carbon (FC) and optimised PCM mixture for two external temperatures

Fig. 23

Case 1 temperature evolution during the filling cycle for full carbon (FC) and optimised PCM mixture for two external temperatures

Table 2 Case 1 temperature amplitude for full carbon (FC) and optimised PCM mixture for two external temperatures

Table 3 Case 1 adsorbed gas volume for full carbon (FC) and optimised PCM mixture for two external temperatures

The summary of the optimised points found for each temperature are presented in Table 4:

Table 4 Summary of case 1 optimised PCM ratios

For cases 2 and 3, the improvement is measured by the total amount of gas the system can deliver by the end of the cycles. The total amount of delivered gas if the difference between the total amount of gas by the end of the charging cycle and the amount of gas by the end of the discharging cycle. Case 2 reached 21.7% of improvement at 331.43 K of phase change temperature for an ambient temperature of 327.5 K. The best PCM distribution is around 15.5%. The optimised amount of PCM increases as ambient temperature increases. If the ambient temperature is 327.5 K, the optimised amount of PCM is 15.5%. Figures 24 and 25 present the contour plot for the improvement in terms of adsorbed gas for all inlet temperature verified for these cases. As in case 1, PCM gains rise as external temperature rises. The temperature reduction during the filling cycle, due to PCM insertion, causes proportionally higher adsorbed gas increase at higher external temperatures; however, for case 2, the heat stored in PCM during the charging cycle aids desorption. As high ambient temperatures favour desorption, which is a slower phenomenon than adsorption, the differences between PCM gains for various ambient temperatures are significant.

Fig. 24

Solution space for case 2. Improvement in function of the phase change temperature and PCM portion. The inlet temperature verified are a 290.0 K, b 302.5 K, c 315.0 K, and d 327.5 K

Fig. 25

Solution space for case 3. Improvement in function of the phase change temperature and PCM portion. The inlet temperature verified are a 290.0 K, b 302.5 K, c 315.0 K, and d 327.5 K

The summary of the optimised points fount for each temperature is presented in Table 5. Figures 21 and 24 present a white region that address negative gains. As these gains are undesired, they are removed to identify the desired areas, which present improvements.

Table 5 Summary of case 2 optimised PCM ratios

Case 3 reached 167.1% of improvement at 290.0K of phase change temperature for an ambient temperature of 290.0K. In this case, the best takes place for low ambient temperatures. The optimised amount of PCM for this case is around 23.5%.

Case 3 presents substantial gains due to the pressure drop in full carbon tanks. After the charging cycle, the vessel is at an elevated temperature; as the temperature drops, the gaseous gas inside the vessel when the temperature was high, is gradually adsorbed. Consequently, the pressure inside the vessel drops. The result is a vessel with lower internal pressure and at a lower temperature. The lower pressure may be considered less gas that will be delivered without desorption, and the lower temperature implies lower rates of desorption. Therefore, the pressure drop is a double loss in terms of delivered gas, and it tends to lead to more residual gas by the end of the discharging cycle.

When PCM is added in case 3, it decreases the pressure drop by reducing the maximum temperature reached during the charging cycle. Consequently, as the vessel reaches thermal equilibrium with the ambient, less gas in the gaseous form will be adsorbed after the charging cycle ended. The result is a vessel with an internal pressure at higher values and able to deliver more gas. Figure 26 shows the pressure drop between the full carbon vessel and the vessel with PCM for two ambient temperatures. At 290.0 K, the full carbon vessel presents a pressure drop of 46% while the 23.5% PCM vessel pressure drops by 8%. At 327.5 K, the full-carbon vessel presents a pressure drop of 42% while the 19.5% PCM vessel pressure drops by 18%. The effect of this pressure variation in the gas delivery capacity is presented in Fig. 27. After an initial increase, the curve stagnates during the filling cycle because the SA model does not consider convection, which means that the system cannot dissipate heat and increase adsorption equilibrium density. The increase of adsorbed gas after 360 s represents the gas that is in the gaseous state and is adsorbed after the charging cycle is finished. The full-carbon vessel has significantly more residual gas than the vessel with PCM by the end of the discharging cycle. The step in the curves after the charging cycle is caused by the pressure drop between the cycles.

Fig. 26

The pressure loss during case 3

Fig. 27

Case 3 adsorbed gas volume evolution during 3600 s

Unlike the other cases, the best option for case 3 would be a PCM with phase change temperature equal to or below the ambient temperature. This contrast arises because desorption is the dominant phenomena. Additionally, the gains steadily increase as ambient temperature decreases. For case 3, the trend is the opposite of that observed in cases 1 and 2, where PCM gain increases when external temperature decreases. The explanation is that the dominant effect, in this case, is the pressure loss due to temperature variation between the charging cycle and discharging cycle. The pressure loss effect represents the adsorption of the gas in gaseous form by the end of the charging cycle but in adsorbed form by the start of the discharging process. Naturally, the full carbon vessel adsorbs less gas at higher ambient temperatures than at lower ambient temperatures. Consequently, the temperature variation at high ambient temperature is lower, resulting in a smaller pressure loss. Because PCM reduces the temperature increase during the charging cycle, it reduces the pressure loss, which is higher at lower ambient temperatures, thereby being more effective.

The summary of the optimised points found for each temperature are presented in Table 6:

Table 6 Summary of case 3 optimised PCM ratios

These results regard the homogeneous distribution of PCM inside an adsorption tank. In case 1, adsorption is the only phenomena taking place. Although case 3 starts with adsorption and ends with desorption, being the latter, the limiting phenomena. This dominance determines if the phase change temperature is higher or lower than the ambient temperature. However, for these cases, varying the ambient temperature does not modify the optimised amount of PCM. In case 2, adsorption and desorption are both taking place, and desorption is influenced by adsorption for the discharging cycle starts in the state that the charging cycle ends. In this case, the favoured phenomenon is adsorption. The reason for that might be related to storing as much energy as possible in the PCM internal energy so it can be used to aid the desorption phenomenon.

5.2.2 Graded material optimisation

In this section, the benefits brought by optimised homogeneous PCM distribution inside an adsorption vessel are quantified. As the semi-analytic model does not consider the effects caused by the boundaries convection boundary conditions, it is expected that it is possible to go beyond the homogeneous optimised solution when applying FGM optimisation to distribute material inside the vessel properly. It is expected that the larger the container, the closer the 2D model and the SA model match, while for smaller tanks, the gain brought by the graded solution tends to be higher.

FGM implementation considers the parameters shown in Fig. 11. The initial PCM condition is a homogeneous distribution with all design variables set according to the homogenised optimised PCM distribution obtained in the previous subsection. For the optimisation of the 2D model, only case 1 will be run. It will consider an ambient temperature of 300 K, the initial PCM distribution is set to ε = 0.0% for all domain, and the Helmholtz filter length is set to z = 0.01. The ROL (Rapid Optimisation Library) (Rapid Optimization Library 2020) optimiser applies augmented Lagrangian method guided by quasi-Newton line search method (Rapid Optimization Library 2020) with L-BFGS-B.

The optimiser chosen for this application is the augmented Lagrangian method from ROL (Rapid Optimisation Library) (Rapid Optimization Library 2020). The new solution is determined by quasi-Newton line search method.

The radial section of the cylindrical vessel considered for optimisation is the same as that used for adsorption validation as depicted in Fig. 11. The 2D FGM optimisation considers the scenario of natural convection and for a convection coefficient of 700 W/m.K, assumed at boundaries, representing a value describing efficient surface cooling.

It is verified that for lower volume rates during the filling cycle, the tanks present the highest efficiency, while for higher volume rates, the efficiency is lower (Sahoo et al. 2010). This happens because, for lower volume rates, the cycle time is higher than for lower volume rates, which allows convection to remove more heat from the system during the filling cycle, resulting in a cooler system. This picture may be addressed as a time-scale problem. For the SA model, which does not consider convection, the time-scale does not affect the result. For the 2D model, this time-scale problem is handled by altering the heat transfer rate, instead of filling time so that convection will take more or less heat from the system.

Figure 28 shows the results obtained for the vessel optimisation considering 300.0 K as ambient temperature, a low convection rate, and a cycle time of 240 s. It also depicts the comparison between the temperature and amount of gas for three-vessel configurations, being them, full carbon, homogenised solution (of 14% PCM), and optimised solution. As expected, the distribution is almost homogeneous throughout most of the domain, placing no PCM where the adsorbent has its temperature reduced by the boundary effect. PCM concentration ranges from zero to 14% for the slower filling cycle. When compared to the homogeneous solution, the amount of gas that the graded vessel is capable of storing is about 1% more. This improvement comes from excluding PCM from the boundary regions, which are already cooled by the air intake and convection. The integral of the total amount of PCM inside the vessel reduces from the homogeneous solution (14.0%) to 13.7%, which is expected as the optimiser removes PCM from the regions close to the borders. The variation between the homogeneous and the graded solution is low because the external convection does not remove enough heat to cause a significant change in results.

Fig. 28

Optimised PCM distribution, functional evolution throughout the optimisation, temperate, and adsorbed gas amount for Eicosane (Kahwaji et al. 2018) at ambient temperature of 300 K and low convection

In Fig. 29 considering 300.0 K as ambient temperature, a high convection rate. As in the low convection case, the border effects such as external convection and inlet gas temperature affects the internal PCM distribution. The optimised PCM distribution in his case stores 2% more gas than the homogenised solution. The low variation between the homogeneous and FGM solution in both cases is related to the low thermal conductivity of the adsorbent and also the adsorption isotherms, which affects how adsorption capacity changes according to the temperature.

Fig. 29

Optimised PCM distribution, functional evolution throughout the optimisation, temperate and adsorbed gas amount for Eicosane (Kahwaji et al. 2018) at ambient temperature of 300 K and high convection

Figure 30 shows the evolution of the total PCM ratio throughout the optimisation. The vessel with low convection converges to 13.7% while the tank with high convection converges to 8.4%. This variation is caused to the external convection boundary condition. Table 7 summarises the total adsorbed gas volume by the end of the analysis for the three-vessel configurations. The FGM solution adsorbs more gas than the other, especially when boundary condition effects are more pronounced. In Table 8, the improvements of each solution are compared. At low convection conditions, PCM brings more improvement to the system. In this case, the variation between the homogeneous solution and the FGM solution is around 1%. For the high convection scenario, the difference between the solutions doubles, reaching 2%. The variation between both solutions is low in both cases. The FGM solution is more suitable for cases with higher boundary effects magnitude. However, the same table shows that at high external convection values, the benefits brought by PCM are lower than those for low convection. The computational time of both models is presented in Table 9. The 2D model spent 24,736 s during its computation while the SA model spent 1304 s (about 5% of the 2D model). Both models were run on an Intel(R) Xeon(R) CPU E5-2630 v2 @ 2.6 GHz with 24 cores and 70 Gb of RAM.

Fig. 30

Optimised PCM ratio evolution throughout the optimisation iterations

Table 7 Volume variation between the homogeneous solution and the graded solution

Table 8 Improvement variation between the homogeneous solution and the graded solution when compared to the full carbon condition

Table 9 Computing time comparison between SA model and 2D model

A virtual analysis for the charging cycle was run with the high convection optimised PCM distribution to compare with the full carbon configuration. Figure 31 presents the evolution of the total amount of gas inside the system during the charging cycle. As expected, the optimised vessel starts the analysis with less gas because there is less adsorbent inside it but finished the process with more gas, because the mixture has a higher adsorbed gas density due to temperature reduction. The temperature and adsorbed gas mass are already presented in Fig. 29.

Fig. 31

Comparison between full carbon vessel and the optimised design in virtual analysis

These results are sensitive to the adsorbent material. The materials here used were chosen because their properties are easily found in the literature. The material adsorption characteristics and the adsorption heat play substantial roles in this optimisation; likewise, the phase change temperature and the phase change enthalpy also does.

It is important to remark that the axisymmetrical nature of this analysis hinders optimisation. It makes it impossible for the optimiser to build 3D patterns. A full 3D analysis may lead to different patterns, offering higher gains; however, the small gains in FGM optimisation suggests that extending it to 3D is unlikely to improve significantly.

6 Conclusions

Two approaches were presented to distribute PCM material inside an adsorption system optimally. The semi-analytic model describes a homogeneous PCM distribution that is suitable for vessels whose dimensions are large compared to the inlet and external convection effects because it does not consider local effects.

The 2D axisymmetric optimisation was compared to the semi-analytic model to verify how much the boundary effects could represent a change in the vessel optimised PCM distribution. Results show that for cases where convection is not negligible, the semi-analytic model has its benefits reduced. The 2D model is indicated for adsorption systems with longer cycle times and/or higher convection rates due to the effect that the boundaries have on the solution. The 2D axisymmetric results use less PCM than the homogeneous result from the semi-analytic model. Consequently, the 2D model may be indicated when the volume of used PCM is a concern.

The semi-analytic model presented a good agreement to the results found in literature when convection is low. The full factorial sweep returned results which provide improvements that are very close to those obtained via FGM optimisation in these cases. Therefore, this approach presents a very attractive cost-benefit when optimising an adsorbent system with mixtures. As the adsorption phenomenon is time transient and complex cycles may demand many time steps, its computational cost may be a problem for the 2D model, which does not happen in the semi-analytic approach.

For all cases, the optimised result is an adsorbent and PCM mixture. The mixture removes part of the adsorbent and increases the adsorbed density of those adsorbent particles that remain. The result is that the vessel stores less gas at standard conditions for temperature and pressure, which is desirable because it means less residual gas by the end of the discharging process, and more gas by the end of the charging process because the temperature amplitude inside the vessel during the cycle is reduced by PCM. For case 3 in SA model, PCM reduced the pressure loss after the charging cycle.

In this study, adsorption simulation was carried out as a transient phenomenon. However, if it could be addressed as a stationary problem, the efficiency and computational cost for the analysis would be reduced, and more complex cycles could be optimised via FG or topology optimisation. The stationary approach is available for further exploration.

Another aspect of evaluating may be whether it is convenient to develop technology to build non-homogeneous adsorbent systems. This technology could employ additive manufacturing or even create several internal chambers inside the vessel, each filled with its respective adsorbent and PCM mixture. Nevertheless, results present small variations between the FG solution and the optimised homogeneous solution. Consequently, the cost and effort to develop the technology for building these vessels are unlikely to be justified.

7 Replication of results

The implementation in the FEniCS platform is direct from the description provided of the equations and numerical implementation in this article. FEniCS is based on a high-level description for the variational formulation (UFL); therefore, the generation of the matrix equations is automated.

The pseudocode of the implementation is indicated in Appendix B and C, where the main FEniCS/dolfin-adjoint functions that are being used are represented between parentheses. When using dolfin-adjoint, the dolfin-adjoint library provides an interface to ROL. In Appendix A, the pseudocode for the semi-analytic model describes the procedure for each case.

Appendices

Appendix A: Phase change model

An analytic model for the phase change phenomena can be found in the literature in the form of a Laplace transform of the thermal energy balance equation. It presents a solution for a system that undergo a unidimensional phase change phenomena. Figure 32 shows a schematic of a system in which the left wall, referred to as a leading surface, has its temperature prescribed at a high temperature during the whole simulation and initial temperature equal to the phase change temperature elsewhere. As the simulation goes by, the domain will receive heat from the left wall, thereby melting from the left side. This model aims to describe the position of the phase change interface as it travels through the domain. Consequently, it is possible to determine the amount of exchanged heat and the temperature according to the position.

Fig. 32

Semi-infinite domain presenting phase change

The equation that describes the energy balance for this system is present in serveral works (Ku and Chan 1990; Ogoh and Groulx 2010; Muhieddine et al. 2009; Jonsson 2013). It is expressed by:

$$ (\rho{}C_{p})_{l} \frac{\partial T_{l}}{\partial t} = k_{l} \frac{\partial^{2} T_{l}}{\partial x^{2}} $$

(43)

with the boundary condition of Stefan’s problem: wall temperature: (T(x = 0,t > 0) = T_w) and melting front temperature: (T(x = δ(t),t > 0) = T_m). Where ρ is the density, C_p is the specific heat, k is the thermal conductivity, t and x are time and space coordinates, respectively, and δ(t) is the position of the solid-liquid interface. The subscript l refers to the liquid phase.

Employing the Laplace transform in (43) and subsequently taking the inverse transform for the assumed boundary conditions, the analytical solution will assume the form seen in Ku and Chan (1990):

$$ \frac{T_{l} - T_{w}}{T_{w} - T_{c}} = \text{erf} (\frac{x}{2(\alpha_{l} t )^{2}}) $$

(44)

where erf is the error function given by $\text {erf}(x)= \frac {2}{\sqrt {\pi }} {{{\int \limits }_{0}^{x}} e^{-t^{2}} dt}$ and T_c is given by:

$$ T_{c} = T_{w} - \frac{T_{w} - T_{m}}{\text{erf}(\lambda)} $$

(45)

and λ is the result of the non-linear equation (Ogoh and Groulx 2010):

$$ \lambda e^{\lambda^{2}} \text{erf}(\lambda) = \frac{St_{l}}{\sqrt{\pi}} = \frac{C_{p,l}(T_{w} - T_{m})}{L \sqrt{\pi}} $$

(46)

The phase change barrier position can be written as Ogoh and Groulx (2010):

$$ \delta(t) = 2 \lambda \sqrt{\alpha_{l} t} $$

(47)

Finally, the solution for the temperature along the system is given by:

$$ T_{l}(x) = \begin{cases} T_{w} + \frac{(T_{w} - T_{m})}{\text{erf}(\lambda)}\text{erf}(\frac{x}{2(\alpha_{l} t )^{2}}) & \text{if } x \leqslant \delta(t)\\ T_{m} & \text{otherwise} \end{cases} $$

(48)

Appendix B: Pseudocode for 2D analysis and optimisation

Input parameters

Pressure, temperature, adsorbed gas portion, optimisation parameters, and constants.

Result

Optimised PCM distribution (optimised distribution of the design variable).

1 - Generate the finite element mesh (“generate_mesh”)

2 - Prepare the state variables (pressure and temperature) and design variable (see Section 4). (CG1 “FiniteElement” with “dim= 2” (Pressure and Temperature), CG0 “FiniteElement” (adsorbed gas portion).

3 - Define the bounds of the design variable ([0, 1]).

4 - Define the initial guess of the distribution (i.e. the initial values of the design variable) (“interpolate”)

5 - Prepare the finite element method and Define the material model (23) and (24)

6 - Apply Helmholtz filter (38)

7 - For the adsorption problem: 7.1 - Define the weak form of the adsorption problem (32) and (33)

7.2 - Define the linear solver for the adsorption simulation (“solve”)

7.3 - Solve the physics equations. When performing this operation, dolfin-adjoint automatically annotates the corresponding adjoint model

8 - Determine the new adsorption equilibrium (7)

9 - Repeat from step 7 until the cycle ends;

10 - Finish preparing the topology optimisation problem

10.1 - Set the design variable (“Control”)

10.2 - Define the objective function (27) (“assemble”)

10.3 - Prepare the ROL solver for topology optimisation (“ReducedFunctional”, “MinimizationProblem”, “ROLSolver”)

10.4 - Run the ROL solver (“ROLSolver.solve”)

11 - Post-process the optimised topology

Appendix C: Pseudocode for 0D analysis

Input parameters

Pressure, temperature, adsorbed gas portion, and constants.

Result

PCM improvement charts (optimised distribution of the design variable).

1 - Prepare the state variables (pressure and temperature) and design variable (see Section 4);

2 - Define the bounds of the design variable and the steps that will be set for analysis;

3 - Define the initial guess of the distribution, set for the lower boundary (i.e. the initial values of the design variable);

4 - For the adsorption problem: 4.1 - Solve the mass balance equation of the adsorption problem (see Section 4.3);

4.2 - Solve the energy balance equation of the adsorption problem (see Section 4.3);

4.3 - Solve the numeric integration for Q;

4.4 - If case 1: repeat step 4 until the cycle ends;

4.4 - If case 2: repeat step 4 until the cycle ends;

4.4 - If case 3: repeat step 4 until the charging cycle ends. Solve (42) to define P_i. Set P and T as P_i and T_amb respectively and repeat step 4 until discharging cycle ends;

5 - Store analysis data and results;

6 - Adjust the design variable and repeat step 4;

7 - Post-process the data and generate the PCM Improvement Charts.

Appendix D: Properties

The data used in this work are available in the literature. The material properties used in the simulation are listed in this appendix. Methane properties are in Table 10, activated methane properties are listed in Table 11 and PCM properties are presented in Table 12. The properties of methane adsorption on carbon are in Table 13.

Table 10 Methane properties (Sahoo et al. 2011; Sahoo et al. 2014)

Table 11 Activated carbon properties (Sahoo et al. 2011)

Table 12 Eicosane (Kahwaji et al. 2018)

Table 13 Adsorption parameters for methane on activated carbon (Sahoo et al. 2011; Sahoo et al. 2014)