Adaptive multi-fidelity sparse polynomial chaos-Kriging metamodeling for global approximation of aerodynamic data

Abstract

The multi-fidelity metamodeling method can dramatically improve the efficiency of metamodeling for computationally expensive engineering problems when multiple levels of fidelity data are available. In this paper, an efficient and novel adaptive multi-fidelity sparse polynomial chaos-Kriging (AMF-PCK) metamodeling method is proposed for accurate global approximation. This approach, by first using low-fidelity computations, builds the PCK model as a model trend for the high-fidelity function and captures the relative importance of the significant sparse polynomial bases selected by least angle regression (LAR). Then, by using high-fidelity model evaluations, the developed method utilizes the trend information to adaptively refine a scaling PCK model using an adaptive correction polynomial expansion-Gaussian process modeling. Here, the most relevant sparse polynomial basis set and the optimal correction expansion are adaptively identified and constructed based on a devised nested leave-one-out cross-validation-based LAR procedure. As a result, the optimal AMF-PCK metamodel is adaptively established, which combines advantages of high flexibility and strong nonlinear modeling ability. Moreover, an adaptive sequential sampling approach is specially developed to further improve the multi-fidelity metamodeling efficiency. The developed method is evaluated by several benchmark functions and two practically challenging transonic aerodynamic modeling applications. A comprehensive comparison with the popular hierarchical Kriging, universal Kriging, and LAR-PCK approaches demonstrates that the proposed method is the most efficient and provides the best global approximation accuracy, with particular superiority for quantities of interest in the multimodal and highly nonlinear landscape. This novel method is very promising for efficient uncertainty analysis and surrogate-based optimization of expensive engineering problems.

Appendices

Appendix 1: Adaptive multi-level multi-fidelity polynomial chaos-Kriging metamodeling

Essentially, there often exist multiple sets of data corresponding to multiple levels of fidelity data. For example, for aerodynamic analysis, an often-employed hierarchy comprises Reynolds averaged Navier-Stokes (RANS) equations with different grid levels, Euler equations, and potential theory. Similar hierarchies of models also exist in other fields of engineering. Therefore, the application of multiple levels of fidelity to assist the HF prediction of the same output quantity is expected to contribute to the reduction of computational cost significantly. Further, a multi-level AMF-PCK metamodel can be built by

(52)

where the function predictors $\left\{{\hat{y}}_{l_0},{\hat{y}}_{l_1},{\hat{y}}_{l_2},\cdots, {\hat{y}}_{l_{\tau }}\right\}$ have the reduced (τ + 1) levels of fidelity and ${\hat{y}}_{l_0}$ denotes the highest-fidelity predictor for the physical model (or the HF function) based on all the sample data, namely, ${\hat{y}}_h$. The lowest-fidelity function predictor ${\hat{y}}_{l_{\tau }}$ is the PCK model built using the lowest-fidelity sample set, namely,

$$ {\hat{y}}_{l_{\tau }}(X)=\sum \limits_{r_i\in A}{\beta}_{r_i}{\psi}_{r_i}(X)+{r}_{l_{\tau}}^{\mathrm{T}}{R}_{l_{\tau}}^{-1}\left({Y}_{l_{\tau }}-{\varPsi}_r{\beta}_r\right) $$

(53)

where A is the index set of the selected polynomials in ${\hat{y}}_{l_{\tau }}\left(\boldsymbol{X}\right)$, as presented in Section 3.1. α_i and C_i(X) denote the i^th level scaling factor and the i^th level adaptive correction polynomial expansion-Gaussian process term, respectively. ${y}_{c_i}\left(\boldsymbol{X}\right)$ is the i^th level correction polynomial expansion defined by

$$ {y}_{c_i}\left(\mathbf{X}\right)=\sum \limits_{c_{i,j}\in {A}_{c_i}}{\alpha}_{c_{i,j}}{\psi}_{c_{i,j}}\left(\mathbf{X}\right), $$

(54)

where ${A}_{c_i}$ and ${\alpha}_{c_{i,j}}$ are the index set of the i^th level correction polynomial expansion and corresponding polynomial coefficient, respectively. Specifically, the index sets of polynomials for (52) should meet the condition of ${A}_{c_0}\subseteq {A}_{c_1}\subseteq \cdots {A}_{c_{\tau -2}}\subseteq {A}_{c_{\tau -1}}\subseteq A$. The building procedures of ${\hat{y}}_{l_i}$ of the i^th level model, ${y}_{c_i}\left(\boldsymbol{X}\right)$ of the i^th level correction expansion, and ${z}_{l_i}\left({\boldsymbol{X}}^{(i)}\right)$ of the i^th level stationary Gaussian process are the same as those presented in Sections 3.1, 3.2, and 3.3. Subsequently, we can build the PC-Kriging model ${\hat{y}}_{l_i}$ for the i^th level with the lower-fidelity PCK ${\hat{y}}_{l_{i+1}}$ serving as its model trend.

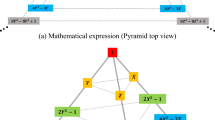
Next, an adaptive LOOCV-based multi-level AMF-PCK metamodeling procedure is applied when multiple levels of fidelity data are available. Figure 17 gives the sketch map of (τ + 1)-level AMF-PCK metamodeling using the proposed correction form.

Fig. 17

The sketch map of (τ + 1)-level AMF-PCK correction procedure

• 1) Represent the response functions for the same output quantity corresponding to (τ + 1) levels of fidelity data as $\left\{{y}_{l_0}\left(\boldsymbol{X}\right),{y}_{l_1}\left(\boldsymbol{X}\right),{y}_{l_2}\left(\boldsymbol{X}\right),\cdots, {y}_{l_{\tau }}\left(\boldsymbol{X}\right)\right\}$. Apply efficient DOE strategies to generate (τ + 1) sets of samples corresponding to (τ + 1) levels of fidelity functions, namely, ${\boldsymbol{S}}_{l_k}={\left\{{\boldsymbol{X}}^{(i)}\right\}}_{i=1}^{N_{l_k}},k=0,1,2,\cdots, \tau$, ($\mathrm{typically}\ {N}_{l_0}\ll {N}_{l_1}\ll \cdots \ll {N}_{l_{\tau }}\Big),$ where ${N}_{l_j}$ represents the number of sample points for the j^th level of fidelity data. Evaluate their responses stored in ${\boldsymbol{Y}}_{l_k}={\left({y}_{l_k}\left({\boldsymbol{X}}^{(1)}\right),{y}_{l_k}\left({\boldsymbol{X}}^{(2)}\right),\cdots, {y}_{l_k}\left({\boldsymbol{X}}^{\left({N}_{l_k}\right)}\right)\right)}^{\mathrm{T}}$ (k = 0, 1, 2, ⋯, τ), respectively. Other initializations are similar with those presented in Section 3.4, e.g., error criterion ϵ_h, candidate polynomials set $\left\{{\psi}_1\left(\boldsymbol{X}\right),{\psi}_2\left(\boldsymbol{X}\right),\cdots, {\psi}_{M_p}\left(\boldsymbol{X}\right)\right\}$.

• 2) Run the adaptive LAR algorithm using the lowest-fidelity sample set $\left\{{\boldsymbol{S}}_{l_{\tau }},{\boldsymbol{Y}}_{l_{\tau }}\right\}$ to obtain a ranked basis set from the candidate polynomial bases, which are chosen depending on their correlation to the current residual at each iteration in decreasing order, i.e., $\left\{{\psi}_{r_1}\left(\boldsymbol{X}\right),{\psi}_{r_2}\left(\boldsymbol{X}\right),\cdots, {\psi}_{r_{M_{l_{\tau }}}}\left(\boldsymbol{X}\right)\right\},$ where ${M}_{l_{\tau }}=\min \left({M}_p,{N}_{l_{\tau }}-1\right)$. The number of lowest-fidelity sample points is sufficient, but their evaluations are much cheaper compared to the computations of the same number of higher-fidelity sample points.

• 3) Build a series of the lowest-fidelity LAR-PCK metamodels $\left\{{\hat{y}}_{l_{\tau}}^{\left({M}_{\tau}\right)}\left(\boldsymbol{X}\right)\right\}$ using the first M_τ PC term(s) from the ranked PC bases functions as the trend functions, i.e., $\left\{{\psi}_{r_1}\left(\boldsymbol{X}\right),{\psi}_{r_2}\left(\boldsymbol{X}\right),\cdots, {\psi}_{r_{M_{\tau }}}\left(\boldsymbol{X}\right)\right\}\ \left({M}_{\tau }=1,2,3,\cdots, {M}_{l_{\tau }}\right)$, by utilizing the lowest-fidelity sample set $\left\{{\boldsymbol{S}}_{l_{\tau }},{\boldsymbol{Y}}_{l_{\tau }}\right\}$. Each polynomial is added one by one to the trend functions.

• 4) For each lowest-fidelity PCK model ${\hat{y}}_{l_{\tau}}^{\left({M}_{\tau}\right)}\left(\boldsymbol{X}\right)$, build a series of two-level AMF-PCK metamodels $\left\{{\hat{y}}_{l_{\tau -1}}^{\left({M}_{\tau },{M}_{c_{\tau -1}}\right)}\left(\boldsymbol{X}\right)\right\}$ using the higher-fidelity sample set $\left\{{\boldsymbol{S}}_{l_{\tau -1}},{\boldsymbol{Y}}_{l_{\tau -1}}\right\}$ with increasing cardinality ${M}_{c_{\tau -1}}$ of the correction expansion ${y}_{c_{\tau -1}}^{\left({M}_{c_{\tau -1}}\right)}\left(\boldsymbol{X}\right)$, as given by (52), where PC basis set in the correction expansion ${y}_{c_{\tau -1}}^{\left({M}_{c_{\tau -1}}\right)}\left(\boldsymbol{X}\right)$ as $\left\{{\psi}_{r_1}\left(\boldsymbol{X}\right),{\psi}_{r_2}\left(\boldsymbol{X}\right),\cdots, {\psi}_{r_{M_{c_{\tau -1}}}}\left(\boldsymbol{X}\right)\right\}$ $\left({M}_{c_{\tau -1}}=1,2,3,\cdots, \min \left({M}_{\tau },{N}_{l_{\tau -1}}\right)\right)$. The fitting procedure of two-level AMF-PCK model is the same as that presented in Section 3.3.

• 5) Proceed the modeling process until τ levels of lower-fidelity data are utilized. For each (τ − 1)-level AMF-PCK metamodel ${\hat{y}}_{l_2}^{\left({M}_{\tau },{M}_{c_{\tau -1}},\cdots, {M}_{c_2}\right)}\left(\boldsymbol{X}\right)$, build a series of τ-level AMF-PCK metamodels $\left\{{\hat{y}}_{l_1}^{\left({M}_{\tau },{M}_{c_{\tau -1}},\cdots, {M}_{c_1}\right)}\left(\boldsymbol{X}\right)\right\}$ using the higher-fidelity sample set $\left\{{\boldsymbol{S}}_{l_1},{\boldsymbol{Y}}_{l_1}\right\}$ with increasing cardinality ${M}_{c_1}$ of the correction expansion ${y}_{c_1}^{\left({M}_{c_1}\right)}\left(\boldsymbol{X}\right)$, where PC basis set in the correction expansion ${y}_{c_1}^{\left({M}_{c_1}\right)}\left(\boldsymbol{X}\right)$ as $\left\{{\psi}_{r_1}\left(\boldsymbol{X}\right),{\psi}_{r_2}\left(\boldsymbol{X}\right),\cdots, {\psi}_{r_{M_{c_1}}}\left(\boldsymbol{X}\right)\right\}$ $\left({M}_{c_1}=1,2,3,\cdots, \min \left({M}_{c_2},{N}_{l_1}\right)\right)$. The fitting procedure of the τ-level AMF-PCK model is similar with that presented in Section 3.3, though it utilizes the (τ − 1)-level AMF-PCK metamodel as the low-fidelity model.

• 6) For $i=1,2,\kern0.5em \cdots, {N}_{l_0}$:

• a) For each τ-level AMF-PCK model ${\hat{y}}_{l_1}^{\left({M}_{\tau },{M}_{c_{\tau -1}},\cdots, {M}_{c_1}\right)}\left(\boldsymbol{X}\right)$ using the sample set $\left\{{\boldsymbol{S}}_{l_0},{\boldsymbol{Y}}_{l_0}\right\}\backslash \left\{{\boldsymbol{X}}^{(i)},{y}_{l_0}\left({\boldsymbol{X}}^{(i)}\right)\right\}$, build a series of (τ + 1)-level AMF-PCK metamodels $\left\{{\hat{y}}_{l_0^{\left(-i\right)}}^{\left({M}_{\tau },{M}_{c_{\tau -1}},\cdots, {M}_{c_0}\right)}\left(\boldsymbol{X}\right)\right\}$ with increasing cardinality ${M}_{c_0}$ of the correction expansion ${y}_{c_0}^{\left({M}_{c_0}\right)}\left(\boldsymbol{X}\right)$, where PC basis set in the correction expansion ${y}_{c_0}^{\left({M}_{c_0}\right)}\left(\boldsymbol{X}\right)$ as $\left\{{\psi}_{r_1}\left(\boldsymbol{X}\right),{\psi}_{r_2}\left(\boldsymbol{X}\right),\cdots, {\psi}_{r_{M_{c_0}}}\left(\boldsymbol{X}\right)\right\}$ $\left({M}_{c_0}=1,2,\cdots, \min \left({M}_{c_1},{N}_{l_0}\right)\right)$. The cardinality of the correction expansions should satisfy ${M}_{c_0}\le {M}_{c_1}\le \cdots \le {M}_{c_{\tau -1}}\le {M}_{\tau}\le {M}_{l_{\tau }}$.

• b) Calculate the prediction residual ${\delta}_{M_{\tau },{M}_{c_{\tau -1}},\cdots, {M}_{c_0}}^{(i)}$ at high-fidelity point X⁽ⁱ⁾ by each (τ + 1)-level AMF-PCK model ${\hat{y}}_{l_0^{\left(-i\right)}}^{\left({M}_{\tau },{M}_{c_{\tau -1}},\cdots, {M}_{c_0}\right)}\left(\boldsymbol{X}\right)$, where ${\delta}_{M_{\tau },{M}_{c_{\tau -1}},\cdots, {M}_{c_0}}^{(i)}={\hat{y}}_{l_0^{\left(-i\right)}}^{\left({M}_{\tau },{M}_{c_{\tau -1}},\cdots, {M}_{c_0}\right)}\left({\boldsymbol{X}}^{(i)}\right)-{y}_{l_0}\left({\boldsymbol{X}}^{(i)}\right)$.

• 7) Calculate the LOOCV error ${\varepsilon}_{M_{\tau },{M}_{c_{\tau -1}},\cdots, {M}_{c_0}}={Err_{LOO}}_{M_{\tau },{M}_{c_{\tau -1}},\cdots, {M}_{c_0}}$ of each (τ + 1)-level AMF-PCK metamodel, where ${Err_{LOO}}_{M_{\tau },{M}_{c_{\tau -1}},\cdots, {M}_{c_0}}={\sum}_{i=1}^{N_{l_0}}{\left({\delta}_{M_{\tau },{M}_{c_{\tau -1}},\cdots, {M}_{c_0}}^{(i)}\right)}^2/{N}_{l_0}$. Find ${\varepsilon}^{\ast }={\varepsilon}_{M_{\tau}^{\ast },{M}_{c_{\tau -1}}^{\ast },\cdots, {M}_{c_0}^{\ast }}=\min \left\{{\varepsilon}_{M_{\tau },{M}_{c_{\tau -1}},\cdots, {M}_{c_0}}\right\}$, (${M}_{\tau }=1,2,\cdots, {M}_{l_{\tau }};{M}_{c_{\tau -1}}=1,2,\cdots, \min \left({M}_{\tau },{N}_{l_{\tau -1}}\right);\cdots; {M}_{c_0}=1,2,\cdots, \min \left({M}_{c_1},{N}_{l_0}\right)$), as well as the corresponding number ${M}_{\tau}^{\ast }$ of the LF PC bases and the corresponding cardinalities ${M}_{c_{\tau -1}}^{\ast },\cdots,$ ${M}_{c_1}^{\ast }$and ${M}_{c_0}^{\ast }$ of the correction expansion sets. Then, the optimal (τ + 1)-level AMF-PCK metamodel ${\hat{\mathrm{y}}}_{l_0}^{\left({M}_{\tau}^{\ast },{M}_{c_{\tau -1}}^{\ast },\cdots, {M}_{c_0}^{\ast}\right)}\left(\boldsymbol{X}\right)\ \left(\mathrm{or}\ {\hat{\mathrm{y}}}_h^{\left({M}_{\tau}^{\ast },{M}_{c_{\tau -1}}^{\ast },\cdots, {M}_{c_0}^{\ast}\right)}\left(\boldsymbol{X}\right)\right)$ can be built, with the optimal PC basis set $\left\{{\psi}_{r_1}\left(\mathbf{X}\right),{\psi}_{r_2}\left(\mathbf{X}\right),\cdots, {\psi}_{r_{M_{\tau}^{\ast }}}\left(\mathbf{X}\right)\right\}$ in the LF PCK ${\hat{y}}_{l_{\tau}}^{\left({M}_{\tau}^{\ast}\right)}\left(\mathbf{X}\right)$ and the corresponding optimal correction expansion sets $\left\{{\psi}_{r_1}\left(\mathbf{X}\right),{\psi}_{r_2}\left(\mathbf{X}\right),\cdots, {\psi}_{r_{M_{c_{\tau -1}}^{\ast }}}\left(\mathbf{X}\right)\right\}$,⋯, $\left\{{\psi}_{r_1}\left(\mathbf{X}\right),{\psi}_{r_2}\left(\mathbf{X}\right),\cdots, {\psi}_{r_{M_{c_1}^{\ast }}}\left(\mathbf{X}\right)\right\},$ $\left\{{\psi}_{r_1}\left(\mathbf{X}\right),{\psi}_{r_2}\left(\mathbf{X}\right),\cdots, {\psi}_{r_{M_{c_0}^{\ast }}}\left(\mathbf{X}\right)\right\}$ in ${y}_{C_{\tau -1}}^{\left({M}_{c_{\tau -1}}^{\ast}\right)}\left(\mathbf{X}\right),\cdots, {y}_{c_1}^{\left({M}_{c_1}^{\ast}\right)}\left(\mathbf{X}\right),{y}_{c_0}^{\left({M}_{c_0}^{\ast}\right)}\left(\mathbf{X}\right)$, respectively.

• 8) If ε^∗ is larger than the target error ϵ_h, the user can enrich the different levels of fidelity sample sets by (multi-fidelity) sequential sampling strategies, and repeat steps 2–7 until the error criterion is satisfied. Build the optimal (τ + 1)-level AMF-PCK metamodel using the selected PC basis sets and all (τ + 1)-level fidelity of data.

Appendix 2: Nomenclature

ψ_i, β_i, p, M_p:

Polynomial basis, polynomial coefficient, polynomial order, and truncated polynomial terms

Ψ :

Polynomial measurement matrix

${y}_l,\kern0.5em {y}_h,\kern0.5em {\hat{y}}_l,\kern0.5em {\hat{y}}_h$ :

Low- and high-fidelity function responses, low-and high-fidelity predictions

${\psi}_{c_i},\kern0.5em {\alpha}_{c_i}$ :

PC basis in correction expansion and corresponding coefficient

α ₀ :

Scaling factor for low-fidelity model

S_l, S_h, Y_l, Y_h, N_l, N_h:

Low- and high-fidelity sample sets and their responses sets and corresponding sample sizes

A, A_c, M, M_c:

Index sets of selected LF PCE and correction PCE and corresponding cardinalities

C(X):

Additive correction term

${z}_l,{z}_h,{\hat{\sigma}}_{z_l}^2,{\hat{\sigma}}_{z_h}^2$ :

Gaussian random process and corresponding stationary process variance

R_l, R_h, R, θ_l, θ_h:

Correlation matrix, autocorrelation function, and corresponding hyper-parameters of R

r_l, r_h:

Correlation vectors

Ma, Re, AoA :

Freestream Mach number, Reynolds number based on airfoil chord, and angle of attack

C_l, C_d, C_m:

Lift, drag, and pitching moment coefficients

Appendix 3: Highlights

• An efficient AMF-PCK metamodeling technique is proposed.

• A nested LOOCV-based LAR adaptive basis-selection procedure for the optimal AMF-PCK is developed.

• An adaptive sequential sampling based on LOOCV-Voronoi-MSD approach is devised for MF metamodeling.

• Comprehensive comparisons among AMF-PCK, HK, UK, and LAR-PCK are made by multiple benchmark examples.

• The AMF-PCK for global approximation appreciably improves efficiency, accuracy, and reliability.