Cryptanalysis of OCB2: Attacks on Authenticity and Confidentiality

Abstract

We present practical attacks on OCB2. This mode of operation of a blockcipher was designed with the aim to provide particularly efficient and provably secure authenticated encryption services, and since its proposal about 15 years ago it belongs to the top performers in this realm. OCB2 was included in an ISO standard in 2009. An internal building block of OCB2 is the tweakable blockcipher obtained by operating a regular blockcipher in ${\text {XEX}}^*$ mode. The latter provides security only when evaluated in accordance with certain technical restrictions that, as we note, are not always respected by OCB2. This leads to devastating attacks against OCB2’s security promises: We develop a range of very practical attacks that, amongst others, demonstrate universal forgeries and full plaintext recovery. We complete our report with proposals for (provably) repairing OCB2. As a direct consequence of our findings, OCB2 is currently in a process of removal from ISO standards. Our attacks do not apply to OCB1 and OCB3, and our privacy attacks on OCB2 require an active adversary.

Appendices

A. Brief History of This Paper

A frequent question we have received is how we came to find the flaws, and how they lead to the devastating attacks. The current article is based on three prior ones [17, 21, 32] that appeared in late 2018 on the IACR ePrint archive. That OCB2 might be flawed was first identified by the authors of [17] when they re-examined the proofs of OCB2 for educational purposes and searched for potential improvements. Instead, they came to find a seemingly tiny crack in the proof that they first tried to fix as they strongly believed OCB2 was a secure design, but after several tries they ended up with existential and (near-)universal forgeries. Only two weeks after these findings became public (in [17]), the author of the second ePrint article [32] announced an IND-CCA vulnerability and first steps toward plaintext recovery, and again three days later, the author of the third ePrint article [21] announced full plaintext recovery. This series of happenings is a good example of “attacks only get better” and how seemingly minor error conditions can rapidly grow to nullify the security of a renowned scheme.

B. Left-Out Details of OCB2

We complete our OCB2 description from Sect. 3 by specifying the details of the PMAC and $\texttt {len}$ functions. For the former, see Fig. 15. The latter takes a string $X\in \{0,1\}^{\le n}$ and encodes its lengths |X| as per $\texttt {len}(X)=0^{n-8}\Vert \ell _X$, where $\ell _X$ denotes the standard binary encoding of |X|. For example, $\texttt {len}(0^n)$ for $n=128$ is $0^{120}10^7$.

Fig. 15

Left: The algorithm ${\text {PMAC}}_E$ for the use in OCB2. Right: A TBC-based PMAC, $\mathbb {PMAC}_{\widetilde{E}}$

C. Proof of OCB2f

We first prove the privacy bound. Let $\mathbf{Adv} ^{ \textsf {cpa}}_{\mathbb {PMAC}_{\widetilde{{\textsf {P}}}}, {\textsf {R}}}(\mathcal{A})$ denote the PRF advantage of $\mathbb {PMAC}_{\widetilde{{\textsf {P}}}}$ for CPA-adversary $\mathcal{A}$. Rog04 showed that it is bounded by ${0.5q^2}/{2^n}$ for $\mathcal{A}$ with q queries. Then, we have

$$\begin{aligned} \mathbf{Adv} ^{ \textsf {priv}}_{{\text {OCB2f}}_{{\textsf {P}}}}({\mathcal {A}})&= \mathbf{Adv} ^{ \textsf {priv}}_{{\Theta }\text {CB2f}_{{\text {XEX}}^*_{{\textsf {P}}}}}({\mathcal {A}}) \nonumber \\&\le \mathbf{Adv} ^{ \textsf {tprp}}_{{\text {XEX}}^*_{{\textsf {P}}}}({\mathcal {B}}) + \mathbf{Adv} ^{ \textsf {priv}}_{{\Theta }\text {CB2f}_{\widetilde{{\textsf {P}}}}}({\mathcal {A}}) \nonumber \\&\le \mathbf{Adv} ^{ \textsf {tprp}}_{{\text {XEX}}^*_{{\textsf {P}}}}({\mathcal {B}}) + \mathbf{Adv} ^{ \textsf {cpa}}_{\mathbb {PMAC}_{\widetilde{{\textsf {P}}}}, {\textsf {R}}}(\mathcal{C}) + \mathbf{Adv} ^{ \textsf {priv}}_{\mathrm {\Theta }\text {CB2f}'_{\widetilde{{\textsf {P}}}}}({\mathcal {A}})\nonumber \\&\le \frac{4.5{\sigma ^2_{{\text {priv}}}}}{2^n} + \frac{0.5{\sigma ^2_{{\text {priv}}}}}{2^n} + 0, \end{aligned}$$

(9)

for $\mathcal{B}$ and $\mathcal{C}$ using $\sigma _{\text {priv}}$ CPA queries. Here, the first inequality follows from the fact that possible tweak values of ${\text {XE}}$ and ${\text {XEX}}$ in ${\text {OCB2f}}$ are distinct and $\mathcal{A}$ is tag-respecting. The last inequality follows from (7) and the aforementioned bound of $\mathbb {PMAC}$, and that the last term of (9) is zero as well as $\mathrm {\Theta }\text {CB2}$ as shown by Rog04.

For the authenticity bound, we have

$$\begin{aligned} \mathbf{Adv} ^{ \textsf {auth}}_{{\text {OCB2f}}_{{\textsf {P}}}}({\mathcal {A}}_\pm )&= \mathbf{Adv} ^{ \textsf {auth}}_{{\Theta }\text {CB2f}_{{\text {XEX}}^*_{{\textsf {P}}}}}({\mathcal {A}}_\pm ) \nonumber \\&\le \mathbf{Adv} ^{ \textsf {tsprp}}_{{\text {XEX}}^*_{{\textsf {P}}}}({\mathcal {B}}_\pm ) + \mathbf{Adv} ^{ \textsf {cpa}}_{\mathbb {PMAC}_{\widetilde{{\textsf {P}}}}, {\textsf {R}}}(\mathcal{C}) + \mathbf{Adv} ^{ \textsf {auth}}_{\mathrm {\Theta }\text {CB2f}'_{\widetilde{{\textsf {P}}}}}({\mathcal {A}}_\pm )\nonumber \\&\le \frac{4.5\sigma _{{\text {auth}}}^2}{2^n} + \frac{0.5\sigma _{{\text {auth}}}^2}{2^n} + q_v\left( \frac{2}{2^\tau } + \frac{2}{2^n}\right) \end{aligned}$$

(10)

for $\mathcal{B}_\pm$ using $\sigma _{\text {auth}}$ CCA queries and $\mathcal{C}_\pm$ using $\sigma _{\text {auth}}$ CPA queries. Here, the first inequality follows from the same reason as the case of privacy bound, and the second follows from an improved CCA bound of ${\text {XEX}}^*$ [30] and $\mathbb {PMAC}$ bound.

All that remains is to prove that $\mathbf{Adv} ^{ \textsf {auth}}_{\mathrm {\Theta }\text {CB2f}'_{\widetilde{{\textsf {P}}}}}({\mathcal {A}}_\pm )$ (the last term of (10)) is at most $q_v(2/2^n + 2/2^\tau )$. We first prove the case of $q_v=1$. Let $(N_i, A_i, M_i, C_i, T_i)$ for $i=1,\ldots ,q$ be the tuples obtained by q encryption queries and let $(N', A', C', T')$ be the decryption query. Let $T^{*}$ denote the valid tag corresponding to $(N', A', C')$. Without loss of generality, we assume the decryption query is made after all the encryption queries. We need to consider the following cases for $(N', A', C', T')$.

• 1. $N' \notin \{N_{1}, \ldots , N_{q}\}$

  Since the tag ($T^*$) computation is done by TURP taking a new tweak, $T^{*}$ is completely random. Thus, the forging probability is $1/2^{\tau }$.

• 2. $1\le \exists \alpha \le q$, $N' = N_{\alpha }$, $C' = C_\alpha$, $A' \ne A_{\alpha }$

  Let $|C'|_n = |C_\alpha |_n = m_c$. We have subcases:

  • (a) Let $A'=\varepsilon$ and $A_{\alpha } \ne \varepsilon$. Then,

    $$\begin{aligned} T^{*} = \texttt {msb}_{\tau }(\widetilde{{\textsf {P}}}^{*, 0, N_{\alpha }, m_c, 1}(\Sigma _{\alpha })) = T_{\alpha } \oplus \texttt {msb}_{\tau }({\textsf {R}}(A_{\alpha })) \end{aligned}$$

    holds. The adversary has to guess $\texttt {msb}_{\tau }({\textsf {R}}(A_{\alpha }))$ to forge $T^{*}$. Thus, the forging probability is $1/2^{\tau }$.

  • (b) Let $A'\ne \varepsilon$, $A' = A_{j}$ for some $j \in \{1, \ldots , q\}$ and $A_{j} \ne A_{\alpha }$. We have

    $$\begin{aligned} T^{*}&= \texttt {msb}_{\tau }(\widetilde{{\textsf {P}}}^{*, 0, N_{\alpha }, m_c, 1}(\Sigma _{\alpha }) \oplus {\textsf {R}}(A_{j})). \end{aligned}$$

    To correctly guess $T^{*}$, the adversary needs to guess $\texttt {msb}_{\tau }({\textsf {R}}(A_{j}))$, thus the forging probability is $1/2^{\tau }$.

  • (c) Let $A'\ne \varepsilon$ and $A'\notin \{A_{1}, \ldots , A_{q}\}$. We have

    $$\begin{aligned} T^{*}&= \texttt {msb}_{\tau }(\widetilde{{\textsf {P}}}^{*, 0, N_{\alpha }, m_c, 1}(\Sigma _{\alpha }) \oplus {\textsf {R}}(A')). \end{aligned}$$

    The same as (b): the adversary needs to guess $\texttt {msb}_{\tau }({\textsf {R}}(A'))$, thus the forging probability is $1/2^{\tau }$.

• 3. $1\le \exists \alpha \le q$, $N' = N_{\alpha }$, $C' \ne C_\alpha$, $|C'|_n = |C_\alpha |_n = m_c$

  In this case, the adversary learns $T_{\alpha }=\texttt {msb}_{\tau }(\widetilde{{\textsf {P}}}^{*, 0, N', m_c, 1}(\Sigma _{\alpha }) \oplus {\textsf {R}}(A_{\alpha }))$ from encryption queries. The TURP $\widetilde{{\textsf {P}}}^{*, 0, N', m_c, 1}$ is invoked again at the decryption query to produce $T^*$. The case $A' \ne A_{\alpha }$ can be analyzed in the same way as Case 2. Thus, we assume $A' = A_{\alpha }$ in this case. Let $\Sigma ^{*}$ and $M^{*}$ denote the valid values of the checksum and plaintext corresponding to $(N', C')$. We define $Z_{\alpha } :=(N_\alpha , A_\alpha , M_\alpha , C_\alpha , T_\alpha )$, and we can bound the forging probability as follows:

  $$\begin{aligned} {\mathrm{Pr}}[T' = T^{*} | Z_{\alpha }] \le {\mathrm{Pr}}[T' = T^{*} | \Sigma ^{*}\ne \Sigma _\alpha , Z_\alpha ] + {\mathrm{Pr}}[\Sigma ^{*}=\Sigma _\alpha | Z_{\alpha }] \end{aligned}$$

  (11)

  • (a) For $1 \le \exists i \le m_c$ and $\forall j \in \{1, \ldots , m_c\} \setminus \{i\}$, we assume $C'[i] \ne C_{\alpha }[i]$, $C'[j] = C_{\alpha }[j]$. We obtain $\Sigma ^{*} \ne \Sigma _{\alpha }$ because $M^{*}[i]\ne M_{\alpha }[i]$ holds, and $M^{*}[j]=M_{\alpha }[j]$ holds for all $j \in \{1, \ldots , m_c\} \setminus \{i\}$. From (11), we obtain the forging probability as follows.

    $$\begin{aligned} {\mathrm{Pr}}[T'=T^{*}|Z_{\alpha }]&\le {\mathrm{Pr}}[T' = T^{*} | \Sigma ^{*}\ne \Sigma _\alpha , Z_\alpha ] + {\mathrm{Pr}}[\Sigma ^{*}=\Sigma _\alpha | Z_{\alpha }]\\&\le \frac{2^{n-\tau }}{2^n-1} \le \frac{2}{2^\tau }. \end{aligned}$$

  • (b) For $1 \le \exists i < \exists j \le m_c$, we assume $C'[i] \ne C_{\alpha }[i]$ and $C'[j] \ne C_{\alpha }[j]$. We also define $\Delta M[i] := M^{*}[i] \oplus M_{\alpha }[i] \ne 0^n$ and $\Delta M[j] := M^{*}[j] \oplus M_{\alpha }[j] \ne 0^n$. As described above, we have

    $$\begin{aligned}&{\mathrm{Pr}}[T'=T^{*}|Z_{\alpha }] \\&\le {\mathrm{Pr}}[T' = T^{*} | \Sigma ^{*}\ne \Sigma _\alpha , Z_\alpha ] + {\mathrm{Pr}}[\Sigma ^{*}=\Sigma _\alpha | Z_{\alpha }],\\&\le {\mathrm{Pr}}[T' = T^{*} | \Sigma ^{*}\ne \Sigma _\alpha , Z_\alpha ] + \max _{\forall \delta \in \{0, 1\}^n} {\mathrm{Pr}}[\Delta M[i] \oplus \Delta M[j] = \delta | Z_{\alpha }],\\&\le \frac{2^{n-\tau }}{2^n-1} + \frac{1}{2^n-1} = \frac{2^{n-\tau }+1}{2^n-1} \le \frac{2}{2^\tau } + \frac{2}{2^n}. \end{aligned}$$

• 4. $N' = N_{\alpha }$, $C' \ne C_\alpha$, $|C'|_n < |C_\alpha |_n$

  Let $|C'|_n = m_{c'}$ and $|C_\alpha |_n = m_{c}$. In this case, unlike $\mathrm {\Theta }\text {CB2}$, $\widetilde{{\textsf {P}}}^{*,1,N',m_{c'},0}$ is invoked to decrypt $C'[m_{c'}]$, while $\widetilde{{\textsf {P}}}^{*,1,N',m_{c'},0}$ is also used in an encryption query. Since the adversary knows $\widetilde{{\textsf {P}}}^{*,1,N',m_{c'},0}(M_{\alpha }[m_{c'}])$, she can manipulate the last block of plaintext $M^{*}[m_{c'}]$ if $M_{\alpha }[m_{c'}] = \texttt {len}(C'[m_{c'}])$. Then, she can control the value of $\Sigma ^{*}$. Nevertheless, she has to guess $T^{*}$ without access to $\widetilde{{\textsf {P}}}^{*,0,N',m_{c'},1}$, which has never been invoked in encryption, since $m_{c'} \ne m_c$. Therefore, the forging probability is $1/2^{\tau }$.

• 5. $N' = N_{\alpha }$, $C' \ne C_\alpha$, $|C'|_n > |C_\alpha |_n$

  As above, the forging probability is $1/2^{\tau }$.

From these five cases, the bound is ${2}/{2^\tau } + {2}/{2^n}$ for $q_v=1$. Finally, we apply the standard conversion from single to multiple decryption queries [5] and obtain the bound $q_v\left( {2}/{2^\tau } + {2}/{2^n}\right)$ for $q_v\ge 1$. This concludes the proof. $\square$

D. Proof of OCB2ff

For the privacy bound, we have

$$\begin{aligned} \mathbf{Adv} ^{ \textsf {priv}}_{{\text {OCB2ff}}_{{\textsf {P}}}}({\mathcal {A}})&= \mathbf{Adv} ^{ \textsf {priv}}_{{\Theta }\text {CB2ff}_{\text {XEX}^*_{{\textsf {P}}}}}({\mathcal {A}}) \nonumber \\&\le \mathbf{Adv} ^{ \textsf {tprp}}_{\text {XEX}^*_{{\textsf {P}}}}({\mathcal {B}}) + \mathbf{Adv} ^{ \textsf {priv}}_{{\Theta }\text {CB2ff}_{\widetilde{{\textsf {P}}}}}({\mathcal {A}}) \nonumber \\&\le \mathbf{Adv} ^{ \textsf {tprp}}_{\text {XEX}^*_{{\textsf {P}}}}({\mathcal {B}}) + \mathbf{Adv} ^{ \textsf {cpa}}_{\mathbb {PMAC}_{\widetilde{{\textsf {P}}}}, {\textsf {R}}}(\mathcal{C}) + \mathbf{Adv} ^{ \textsf {priv}}_{{\Theta }\text {CB2ff}'_{\widetilde{{\textsf {P}}}}}({\mathcal {A}})\nonumber \\&\le \frac{4.5{\sigma ^2_{{\text {priv}}}}}{2^n} + \frac{0.5{\sigma ^2_{{\text {priv}}}}}{2^n} + 0, \end{aligned}$$

(12)

for $\mathcal{B}$ and $\mathcal{C}$ using $\sigma _{\text {priv}}$ CPA queries. Here, the first inequality follows since possible tweak values of ${\text {XE}}$ and ${\text {XEX}}$ in ${\text {OCB2ff}}$ are distinct and $\mathcal{A}$ is tag-respecting. The last inequality follows from (7) and the bound of $\mathbb {PMAC}$, and the last term of (12) is zero with the same reasoning as $\mathrm {\Theta }\text {CB2}$ shown by Rog04.

For the authenticity bound, we have

$$\begin{aligned} \mathbf{Adv} ^{ \textsf {auth}}_{{\text {OCB2ff}}_{{\textsf {P}}}}({\mathcal {A}}_\pm )&= \mathbf{Adv} ^{ \textsf {auth}}_{{\Theta }\text {CB2ff}_{\text {XEX}^*_{{\textsf {P}}}}}({\mathcal {A}}_\pm ) \nonumber \\&\le \mathbf{Adv} ^{ \textsf {tsprp}}_{\text {XEX}^*_{{\textsf {P}}}}({\mathcal {B}}_\pm ) + \mathbf{Adv} ^{ \textsf {cpa}}_{\mathbb {PMAC}_{\widetilde{{\textsf {P}}}}, {\textsf {R}}}(\mathcal{C}) + \mathbf{Adv} ^{ \textsf {auth}}_{{\Theta }\text {CB2ff}'_{\widetilde{{\textsf {P}}}}}({\mathcal {A}}_\pm )\nonumber \\&\le \frac{4.5\sigma _{{\text {auth}}}^2}{2^n} + \frac{0.5\sigma _{{\text {auth}}}^2}{2^n} + q_v\left( \frac{2}{2^\tau } + \frac{2}{2^n}\right) \end{aligned}$$

(13)

for $\mathcal{B}_\pm$ using $\sigma _{\text {auth}}$ CCA queries and $\mathcal{C}_\pm$ using $\sigma _{\text {auth}}$ CPA queries. Note that the algorithm of ${\Theta }\text {CB2ff}'$ is obtained by replacing $\mathbb {PMAC}$ of ${\Theta }\text {CB2ff}$ with a URF ${\textsf {R}}$.

Then, the first inequality follows from the same reason as the case of privacy bound, and the second follows from an improved CCA bound of ${\text {XEX}}^*$ [30] and $\mathbb {PMAC}$ bound.

It remains is to prove that $\mathbf{Adv} ^{ \textsf {auth}}_{{\Theta }\text {CB2ff}'_{\widetilde{{\textsf {P}}}}}({\mathcal {A}}_\pm )$ (the last term of (13)) is at most $q_v(2/2^n + 2/2^\tau )$.

We first prove the case of $q_v=1$. We use the same case analysis as ${\Theta }\text {CB2f}$.

• 1. $N' \notin \{N_{1}, \ldots , N_{q}\}$

  Since the tag ($T^*$) computation is done by TURP taking a new tweak, $T^{*}$ is completely random. Thus, the forging probability is $1/2^{\tau }$.

• 2. $1\le \exists \alpha \le q$, $N' = N_{\alpha }$, $C' = C_\alpha$, $A' \ne A_{\alpha }$

  Let $|C'|_n = |C_\alpha |_n = m_c$. The analysis of this case is almost the same as that of Case 2 in Appendix C except for the indices of tweaks. We have subcases:

  • (a) Let $A'=\varepsilon$ and $A_{\alpha } \ne \varepsilon$. Then,

    $$\begin{aligned} T^{*} = \texttt {msb}_{\tau }(\widetilde{{\textsf {P}}}^{*, 0, N_{\alpha }, m_c-1, 1, 1}(\Sigma _{\alpha })) = T_{\alpha } \oplus \texttt {msb}_{\tau }({\textsf {R}}(A_{\alpha })) \end{aligned}$$

    holds. The adversary has to guess $\texttt {msb}_{\tau }({\textsf {R}}(A_{\alpha }))$ to forge $T^{*}$. Thus, the forging probability is $1/2^{\tau }$.

  • (b) Let $A'\ne \varepsilon$, $A' = A_{j}$ for some $j \in \{1, \ldots , q\}$ and $A_{j} \ne A_{\alpha }$. We have

    $$\begin{aligned} T^{*}&= \texttt {msb}_{\tau }(\widetilde{{\textsf {P}}}^{*, 0, N_{\alpha }, m_c-1, 1, 1}(\Sigma _{\alpha }) \oplus {\textsf {R}}(A_{j})). \end{aligned}$$

    To correctly guess $T^{*}$, the adversary needs to guess $\texttt {msb}_{\tau }({\textsf {R}}(A_{j}))$, thus the forging probability is $1/2^{\tau }$.

  • (c) Let $A'\ne \varepsilon$ and $A'\notin \{A_{1}, \ldots , A_{q}\}$. We have

    $$\begin{aligned} T^{*}&= \texttt {msb}_{\tau }(\widetilde{{\textsf {P}}}^{*, 0, N_{\alpha }, m_c-1, 1, 1}(\Sigma _{\alpha }) \oplus {\textsf {R}}(A')). \end{aligned}$$

    The same as (b): the adversary needs to guess $\texttt {msb}_{\tau }({\textsf {R}}(A'))$, thus the forging probability is $1/2^{\tau }$.

• 3. $1\le \exists \alpha \le q$, $N' = N_{\alpha }$, $C' \ne C_\alpha$, $|C'|_n = |C_\alpha |_n = m_c$

  The analysis of this case is exactly the same as that of Case 3 in Appendix C. Thus, the forging probability can be evaluated as $2/2^\tau + 2/2^n$.

• 4. $N' = N_{\alpha }$, $C' \ne C_\alpha$, $|C'|_n < |C_\alpha |_n$

  Let $|C'|_n = m_{c'}$ and $|C_\alpha |_n = m_{c}$. In the proof of ${\Theta }\text {CB2f}$, we had to take care of the fact that the adversary can control the last block of $M^{*}$ because the last block of $C'$ is decrypted by TURP which has been invoked in the $\alpha$-th encryption query. In the case of ${\Theta }\text {CB2ff}$, however, we do not have to care such a case since TURP to decrypt $C'[m_{c'}]$ takes a new tweak and the adversary cannot control $M^{*}[m_{c'}]$ at all. Moreover, she has no information about $\widetilde{{\textsf {P}}}^{*, 1, N', m_{c'}-1, 1, 1}$ which produces $T^{*}$, since $m_{c'} \ne m_{c}$. Therefore, the forging probability is $1/2^{\tau }$.

• 5. $N' = N_{\alpha }$, $C' \ne C_\alpha$, $|C'|_n > |C_\alpha |_n$ As above, the forging probability is $1/2^{\tau }$.

From these five cases, the bound is ${2}/{2^\tau } + {2}/{2^n}$ for $q_v=1$. Finally, we apply the standard conversion from single to multiple decryption queries [5] and obtain the bound $q_v\left( {2}/{2^\tau } + {2}/{2^n}\right)$ for $q_v\ge 1$. This concludes the proof. $\square$

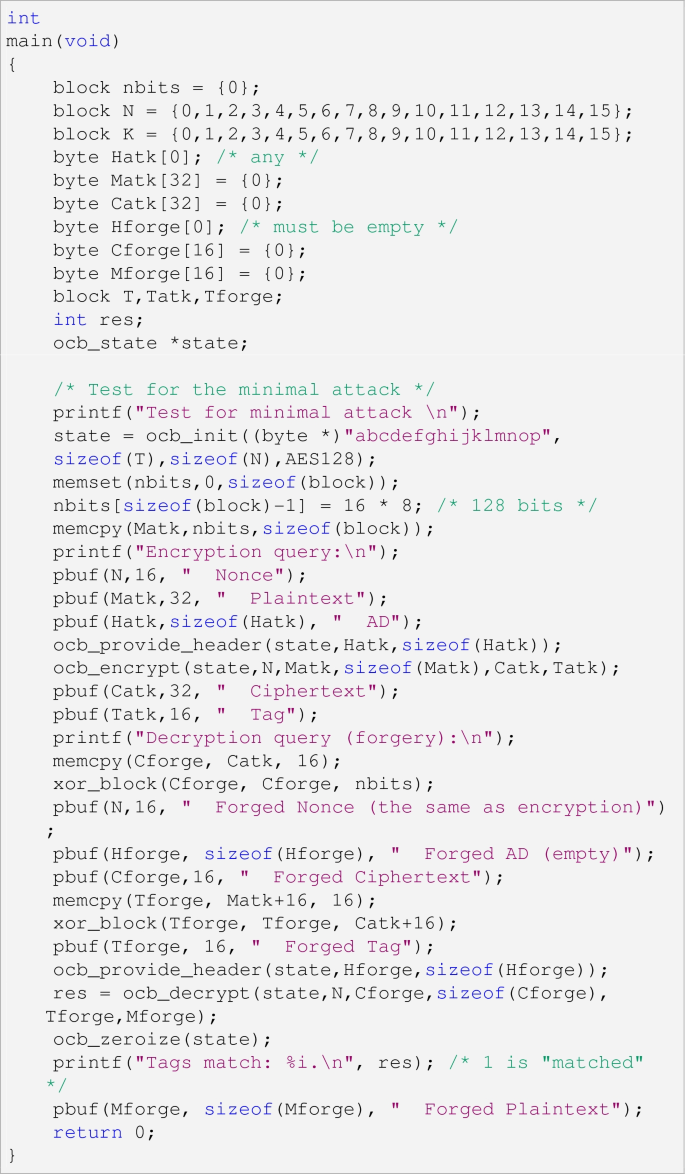
E. Code Example for Minimal Forgery Attack

• 1. Retrieve OCB2 reference code from http://web.cs.ucdavis.edu/~rogaway/ocb/code-2.0.htm and AES reference code (rijndael-alg-fst.c).

• 2. Change the $\texttt {main}$ routine of ocb.c to the following snippet: