Point cloud registration with quantile assignment

Abstract

Point cloud registration is a fundamental problem in computer vision. The problem encompasses critical tasks such as feature estimation, correspondence matching, and transformation estimation. The point cloud registration problem can be cast as a quantile matching problem. We refined the quantile assignment algorithm by integrating prevalent feature descriptors and transformation estimation methods to enhance the correspondence between the source and target point clouds. We evaluated the performances of these descriptors and methods with our approach through controlled experiments on a dataset we constructed using well-known 3D models. This systematic investigation led us to identify the most suitable methods for complementing our approach. Subsequently, we devised a new end-to-end, coarse-to-fine pairwise point cloud registration framework. Finally, we tested our framework on indoor and outdoor benchmark datasets and compared our results with state-of-the-art point cloud registration methods.

1 Introduction

We propose a new coarse-to-fine approach to solving the pairwise 3D point cloud registration (PCR) problem. PCR aims to align two or more point clouds in a standard coordinate system by estimating the transformation that maps one point cloud onto another. A point cloud is a set of data points in X, Y, and Z coordinates representing a 3D shape or object. Range sensors, such as ultrasonic sensors, Kinect, and LiDAR, are widely used technologies to gather point cloud data [1]. Since these sensors have a limited view range, the existing technologies cannot represent a complete scene for larger shapes or objects. PCR combines the point clouds and obtains a complete 3D scene; therefore, it is a fundamental task in computer vision and robotics with many applications such as 3D reconstruction, 3D localization, and pose estimation [2].

The pairwise PCR problem mainly involves detecting the corresponding point pairs between the two clouds (source and target) and calculating the transformation matrix (rotation and translation) that minimizes the distance between the corresponding points. For many applications, the source and the target point cloud only partially overlap [3]. To deal with this challenge, we defined the quantile assignment problem to obtain the correspondence set using a bipartite assignment approach where we aim to detect the point pairs that belong to the overlapping region and find an accurate matching for those pairs only.

1.1 Problem definition

Let ${{\mathcal {S}}} = \{ p_1, \ldots , p_N\}$ and ${{\mathcal {T}}} = \{ q_1, \ldots , q_M\}$ be the source and the target point clouds where $p_i$ and $q_j$ are the coordinate vectors of the $i{\text {th}}$ and $j{\text {th}}$ points of their respective point cloud, ${{\mathcal {S}}}, {{\mathcal {T}}} \subset {\mathbb {R}}^3$. The goal of PCR is to find the rotation matrix R and the translation vector t minimizing the distance between the source and target point clouds, i.e., solve the following optimization problem: $\min _{\begin{array}{c} R \in {\mathbb {R}}^{3 \times 3}, t \in {\mathbb {R}}^3 \end{array}} d(R{{\mathcal {S}}} + t, {{\mathcal {T}}}).$ We define the correspondence set ${{\mathcal {C}}} \subset {\mathbb {N}}^{2}$ as the one-to-one mapping between ${{\mathcal {S}}}$ and ${{\mathcal {T}}}$. For a tuple (i, j) in ${\mathcal {C}}$, the points $p_i \in {\mathcal {S}}$ and $q_j \in {\mathcal {T}}$ are said to correspond. When ${\mathcal {C}}$ is known, the distance between ${\mathcal {S}}$ and ${\mathcal {T}}$ is defined as $d({{\mathcal {S}}}, {{\mathcal {T}}})=\sum \limits _{(i,j)\in {{\mathcal {C}}}} {\Vert p_i - q_j \Vert ^2}.$ and the optimization problem above has a closed-form solution [4]. However, obtaining an accurate enough correspondence set is a challenging task.

1.2 Challenges

Range sensing technologies have evolved rapidly throughout recent years; however, the point cloud data gathered is still subject to noise and outliers. Moreover, the point clouds to be registered have only partial overlaps. These limitations make it difficult to accurately detect the points in the source point cloud belonging to the overlapping region and the points in the target point cloud they correspond to. Since the initial positions of the two clouds are on different coordinate systems, only using the Euclidean distance between the data points for registration may result in false alignments. Therefore, pose-invariant local descriptors are widely utilized [5] to detect the corresponding pairs, and remarkable developments have been made regarding these descriptors. Still, the accuracy of the 3D point cloud registration is limited by the robustness of descriptors, and improvement is needed for better results.

In general, input point clouds may contain up to billions of points, and therefore PCR applications have been limited by high memory footprint and slow speed [6]. Downsampling methods are utilized to deal with more extensive data. However, downsampling the point clouds may result in losing some of the descriptive features of surfaces. Thus, there is a trade-off between accuracy and computational complexity, which makes it challenging to deal with these large point clouds without suffering from inaccurate correspondences. The resulting transformation fails to align when the correspondence set does not contain enough accurate corresponding pairs.

1.3 Applications

PCR plays a critical role in computer vision and robotics. PCR algorithms represent scenes and objects in 3D by registering multiple point cloud data. This process is called 3D reconstruction [7], which can be used for medical imaging [8], constructions of buildings, roads and bridges [9], 3D animation and face recognition [10], and autonomous driving [11]. Simultaneous localization and mapping (SLAM) is another process in robotics that utilizes PCR methods for estimating the real-time positions of objects in unknown environments.

1.4 Motivation

The interest in PCR has increased in recent years due to its critical applications. Although existing efficient learning and optimization-based algorithms can achieve accurate point cloud registration, there is still a need for improvement due to the many challenges of dealing with large and noisy point clouds. The low overlap ratio between the source and target cloud imposes difficulties in estimating accurate transformations. Our study focused on detecting the overlapping region and adaptively achieving accurate registration by utilizing only the points in this region. We developed an optimization-based algorithm that does not require any initialization.

2 Related work

There are notable algorithms to achieve efficient and accurate PCR. There are two PCR types: global registration and local registration. Global registration methods do not only use the point clouds’ positions; hence, they do not require initialization. In contrast, local registration methods utilize the coordinates of points and rely on a rough initial alignment. The initial alignment may affect the registration result adversely. A common strategy to deal with this challenge is to adopt a coarse-to-fine approach: first estimating an initial approximate transformation with coarse registration (based on pose-invariant features), and then refining this transformation with fine registration (based on coordinates) [12].

The local registration (refinement) is performed generally with the well-known iterative closest point (ICP) method [13] [14] or its variants. ICP matches each point in the source cloud to its geometrically nearest point in the target cloud and transforms the source cloud such that the distance between these corresponding points is minimized. This procedure is repeated until the distance is below a threshold. There are several standard methods for calculating the transformation: SVD, Lucas–Kanade algorithm, and Procrustes analysis [2]. In addition to the point-point distance metric, the point-plane and plane-plane distance metrics are also used. Although fast and straightforward, ICP converges to the nearest local minimum, and therefore, its registration performance is highly dependent on the initial position of the point clouds [12]. There are many improved variants of ICP. Scale-adaptive ICP [15] integrates the scale factor into the optimization process and handles the PCR problem when a scale difference between the input clouds is present. In the Sparse ICP method [16], the registration optimization is formulated using sparsity-inducing norms to become more robust to noise and outliers. Zhang et al. [17] developed a fast converging method using an Anderson acceleration approach. The refinement is typically performed with an ICP-based method. Different approaches can be used to obtain the rough alignment needed for ICP. We classified these approaches as learning-based and optimization-based.

2.1 Learning-based approaches

Deep neural networks (DNNs) are extensively used to perform PCR. DNN is commonly used for feature extraction and transformation estimation [2]. One common approach is establishing the features with a feature-learning model and using a robust estimation tool to obtain the transformation. Random sample consensus (RANSAC) [18] is commonly used to estimate the transformation matrix. It is a search algorithm using repeated random subsampling to estimate parameters iteratively. An alternative to RANSAC is the optimized sample consensus [19], which has a similar principle but uses a different error metric. For both algorithms, a different set of correspondences are obtained at each iteration.

R-PointHop [20] is a green, unsupervised feature-learning method with lower memory consumption and reduced training time than its alternatives. Zeng et al. introduced 3DMatch [21], a learning model that uses 3D local volumetric data and extracts 512-dimensional features representing local patches. Instead of learning from volumetric data, PPFNet [22] learns local descriptors on pure geometry and extracts 64-dimensional descriptors. FCGF [23], PointNet [24], and CGF [25] are other notable state-of-the-art feature-learning models. PCR can be performed using the extracted features by one of these models and estimating a transformation via RANSAC.

DNNs are also utilized for transformation estimation with an end-to-end framework. PCR can be solved with end-to-end neural networks by transforming the registration problem into a regression problem [2]. 3DRegNet [26] uses DNN to classify the inliers/outliers among correspondences and perform regression of the transformation parameters. Alternative to DNN, the authors also adopted a Procrustes approach for regression. Similarly, Choy et al. introduced the deep global registration framework [27], which uses a differentiable weighted Procrustes algorithm for transformation estimation. Deep global registration uses a six-dimensional convolutional network for correspondence confidence prediction and a robust gradient-based optimizer for pose refinement.

Learning-based methods can perform fast and accurate registration. However, they have a training process requiring extensive data, and their performance can drop significantly for unknown scenes much different than the training data [2].

2.2 Optimization-based approaches

Handcrafted features are commonly used instead of feature-learning models. These features are based on spatial and geometric attributes or relationships between different points in the cloud [5]. Spin image [28] is generated by accumulating two parameters in a 2D array describing the position of a point with respect to its neighboring points. Lei et al. [29] designed an efficient local descriptor formed with eigenvalues and normals computed from multiple scales. Local feature statistics histogram (LFSH) [19] describes local shape geometries using local depth, point density, and angles between normals. Some handcrafted descriptors are built using a local reference frame (LRF). Signature of Histograms of OrienTations (SHOT) [30] is based on spatial distributions of the local neighborhoods of the key points. Fast point feature histograms (FPFH) [31] is a robust descriptor based on geometric relations within the local neighborhood of a key point. Fast global registration (FGR) [32] is a state-of-the-art optimization-based global registration method. FGR uses FPFH features for correspondence search and estimates the transformation with an alternating optimization algorithm that utilizes the Jacobian of the feature differences and the Gauss–Newton method.

Probabilistic approaches utilizing Gaussian mixture models (GMMs), such as the coherent point drift (CPD) [33] algorithm, are also adopted for optimization-based registration. KSS-ICP [34] method performs registration in Kendall shape space (KSS) that removes influences of translations, scales, and rotations for shape feature-based analysis. Another popular approach is to use graph matching to establish the correspondence set. The iterative global similarity point (IGSP) algorithm [35] is a variant of the ICP algorithm where correspondences are obtained with the Hungarian algorithm using a hybrid distance metric that utilizes the points’ local and geometric features. Chaudhury [36] proposed a method that also leverages the point clouds’ local and global structures and uses the Gauss–Newton optimization method for estimating the transformation. A method that utilizes GMM for noise handling and an expectation-maximization (EM) algorithm for registration was proposed in [37]. The singular value decomposition (SVD) method calculates the transformation matrix. Since optimization-based registration methods do not need training, they can be generalized well to unknown scenes. However, they might suffer from high computation costs. Shen et al. [38] leveraged robust optimal transport for point cloud registration. The authors show that optimal transport (OT) solvers improve the performances of deep learning- and optimization-based approaches for point cloud registration. They utilize the latest OT solvers to improve memory usage and numerical stability, which helps to handle fine-grained details effectively. Their improvements increase accuracy at a reasonable computational cost.

Significant advancements in point cloud registration have been made in recent years, with a predominant emphasis on feature extraction and transformation estimation. However, we have observed a relative need for more attention to the crucial task of feature-matching or correspondence estimation. Existing techniques, such as maximum matching or nearest neighbor approaches, are employed for this task, but they need to improve accuracy in the presence of noise and partial overlap. The correspondence set directly affects the end transformation and, thus, is a crucial part of the registration process. Therefore, integrating more sophisticated novel feature-matching techniques to point cloud registration frameworks would help to achieve higher accuracy and precision. Our primary focus is developing and applying the quantile assignment algorithm for precise correspondence estimation. To this end, we define the quantile assignment problem specifically for the registration task, considering the limitations such as noise, outliers, and partial overlap between the point clouds. We analyzed different feature descriptors and transformation estimation methods to combine with our correspondence estimation algorithm and proposed a new optimization-based, two-stage coarse-to-fine framework.

3 Quantile assignment

We used the quantile assignment (QA) algorithm [3]¹ to obtain the correspondence set. The assignment problem is polynomially solvable [39], and the QA problem is a variant of the maximum bipartite assignment problem.

3.1 Problem definition

Consider the source and target clouds and assume ${M \ge N}$. The feature of each point is calculated using a local descriptor. Note that these features can be scalars or vectors depending on the descriptor. Let $p_i$ be the feature value/vector of $i\text {{th}}$ point in ${{\mathcal {S}}}$ and $q_j$ be the feature value/vector of $j\text {{th}}$ point in ${{\mathcal {T}}}$. Using these features, we construct the affinity matrix ${A}_{N\times M}$ where ${A}_{ij} = -\rho e^{{\Vert p_i - q_j \Vert }_2}$ and $\rho$ is the penalty coefficient. The maximum weight assignment problem corresponding to this data solves the following mathematical model

$$\begin{aligned} \max _{X{\in }{{\mathcal {X}}}} \; \sum _{n=1}^N \sum _{m=1}^M \ A_{nm} X_{nm}, \text { where } \end{aligned}$$

$$\begin{aligned} \begin{array}{llll} {{\mathcal {X}}}{=} &{} \left\{ X{\in }\{0,1\}^{{ N}\times {M}}{:}\sum _{n=1}^N\right. &{}\!\!X_{nm}{=}1, \forall m, &{} \\ &{} &{} \left. \sum _{m=1}^M X_{nm}{=}1, \forall n \right\} &{} \end{array} \end{aligned}$$

is the set of all bipartite matchings. We defined $\alpha \in [0,1]$ as the overlap ratio between the source and the target clouds. In practical applications, noise makes the overlap ratio difficult to estimate. Let us assume there is no noise, and ${\mathcal {K}} \subseteq {\mathbb {N}}$ is the set of points in the source cloud that matches exactly the points in the target cloud. Then, we set $\alpha = {|{\mathcal {K}}|}/{N}$, representing the ratio of expected matches for the smaller point cloud. Using this value, we define $k_{\alpha } = \max \left( 1, \lceil (1{-}\alpha )N \rceil \right)$ and denote the distinct entries of the matrix A as q values. The $k_{\alpha }^{th}$ smallest q value is called the $\alpha$-quantile, $q_{\alpha }$. Given an affinity matrix A and $\alpha$, the objective of QA is to find the bipartite matching that maximizes the $\alpha$-quantile of the weights associated, i.e., solve $\max _{X{\in }{{\mathcal {X}}}} \; q_\alpha \left( A_{nm} X_{nm}, \ \forall n, m\} \right) .$ that was shown in [3] to be polynomially solvable. After the correspondence set is established using the QA problem, the transformation matrix is estimated using only the matches with larger affinity values than the optimal $k_{\alpha }^{\text {th}}$ smallest affinity value since we assume that the matches with smaller affinity values belong to the non-overlapping region. Hence, we avoid using faulty matches.

3.2 Solution method

We can solve the QA problem by conducting a binary search on the affinity matrix’s q values. A particular q value is considered $\alpha$-feasible if there exists $X \in {{\mathcal {X}}}$ such that the $k_{\alpha }^{th}$ smallest affinity value in $\{ A_{nm} X_{nm}, \ \forall n, m \}$ is at least as high as q. Only the matched pairs with higher affinity values than this q value are later utilized to obtain a final matching. Therefore, we need this q value to be $\alpha$-feasible to end up with a number of matched pairs enough to meet the specified overlap ratio. We aim to find the largest $\alpha$-feasible affinity value q, i.e., the largest $\alpha$-quantile value. We propose a Hungarian-based method to test whether a q value is $\alpha$-feasible. This method first constructs a binary cost matrix C by assigning each entry of A the value one if that entry is smaller than q and zero if not. Then, the minimum cost matching problem can be solved on C using the Hungarian algorithm [40]. The current q value is considered $\alpha$-feasible if the minimum cost found is less than or equal to $k_{\alpha }{-}1$. Note that the source and target clouds are generally different sizes; hence, our matrix C may not be square. Since the Hungarian algorithm can only be performed in square matrices, we appropriately complement C to a square one.

Alternatively, we propose a Hopcroft–Karp-based method. We apply the Hopcroft–Karp maximum cardinality matching algorithm [41] on a bipartite graph to test the $\alpha$-feasibility of a q value. The edges of this bipartite graph correspond to pairs in ${{\mathcal {C}}}$ having zero costs. Augmenting the maximum cardinality matching edges in this graph with enough edges with cost values as one will result in a minimum cost matching. Similarly, if the cost computed for C is less than or equal to $k_{\alpha }-1$, one can conclude that the current q value is $\alpha$-feasible. When the largest $\alpha$-feasible q value is obtained, the matching found for that q is utilized for constructing the correspondence set. Matched points with an affinity value smaller than q are excluded from the matching, and the remaining pairs are used for estimating the transformation matrix. However, recall that the matching is calculated on the binary cost matrix C; therefore, each potential pair with an affinity value higher than q is treated the same. The overlapping region can be determined with the so far explained method. However, it is not enough to ensure a successful matching within the overlapping region since the used matrix is binary. To further differentiate between the potential point pairs, we used the alternative cost matrix $C_q$, where the affinity values smaller than q are replaced by zeroes, and the rest remains the same. Once the largest $\alpha$-feasible q value is found, the maximum cost matching problem is solved on this matrix one last time to obtain the final matching. With this modification, we aim to detect the pairs belonging to the overlapping region of the two point clouds and search for the best matching among the overlapping pairs. In the sequel, we refer to this method as Hungarian cost sensitive.

Lemma 1

Given $\alpha$, q, and A, deciding whether there exists a matching such that the $k_{\alpha }^{th}$ smallest entry in this matching is at least q can be done in $O(M^{1.5}N)$ time.

Theorem 1

A matching that maximizes the $\alpha$-quantile can be found in $O(M^{1.5}N \log M)$ time.

Please refer to [3] for the proofs of Lemma 1 and Theorem 1. Algorithm 1 solves the QA problem [3].

Algorithm 1

Quantile Assignment

As an example, consider the following affinity matrix and $\alpha = 0.55$. The perfect matching entries are bracketed.

$$\begin{aligned} A = \left[ \begin{array}{rrrrr} \fbox {19} &{} 13 &{} 8 &{} 1 &{} 14\\ 9 &{} 3 &{} 18 &{} 2 &{} \fbox {18} \\ 17 &{} 15 &{} 7 &{} \fbox {14}&{} 19 \\ 2 &{} 1 &{} \fbox {9} &{} 6 &{} 13 \\ 17 &{} \fbox {20} &{} 13 &{} 14 &{} 15\\ \end{array} \right] . \end{aligned}$$

Since $k_{\alpha }=3$, the q value is the third smallest value in the matched element set, i.e., 18. However, the following optimal assignment is preferable since it gives a better value of 19.

$$\begin{aligned} A = \left[ \begin{array}{rrrrr} \fbox {19} &{} 13 &{} 8 &{} 1 &{} 14\\ 9 &{} 3 &{} 18 &{} \fbox {2} &{} {18} \\ 17 &{} 15 &{} 7 &{} {14}&{} \fbox {19} \\ 2 &{} 1 &{} \fbox {9} &{} 6 &{} 13 \\ 17 &{} \fbox {20} &{} 13 &{} 14 &{} 15\\ \end{array} \right] . \end{aligned}$$

4 Computational experiments

Our proposed approach is tested by conducting a series of PCR experiments. We constructed a synthetic dataset inspired by the experiments conducted by Zhou et al. [32]. Our dataset contains five models: the Angel, Bunny, Happy Buddha, Dragon, and Horse [42]. We generated five partially overlapping clouds for each model by cropping the models, and we added Gaussian noise to each partial cloud using three noise levels. We set the Gaussian standard deviation parameter $\sigma$ equal to 0 (no noise), 0.0025 (noise level 1), and 0.005 (noise level 2) for each noise level, respectively, and multiplied this parameter with the diameter of the partial cloud. Our dataset contains 75 different point clouds, three noise levels for each model, and five point clouds for each noise level. The overlap ratio varies between $51\%$ and $94\%$. Figure 1 shows partial clouds from each model’s three noise levels. Figure 2 illustrates an example of the PCR process.

Fig. 1

Noise added partial point clouds in the synthetic dataset (color figure online)

Fig. 2

a shows the initial position of the two partially overlapping clouds. Then, the source cloud (blue) is rotated by the matrix R and translated by the vector t as shown in (b) where R is constructed from the XYZ Euler angles [43] $\left[ \dfrac{\pi }{3}, \dfrac{\pi }{2}, \pi \right]$, and $t = [0.5, 0.5, 0.5]$. The correspondence set for the point clouds is constructed using our QA algorithm. The correspondence lines between the point clouds for the top 50 affinity values are visualized in (c). Then, the transformation matrix is calculated using the correspondence set and applied to the source cloud. The final registration is shown in (d) (color figure online)

Ground-truth rotation and translation for the experiments conducted with synthetic data can be found by calculating the inverse of R and t. The registration performance is evaluated using the ground truth rotation and translation. The registration is successful if the difference between the calculated and the ground-truth transformation is below a threshold. For the synthetic dataset, the rotation threshold is $5^{\circ }$, and the translation threshold is 2 cm. We used the evaluation metric recall in our experiments, representing the ratio of successfully registered point cloud pairs to all pairs [2].

4.1 Framework

We adopted a coarse-to-fine approach to perform PCR, consisting of global and local registration as explained in Sect. 2. The workflow of our registration process can be found in Fig. 3. The inputs of our algorithm are the source and target point clouds. The point clouds are simplified using voxel or uniform downsampling methods to deal with large data. In voxel downsampling, points in the cloud are bucketed into voxels for a given measure, and each occupied voxel generates one point by averaging all points inside [44]. An alternative method is uniform downsampling that samples the point cloud in the order of the points. The selected point indices are $[0, k, 2k, \ldots ]$ for a given parameter k [44].

Fig. 3

Our workflow

The features of the simplified point clouds are extracted with the chosen descriptor. We tested our algorithm with three feature descriptors: curvatures [45], FPFH [31], and LFSH [19]. We explain the computation of each descriptor and analyze their performances in Sect. 4.2.

The affinity matrix is constructed using the chosen descriptor, as explained in Sect. 3.1, and the QA problem is solved on this affinity matrix with one of the algorithms in Sect. 3.2. The registration performances of different algorithms are analyzed in Sect. 4.3. The QA algorithm requires an $\alpha$ value as input representing the overlap ratio between the source and target point clouds. The estimation of this ratio is a challenging problem. We manually synthesized the partial point cloud pairs from a single model for our synthetic dataset; hence, the overlap ratio is easily computed.

Fig. 4

Feature visualizer tool outputs (color figure online)

The resulting matching of our QA algorithm is the initial correspondence set. We apply a test called tuple normal alignment to the initial correspondence set to eliminate false correspondences (cf. Sect. 4.4) and obtain the final correspondence set to estimate the transformation.

Given the correspondence set, we implemented two methods to estimate the transformation matrix. The first option is to perform singular value decomposition (SVD), a well-known method for estimating the rotation matrix. After the rotation matrix is calculated with SVD and applied to the source point cloud, the translation vector is calculated by simply using the difference between the mean coordinates of the matched points among the target cloud and the rotated source cloud. We also implemented the algorithm by Zhou et al. [32], referred to as the FGR optimization method. Both methods are explained, and their registration performances are evaluated in Sect. 4.5.

The process so far is the global registration part of our framework. We then perform local registration after the found transformation is applied to the source cloud. The point-to-plane ICP algorithm (cf. Sect. 4.6) performs fast and accurate registration if the initial alignment of the input point clouds is close enough. The original target cloud and the previously transformed source cloud are fed to the ICP algorithm to perform local refinement, and the final registration is obtained.

4.2 Feature investigation

The choice of feature descriptor is crucial. The main idea is that one should associate with each point a number or a vector that does not change with the set of transformations that the point cloud may have to go through to achieve an optimal registration with another point cloud. We explain the computations of each implemented local descriptor and compare their performances according to their registration performance and descriptiveness.

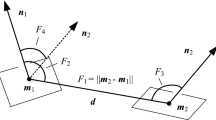
Our first choice as a descriptor was curvatures. Curvature is a quantity preserved under rigid transformation. Histogram shapes of local curvature for K-nearest neighbors are invariant under, e.g., affine transformations. The curvature computation for point clouds is performed as follows. For each point $x_i$, $i{=}1,\ldots , n$ in the point cloud, let $M_i$ be the associated unit normal vector. Fix one point $P{=}x_{i_0}$ and let $N{=}M_{i_0}$ denote its normal vector. Let another point $Q_i = x_i$ be chosen in a close neighborhood of P. The normal curvature $\tau _i$ can be estimated at any point by $\tau _i{=}\frac{\sin (\beta )}{|PQ_i|\sin (\alpha )},$ where $\alpha$ denotes the angle between $-N$ and $P Q_i$, and $\beta$ represents the angle between N and $M_i$ (see [45] for details).

Alternative pose-invariant local features are FPFH, a modification of previously reported point feature histograms (PFH) to be more robust. The default implementation uses 11 binning subdivisions, resulting in a 33-dimensional feature for each key point. The computational cost of FPFH is significantly lower than PFH, and most of the discriminative power of PFH is retained [31].

The third local descriptor we implement for our PCR algorithm is Local Feature Statistics Histograms (LFSH). LFSH describes local shape geometries by encoding their statistical properties on local depth, point density, and angles between normals. Three sub-histograms are obtained using these feature statistics containing 10, 15, and 5 bins, respectively. The LFSH descriptor is obtained by concatenating these three sub-histograms into one histogram [19].

The performances of the three local descriptors, curvatures, FPFH, and LFSH, are first tested using the Feature Visualizer tool we designed using the Open3D library [44]. For any given point in the source cloud, the location of the closest point in the target cloud regarding its feature value/vector for the given local descriptor is shown via the Feature Visualizer.

The given point for the point cloud on the left side of Fig. 4 is shown as green. The points in the point cloud on the right are colored from red to blue using the heat map technique depending on their closeness (in terms of the used feature) to the green point. The colors are normalized; the closest points are colored red, and the furthest points are colored blue accordingly. According to our tool, the FPFH feature seems more discriminative than the other two.

We used the Bunny model from our synthetic dataset to test the registration performances of the descriptors. For each descriptor, our PCR framework is used on the ten partially overlapping pairs from each noise level, with voxel and uniform downsampling for simplification. The recall values are plotted for the cases of no noise, noise level 1, and noise level 2 in Figs. 5, 6, and 7, respectively. Our experiments showed that the FPFH feature achieved better registration performance in our PCR framework for each noise level and downsampling method compared to curvatures and LFSH.

Fig. 5

Feature recalls with no noise (color figure online)

Fig. 6

Feature recalls with noise Level 1 (color figure online)

Fig. 7

Feature recalls with noise Level 2 (color figure online)

4.3 Correspondence set

The initial correspondence set is obtained by solving the QA problem. Several solution methods are proposed in Sect. 3. The Hungarian-based and Hopcroft–Karp-based methods have similar performances. The results were expected to differ for the Hungarian cost-sensitive method since the cost matrix construction was modified. Among the proposed solution methods, we used the Hopcroft–Karp-based and Hungarian cost-sensitive methods for our computational PCR experiments.

We compare the registration performances of the two methods using the bunny model. Figure 8 depicts the two methods’ recall values with voxel and uniform downsampling, respectively. The recall values of the Hopcroft–Karp-based and the Hungarian cost-sensitive methods are similar.

Fig. 8

Hungarian cost-sensitive and Hopcroft–Karp-based recalls with voxel and uniform downsampling (color figure online)

4.4 Tuple normal alignment test

We adopted the tuple test in [32] and used it on our initial correspondence set to eliminate the faulty matches. Three correspondence pairs $(p_1, q_1)$, $(p_2, q_2)$, $(p_3, q_3)$ are randomly selected. The tuples $(p_1, p_2, p_3)$ and $(q_1, q_2, q_3)$ are considered compatible and pass the test if the condition below is satisfied:

$$\begin{aligned} \tau< \dfrac{||p_i - p_j||}{||q_i - q_j||} < \dfrac{1}{\tau }, \quad \forall \;\; i,j = 1,2,3 \quad \text {and} \quad i \ne j \end{aligned}$$

where $\tau$ is selected as 0.9. For any two corresponding pairs $(p_i,q_i)$, $(p_j,q_j)$, the ratio of their distances must be close to one if any of the correspondences is not false.

The source cloud is transformed using the correspondences that pass the tuple test. Then, to further eliminate the faulty correspondences, we applied one more test, called tuple normal alignment test, using the normal alignments of the triangles. This test is applied as follows. Three correspondence pairs $(p_1, q_1)$, $(p_2, q_2)$, $(p_3, q_3)$ are randomly selected from the set. Let $n_p$ be the surface normal of the triangle formed by the tuple $(p'_1, p'_2, p'_3)$ and $n_q$ be the surface normal of the triangle formed by the tuple $(q_1, q_2, q_3)$, where $(p'_1, p'_2, p'_3)$ are the points in the source cloud after the transformation is applied. The correspondence pairs $(p_1, q_1)$, $(p_2, q_2)$, $(p_3, q_3)$ remain in the final correspondence set if the angle between $n_p$ and $n_q$ is less than or equal to our threshold, which is $15^{\circ }$. We obtain the final correspondence set by applying the tuple test and the tuple normal test to the initial correspondence set.

4.5 Transformation estimation

The well-known singular value decomposition (SVD) method can estimate the transformation matrix. After the final correspondence set is established, our aim is to compute the rotation matrix R and the translation vector t that minimizes the weighted sum of squared errors, i.e., solve $\min _{\begin{array}{c} R \in {\mathbb {R}}^{3 \times 3}, t \in {\mathbb {R}}^3 \end{array}} \sum \limits _{(i,j)\in {{\mathcal {C}}}} {\Vert (Rp_i + t) - q_j \Vert ^2} w_{ij}$

where $w_{ij}$ is the weight of the corresponding pair $(p_i,q_j)$ is solved. We used the affinity matrix values, which show the closeness of two points in terms of their features as weights. A direct optimal solution for the rotation matrix can be found via SVD. First, the weighted mean values $p_0$ and $q_0$ for the source and the target clouds, respectively, are calculated as $p_0{=}\frac{\sum _{(i,j) \in {\mathcal {C}}} p_i w_{ij}}{\sum _{(i,j) \in {\mathcal {C}}} w_{ij}}, \; q_0{=}\frac{\sum _{(i,j) \in {\mathcal {C}}} q_j w_{ij}}{\sum _{(i,j) \in {\mathcal {C}}} w_{ij}}.$ Next, the covariance matrix $H{=}\sum _{(i,j) \in {\mathcal {C}}} (q_j{-}q_o)(p_i{-}p_0)^\top w_{ij}.$ Finally, we apply SVD to H to decompose H into matrices U, D, and V: $\textit{SVD(H)}{=}{} \textit{UDV}^\top .$ Using the SVD decomposition, the rotation matrix R is $R{=}VU^\top .$ Once R is computed, the translation vector is calculated as a shift between the means of the matched points from the two point clouds as $t{=}q_0{-}Rp_0.$ It was shown that this (R, t) is the optimal solution to the optimization problem defined above (see [46] for details).

Our second option to estimate the transformation matrix is to use the FGR optimization proposed by Zhou et al. [32] with the objective function $E(R,t){=}\sum _{(i,j) \in {\mathcal {C}}} \rho (||(Rp_i{+}t){-}q_j||)$

where a scaled Geman–McClure estimator is used as the robust penalty function $\rho (.)$: $\rho (x){=}\dfrac{\mu x^2}{\mu {+}x^2}.$ Since optimizing E(R, t) is difficult, the authors proposed an equivalent joint objective using Black-Rangarajan duality and optimized it with an alternate algorithm.

The registration performances of the two methods are compared using the bunny model. As shown in Figs. 9, 10, 11, the FGR optimization achieves more accurate PCR results. The parameter $\mu$ used in the objective in the FGR optimization controls the correspondences that significantly affect the objective. It is more successful in dealing with outlier correspondences.

Fig. 9

FGR optimization and SVD recalls with no noise (color figure online)

Fig. 10

FGR optimization and SVD recalls with noise Level 1 (color figure online)

Fig. 11

FGR optimization and SVD recalls with noise Level 2 (color figure online)

4.6 Local refinement via ICP

The resulting alignment of the source and target point clouds from our global registration algorithm requires further refinement to achieve a more accurate registration result. The point-to-plane ICP method [13] is used in our implementation for local refinement. First, the correspondence set is established by matching each point in the source cloud to its closest neighbor point in the target point cloud. The point-to-plane ICP method considers the surface normal of the target scan. The optimization problem $\min _{\begin{array}{c} R \in {\mathbb {R}}^{3 \times 3}, t \in {\mathbb {R}}^3 \end{array}} \sum _{(i,j) \in {\mathcal {C}}} ||((Rp_i + t) - q_j) \cdot n_j||^{2},$

where $n_j$ is the surface normal of the point $q_j$, is solved. This error function is minimized using the least squares approach. The Gauss–Newton method is used to compute the least squares solution, and the resulting transformation is applied to the source cloud. This process is iterated until the error function is below a certain threshold.

5 Point cloud registration experiments

We tested the registration performance of our algorithm with three different datasets and compared our results with some of the state-of-the-art PCR methods. We used a synthetic dataset containing commonly used 3D models, one indoor benchmark dataset (3DMatch [21]), and one outdoor benchmark dataset (KITTI [47]). For better comparison with learning-based state-of-the-art methods on the benchmark datasets, we also integrated the pre-trained feature-learning model FCGF [23] into our framework instead of the feature descriptors explained in Sect. 4 to perform registration. All tests were performed on a PC with 64-bit Operating System, x64-based Intel(R) E5-2620 v4 processor, CPU @2.10GHz, and RAM 64.00 GB. FCGF-based tests on 3Dmatch and KITTI are performed on a separate PC with 64-bit Ubuntu 22.04, x64-based AMD(R) Ryzen 7 6800 H processor at @3.2GHz, NVIDIA(R) RTX 3070Ti, and RAM 16.00 GB.

5.1 Synthetic dataset

We ran our point cloud registration algorithm on 150 pairs in our synthetic dataset and compared our results with a state-of-the-art optimization-based method, FGR algorithm [32]. After using voxel and uniform downsampling with several different downsample parameters, we registered each point cloud pair. The overlap ratio is computed easily for each cloud pair in our experiments since the point clouds are manually created, and our $\alpha$ parameter is set accordingly. The recall plots for different downsampling sizes and each noise level for the Angel model in our synthetic dataset are depicted in Fig. 12. Please refer to the Appendix for the recall plots for the other models in our synthetic dataset. The average recall values of the two methods are compared in Table 1.

Fig. 12

Registration with QA and FGR on Angel (color figure online)

Table 1 Average recalls of QA and FGR on the synthetic dataset. We use the FPFH feature in QA

For the synthetic dataset, FGR is selected for comparison since it is one of the state-of-the-art optimization-based algorithms like our approach, and the implementation was available online [44]. The average recall values are computed for 30 cases where registrations are performed with different 3D models, noise levels, and downsampling method combinations. Out of these 30 cases, our algorithm outperforms the FGR method in 17, resulting in a tie in three. Overall, the average recall values for the two methods are comparable.

Standard Assignment Comparison

The standard assignment is integrated into our correspondence search framework to show the effectiveness of our approach in point cloud registration. Registration experiments are conducted on the synthetic dataset using QA and Standard Assignment (SA), and recall values are compared for various downsampling sizes. Figure 13 shows the recall plots for various noise levels of the Angel model. Please refer to the appendix for the recall plots of the other models for various noise levels in the synthetic dataset. Some example registration results are given in Fig. 14. Significant improvement in registration accuracy can be achieved by using QA instead of SA for correspondence estimation. The average computation times of our framework with QA, with SA, and the FGR framework on the Bunny model for different downsampling sizes are tabulated in Table 2. Our QA algorithm runs slower on the synthetic dataset than SA and FGR; however, it achieves registration with higher accuracy.

Fig. 13

Recall values for QA and SA on Angel (color figure online)

Fig. 14

Registration results of QA and SA (color figure online)

Table 2 Average computation times (sec) of QA, SA, and FGR on Bunny

5.2 3DMatch dataset

3DMatch benchmark [21] is a large-scale real-world indoor dataset containing eight sets of indoor scene fragments captured by the RGBD sensor. Sample fragments are shown in Fig. 15. Each set contains 37–66 fragments; each fragment is a 3D point cloud of a surface. Unfortunately, computing the overlap ratio of the point cloud pairs in 3DMatch was not possible; however, it is known that the pairs have $>30\%$ overlap. Therefore, we set our parameter $\alpha$ as 0.3 in our experiments for all point cloud pairs. We downsampled our point clouds to 10 cm using voxel downsampling. For FCGF, we downsampled after the features were obtained and used the average of feature values for voxel downsampling. After registration, we applied the tuple test [32] and point-to-point ICP. We also used FGR transformation estimation. Figure 16 shows the registration result for one point cloud pair.

Table 3 gives the registration recall values for some state-of-the-art PCR methods using the RANSAC algorithm on the 3DMatch dataset. We obtained higher precision and recall values on most scenes and on average. It was reported that the R-PointHop [20] method achieves similar results to the methods presented in Table 3 with 0.72 and 0.26 average recall and precision values on 3DMatch. The proposed QA algorithm surpasses earlier approaches in recall performance and significantly improves the precision metric. We also compared our average and maximal recall and precision results with FGR [32] and recall values with FCGF+RANSAC in Table 4. We obtained the results for FGR using the implementation in [44]. Even though our registration results were poor compared to FGR [32] when we used the FPFH descriptor in the QA algorithm, we achieved significant improvement in accuracy over FGR when we used FCGF features [23]. Our results are also closer to FCGF with RANSAC than FGR.

Fig. 15

Scene fragments from 3DMatch dataset (color figure online)

Fig. 16

Registration result of QA on a point cloud pair in the 3DMatch dataset (color figure online)

Table 3 Evaluation results on 3DMatch

5.3 KITTI dataset

Karlsruhe Institute of Technology and Toyota Technological Institute (KITTI) benchmark is a large-scale real-world outdoor dataset containing 555 point cloud pairs. The scenes are captured by driving around Karlsruhe with two high-resolution color and grayscale video cameras using the autonomous driving platform Annieway [47]. Figure 17 shows sample point clouds in the dataset.

Table 4 QA, FGR, and FCGF evaluation results on 3DMatch

Fig. 17

Some examples from the KITTI dataset

Table 5 Evaluation results on KITTI

We used the relative rotation error (RRE), relative translation error (RTE), and registration recall (RR) metrics in our experiments on KITTI where RRE is the geodesic distance between estimated and ground-truth rotation matrices and RTE is the Euclidean distance between the estimated and ground-truth translation vectors. A registration result is successful if RRE is below $5^{\circ }$ and RTE is below 2 m.

Computing the exact overlap ratio between the source and target clouds was impossible for point clouds in the KITTI dataset. In our experiments, there are at least ten meters of distance between each point cloud pair, and the sensor range for collecting the point clouds is 120 ms [49]. Using this information, we expected the overlap ratio to be high for any two cloud pairs in our experiments but not more than $95\%$. We set our parameter $\alpha$ equal to 0.90 through experiments with different values. The comparison of our QA algorithm’s registration results and some state-of-the-art methods can be found in Table 5. Similar to the process in 3DMatch, we applied uniform downsampling, tuple test, and point-to-point ICP and FGR transformation estimation. Although the success rate of QA is slightly lower than that of DGR [27], our approach achieves the lowest RTE and RRE values among the presented state-of-the-art methods in the table. We observed that our results for the KITTI dataset were much better than the 3DMatch dataset. This may be due to the overlap ratio between the source and target point cloud pairs in KITTI having much less variation than 3DMatch; thus, we were able to set our parameter $\alpha$ more precisely.

5.4 Summary of results

Our results on the synthetic dataset show that the QA algorithm outperforms FGR in accuracy in 17 cases out of 30 cases (see Table 1), although it runs slower (see Table 2). Using the 3DMatch dataset, we tested our algorithm combined with the features FPFH and FCGF. We showed that the performance of QA significantly improves with FCGF by increasing our average recall from 9.25 to 74.08 and average precision from 15.56 to 87.52 (see Table 4). For the 3DMatch dataset, our approach outperforms the compared methods with an average recall of 0.74 and precision of 0.48. Of the eight scenes in the dataset, QA achieves higher recall values in four of them and higher precision values in all (see Table 3). For the KITTI dataset, the success rate of our approach is lower than that of DGR [27] by 0.7%. QA outperforms the compared methods in other metrics with 10.5 cm RTE and 0.17 $^{\circ }$ RRE (see Table 5).

6 Conclusion

As our main contribution, we propose a new coarse-to-fine pairwise point cloud registration framework. The preliminary version of the QA algorithm [3] that establishes the correspondence between the source and target point clouds has been improved and refined by integrating it with different handcrafted descriptors and a feature-learning model, resulting in an enhanced feature-matching performance.

We demonstrated the effectiveness of our approach against the standard assignment through experiments on our synthetic dataset. We evaluated the performance of our framework using three datasets; our registration results are better than or compatible with the state-of-the-art PCR methods in terms of accuracy.

The accuracy of our approach can be further improved for real-world datasets like 3DMatch and KITTI with overlap ratio estimation techniques. Our experiments showed that the QA algorithm is susceptible to the $\alpha$ parameter. Estimating the overlap ratio is difficult for these datasets. Setting the parameters that achieve the best possible results is challenging. A possible research direction is developing a method for estimating the overlap ratio for any two input point clouds using a learning model.

QA algorithm is computationally costly for real applications since the affinity matrix constructed is generally dense. Another future research direction is to explore sparser affinity matrix construction techniques to reduce computational costs while maintaining accuracy.

Further results

Figures 18, 19, 20, 21 show the recall plots for different downsampling sizes and each noise level of the Buddha, Bunny, Dragon, and Horse models, respectively. Figures 22, 23, 24, 25 show the recall plots using QA and SA for various noise levels of the Buddha, Bunny, Dragon, and Horse models, respectively.

Fig. 18

Registration with QA and FGR on Buddha (color figure online)

Fig. 19

Registration with QA and FGR on Bunny (color figure online)

Fig. 20

Registration with QA and FGR on Dragon (color figure online)

Fig. 21

Registration with QA and FGR on Horse (color figure online)

Fig. 22

Recall values for QA and SA on Buddha (color figure online)

Fig. 23

Recall values for QA and SA on Bunny (color figure online)

Fig. 24

Recall values for QA and SA on Dragon (color figure online)

Fig. 25

Recall values for QA and SA on Horse (color figure online)