1 Introduction

X-ray scanning technologies are increasingly used at sawmills to quality-grade logs and to optimise the log position for sawing (Berglund et al. 2014b; Rais et al. 2017). X-ray tomography can be used for measuring heartwood diameter (Skog and Oja 2009), wood density (Skog and Oja 2010) and knot sizes and geometry (Oja 2000; Johansson et al. 2013). Automatic scanners are used to grade sawn boards after sawing according to customer needs as illustrated by Berglund et al. (2014a).

In Nordic countries, the felling and processing of trees into various products is almost entirely carried out by single-grip harvesters using a cut-to-length approach (CTL). The determination of the optimal bucking pattern is challenging because stem shapes and wood properties for individual trees are typically unknown at the time of felling. Improper bucking in forests leads to financial losses because stem bucking is not properly connected with the production planning at sawmills. Costs from inadequate bucking are difficult or impossible to recover at subsequent stages of the value-chain because processing opportunities for a log and the eventual value of sawn products depend on the success of the bucking (Sessions 1988; Barth et al. 2015; Andersson et al. 2016).

Several studies have shown that increasing resources, including nutrient and light availability, increase tree and branch growth (Niinemets and Lukjanova 2003; Mäkinen and Hein 2006; Chen and Sumida 2018). Hence, current stem and wood properties relate to past tree growth, which is affected by geographical origin, site properties, stand dynamics and silvicultural regime (Auty et al. 2012; Mäkinen et al. 2015; Wang et al. 2018). Studies have been published over the years that report the effects of stand density and thinning on branch properties for several tree species (Weiskittel et al. 2009; Huuskonen et al. 2014; Grace et al. 2015). Although the general relationship between tree growth rate and branch dimensions is well-known, approaches that integrate information about past tree growth into the harvesting and bucking process are rarely used.

Current stem and crown dimensions are unreliable for predicting knot properties within stems because they may not adequately represent the conditions during the development of branches (Grace et al. 2006; Kantola et al. 2007; Ojansuu et al. 2018). Consequently, Reed et al. (1987) and Gobakken (2000) concluded that it is virtually impossible to predict timber grade recovery for individual trees. Thus, further development and new tools are needed to automatically record detailed information about tree properties during harvesting. Information about past growth rates is important for analysing knot properties within stems; these data, combined with stem dimensions, allow for the prediction of different quality zones within tree stems (Uusitalo et al. 2018).

Moberg and Nordmark (2006) showed that lumber volume and grade recovery could be predicted by integrating models for stem shape and knottiness with sawmill conversion simulation. Based on tree age and stand location (i.e., latitude, altitude), such models can be utilised during harvesting and production planning, as long as that input information can be automatically detected by CTL harvesters. X-ray scanning cannot be performed in a harvester; therefore, required information must be gathered by indirect techniques, such as using acoustic or near-infrared spectroscopy tools installed on a harvester head (Acuna and Murphy 2005; Walsh et al. 2014).

Image acquisition for bucking control may soon be feasible during felling. A camera system can be mounted on a harvester head for detecting variable and detailed information from the log end face, such as annual ring widths, boundary between sapwood and heartwood, pith eccentricity and the presence of rot. The aim of this study was to develop and demonstrate the potential for new models to integrate information about external and internal stem characteristics detected during harvesting that will aid stem bucking procedures for CTL harvesters. The approach incorporates explicit information on past growth rate of a tree and stem geometry.

2 Materials and methods

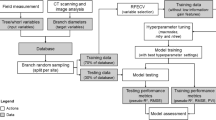
2.1 Stands and field measurements

Materials were collected from six pure or nearly-pure Scots pine (Pinus sylvestris L.) stands in 2017 and from three stands in 2018. The stands were at final felling stage and were located in southern Finland. The sites were on relatively infertile mineral soils classified as Myrtillus (medium fertility) or Vaccinium (lower fertility and moisture) forest types that are typical for Scots pine growth (Cajander 1949). The region represents the southern boreal zone with 3.3 °C annual mean temperature and 713 mm annual precipitation (Drebs et al. 2002).

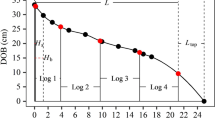
From each stand, 3–35 dominant trees without severe damage were randomly selected, for a total of 221 sample trees (Table 1). Stem diameter at breast height (1.3 m), tree height and height of the crown base were measured using Vertex III-60 instrument (Haglöf, Sweden) prior to felling the sample trees. The stems were cut to sawlogs and pulpwood by a harvester as part of normal logging operations by the UPM company. Sawlog lengths were defined using 30 cm intervals (3.7 m, 4.0 m, and up to 5.8 m), and upper diameters varied from 15 cm to 40 cm, depending on log quality and length.

Table 1 The number of sample trees and their mean stem diameter at breast height (dbh), height, height to crown base and age in each stand
Full size table

After felling, a single RGB image was taken under non-standardised conditions from the end face of each butt log by using a regular digital camera (Nikon D7200, Tokyo, Japan, resolution 6000 × 4000). The widths of the individual annual rings were manually measured from the pith to the bark by using image analysis software (ImageJ, Schneider et al. 2012). The mean width of rings 11−20 from the pith was used in the modelling for describing the growth rate at the pole stage, which is critical for quantifying the branchiness of the lower stem (Uusitalo and Isotalo 2005).

2.2 X-ray scanning of logs

The logs cut from the 221 sample trees were scanned at the UPM Korkeakoski sawmill by using a 4D X-ray log scanner with four scanner units and a conveyor speed of 150 m/min produced by Finnos (Lappeenranta, Finland). The discrete X-ray tomography scanner measured the total volume of knots in each whorl within the heartwood area of a stem based on density differences (Natterer 1986), hereafter referred to as knot volume, which is a relative dimensionless parameter without any exact physical unit. The scanning system also measures stem diameter at the point of a whorl. The scanned logs from a stem were merged to construct a knot volume profile for the entire log section for each stem.

The trees sampled from stands 1–6 were scanned in 2017, and the trees from stands 7–9 were scanned in 2018. The settings for the X-ray scanner were adjusted between years to better examine logs with low branchiness quality. The between-year difference in the knot volume profiles was accounted for in the modelling by introducing a dummy variable that indicated the measurement year.

In addition, an independent evaluation data set was measured that consisted of 102 butt logs of various lengths and diameters randomly selected from the normal log batch at the UPM Korkeakoski sawmill. The knot volumes in the evaluation data set were measured using the same methods as those used for the 221 trees sampled from the nine stands described above.

2.3 Test sawing

One sample tree from stands 2, 3, 4 and 5, as well as three sample trees each from stands 7, 8 and 9, were randomly selected for test sawing, for a total of 13 sample trees. The logs from stands 2, 3, 4 and 5 were first sawn through the pith. Then, 25-mm-thick boards were sawn through both log halves from the pith outwards (through-and-through sawing, unedged). The diameter and quality (sound, loose, decayed) of knots, as well as their vertical distance from the board base, were manually measured for each board. The X-ray scanner measures the total knot volume in the heartwood area of a log, therefore, the maximum knot diameter of each whorl was determined at the heartwood-sapwood boundary based on the measured knot diameters. Then, the profile for the log section of the stem was reconstructed by merging the logs for a stem.

The test sawing process was modified after the first four stems because knot information was only needed from the heartwood area. The logs from stands 7, 8 and 9 were cant sawn, i.e., side boards from four log sides were cut based on the heartwood-sapwood boundary for each log. The faces of the remaining quadrangle block corresponded to the centre boards of a typical sawing process. Then, the knots were measured similar to those of the first trees.

2.4 Statistical analyses

The system for predicting diameter of the thickest knot from each whorl along a stem consists of two submodels. The first submodel predicts the knot volume profile from the stem base upwards, and the second submodel converts the predicted knot volume to the maximum knot diameter. The first submodel is based on all 221 sample trees measured by the X-ray log scanner, and the second submodel is based on the 13 sample trees selected for test sawing.

Different combinations of variables used to describe the sample trees, stem dimensions, radial growth rate and measurement year, as well as their transformations, were tested. Highly correlated independent variables were avoided.

The data set had hierarchical structure with stand, tree and whorl levels. Therefore, mixed linear models were applied using the MIXED procedure in SAS (version 9.4, SAS Institute Inc. 2017). Two-level nested random effects were used for the intercepts to account for the hierarchical data structure. A first-order autoregressive model [AR(1)] was used to describe autocorrelation structure of the residuals along the stem because a series of consecutive whorls are measured from the same stem. The final models were selected based on visual examination of the residuals, statistical significance of the fixed variables (p < 0.05), and the Bayesian information criteria (BIC; Schwarz 1978), which indicates the overall fit of the model.

The knot volumes and maximum knot diameters were predicted using the fixed part of both models, and the predicted values were transformed back to the original scale to examine the performance of the models. A logarithmic transformation was used to stabilise the variance for the dependent variables. Therefore, a variance correction term [(\(\sigma_{i}^{2} + \sigma_{ij}^{2} + \sigma_{ijk}^{2}\))/2] was added to correct the bias caused by the log transformation (Baskerville 1972), where \(\sigma_{i}^{2}\), \(\sigma_{ij}^{2}\) and \(\sigma_{ijk}^{2}\) are the mean square errors for stands, trees and whorls, respectively.

3 Results

3.1 Model for knot volume along the stem

Model (1) predicts the total knot volume in whorls along a stem.

$$\ln \left( {kv_{ijk} } \right) = \beta_{0} + \beta_{1} \ln \left( {dw_{ijk} } \right) + \beta_{2} \ln \left( {dbh_{ij} } \right) + \beta_{3} ds_{ijk} /dbh_{ij} + \beta_{4} \left( {ds_{ijk} /dbh_{ij} } \right) \times Year + \beta_{5} \ln \left( {ir_{ij} } \right) + \beta_{6} Year + Stand_{i} + Tree_{ij} + Whorl_{ijk}$$
(1)

where kv is the knot volume, dw is the distance of whorl k from the stem base (m), dbh is the stem diameter (cm) of tree j from stand i at breast height, ds is the stem diameter at the height of whorl k, ir is the mean width of annual rings 11‒20 from the pith at the stem base (mm), Year is a dummy variable indicating the sampling year (0 = 2017, 1 = 2018) and β0,… β6 are fixed regression coefficients. Standi is a random stand effect i = 1, 2, 3,…, 9. Treeij is a random tree effect, j = 1, 2,…,nj. Whorlijk is a random whorl effect, k = 1, 2,…, nk with AR(1) correlation structure between the measurements of the same tree in successive whorls along the stem.

Knot volume increased with increasing stem diameter and growth rate at the pole stage (Table 2). In the model-building data set, no clear trend in the residuals was found relative to whorl distance from the stem base (Fig. 1a). Accordingly, in the evaluation data set consisting of 102 butt logs, no trend was found from the stem base upwards, but the predicted knot volumes were lower, on average, than the measured values (Fig. 1b).

Table 2 Regression coefficients, covariance parameter estimates and their standard errors (SEs) for the model predicting the knot volume along the stem (Eq. 1)
Full size table
Fig. 1
figure 1

Residuals (measured-predicted) of the knot volume model (Eq. 1) plotted against whorl distance from the stem base in the model-building data set (a) and in the evaluation data set (b). The bottom and top edges of the box are located at the sample 25th and 75th percentiles and the centre line is at the median. The vertical lines are drawn from the box to the most extreme point within the 1.5 interquartile ranges

Full size image

The knot volume for the sample trees increased from the stem base upwards but levelled off at the height of 4–10 m and started to decrease further towards the tree top (Fig. 2). In most cases, the model gave an unbiased prediction of knot volume, but in stand 9, which was of very poor quality, knot volumes were clearly underestimated.

Fig. 2
figure 2

Measured (dots) and predicted (dashed lines) knot volumes (Eq. 1) plotted against whorl distance from the stem base upwards for four randomly selected test-sawn sample trees (upper row). Measured (dots) and predicted knot diameters (Eq. 2) are shown for the same trees (lower row). The continuous lines show the predictions based on the measured knot volumes and the dashed lines show the predictions based on the predicted knot volumes. The knot volumes and knot diameters were predicted using only the fixed parts of Eqs. 1 and 2

Full size image

3.2 Model for maximum knot diameter

The model for maximum knot diameter in a whorl was based on the test sawing of 13 stems sampled in 2017 and 2018. Knot diameter was mainly related to knot volume in the same whorl (kv).

$$ln\left( {kd_{jk} } \right) = \alpha_{0} + \alpha_{1} kv_{jk} + \alpha_{2} \ln \left( {kv_{jk} } \right) + \alpha_{3} dw_{ijk} + \alpha_{4} Year + Tree_{j} + Whorl_{jk}$$
(2)

where kd is the maximum knot diameter of whorl k in tree j, and the other fixed variables are defined above. α0, α1, α2, a3 and α4 are fixed regression coefficients. Random variables include the tree and whorl level (Treeij and Whorljk, respectively), with Whorljk having an AR(1) correlation structure between the measurements of the successive whorls. The stand and tree levels could not be properly separated from each other because only one tree was selected for sawing from four out of the seven stands from which sample trees were test-sawn; therefore, no random variable at the stand level was included in the model.

Maximum knot diameter increased at a slower rate when the knot volume increased (Table 3; Fig. 3). However, knot volume did not entirely account for the change in knot diameters along the stem, i.e., whorl distance from the stem base also had an effect, even though knot volume was already included in the model. Although the models predicted the average variation of knot diameter in a relatively unbiased manner, the highest and lowest values appeared to occur randomly and were not related to any of the independent variables that were tested (Fig. 3).

Table 3 Regression coefficients, covariance parameter estimates and their standard errors (SEs) for the model predicting maximum knot diameter (Eq. 2)
Full size table
Fig. 3
figure 3

Measured and predicted maximum knot diameters (dots and stars, respectively) plotted against the measured knot volumes (a), and predicted knot diameters (b)

Full size image

Maximum knot diameters increased from the stem base upwards, but then began to decrease near the top logs (Fig. 2). The behaviour of the model, as well as the combined system of Eqs. 1 and 2, is demonstrated in the lower row of Fig. 2. In most cases, the models gave an unbiased prediction for knot diameters relative to the distance from the stem base, regardless of whether the predictions were based on the measured or predicted knot volumes. However, when the predicted knot volumes were biased, the error accumulated from one model to another, and the bias from the recursive system of models was larger.

Knot diameters were predicted for 5-m-long butt logs from all sample trees to further demonstrate the performance of the models in log grading (Table 4). In this simplified example, a log belonged to the highest quality class (grade A) when all the predicted knots were not more than 22 mm thick. When knot diameters were predicted using the measured knot volumes, on average, 45% of the logs were classified as grade A; the proportion varied from 4 to 100% among the stands. When the predicted knot volumes were used, the average proportion was slightly higher (52%). However, for individual stands, the difference was not systematic. In six stands, the proportion of grade A logs based on the predicted knot volumes was higher than that based on the measured knot volume; whereas in two stands it was lower.

Table 4 Number and proportion of high quality butt logs (grade A) predicted using the measured and predicted knot volume
Full size table

4 Discussion

A model system was developed for predicting knot properties inside a stem based on widths of annual rings and stem diameters along the stem; both were measured at the time of harvesting. The results of this study demonstrate the potential of wood quality modelling for identifying between-stand differences regarding knot properties, as well as between-tree differences within a stand. The results also showed that knottiness of stems of a given size varies depending on their early growth rate.

The applicability of the current model system is based on the premise that high quality images from log end faces can be captured by a harvester during felling. Then, various variables, including growth rate and age of stems, can be automatically measured through advanced image analysis and eventually linked to bucking optimisation. In addition to stem internal knottiness, growth rate of trees is strongly correlated with wood density and strength (e.g., Auty et al. 2016). The identification of pith location at the log end face at the time of harvesting is important for further analyses of ring widths. For example, pith eccentricity is related to the occurrence of compression wood and basal sweep (Rune and Warensjö 2002; Nordmark 2003; Norell and Borgefors 2008).

Early growth rate, expressed as average width of rings 11–20 from the pith, explained a significant amount of the variation in the knot volume. As shown in several previous studies, high growth rate at an early age results in thick branches, which live for a long time and self-prune slowly (e.g., Mäkinen and Hein 2006; Weiskittel et al. 2009; Auty et al. 2012). In this study, stand 9 was of particularly poor quality, and the difference between it and other stands was not properly represented by early growth rate. This could be explained by the genetic potential of trees, which influences branch growth relative to stem growth (e.g., Mäkinen 1996; Haapanen et al. 2016).

The relationship between early growth rate and knottiness found in this study supports earlier Finnish attempts to model the quality of butt logs for pricing (Heiskanen 1965), bucking (Uusitalo et al. 2004; Uusitalo and Isotalo 2005) and sawing production planning (Uusitalo 1997). In Sweden, early growth rate has also been used as a quality indicator for wood pricing (VMR 1-07, Swedish Timber Measurement Council 2008), even though it is laborious and destructive to measure from standing trees. Automatic measurement systems attached to the harvester head offer new possibilities to utilise information about early growth rate for logging operations (cf., Uusitalo et al. 2018).

Knot volume data was gathered by using an X-ray tomography system, which delivers the total volume of all knots in a whorl, but not dimensions of individual knots. Even though the model converting knot volumes to diameters for the thickest knots provided an unbiased fit of the data, the variation in the residuals around the predicted knot diameters was due, at least in part, to the fact that a certain volume can be dated back to a few larger or several smaller knots.

The X-ray measurements appeared to be sensitive to the settings of the X-ray scanner. They were adjusted between the study years, but the difference was represented by a dummy variable that indicated the measurement year for both models. In the recursive model system, knot volume is an auxiliary variable assisting in estimating knot diameters. As they are not part of the main analysis, the between-year difference in knot volume results in no error to knot diameters.

5 Conclusion

The developed system will guide logging operations to reach more profitable bucking procedures. The system allows the use of any grading rules in stem bucking based on minimum and maximum log dimensions and maximum allowed knot diameters. As the typical price difference between the two highest u/s sawn good grades is approximately 20%, even small improvements in the detection of quality zones and increasing the proportion of the most valuable lumber grades may result in a large increase in the total value of primary wood products. According to the rough estimate, increasing the proportion of the best quality sawn timber (U/S I) in Finland and Sweden by one percent by means of improved bucking of Scots pine logs based on knot properties would result in a revenue increase of ~ 10 million € per year.