Skip to main content
SpringerLink
Log in

Nonlinear Phase Unwinding of Functions

  • Published:
Journal of Fourier Analysis and Applications Aims and scope Submit manuscript

Abstract

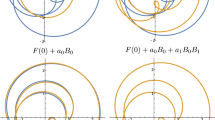
We study a natural nonlinear analogue of Fourier series. Iterative Blaschke factorization allows one to formally write any holomorphic function F as a series which successively unravels or unwinds the oscillation of the function

$$\begin{aligned} F = a_1 B_1 + a_2 B_1 B_2 + a_3 B_1 B_2 B_3 + \cdots \end{aligned}$$

where \(a_i \in \mathbb {C}\) and \(B_i\) is a Blaschke product. Numerical experiments point towards rapid convergence of the formal series but the actual mechanism by which this is happening has yet to be explained. We derive a family of inequalities and use them to prove convergence for a large number of function spaces: for example, we have convergence in \(L^2\) for functions in the Dirichlet space \(\mathcal {D}\). Furthermore, we present a numerically efficient way to expand a function without explicit calculations of the Blaschke zeroes going back to Guido and Mary Weiss.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

References

  1. Beurling, A., Deny, J.: Espaces de Dirichlet I. Le cas elementaire. Acta Math. 99, 203–224 (1958)

    Article  MathSciNet  MATH  Google Scholar 

  2. Beurling, A., Deny, J.: Dirichlet spaces. Proc. Natl. Acad. Sci. USA 45, 208–215 (1959)

    Article  MATH  Google Scholar 

  3. Carleson, L.: A representation formula for the Dirichlet integral. Math. Z. 73, 190–196 (1960)

    Article  MathSciNet  MATH  Google Scholar 

  4. Coifman, R., Weiss, G.: A kernel associated with certain multiply connected domains and its applications to factorization theorems. Stud. Math. 28(1966), 31–68 (1967)

    MathSciNet  MATH  Google Scholar 

  5. Eisner, T., Pap, M.: Discrete orthogonality of the Malmquist Takenaka system of the upper half plane and rational interpolation. J. Fourier Anal. Appl. 20(1), 1–16 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  6. El-Fallah, O., Kellay, K., Mashreghi, J., Ransford, T.: A primer on the Dirichlet space. Cambridge Tracts in Mathematics, 203. Cambridge University Press, Cambridge (2014)

    MATH  Google Scholar 

  7. Feichtinger, H., Pap, M.: Hyperbolic wavelets and multiresolution in the Hardy space of the upper half plane. Blaschke products and their applications. Fields Inst. Commun. 65, 193–208 (2013)

  8. Gabor, D.: Theory of communication. J. Inst. Electr. Eng. Part III Radio Commun. Eng. 93(26), 429–457 (1946)

    Google Scholar 

  9. Healy, D. Jr: Multi-resolution phase, modulation, Doppler ultrasound velocimetry, and other Trendy Stuff, talk, slides via personal communication

  10. Healy, D.: Phase analysis. Talk given at the University of Maryland, slides as private communication

  11. Letelier, J., Saito, N.: Amplitude and phase factorization of signals via Blaschke product and its applications, talk given at JSIAM09, https://www.math.ucdavis.edu/~saito/talks/jsiam09.pdf

  12. Mallat, S.: Group invariant scattering. Commun. Pure Appl. Math. 65(10), 1331–1398 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  13. Nahon, M.: Phase Evaluation and Segmentation. Ph.D. Thesis, Yale University, 2000

  14. Picinbino, B.: On instantaneous amplitude and phase of signals. IEEE Trans. Signal Process. 45, 552–560 (1997)

    Article  Google Scholar 

  15. Pap, M.: Hyperbolic wavelets and multiresolution in \(H^2(\mathbb{T})\). J. Fourier Anal. Appl. 17(5), 755–776 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  16. Mi, W., Qian, T., Wan, F.: A fast adaptive model reduction method based on Takenaka–Malmquist systems. Syst. Control Lett. 61(1), 223–230 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  17. Qian, T.: Adaptive Fourier decomposition, rational approximation, part 1: theory, invited to be included in a special issue of Int. J. Wavelets Multiresolut. Inf. Process

  18. Qian, T.: Intrinsic mono-component decomposition of functions: an advance of Fourier theory. Math. Methods Appl. Sci. 33(7), 880–891 (2010)

    MathSciNet  MATH  Google Scholar 

  19. Qian, T., Ho, I.T., Leong, I.T., Wang, Y.B.: Adaptive decomposition of functions into pieces of non-negative instantaneous frequencies. Int. J. Wavelets Multires. Inf. Process. 8(5), 813–833 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  20. Qian, T., Tan, L.H., Wang, Y.B.: Adaptive decomposition by weighted inner functions: a generalization of Fourier series. J. Fourier Anal. Appl. 17(2), 175–190 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  21. Qian, T., Zhang, L.: Mathematical theory of signal analysis vs. complex analysis method of harmonic analysis. Appl. Math. J. Chin. Univ. 28(4), 505–530 (2013)

    Article  MATH  Google Scholar 

  22. Qian, T., Zhang, L., Li, Z.: Algorithm of adaptive Fourier decomposition. IEEE Trans. Signal Process. 59(12), 5899–5906 (2011)

    Article  MathSciNet  Google Scholar 

  23. Rado, T.: A lemma on the topological index. Fund. Math. 27, 212–225 (1936)

    MATH  Google Scholar 

  24. Vakman, D.E.: On the definition of concepts of amplitude, phase and instantaneous frequency of a signal. Radiotekhnika i Elektronika 17(5), 972–978 (1972)

    Google Scholar 

  25. Weiss, G., Weiss, M.: A derivation of the main results of the theory of \(H^p\)-spaces. Rev. Un. Mat. Argent. 20, 63–71 (1962)

    MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Program in Applied Mathematics, Yale University, New Haven, CT, 06510, USA

    Ronald R. Coifman

  2. Department of Mathematics, Yale University, New Haven, CT, 06510, USA

    Stefan Steinerberger

Authors
  1. Ronald R. Coifman
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Stefan Steinerberger
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Stefan Steinerberger.

Additional information

Communicated by Thomas Strohmer.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Coifman, R.R., Steinerberger, S. Nonlinear Phase Unwinding of Functions. J Fourier Anal Appl 23, 778–809 (2017). https://doi.org/10.1007/s00041-016-9489-3

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00041-016-9489-3

Keywords

Mathematics Subject Classification

Search

Navigation