On Closed Geodesics in Lorentz Manifolds

Abstract

We construct compact Lorentz manifolds without closed geodesics.

1 Introduction

It is well known that (non-trivial) closed geodesics in compact Riemannian manifolds always exist (see for example [Kli78]). There has been, then, a lot of activity around the semi-Riemannian counterpart, mainly the Lorentzian case. Before going further, let us first introduce the following definition. A (non-trivial) geodesic γ:I→M in a semi-Riemannian manifold (M,g) is called weakly closed if there exists s,t∈I with t≠s, such that γ(s)=γ(t) and $\dot{\gamma}(s)$ is proportional but not equal to $\dot{\gamma}(t)$ and called closed if $\dot{\gamma}(s)=\dot{\gamma}(t)$. Observe that weakly closed geodesics are necessarily isotropic and incomplete.

Our first result provides an example of a compact semi-Riemannian manifold without closed or weakly closed geodesics. More precisely, let SOL and Euc be the identity components of the isometry groups of the Minkowski and the Euclidean planes respectively and put G=SOL×Euc. Then

Theorem 1.1

There exists a left invariant metric on G, of signature (2,4), and a cocompact lattice Γ⊂G such that Γ∖G is without closed or weakly closed geodesics.

The study of closed geodesics in semi-Riemannian manifolds received more attention in the Lorentzian case. The first result we want to mention in this direction is due to Tipler [Tip79] where it is shown that a compact spacetime with a covering space containing a compact Cauchy surface admits closed timelike geodesics. The compactness assumption of the Cauchy surface is necessary as shown by Guediri [Gue02] where he provides examples of compact flat Lorentz space forms without closed timelike geodesic, but they admit, however, closed lightlike geodesics.

In [Gal86], Galloway shows that every compact two-dimensional Lorentzian manifold contains at least one closed non-lightlike or (weakly) closed lightlike geodesic. He also constructed a three-dimensional example without closed non-spacelike geodesics. Galloway’s result doesn’t ensure existence of closed geodesics in Lorentzian surfaces. This was settled later by Suhr in [Suh13] where he shows that every compact Lorentzian surface contains at least two closed geodesics, one of them is non-lightlike and then constructs examples showing optimality of this bound.

Galloway in [Gal84], Guediri in [Gue02, Gue07], Sánchez in [San06] and Flores et al. in [FJP11] provide many existence (and non-existence) results of closed timelike geodesics in compact Lorentzian manifolds. See also [C+21, Mas92, Mas93] for further investigations.

The question whether a compact Lorentzian manifold admits closed geodesics remained open (see Question 9.1.1 in the recent survey [BM21]). The following examples provide a negative answer:

Theorem 1.2

Let G be either ${\textsf{SL}}(2,\mathbb{R})$ or SOL. Then there exists a left invariant Lorentzian metric on G such that every compact quotient Γ∖G is without closed geodesics. However, Γ∖G admits a countable collection of weakly closed null geodesics.

Unlike the locally homogeneous case, closed geodesics always exist in the homogeneous setting. More precisely

Theorem 1.3

A compact homogeneous semi-Riemannian manifold (M,g) admits closed geodesics. If, in addition, (M,g) is Lorentzian then it admits both timelike and spacelike closed geodesics.

1.1 Organization of the paper

Section 2 is dedicated to the proof of Theorem 1.3. In Sect. 3 we present some background about geodesics of left invariant metrics needed for the constructions later. We prove Theorems 1.2 and 1.1 in Sects. 4 and 5 respectively.

2 The homogeneous case: proof of Theorem 1.3

The main purpose of this section is to show existence of closed geodesics in the case of compact homogeneous semi-Riemannian manifolds.

Lemma 2.1

Let X be a Killing vector field on a compact semi-Riemannian manifold (M,g). The X-orbits of critical points of the function p↦g(X(p),X(p)) are geodesics. If X generates a precompact one-parameter subgroup of Isom(M,g) then it can be approximated by a Killing field X′ whose flow defines a circle action. It follows that (M,g) has closed geodesics. Moreover, (M,g) has a spacelike (resp. timelike) closed geodesic if X′ is spacelike (resp. timelike) somewhere.

Proof

For the proof of the first statement see [KN63] Proposition 5.7 or [FJP11] Lemma 2.3 for more details. If X generates a precompact one-parameter subgroup I then its closure in Isom(M,g) is a compact connected torus $\mathbb{T}^{k}$ and it follows that I can be approximated by closed one-parameter subgroups. The rest follows from the compactness of M. □

Corollary 2.2

A compact homogeneous semi-Riemannian manifold (M,g), whose identity component of its isometry group is compact, admits both timelike and spacelike closed geodesics.

Now, suppose that (M,g) is homogeneous and let G=Isom₀(M,g) be the identity component of the isometry group with Lie algebra ${\mathfrak{g}}={\mathfrak{s}}\ltimes {\mathfrak{r}}$ where ${\mathfrak{s}}$ is the semisimple Levi factor and ${\mathfrak{r}}$ is the solvable radical.

If G admits a non-trivial compact semisimple Levi factor K, then applying Lemma 2.1 one deduces existence of closed geodesics. Indeed, K contains many closed one-parameter groups. In fact, the set of linear lines in the algebra ${\mathfrak{k}}$ of K, generating closed one-parameter subgroups, is dense in the projective space $\mathbb{P}({\mathfrak{k}})$.

On the other hand, if ${\mathfrak{s}}$ has no compact factor then by [BGZ19] (Theorem A.) the G-action is locally free i.e the isotropy subgroup Γ⊂G is discrete. Moreover, the left invariant metric on G, obtained by pulling-back the metric g to G, is in fact bi-invariant. Therefore, geodesics in G are right and left cosets of one-parameter subgroups. We distinguish two cases:

• Case ${\mathfrak{s}}\neq \{0\}$: let $u\in {\mathfrak{s}}$ be an elliptic element, that is, $\mathrm {ad}_{u}:{\mathfrak{s}}\to {\mathfrak{s}}$ is $\mathbb{C}$-diagonalizable with imaginary eigenvalues. Elliptic elements u in ${\mathfrak{s}}$ always exist and the ad_u-action on ${\mathfrak{g}}={\mathfrak{s}}\ltimes {\mathfrak{r}}$ is also elliptic (in fact for any representation ${\mathfrak{s}}\to {\mathfrak{gl}} (V)$, the image of an elliptic element is elliptic). The right (or left) invariant Killing field X_u determined by u is equi-continuous i.e it generates a precompact flow. Indeed, ad_u preserves a positive definite inner product on ${\mathfrak{g}}$ and, hence, the left action of exp(tu) on G/Γ preserves a right invariant Riemannian metric. Finally, by applying Lemma 2.1 we deduce existence of closed geodesics.

• Case ${\mathfrak{s}}= \{0\}$: so ${\mathfrak{g}}={\mathfrak{r}}$ is solvable and, as discussed above, M=G/Γ with G endowed with a bi-invariant semi-Riemannian metric. Therefore, one-parameter groups in G are geodesic and if γ∈Γ belongs to a one-parameter group I, then I projects to a closed geodesic in G/Γ. The exponential map for solvable groups fails to be surjective in general but it is, however, a diffeomorphism for nilpotent (simply connected) groups. Since every lattice in a solvable group intersects the nil-radical in a lattice, we deduce existence of closed geodesics in our case.

The Lorentzian case

If (M,g) is a homogeneous compact Lorentzian manifold we can in fact deduce existence of both timelike and spacelike closed geodesics. Indeed, if the identity component G of its isometry group is compact, then this follows from Corollary 2.2. If G is non-compact, then it follows by a classification in [Zeg981] that (M,g) is covered by a metric product H×N where N is a compact homogeneous Riemannian manifold and H is a Lie group endowed with a bi-invariant metric. This Lie group is either $\widetilde{{\textsf{SL}}}(2,\mathbb{R})$ or an oscillator group i.e an elliptic extension $\mathbb{S}^{1}\ltimes {\textsf{Heis}}_{2n+1}$ of the Heisenberg group Heis_2n+1 (let us mention, in fact, that general non necessarily transitive actions of Lie groups on compact Lorentz manifolds were also classified in [AS971, AS972, Zeg982]). We deduce:

• Closed spacelike geodesics: if N is non-trivial then we have closed spacelike geodesics. Suppose N is trivial, so M=H/Γ with Γ⊂H a cocompact lattice. If $H=\widetilde{{\textsf{SL}}}(2,\mathbb{R})$ then any one-parameter subgroup intersecting Γ in a hyperbolic element projects to a closed spacelike geodesic. If $H=\mathbb{S}^{1}\ltimes {\textsf{Heis}}_{2n+1}$ then for the bi-invariant metric the subgroup Heis_2n+1 is degenerate (i.e lightlike) and totally geodesic. Since Γ intersects Heis_2n+1 in a lattice, we deduce existence of closed spacelike geodesics.

• Closed timelike geodesics: In all cases, elliptic elements in the Lie algebra ${\mathfrak{h}}$ of H exist and are timelike with respect to the bi-invariant metric. They give rise to closed timelike geodesics.

3 The geodesic equation for left invariant metrics

To a C¹-curve γ:I→G in a Lie group G, one associates the curve $D_{\gamma}:I\to {\mathfrak{g}}$ in the Lie algebra ${\mathfrak{g}}$ as follows: for t∈I the velocity vector $\dot{\gamma}(t)$ lives in T_γ(t)G which is identified with ${\mathfrak{g}}$ via the left translation L_γ(t). Put $D_{\gamma}(t)=(L_{\gamma (t)})_{*}^{-1}(\dot{\gamma}(t))$. One observes that D_γ is constant if and only if γ is the restriction to I of a parameterized left coset of a one parameter group.

Suppose that G is endowed with a left invariant semi-Riemannian metric, or equivalently, ${\mathfrak{g}}$ is endowed with a semi-Riemannian inner product 〈.,.〉. Then a C²-curve γ:I→G is a geodesic if and only if D_γ solves the first order ODE, introduced in [Arn66], which we refer to as the geodesic equation (also called the Euler-Arnold equation):

$$ \dot{x}(t)=\mathrm {ad}_{x(t)}^{*}(x(t)). $$

(1)

In other words, one has the vector field on ${\mathfrak{g}}$ given by $x\mapsto \mathrm {ad}_{x}^{*}(x)$ and γ is a geodesic if and only if D_γ is a parameterized trajectory of the generated (local) flow. Clearly this vector field is 2-homogeneous.

It is known that the geodesic equation (1) admits at least one radial solution $\mathrm {ad}_{v}^{*}v=\lambda v$ with v≠0. Indeed, the fact that the geodesic vector field given by (1) is 2-homogeneous implies that it induces a map $\psi :\mathbb{P}^{+}({\mathfrak{g}})\to \mathbb{P}^{+}({\mathfrak{g}})$ if it does not vanish on ${\mathfrak{g}}-\{0\}$, where $\mathbb{P}^{+}({\mathfrak{g}})$ is the space of half lines from the origin. In this case, ψ has even degree since it satisfies ψ(x)=ψ(−x) which implies that it has fixed points. Also, observe that λ≠0 implies that v is null.

Recall that 〈.,.〉 is bi-invariant if and only if $\mathrm {ad}_{x}^{*}=-\mathrm {ad}_{x}$ for all $x\in {\mathfrak{g}}$, which implies that equation (1) becomes $\dot{x}=0$. In this case all solutions are constant which means that geodesics in G are nothing but left cosets of one-parameter groups.

Moreover, the case when the algebra ${\mathfrak{g}}$ is quadratic i.e ${\mathfrak{g}}$ admits a bi-invariant semi-Riemannian inner product 〈.,.〉, the geodesic equation for any given metric on ${\mathfrak{g}}$ can be simplified. More precisely, let $({\mathfrak{g}}, \langle .,. \rangle )$ be such an algebra and q is any inner product on ${\mathfrak{g}}$, then there is a unique 〈.,.〉-self-adjoint isomorphism $A_{q}:{\mathfrak{g}}\to {\mathfrak{g}}$ such that q(v,w)=〈v,A_q(w)〉 for all $v,w\in {\mathfrak{g}}$. The geodesic equation for q can be rewritten as follows (see [EFR23] Proposition 4.2):

$$ A_{q}(\dot{x})=[A_{q}(x),x]=-\mathrm {ad}_{x}(A_{q}(x)). $$

(2)

Remark 3.1

Let K be a compact semisimple Lie group with Lie algebra ${\mathfrak{k}}$ and Killing form κ. Let A be a κ-self-adjoint isomorphism and q(.,.)=κ(.,A.) the associated semi-Riemannian inner product. Consider the left invariant metric generated by q. By Lemma 2.1 the left action of any one-parameter subgroup I=exp(tu) admits an orbit Ig which is a geodesic. Thus, the one-parameter subgroup g⁻¹Ig is a geodesic. In other words, it corresponds to a singular solution of the geodesic equation (2) which means [Au′,u′]=0 where u′=Ad(g⁻¹)u. Therefore, every $u\in {\mathfrak{k}}$ is conjugate to $u^{\prime}\in {\mathfrak{k}}$ such that u′ and Au′ commute.

3.1 Dynamics of the geodesic flow

The fact that the vector field given by the ODE (1) is 2-homogeneous, implies that the scaling action sends solution to solution, up to affine reparameterization. This induces a (singular) foliation by curves on the projectivization $\mathbb{P}({\mathfrak{g}})$ seen as the “dynamics” of the geodesic flow on the projective space. Similarly, we have a directed foliation on the spherization $\pi :{\mathfrak{g}}\to \mathbb{P}^{+}({\mathfrak{g}})$. In the case of Lorentzian signature, this “flow” on $\mathbb{P}^{+}({\mathfrak{g}})$ leaves invariant two conformal copies of the hyperbolic space $\mathbb{H}^{n-1}$, a conformal copy of the de Sitter space dS_n−1, and two conformal Riemannian spheres π(C⁺),π(C⁻) where C⁺ and C⁻ are the half null cones.

A solution in ${\mathfrak{g}}$, of the geodesic equation (1), is called direction-periodic if it projects to a closed (possibly singular) trajectory in the spherization $\mathbb{P}^{+}({\mathfrak{g}})$. Observe that both closed and weakly closed geodesics are direction-periodic.

3.2 Compact quotients

Let Γ⊂G be a cocompact lattice and consider the compact quotient M=Γ∖G. The left invariant metric on G descends to M. Projections to M of left invariant vector fields are fundamental vector fields of the right G-action on M. The tangent bundle TG of G, under left translations, is identified with $G\times {\mathfrak{g}}$. Therefore, we have a trivialisation $T M \to M \times {\mathfrak{g}}$. For a curve (x(t),v(t)) in TM, one associates the curve v(t) in ${\mathfrak{g}}$, and this applies in particular to the case $v(t) = \dot{x}(t)$. A curve x(t) in M is a geodesic if and only if $\dot{x}(t)$ solves the equation (1) on ${\mathfrak{g}}$.

Let Φ^t be the geodesic (local) flow. Then Φ^t(x,u)=(ϕ(t,x,u),u(t)), where u(t) is a solution of the geodesic equation (1). In particular, the map $(x, u) \in T M \mapsto u \in {\mathfrak{g}}$ semi-conjugates the geodesic (local) flow on TM to the (local) flow of the geodesic equation (1). Let us pass to the projectivization of the tangent bundle $\mathbb{P}(T M ) = M \times \mathbb{P}({\mathfrak{g}})$. The (singular) foliation on $\mathbb{P}(T M )$ induced by Φ^t projects to the (singular) foliation induced by the flow of the geodesic equation (1) on $\mathbb{P}({\mathfrak{g}})$.

Let $v\in {\mathfrak{g}}$ be a constant solution of the equation (1) i.e $\mathrm {ad}_{v}^{*}v=0$. Let I_v=exp(tv) be the associated one-parameter group in G. The left cosets of I_v are therefore geodesics. In other words, the orbits of the right action of I_v on both G and M=Γ∖G are geodesics. Furthermore, a left coset gI_v projects a closed geodesic in M if and only if gI_vg⁻¹∩Γ is a lattice in gI_vg⁻¹.

On the other hand, if $v\in {\mathfrak{g}}$ is a non-trivial radial solution, i.e $\mathrm {ad}_{v}^{*}v=\lambda v$ with λ≠0, then the left cosets of the one-parameter group I_v=exp(tv) are geodesics but only up to parameterizations. Thus, the orbits of the right action are, up to reparameterizing, geodesics. Similarly, a left coset gI_v projects a weakly closed geodesic, up to parameterizing, in M if and only if gI_vg⁻¹∩Γ is a lattice in gI_vg⁻¹.

4 No closed geodesics: proof of Theorem 1.2

In this section we construct a left invariant Lorentzian metric on $G={\textsf{SL}}(2,\mathbb{R})$ or SOL with the property that every compact quotient Γ∖G admits no closed geodesics but they admit, however, a countable collection (up to reparameterizations) of weakly closed null geodesics. For further details on the structure of Lie algebras and lattices in Lie groups we refer to [Kir08] and [Rag72].

4.1 ${\textsf{SL}}(2,\mathbb{R})$ case

Endow the algebra ${\mathfrak{sl}}(2,\mathbb{R})$ with its Killing form 〈.,.〉 and let e,h,f be a basis of ${\mathfrak{sl}}(2,\mathbb{R})$ such that [f,e]=h [h,e]=−e [h,f]=f. Then

$$ \langle e,e\rangle =\langle e,h\rangle =\langle h,f\rangle =\langle f,f \rangle =0 \ \ \text{and} \ \ \langle e,f\rangle =\langle h,h\rangle =2. $$

Let A be the 〈.,.〉-self-adjoint isomorphism of ${\mathfrak{sl}}(2,\mathbb{R})$ whose matrix with respect to e,h,f is

$$ A= \begin{pmatrix} 1 & 1 & 0 \\ 0 & 1 & 1 \\ 0 & 0 & 1 \end{pmatrix} . $$

Let q be the Lorentzian metric given by q(v,w)=〈v,Aw〉 for all $v,w\in {\mathfrak{sl}}(2,\mathbb{R})$. We have seen in (2) that the geodesic equation for q is $A\dot{v}=[Av,v]$.

Lemma 4.1

The plane P=span(e,h) is invariant under the geodesic flow. More precisely, the geodesic vector field on P has the form v=(x,y)∈P↦y²e.

Proof

Put v=xe+yh, then [Av,v]=[(x+y)e,yh]+[yh,xe]=[ye,yh]=y²e. Thus A⁻¹[Av,v]=y²e. □

One observes, in fact, that the plane P is an A-invariant subalgebra of ${\mathfrak{sl}}(2,\mathbb{R})$ isomorphic to the algebra of the affine group of the real line. This subalgebra, as Lemma 4.1 shows, is lightlike and totally geodesic for the Lorentzian metric q.

Corollary 4.2

All solutions with initial conditions in P are complete with trajectories affine lines parallel to $\mathbb{R}e$.

One checks that the vector $v_{0}=(\frac{3}{8},\frac{-1}{2},1)$ with respect to the basis e,h,f is null and satisfies Av₀=[Av₀,v₀] and $\mathbb{R}v_{0}, \mathbb{R}e$ are the only radial directions. Therefore, the line $\mathbb{R}v_{0}$ is invariant under the geodesic flow and the geodesic vector field on $\mathbb{R}v_{0}$ is λv₀↦λ²v₀. Hence, every solution in $\mathbb{R}v_{0}-\{0\}$ is incomplete. More precisely, for λ>0 the solution through λv₀ is defined on a maximal interval of the form (−∞,b) and for λ<0 it is defined on a maximal interval of the form (a,+∞). For more details about completeness of left invariant metrics on ${\textsf{SL}}(2,\mathbb{R})$ see [BM08] or [EFR23].

Now, define the map $\sigma :{\mathfrak{sl}}(2,\mathbb{R})\to \mathbb{R}v_{0}$ to be the projection on $\mathbb{R}v_{0}$ with respect to the new basis e,h,v₀. We have

Proposition 4.3

The projection σ is equivariant with respect to the geodesic flow.

Proof

Let v=w+cv₀ with w∈P=ker(σ), then

$$ [Av,v]=[A(w+cv_{0}),w+cv_{0}]=[Aw,w]+c([Av_{0},w]+[Aw,v_{0}])+[cAv_{0},cv_{0}]. $$

Since P is an A-invariant subalgebra we have σ(A⁻¹[Av,v])=A⁻¹[Aσ(v),σ(v)] if and only if ([Av₀,w]+[Aw,v₀])∈P. Put v₀=z+αf for z∈P, then

$$ [Av_{0},w]+[Aw,v_{0}]=[\alpha f+w_{1},w]+[Aw,z+\alpha f] $$

for w₁∈P. So it remains to show that ([f,w]+[Aw,f])∈P. This follows from the fact that $Aw-w\in \mathbb{R}e$ and [f,e]=h∈P. □

Corollary 4.4

A solution of the geodesic equation with initial condition $v\in {\mathfrak{sl}}(2,\mathbb{R})$ is complete if and only if v∈P, i.e, σ(v)=0. It is $\mathbb{R}_{+}$ (resp. $\mathbb{R}_{-}$) incomplete if σ(v)>0 (resp. σ(v)<0).

Remark 4.5

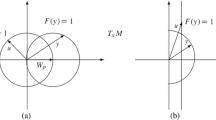
The dynamics on $\mathbb{P}^{+}({\mathfrak{sl}}(2,\mathbb{R}))$ has exactly four fixed points $e^{+},e^{-},v_{0}^{+}$ and $v_{0}^{-}$ corresponding to the half lines through e and v₀. The plane P corresponds to a circle $\mathbb{P}^{+}(P)$. Every point in $\mathbb{P}^{+}(P)$ different from e⁻ and e⁺ converges in the future to e⁺ and to e⁻ in the past. The three invariant circles $\mathbb{P}^{+}(P)$, π(C⁺), and π(C⁻) divide the sphere $\mathbb{P}^{+}({\mathfrak{sl}}(2,\mathbb{R}))$ into four invariant open disks, where π(C⁺) and π(C⁻) are the spherizations of the half null cones (see Figure (1)). Each of these open disks is invariant and solutions are unbounded inside it (i.e they converge to the boundary of the disk). Indeed, a bounded solution forces the existence of a constant one (i.e radial) inside the disk which is impossible.

Figure 1

The dynamics on $\mathbb{P}^{+}({\mathfrak{sl}}(2,\mathbb{R}))$.

Proposition 4.6

Let g be the left invariant metric on ${\textsf{SL}}(2,\mathbb{R})$ generated by q and $\Gamma \subset {\textsf{SL}}(2,\mathbb{R})$ be a cocompact lattice. Then $(\Gamma \backslash {\textsf{SL}}(2,\mathbb{R}), g)$ is without closed geodesics. It admits, however, a countable collection of weakly closed geodesics.

Proof

Let δ be a closed or weakly closed geodesic in $(\Gamma \backslash {\textsf{SL}}(2,\mathbb{R}), g)$ and $\widetilde{\delta}$ its maximal lift to ${\textsf{SL}}(2,\mathbb{R})$. Since the only closed orbits in $\mathbb{P}({\mathfrak{sl}}(2,\mathbb{R}))$ are the constant ones, then $\widetilde{\delta}$ is mapped to a constant solution $d_{\delta}\in \mathbb{P}({\mathfrak{sl}}(2,\mathbb{R}))$ which shows that $\widetilde{\delta}$ is a leaf of the left invariant line field generated by d_δ. Hence, δ is, up to reparameterization, the projection of a left coset of the one-parameter group tangent to d_δ. The line d_δ is either $\mathbb{R}e$ or $\mathbb{R}v_{0}$. But $\mathbb{R}e$ is nilpotent i.e it generates a parabolic subgroup of ${\textsf{SL}}(2,\mathbb{R})$, hence the projection of each of its left cosets is dense in $\Gamma \backslash {\textsf{SL}}(2,\mathbb{R})$ (the right action of a parabolic subgroup on $\Gamma \backslash {\textsf{SL}}(2,\mathbb{R})$ is nothing but the horocyle flow). If $d_{\delta}=\mathbb{R}v_{0}$ then it is hyperbolic and δ is, up to parameterization, the projection of a left coset gH of the hyperbolic one-parameter group H generated by $\mathbb{R}v_{0}$. Moreover, a left coset gH projects to a closed orbit if and only if gHg⁻¹ intersects Γ non-trivially. Thus weakly closed null geodesics are in one-to-one correspondence with conjugates of H intersecting Γ non-trivially. This is a countable collection and all of them are incomplete. □

Remark 4.7

The left action of an elliptic one-parameter subgroup K on ${\textsf{SL}}(2,\mathbb{R})$ is, by assumption, isometric. Let X be its associated right invariant Killing vector field. The length function $p\in {\textsf{SL}}(2,\mathbb{R})\mapsto g(X(p),X(p))$ is without critical points. Indeed, the X-orbit of a critical point is a closed geodesic which projects to a closed geodesic in $\Gamma \backslash {\textsf{SL}}(2,\mathbb{R})$ and this contradicts the previous proposition. On the other hand, the vector field Y on $\Gamma \backslash {\textsf{SL}}(2,\mathbb{R})$ that generates the right action of K has constant length function, since it is the projection of a left invariant vector field, but clearly it is not Killing. The right K-action on $\Gamma \backslash {\textsf{SL}}(2,\mathbb{R})$ defines a fibration by (non-geodesic) circles which is locally homogeneous (the left action is defined locally on $\Gamma \backslash {\textsf{SL}}(2,\mathbb{R})$ and sends circle to circle). In particular, these circles have constant geodesic curvature and when K converges to the parabolic one-parameter group generated by e, these fibrations converge to a foliation by dense null geodesics.

4.2 SOL case

The construction will be similar to the ${\textsf{SL}}(2,\mathbb{R})$ case. Let SOL be the solvable unimodular three-dimensional group $\mathbb{R}\ltimes \mathbb{R}^{2}$ where $\mathbb{R}$ acts on $\mathbb{R}^{2}$ via the representation $t\mapsto \begin{pmatrix} e^{t} & 0 \\ 0 & e^{-t} \end{pmatrix}$. This is the identity component of the isometry group of the quadratic form (x,y)↦xy on $\mathbb{R}^{2}$. Its Lie algebra ${\mathfrak{sol}}$ has a basis e₁,e₂,h with brackets [h,e₁]=e₁ [h,e₂]=−e₂. Let q be the Lorentzian inner product satisfying

$$ q( e_{1},e_{1})=q( e_{1},e_{2})=q( h,e_{2})=q( h,h)=0 \ \ \text{and} \ \ q( e_{1},h)=q( e_{2},e_{2})=1 $$

Therefore, with respect to this basis we have

$$ \mathrm {ad}_{e_{1}}= \begin{pmatrix} 0 & 0 & -1 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix} \ \ \mathrm {ad}_{e_{2}}= \begin{pmatrix} 0 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \end{pmatrix} \ \ \mathrm {ad}_{h}= \begin{pmatrix} 1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 0 \end{pmatrix} $$

and one checks that

$$ \mathrm {ad}_{e_{1}}^{*}= \begin{pmatrix} 0 & 0 & -1 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix} \ \ \mathrm {ad}_{e_{2}}^{*}= \begin{pmatrix} 0 & 1 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix} \ \ \mathrm {ad}_{h}^{*}= \begin{pmatrix} 0 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 1 \end{pmatrix} . $$

It is clear that the abelian subalgebra P=span(e₁,e₂) is invariant under the geodesic flow and the geodesic vector field on P has the form v=(x,y,0)∈P↦y²e₁ since for v=xe₁+ye₂ we have $\mathrm {ad}_{v}^{*}v=(x\mathrm {ad}_{e_{1}}^{*}+y\mathrm {ad}_{e_{2}}^{*})(xe_{1}+ye_{2})=y^{2}e_{1}$. One also checks easily that the equation $\mathrm {ad}_{v}^{*}v=\lambda v$ for some $\lambda \in \mathbb{R}$ admits exactly $\mathbb{R}e_{1}$ and $\mathbb{R}h$ as solutions with $\mathrm {ad}_{e_{1}}^{*}e_{1}=0$ and $\mathrm {ad}_{h}^{*}h=h$. Therefore, the null line $\mathbb{R}h$ is invariant under the geodesic flow and every solution in $\mathbb{R}h-\{0\}$ is incomplete.

Similar to the ${\textsf{SL}}(2,\mathbb{R})$ define the projection $\sigma :{\mathfrak{sol}} \to \mathbb{R}h$ with respect to the basis e₁,e₂,h. Then

Proposition 4.8

The projection σ is equivariant with respect to the geodesic flow.

Proof

Let v=xe₁+ye₂+zh, then

$$ \mathrm {ad}_{v}^{*}v=(x\mathrm {ad}_{e_{1}}^{*}+y\mathrm {ad}_{e_{2}}^{*}+z\mathrm {ad}_{h}^{*})(xe_{1}+ye_{2}+zh)=(y^{2}-xz)e_{1}-yze_{2}+z^{2}h. $$

Therefore, $\sigma (\mathrm {ad}_{v}^{*}v)=z^{2}h=\mathrm {ad}_{zh}^{*}zh=\mathrm {ad}_{\sigma (v)}^{*} \sigma (v)$ □

One observes that the situation is similar to the previous case of ${\mathfrak{sl}}(2,\mathbb{R})$, the dynamics on $\mathbb{P}^{+}({\mathfrak{sol}} )$ is as described in Remark 4.5. One concludes

Corollary 4.9

Let g be the left invariant metric on SOL generated by q and Γ⊂SOL be a cocompact lattice. Then (Γ∖SOL,g) is without closed geodesics. It admits, however, a countable collection of weakly closed geodesics.

Proof

Let δ be a closed or weakly closed geodesic in (Γ∖SOL,g) and $\widetilde{\delta}$ its maximal lift to SOL. The geodesic $\widetilde{\delta}$ is mapped to a constant solution $d_{\delta}\in \mathbb{P}({\mathfrak{sol}} )$ for the same reason as in the ${\mathfrak{sl}}(2,\mathbb{R})$ case, which shows that $\widetilde{\delta}$ is a leaf of the left invariant line field generated by d_δ. The line d_δ is either $\mathbb{R}e_{1}$ or $\mathbb{R}h$. But $\mathbb{R}e$ is impossible since Γ intersects the stable and the unstable lines in $\mathbb{R}^{2}$ trivially. So $d_{\delta}=\mathbb{R}h$ and δ is, up to parameterization, the projection of a left coset gH of the one-parameter group H generated by $\mathbb{R}h$. Moreover, a left coset gH projects to a closed orbit if and only if gHg⁻¹ intersects Γ non-trivially. Thus weakly closed null geodesics are in one-to-one correspondence with conjugates of H intersecting Γ non-trivially. □

5 The SOL×Euc case: proof of Theorem 1.1

Let ${\textsf{Euc}}={\textsf{SO}}(2)\ltimes \mathbb{R}^{2}$ be the identity component of the isometry group of the Euclidean plane. Its Lie algebra ${\mathfrak{euc}}$ has a basis f₁,f₂,e with brackets [e,f₁]=−f₂ and [e,f₂]=f₁. We have, with respect to this basis,

$$ \mathrm {ad}_{f_{1}}= \begin{pmatrix} 0 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \end{pmatrix} \ \ \mathrm {ad}_{f_{2}}= \begin{pmatrix} 0 & 0 & -1 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix} \ \ \mathrm {ad}_{e}= \begin{pmatrix} 0 & 1 & 0 \\ -1 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix} . $$

Let g be the Lorentz metric on ${\mathfrak{euc}}$ satisfying

$$ g( f_{1},f_{1})=g( f_{1},f_{2})=g( e,f_{2})=g( e,e)=0 \ \ \text{and} \ \ g( f_{1},e)=g( f_{2},f_{2})=1. $$

One checks that

$$ \mathrm {ad}_{f_{1}}^{*}= \begin{pmatrix} 0 & 1 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix} \ \ \mathrm {ad}_{f_{2}}^{*}= \begin{pmatrix} 0 & 0 & -1 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix} \ \ \mathrm {ad}_{e}^{*}= \begin{pmatrix} 0 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & -1 & 0 \end{pmatrix} . $$

The geodesic equation (1) in this case is: for v=(x,y,z) we have

$$ \mathrm {ad}_{v}^{*}v= \begin{pmatrix} 0 & x & -y \\ 0 & 0 & z \\ 0 & -z & 0 \end{pmatrix} \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} xy-yz \\ z^{2} \\ -yz \end{pmatrix} . $$

Therefore, the abelian subalgebra P={z=0} is invariant under the geodesic flow and the geodesic vector field on P has the form (x,y,0)∈P↦(xy,0,0)∈P. Thus, on P, the constant solutions are the only periodic ones.

• Periodic solutions: One sees that the vector field (x,y,z)↦(xy−yz,z²,−yz) on the algebra ${\mathfrak{euc}}$ is everywhere transverse to the plane distribution {y=0} outside the subalgebra P. Hence, there are no periodic solutions in ${\mathfrak{euc}}$ except the obvious constant ones inside the plane P.

• Radial solutions: Suppose that (xy−yz,z²,−yz)=λ(x,y,z) for some λ≠0. Since there is no such a solution in P, then we can assume z=1. Thus, (xy−y,1,−y)=(λx,λy,λ) which implies −y²=1 and this is impossible. Therefore, radial non-trivial solutions do not exist and constant solutions exist only in P.

• Direction-periodic solutions: The sphere $\mathbb{P}^{+}({\mathfrak{euc}} )$ is divided into four invariant open disks, bounded by $\mathbb{P}^{+}(P)$ and the two null circles similar to Figure (1). A closed trajectory inside some open disk corresponds to a genuine periodic solution which is impossible as explained above. Therefore, direction-periodic solutions are necessarily radial.

5.1 The product SOL×Euc

Recall that in Sect. 4.2 we constructed a Lorentz metric q on ${\mathfrak{sol}}$, endowed with the basis e₁,e₂,h, having the following properties:

• ∘ Constant solutions of the geodesic equation are exactly the elements of $\mathbb{R}e_{1}$.

• ∘ The line generated by h is the only non-trivial radial direction.

• ∘ There are no direction-periodic solutions except the radial ones.

Now, put the metric q⊕g on the algebra ${\mathfrak{g}}={\mathfrak{sol}} \oplus {\mathfrak{euc}}$ endowed with the product basis e₁,e₂,h,f₁,f₂,e. We have the immediate observations:

• ∘ Constant solutions for the geodesic equation on ${\mathfrak{g}}$ project to constant solutions on both factors. Therefore, they consist of span(e₁,f₁)∪span(e₁,f₂).

• ∘ Non-trivial radial solutions project to radial solutions with the same scaling factor. Thus, they consist of elements of $\mathbb{R}h-\{0\}$.

• ∘ Direction-periodic solutions are radial and given by the above cases. Indeed, a direction-periodic solution projects to radial solutions on both factors, so it either corresponds to constant solutions on both factors or a non-trivial radial solution on the first factor and the zero solution on the second.

5.2 A compact quotient without closed or weakly closed geodesics

Choose a hyperbolic element $A= \begin{pmatrix} \lambda & 0 \\ 0 & \lambda ^{-1} \end{pmatrix}$ and an irrational rotation R_α∈SO(2) such that the 4×4 matrix $\varphi = \begin{pmatrix} A & 0 \\ 0 & R_{\alpha} \end{pmatrix}$ preserves a lattice $\Gamma _{0}\subset \mathbb{R}^{4}$, that is, φ is conjugate to an element of ${\textsf{SL}}(4,\mathbb{Z})$. Such a map φ exists (see Remark 5.2). Define the semi-direct product $\Gamma =\mathbb{Z}\ltimes \Gamma _{0}$ where $\mathbb{Z}$ acts on Γ₀ via φ. The discrete group Γ is, in the obvious way, a cocompact lattice in G=SOL×Euc. We have

Proposition 5.1

Endow G with the left invariant metric given by q⊕g on the algebra ${\mathfrak{g}}={\mathfrak{sol}} \oplus {\mathfrak{euc}}$. Then the compact quotient Γ∖G admits no closed or weakly closed geodesics.

Proof

Let δ be a (weakly) closed geodesic in Γ∖G and $\widetilde{\delta}$ its maximal lift to G. Then $\widetilde{\delta}$ is mapped to a direction-periodic solution in ${\mathfrak{g}}$. Discussion (5.1) shows that $\widetilde{\delta}$ is mapped, in fact, to a radial direction d_δ. Also, we have seen in (5.1) that d_δ is either $\mathbb{R}h$ or any linear line contained in span(e₁,f₁)∪span(e₁,f₂). We claim that this is impossible in both cases. Indeed, $\widetilde{\delta}$ is, as an unparameterized curve, a left coset gI_δ, of the one-parameter group I_δ tangent to d_δ, such that gI_δg⁻¹ intersects Γ non-trivially. But this is impossible because:

⋆:

$\Gamma \cap \exp \bigl({\textsf{span}} (e_{1},f_{1},f_{2})\bigr)=\{0\}$ since the action of φ on $\exp (\mathbb{R}e_{1})$ is expanding and its action on exp(span(f₁,f₂)) is an irrational rotation. Also, since $\exp \bigl({\textsf{span}} (e_{1},f_{1},f_{2})\bigr)$ is normal in G then its intersection with Γ, even up to conjugacy, is trivial.

⋆:

All conjugates of $\exp (\mathbb{R}h)$ intersect Γ trivially since the conjugacy action of every element of Γ on $\mathbb{R}^{4}$ is either identically trivial or has an irrational rotational part.

We conclude that closed or weakly closed geodesics do not exist in Γ∖G. □

Remark 5.2

By Borel-Harish-Chandra’s theorem, the intersection $\Lambda ={\textsf{SO}}(1,3)\cap {\textsf{SL}}(4,\mathbb{Z})$ is a lattice in SO(1,3). The lattice Λ contains, in particular, many loxodromic elements. These are the elements of SO(1,3) that have exactly two fixed points when acting on the boundary at infinity of the hyperbolic space $\mathbb{H}^{3}$. They admit, then, hyperbolic and elliptic factors. If the elliptic part of a loxodromic element in Λ has finite order then its invariant plane P is rational i.e $P\cap \mathbb{Z}^{4}$ is a lattice in P. Since, up to conjugacy, there are only finitely many elliptic elements in ${\textsf{SL}}(2,\mathbb{Z})$, then there is k such that A^k fixes a plane for every loxodromic element A∈Λ whose elliptic part is of finite order. Suppose Λ is torsion free (this is always possible up to finite index). If all loxodromic elements of Λ have finite order elliptic parts then the (polynomial) function f:A∈Λ↦det(A^k−Id) vanishes on Λ (since Λ in this case contains only unipotent and loxodromic elements). But, Borel’s density theorem implies that f vanishes identically on SO(1,3) which is impossible. Thus, Λ contains (in fact many) loxodromic elements with irrational elliptic parts.