Relations between scaling exponents in unimodular random graphs

Abstract

We investigate the validity of the “Einstein relations” in the general setting of unimodular random networks. These are equalities relating scaling exponents:

$$\begin{aligned} d_{w} &= d_{f} + \tilde{\zeta }, \\ d_{s} &= 2 d_{f}/d_{w}, \end{aligned}$$

where d_w is the walk dimension, d_f is the fractal dimension, d_s is the spectral dimension, and $\tilde{\zeta }$ is the resistance exponent. Roughly speaking, this relates the mean displacement and return probability of a random walker to the density and conductivity of the underlying medium. We show that if d_f and $\tilde{\zeta } \geqslant 0$ exist, then d_w and d_s exist, and the aforementioned equalities hold. Moreover, our primary new estimate $d_{w} \geqslant d_{f} + \tilde{\zeta }$ is established for all $\tilde{\zeta } \in \mathbb{R}$.

For the uniform infinite planar triangulation (UIPT), this yields the consequence d_w=4 using d_f=4 (Angel in Geom. Funct. Anal. 13(5):935–974, 2003) and $\tilde{\zeta }=0$ (established here as a consequence of the Liouville Quantum Gravity theory, following Gwynne-Miller 2020 and (Ding and Gwynne in Commun. Math. Phys. 374(3):1877–1934, 2020)). The conclusion d_w=4 had been previously established by Gwynne and Hutchcroft (2018) using more elaborate methods. A new consequence is that d_w=d_f for the uniform infinite Schnyder-wood decorated triangulation, implying that the simple random walk is subdiffusive, since d_f>2.

1 Introduction

Consider an infinite, locally-finite graph $\mathcal {G}$ and a subgraph G of $\mathcal {G}$. For $x \in V(\mathcal {G})$, let $B^{\mathcal {G}}(x,R)$, denote the graph ball of radius R, and let $\tilde{B}(x,R) \mathrel{ \mathop {:}}=B^{\mathcal {G}}(x,R) \cap V(G)$ denote this ball restricted to G. Let $d^{\mathcal {G}}(x,y)$ denote the path distance between a pair $x,y \in V(\mathcal {G})$. Denote by {X_n} the simple random walk on G, and the discrete-time heat kernel

$$ p^{G}_{n}(x,y) \mathrel{\mathop {:}}=\operatorname{ \mathbb{P}}[X_{n} = y \mid X_{0} = x]. $$

We write $\mathsf{R}_{\mathrm{eff}}^{G}(S \leftrightarrow T)$ for the effective resistance between two subsets S,T⊆V(G). One can consult [LP16, Ch. 2 & 9] for background on electrical network theory in finite and infinite graphs.

For a variety of models arising in statistical physics, certain asymptotic geometric and spectral properties of the graph are known or conjectured to have scaling exponents:

$$\begin{aligned} |\tilde{B}(x,R)| &\approx R^{d_{f}} \\ \max _{1 \leqslant t \leqslant n} d^{\mathcal {G}}(X_{0},X_{t}) & \approx n^{1/d_{w}} \\ \mathsf{R}_{\mathrm{eff}}^{G}\left (\tilde{B}(x,R) \leftrightarrow V(G) \setminus \tilde{B}(x, 2R)\right ) &\approx R^{\tilde{\zeta}} \\ p_{2n}^{G}(x,x) &\approx n^{-d_{s}/2}, \end{aligned}$$

(1.1)

where one takes n,R→∞, but we leave the meaning of “≈” imprecise for a moment. These exponents are, respectively, referred to as the fractal dimension, walk dimension, resistance exponent, and spectral dimension. We refer to the extensive discussion in [BH00, Ch. 5–6].

Moreover, by modeling the subgraph G as a homogeneous underlying substrate with density and conductivity prescribed by d_f and $\tilde{\zeta}$, one obtains the plausible relations

$$\begin{aligned} d_{w} &= d_{f} + \tilde{\zeta} \end{aligned}$$

(1.2)

$$\begin{aligned} d_{s} &= \frac{2 d_{f}}{d_{w}}. \end{aligned}$$

(1.3)

In the regime $\tilde{\zeta} > 0$, these relations have been rigorously verified under somewhat stronger assumptions in the setting of strongly recurrent graphs (see [Tel90, Tel95] and [Bar98, KM08, Tak142]). In the latter set of works, the most significant departure from our assumptions is the stronger requirement for uniform control on pointwise effective resistances of the form

$$ \max \left \{ \mathsf{R}_{\mathrm{eff}}^{G}(x \leftrightarrow y) : y \in B^{G}(x,R) \right \} \leqslant R^{\tilde{\zeta}+o(1)}, \quad x \in V(G). $$

(1.4)

Such methods have been extended to the setting where (G,ρ) is a random rooted graph ([KM08, B+08]) under the statistical assumption that (1.4) holds sufficiently often for all sufficiently large scales around the root.

Our main contribution is to establish (1.2) and (1.3) under somewhat less restrictive conditions, but using an additional feature of many such models: Unimodularity of the random rooted graph (G,ρ). When $\tilde{\zeta} \leqslant 0$, it has been significantly more challenging to characterize situations where (1.2)–(1.3) hold; see, for instance, Open Problem III in [Tak141]. Our main new estimate is the speed relation $d_{w} \geqslant d_{f} + \tilde{\zeta}$, which is established for all $\tilde{\zeta} \in \mathbb{R}$. In particular, this shows that the random walk is subdiffusive whenever $d_{f}+ \tilde{\zeta} > 2$, and applies equally well to models where the random walk is transient. Let us now highlight some notable settings in which the relations can be applied.

The IIC in high dimensions

As a prominent example, consider the resolution by Kozma and Nachmias [KN09] of the Alexander-Orbach conjecture for the incipient infinite cluster (IIC) of critical percolation on $\mathbb{Z}^{d}$, with d sufficiently large. If (G,0) denotes the IIC, then in our language, $\mathcal {G}=G$, as they consider the intrinsic graph metric; the authors establish that for every λ>1 and r⩾1, with probability at least 1−p(λ), it holds that

$$\begin{gathered} \lambda ^{-1} r^{2} \leqslant |B^{G}(0,r)| \leqslant \lambda r^{2}, \end{gathered}$$

(1.5)

$$\begin{gathered} \mathsf{R}_{\mathrm{eff}}^{G}(0 \leftrightarrow \partial B^{G}(0,r)) \geqslant \lambda ^{-1} r, \end{gathered}$$

(1.6)

where p(λ)⩽O(λ^−q) for some q>1. One should consider this a statistical verification that d_f=2 and $\tilde{\zeta} = 1$, as in this setting, one gets the analog of (1.4) for free from the trivial bound $\mathsf{R}_{ \mathrm{eff}}^{\textrm{IIC}}(0 \leftrightarrow x) \leqslant d^{ \textrm{IIC}}(0,x)$.

Earlier, Barlow, Járai, Kumagai, and Slade [B+08] verified (1.2)–(1.3) under these assumptions, allowing Kozma and Nachmias to confirm the conjectured values d_w=3 and d_s=4/3. One can consult [Tak141, §4.2.2] for several further examples where $\tilde{\zeta} > 0$ and (1.2)–(1.3) hold using the strongly recurrent theory.

The uniform infinite planar triangulation

Consider, on the other hand, the uniform infinite planar triangulation (UIPT) considered as a random rooted graph (G,ρ). In this case, Angel [Ang03] established that almost surely

$$ \lim _{R \to \infty} \frac{\log |B^{G}(\rho ,R)|}{\log R} = 4, $$

(1.7)

and Gwynne and Miller [GM21] showed that almost surely

$$ \lim _{R \to \infty} \frac{\log \mathsf{R}_{\mathrm{eff}}^{G}(\rho \leftrightarrow V(G) \setminus B^{G}(\rho ,R))}{\log R} = 0\,. $$

This equality falls short of verifying (1.1). Nevertheless, we show in Section 4.3 that $\tilde{\zeta}=0$ is a consequence of the Liouville Quantum Gravity (LQG) estimates derived in [DMS21, GM21, GMS19, GHS20, DG20]. But while the known statistics of |B^G(ρ,R)| are suitable to allow application of the strongly recurrent theory, this does not hold for the effective resistance bounds.

This is highlighted by Gwynne and Hutchcroft [GH20] who establish d_w=4 using even finer aspects of the LQG theory. The authors state “while it may be possible in principle to prove d_w⩾4 using electrical techniques, doing so appears to require matching upper and lower bounds for effective resistances [...] differing by at most a constant order multiplicative factor.” Our methods show that, when leveraging unimodularity, even coarse estimates with subpolynomial errors suffice.

It is open whether $\tilde{\zeta} = 0$ or d_w=4 for the uniform infinite planar quadrangulation (UIPQ), but our verification of (1.2) shows that only one such equality needs to be established.

Random planar maps in the γ-LQG universality class

More generally, we will establish in Section 4.3 that $\tilde{\zeta}=0$ whenever a random planar map (G,ρ) can be coupled to a γ-mated-CRT map with γ∈(0,2). The connection between such maps and LQG was established in [DMS21].

This family includes the UIPT (where $\gamma = \sqrt{8/3}$). Ding and Gwynne [DG20] have shown that d_f exists for such maps, and Gwynne and Huthcroft [GH20] established that d_w=d_f for most known examples, but not for the uniform infinite Schnyder-wood decorated triangulation [LSW17] (where γ=1), for a technical reason underlying the construction of a certain coupling (see [GH20, Rem. 2.11]). We mention this primarily to emphasize the utility of a general theorem, since it is likely the technical obstacle could have been circumvented with sufficient effort.

The IIC in dimension two

Consider the incipient infinite cluster for 2D critical percolation [Kes86], which can be realized as a unimodular random subgraph (G,0) of $\mathcal {G}=\mathbb{Z}^{2}$ [Ant03]. It is known that d_f=91/48 in the 2D hexagonal lattice [LSW02, Smi01], and the same value is conjectured to hold for all 2D lattices regardless of the local structure.

Existence of the exponent $\tilde{\zeta}$ is open for any lattice; experiments give the estimate $\tilde{\zeta} = 0.9825 \pm 0.0008$ [Gra99]. The most precise experimental estimate for d_w=2.8784±0.0008 is derived from estimates for $\tilde{\zeta}$, and our verification of (1.2) puts this on rigorous footing (assuming, of course, that $\tilde{\zeta}$ is well-defined).

1.1 Reversible random networks

We consider random rooted networks (G,ρ,c^G,ξ) where G is a locally-finite, connected graph, ρ∈V(G), and c^G:E(G)→[0,∞) are edge conductances. We allow E(G) to contain self-loops {v,v} for v∈V(G). Here, ξ:V(G)∪E(G)→Ξ is an auxiliary marking, where Ξ is some Polish mark space. We will sometimes use the notation (G,ρ,ξ₁,ξ₂,…,ξ_k) to reference a random rooted network with marks ξ_i:V(G)∪E(G)→Ξ_i, which we intend as shorthand for (G,ρ,(ξ₁,ξ₂,…,ξ_k)), where the mark space is the Cartesian product Ξ₁×⋯×Ξ_k.

Denote by {X_n} the random walk on G with X₀=ρ and transition probabilities

$$ p^{G}_{1}(u,v) \mathrel{\mathop {:}}=\operatorname{ \mathbb{P}}\left [X_{1} = v \mid X_{0} = u\right ] = \frac{c^{G}(\{u,v\})}{c^{G}_{u}}, $$

(1.8)

where we denote $c^{G}_{u} \mathrel{\mathop {:}}=\sum _{v : \{u,v\} \in E(G)} c^{G}(\{u,v\})$. Say that (G,ρ,c^G,ξ) is a reversible random network if:

• 1. Almost surely $c^{G}_{\rho} > 0$.

• 2. (G,X₀,X₁,c^G,ξ) and (G,X₁,X₀,c^G,ξ) have the same law.

We will usually write a reversible random network as (G,ρ,ξ), allowing the conductances to remain implicit. Note that we allow the possibility c^G({u,v})=0 when {u,v}∈E(G). In this sense, random walks occur on the subnetwork G₊ with $V(G_{+}) = \{ x \in V(G) : c^{G}_{x} > 0 \}$ and E(G₊)={{x,y}∈V(G):c^G({x,y})>0}, while distances are measured in the path metric d^G.

Example 1.1

Examples of markings

Aside from edge conductances, we will use auxiliary markings primarily for analyzing the geometry of the random rooted graph (G,ρ).

• 1. Edge weights that deform the graph metric. Consider a random nonnegative weight $\omega : E(G) \to \mathbb{R}_{+}$. Such a weight assigns a length to every finite path in G, and this yields a weighted path metric $\operatorname{dist}^{G}_{\omega}$ on G. See Section 1.4.

• 2. Breaking G into finite subgraphs. A bond percolation is a random marking ξ:E(G)→{0,1}. We will use $K^{G}_{\xi}( \rho )$ to denote the connected component of the root in the subgraph of G with edge set ξ⁻¹(1)⊆E(G). Of particular interest will be finitary bond percolations in which the component $K^{G}_{ \xi}(\rho )$ is almost surely finite.

Remark 1.2

Conductance at the root

Throughout, we will make the following mild boundedness assumption (it is stated explicitly at every occurrence):

$$ \operatorname{ \mathbb{E}}[1/c^{G}_{\rho}] < \infty \,. $$

This is analogous to the assumption $\operatorname{ \mathbb{E}}[\deg _{G}(\rho )] < \infty$ that appears often in the setting of unimodular random graphs, which are defined in Section 2.3 when we need to employ the Mass-Transport Principle.

For now, it suffices to say that if $(\tilde{G},\tilde{\rho}, \tilde{\xi})$ is a unimodular random graph with law $\tilde{\mu}$ and $\operatorname{ \mathbb{E}}[c_{\tilde{\rho}}^{\tilde{G}}] < \infty$, then the random graph (G,ρ,ξ) with law μ is a reversible random graph, where

$$ \frac{d\mu}{d\tilde{\mu}}(G_{0},\rho _{0},\xi _{0}) = \frac{c^{G_{0}}_{\rho _{0}}}{\operatorname{ \mathbb{E}}[c^{\tilde{G}}_{\tilde{\rho}}]}\,, $$

and $d\mu /d\tilde{\mu}$ is the Radon-Nikodym derivative. We refer to [AL07] for an extensive reference on unimodular random graphs, and to [BC12, Prop. 2.5] for the connection between unimodular and reversible random graphs.

1.2 Almost sure scaling exponents

Consider two sequences {A_n} and {B_n} of positive real-valued random variables. Write A_n⪅B_n if almost surely:

$$ \limsup _{n \to \infty} \frac{\log A_{n} - \log B_{n}}{\log n} \leqslant 0, $$

and for the conjunction of A_n⪅B_n and B_n⪅A_n. Note our primary motivation for this relation: It holds that A_n⪅n^d if and only if, for every δ>0, almost surely A_n⩽n^d+δ for n sufficiently large.

In what follows, we consider a reversible random network (G,ρ) (see Section 1.1). Define the random variables:

$$\begin{aligned} \sigma _{R} &\mathrel{\mathop {:}}=\min \{ n \geqslant 0 : d^{G}(X_{0},X_{n}) > R \}, \\ \mathcal {M}_{n} &\mathrel{\mathop {:}}=\max _{0 \leqslant t \leqslant n} d^{G}(X_{0},X_{t}), \end{aligned}$$

and define the walk exponents d_w and β by

assuming the corresponding limits exist. In that case we, we will use the language “d_w exists” or “β exists.”¹

Denote the volume function

$$ \operatorname{vol}^{G}(x,R) \mathrel{\mathop {:}}=\sum _{y \in B^{G}(x,R)} c^{G}_{y}, $$

and define d_f as the asymptotic growth rate of the volume:

Define the spectral dimension by

Let us define upper and lower resistance exponents. Denote the complement of B^G(ρ,R) in G by

$$ \bar{B}^{G}(\rho ,R) \mathrel{\mathop {:}}=V(G) \setminus B^{G}(\rho ,R), $$

and define $\tilde{\zeta}$ and $\tilde{\zeta}_{0}$ as the largest and smallest values, respectively, such that, for every δ∈(0,1), almost surely, for all but finitely many $R \in \mathbb{N}$:

$$ R^{\tilde{\zeta}-\delta} \leqslant \mathsf{R}_{\mathrm{eff}}^{G} \left (B^{G}(\rho ,R^{1-\delta}) \leftrightarrow \bar{B}^{G}(\rho , R) \right ) \leqslant \mathsf{R}_{\mathrm{eff}}^{G}\left (\rho \leftrightarrow \bar{B}^{G}(\rho ,R)\right ) \leqslant R^{ \tilde{\zeta}_{0}+\delta}. $$

(1.9)

It helps to note that the three occurrences of δ in (1.9) could equally well be replaced by distinct values δ₁,δ₂,δ₃∈(0,1) without changing the definition of $\tilde{\zeta}$ and $\tilde{\zeta}_{0}$, as increasing δ>0 weakens the first and last inequalities, and the middle inequality always holds. Accordingly, the exponents $\tilde{\zeta} \leqslant \tilde{\zeta}_{0}$ always exist, and $\tilde{\zeta}_{0} \geqslant 0$. The exponent $\tilde{\zeta}$ is referred to as the “resistance exponent” in the statistical physics literature; see [BH00, §5.3] and Remark 1.4 below.

We emphasize that all the exponents we define are not random variables, but functions of the law of (G,ρ). Our main theorem can then be stated as follows.

Theorem 1.3

Suppose that (G,ρ) is a reversible random network satisfying $\operatorname{ \mathbb{E}}[1/c^{G}_{\rho}] < \infty$. If d_f exists and $\tilde{\zeta}= \tilde{\zeta}_{0}$, then the exponents d_w, β, and d_s exist and it holds that

$$\begin{aligned} d_{w} &= \beta = d_{f} + \tilde{\zeta}, \\ d_{s} &= \frac{2 d_{f}}{d_{w}}. \end{aligned}$$

See Corollary 1.10 for further equalities involving annealed versions of d_w and β.

Remark 1.4

The resistance exponents

The resistance exponent is usually characterized heuristically as the value $\tilde{\zeta}$ such

(1.10)

So the left-hand side of (1.9) would naturally be replaced by

$$ \mathsf{R}_{\mathrm{eff}}^{G}\left (B^{G}(\rho ,R) \leftrightarrow \bar{B}^{G}(\rho ,2R)\right ) \geqslant R^{\tilde{\zeta}-\delta}. $$

The lower bound we require is substantially weaker, allowing one to consider spatial fluctuations of magnitude R^o(1). The upper bound in (1.9), on the other hand, is somewhat stronger than (1.10), and encodes a level of spectral regularity. For instance, if G satisfies an elliptic Harnack inequality and is “strongly recurrent” in the sense of [Tel06, Def. 2.1], then

See [Tel06, Thm. 4.6] and Theorem 4.9.

Comparison to the strongly recurrent theory

Let us try to interpret the strongly recurrent theory (cf. Assumption 1.2 in [KM08]) in the setting of subpolynomial errors. The resistance assumptions would take the form: For every δ>0, almost surely, for R sufficiently large:

$$\begin{gathered} \max \left \{ \mathsf{R}_{\mathrm{eff}}^{G}(\rho \leftrightarrow x) : x \in B^{G}(\rho ,R) \right \} \leqslant R^{\zeta +\delta}, \end{gathered}$$

(1.11)

$$\begin{gathered} \mathsf{R}_{\mathrm{eff}}^{G}\left (\rho \leftrightarrow \bar{B}^{G}( \rho ,R)\right ) \geqslant R^{\zeta -\delta}. \end{gathered}$$

(1.12)

These assumptions imply that when ζ>0, it holds that $\tilde{\zeta}=\tilde{\zeta}_{0}=\zeta$; this is proved in Theorem 4.9. Hence the theory we present (in the setting of reversible random graphs) is more general, at least in terms of concluding the exponent relations (1.2) and (1.3).

Under assumptions (1.11) and (1.12), one can uniformly lower bound the Green kernel $\mathsf{g}_{B^{G}(\rho ,R')}(\rho ,x)$ (see Section 4.2 for definitions) for all points x∈B^G(ρ,R) and some R′≫R. In other words, every point in B^G(ρ,R) is visited often on average before the random walk exits B^G(ρ,R′). See, for instance, [BCK05, §3.2]. This yields a subdiffusive estimate on the speed of the random walk, specifically an almost sure lower bound on $\operatorname{ \mathbb{E}}[\sigma _{R} \mid (G,\rho )]$.

Instead of a pointwise bound, we use a lower bound on $\tilde{\zeta}$ to deform the graph metric d^G (see the next section). The effective resistance across an annulus being large is equivalent to its discrete extremal length being large (see Section 2.1). Thus in most scales and localities, we can extract a metric that locally “stretches” the space. By randomly covering the space with annuli at all scales, we obtain a “quasisymmetric” deformation (only in an asymptotic, statistical sense) that is bigger by a power than the graph metric. This argument is similar in spirit to one of Keith and Laakso [KL04, Thm. 5.0.10] which shows that the Assouad dimension of a metric measure space can be reduced through a quasisymmetric homeomorphism if the discrete modulus across annuli is large.

Finally, by applying Markov type theory, we bound the speed of the walk in the stretched metric, which leads to a stronger bound in the graph metric.

1.3 Upper and lower exponents

Even when scaling exponents do not exist, our arguments give inequalities between various superior and inferior limits. Given a sequence $\{ \mathcal {E}_{n} : n \geqslant 1\}$ of events on some probability space, let us say that they occur almost surely eventually (a.s.e.) with respect to n if $\operatorname{ \mathbb{P}}[\# \{ n \geqslant 1 : \neg \mathcal {E}_{n} \} < \infty ] = 1$.

For a family {A_n} of random variables, we will define and $\bar{d}$ to be the largest and smallest values, respectively, such that for every δ>0, almost surely eventually,

where we allow the exponents to take values {−∞,+∞} if no such number exists. Note that (i.e., the exponent d “exists”) if and only if.

Let us consider the corresponding extremal exponents such that for every δ>0 the following relations hold almost surely eventually (with respect to n,R⩾1):

We will establish the following chains of inequalities, which together prove Theorem 1.3.

Theorem 1.5

Suppose that (G,ρ) is a reversible random network satisfying $\operatorname{ \mathbb{E}}[1/c^{G}_{\rho}] < \infty$. Then,

Theorem 1.6

Suppose that (G,ρ) is a random rooted network. Then it holds that

and

To see that this yields Theorem 1.3, simply note that when $\tilde{\zeta}=\tilde{\zeta}_{0}$ and , then the upper and lower bounds in (1.13) and (1.18) match, and the upper and lower bounds in (1.19) are both equal to 2d_f/d_w because the first set of inequalities implies $d_{w}=d_{f}+ \tilde{\zeta}$.

Remark 1.7

Negative resistance exponent

For $\tilde{\zeta} < 0$ (and assuming d_s,d_w,d_f exist), the preceding two theorems give

$$\begin{gathered} d_{w} \geqslant d_{f} + \tilde{\zeta} \\ 2 \leqslant d_{s} \leqslant \frac{2 d_{f}}{d_{f}+\tilde{\zeta}}. \end{gathered}$$

Without further assumptions, the last inequality cannot be replaced by an equality. Indeed, for every ε>0, there are unimodular random planar graphs of almost sure uniform polynomial growth and $\tilde{\zeta} \leqslant -1+\varepsilon$ [EL21]. Yet these graphs must satisfy d_s⩽2 [Lee21].

In the general setting of Dirichlet forms on metric measure spaces, the “resistance conjecture” [GHL15, pg. 1493] asserts conditions under which (1.2)–(1.3) might hold even for $\tilde{\zeta} < 0$. The primary additional condition is a Poincaré inequality with matching exponent. In our setting, the existence of d_f does not yield the “bounded covering” property, that almost surely every ball B^G(ρ,R) can be covered by O(1) balls of radius R/2. It seems likely that a variant of this condition should also be imposed to recover (1.2)–(1.3).

Let us give a brief outline of how Theorem 1.6 is proved. The unlabeled inequality is trivial. Both inequalities (1.14) and (1.17) are a straightforward consequence of Markov’s inequality and the Borel-Cantelli Lemma. Since this sort of application will be frequent, let us formalize it.

Lemma 1.8

Suppose $\{X_{n} \in \mathbb{R}_{+} : n \geqslant 1 \}$ is a sequence of random numbers on some probability space $(\Omega ,\mathcal {F},\mu )$ such that {X_n} is almost surely non-decreasing, and {α_n:n⩾1} is a non-decreasing sequence of real numbers. If $\mathcal {G}\subseteq \mathcal {F}$ is a σ-algebra and $\operatorname{ \mathbb{E}}[X_{n} \mid \mathcal {G}] \lessapprox \alpha _{n}$, then X_n⪅α_2n. In particular, if α_n=n^d for some d⩾0, then X_n⪅n^d.

Proof

The assumption $\operatorname{ \mathbb{E}}[X_{n} \mid \mathcal {G}] \lessapprox \alpha _{n}$ asserts that for every δ>0, almost surely eventually

$$ \operatorname{ \mathbb{E}}[X_{n} \mid \mathcal {G}] \leqslant n^{\delta} \alpha _{n}\,. $$

Markov’s inequality gives that almost surely eventually, $\operatorname{ \mathbb{P}}[X_{n} \geqslant n^{2\delta} \alpha _{n} \mid \mathcal {G}] \leqslant n^{- \delta}$.

Applying this to dyadic values n=2^k for k=1,2,…, the Borel-Cantelli Lemma implies that almost surely, for k sufficiently large,

$$ X_{2^{k}} \leqslant 2^{2 \delta k} \alpha _{2^{k}}. $$

Since {X_n} is almost surely non-decreasing and {α_n} is non-decreasing, this implies that almost surely eventually

$$ X_{n} \leqslant (2n)^{2\delta} \alpha _{2n}. $$

Since this holds for every δ>0, we conclude that X_n⪅α_2n. □

The content of inequalities (1.15) and (1.16) lies in the relations and $\bar{\beta } \leqslant \bar{d}_{w}$. These follow from the elementary inequality

(1.20)

which gives the implications, for every δ>0,

Since these hold for every δ>0, we obtain the desired inequalities. Inequalities (1.18) and (1.19) are proved in Section 4.2 using the standard relationships between effective resistance, the Green kernel, and return probabilities. That leaves (1.13), which relies on Markov type theory, as we now explain.

1.4 Reversible random weights

Consider a reversible random graph (G,ρ) and random edge weights $\omega : E(G) \to \mathbb{R}_{+}$. Denote by $\operatorname{dist}_{\omega}^{G}$ the ω-weighted path metric in G.² When (G,ρ,ω) is a reversible random network and (G,ρ) is clear from context, we will say simply that the weight ω is reversible. The next theorem (proved in Section 3) is a variant of the approach pursued in [Lee21].

Theorem 1.9

Suppose (G,ρ,ω) is a reversible random network with $\operatorname{ \mathbb{E}}[1/c^{G}_{ \rho}] < \infty$ and such that almost surely

$$ \lim _{R \to \infty} \frac{\log \log \operatorname{vol}^{G}(\rho ,R)}{\log R} = 0. $$

(1.21)

Suppose, moreover, that

$$ \operatorname{ \mathbb{E}}\left [\omega (X_{0},X_{1})^{2}\right ] < \infty , $$

(1.22)

where {X_n} is random walk on G started from X₀=ρ. Then it holds that

$$ \operatorname{ \mathbb{E}}\left [\max _{0 \leqslant t \leqslant n} \operatorname{dist}_{\omega}^{G}(X_{0},X_{t})^{2} \mid (G,\rho ,\omega )\right ] \lessapprox n. $$

(1.23)

Given this theorem, let us now sketch the proof of (1.13). Consider a graph annulus

$$ \mathcal {A}\mathrel{\mathop {:}}=\{ x \in V(G) : R \leqslant d^{G}( \rho ,x) \leqslant R^{1+\delta}\}. $$

If the effective resistance across $\mathcal {A}$ is at least $R^{ \tilde{\zeta}}$, then by the duality between effective resistance and discrete extremal length (see Section 2.1), there is a length functional $L : E(G[\mathcal {A}]) \to \mathbb{R}_{+}$ satisfying

$$\begin{gathered} \sum _{\{x,y\} \in E(G[\mathcal {A}])} c^{G}(\{x,y\}) L(x,y)^{2} \leqslant R^{-\tilde{\zeta}} \\ \operatorname{dist}_{L}^{G[\mathcal {A}]}\left (B^{G}(x,R), \bar{B}^{G}(x,R^{1+ \delta})\right ) \geqslant 1, \end{gathered}$$

where $G[\mathcal {A}]$ is the subgraph induced on $\mathcal {A}$.

Let us suppose that the total volume in $\mathcal {A}$ satisfies

$$ V_{\mathcal {A}} \mathrel{\mathop {:}}=\sum _{e \in E(G[\mathcal {A}])} c^{G}(e) \approx R^{d_{f}}, $$

and we normalize L to have expectation squared ⩽1 under the measure $c^{G}(\{x,y\})/ V_{\mathcal {A}}$ on $E(G[\mathcal {A}])$:

$$ \hat{L} \mathrel{\mathop {:}}=R^{(\tilde{\zeta}+d_{f})/2} L \approx \left (R^{\tilde{\zeta}}\cdot V_{\mathcal {A}}\right )^{1/2} L. $$

This yields:

$$ \operatorname{dist}_{\hat{L}}^{G[\mathcal {A}]}\left (B^{G}(x,R), \bar{B}^{G}(x,R^{1+ \delta})\right ) \geqslant R^{(\tilde{\zeta}+d_{f})/2}, $$

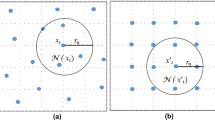
meaning that, with normalized unit area, $\hat{L}$ “stretches” the graph annulus by a positive power when $\tilde{\zeta}+d_{f} > 2$ (see Figure 1(a)).

Figure 1

Stretching the graph at a fixed scale.

If G is sufficiently regular (e.g., a lattice), then we could tile annuli at this scale (as in Figure 1(b)) so that if we define ω_R as the sum of the length functionals over the tiled annuli, then for any pair x,y∈V(G) with d^G(x,y)⩾R^1+δ and at least one of x or y near the center of an annulus, we would have $\operatorname{dist}_{\omega _{R}}^{G}(x,y) \geqslant R^{( \tilde{\zeta}+d_{f})/2}$. In a finite-dimensional lattice, a bounded number of shifts of the tiling is sufficient for every vertex to reside near the center of some annulus.

By combining length functionals over all scales, and replacing the regular tiling by a suitable random family of annuli, we obtain, for every δ>0, a reversible random weight $\omega : E(G) \to \mathbb{R}_{+}$ satisfying (1.22) (intuitively, because of the unit area normalization), and such that almost surely eventually

$$ \operatorname{dist}_{\omega}^{G}\left (\rho , \bar{B}^{G}(\rho ,R)\right ) \geqslant R^{(d-\delta )/2}, $$

(1.24)

where $d \mathrel{\mathop {:}}=d_{f} + \tilde{\zeta}$. In other words, distances in $\operatorname{dist}_{\omega}^{G}$ are (asymptotically) increased by power (d−δ)/2.

Thus (1.23) gives for every δ>0, eventually almost surely

$$ \operatorname{ \mathbb{E}}\left [\mathcal {M}_{n}^{2} \mid (G,\rho )\right ] \leqslant n^{2(1+ \delta )/(d-\delta )}. $$

Taking δ→0 yields . This is carried out formally in Section 4.1.

1.4.1 Annealed vs. quenched subdiffusivity

One can express $\operatorname{ \mathbb{E}}[\sigma _{R} \mid (G,\rho )]$ in terms of electrical potentials. Suppose that, accordingly, one is able to establish, for some d>0, a two-sided annealed estimate:

$$ R^{d-o(1)} \leqslant \operatorname{ \mathbb{E}}[\sigma _{R}] \leqslant R^{d+o(1)} \quad \textrm{as } R \to \infty , $$

where expectation is taken over both the walk and the random network (G,ρ). Then a standard application of Borel-Cantelli (cf. Lemma 1.8) gives that almost surely σ_R⩽R^d+o(1), but not an almost sure lower bound. On the other hand, a bound of the form

$$ \operatorname{ \mathbb{E}}[\mathcal {M}_{n}^{2}] \leqslant n^{2/d+o(1)}\quad \textrm{as } n \to \infty $$

provides that $\mathcal {M}_{n} \leqslant n^{1/d+o(1)}$ almost surely, which entails σ_R⩾R^d−o(1) almost surely.

In this way, the two exponents β and d_w are complementary, allowing one to obtain two-sided quenched estimates from two-sided annealed estimates. This is crucial for establishing d_s=2d_f/d_w, as the upper bound in (1.19) uses the fully quenched exponent which, in the setting of Theorem 1.3, arises from the lower bound (1.13) on the annealed exponent .

We remark on the following strengthening of Theorem 1.3.

Corollary 1.10

Under the assumptions of Theorem 1.3, it additionally holds that $\beta = \beta ^{\mathcal {A}}$ and $d_{w} = d_{w}^{\mathcal {A}}$.

Proof

We may assume that d_w and β exist, and d_w=β. From Theorem 1.6 we obtain:

The relations and $\bar{\beta }^{ \mathcal {A}} \leqslant \bar{d}_{w}$ follow from (1.20), yielding

 □

2 Reversible random weights

Throughout this section, (G,ρ) is a reversible random network satisfying $\operatorname{ \mathbb{E}}[1/c^{G}_{\rho}] < \infty$.

2.1 Modulus and effective resistance

For a network H and two disjoint subsets S,T⊆V(H), define the modulus

$$ \mathsf{Mod}^{H}(S\leftrightarrow T) \mathrel{\mathop {:}}=\min \left \{ \|\omega \|_{\ell ^{2}(c^{H})}^{2} : \operatorname{dist}^{H}_{\omega}(S,T) \geqslant 1 \right \}, $$

(2.1)

where the minimum is over all weights $\omega : E(H) \to \mathbb{R}_{+}$, and

$$ \|\omega \|^{2}_{\ell ^{2}(c^{H})} = \sum _{e \in E(H)} c^{H}(e) | \omega (e)|^{2}. $$

For x∈V(H) and 0<r<R, define the annular modulus:

$$ \mathsf{M}^{H}(x,r,R) \mathrel{\mathop {:}}=\mathsf{Mod}^{H}\left (B^{H}(x,r) \leftrightarrow \bar{B}^{H}(x,R)\right ). $$

Note that when H is finite, the minimizer in (2.1) exists and is unique (as it is the minimum of a strictly convex function over a compact set). In particular, even when H is infinite, this also holds for M^H(x,r,R), as we have

$$ \mathsf{Mod}^{H}\left (B^{H}(x,r) \leftrightarrow \bar{B}^{H}(x,R) \right ) = \mathsf{Mod}^{H[B^{H}(x,R+1)]}\left (B^{H}(x,r) \leftrightarrow \bar{B}^{H}(x,R)\right ). $$

Denote this minimal weight by $\omega ^{*}_{(H,x,r,R)}$. The standard duality between effective resistance and discrete extremal length [Duf62] gives an alternate characterization of M^H(x,r,R), as follows.

Lemma 2.1

For any finite graph H and disjoint subsets S,T⊆V(H), it holds that

$$ \mathsf{Mod}^{H}(S \leftrightarrow T) = \left (\mathsf{R}_{ \mathrm{eff}}^{H}(S \leftrightarrow T)\right )^{-1}. $$

(2.2)

Hence for any (possibly infinite graph) G, all x∈V(G) and 0⩽r⩽R,

$$ \mathsf{M}^{H}(x,r,R) = \left (\mathsf{R}_{\mathrm{eff}}^{G}\left (B^{G}(x,r) \leftrightarrow \bar{B}^{G}(x,R)\right )\right )^{-1}. $$

For a function $g : V(H) \to \mathbb{R}$, we denote the Dirichlet energy

$$ \mathscr{E}^{H}(g) \mathrel{\mathop {:}}=\sum _{\{x,y\} \in E(H)} c^{H}( \{x,y\}) |g(x)-g(y)|^{2}. $$

We will make use of the Dirichlet principle (see [LP16, Ch. 2]): When H is finite and S∩T=∅,

$$ \mathsf{R}_{\mathrm{eff}}^{H}(S \leftrightarrow T) = \left (\min \left \{ \mathscr{E}^{H}(g) : g|_{S} \equiv 0, g|_{T} \equiv 1 \right \}\right )^{-1}, $$

(2.3)

and when H is additionally connected, the minimizer of (2.3) is the unique function harmonic on V(H)∖(S∪T) with the given boundary values.

2.2 Approximate nets

We now define some objects that will act as random approximate nets in the metric space (V(G),d^G). The definitions are made conditioned on (G,ρ), and the random variables are otherwise taken to be mutually independent.

Fix R′⩾R⩾1 and λ⩾1. For v∈V(G), define

$$ \gamma _{R,R'}(v) \mathrel{\mathop {:}}=\max \left \{ \operatorname{vol}^{G}(y,R) : y \in B^{G}(v,R') \right \}. $$

Let {u_v:v∈V(G)} be an independent family of Bernoulli {0,1} random variables where

$$ \operatorname{ \mathbb{P}}\left (\boldsymbol{u}_{v} = 1\right ) = \min \left (1,\lambda \frac{c^{G}_{v}}{\gamma _{R,R'}(v)}\right ), $$

(2.4)

and define $\boldsymbol{U}_{R,R'}(\lambda ) \mathrel{\mathop {:}}=\left \{ x \in V(G) : \boldsymbol{u}_{v} = 1 \right \}$. Observe the inequality, valid for every x∈V(G) and 1⩽r⩽R:

$$\begin{aligned} \operatorname{ \mathbb{P}}[d^{G}(x, \boldsymbol{U}_{R,R'}(\lambda )) > r] &\leqslant \prod _{v \in B^{G}(x,r)} \left (1-\frac{\lambda c^{G}_{v}}{\gamma _{R,R'}(v)} \right )_{+} \\ &\leqslant \exp \left (-\lambda \sum _{v \in B^{G}(x,r)} \frac{c^{G}_{v}}{\gamma _{R,R'}(v)}\right ) \leqslant \exp \left (- \lambda \frac{\operatorname{vol}^{G}(x,r)}{\operatorname{vol}^{G}(x,2R')}\right ), \vphantom{\frac{\bigoplus}{\bigoplus}} \end{aligned}$$

(2.5)

where we have employed the two inequalities

$$\begin{aligned} \sum _{v \in B^{G}(x,r)} c^{G}_{v} &= \operatorname{vol}^{G}(x,r), \\ \max _{v \in B^{G}(x,r)} \gamma _{R,R'}(v) &\leqslant \operatorname{vol}^{G}(x,2R'). \end{aligned}$$

The idea here is that, by (2.5), the balls {B^G(u,R):u∈U_R,R′(λ)} tend to cover vertices x∈V(G) for which $\operatorname{vol}^{G}(x,R) \approx \operatorname{vol}^{G}(x,2R')$, as long as λ is chosen sufficiently large. On the other hand, the sampling rate (2.4) allow us to control $\operatorname{ \mathbb{E}}|B^{G}(\rho ,R') \cap \boldsymbol{U}_{R,R'}( \lambda )|$. Referring to the argument sketched at the end of Section 1.3, we will center an annulus at every x∈U_R,R′(λ), and thus we need to control the average covering multiplicity to keep $\operatorname{ \mathbb{E}}[\omega (X_{0},X_{1})^{2}]$ finite.

Since the law of U_R,R′(λ) does not depend on the root, we have the following.

Lemma 2.2

The triple (G,ρ,U_R,R′(λ)) is a reversible random network.

Our construction of reversible random networks are all of this form: Starting with a reversible random network (G,ρ), we augment G by some markings in a manner that “doesn’t depend on the root ρ,” to obtain a reversible random network (G,ρ,ξ). This notion is formalized in the next section.

2.3 The mass-transport principle

Let 𝒢_• denote the collection of isomorphism classes of rooted, connected, locally-finite networks, and let 𝒢_•• denote the collection of isomorphism classes of doubly-rooted, connected, locally-finite networks. We will consider functionals F:𝒢_••→[0,∞). Equivalently, these are functionals F(G₀,x₀,y₀,ξ₀) that are invariant under automorphisms of ψ of G₀: F(G₀,x₀,y₀,ξ₀)=F(ψ(G₀),ψ(x₀),ψ(y₀),ξ₀∘ψ⁻¹).

The mass-transport principle (MTP) for a random rooted network (G,ρ,ξ) asserts that for any nonnegative Borel F:𝒢_••→[0,∞), it holds that

$$ \operatorname{ \mathbb{E}}\left [\sum _{x \in V(G)} F(G,\rho ,x,\xi )\right ] = \operatorname{ \mathbb{E}}\left [ \sum _{x \in V(G)} F(G,x,\rho ,\xi )\right ]. $$

Unimodular random networks are precisely those that satisfy the MTP (see [AL07]).

Using the fact that biasing the law of a reversible random network (G,ρ,ξ) with $\operatorname{ \mathbb{E}}[1/c^{G}_{\rho}] < \infty$ by $1/c^{G}_{\rho}$ (see [BC12, Prop. 2.5]) yields a unimodular random network, one arrives at the following biased MTP.

Lemma 2.3

If (G,ρ,ξ) is a reversible random network with $\operatorname{ \mathbb{E}}[1/c^{G}_{ \rho}] < \infty$, then for any nonnegative Borel functional F:𝒢_••→[0,∞), it holds that

$$ \operatorname{ \mathbb{E}}\left [\frac{1}{c^{G}_{\rho}} \sum _{x \in V(G)} F(G,\rho ,x,\xi ) \right ] = \operatorname{ \mathbb{E}}\left [\frac{1}{c^{G}_{\rho}} \sum _{x \in V(G)} F(G,x, \rho ,\xi )\right ]. $$

(2.6)

Let us now explain the claim of Lemma 2.2 further. The following is a special case of [O+18, Lem. 2.2], where it is stated for unimodular random networks. Its proof is a straightforward consequence of the characterization of unimodular random graphs via the mass-transport principle.

Lemma 2.4

Suppose that (G,ρ,ξ) is a reversible random network with $\operatorname{ \mathbb{E}}[1/c_{\rho}^{G}] < \infty$ and (G,ρ,ξ′) is a random rooted network such that for every pair of vertices u,v∈V(G), the conditional distribution of (G,u,v,ξ′) given (G,ρ,ξ) coincides almost surely with some measurable function of the (doubly-rooted) isomorphism class of (G,u,v,ξ). Then (G,ρ,ξ′) is a reversible random network.

2.4 Construction of the weights

Recall that (G,ρ) is a reversible random network satisfying $\operatorname{ \mathbb{E}}[1/c^{G}_{\rho}] < \infty$. Denote . Our goal is to prove the following.

Theorem 2.5

There is a reversible random weight $\omega : E(G) \to \mathbb{R}_{+}$ such that $\operatorname{ \mathbb{E}}[\omega (X_{0},X_{1})^{2}] < \infty$, and such that, for every δ>0, almost surely eventually

$$ \operatorname{dist}_{\omega}^{G}\left (\rho , \bar{B}^{G}(\rho ,R)\right ) \geqslant R^{(d_{*}-\delta )/2}. $$

(2.7)

To this end, for ε∈(0,1), define the set of networks with controlled geometry at scale R:

where we recall the definition of the annular modulus M^G from Section 2.1.

Lemma 2.6

For every ε>0 and R⩾1, there is a reversible random weight $\omega _{R} : E(G) \to \mathbb{R}_{+}$ such that

$$ \operatorname{ \mathbb{E}}\left [\omega _{R}(X_{0},X_{1})^{2}\right ] \leqslant 2 R^{-d_{*}+ \varepsilon (3+3\bar{d}_{f}-\tilde{\zeta})}, $$

(2.8)

and if x∈V(G) satisfies d^G(ρ,x)⩾3R^1+ε, then

(2.9)

Before proving the lemma, let us see that it establishes Theorem 2.5.

Proof of Theorem 2.5

Clearly we may assume d_∗>0. Fix a value ε∈(0,d_∗), and define the sets

$$\begin{aligned} \mathcal {S}_{R_{0}}(\varepsilon ) &\mathrel{\mathop {:}}=\bigcap _{R \geqslant R_{0}} \mathcal {S}(\varepsilon ,R)\,, \\ \mathcal {S}(\varepsilon ) &\mathrel{\mathop {:}}=\bigcup _{R_{0} \geqslant 1} \mathcal {S}_{R_{0}}(\varepsilon )\,. \end{aligned}$$

Lemma 2.7

Almost surely $(G,\rho ) \in \mathcal {S}(\varepsilon )$.

Proof

To establish the claim, we need to show that almost surely: $(G,\rho ) \in \mathcal {S}(\varepsilon ,R)$ for R sufficiently large. By definition of the exponents , for every δ>0, it holds that almost surely eventually $\mathsf{M}^{G}(\rho ,R,R^{1+\delta}) \leqslant R^{-\tilde{\zeta}+ \delta}$ (recall Lemma 2.1) and .

Therefore we have, for every δ>0, almost surely eventually

where the second inequality holds for R sufficiently large (depending on δ>0).

Similarly, we have that, for every δ>0, almost surely eventually

where the latter inequality holds for R sufficiently large (depending on δ>0). Choosing δ>0 sufficiently small shows that $(G, \rho ) \in \mathcal {S}(\varepsilon ,R)$ whenever (2.10) and (2.11) hold. □

Define $\alpha \mathrel{\mathop {:}}=3+3\bar{d}_{f} - \tilde{\zeta}$. For k⩾1, let $\omega _{2^{k}}$ be the weight guaranteed by Lemma 2.6, and define the random weight

$$ \omega \mathrel{\mathop {:}}=\left (\sum _{k \geqslant 1} \frac{2^{k(d_{*}-\varepsilon \alpha )}}{k^{2}} \omega _{2^{k}}^{2} \right )^{1/2}, $$

so that

$$ \operatorname{ \mathbb{E}}\left [\omega (X_{0},X_{1})^{2}\right ] \stackrel{\text{(2.8)}}{\leqslant } 2 \sum _{k \geqslant 1} k^{-2} \leqslant O(1). $$

Moreover, for any k⩾1 and x∈V(G), if d^G(ρ,x)⩾3⋅2^k(1+ε), then (2.9) gives

hence for all x∈V(G),

Now by Lemma 2.7, this shows that almost surely eventually (with respect to k),

$$ d^{G}(\rho ,x)\in [3\cdot 2^{k(1+\varepsilon )}, 3 \cdot 2^{(k+1)(1+ \varepsilon )}) \implies \operatorname{dist}_{\omega}^{G}(\rho ,x) \geqslant d^{G}( \rho ,x)^{(d_{*}-\varepsilon \alpha )/(2(1+\varepsilon ))- \varepsilon }, $$

and, therefore, almost surely eventually with respect to R,

$$ d^{G}(\rho ,x) \geqslant R \implies \operatorname{dist}_{\omega}^{G}(\rho ,x) \geqslant d^{G}(\rho ,x)^{(d_{*}-\varepsilon \alpha ))/(2(1+ \varepsilon ))-\varepsilon }. $$

Since we can take ε>0 arbitrarily small, the desired result follows.  □

Let us now prove the lemma.

Proof of Lemma 2.6

Fix R⩾1, and define

Lemma 2.8

If $(G,\rho ) \in \mathcal {S}(\varepsilon ,R)$ and d^G(ρ,z)⩽R, then $z \in \mathcal {S}'(\varepsilon ,R)$.

Proof

Note that d^G(ρ,z)⩽R gives

$$ \mathsf{M}^{G}(z,R,2 R^{1+\varepsilon }) \leqslant \mathsf{M}^{G}( \rho ,2R,R^{1+\varepsilon }). $$

Similarly, we have $\operatorname{vol}^{G}(z,4 R^{1+\varepsilon }) \leqslant \operatorname{vol}^{G}( \rho ,5 R^{1+\varepsilon })$, and

$$ \max \left \{ \operatorname{vol}^{G}(y,R) : y \in B^{G}(z,R) \right \} \geqslant \operatorname{vol}^{G}(\rho ,R). $$

 □

Denote R′:=5R^1+ε and, recalling Section 2.1, define

(2.12)

where we recall the definition of $\omega ^{*}_{(H,x,r,R)}$ from Section 2.1. Then define: $\omega _{R} : E(G) \to \mathbb{R}_{+}$ by

$$\begin{aligned} \hat{\omega} &\mathrel{\mathop {:}}=\sum _{z \in \boldsymbol{U}_{R,R'}( \lambda )} \omega ^{(z)}\,, \\ \tilde{\omega}(\{x,y\}) & \mathrel{\mathop {:}}= \textstyle\begin{cases} 1 & \{x,y\} \nsubseteq B^{G}(\boldsymbol{U}_{R,R'}(\lambda ),R) \textrm{ and } \{(G,x),(G,y)\} \cap \mathcal {S}(\varepsilon ,R) \neq \emptyset \\ 0 & \textrm{otherwise.} \end{cases}\displaystyle \\ \omega _{R} &\mathrel{\mathop {:}}=\hat{\omega} + \tilde{\omega}\,, \end{aligned}$$

where λ>0 is a number (depending on R) that we will choose later.

Lemma 2.9

If x∈V(G) satisfies d^G(ρ,x)⩾3R^1+ε, then .

Proof

If d^G(ρ,U_R,R′(λ))>R and $(G,\rho ) \in \mathcal {S}(\varepsilon ,R)$, then $\tilde{\omega}(\{\rho ,y\}) \geqslant 1$ for every {ρ,y}∈E(G), implying $\operatorname{dist}^{G}_{ \tilde{\omega}}(\rho ,x) \geqslant 1$.

Now suppose that z∈U_R,R′(λ) satisfies d^G(ρ,z)⩽R and $(G,\rho ) \in \mathcal {S}(\varepsilon ,R)$. By Lemma 2.8, we have $z \in \mathcal {S}'(\varepsilon ,R)$, and therefore $\hat{\omega} \geqslant \omega ^{*}_{(G,z,R,2 R^{1+ \varepsilon })}$. Thus by definition,

$$ \operatorname{dist}_{\omega _{R}}^{G}(\rho ,x) \geqslant \operatorname{dist}^{G}_{\omega ^{*}_{(G,z,R,2 R^{1+\varepsilon })}}\left (B^{G}(z,R), \bar{B}^{G}(z,2 R^{1+ \varepsilon })\right ) \geqslant 1, $$

since ρ∈B^G(z,R), and x∉B^G(z,2R^1+ε). □

What remains is to bound $\operatorname{ \mathbb{E}}[\omega _{R}(X_{0},X_{1})^{2}]$. Use Cauchy-Schwarz to write

(2.13)

where we have used the fact that ω^(z) is supported on edges e such that e⊆B^G(z,2R^1+ε).

Define the functional

so that the expression in (2.13) is equal to

$$\begin{aligned} \operatorname{ \mathbb{E}}\left [\frac{1}{c_{\rho}^{G}} \sum _{z \in V(G)} F(G,\rho ,z, \boldsymbol{U}_{R,R'}(\lambda ))\right ] &= \operatorname{ \mathbb{E}}\left [\frac{1}{c_{\rho}^{G}} \sum _{z \in V(G)} F(G,z,\rho ,\boldsymbol{U}_{R,R'}(\lambda ))\right ], \end{aligned}$$

where the equality is a consequence of the biased Mass-Transport Principle (2.6). It follows that

where in the last line we have used the definition of ω^(ρ) from (2.12).

Now (2.4) gives, for every x∈B^G(ρ,4R^1+ε),

$$ \begin{aligned} \operatorname{ \mathbb{P}}[x \in \boldsymbol{U}_{R,R'}(\lambda ) \mid (G,\rho )] &\leqslant \frac{\lambda c^{G}_{x}}{\max \{ \operatorname{vol}^{G}(y,R): y \in B^{G}(x,R') \}} \\ &\leqslant \frac{\lambda c^{G}_{x}}{\max \{ \operatorname{vol}^{G}(y,R): y \in B^{G}(\rho ,R) \}}, \end{aligned}$$

where we have used R′=5R^1+ε⩾4R^1+ε+R.

For notational convenience, define the value $V \mathrel{\mathop {:}}= \max \{ \operatorname{vol}^{G}(y,R): y \in B^{G}(\rho ,R) \}$. Then the preceding inequality yields

and the latter expectation is

$$ \sum _{x \in B^{G}(\rho ,4 R^{1+\varepsilon })} \operatorname{ \mathbb{P}}\left [x \in \boldsymbol{U}_{R,R'}(\lambda ) \mid (G,\rho ), \rho \in \boldsymbol{U}_{R,R'}( \lambda )\right ] \leqslant 1 + \lambda \frac{\operatorname{vol}^{G}(\rho ,4R^{1+\varepsilon })}{V}, $$

using independence of the Bernoullis {u_x:x∈V(G)} in the sampling procedure.

Therefore,

by definition of $\mathcal {S}'(\varepsilon ,R)$.

Let us use (2.5) with r=R−1 to bound

where the last line follows from the definition of $\mathcal {S}( \varepsilon ,R)$, and in the first line we have used that $\tilde{\omega}(X_{0},X_{1})=0$ if $(G,\rho ) \notin \mathcal {S}( \varepsilon ,R)$.

Now choose , yielding

$$ \operatorname{ \mathbb{E}}\left [\omega _{R}(X_{0},X_{1})^{2}\right ] \leqslant 2 \left (\operatorname{ \mathbb{E}}[ \hat{\omega}(X_{0},X_{1})^{2}+\tilde{\omega}(X_{0},X_{1})^{2}]\right ) \leqslant R^{-d_{*}} + R^{-d_{*} + \varepsilon (3+3\bar{d}_{f}- \tilde{\zeta})}\,. $$

 □

3 Markov type and the rate of escape

Our goal now is to prove Theorem 1.9. It is essentially a consequence of the fact that every N-point metric space has maximal Markov type 2 with constant O(logN) (see Section 3.2 below), and that the random walk on a reversible random graph with almost sure subexponential growth (in the sense of (1.21)) can be approximated, quantitatively, by a limit of random walks restricted to finite subgraphs.

3.1 Restricted walks on clusters

Definition 3.1

Restricted random walk

Consider a network G=(V,E,c^G) and a finite subset S⊆V. Let

$$ N_{G}(x) \mathrel{\mathop {:}}=\{ y \in V : \{x,y\} \in E \} $$

denote the neighborhood of a vertex x∈V.

Define a measure π_S on S by

(3.1)

where $E^{G}(S) \mathrel{\mathop {:}}=\left \{ \{x,y\} \in E(G) : \{x,y \} \cap S \neq \emptyset \right \}$ is the set of edges incident on S.

We define the random walk restricted to S as the following process {Z_t}: For t⩾0, put

$$ \operatorname{ \mathbb{P}}(Z_{t+1} = y \mid Z_{t} = x) = \textstyle\begin{cases} \frac{c^{G}(E^{G}(x, V \setminus S))}{c^{G}_{x}} & y = x \\ \frac{c^{G}(\{x,y\})}{c^{G}_{x}} & y \in N_{G}(x) \cap S \\ 0 & \textrm{otherwise,} \end{cases} $$

where we have used the notation $E^{G}(x, U) \mathrel{\mathop {:}}= \left \{ \{x,y\} \in E : y \in U \right \}$. It is straightforward to check that {Z_t} is a reversible Markov chain on S with stationary measure π_S. If Z₀ has law π_S, we say that {Z_t} is the stationary random walk restricted to S.

A bond percolation on G is a mapping ξ:E(G)→{0,1}. For a vertex v∈V(G) and a bond percolation ξ, we let $K^{G}_{ \xi}(v)$ denote the connected component of v in the subgraph of G given by ξ⁻¹(1). Say that a bond percolation ξ:E(G)→{0,1} is finitary if $K^{G}_{\xi}(\rho )$ is almost surely finite. In what follows, if H is a subgraph of G, we use the notation $c^{G}(H) \mathrel{\mathop {:}}=\sum _{x \in V(H)} c_{x}^{G}$.

Lemma 3.2

Suppose (G,ρ,ξ) is a reversible random network and ξ is finitary. Let $\hat{\rho} \in V(G)$ be chosen according to the measure $\pi _{K^{G}_{ \xi}(\rho )}$ from Definition 3.1. Then (G,ρ) and $(G, \hat{\rho})$ have the same law.

Proof

Define the transport

where $\mathcal {S}$ denotes some Borel measurable subset of 𝒢_• (recall the definition from Section 2.3). Then the biased mass-transport principle (2.6) gives

and

 □

We will also need the following simple lemma relating the cardinality of clusters to their volume.

Lemma 3.3

Suppose (G,ρ,ξ) is a reversible random network satisfying $\operatorname{ \mathbb{E}}[1/c^{G}_{\rho}] < \infty$ and ξ is a finitary bond percolation. Then,

$$ \operatorname{ \mathbb{E}}\left [\frac{|V(K^{G}_{\xi}(\rho ))|}{c^{G}(K^{G}_{\xi}(\rho ))} \right ] = \operatorname{ \mathbb{E}}[1/c^{G}_{\rho}]\,. $$

Proof

Define the transport

Then the biased mass-transport principle (2.6) gives

$$ \begin{aligned} \operatorname{ \mathbb{E}}\left [\frac{|V(K^{G}_{\xi}(\rho ))|}{c^{G}(K^{G}_{\xi}(\rho ))} \right ] &= \operatorname{ \mathbb{E}}\left [\frac{1}{c^{G}_{\rho}}\sum _{x \in V(G)} F(G, \rho ,x,\xi )\right ] \\ &= \operatorname{ \mathbb{E}}\left [\frac{1}{c^{G}_{\rho}}\sum _{x \in V(G)} F(G,x,\rho ,\xi )\right ] = \operatorname{ \mathbb{E}}[1/c^{G}_{\rho}]. \end{aligned}$$

 □

3.2 Maximal Markov type

A metric space $(\mathcal {X},d_{\mathcal {X}})$ has maximal Markov type 2 with constant K if it holds that for every finite state space Ω, every map f:Ω→X, and every stationary, reversible Markov chain {Z_n} on Ω,

$$ \operatorname{ \mathbb{E}}\left [\max _{0 \leqslant t \leqslant n} d_{\mathcal {X}}(Z_{0},Z_{t})^{2} \right ] \leqslant K^{2} n \operatorname{ \mathbb{E}}\left [d_{\mathcal {X}}(Z_{0},Z_{1})^{2} \right ],\quad \forall n \geqslant 1. $$

This is a maximal variant of K. Ball’s Markov type [Bal92]. Note that every Hilbert space has maximal Markov type 2 with constant K for some universal K (independent of the Hilbert space); see, e.g., [A+06, §8]. Bourgain’s embedding theorem [Bou85] asserts that every N-point metric space embeds into a Hilbert space with bilipschitz distortion O(logN), yielding the following.

Lemma 3.4

If $(\mathcal {X},d_{\mathcal {X}})$ is a finite metric space with $N = | \mathcal {X}|$, then for every stationary, reversible Markov chain {Z_n} on $\mathcal {X}$, it holds that

$$ \operatorname{ \mathbb{E}}\left [\max _{0 \leqslant t \leqslant n} d_{\mathcal {X}}(Z_{0},Z_{t})^{2} \right ] \leqslant O(n) (\log N)^{2} \operatorname{ \mathbb{E}}\left [d_{\mathcal {X}}(Z_{0},Z_{1})^{2} \right ],\quad \forall n \geqslant 1. $$

Note that the lemma holds vacuously when N=1.

3.3 Reduction to finite subgraphs

Consider now a reversible random network (G,ρ,ω,ξ), where ξ is a finitary bond percolation, and define the random time

$$ \tau _{\xi} \mathrel{\mathop {:}}=\max \{ t \geqslant 0 : X_{0},X_{1}, \ldots ,X_{t} \in K^{G}_{\xi}(\rho ) \}, $$

(3.2)

where {X_t} is the random walk on G with X₀=ρ. For a number L⩾1, let $\mathcal {S}_{L}$ denote the event $\{ \log |V(K_{ \xi}^{G}(\rho ))| \leqslant L \}$.

Lemma 3.5

Suppose (G,ρ,ω,ξ) is a reversible random network, where ξ is a finitary bond percolation. Then for any L⩾1, it holds that

Proof

Let $\{X^{\xi}_{n}\}$ be the restricted random walk on $K^{G}_{\xi}( \rho )$, where $X^{\xi}_{0}$ has law $\pi _{K^{G}_{\xi}(\rho )}$ conditioned on (G,ρ,ω,ξ). Let us furthermore use $\{\tilde{X}_{n}^{ \xi}\}$ for the random walk on G started from $\tilde{X}^{\xi }_{0} = X_{0}^{\xi}$, and note that we take both $\{\tilde{X}_{n}^{\xi}\}$ and $\{X_{n}^{\xi}\}$ to be independent of the random walk {X_n} on G with X₀=ρ.

Define the sets

$$\begin{aligned} \mathcal {A}_{L} &\mathrel{\mathop {:}}=\left \{ (G_{0},u,\xi _{0}) : \log \left |V(K^{G_{0}}_{\xi _{0}}(u))\right | \leqslant L \right \}, \\ \mathcal {B}_{t} &\mathrel{\mathop {:}}=\left \{ (G_{0},u,\{v_{0},v_{1}, \ldots ,v_{t}\},\xi _{0}) : v_{0},v_{1},\ldots ,v_{t} \in K^{G_{0}}_{ \xi _{0}}(u) \right \}, \end{aligned}$$

where (G₀,u) is a rooted graph, v₀,v₁,…,v_t∈V(G₀), and ξ₀:E(G)→{0,1}.

Note that there is a natural coupling of $\{\tilde{X}^{\xi}_{t}\}$ and $\{X_{t}^{\xi}\}$ such that

$$ (G,\rho ,\{\tilde{X}_{t}^{\xi} : 0 \leqslant t \leqslant n \},\xi ) \in \mathcal {B}_{n} \implies \{\tilde{X}^{\xi}_{0},\tilde{X}^{\xi}_{1}, \ldots ,\tilde{X}^{\xi}_{n}\} = \{X_{0}^{\xi}, X_{1}^{\xi},\ldots ,X_{n}^{ \xi}\}\,. $$

(3.3)

Applying Lemma 3.4 to the stationary, reversible Markov chain $\{X_{n}^{\xi}\}$ on $K^{G}_{\xi}(\rho )$ and the metric space $(V(K^{G}_{ \xi}(\rho )), \operatorname{dist}^{K^{G}_{\xi}(\rho )}_{\omega})$, we obtain that almost surely over the choice of (G,ρ,ω,ξ),

$$\begin{aligned} &\operatorname{ \mathbb{E}}\left [\max _{0 \leqslant t \leqslant n} \operatorname{dist}_{\omega}^{K^{G}_{ \xi}(\rho )}(X_{0}^{\xi}, X_{t}^{\xi})^{2} \mid (G,\rho ,\omega ,\xi ) \right ] \\ &\quad \leqslant O(n) \left (\log |K^{G}_{\xi}(\rho )|\right )^{2} \operatorname{ \mathbb{E}}\left [\operatorname{dist}_{\omega}^{K^{G}_{\xi}(\rho )}(X_{0}^{\xi},X_{1}^{\xi})^{2} \mid (G,\rho ,\omega ,\xi )\right ] \\ &\quad \leqslant O(n) \left (\log |K^{G}_{\xi}(\rho )|\right )^{2} \operatorname{ \mathbb{E}}\left [\omega (X_{0}^{\xi},X_{1}^{\xi})^{2} \mid (G,\rho ,\omega , \xi )\right ]. \end{aligned}$$

Using the fact that $\operatorname{dist}^{G}_{\omega}(x,y) \leqslant \operatorname{dist}^{K^{G}_{ \xi}(\rho )}_{\omega}(x,y)$ for all $x,y \in V(K^{G}_{\xi}(\rho ))$ and the definition of $\mathcal {A}_{L}$ gives

Employing the coupling given by (3.3) yields

and taking expectations gives

(3.4)

where for the right-hand side, we have used Lemma 3.2 to conclude that (G,X₀) (recall X₀=ρ) and $(G,X_{0}^{\xi})$ have the same law, and we have used the fact that the steps $(X_{0}^{\xi},X_{1}^{ \xi})$ of the restricted walk can be coupled to (X₀,X₁) so that when $X_{1} \neq X_{1}^{\xi}$, we have X₁=X₀.

Let us now make a key observation: The left-hand side of (3.4) is equal to

since $K^{G}_{\xi}(\rho )=K^{G}_{\xi}(\tilde{X}_{0}^{\xi})$.

Now Lemma 3.2 shows that (G,X₀,X₁,…,X_n) and $(G,\tilde{X}^{\xi}_{0},\tilde{X}^{\xi}_{1},\ldots ,\tilde{X}^{\xi}_{n})$ have the same law, hence (3.4) gives

which is the claimed bound. □

3.3.1 A unimodular random partitioning scheme

We need a unimodular random partitioning scheme that adapts to the volume measure. Here we state it for any unimodular vertex measure. This argument employs a unimodular variation on the method and analysis from [CKR01], adapted to an arbitrary underlying measure as in [K+05]. We will use the notation $\mathrm{diam}^{G}(S) \mathrel{\mathop {:}}=\max \{ \operatorname{dist}^{G}(x,y) : x,y \in S \}$.

Lemma 3.6

Suppose (G,ρ,μ) is a reversible random network, where $\mu : V(G) \to \mathbb{R}_{+}$ satisfies μ(ρ)>0 almost surely. Then for every Δ>0, there is a bond percolation χ_Δ:E(G)→{0,1} such that

• 1. (G,ρ,χ_Δ) is a reversible random network.

• 2. Almost surely $\mathrm{diam}^{G}(K^{G}_{\chi _{\Delta}}(\rho )) \leqslant \Delta$.

• 3. For every r⩾0, it holds that almost surely

  $$ \operatorname{ \mathbb{P}}\left [B^{G}(\rho ,r) \nsubseteq K^{G}_{\chi _{\Delta}}(\rho ) \mid (G,\rho )\right ] \leqslant \frac{16 r}{\Delta} \left (1+\log \left ( \frac{\mu \left (B^{G}(\rho ,\frac{5}{8} \Delta )\right )}{\mu \left (B^{G}(\rho ,\frac{1}{8} \Delta \right )} \right )\right ), $$

where we use the notation μ(S):=∑_x∈Sμ(x) for S⊆V(G).

Proof

By assumption, G is locally finite, hence B^G(ρ,Δ) is finite. Thus we may assume that μ(x)>0 for all x∈V(G) as follows: Define $\hat{\mu}(x) = \mu (x)$ if μ(x)>0 and $\hat{\mu}(x)=1$ otherwise. We may then prove the lemma for $\hat{\mu}$, and observe that because properties (2) and (3) only refer to finite neighborhoods of the root, μ and $\hat{\mu}$ are identical on these neighborhoods, except for a set of zero measure.

Let {β_x:x∈V(G)} be a sequence of independent random variables where β_x is an exponential with rate μ(x). Let $R \in [ \frac{\Delta}{4},\frac{\Delta}{2})$ be independent and chosen uniformly random. For a finite subset S⊆V(G), write μ(S):=∑_x∈Sμ(x). We need the following elementary lemma.

Lemma 3.7

For any finite subset S⊆V(G), it holds that

$$ \operatorname{ \mathbb{P}}\left [\beta _{x} = \min \{ \beta _{v} : v \in S \} \mid (G, \mu )\right ] = \frac{\mu (x)}{\mu (S)},\qquad \forall x \in S. $$

Proof

A straightforward calculation shows that min{β_v:v∈S∖{x}} is exponential with rate μ(S∖{x}). Moreover, if β and β′ are independent exponentials with rates λ and λ′, respectively, then

$$ \operatorname{ \mathbb{P}}[\beta =\min (\beta ,\beta ')]= \frac{\lambda}{\lambda +\lambda '}. $$

 □

Define a labeling ℓ:V(G)→V(G), where ℓ(x)∈B^G(x,R) is such that

$$ \beta _{\ell (x)} = \min \left \{ \beta _{y} : y \in B^{G}(x,R) \right \}. $$

Define the bond percolation χ_Δ by

In other words, we remove edges whose endpoints receive different labels.

Since the law of χ_Δ does not depend on ρ (cf. the discussion in Section 2.3), it follows that (G,ρ,χ_Δ) is a reversible random network, yielding claim (1). Moreover, since ℓ(x)=z implies that $\operatorname{dist}^{G}(x,z) \leqslant R \leqslant \Delta$, it holds that almost surely

$$ \mathrm{diam}^{G}(K^{G}_{\chi _{\Delta}}(\rho )) = \mathrm{diam}^{G}( \ell ^{-1}(\ell (\rho ))) \leqslant \Delta , $$

yielding claim (2).

Since the statement of the lemma is vacuous for r>Δ/8, consider some r∈[0,Δ/8]. Let x^∗∈B^G(ρ,r+R) be such that

$$ \beta _{x^{*}} = \min \left \{ \beta _{x} : x \in B^{G}(\rho ,R+r) \right \}. $$

Then we have

$$ \operatorname{ \mathbb{P}}\left [B^{G}(\rho , r) \nsubseteq K^{G}_{\chi _{\Delta}}( \rho )\right ] \leqslant \operatorname{ \mathbb{P}}\left [\operatorname{dist}^{G}(\rho ,x^{*}) \geqslant R - r\right ]. $$

(3.5)

For x∈B^G(ρ,2Δ), define the interval $I(x) \mathrel{ \mathop {:}}=[\operatorname{dist}^{G}(\rho ,x) - r, \operatorname{dist}^{G}(\rho ,x)+r]$. Note that the bad event $\{ \operatorname{dist}^{G}(\rho ,x^{*}) \geqslant R - r \}$ coincides with the event {R∈I(x^∗)}. Order the points of B^G(ρ,2Δ) in non-decreasing order from ρ: x₀=ρ,x₁,x₂,…,x_N. Then (3.5) yields

$$\begin{aligned} \operatorname{ \mathbb{P}}\left [B^{G}(\rho ,r) \nsubseteq K^{G}_{\chi _{\Delta}}(\rho ) \right ] &\leqslant \operatorname{ \mathbb{P}}[R \in I(x^{*})] \\ &=\sum _{j=1}^{N} \operatorname{ \mathbb{P}}[R \in I(x_{j})] \cdot \operatorname{ \mathbb{P}}[x_{j} = x^{*} \mid R \in I(x_{j})] \\ &\leqslant \frac{2r}{\Delta /8}\sum _{j=1}^{N} \operatorname{ \mathbb{P}}[x_{j} = x^{*} \mid R \in I(x_{j})]. \end{aligned}$$

(3.6)

Note that since R⩾Δ/4 and r⩽Δ/8,

$$ R \in I(x_{j}) \implies x_{j} \in B^{G}(\rho ,\tfrac{5}{8}\Delta ) \setminus B^{G}(\rho ,\tfrac{1}{8} \Delta ). $$

Observe, moreover, that R∈I(x_j) implies x₁,x₂,…,x_j∈B^G(ρ,R+r), hence

$$ \begin{aligned}&\operatorname{ \mathbb{P}}[x_{j}=x^{*} \mid R \in I(x_{j})] \\ &\quad = \operatorname{ \mathbb{P}}\left [\beta _{x_{j}} = \min \left \{\beta _{x} : x \in B^{G}(\rho ,R+r)\right \} \mid R \in I(x_{j})\right ] \leqslant \frac{\mu (x_{j})}{\mu (\{x_{1},x_{2},\ldots ,x_{j}\})}, \end{aligned}$$

where the last inequality follows from Lemma 3.7.

Plugging these bounds into (3.6) gives

$$\begin{aligned} \operatorname{ \mathbb{P}}\left [B^{G}(\rho ,r) \nsubseteq K^{G}_{\chi _{\Delta}}(\rho ) \right ] &\leqslant \frac{16r}{\Delta} \sum _{j=|B^{G}(\rho , \frac{1}{8} \Delta )|+1}^{|B^{G}(\rho , \frac{5}{8} \Delta )|} \frac{\mu (x_{j})}{\mu (x_{1})+\cdots +\mu (x_{j})}. \end{aligned}$$

Finally, observe that for any a₀,a₁,a₂,…,a_m>0,

$$\begin{aligned} \sum _{j=1}^{m} \frac{a_{j}}{a_{0}+a_{1}+a_{2}+\cdots +a_{j}} &= \sum _{j=1}^{m} \frac{a_{j}/a_{0}}{1+a_{1}/a_{0}+\cdots +a_{j}/a_{0}} \\ &\leqslant \int _{0}^{(a_{1}+\cdots +a_{m})/a_{0}} \frac{1}{t+1}\,dt = \log \left (1+\frac{a_{1}+\cdots +a_{m}}{a_{0}}\right ), \end{aligned}$$

and therefore

$$ \operatorname{ \mathbb{P}}\left [B^{G}(\rho ,r) \nsubseteq K^{G}_{\chi _{\Delta}}(\rho ) \right ] \leqslant \frac{16r}{\Delta} \log \left (1 + \frac{\mu (B^{G}(\rho ,\tfrac{5}{8} \Delta ))}{\mu (B^{G}(\rho ,\tfrac{1}{8} \Delta ))} \right ), $$

as desired (noting that log(1+y)⩽1+log(y) for y⩾1).  □

3.4 Proof of Theorem 1.9

The next lemma outlines our strategy for proving Theorem 1.9.

Lemma 3.8

Suppose (G,ρ,ω,ξ) is a reversible random network and for every 0<ε<1, there is a sequence of events $\{ \mathcal {E}_{k} : k \geqslant 1\}$ such that each $\mathcal {E}_{k}$ is measurable with respect to the σ-algebra generated by (G,ρ,ω,ξ), and such that:

• 1. Almost surely, $\mathcal {E}_{k}$ holds for all but finitely many k.

• 2. It holds that for all k⩾1,

  

  (3.7)

Then (1.23) holds.

The reader should take note of the crucial property: The events $\{ \mathcal {E}_{k}\}$ are independent of the random walk {X_t}, conditioned on (G,ρ).

Proof

Using assumption (2) in conjunction with Markov’s inequality and the Borel-Cantelli Lemma, it holds that almost surely, for all but finitely many k,

where expectation is taken over the random walk {X_t}. Now using assumption (1) yields that almost surely, for all but finitely many k,

$$ \operatorname{ \mathbb{E}}\left [\max _{0 \leqslant t \leqslant 4^{(1-\varepsilon )k}} \operatorname{dist}_{\omega}^{G}(X_{0},X_{t})^{2} \mid (G,\rho ,\omega ,\xi ) \right ] \leqslant 4^{(1+2\varepsilon ) k}, $$

and as a consequence, for all but finitely many n,

$$ \operatorname{ \mathbb{E}}\left [\max _{0 \leqslant t \leqslant n} \operatorname{dist}_{\omega}^{G}(X_{0},X_{t})^{2} \mid (G,\rho ,\omega ,\xi )\right ] \leqslant 4^{1+2\varepsilon } n^{(1+2 \varepsilon )/(1-\varepsilon )}. $$

Since this holds for every ε>0, (1.23) follows. □

With this in hand, we can proceed to our goal of proving Theorem 1.9.

Proof of Theorem 1.9

Recall that (G,ρ,ω) is a reversible random network and {X_n} is the random walk on G started from X₀=ρ.

Define the random vertex measure $\mu (x) \mathrel{\mathop {:}}=c^{G}_{x}$ for x∈V(G). For each k⩾1, let $\xi _{k} \mathrel{ \mathop {:}}=\chi _{4^{k}}$ denote the bond percolation provided by applying Lemma 3.6 with μ and Δ=4^k, where we take the sequence {ξ_k:k⩾1} to be mutually independent given (G,ρ). This makes the ensemble (G,ρ,ω,〈ξ_k:k⩾1〉) a reversible random network.

Denote

$$ \boldsymbol{n}_{k} \mathrel{\mathop {:}}= \frac{4^{k}}{16 k^{2} \left (1+\log \frac{\operatorname{vol}^{G}(\rho ,4^{k})}{c_{\rho}^{G}}\right )} $$

(3.8)

so that according to the guarantees of Lemma 3.6, for k⩾1, almost surely,

$$\begin{gathered} V(K^{G}_{\xi _{k}}(\rho )) \subseteq B^{G}(\rho ,4^{k})\,, \end{gathered}$$

(3.9)

$$\begin{gathered} \operatorname{ \mathbb{P}}[B^{G}(\rho ,\boldsymbol{n}_{k}) \nsubseteq V(K^{G}_{\xi _{k}}(\rho )) \mid (G,\rho ,\omega )] \leqslant O(k^{-2})\,. \end{gathered}$$

(3.10)

Define the events:

$$\begin{aligned} \mathcal {A}_{k} &\mathrel{\mathop {:}}=\left \{ B^{G}(\rho ,\boldsymbol{n}_{k}) \subseteq V(K_{\xi _{k}}^{G}(\rho )) \right \} \\ \mathcal {B}_{k}(\varepsilon ) &\mathrel{\mathop {:}}=\left \{ \log \operatorname{vol}^{G}(\rho ,4^{k}) \leqslant 4^{\varepsilon k}\right \} \\ \mathcal {C}_{k} &\mathrel{\mathop {:}}=\left \{ |V(K^{G}_{\xi}(\rho ))| \leqslant k^{2} c^{G}(K^{G}_{\xi}(\rho )) \right \} \\ \mathcal {D}_{k} &\mathrel{\mathop {:}}=\left \{ c_{\rho}^{G} \geqslant k^{-2} \right \}. \end{aligned}$$

Lemma 3.9

For every ε>0, almost surely $\mathcal {A}_{k},\mathcal {B}_{k}( \varepsilon ),\mathcal {C}_{k},\mathcal {D}_{k}$ hold for all but finitely many k.

Proof

For $\mathcal {A}_{k}$, this follows from an application of the Borel-Cantelli Lemma and (3.10). For $\mathcal {D}_{k}$, this similarly follows from the fact that $c^{G}_{\rho}$ is almost surely positive. For $\mathcal {B}_{k}(\varepsilon )$, this follows from the assumption (1.21). Finally, for $\mathcal {C}_{k}$ this follows from another application of Markov’s inequality and the Borel-Cantelli Lemma in conjunction with Lemma 3.3 and the fact that $\operatorname{ \mathbb{E}}[1/c^{G}_{\rho}] < \infty$. □

In light of Lemma 3.8, the next lemma suffices to complete the proof of Theorem 1.9.

Lemma 3.10

Consider ε>0 and the event $\mathcal {E}_{k} \mathrel{ \mathop {:}}=\mathcal {A}_{k} \cap \mathcal {B}_{k}(\varepsilon ) \cap \mathcal {C}_{k}(\varepsilon ) \cap \mathcal {D}_{k}$. Then,

(3.11)

Proof

Note first that for k sufficiently large,

$$ \mathcal {B}_{k}(\varepsilon ) \cap \mathcal {D}_{k} \implies \boldsymbol{n}_{k} \geqslant 4^{(1-2\varepsilon )k}. $$

Moreover, (3.9) gives, for k sufficiently large,

$$ \mathcal {B}_{k}(\varepsilon ) \cap \mathcal {C}_{k} \implies \log |V(K^{G}_{ \xi}(\rho ))| \leqslant 4^{2 \varepsilon k}. $$

Finally, we have $\mathcal {A}_{k} \implies \tau _{\xi _{k}} \geqslant \boldsymbol{n}_{k}$, where we recall the definition of $\tau _{\xi _{k}}$ from (3.2).

Thus applying Lemma 3.5 with $\xi = \hat{\xi}_{k}$ and L=4^2εk gives that, for k sufficiently large,

Since $\operatorname{ \mathbb{E}}[\omega (X_{0},X_{1})^{2}] < \infty$ by assumption, it follows that (3.11) holds for k sufficiently large. □

 □

4 Exponent relations

Let us first prove Theorem 1.6. In Section 4.3, we apply our main theorem to some random network models.

4.1 The speed upper bound

The next theorem verifies (1.13).

Theorem 4.1

If (G,ρ) is a reversible random network satisfying $\operatorname{ \mathbb{E}}[1/c_{ \rho}^{G}] < \infty$, then .

Proof

Recall that {X_n} is the random walk on G (cf. (1.8)) started from X₀=ρ. Let us denote . If d_∗⩽2, we can use the weight ω≡1 for which $\operatorname{dist}_{\omega}^{G} = d^{G}$, and (1.23) yields . Consider now d_∗>2 and fix δ∈(0,d^∗−2). Apply Theorem 2.5 to arrive at a reversible random weight $\omega : E(G) \to \mathbb{R}_{+}$ such that $\operatorname{ \mathbb{E}}[ \omega (X_{0},X_{1})^{2}] < \infty$ and almost surely eventually (with respect to R),

$$ \operatorname{dist}_{\omega}^{G}(\rho ,\bar{B}^{G}(\rho ,R)) \geqslant R^{(d_{*}- \delta )/2}. $$

(4.1)

Now, since $\bar{d}_{f} < \infty$, it follows that (1.21) holds, and we can apply Theorem 1.9 to (G,ρ,ω) yielding: Almost surely eventually (with respect to n),

$$ \operatorname{ \mathbb{E}}\left [\max _{0 \leqslant t \leqslant n} \operatorname{dist}_{\omega}^{G}(X_{0},X_{t})^{2} \mid (G,\rho ,\omega )\right ] \leqslant n^{1+\delta}. $$

Combining this with (4.1) yields almost surely eventually

$$ \operatorname{ \mathbb{E}}\left [\max _{0 \leqslant t \leqslant n} d^{G}(X_{0},X_{t})^{d_{*}- \delta} \mid (G,\rho ,\omega )\right ] \leqslant n^{1+\delta}. $$

Now since d_∗−δ>2, convexity of $y \mapsto y^{(d_{*}- \delta )/2}$ gives

$$ \operatorname{ \mathbb{E}}\left [\max _{0 \leqslant t \leqslant n} d^{G}(X_{0},X_{t})^{2} \mid (G,\rho ,\omega )\right ] \leqslant n^{2(1+\delta )/(d_{*}- \delta )}. $$

Since we can take δ>0 arbitrarily small, this yields , completing the proof. □

4.2 Effective resistance and the Green kernel

For the present subject, we assume only that (G,ρ) is a random rooted network (i.e., we will not employ reversibility). First, let us recall the standard relationship between effective resistances and commute times [C+96/97] gives the following.

Lemma 4.2

For any R⩾1, almost surely:

$$ \operatorname{ \mathbb{E}}[\sigma _{R} \mid (G,\rho ), X_{0} = \rho ] \leqslant \mathsf{R}_{ \mathrm{eff}}^{G}(\rho \leftrightarrow \bar{B}^{G}(\rho ,R))\, \operatorname{vol}^{G}( \rho ,R). $$

This immediately yields (1.18):

Theorem 4.3

It holds that $\bar{d}^{\mathcal {A}}_{w} \leqslant \bar{d}_{f} + \tilde{\zeta}_{0}$.

Let us now prove the upper and lower bounds in (1.19).

Theorem 4.4

It holds that

Proof

Using reversibility of the random walk conditioned on (G,ρ), we have almost surely

$$\begin{aligned} p^{G}_{2n}(\rho ,\rho ) \geqslant \sum _{x \in B^{G}(\rho ,R)} p_{n}^{G}( \rho ,x) p_{n}^{G}(x,\rho ) = c^{G}_{\rho} \sum _{x \in B^{G}(\rho ,R)} \frac{p_{n}^{G}(\rho ,x)^{2}}{c^{G}_{x}} . \end{aligned}$$

Thus applying Cauchy-Schwarz yields

$$\begin{aligned} \frac{p^{G}_{2n}(\rho ,\rho )}{c^{G}_{\rho}} \geqslant \frac{\left (\sum _{x \in B^{G}(\rho ,R)} p^{G}_{n}(\rho ,x)\right )^{2}}{\operatorname{vol}^{G}(\rho ,R)} \geqslant \frac{\left (\operatorname{ \mathbb{P}}[X_{n} \in B^{G}(\rho ,R) \mid (G,\rho )]\right )^{2}}{\operatorname{vol}^{G}(\rho ,R)}. \end{aligned}$$

(4.2)

Observe that

$$ \operatorname{ \mathbb{P}}[X_{n} \in B^{G}(\rho ,R) \mid (G,\rho )] \geqslant \operatorname{ \mathbb{P}}[ \sigma _{R} > n \mid (G,\rho )]. $$

(4.3)

By definition, for every δ>0, almost surely eventually (with respect to R), and $\operatorname{vol}^{G}(\rho ,R) \leqslant R^{\bar{d}_{f}+\delta}$. Combining these with (4.2) and (4.3) gives almost surely eventually (with respect to n),

As this holds for every δ>0, it yields the claimed inequality. □

We now move on to the lower bound in (1.19). Define the random variable

We need a preliminary application of the 2nd moment method.

Lemma 4.5

Suppose that $p^{G}_{2n}(\rho ,\rho ) \geqslant n^{\varepsilon -1}$ for some n⩾1 and ε>0. Then,

$$ \operatorname{ \mathbb{P}}\left [Z_{2n} \geqslant \frac{1}{2} n^{\varepsilon } ~\big|~(G, \rho ) \right ] \geqslant \frac{1}{12}. $$

Proof

For the proof that follows, we condition on (G,ρ) and recall that X₀=ρ. Define $q_{t} \mathrel{\mathop {:}}=p^{G}_{t}(\rho , \rho )$. Then,

$$\begin{aligned} \operatorname{ \mathbb{E}}[Z_{2n}] &= q_{1}+q_{2}+\cdots +q_{2n}, \\ \operatorname{ \mathbb{E}}[Z_{2n}^{2}] &= \sum _{t=1}^{2n} q_{t} + 2 \sum _{t=1}^{2n} \sum _{s=t+1}^{2n} \operatorname{ \mathbb{P}}[X_{t}=\rho , X_{s}=\rho ] \\ &= \operatorname{ \mathbb{E}}[Z_{2n}] + 2 \sum _{t=1}^{2n} \sum _{s=1}^{2n-t} q_{t} q_{s}, \end{aligned}$$

where in the final equality we have used the Markov property $\operatorname{ \mathbb{P}}[X_{s}=\rho \mid X_{t}=\rho ] = \operatorname{ \mathbb{P}}[X_{s-t}=\rho ]$.

Since the even return times are non-increasing (see, e.g., [LPW09, Prop. 10.18]), we have q_2j⩾q_2n⩾n^ε−1 for all j=1,2,…,n, hence

$$ \operatorname{ \mathbb{E}}[Z_{2n}] \geqslant n \cdot n^{\varepsilon -1} = n^{\varepsilon }. $$

(4.4)

In particular, $(\operatorname{ \mathbb{E}}[Z_{2n}])^{2} \geqslant \operatorname{ \mathbb{E}}[Z_{2n}]$, and therefore

$$ 3 \left (\operatorname{ \mathbb{E}}[Z_{2n}]\right )^{2} \geqslant \operatorname{ \mathbb{E}}[Z_{2n}] + 2 \left (q_{1}+q_{2}+ \cdots +q_{2n}\right )^{2} \geqslant \operatorname{ \mathbb{E}}[Z_{2n}^{2}]. $$

The Payley-Zygmund inequality now asserts that

$$ \operatorname{ \mathbb{P}}\left (Z_{2n} \geqslant \frac{1}{2} \operatorname{ \mathbb{E}}[Z_{2n}]\right ) \geqslant \frac{1}{4} \frac{(\operatorname{ \mathbb{E}}[Z_{2n}])^{2}}{\operatorname{ \mathbb{E}}[Z_{2n}^{2}]} \geqslant \frac{1}{12}. $$

Combined with (4.4), this yields the desired bound. □

Corollary 4.6

For any ε>0, it holds that if $Z_{2n} \leqslant \frac{1}{2} n^{\varepsilon }$ almost surely eventually, then $p_{2n}^{G}( \rho ,\rho ) \leqslant n^{\varepsilon -1}$ almost surely eventually.

Proof

Suppose $\mathcal {E}$ is the event that $p_{2n}^{G}(\rho ,\rho ) > n^{ \varepsilon -1}$ infinitely often. Then Lemma 4.5 gives

$$ \frac{1}{12} \leqslant \liminf _{n \to \infty} \operatorname{ \mathbb{P}}[Z_{2n} \geqslant \tfrac{1}{2} n^{\varepsilon } \mid \mathcal {E}] \leqslant \operatorname{ \mathbb{P}}[Z_{2n} \geqslant \tfrac{1}{2} n^{\varepsilon } \textrm{ infinitely often} \mid \mathcal {E}]\,, $$

where the latter inequality is a consequence of Fatou’s Lemma. Thus if $Z_{2n} \leqslant \frac{1}{2} n^{\varepsilon }$ almost surely eventually, we must have $\operatorname{ \mathbb{P}}(\mathcal {E})=0$. □

Definition 4.7

Green kernels

For S⊆V(G), let τ_S:=min{n⩾0:X_n∈S}, and define the Green kernel killed off S by

It is well-known (see [LP16, Ch. 2]) that for any x∈V(G) and S⊆V(G):

$$ c^{G}_{x}\,\mathsf{R}_{\mathrm{eff}}^{G}(x \leftrightarrow V(G) \setminus S) =\mathsf{g}_{S}^{G}(x,x)\,. $$

(4.5)

Theorem 4.8

It holds that

Proof

Fix δ>0. Define the random variable

where . Then we have:

where the latter inequality holds almost surely for n sufficiently large, by the definition of $\tilde{\zeta}_{0}$.

Now Markov’s inequality and the Borel-Cantelli Lemma (recall Lemma 1.8) give that almost surely eventually

For convenience, let us note the consequence: Almost surely eventually,

By definition of , it holds that almost surely eventually and therefore almost surely eventually,

From Corollary 4.6, we conclude that almost surely eventually

Since this holds for every δ>0, we conclude that , as desired. □

4.2.1 Comparison to the strongly recurrent regime

Finally, let us prove that the assumptions (1.11) and (1.12) imply $\tilde{\zeta}=\tilde{\zeta}_{0}$ in the case ζ>0. The first part of the argument follows [BCK05, §3.2].

Theorem 4.9

If (1.11) and (1.12) hold for some ζ>0, then $\tilde{\zeta}=\tilde{\zeta}_{0}=\zeta$.

Proof

First note that if d^G(ρ,x)=R+1, then

$$ \mathsf{R}_{\mathrm{eff}}^{G}(\rho \leftrightarrow \bar{B}^{G}(\rho ,R)) \leqslant \mathsf{R}_{\mathrm{eff}}^{G}(\rho \leftrightarrow x) \stackrel{\text{(1.11)}}{\leqslant } (R+1)^{\tilde{\zeta}+\delta}, $$

(4.6)

hence (1.11) yields

$$ \tilde{\zeta}_{0} \leqslant \zeta . $$

(4.7)

Thus we are left to prove that $\tilde{\zeta} \geqslant \zeta$.

For y∈V(G) and R⩾1, define

$$ Q^{R}_{\rho}(y) \mathrel{\mathop {:}}=\operatorname{ \mathbb{P}}\left [\tau _{\{\rho \}} < \tau _{\bar{B}^{G}(\rho ,R)} \mid X_{0}=y\right ] = \frac{c^{G}_{\rho}}{c^{G}_{y}} \frac{\mathsf{g}_{B^{G}(\rho ,R)}(\rho ,y)}{\mathsf{g}_{B^{G}(\rho ,R)}(\rho ,\rho )}, $$

(4.8)

where the latter equality arises because both $Q^{R}_{\rho}$ and the function $y \mapsto \mathsf{g}_{B^{G}(\rho ,R)}(\rho ,y)/ c^{G}_{y}$ are harmonic on B^G(ρ,R)∖{ρ}. Moreover, $Q^{R}_{\rho}$ and the right-hand side vanish on $\bar{B}^{G}(\rho ,R)$ and are equal to 1 at ρ.

Hence, the Dirichlet principle (2.3) yields

$$ \mathscr{E}^{G}(Q_{\rho}^{R}) = \frac{1}{\mathsf{R}_{\mathrm{eff}}^{G}(\rho \leftrightarrow \bar{B}^{G}(\rho ,R))} \,. $$

(4.9)

In particular, we have

$$ \left |1-Q^{R}_{\rho}(y)\right |^{2} = \left |Q^{R}_{\rho}(\rho )-Q^{R}_{ \rho}(y)\right |^{2} \leqslant \mathsf{R}_{\mathrm{eff}}^{G}(\rho \leftrightarrow y)\,\mathscr{E}^{G}(Q^{R}_{\rho}) = \frac{\mathsf{R}_{\mathrm{eff}}^{G}(\rho \leftrightarrow y)}{\mathsf{R}_{\mathrm{eff}}^{G}(\rho \leftrightarrow \bar{B}^{G}(\rho ,R))}, $$

(4.10)

where the inequality is another application of the Dirichlet principle (2.3).

Assume now that ζ>0, and fix δ∈(0,ζ). Denote R′:=R^{(ζ+2δ)/(ζ−δ)} and $Q_{ \rho} \mathrel{\mathop {:}}=Q_{\rho}^{R'}$. Using (1.11) and (1.12), we have almost surely eventually

$$\begin{aligned} \max \{ \mathsf{R}_{\mathrm{eff}}^{G}(\rho \leftrightarrow x) : x \in B^{G}(\rho ,R) \} &\leqslant R^{\zeta +\delta}, \end{aligned}$$

(4.11)

$$\begin{aligned} \mathsf{R}_{\mathrm{eff}}^{G}\left (\rho \leftrightarrow \bar{B}^{G}( \rho ,R')\right ) &\geqslant R^{\zeta +2\delta}. \end{aligned}$$

(4.12)

So by (4.10), almost surely eventually

$$ \min \left \{ Q_{\rho}(y) : y \in B^{G}(\rho ,R) \right \} \geqslant 1-R^{- \delta /2} > \frac{1}{2}. $$

(4.13)

Remark 4.10

Here one notes that this conclusion cannot be reached for ζ=0 because we cannot choose R′ large enough with respect to R so as to create a gap between the respective upper and lower bounds in (4.11) and (4.12). Indeed, it is this sort of gap that Telcs defines as “strongly recurrent” (see [Tel01, Def. 2.1]), although his quantitative notion (which requires a uniform multiplicative gap with R′=O(R)) is too strong for us, as it entails $\tilde{\zeta} > 0$.

Let us assume that R is such that (4.13) holds. Define the function

$$ \tilde{Q}_{\rho}(x) \mathrel{\mathop {:}}=2 \min \{Q_{\rho}(x), \tfrac{1}{2}\}. $$

Then $\tilde{Q}_{\rho}$ vanishes outside B^G(ρ,R′) (as Q_ρ does) and is identically 1 on B^G(ρ,R), and moreover

$$ \mathscr{E}^{G}(\tilde{Q}_{\rho}) \leqslant 4\,\mathscr{E}^{G}(Q_{ \rho}). $$

So the Dirichlet principle gives

$$ \begin{aligned}\mathsf{R}_{\mathrm{eff}}^{G}(B^{G}(\rho ,R) \leftrightarrow \bar{B}^{G}( \rho ,R')) &\geqslant \frac{1}{4 \mathscr{E}^{G}(Q_{\rho})} \\ &= \frac{\mathsf{R}_{\mathrm{eff}}^{G}(\rho \leftrightarrow \bar{B}^{G}(\rho ,R'))}{4} \geqslant \frac{\mathsf{R}_{\mathrm{eff}}^{G}(\rho \leftrightarrow \bar{B}^{G}(\rho ,R))}{4} \geqslant R^{\zeta -\delta}, \end{aligned}$$

where the last inequality follows from (1.12) and holds almost surely eventually (with respect to R). Since this holds for any δ>0, we conclude that $\tilde{\zeta} \geqslant \zeta$, as required.  □

4.3 Resistance exponent for planar maps coupled to a mated-CRT

We first establish that $\tilde{\zeta}=0$ for the γ-mated-CRT with γ∈(0,2). It is known that $\tilde{\zeta}_{0} = 0$ [GM21, Prop. 3.1]. While the following argument is somewhat technical and, to our knowledge, does not appear elsewhere, we stress that it is a relatively straightforward consequence of [GMS19, DG20].

Fix some γ∈(0,2) and for ε>0, let $\mathcal {G}^{\varepsilon }$ be the γ-mated-CRT with increment ε. See, for instance, the description in [GMS19]. For our purposes, we may consider this as a random planar multigraph. When needed, we can replace multiple edges by appropriate conductances.

From [DMS21, Thm. 1.9], one can identify $V(\mathcal {G}^{ \varepsilon })=\varepsilon \mathbb{Z}$ and there is a space-filling SLE curve $\eta : \mathbb{R}\to \mathbb{C}$ parameterized by the LQG mass of the γ-quantum cone, with η(0)=0 and such that $\{a,b \} \in E(\mathcal {G}^{\varepsilon })$ are connected by an edge if and only if the corresponding cells η([a−ε,a]) and η([b−ε,b]) share a non-trivial connected boundary arc. Thus we can envision η as an embedding of $V(\mathcal {G}^{\varepsilon })$ into the complex plane, where a vertex $v \in V(\mathcal {G}^{\varepsilon })$ is sent to η(v). Let us denote the Euclidean ball $B^{ \mathbb{C}}(z,r) \mathrel{\mathop {:}}=\{ y \in \mathbb{C}: |y-z| \leqslant r \}$.

The underlying idea is simple: We will arrange that, with high probability, the image of a graph annulus under η contains a Euclidean annulus $\mathcal {A}$ of large width. Then we pull back a Lipschitz test functional from $\mathcal {A}$ to $\mathcal {G}^{\varepsilon }$, and use the Dirichlet principle (2.3) to lower bound the effective resistance across the annulus.

By [DG20, Prop. 4.6], there is a number d_γ>2 such that the following holds: For every θ∈(0,1) and δ>0, there is an α=α(δ,γ,θ)>0 such that as ε→0,

$$\begin{aligned} \operatorname{ \mathbb{P}}\left [\eta \left (B^{\mathcal {G}^{\varepsilon }}(0, \varepsilon ^{-1/(d_{\gamma}+\delta )})\right ) \subseteq B^{ \mathbb{C}}(0,\theta )\right ] &\geqslant 1 - O(\varepsilon ^{\alpha}) \\ \operatorname{ \mathbb{P}}\left [\eta ^{-1}\!\left (B^{\mathbb{C}}(0,\theta ) \cap \eta (\varepsilon \mathbb{Z})\right ) \subseteq B^{\mathcal {G}^{ \varepsilon }}(0, \varepsilon ^{-1/(d_{\gamma}-\delta )})\right ] & \geqslant 1 - O(\varepsilon ^{\alpha}). \end{aligned}$$

In particular, taking θ=1/4 and θ=3/4, respectively, yields, for some α=α(δ,γ)>0:

$$\begin{aligned} \operatorname{ \mathbb{P}}\left [ \eta \left (B^{\mathcal {G}^{\varepsilon }}(0, \varepsilon ^{-1/(d_{\gamma}+\delta )})\right )\right . &\subseteq B^{ \mathbb{C}}(0,1/4) \cap \eta (\varepsilon \mathbb{Z}) \\ &\left .\subseteq B^{\mathbb{C}}(0,3/4) \cap \eta (\varepsilon \mathbb{Z})\right. \\ &\left.\subseteq \eta \left (B^{\mathcal {G}^{\varepsilon }}(0, \varepsilon ^{-1/(d_{\gamma}-\delta )})\right )\right ] \geqslant 1 - O( \varepsilon ^{\alpha})\,. \end{aligned}$$

(4.14)

For a subset $D \subseteq \mathbb{C}$, denote

$$\begin{aligned} \mathcal {V}\mathcal {G}^{\varepsilon }(D) &\mathrel{\mathop {:}}=\{ x \in \varepsilon \mathbb{Z}: \eta ([x-\varepsilon ,x]) \cap D \neq \emptyset \}, \end{aligned}$$

and let $\mathcal {G}^{\varepsilon }(D)$ be the subgraph of $\mathcal {G}^{ \varepsilon }$ induced on $\mathcal {V}\mathcal {G}^{\varepsilon }(D)$. For a function $f : \overline{D} \to \mathbb{R}$, define $f^{ \varepsilon } : \mathcal {V}\mathcal {G}^{\varepsilon }(D) \to \mathbb{R}$ by

$$ f^{\varepsilon }(z) \mathrel{\mathop {:}}= \textstyle\begin{cases} f(\eta (z)) & z \in \mathcal {V}\mathcal {G}^{\varepsilon }(D) \setminus \mathcal {V}\mathcal {G}^{\varepsilon }(\partial D) \\ \sup _{x \in \eta ([z-\varepsilon ,z]) \cap \partial D} f(z) & z\in \mathcal {V}\mathcal {G}^{\varepsilon }(\partial D). \end{cases} $$

Take now $D \mathrel{\mathop {:}}=B^{\mathbb{C}}(0,1)$ and define $f : D\to \mathbb{R}$ by $f(z) \mathrel{\mathop {:}}=\min (1, 4 \left (|z|-3/8 \right )_{+})$, which is a 4-Lipschitz function satisfying

$$ f|_{B^{\mathbb{C}}(0,3/8)} \equiv 0, \qquad f|_{B^{\mathbb{C}}(0,1) \setminus B^{\mathbb{C}}(0,5/8)} \equiv 1. $$

(4.15)

Let {f_n} be a sequence of continuously differentiable, uniformly Lipschitz functions such that f_n→f uniformly on D. Then we may apply [GMS19, Lem. 3.3] to each f_n to obtain, for every n⩾1,

$$ \operatorname{ \mathbb{P}}\left (\mathscr{E}^{\mathcal {G}^{\varepsilon }(D)}(f_{n}^{ \varepsilon }) \leqslant \varepsilon ^{\alpha} + A \int _{D} |\nabla f_{n}(z)|^{2} \,dz\right ) \geqslant 1- O(\varepsilon ^{\alpha}), $$

where A=A(γ),α=α(γ)>0. We conclude that with probability at least 1−O(ε^α), the Dirichlet energy of $f_{n}^{\varepsilon }$ is uniformly (in n) bounded. Taking $f^{ \varepsilon } = \lim _{n \to \infty} f^{\varepsilon }_{n}$, we obtain the following in conjunction with (4.14) and (4.15).

Lemma 4.11

For every γ∈(0,2) and δ>0, there are numbers α,A>0 such that for every ε>0, with probability at least 1−O(ε^α), there is a function $f^{ \varepsilon } : V(\mathcal {G}^{\varepsilon }) \to \mathbb{R}$ such that

• 1. f^ε vanishes on $B^{\mathcal {G}^{\varepsilon }}(0, \varepsilon ^{-1/(d_{\gamma}+\delta )})$,

• 2. f^ε is identically 1 on $\partial _{\mathcal {G}^{ \varepsilon }} B^{\mathcal {G}^{\varepsilon }}(0, \varepsilon ^{-1/(d_{ \gamma}-\delta )})$.

• 3. $\mathscr{E}^{\mathcal {G}^{\varepsilon }}(f^{\varepsilon }) \leqslant A$.

In particular, the Dirichlet principle (2.3) gives, with probability at least 1−O(ε^α),

$$ \mathsf{R}_{\mathrm{eff}}^{\mathcal {G}^{\varepsilon }}\left (\partial _{ \mathcal {G}^{\varepsilon }} B^{\mathcal {G}^{\varepsilon }}(0, \varepsilon ^{-1/(d_{\gamma}+\delta )})) \leftrightarrow \partial _{ \mathcal {G}^{\varepsilon }} B^{\mathcal {G}^{\varepsilon }}(0, \varepsilon ^{-1/(d_{\gamma}-\delta )})\right ) \geqslant 1/A. $$

Note that the law of $\mathcal {G}^{\varepsilon }$ is independent of ε>0, and therefore denoting its law by $\mathcal {G}$ and taking R:=1/ε, we arrive at the following.

Corollary 4.12

Let $\mathcal {G}$ denote the γ-mated-CRT for γ∈(0,2). Then for every δ>0, there are numbers α,κ>0 such that with probability at least 1−O(R^−α)

$$ \mathsf{R}_{\mathrm{eff}}^{\mathcal {G}}\left (\partial _{\mathcal {G}} B^{ \mathcal {G}}(0, R) \leftrightarrow \partial _{\mathcal {G}} B^{ \mathcal {G}}(0, R^{1+\delta})\right ) \geqslant \kappa . $$

(4.16)

In particular, it holds that for every δ>0, almost surely eventually

$$ \mathsf{R}_{\mathrm{eff}}^{\mathcal {G}}\left (\partial _{\mathcal {G}} B^{ \mathcal {G}}(0, R) \leftrightarrow \partial _{\mathcal {G}} B^{ \mathcal {G}}(0, R^{1+\delta})\right ) \geqslant \kappa . $$

Since this holds for every δ>0, and $(\mathcal {G},0)$ is a unimodular random network, we have $\tilde{\zeta} = 0$.

Proof

(4.16) follows immediately from Lemma 4.11. The other conclusion is a standard consequence: The Borel-Cantelli Lemma implies that almost surely, for all but finitely many $k \in \mathbb{N}$, we have

$$ \mathsf{R}_{\mathrm{eff}}^{\mathcal {G}}\left (\partial _{\mathcal {G}} B^{ \mathcal {G}}(0, 2^{k}) \leftrightarrow \partial _{\mathcal {G}} B^{ \mathcal {G}}(0, 2^{(1+\delta )k})\right ) \geqslant \kappa , $$

so by the series law for effective resistances, it holds that almost surely eventually

$$ \begin{aligned}&\mathsf{R}_{\mathrm{eff}}^{\mathcal {G}}\left (\partial _{\mathcal {G}} B^{ \mathcal {G}}(0, R) \leftrightarrow \partial _{\mathcal {G}} B^{ \mathcal {G}}(0, 2 R^{1+\delta})\right ) \\ &\quad \geqslant \mathsf{R}_{ \mathrm{eff}}^{\mathcal {G}}\left (\partial _{\mathcal {G}} B^{\mathcal {G}}(0, 2^{\lfloor \log _{2} R\rfloor}) \leftrightarrow \partial _{\mathcal {G}} B^{\mathcal {G}}(0, 2^{\lceil \log _{2} (R^{1+\delta})\rceil})\right ) \geqslant \kappa , \end{aligned}$$

and thus for any δ′>δ, almost surely eventually $\mathsf{R}_{\mathrm{eff}}^{\mathcal {G}} (\partial _{\mathcal {G}} B^{ \mathcal {G}}(0, R) \leftrightarrow \partial _{\mathcal {G}} B^{ \mathcal {G}}(0, R^{1+\delta '}) ) \geqslant \kappa$. □

Note that since $\tilde{\zeta}=\tilde{\zeta}_{0}=0$ and d_f exists [DG20], it follows from Theorem 1.3 that d_w=d_f and d_s=2. Both equalities were known previously: d_s⩽2 from [Lee21], d_w⩽d_f and d_s⩾2 from [GM21], and d_w⩾d_f from [GH20]. Let us remark that the preceding argument requires somewhat less detailed information about $\mathcal {G}$ than that of [GH20]. In particular, bounding $\tilde{\zeta}$ only requires control of one scale at a time.

4.3.1 Other planar maps

We consider now the case of random planar maps that can be appropriately coupled to a γ-mated CRT for some γ∈(0,2); we refer to [GHS20] for a discussion of such examples, including the UIPT, and random planar maps whose law is biased by the number of different spanning trees ($\gamma =\sqrt{2}$), bipolar orientations $(\gamma =\sqrt{4/3})$, or Schynder woods (γ=1).

Our goal is to prove that $\tilde{\zeta}=0$ for each of these random planar maps (M,ρ). We employ the same approach as in the preceding section, arguing that an annulus in (M,ρ) can be mapped into $\mathcal {G}$ so that its image contains an annulus of large width, and that the Dirichlet energy of functionals in $\mathcal {G}$ is controlled when pulling them back to M.

Fix γ∈(0,2) and let $\mathcal {G}$ be the γ-mated-CRT with increment 1. Let $\mathcal {G}_{n}$ be the subgraph of $\mathcal {G}$ induced on the vertices $[-n,n] \cap \mathbb{Z}$. Parts (1)–(3) in the following theorem are the conjunction of Lemma 1.11 and Theorem 1.9 in [GHS20]. Part (4) is [GM21, Lem. 4.3].

Theorem 4.13

For each model considered in [GHS20], the following holds. There is a coupling of (M,ρ) and $(\mathcal {G},0)$, and a family of random rooted graphs {(M_n,ρ_n):n⩾1} and numbers α,K,q>0 such that for every n⩾1, with probability at least 1−O(n^−α):

• 1. $B^{\mathcal {G}}(0,n^{1/K}) \subseteq V(\mathcal {G}_{n})$,

• 2. The induced, rooted subnetworks B^M(ρ,n^1/K) and $B^{M_{n}}( \rho _{n},n^{1/K})$ are isomorphic.

• 3. There is a mapping $\phi _{n} : V(M_{n}) \to V(\mathcal {G}_{n})$ with ϕ_n(ρ_n)=0, and for all 3⩽r⩽R,

  $$\begin{aligned} \phi _{n}\left (B^{M_{n}}\!\left (\rho _{n}, (K \log n)^{-q} (r-2) \right )\right ) &\subseteq B^{\mathcal {G}_{n}}(0,r) \\ \phi _{n}\left (V(M_{n}) \setminus B^{M_{n}}\!\left (\rho _{n}, (K \log n)^{q} R - 1\right )\right ) &\subseteq V(\mathcal {G}_{n}) \setminus B^{\mathcal {G}_{n}}(0,R). \end{aligned}$$

• 4. For every $f : V(\mathcal {G}_{n}) \to \mathbb{R}$, it holds that

  $$ \mathscr{E}^{M_{n}}(f \circ \phi _{n}) \leqslant K (\log n)^{q} \mathscr{E}^{\mathcal {G}_{n}}(f). $$

Corollary 4.14

For any model considered in [GHS20], it holds that $\tilde{\zeta}=0$.

We prove this momentarily, but first note the following consequence. Since d_f>2 for each of these models [DG20, Prop. 4.7], and $\tilde{\zeta}_{0}=0$ by [GM21, Prop. 4.4], Theorem 1.3 yields:

Theorem 4.15

For any model considered in [GHS20], it holds that d_w=d_f>2 and d_s=2.

Remark 4.16

We remark that the lower bound d_s⩾2 is established in [GM21], and the upper bound d_s⩽2 follows for any unimodular random planar graph where the law of the degree of the root has tails that decay sufficiently fast [Lee21] (which is true for each of these models; see [GM21, §1.3]). The consequence d_w=d_f is proved in [GH20] for every model except the uniform infinite Schynder-wood decorated triangulation. This is for a technical reason underlying the identification of V(M_n) with a subset of V(M) used in the proof of [GHS20, Lem. 1.11] (see [GHS20, Rem. 1.3] and [GH20, Rem. 2.11]).

Proof of Corollary 4.14

Fix δ>0 and R⩾2. Denote

$$\begin{aligned} \tilde{r} &\mathrel{\mathop {:}}=(K \log n)^{-q} (R-2), \\ \tilde{R} &\mathrel{\mathop {:}}=(K \log n)^{q} R^{1+\delta}, \\ n &\mathrel{\mathop {:}}=\lceil \tilde{R}^{K}\rceil , \end{aligned}$$

and let $\mathcal {E}_{n}$ be an event on which Theorem 4.13(1)–(4) and (4.16) hold. Note that we can take $\operatorname{ \mathbb{P}}( \mathcal {E}_{n}) \geqslant 1-O(R^{-\alpha '})$ for some α′=α′(δ,K)>0.

Assume now that $\mathcal {E}_{n}$ holds. Then (4.16) and the Dirichlet principle (2.3) give a test function $f : V( \mathcal {G}) \to \mathbb{R}$ such that

$$ f(B^{\mathcal {G}}(0,R)) = 0, \qquad f(\partial _{\mathcal {G}} B^{ \mathcal {G}}(0,R^{1+\delta}))=1, \qquad \mathscr{E}^{\mathcal {G}}(f) \leqslant 1/\kappa . $$

Theorem 4.13(1) asserts that the restriction of f to $B^{ \mathcal {G}}(0,R^{1+\delta})$ gives a function $\tilde{f} : V( \mathcal {G}_{n}) \to \mathbb{R}$ on which

$$ \tilde{f}(B^{\mathcal {G}_{n}}(0,R))=0, \qquad \tilde{f}(\partial _{ \mathcal {G}} B^{\mathcal {G}_{n}}(0,R^{1+\delta}))=1, \qquad \mathscr{E}^{ \mathcal {G}_{n}}(\tilde{f}) \leqslant 1/\kappa . $$

Without increasing the energy of $\tilde{f}$, we may assume that $\tilde{f}(V(\mathcal {G}_{n}) \setminus B^{\mathcal {G}_{n}}(0,R^{1+ \delta}))=1$ as well.

By our choice of $\tilde{r}$ and $\tilde{R}$, Theorem 4.13(3) implies that

$$ \begin{aligned}\tilde{f} \circ \phi _{n}(B^{M_{n}}(\rho ,\tilde{r})) &= 0, \qquad \tilde{f} \circ \phi _{n}(\partial _{M_{n}} B^{M_{n}}(\rho ,\tilde{R}))=1, \\ \mathscr{E}^{M_{n}}(\tilde{f} \circ \phi _{n}) &\leqslant K' ( \log R)/\kappa , \end{aligned}$$

where the last inequality is from Theorem 4.13(4), and K′=K′(K,q,δ). Now the Dirichlet principle (2.3) yields

$$ \mathsf{R}_{\mathrm{eff}}^{M_{n}}\left (\partial _{M_{n}} B^{M_{n}}( \rho _{n},\tilde{r}) \leftrightarrow \partial _{M_{n}} B^{M_{n}}( \rho _{n},\tilde{R})\right ) \geqslant \frac{1}{K' (\log R)/\kappa}, $$

and from the graph isomorphism Theorem 4.13(2) and the fact that $n^{1/K} \geqslant \tilde{R}$, we conclude that

$$ \mathsf{R}_{\mathrm{eff}}^{M}\left (\partial _{M} B^{M}(\rho , \tilde{r}) \leftrightarrow \partial _{M} B^{M}(\rho ,\tilde{R}) \right ) \geqslant \frac{1}{K' (\log R)/\kappa}. $$

Since this conclusion holds with probability at least 1−O(R^−α′), we conclude (using Borel-Cantelli as in the proof of Corollary 4.12) that for every δ>0, almost surely eventually

$$ \mathsf{R}_{\mathrm{eff}}^{M}\left (\partial _{M} B^{M}(\rho ,R) \leftrightarrow \partial _{M} B^{M}(\rho ,R^{1+\delta})\right ) \geqslant R^{-\delta}. $$

This yields $\tilde{\zeta}=0$, completing the proof. □