1 Introduction

Kerr frequency combs generated in an externally driven Kerr nonlinear microresonator are very promising devices in optical communications or frequency metrology, enabling, for instance, high-speed data transmission of up to 1.44 Tbit/s, cf. [43]. They are optical signals consisting of a multitude of equally spaced excited modes in frequency space and are modeled by stable highly localized stationary periodic solutions of the Lugiato–Lefever equation (LLE)

$$\begin{aligned} \textrm{i}u_t = - d u_{xx} + (\zeta -\textrm{i}) u - |u|^2 u + \textrm{i}f, \qquad (x,t) \in \mathbb {R}^2. \end{aligned}$$
(1.1)

Here, \(u = u(x,t) \in \mathbb {C}\) is the field amplitude in the resonator, \(d \not =0\) is the dispersion, \(\zeta \in \mathbb {R}\) is the offset between the external forcing frequency and the resonant frequency in the resonator called detuning, and \(f\in \mathbb {R}\) describes the pump power inside the resonator of the external forcing. A physical derivation of (1.1) can be found in [34]. From a mathematical point of view, LLE is a damped and driven nonlinear Schrödinger equation (NLS). Motivated by the promising applications of Kerr frequency combs, the existence of stationary solutions of LLE has received considerable attention. A plethora of stationary solutions have been found in numerical simulations [4, 17, 38,39,40,41] or have been constructed analytically [5, 16, 21, 33, 36, 37]. The naturally associated question of their spectral as well as their nonlinear stability with respect to different types of perturbations has gained interest recently [3, 11, 12, 14, 22,23,24,25,26, 42, 46, 47]. Whereas nonlinear stability can be obtained under general spectral stability assumptions, spectral stability analyses themselves rely on the specific structure of the solutions and typically employ similar methods as were used to construct them. So far, spectral stability has been obtained for periodic small amplitude solutions of (1.1) arising through a Turing bifurcation of a homogeneous rest state [12]. The only spectral stability result of far-from-equilibrium solutions of (1.1) that the author is aware of is that in [23], where solutions to (1.1) are constructed by bifurcation from the dnoidal wave solutions solving NLS equation on the torus. Stability results for explicitly available solitary wave solutions in the forced NLS equation without damping have been obtained in [2] and also recently in [14]. Here, we present the first spectral stability result of far-from-equilibrium soliton solutions of the damped and driven NLS (1.1). The solutions under consideration are highly nonlinear and arise by bifurcation from bright solitons in the NLS equation in the anomalous regime \(d>0\). They satisfy the approximation formula

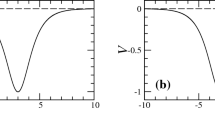
$$\begin{aligned} u(x) \approx u_\infty + \sqrt{2\zeta } {{\,\textrm{sech}\,}}\left( \sqrt{\frac{\zeta }{d}} x\right) \textrm{e}^{\textrm{i}\theta _0}, \qquad x \in \mathbb {R}, \end{aligned}$$
(1.2)

where \(u_\infty \in \mathbb {C}\) is a constant background due to the forcing in (1.1) and the angle \(\theta _0\) is found by solving the equation \(\cos \theta _0 = 2 \sqrt{2\zeta }/(\pi f)\). Although they are non-periodic solutions of (1.1), their exponential localization makes them a valid approximation of a frequency comb, cf. Fig. 1. We emphasize that the approximation (1.2) is frequently used in the physics literature to approximate Kerr frequency combs [8, 27, 48], which facilitates (formal) computations.

Contributions of this paper are threefold. In Theorem 1, we prove the existence of solitary wave solutions of (1.1) that verify the approximation (1.2). Therefore, we consider the LLE with dispersion rescaled to \(d=1\) as a perturbation of the focusing NLS in the following sense:

$$\begin{aligned} \textrm{i}u_t = - u_{xx} + \zeta u - |u|^2 u + \varepsilon \textrm{i}\Psi (u), \qquad (x,t) \in \mathbb {R}^2, \end{aligned}$$
(1.3)

where

$$\begin{aligned} \Psi (u) = -u + f, \end{aligned}$$

and \(\varepsilon \) is the bifurcation parameter. We show that solitary wave solutions \(u = u(\varepsilon )\) bifurcate at \(\varepsilon = 0\) from the rotated NLS soliton

$$\begin{aligned} \phi _{\theta _0}(x):= \sqrt{2 \zeta } {{\,\textrm{sech}\,}}(\sqrt{\zeta }x) \textrm{e}^{\textrm{i}\theta _0}. \end{aligned}$$

In Theorem 2, we prove spectral stability of the solitary waves satisfying \(\sin \theta _0,\varepsilon >0\) and spectral instability for all other sign configurations of \(\varepsilon ,\sin \theta _0\). This result relies on a detailed analysis of the spectral problem, where the crucial point is to understand the behavior of small eigenvalues for \(\varepsilon \) small in the linearized problem.

Finally, in Theorem 3 we prove nonlinear asymptotic orbital stability of spectrally stable solitary waves. For the linear estimates, we establish high-frequency resolvent estimates for families of operators in Hilbert spaces, see Theorem 4, which we then use to prove linear stability. Indeed, the resolvent estimates are needed to overcome the problem that a spectral mapping theorem for the non-sectorial operator arising in the linearized equation is a-priori not available. Nonlinear stability then follows as a corollary of the linear stability result.

Remark 1

Existence of solitary waves bifurcating from the NLS soliton has already been proven in [18] using the Crandall–Rabinowitz theorem of bifurcation from a simple eigenvalue. Here, we use a different approach based on a Lyapunov–Schmidt reduction in parameter-dependent spaces. This is advantageous because it directly yields an expansion of the solution needed in the spectral stability analysis. Further, we believe that our approach is flexible enough for possible extensions to bifurcation problems with higher dimensional kernels.

Remark 2

There is a long list of literature on persistence and stability of solitary solutions for other variants of the perturbed NLS, cf.  [1, 6, 31, 44] and the references therein.

Fig. 1
figure 1

Approximation of a periodic solution on \(\mathbb {R}/\mathbb {Z}\) by a solitary wave on \(\mathbb {R}\)

Full size image

1.1 Main results

Solitary wave solutions of the perturbed NLS (1.3) are solutions of the stationary equation

$$\begin{aligned} -u'' + \zeta u - |u|^2 u + \textrm{i}\varepsilon (-u + f) = 0, \quad x \in \mathbb {R}, \end{aligned}$$
(1.4)

which decay to a limit state \(u_\infty \in \mathbb {C}\) as \(|x| \rightarrow \infty \).

The following theorem provides the first result of the paper on the existence of solitary waves for a suitable parameter region.

Theorem 1

Let \(\zeta , f>0\) be fixed and suppose that \(\theta _0 \in \mathbb {R}\) is a simple zero of the function

$$\begin{aligned} \theta \mapsto \pi f \cos \theta - 2\sqrt{2 \zeta }. \end{aligned}$$

Then, there exist \(\varepsilon ^*>0\) and a branch \((-\varepsilon ^*,\varepsilon ^*) \ni \varepsilon \mapsto u(\varepsilon ) \in \mathbb {C}+ H^2(\mathbb {R})\) of solutions to the perturbed problem (1.4) bifurcating from the rotated soliton

$$\begin{aligned} \phi _{\theta _0}(x) = \sqrt{2\zeta } {{\,\textrm{sech}\,}}\big ( \sqrt{\zeta } x \big ) \textrm{e}^{\textrm{i}\theta _0}. \end{aligned}$$

More precisely, the branch is of the form

$$\begin{aligned} u (\varepsilon ) = \phi _{\theta (\varepsilon )} + u_\infty (\varepsilon ) + \varphi (\varepsilon ),\quad u (0) = \phi _{\theta _0}, \end{aligned}$$

where

  • the map \((-\varepsilon ^*,\varepsilon ^*) \ni \varepsilon \mapsto \theta (\varepsilon ) \in \mathbb {R}\) is real analytic and describes the rotational angle of the soliton,

  • the map \((-\varepsilon ^*,\varepsilon ^*) \ni \varepsilon \mapsto u_\infty (\varepsilon ) \in \mathbb {C}\) is real analytic and consists of the constant background of the solution at \(\pm \infty \),

  • the map \((-\varepsilon ^*,\varepsilon ^*) \ni \varepsilon \mapsto \varphi (\varepsilon )\in H^2(\mathbb {R})\) is real analytic and describes a small correction term of order \({\mathcal {O}}(|\varepsilon |)\).

Remark 3

In Theorem 1, a necessary and sufficient condition on the parameters \(\zeta ,f\) to find simple zeros is \(\pi ^2 f^2 > 8 \zeta \), which yields an existence region in the \(\zeta \)-f-plane, already obtained analytically or numerically in [3, 16, 18, 48]. Furthermore, it should be noted that solutions for negative forcing parameters \(f<0\) are obtained through the transformation \(u \mapsto - u\).

Theorems 2 and 3 provide the two main results on the spectral and nonlinear stability of solitary waves of Theorem 1 against localized perturbations in \(H^1\).

Let \(u = u(\varepsilon ) \in \mathbb {C}+ H^2(\mathbb {R})\) be a solution of the stationary LLE as in Theorem 1 for sufficiently small \(\varepsilon \not =0\). Expanding the solution as \(\psi (x,t) = u(x) + v(x,t)\) results in the perturbation equation

$$\begin{aligned} \textrm{i}v_t = - v_{xx} + \zeta v - 2 |u|^2 v - u^2 {\bar{v}} - \textrm{i}\varepsilon v - 2 |v|^2 u - v^2 {\bar{u}} - |v|^2 v. \end{aligned}$$

The evolution of the perturbation v is coupled with the evolution of the complex conjugate \({{\bar{v}}}\) so that we obtain the system:

$$\begin{aligned} \left\{ \begin{array}{rl} \textrm{i}v_t &{}= - v_{xx} + \zeta v - 2 |u|^2 v - u^2 {\bar{v}} - \textrm{i}\varepsilon v - 2 |v|^2 u - v^2 {\bar{u}} - |v|^2 v, \\ -\textrm{i}{{\bar{v}}}_t &{}= - {{\bar{v}}}_{xx} + \zeta {{\bar{v}}} - 2 |u|^2 {{\bar{v}}} - {{\bar{u}}}^2 v + \textrm{i}\varepsilon {{\bar{v}}} - 2 |v|^2{{\bar{u}}} - {{\bar{v}}}^2 u - |v|^2 {{\bar{v}}}, \end{array}\right. \end{aligned}$$
(1.5)

for which the mild formulation is locally well-posedFootnote 1 in \((H^1(\mathbb {R}))^2\). The linearized equation is then given by

$$\begin{aligned} V_t = ({\mathcal {L}}-\varepsilon ) V, \quad V = (v_1,v_2)^T, \end{aligned}$$

for the operator \({\mathcal {L}}:=J L: (H^2(\mathbb {R}))^2 \rightarrow (L^2(\mathbb {R}))^2\), with

$$\begin{aligned} J := \begin{pmatrix} - \textrm{i}&{} 0 \\ 0 &{} \textrm{i}\end{pmatrix}, \quad L:= \begin{pmatrix} - \partial _x^2 + \zeta - 2 |u|^2 &{} - u^2 \\ -{\bar{u}}^2 &{} - \partial _x^2 + \zeta - 2 |u|^2 \end{pmatrix}, \end{aligned}$$
(1.6)

and the associated eigenvalue problem reads

$$\begin{aligned} \lambda V = ({\mathcal {L}}-\varepsilon ) V, \quad V = (v_1,v_2)^T. \end{aligned}$$
(1.7)

Spectral stability is now determined by the location of the spectrum of the linearized operator \(\sigma ({\mathcal {L}}-\varepsilon ) = \sigma ({\mathcal {L}})-\varepsilon \) according to the following definition.

Definition 1

A solution \(u = u(\varepsilon ) \in \mathbb {C}+ H^2(\mathbb {R})\) of (1.4) is called spectrally unstable, if there exists \(\lambda \in \sigma ({\mathcal {L}}-\varepsilon )\) such that \({\text {Re}}(\lambda )>0\). Otherwise the solution is called spectrally stable, i.e., if and only if \(\sigma ({\mathcal {L}}) \subset \{z \in \mathbb {C}:\ {\text {Re}}z \le \varepsilon \}\).

The following theorem clarifies the spectral stability of the solitary wave solutions found in Theorem 1.

Theorem 2

Suppose that \(u = u(\varepsilon ) \in \mathbb {C}+ H^2(\mathbb {R})\) is a solution of (1.4) as in Theorem 1 for \(\varepsilon \not =0\) sufficiently small, that bifurcates from the NLS soliton

$$\begin{aligned} \phi _{\theta _0}(x) = \sqrt{2\zeta } {{\,\textrm{sech}\,}}\big ( \sqrt{\zeta } x \big ) \textrm{e}^{\textrm{i}\theta _0}, \end{aligned}$$

with \(\sin \theta _0 \not = 0\). Then, the spectrum of \({\mathcal {L}}-\varepsilon \) is given by the disjoint union of essential and discrete spectrum \(\sigma ({\mathcal {L}}-\varepsilon ) = \sigma _ess ({\mathcal {L}}-\varepsilon ) \cup \sigma _d({\mathcal {L}}-\varepsilon )\), where the essential spectrum is explicitly computable:

$$\begin{aligned} \sigma _ess ({\mathcal {L}}-\varepsilon ) = \left\{ \textrm{i}\omega \in \textrm{i}\mathbb {R}: \ |\omega | \in [\zeta _\varepsilon ,\infty ) \right\} -\varepsilon , \quad \zeta _\varepsilon = \zeta + {\mathcal {O}}(\varepsilon ^2). \end{aligned}$$

Moreover,

  1. (i)

    if \(\varepsilon <0\), then the solution u is spectrally unstable. The same is true if \(\varepsilon ,-\sin \theta _0>0\).

  2. (ii)

    if \(\varepsilon ,\sin \theta _0>0\), then the solution \(u(\varepsilon )\) is spectrally stable and the spectrum satisfies

    $$\begin{aligned} \sigma ({\mathcal {L}}-\varepsilon ) \subset \{-2 \varepsilon \} \cup \{z \in \mathbb {C}:\ {\text {Re}}z = -\varepsilon \} \cup \{0\} \end{aligned}$$

    with (algebraically) simple eigenvalues \(\lambda = 0,-2\varepsilon \).

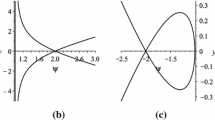
The different stability configurations of Theorem 2 are depicted in Fig. 2.

Fig. 2
figure 2

Stability configurations of Theorem 2. Blue dots = discrete spectrum, red lines = essential spectrum. Top: spectrum of the unperturbed stable NLS soliton. Left and bottom: spectrum of unstable solitary waves of LLE. Right: spectrum of a stable solitary wave of LLE (Color figure online)

Full size image

Remark 4

In case (i) of Theorem 2, the instability is triggered by two different mechanism. If \(\varepsilon <0\), the essential spectrum of \({\mathcal {L}}-\varepsilon \) is unstable. If \(\varepsilon>0>\sin \theta _0\), we find exactly one simple real unstable eigenvalue \(\lambda _+ \in \sigma _d({\mathcal {L}})\) of order \({\mathcal {O}}(\varepsilon ^{1/2})\).

Remark 5

A similar spectral stability result for periodic solutions of (1.3) bifurcating from dnoidal wave solutions of the NLS has been obtained in [46]. Moreover, in [2, 14] stability and instability of purely imaginary soliton solutions of the forced NLS equation is proven. Here, the stable solutions have a strictly positive imaginary part, which is in agreement with our sign condition on \(\sin \theta _0\).

The next theorem provides the nonlinear stability result for spectrally stable solutions of Therorem 2.

Theorem 3

Suppose that \(u = u(\varepsilon ) \in \mathbb {C}+ H^2(\mathbb {R})\) is a spectrally stable solution as in Theorem 2. Then, the solution \(u(\varepsilon )\) is asymptotically orbitally stable. More precisely, there exist constants \(\delta ,\eta ,C>0\) such that for all \(v_0 \in H^1(\mathbb {R})\) satisfying \(\Vert v_0\Vert _{H^1}< \delta \) there exists the unique global (mild) solution \((v,{\bar{v}}) \in C([0,\infty ),(H^1(\mathbb {R}))^2)\), \((v(0),{\bar{v}}(0)) =(v_0,{\bar{v}}_0)\) of (1.5) and \(\sigma _\infty \in \mathbb {R}\) such that with \(\psi = u + v\) we have

$$\begin{aligned} \Vert \psi (\cdot ,t) - u(\cdot - \sigma _\infty )\Vert _{H^1} \le C \delta \textrm{e}^{-\eta t} \qquad \text {for } t \ge 0. \end{aligned}$$

Remark 6

In [46], asymptotic orbital stability of spectrally stable periodic solutions against co-periodic perturbations is proven. Theorem 3 can be seen as an analogous version of this result for stability of solitary wave solutions on \(\mathbb {R}\) against localized perturbations.

Remark 7

If we restrict perturbations to the class of even functions the asymptotic orbital stability can be improved to asymptotic stability by exploiting a spectral gap in the linear stability problem.

1.2 Outline of the paper

In Sect. 2, we show that solitary waves for the LLE bifurcate from the NLS soliton as stated in Theorem 1. The spectral stability problem is analyzed in Sect. 3.1 and the proof of Theorem 2 is presented. The asymptotic orbital stability result of Theorem 3 is proven in Sect. 3.2. It relies upon uniform resolvent estimates for the linearized LLE, which we derive from high-frequency resolvent estimates. These estimates are obtained in an abstract functional analytical setup and can therefore also be applied to other NLS type equations.

2 Existence of solitary wave solutions

The goal of this section is to prove Theorem 1. We work in the Sobolev spaces \(H^k(\mathbb {R}) = H^k(\mathbb {R},\mathbb {C})\), \(k \in \mathbb {N}_0\) of complex valued functions over the field \(\mathbb {R}\). By this choice of function spaces, the map \(H^2(\mathbb {R}) \ni u \mapsto |u|^2 u \in H^2(\mathbb {R})\) is Fréchet differentiable. Moreover, the \(L^2\) scalar product is defined by the \(\mathbb {R}\)-valued map

$$\begin{aligned} \forall f,g \in L^2(\mathbb {R},\mathbb {C}): \quad \langle f, g \rangle _{L^2} = {\text {Re}}\int _\mathbb {R}f {\bar{g}} dx. \end{aligned}$$

Let us fix the parameters \(\zeta ,f>0\) such that \(2 \sqrt{2 \zeta } < \pi f\) and let \(\theta _0 \in \mathbb {R}\) be a simple zero of \(\theta \mapsto \pi f\cos \theta - 2\sqrt{2\zeta }\). Recall that \(\phi _0(x) = \sqrt{2 \zeta } {{\,\textrm{sech}\,}}\big ( \sqrt{\zeta } x \big )\) denotes the soliton solution of the focusing cubic NLS equation

$$\begin{aligned} -\phi '' + \zeta \phi - |\phi |^2 \phi = 0, \end{aligned}$$

which decays exponentially to zero as \(|x| \rightarrow \infty \). Let us introduce the manifold of rotated solitons

$$\begin{aligned} {\mathcal {M}}:= \Big \{\phi _\theta = \phi _0 \textrm{e}^{\textrm{i}\theta }: \theta \in \mathbb {R}\Big \}. \end{aligned}$$

By the gauge invariance of NLS every \(\phi \in {\mathcal {M}}\) is a solution of the NLS. In addition, NLS possesses a translational symmetry, i.e., \(\phi (\cdot -\sigma )\) is a solution of NLS for all shifts \(\sigma \in \mathbb {R}\). In the Lugiato–Lefever equation, the gauge symmetry is broken, and only the translational symmetry persists. Consequently, the continuation for \(\varepsilon \not =0\) is expected to be successful only for suitably rotated solitons \(\phi \in {\mathcal {M}}\). To handle the translational symmetry, we fix the shift parameter \(\sigma = 0\) and restrict our analysis to the spaces \(H_\text {ev}^2(\mathbb {R}),L_\text {ev}^2(\mathbb {R})\) of even functions.

It is now important to note that the presence of the forcing term f in (1.4) prevents solutions from decaying to zero as \(|x| \rightarrow \infty \). More precisely, the tails at \(\pm \infty \) of every localized solution satisfy the algebraic equation

$$\begin{aligned} \zeta u_\infty - |u_\infty |^2 u_\infty + \textrm{i}\varepsilon \big ( - u_\infty + f) = 0, \quad u_\infty \in \mathbb {C}. \end{aligned}$$
(2.1)

Thus, we adapt an ansatz of the form

$$\begin{aligned} u = \phi _\theta + u_\infty + \varphi , \end{aligned}$$

where \(\phi _\theta \in {\mathcal {M}}\) is a suitably rotated soliton, \(u_\infty \in \mathbb {C}\) is the constant background solving the algebraic equation (2.1), and \(\varphi \in H_\text {ev}^2(\mathbb {R})\) is a small correction. For the background, we solve  (2.1) to leading order by

$$\begin{aligned} u_\infty (\varepsilon ) = -\frac{\textrm{i}f}{\zeta } \varepsilon + {\mathcal {O}}(\varepsilon ^2), \end{aligned}$$
(2.2)

which is the unique solutionFootnote 2 close to 0. Inserting our ansatz into (1.4) yields the equation for the correction \(\varphi \) and rotational angle \(\theta \):

$$\begin{aligned} L_\theta \varphi = N(\varphi , \varepsilon , \theta ) \end{aligned}$$
(2.3)

where

$$\begin{aligned} L_\theta \varphi := -\varphi '' + \zeta \varphi - 2 |\phi _\theta |^2 \varphi - \phi _\theta ^2 {\bar{\varphi }}, \qquad \varphi \in H_\text {ev}^2(\mathbb {R}), \end{aligned}$$

and

$$\begin{aligned} N(\varphi , \varepsilon , \theta ) :&= 2 |u_\infty (\varepsilon ) + \varphi |^2 \phi _\theta +(u_\infty (\varepsilon ) + \varphi )^2 {\bar{\phi }}_\theta + |u_\infty (\varepsilon ) + \varphi |^2 (u_\infty (\varepsilon ) + \varphi ) \\&\quad - |u_\infty (\varepsilon )|^2 u_\infty (\varepsilon ) +2 |\phi _\theta |^2 u_\infty (\varepsilon ) + \phi _\theta ^2 {{\bar{u}}}_\infty (\varepsilon ) + \textrm{i}\varepsilon (\phi _\theta + \varphi ). \end{aligned}$$

Note that we have \(N(\varphi ,\varepsilon ,\theta ) \in H_\text {ev}^2(\mathbb {R})\) for \(\varphi \in H_\text {ev}^2(\mathbb {R})\). Our goal is to solve (2.3) by means of the Lyapunov–Schmidt reduction method. Therefore, let us collect relevant properties of the linearized operator \(L_\theta \).

Lemma 1

For every \(\theta \in \mathbb {R}\), the \(\mathbb {R}\)-linear operator \(L_\theta : H^2(\mathbb {R}) \rightarrow L^2(\mathbb {R})\) is self-adjoint and Fredholm of index zero. Moreover, we have

$$\begin{aligned} {{\,\textrm{Ker}\,}}(L_\theta ) = {{\,\textrm{Span}\,}}\{ \textrm{i}\phi _\theta , \phi _\theta ' \}. \end{aligned}$$

Proof

The fact that \(L_\theta \) is Fredholm of index zero follows from \(0 \not \in \sigma _\text {ess}(L_\theta ) = \sigma _\text {ess}(-\partial _x^2 + \zeta ) = [\zeta ,\infty )\) and the first equality is a consequence of Weyl’s theorem. Moreover, the operator \( -\partial _x^2: H^2(\mathbb {R}) \rightarrow L^2(\mathbb {R})\) is self-adjoint and hence the same holds for \(L_\theta \) since it is a symmetric bounded perturbation of \(-\partial _x^2:H^2(\mathbb {R})\rightarrow L^2(\mathbb {R})\). Finally, the identity for the kernel follows from a similarity transformation and explicit formulas for the kernel of the linearized NLS operator, cf. [30]. \(\square \)

Since we aim to solve (2.3) in the space of even functions, we note that the restricted operator \(L_\theta |_{H_\text {ev}^2}\) has a one-dimensional kernel. Indeed, by Lemma 1 the kernel is explicitly given by \({{\,\textrm{Ker}\,}}(L_\theta |_{H_\text {ev}^2}) = {{\,\textrm{Span}\,}}\{ \textrm{i}\phi _\theta \}\). Lyapunov–Schmidt reduction now relies on the decomposition of \(L_\text {ev}^2\) with the orthogonal projection onto \({{\,\textrm{Ker}\,}}(L_\theta |_{H_\text {ev}^2})\) defined by

$$\begin{aligned} P_\theta \varphi : = \frac{\langle \textrm{i}\phi _\theta , \varphi \rangle _{L^2}}{\Vert \phi _0\Vert _{L^2}^2} \textrm{i}\phi _\theta , \qquad \varphi \in H_\text {ev}^2(\mathbb {R}). \end{aligned}$$

The operator \(P_\theta \) allows us to split the equation (2.3) into a singular and non-singular part:

$$\begin{aligned}&(I-P_\theta ) L_\theta (I-P_\theta ) \varphi = (I-P_\theta ) N(\varphi ,\varepsilon ,\theta ) \end{aligned}$$
(2.4)
$$\begin{aligned}&P_\theta N(\varphi ,\varepsilon ,\theta ) = 0 \end{aligned}$$
(2.5)

where we additionally impose the phase condition:

$$\begin{aligned} P_\theta \varphi = 0. \end{aligned}$$
(2.6)

Note that the condition (2.6) depends on the free rotational parameter \(\theta \) which means that our decomposition of \(L_\text {ev}^2\) is parameter dependent:

$$\begin{aligned} L_\text {ev}^2(\mathbb {R}) = {{\,\textrm{Ker}\,}}(P_\theta ) \oplus {{\,\textrm{Ran}\,}}(P_\theta ). \end{aligned}$$

In the following lemma, we solve the non-singular equation (2.4) subject to the phase condition (2.6).

Lemma 2

There exist open neighborhoods \(U \subset \mathbb {R}^2\) of \((0,\theta _0)\), \(V \subset H_ev ^2(\mathbb {R})\) of 0 and an real-analytic map \(U \ni (\varepsilon ,\theta ) \mapsto \varphi (\varepsilon ,\theta ) \in V\) such that \(\varphi (\varepsilon ,\theta )\) solves (2.4) subject to the phase condition (2.6) and \(\varphi (0,\theta ) = 0\) for all \((0,\theta ) \in U\).

Proof

Define the function \(F: H_\text {ev}^2(\mathbb {R}) \times \mathbb {R}\times \mathbb {R}\rightarrow L_\text {ev}^2(\mathbb {R})\) given by

$$\begin{aligned} F(\varphi ,\varepsilon ,\theta ):= (I-P_\theta ) L_\theta (I-P_\theta ) \varphi - (I-P_\theta ) N(\varphi ,\varepsilon ,\theta ) + P_\theta \varphi . \end{aligned}$$

Then, F is real analytic in \((\varphi ,\varepsilon ,\theta )\) as a composition of real-analytic functions (cf. [9] Theorem 4.5.7), \(F(0,0,\theta _0) = 0\) and

$$\begin{aligned} \partial _{\varphi }F(0,0,\theta _0) = (I-P_{\theta _0}) L_\theta (I-P_{\theta _0}) + P_{\theta _0}:H_\text {ev}^2(\mathbb {R}) \rightarrow L_\text {ev}^2(\mathbb {R}) \end{aligned}$$

is a homeomorphism by construction. The implicit function theorem for analytic functions ( [9] Theorem 4.5.4) yields the existence of open neighborhoods \(U \subset \mathbb {R}^2\) of \((0,\theta _0)\), \(V \subset H_\text {ev}^2(\mathbb {R})\) of 0 and a real-analytic map \(U \ni (\varepsilon ,\theta ) \mapsto \varphi (\varepsilon ,\theta ) \in V\) such that the unique solution of \(F(\varphi ,\varepsilon ,\theta ) = 0\) in \(V \times U\) is given by \((\varphi , \varepsilon , \theta ) = (\varphi (\varepsilon ,\theta ), \varepsilon , \theta )\). Finally, since \(F(0,0,\theta ) = 0\), we find \(\varphi (0,\theta ) = 0\) by the local uniqueness of the solution. \(\square \)

Substitution of the solution obtained in Lemma 2 into (2.5) amounts to

$$\begin{aligned} P_\theta N(\varphi (\varepsilon ,\theta ),\varepsilon ,\theta ) = 0 \quad \Longleftrightarrow \quad f(\varepsilon ,\theta ):=\langle N(\varphi (\varepsilon ,\theta ),\varepsilon ,\theta ), \textrm{i}\phi _\theta \rangle _{L^2} = 0, \end{aligned}$$

where \(f: U \subset \mathbb {R}^2 \rightarrow \mathbb {R}\) is again real analytic as a composition of real-analytic functions and admits the expansion

$$\begin{aligned} f(\varepsilon ,\theta ) = \langle \varepsilon \textrm{i}\phi _\theta + 2 |\phi _\theta |^2 u_\infty (\varepsilon ) + \phi _\theta ^2 {{\bar{u}}}_\infty (\varepsilon ), \textrm{i}\phi _\theta \rangle _{L^2} + {\mathcal {O}}(\varepsilon ^2). \end{aligned}$$

Clearly, \(f(0,\theta ) = 0\) for all \((0,\theta ) \in U\) and thus we find a real-analytic function \({\tilde{f}}\) with \(f(\varepsilon ,\theta ) = \varepsilon {\tilde{f}}(\varepsilon ,\theta )\). Nontrivial solutions of \(f(\varepsilon ,\theta ) = 0\) then satisfy \({\tilde{f}}(\varepsilon ,\theta ) = 0\) and the equation is again solved by the implicit function theorem. Indeed, in the subsequent Lemma 3 we show \({\tilde{f}}(0,\theta _0) = 0\) and \(\partial _\theta {\tilde{f}}(0,\theta _0) \not = 0\) and thus there exist open intervals \((-\varepsilon ^*,\varepsilon ^*)\), \(\Theta \subset \mathbb {R}\), \(\theta _0 \in \Theta \) and a real-analytic branch \((-\varepsilon ^*,\varepsilon ^*) \ni \varepsilon \mapsto \theta (\varepsilon ) \in \Theta \) such that \({\tilde{f}}(\varepsilon ,\theta ) = 0\) in \((-\varepsilon ^*,\varepsilon ^*) \times \Theta \) is uniquely solved by \((\varepsilon ,\theta (\varepsilon )) = (\varepsilon ,\theta )\). In summary, we have constructed a solitary wave solution

$$\begin{aligned} u (\varepsilon ) = \phi _{\theta (\varepsilon )} + u_\infty (\varepsilon ) + \varphi (\varepsilon ,\theta (\varepsilon )) \in \mathbb {C}+ H^2(\mathbb {R}), \quad \varepsilon \in (-\varepsilon ^*,\varepsilon ^*) \end{aligned}$$

of the Lugiato–Lefever equation (1.4). It remains to prove Lemma 3.

Lemma 3

Let \(\theta _0 \in \mathbb {R}\) be a simple zero of \(\theta \mapsto \pi f\cos \theta - 2\sqrt{2\zeta }\). Then, \({\tilde{f}}(0,\theta _0) = 0\) and \(\partial _\theta {\tilde{f}}(0,\theta _0) \not = 0\).

Proof

By definition of \({\tilde{f}}\), formula (2.2), and since \(\pi f\cos \theta _0 = 2 \sqrt{2\zeta }\), we have

$$\begin{aligned} {\tilde{f}}(0,\theta _0)&= \langle \textrm{i}\phi _{\theta _0} + 2 |\phi _{\theta _0}|^2 \partial _\varepsilon u_\infty (0) + \phi _{\theta _0}^2 \partial _\varepsilon {{\bar{u}}}_\infty (0) , \textrm{i}\phi _{\theta _0} \rangle _{L^2} \\&= {\text {Re}}\int _\mathbb {R}|\phi _0|^2 - 2 \textrm{i}|\phi _0|^2 {\bar{\phi }}_{\theta _0} \partial _\varepsilon u_\infty (0) - \textrm{i}|\phi _0|^2 \phi _{\theta _0} \partial _\varepsilon {{\bar{u}}}_\infty (0) dx \\&= 4 \sqrt{\zeta } - \frac{f}{\zeta } {\text {Re}}\int _\mathbb {R}2 |\phi _0|^2 {\bar{\phi }}_{\theta _0} - |\phi _0|^2 \phi _{\theta _0} dx \\&= 4 \sqrt{\zeta } - \frac{f}{\zeta } \cos \theta _0 \int _\mathbb {R}\phi _0^3 dx \\&= 4 \sqrt{\zeta } - \sqrt{2}\pi f \cos \theta _0 = 0 \end{aligned}$$

and similar computations lead to

$$\begin{aligned} \partial _\theta {\tilde{f}}(0,\theta _0) = \sqrt{2} \pi f \sin \theta _0 \not = 0, \end{aligned}$$

where \(\sin \theta _0\not =0\) by simplicity of the root \(\theta _0\), which proves the statement. \(\square \)

Corollary 1

The solutions \(u (\varepsilon ) \in \mathbb {C}+ H^2(\mathbb {R})\) of Theorem 1 decay exponentially fast to their limit states \(u_\infty (\varepsilon ) \in \mathbb {C}\) as \(|x| \rightarrow \infty \).

Proof

Re-writing (1.4) in its dynamical system formulation

$$\begin{aligned} \partial _x U= \begin{pmatrix} U_3 \\ U_4 \\ \zeta U_1 - (U_1^2+U_2^2)U_1 + \varepsilon U_2 \\ \zeta U_2 - (U_1^2+U_2^2)U_2 + \varepsilon (-U_1 + f) \end{pmatrix}, \quad U = \begin{pmatrix} u_1(\varepsilon ) \\ u_2(\varepsilon ) \\ \partial _x u_1(\varepsilon ) \\ \partial _x u_2(\varepsilon ) \end{pmatrix} \end{aligned}$$

for \(u_1(\varepsilon ) = {\text {Re}}(u(\varepsilon )), u_2(\varepsilon ) = {\text {Im}}(u(\varepsilon ))\) we easily see that U is homoclinic to a hyperbolic equilibrium and thus converges exponentially fast to its limit state \( U_\infty = ({\text {Re}}(u_{\infty }(\varepsilon )), {\text {Im}}(u_{\infty }(\varepsilon )), 0, 0)^T. \) \(\square \)

3 Stability analysis

In this section, we prove the stability results of Theorem 2 and Theorem 3. From now on \(H^k(\mathbb {R})=H^k(\mathbb {R}, \mathbb {C})\), \(k \in \mathbb {N}_0\) denotes the Sobolev spaces over the field \(\mathbb {C}\). In particular, the \(L^2\)-scalar product is now given by the \(\mathbb {C}\)-valued map

$$\begin{aligned} \forall f,g \in L^2(\mathbb {R},\mathbb {C}): \quad \langle f, g \rangle _{L^2} = \int _\mathbb {R}f {{\bar{g}}} dx. \end{aligned}$$

Let us start with the proof of the spectral stability result of Theorem 2.

3.1 Proof of Theorem 2

Suppose that \(u = u(\varepsilon ) \in \mathbb {C}+ H^2(\mathbb {R})\) is a solution of (1.4) as in Theorem 2 for \(\varepsilon \not =0\) sufficiently small. We determine the location of the spectrum of the operator \({\mathcal {L}}=JL\) defined in (1.6).

It is well known [30] that we have a decomposition into essential and discrete spectrum

$$\begin{aligned} \sigma ({\mathcal {L}}) = \sigma _\text {ess}({\mathcal {L}}) \cup \sigma _d({\mathcal {L}}). \end{aligned}$$
(3.1)

3.1.1 Essential spectrum of \({\mathcal {L}}\)

The essential spectrum can be computed explicitly.

Lemma 4

Let \(\varepsilon \) be sufficiently small. The essential spectrum is given by

$$\begin{aligned} \sigma _\text {ess}({\mathcal {L}}) = \{\textrm{i}\omega \in \textrm{i}\mathbb {R}: \ |\omega | \in [\zeta _\varepsilon , \infty ) \}, \end{aligned}$$

where \(\zeta _\varepsilon = \zeta + {\mathcal {O}}(\varepsilon ^2)\).

Proof

Since \(u(x) \rightarrow u_\infty \) as \(|x| \rightarrow \infty \) exponentially fast, cf. Corollary 1, we can use Weyl’s theorem [30] to find

$$\begin{aligned} \sigma _\text {ess}({\mathcal {L}}) = \sigma _\text {ess}({\mathcal {L}}^\infty ) \end{aligned}$$

where the asymptotic constant coefficient operator is given by

$$\begin{aligned} {\mathcal {L}}^\infty = \begin{pmatrix} - \textrm{i}&{} 0 \\ 0 &{} \textrm{i}\end{pmatrix} \begin{pmatrix} - \partial _x^2 + \zeta - 2 |u_\infty |^2 &{} - u_\infty ^2 \\ -{\bar{u}}_\infty ^2 &{} - \partial _x^2 + \zeta - 2 |u_\infty |^2 \end{pmatrix}. \end{aligned}$$

We calculate the essential spectrum of \({\mathcal {L}}^\infty \). Therefore, we write the spectral problem for \({\mathcal {L}}^\infty \) in its first-order reformulation \(\partial _x V = A(\lambda )V\) with

$$\begin{aligned} A(\lambda ) = \begin{pmatrix} 0 &{} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 1 \\ \zeta - 2|u_\infty |^2-\textrm{i}\lambda &{} u_\infty ^2 &{} 0 &{} 0 \\ {\bar{u}}_\infty ^2 &{} \zeta - 2|u_\infty |^2+\textrm{i}\lambda &{} 0 &{} 0 \end{pmatrix}, \quad V = \begin{pmatrix} v_1 \\ v_2 \\ \partial _x v_1 \\ \partial _x v_2 \end{pmatrix}. \end{aligned}$$

Then, the essential spectrum is characterized as follows (see for instance [30]):

$$\begin{aligned} \lambda \in \sigma _\text {ess}({\mathcal {L}}^\infty ) \quad \Longleftrightarrow \quad \sigma (A(\lambda ))\cap \textrm{i}\mathbb {R}\not = \emptyset . \end{aligned}$$

Computing

$$\begin{aligned} p(k,\lambda ):=\det (A(\lambda )- \textrm{i}k) = k^4 + 2( \zeta -2|u_\infty |^2 ) k^2 + (\zeta -2|u_\infty |^2)^2-|u_\infty |^4 +\lambda ^2 \end{aligned}$$

we find that \(A(\lambda )\) is nonhyperbolic if and only if

$$\begin{aligned} \exists k \in \mathbb {R}: \quad p(k,\lambda )=0 \end{aligned}$$

which is equivalent to

$$\begin{aligned} \lambda \in \{ \textrm{i}\omega \in \textrm{i}\mathbb {R}: \ |\omega | \in [\zeta _\varepsilon , \infty ) \}, \end{aligned}$$

with \(\zeta _\varepsilon = \zeta + {\mathcal {O}}(\varepsilon ^2)\) since \(u_\infty = {\mathcal {O}}(\varepsilon )\) and thus the claim follows. \(\square \)

An immediate consequence of Lemma 4 is the spectral instability of the wave u if \(\varepsilon <0\). However, if \(\varepsilon >0\), the essential spectrum is stable and spectral stability is solely determined by the location of the discrete spectrum. From now on we focus on the case \(\varepsilon >0\).

3.1.2 Discrete spectrum of \({\mathcal {L}}\)

Recall that the discrete spectrum can be determined from the eigenvalue problem (1.7) which can be written as

$$\begin{aligned} \left\{ \begin{array}{rl} \textrm{i}\lambda v_1 &{}= - v_{1xx} + \zeta v_1 - 2 |u|^2 v_1 - u^2 v_2 - \textrm{i}\varepsilon v_1, \\ -\textrm{i}\lambda v_2 &{}= - v_{2xx} + \zeta v_2 - 2 |u|^2 v_2 - {{\bar{u}}}^2 v_1 + \textrm{i}\varepsilon v_2. \end{array}\right. \end{aligned}$$

For \(\varepsilon =0\), we recover the spectral stability problem for the rotated soliton \(\phi _{\theta _0}\) of NLS and \(\lambda =0\) is an isolated eigenvalue of geometric multiplicity two and algebraic multiplicity four. More precisely, we find two Jordan chains of length two and by Lemma 1 we have that the corresponding eigenspace is spanned by the vectors \((\textrm{i}\phi _{\theta _0},-\textrm{i}\bar{\phi }_{\theta _0})\) and \((\phi _{\theta _0}',\bar{\phi }_{\theta _0}')\). Consequently, it follows from standard perturbation theory [32], that for small values of \(\varepsilon \) the total multiplicity of all eigenvalues in a small neighborhood of zero is also four. We now focus on the bifurcations of these eigenvalues which in the end will determine the spectral stability.

3.1.3 Eigenvalues close to the origin

We compute expansions in \(\varepsilon \) of all eigenvalues of \({\mathcal {L}}=JL\) close to zero. Observe that we always find \(0 \in \sigma ({\mathcal {L}}-\varepsilon )\) due to the translational invariance of (1.4). This yields \(\varepsilon \in \sigma (JL)\) and the corresponding eigenfunction is given by \((\partial _x u, \partial _x {\bar{u}})\). Since the spectrum of JL is symmetric w.r.t. the imaginary axis we also find \(-\varepsilon \in \sigma (JL)\). Note that the symmetry is an immediate consequence of the structure of JL, a composition of a skew-adjoint and self-adjoint operator. Thus, in the neighborhood of \(\lambda =0\) only two unknown eigenvalues remain and they correspond to the broken gauge symmetry in the LLE.

To compute the expansions of the perturbed rotational eigenvalues, we restrict to spaces of even functions. Following [32], we expand both remaining eigenvalues along with their corresponding eigenfunctions in a Puiseux series:

$$\begin{aligned} \lambda = \sqrt{\varepsilon } \lambda _1+ \varepsilon \lambda _2 + {\mathcal {O}}(\varepsilon ^{3/2}), \quad V =V_0 + \sqrt{\varepsilon } V_1 + \varepsilon V_2 + {\mathcal {O}}(\varepsilon ^{3/2}),\quad V_0 = \begin{pmatrix} \textrm{i}\phi _{\theta _0} \\ - \textrm{i}{\bar{\phi }}_{\theta _0} \end{pmatrix}, \end{aligned}$$

and the expansions are in powers of \(\varepsilon ^{1/2}\) since we consider the splitting of a Jordan chain of length two. Moreover, we expand the operator L in powers of \(\varepsilon \) which relies on expansions of the solution u:

$$\begin{aligned} L&= L_0 + \varepsilon L_1 + {\mathcal {O}}(\varepsilon ^2) \\ L_0&= \begin{pmatrix} - \partial _x^2 + \zeta - 2 |u_0|^2 &{} - u_0^2 \\ -{\bar{u}}_0^2 &{} - \partial _x^2 + \zeta - 2 |u_0|^2 \end{pmatrix}, \ L_1 = \begin{pmatrix} -2(u_0 {\bar{u}}_1 + {\bar{u}}_0 u_1) &{} -2 u_0 u_1 \\ -2 {\bar{u}}_0 {\bar{u}}_1 &{} -2 (u_0 {\bar{u}}_1 + {\bar{u}}_0 u_1) \end{pmatrix}, \\ u&= u_0 + \varepsilon u_1 + {\mathcal {O}}(\varepsilon ^2) , \qquad u_0 = \phi _{\theta _0}, \qquad u_1 = \textrm{i}\partial _\varepsilon \theta (0) \phi _{\theta _0} - \textrm{i}\frac{f}{\zeta } + \varphi _1, \end{aligned}$$

and the equation for \(\varphi _1\) is found from differentiating (2.3) w.r.t. \(\varepsilon \) at \(\varepsilon =0\) (see also part two of the proof of Lemma 2),

$$\begin{aligned} L_{\theta _0} \varphi _1 = 2 |\phi _{\theta _0}|^2 \partial _\varepsilon u_\infty (0) + \phi _{\theta _0}^2 \partial _\varepsilon {\bar{u}}_\infty (0) + \textrm{i}\phi _{\theta _0}, \qquad \varphi _1 \perp \textrm{i}\phi _{\theta _0}. \end{aligned}$$

Substituting the expansions into the spectral problem \(JL V = \lambda V\) yields equations at order \(\varepsilon ^{1/2}\) and \(\varepsilon \),

$$\begin{aligned} L_0 V_1 = \lambda _1 J^{-1} V_0, \quad L_0 V_2 + L_1 V_0 = \lambda _1 J^{-1}V_1 + \lambda _2 J^{-1} V_0. \end{aligned}$$

Since \(J^{-1} V_0 \perp {{\,\textrm{Ker}\,}}(L_0)\), we find \(V_1 = \lambda _1 L_0^{-1} J^{-1} V_0 + \alpha V_0\), \(\alpha \in \mathbb {C}\). Inserting this into the second equation amounts to

$$\begin{aligned} L_0 V_2 = - L_1 V_0 + \lambda _1^2 J^{-1} L_0^{-1} J^{-1} V_0+ \alpha \lambda _1 J^{-1} V_0 + \lambda _2 J^{-1} V_0 \end{aligned}$$
(3.2)

and by the Fredholm alternative, (3.2) is solvable if and only if

$$\begin{aligned} - L_1 V_0 + \lambda _1^2 J^{-1} L_0^{-1} J^{-1} V_0+ \alpha \lambda _1 J^{-1} V_0 + \lambda _2 J^{-1} V_0 \perp {{\,\textrm{Ker}\,}}(L_0). \end{aligned}$$

Since \( J^{-1} V_0 \perp {{\,\textrm{Ker}\,}}(L_0)\), this yields

$$\begin{aligned} \lambda _1^2 \langle J^{-1} L_0^{-1} J^{-1} V_0,V_0\rangle _{L^2} = \langle L_1 V_0, V_0\rangle _{L^2}. \end{aligned}$$
(3.3)

Lemma 5

Let \(\varepsilon ,\delta >0\) be sufficiently small and \(B_\delta (0) \subset \mathbb {C}\) be the ball of radius \(\delta \) centered at \(\lambda =0\). Then, \(B_\delta (0) \cap \sigma _d({\mathcal {L}})\) consists of four distinct simple eigenvalues, given by

$$\begin{aligned} \pm \varepsilon , \pm \sqrt{\varepsilon } \sqrt{- \pi f \sqrt{2\zeta }\sin \theta _0 } + {\mathcal {O}}(\varepsilon ) \in \sigma _d({\mathcal {L}}). \end{aligned}$$

In particular, if \(\sin \theta _0>0\), we have one unstable eigenvalue \(\lambda = \varepsilon \) of \({\mathcal {L}}\), which corresponds to a simple zero eigenvalue of \({\mathcal {L}} - \varepsilon \), and two purely imaginary eigenvalues of \({\mathcal {L}}\):

$$\begin{aligned} \lambda _\pm =\pm \textrm{i}\left( \sqrt{\varepsilon } \sqrt{\pi f \sqrt{2\zeta }\sin \theta _0} + {\mathcal {O}}(\varepsilon )\right) . \end{aligned}$$

If \(\sin \theta _0< 0\), we have two real unstable eigenvalues of \({\mathcal {L}}\):

$$\begin{aligned} \lambda =\varepsilon \quad \text {and}\quad \lambda _+=\sqrt{\varepsilon } \sqrt{\pi f \sqrt{2\zeta }|\sin \theta _0|} + {\mathcal {O}}(\varepsilon ), \end{aligned}$$

where \(\lambda _+\) is also an unstable eigenvalue of the operator \({\mathcal {L}} - \varepsilon \) since it is of order \({\mathcal {O}}(\varepsilon ^{1/2})\).

Proof

From the preceding discussion, it remains to calculate the scalar products in (3.3). Let us start with \(\langle J^{-1} L_0^{-1} J^{-1} V_0,V_0\rangle _{L^2}\). Consider the NLS

$$\begin{aligned} - \phi _{\theta _0}'' + \zeta \phi _{\theta _0} - |\phi _{\theta _0}|^2\phi _{\theta _0} = 0. \end{aligned}$$

Taking derivative w.r.t. \(\zeta \) yields

$$\begin{aligned} L_0 \begin{pmatrix} \partial _\zeta \phi _{\theta _0} \\ \partial _\zeta {\bar{\phi }}_{\theta _0} \end{pmatrix} = - \begin{pmatrix} \phi _{\theta _0} \\ {\bar{\phi }}_{\theta _0} \end{pmatrix} = J^{-1} V_0. \end{aligned}$$

The function \(\partial _\zeta \phi _{\theta _0}\) is found from differentiating the formula of the NLS soliton and a straight forward calculation gives

$$\begin{aligned} \left\langle J^{-1} L_0^{-1} J^{-1} V_0 ,V_0\right\rangle _{L^2}&= \int _\mathbb {R}\partial _\zeta \phi _{\theta _0} {\bar{\phi }}_{\theta _0} + \partial _\zeta {\bar{\phi }}_{\theta _0} \phi _{\theta _0} dx = 2 \zeta ^{-1/2}. \end{aligned}$$

Next, we calculate the scalar product \(\langle L_1 V_0, V_0\rangle _{L^2}\). We have

$$\begin{aligned} \langle L_1 V_0, V_0\rangle _{L^2} = 2 \int _\mathbb {R}\begin{pmatrix} -\textrm{i}u_0^2 {{\bar{u}}}_1 \\ \textrm{i}{{\bar{u}}}_0^2 u_1 \end{pmatrix} \cdot \overline{ \begin{pmatrix} \textrm{i}u_0 \\ -\textrm{i}{{\bar{u}}}_0 \end{pmatrix}} dx = - 4 {\text {Re}}\int _\mathbb {R}|u_0|^2 u_0 {{\bar{u}}}_1 dx. \end{aligned}$$

Inserting the formula for \(u_1\) into the integral yields

$$\begin{aligned}&{\text {Re}}\int _\mathbb {R}|u_0|^2 u_0 {{\bar{u}}}_1 dx = - \frac{f}{\zeta } \Vert \phi _0\Vert _{L^3}^3 \sin \theta _0 + {\text {Re}}\int _\mathbb {R}|\phi _{\theta _0}|^2 \phi _{\theta _0} {\bar{\varphi }}_1 dx \\&\quad = -\frac{f}{\zeta } \Vert \phi _0\Vert _{L^3}^3 \sin \theta _0 + {\text {Re}}\int _\mathbb {R}|\phi _{\theta _0}|^2 \phi _{\theta _0} \overline{L_{\theta _0}^{-1} ( 2 |\phi _{\theta _0}|^2 \partial _\varepsilon u_\infty (0) + \phi _{\theta _0}^2 \partial _\varepsilon {\bar{u}}_\infty (0) + \textrm{i}\phi _{\theta _0})} dx \\&\quad = - \frac{f}{\zeta } \Vert \phi _0\Vert _{L^3}^3 \sin \theta _0 +{\text {Re}}\int _\mathbb {R}L_{\theta _0}^{-1}(|\phi _{\theta _0}|^2 \phi _{\theta _0}) (\overline{ 2 |\phi _{\theta _0}|^2 \partial _\varepsilon u_\infty (0) + \phi _{\theta _0}^2 \partial _\varepsilon {\bar{u}}_\infty (0) + \textrm{i}\phi _{\theta _0}}) dx. \end{aligned}$$

Using that \(L_{\theta _0} \phi _{\theta _0} = - 2|\phi _{\theta _0}|^2 \phi _{\theta _0}\) gives

$$\begin{aligned}&{\text {Re}}\int _\mathbb {R}L_{\theta _0}^{-1}(|\phi _{\theta _0}|^2 \phi _{\theta _0}) (\overline{ 2 |\phi _{\theta _0}|^2 \partial _\varepsilon u_\infty (0) + \phi _{\theta _0}^2 \partial _\varepsilon {\bar{u}}_\infty (0) + \textrm{i}\phi _{\theta _0}}) dx \\&\quad = -\frac{1}{2} {\text {Re}}\int _\mathbb {R}\phi _{\theta _0}( \overline{ 2 |\phi _{\theta _0}|^2 \partial _\varepsilon u_\infty (0) + \phi _{\theta _0}^2 \partial _\varepsilon {\bar{u}}_\infty (0) + \textrm{i}\phi _{\theta _0}}) dx \\&\quad = \frac{3f}{2 \zeta } \Vert \phi _0\Vert _{L^3}^3\sin \theta _0. \end{aligned}$$

Finally, since \(\Vert \phi _0\Vert _{L^3}^3 = \sqrt{2} \zeta \pi \), we have

$$\begin{aligned} \langle L_1 V_0, V_0\rangle _{L^2} = - 2 \frac{f}{\zeta } \Vert \phi _0\Vert _{L^3}^3 \sin \theta _0 = - 2\sqrt{2} f \pi \sin \theta _0 \end{aligned}$$

and thus from (3.3) we obtain the desired formula for the simple eigenvalues

$$\begin{aligned} \lambda _\pm = \pm \sqrt{\varepsilon } \sqrt{-\pi f \sqrt{2\zeta }\sin \theta _0} + {\mathcal {O}}(\varepsilon ), \end{aligned}$$

where in the case \(\sin \theta _0>0\) the \({\mathcal {O}}(\varepsilon )\) remainder is purely imaginary because of the Hamiltonian symmetry of the spectrum. \(\square \)

Lemma 5 proves the spectral instability of the wave u if \(\sin \theta _0<0\). However, if \(\sin \theta _0>0\), no unstable eigenvalues of \({\mathcal {L}}-\varepsilon \) occur from the splitting of the zero eigenvalue. Instead, we find a pair of purely imaginary eigenvalues \(\lambda _\pm \in \textrm{i}\mathbb {R}\) of \({\mathcal {L}}\). Hence, we now focus on the case \(\sin \theta _0>0\) and show that the only unstable eigenvalue of \({\mathcal {L}}\) is given by \(\lambda = \varepsilon \), which then proves the spectral stability of the wave u. For this purpose, we employ the instability index count developed in [28, 29] and also in [10]. To apply the instability count, we need to transform the spectral stability problem (1.7) into a problem with real-valued coefficients. Using similarity transformations with the matrices

$$\begin{aligned} T_1 = \frac{1}{2} \begin{pmatrix} 1 &{} 1 \\ -\textrm{i}&{} \textrm{i}\end{pmatrix},\quad T_2 = \begin{pmatrix} \cos \theta _0 &{} \sin \theta _0 \\ -\sin \theta _0 &{} \cos \theta _0 \end{pmatrix} \end{aligned}$$

such that \({{\tilde{J}}} = T_2T_1 J T_1^{-1}T_2^{-1}\), \({{\tilde{L}}} = T_2T_1 L T_1^{-1}T_2^{-1}\) we obtain the equivalent problem

$$\begin{aligned} \lambda {{\tilde{V}}} = ({\tilde{J}}{\tilde{L}} -\varepsilon ) {{\tilde{V}}}, \end{aligned}$$

and the eigenfunctions are related by \({{\tilde{V}}} = T_2T_1V\). The real-valued operators \({{\tilde{J}}},{{\tilde{L}}}\) are then of the form

$$\begin{aligned} {\tilde{J}} = \begin{pmatrix} 0 &{} 1 \\ -1 &{} 0 \end{pmatrix}, \qquad {\tilde{L}} = \begin{pmatrix} - \partial _x^2 + \zeta - 3 \phi _0^2 &{} 0\\ 0 &{} - \partial _x^2 + \zeta - \phi _0^2 \end{pmatrix} + {\mathcal {O}}(\varepsilon ). \end{aligned}$$

We recall necessary notation from [30]:

  • n(A) denotes the number of negative eigenvalues (counting multiplicities) of a linear operator A.

  • Let \(\lambda \in \sigma _d({\tilde{J}}{\tilde{L}}) \cap (\textrm{i}\mathbb {R}{\setminus }\{0\})\) be an eigenvalue with algebraic multiplicity \(m_a(\lambda )\) and \({{\,\textrm{Ker}\,}}(\bigcup _{n \in \mathbb {N}}({\tilde{J}}{\tilde{L}} - \lambda )^{n}) ={{\,\textrm{Span}\,}}\{v_1,\dots ,v_{m_a(\lambda )}\}\) be the generalized eigenspace. Then, the negative Krein index of \(\lambda \) is defined by

    $$\begin{aligned} k_i^-(\lambda ):= n (H), \quad \text {with}\quad H_{ij}:= \langle {\tilde{L}} v_i,v_j \rangle , \end{aligned}$$

    and the total negative index is defined by \( k_i^-:= \sum _{\lambda \in \sigma _d({\tilde{J}}{\tilde{L}}) \cap \textrm{i}\mathbb {R}{\setminus }\{0\}} k_i^-(\lambda ). \)

  • The real Krein index is defined by \( k_r:= \sum _{\lambda \in \sigma _d({\tilde{J}}{\tilde{L}}) \cap (0,\infty )} m_a(\lambda ). \)

  • The complex Krein index is defined by \( k_c:= \sum _{\lambda \in \sigma _d({\tilde{J}}{\tilde{L}}), {\text {Re}}(\lambda )>0, {\text {Im}}(\lambda )\not = 0} m_a(\lambda ). \)

Applying the instability index counting theory from [10, 28, 29] yields for \(\varepsilon >0\) sufficiently small the formula

$$\begin{aligned} k_r+k_i^- +k_c = n({\tilde{L}}). \end{aligned}$$
(3.4)

Remark 8

In [28, 29], there appears an additional number n(D) in formula (3.4), which accounts for a nontrivial kernel generated by various symmetries of the problem. However, in Lemma 5 we proved that \({{\,\textrm{Ker}\,}}({\tilde{L}}) = \{0\}\) provided \(\varepsilon >0\) is sufficiently small explaining the absence of this number in our situation (see also [10]).

In the next lemma, we use (3.4) to show that \(\varepsilon \in \sigma ({\mathcal {L}})\) is the only unstable eigenvalue of \({\mathcal {L}}\) proving that \(\sigma _d({\mathcal {L}}-\varepsilon ) \subset \{-2\varepsilon \} \cup \{{\text {Re}}= - \varepsilon \} \cup \{0\}\) with simple eigenvalues \(\lambda =0,-2\varepsilon \).

Lemma 6

Let \(\varepsilon >0\) be sufficiently small and \(\sin \theta _0>0\). Then, \(n({\tilde{L}})= 3\), \(k_r = 1\), and \(k_i^- = 2\).

Proof

\(k_r \ge 1\) is clear since \(\varepsilon \in \sigma _d({\tilde{J}}{\tilde{L}})\) due to the translational symmetry. Now consider the Sturm–Liouville operators on the line \(\mathbb {R}\),

$$\begin{aligned} L_+:= -\partial _x^2 + \zeta - 3 \phi _0^3, \quad L_-:= -\partial _x^2 + \zeta - \phi _0^3. \end{aligned}$$

We have \({{\,\textrm{Ker}\,}}(L_+) = {{\,\textrm{Span}\,}}\{\phi _0'\}\), \({{\,\textrm{Ker}\,}}(L_-) = {{\,\textrm{Span}\,}}\{\phi _0\}\) and since \(\phi _0'\) has one zero and \(\phi _0>0\) on \(\mathbb {R}\) we find \(n(L_+) = 1\), \(n(L_-) = 0\) by the standard theory for Sturm–Liouville operators. In particular, we obtain

$$\begin{aligned} n \left( \begin{pmatrix} L_+ &{} 0 \\ 0 &{} L_- \end{pmatrix} \right) = 1, \quad 0 \in \sigma _d \left( \begin{pmatrix} L_+ &{} 0 \\ 0 &{} L_- \end{pmatrix}\right) , \quad m_a(0) = 2, \end{aligned}$$

and by means of perturbation theory for eigenvalues we conclude that there are at most three negative eigenvalues of \({\tilde{L}}\) for \(\varepsilon \) sufficiently small, which proves \(n({\tilde{L}}) \le 3\). Moreover, by Lemma 5 we find purely imaginary simple eigenvalues \(\lambda _\pm \in \textrm{i}\mathbb {R}\) with \(\bar{\lambda }_+=\lambda _-\) by the symmetry of the spectrum and we show that \(k_i^-(\lambda _\pm ) = 1\). Indeed, from Lemma 5 and the discussion before, we have Puiseux expansions for the eigenvalue and corresponding eigenfunction

$$\begin{aligned} \lambda _+ = \sqrt{\varepsilon } \lambda _1 + {\mathcal {O}}(\varepsilon ), \quad {{\tilde{V}}} = \begin{pmatrix} 0 \\ \phi _0 \end{pmatrix} - \sqrt{\varepsilon } \left[ \lambda _1 \begin{pmatrix} L_+^{-1}\phi _0 \\ 0\end{pmatrix} + \alpha \begin{pmatrix} 0 \\ \phi _0 \end{pmatrix} \right] + {\mathcal {O}}(\varepsilon ) \end{aligned}$$

where the eigenfunction is found from the relation \({\tilde{V}} = T_2T_1 V\). Hence, direct calculations yield

$$\begin{aligned} \langle {\tilde{L}} {{\tilde{V}}},{{\tilde{V}}} \rangle _{L^2} = - \lambda _1 \langle {\tilde{J}}{{\tilde{V}}},{{\tilde{V}}} \rangle _{L^2} =\varepsilon 2 |\lambda _1|^2 \langle L_+^{-1} \phi _0 ,\phi _0 \rangle _{L^2} + {\mathcal {O}}(\varepsilon ^{3/2}). \end{aligned}$$

Since \(\langle L_+^{-1}\phi _0, \phi _0 \rangle _{L^2} =- \langle \partial _\zeta \phi _0, \phi _0 \rangle _{L^2}<0\), cf. the proof of Lemma 5, we find \(k_i^-(\lambda _+) = 1\) and from \(k_i^-(\lambda _+)=k_i^-(\bar{\lambda }_+)\) and \(\bar{\lambda }_+=\lambda _-\) it follows that \(k_i^- \ge 2\). Thus, using (3.4) we infer \(n(L)=3\), \(k_r=1\), and \(k_i^- = 2\), which finishes the proof. \(\square \)

Combining our results on the discrete and essential spectrum, we finally obtain

$$\begin{aligned} \sigma ({\mathcal {L}}-\varepsilon )\subset \{-2\varepsilon \} \cup \{z \in \mathbb {C}: \ {\text {Re}}z = -\varepsilon \} \cup \{0\} \end{aligned}$$

with simple eigenvalues \(\lambda = -2 \varepsilon , 0\). Thus, the wave is spectrally stable, provided that \(\varepsilon ,\sin \theta _0>0\) as claimed.

3.2 Proof of Theorem 3

We prove the asymptotic orbital stability in \(H^1\) of the spectrally stable solitary waves of Theorem 2. The strategy of the proof follows the work in [46] where asymptotic orbital stability is obtained for periodic spectrally stable solutions of LLE. Our method deviates from [46] when establishing uniform resolvent bounds. Indeed, high-frequency resolvent estimates in [46] are only proven for the linearization operator with periodic coefficients. Using an abstract functional analytic approach, we extend this result to the case of localized perturbations.

3.2.1 Linearized stability

Let \(u \in \mathbb {C}+ H^2(\mathbb {R})\) be a spectrally stable solution of (1.4) for \(\varepsilon >0\) sufficiently small and denote by \({\mathcal {L}}-\varepsilon \) the linearization about u. In a first step, we prove linearized stability. Note that decay of the semigroup \(\left( \textrm{e}^{({\mathcal {L}}-\varepsilon )t}\right) _{t \ge 0}\) cannot be concluded immediately from the spectral stability of \({\mathcal {L}}-\varepsilon \), since the spectrum of the operator is not confined to a sector of \(\mathbb {C}\) and therefore the spectral mapping theorem is a-priori not available. However, we can use the following characterization of exponential stability of semigroups in Hilbert spaces called the Prüss Theorem, cf. [45] Corollary 4.

Theorem

(Prüss, [45], Corollary 4) Let A be the generator of a \(C_0\)-semigroup \((\textrm{e}^{At})_{t \ge 0}\) in a Hilbert space H. Then, \((\textrm{e}^{At})_{t \ge 0}\) is exponentially stable if and only if

$$\begin{aligned} \{\lambda \in \mathbb {C}:\ {\text {Re}}(\lambda ) \ge 0\} \subset \rho (A) \quad \text {and}\quad \sup \left\{ \Vert (A-\lambda )^{-1}\Vert _{H \rightarrow H}:\ \lambda \in \mathbb {C}, {\text {Re}}(\lambda )\ge 0 \right\} < \infty . \end{aligned}$$

Recall that by the presence of the translational symmetry, \(0 \in \sigma ({\mathcal {L}} - \varepsilon )\), which violates the spectral condition in Prüss Theorem. To overcome this problem, we introduce the spectral projection \(P_0\) onto \({{\,\textrm{Ker}\,}}({\mathcal {L}} - \varepsilon )\) and show that the restricted operator \(({\mathcal {L}} - \varepsilon )|_E\) satisfies the conditions in Prüss Theorem, where \(E:={{\,\textrm{Ker}\,}}(P_0)\). This then leads to decay of the semigroup restricted to the subspace E, which is enough to establish the orbital stability result (cf. Theorem 4.3.2 in [30]).

Recall the basic properties of the spectral projection: \(({\mathcal {L}} - \varepsilon )P_0 =P_0 ({\mathcal {L}} - \varepsilon ) = 0\) and

$$\begin{aligned} \sigma (({\mathcal {L}} - \varepsilon )|_E) = \sigma ({\mathcal {L}} - \varepsilon ) \setminus \{0\} \subset \{\lambda \in \mathbb {C}:\ {\text {Re}}(\lambda ) \le -\varepsilon \}. \end{aligned}$$
(3.5)

Lemma 7

There exist constants \(\eta >0,C\ge 1\) such that

$$\begin{aligned} \Vert \textrm{e}^{({\mathcal {L}} - \varepsilon )t}|_E\Vert _{H^1 \rightarrow H^1} \le C \textrm{e}^{-\eta t} \quad \text {for } t \ge 0. \end{aligned}$$

Proof

It follows from the Lumer–Phillips theorem (Theorem II.3.15 in [13]) and the bounded perturbation theorem (Theorem III.1.3 in [13]) that \({\mathcal {L}} - \varepsilon \) is the generator a \(C_0\)-semigroup on \((H^1(\mathbb {R}))^2\) and the same holds after restricting the operator to \(E={{\,\textrm{Ker}\,}}(P_0)\). According to the Prüss Theorem and (3.5), the claim of the lemma follows if we show the uniform resolvent bound

$$\begin{aligned} \exists C>0: \quad \sup _{{\text {Re}}(\lambda )\ge 0}\Vert ({\mathcal {L}} - \varepsilon -\lambda )^{-1}(I-P_0)\Vert _{H^1 \rightarrow H^1} \le C. \end{aligned}$$

This estimate is obtained in two steps.

Step 1 (Uniform bound in \(L^2\)): We show uniform resolvent estimates for the operator \(({\mathcal {L}} - \varepsilon -\lambda )^{-1}(I-P_0):L^2 \rightarrow L^2\). First note that the Hille–Yosida Theorem ( [13] Theorem 3.8) ensures existence of constants \(\gamma _1, C' > 0\) such that

$$\begin{aligned} \sup _{{\text {Re}}(\lambda )\ge \gamma _1}\Vert ({\mathcal {L}} - \varepsilon -\lambda )^{-1}\Vert _{L^2 \rightarrow L^2} \le C'. \end{aligned}$$

Moreover, using Theorem 4 and Remark 9 with \(H= L^2(\mathbb {R}), A_\pm = -\partial _x^2 + \zeta - 2|u|^2, B = -u^2\) we find constants \(\gamma _2, C''>0\) such that

$$\begin{aligned} \sup _{{\text {Re}}(\lambda )\ge 0, |{\text {Im}}(\lambda )|\ge \gamma _2}\Vert ({\mathcal {L}} - \varepsilon -\lambda )^{-1}\Vert _{L^2 \rightarrow L^2} \le C''. \end{aligned}$$

Finally, observe that \(\lambda \mapsto ({\mathcal {L}} - \varepsilon -\lambda )^{-1}(I-P_0)\) is an analytic function on \(\{\lambda \in \mathbb {C}:\ {\text {Re}}(\lambda ) \ge 0\}\) and hence uniformly bounded on the compact set \(\{\lambda \in \mathbb {C}:\ 0 \le {\text {Re}}(\lambda ) \le \gamma _1, |{\text {Im}}(\lambda )|\le \gamma _2\}\) with a bound \(C''' \ge 0\). Thus for \(C:= \max \{C',C'',C'''\}\) we have

$$\begin{aligned} \sup _{{\text {Re}}(\lambda )\ge 0}\Vert ({\mathcal {L}} - \varepsilon -\lambda )^{-1}(I-P_0)\Vert _{L^2 \rightarrow L^2} \le C. \end{aligned}$$

Step 2 (Uniform bound in \(H^1\)): First, we establish a uniform bound in \(H^2\) and then use an interpolation argument to find the desired \(H^1\) bound. Note that there exist constants \(c, \gamma \gg 1\) such that

$$\begin{aligned} \forall V = (v_1,v_2)^T \in (H^2(\mathbb {R}))^2: \quad \Vert V\Vert _{H^2} \le c \Vert (L + J \varepsilon + \gamma )V\Vert _{L^2}, \quad \Vert (JL - \varepsilon )V\Vert _{L^2} \le c\Vert V\Vert _{H^2}, \end{aligned}$$

where we recall the decomposition \({\mathcal {L}} = JL\) from (1.6). Hence, we find for \({\text {Re}}(\lambda )\ge 0,V \in H^2\),

$$\begin{aligned}&\Vert (JL - \varepsilon -\lambda )^{-1}(I -P_0)V\Vert _{H^2} \\&\quad \le c \Vert (L + J \varepsilon + \gamma )(JL - \varepsilon -\lambda )^{-1}(I-P_0)V\Vert _{L^2} \\&\quad \le c \Vert (JL - \varepsilon )(JL - \varepsilon -\lambda )^{-1}(I-P_0)V\Vert _{L^2} \\&\qquad + c \gamma \Vert (JL - \varepsilon -\lambda )^{-1}(I-P_0)V\Vert _{L^2} \\&\quad \le c \Vert (JL - \varepsilon -\lambda )^{-1}(I-P_0)(JL - \varepsilon )V\Vert _{L^2} + c \gamma C \Vert V\Vert _{H^2} \\&\quad \le cC (c+\gamma ) \Vert V\Vert _{H^2}, \end{aligned}$$

by step 1, which implies the uniform bound

$$\begin{aligned} \sup _{{\text {Re}}(\lambda )\ge 0}\Vert (JL - \varepsilon -\lambda )^{-1}(I-P_0)\Vert _{H^2 \rightarrow H^2} \le cC (c+\gamma ). \end{aligned}$$

Interpolation of both estimates according to [35] Theorem 2.6 yields

$$\begin{aligned} \sup _{{\text {Re}}(\lambda )\ge 0}\Vert (JL - \varepsilon -\lambda )^{-1}(I-P_0)\Vert _{H^1 \rightarrow H^1} \le C \end{aligned}$$

for some constant \(C>0\) and thus the claim follows. \(\square \)

We still need to prove the uniform resolvent estimate for \(\lambda \in \mathbb {C}\) with \({\text {Re}}\lambda \ge 0\), \(|{\text {Im}}\lambda | \gg 1\) and conclude the nonlinear stability.

3.2.2 High-frequency resolvent estimates

We establish uniform resolvent estimates for a family of operators in Hilbert spaces which generalizes the linearization operator \({\mathcal {L}}-\varepsilon \). Our proof relies on techniques from [15] Section 3 where uniform resolvent estimates for NLS are considered. Similar resolvent estimates can also be found in [7, 44, 46].

Let H be a complex Hilbert space with scalar product \(\langle \cdot , \cdot \rangle \) and norm \(\Vert \cdot \Vert = \sqrt{\langle \cdot , \cdot \rangle }\). On \(H \times H\), we consider the spectral problem

$$\begin{aligned} \left[ \begin{pmatrix} -\textrm{i}&{} 0 \\ 0 &{} \textrm{i}\end{pmatrix} \begin{pmatrix} A_+ &{} B \\ B^* &{} A_- \end{pmatrix} - \lambda \begin{pmatrix} I &{} 0 \\ 0 &{} I \end{pmatrix} \right] \begin{pmatrix} \phi _1 \\ \phi _2 \end{pmatrix} = \begin{pmatrix} \psi _1 \\ \psi _2 \end{pmatrix}, \end{aligned}$$
(3.6)

where \(\lambda = \lambda _r + \textrm{i}\lambda _i \in \mathbb {C}\) is a spectral parameter, \(A_\pm : D \subset H \rightarrow H\) are closed self-adjoint linear operators with common domains \(D = {{\,\textrm{Dom}\,}}(A_\pm )\) which are either both bounded from below or from above by the bound \(\gamma \in \mathbb {R}\), \(B:H \rightarrow H\) is a bounded linear operator, \(I:H \rightarrow H\) is the identity, \(\phi _1,\phi _2 \in D\) and \(\psi _1,\psi _2 \in H\). Under these assumptions, the following theorem on uniform high-frequency resolvent estimates holds.

Theorem 4

There exists \(\rho = \rho (\gamma ,\Vert B\Vert _{H \rightarrow H})>0\) such that for all \(\lambda = \lambda _r + \textrm{i}\lambda _i \in \mathbb {C}\) with \(|\lambda _i| \ge \rho \) and \(\lambda _r \not = 0\) we have that for every given \((\psi _1,\psi _2) \in H \times H\) the spectral problem (3.6) has a unique solution \((\phi _1, \phi _2) \in D \times D\) such that

$$\begin{aligned} \Vert \phi _1\Vert + \Vert \phi _2\Vert \lesssim |\lambda _r|^{-1} (\Vert \psi _1\Vert + \Vert \psi _2\Vert ). \end{aligned}$$

Remark 9

Theorem 4 gives a uniform resolvent estimate for the linear operator

$$\begin{aligned} \begin{pmatrix} -\textrm{i}&{} 0 \\ 0 &{} \textrm{i}\end{pmatrix} \begin{pmatrix} A_+ &{} B \\ B^* &{} A_- \end{pmatrix}: D \times D \rightarrow H \times H \end{aligned}$$

for high frequencies \(\lambda \in \mathbb {C}\) such that \(|{\text {Im}}(\lambda )| \gg 1\), \({\text {Re}}(\lambda ) \not =0\). For \({\text {Re}}(\lambda ) = 0\), we cannot expect such an estimate to be true, since the intersection of the spectrum and the imaginary axis is typically non-empty.

Remark 10

Theorem 4 can be applied to different variants of LLE. Indeed, consider the extended LLE

$$\begin{aligned} \textrm{i}u_t = \sum _{k =1}^{2n} d_k \left( \textrm{i}\partial _x \right) ^k u + (\zeta (x) - \textrm{i}\mu ) u - |u|^2 u + \textrm{i}f(x),\quad (x,t) \in \Omega \times \mathbb {R}, \end{aligned}$$

where \(\Omega \in \{\mathbb {R}, \mathbb {R}/ \mathbb {Z}\}\), \(n \in \mathbb {N}\), \(d_{2n}\not = 0\), \(d_{2n-1},\dots ,d_1 \in \mathbb {R}\), \(\zeta \in L^\infty (\Omega ,\mathbb {R})\), \(f \in H^2(\Omega ,\mathbb {C})\), and \(\mu \ge 0\). A similar equation is studied in [7, 19, 20]. Then, the linearization \({\mathcal {L}}: (H^{2n}(\Omega ))^2 \rightarrow (L^2(\Omega ))^2\) about a stationary solution \(u=u(x)\) reads

$$\begin{aligned} {\mathcal {L}}:= \begin{pmatrix} - \textrm{i}&{} 0 \\ 0 &{} \textrm{i}\end{pmatrix} \begin{pmatrix} \sum _{k =1}^{2n} d_k \left( \textrm{i}\partial _x \right) ^k + \zeta (x) - 2 |u|^2 &{} -u^2 \\ -{\bar{u}}^2 &{} \sum _{k =1}^{2n} d_k \left( -\textrm{i}\partial _x \right) ^k + \zeta (x) - 2 |u|^2 \end{pmatrix} - \mu . \end{aligned}$$

If we set \(A_\pm = \sum _{k =1}^{2n} d_k \left( \pm \textrm{i}\partial _x \right) ^k + \zeta (x) - 2 |u|^2\), \(B = -u^2\), and replaced \(\lambda \) by \(\lambda +\mu \), the associated spectral problem fits into the framework of Theorem 4. In particular, the uniform resolvent estimates can be used to study the dynamics of the extended LLE close to stationary waves.

We need the following property of self-adjoint operators.

Lemma

([32], Chapter 5, Section 5) Let \(A: {{\,\textrm{Dom}\,}}(A) \subset H \rightarrow H\) be a self-adjoint operator and \(\lambda \in \rho (A)\) be in the resolvent set of A. Then,

$$\begin{aligned} \Vert (A-\lambda )^{-1}\Vert _{H \rightarrow H} = \frac{1}{dist (\sigma (A),\lambda )}. \end{aligned}$$

Proof of Theorem 4

We follow the strategy in [15] Section 3. Let us assume that \(A_\pm \) are both bounded from below, i.e., \(A_\pm \ge -\gamma \) for \(\gamma >0\). The proof for the case that \(A_\pm \) is bounded from above is similar. We write the spectral problem (3.6) as the system

$$\begin{aligned} \left\{ \begin{array}{l} (A_+ + \lambda _i-\textrm{i}\lambda _r) \phi _1 + B \phi _2 = \psi _1, \\ (A_- - \lambda _i+\textrm{i}\lambda _r) \phi _2 + B^* \phi _1 = \psi _2, \end{array}\right. \end{aligned}$$
(3.7)

where we have replaced \(\textrm{i}\psi _1\) by \(\psi _1\) and \(-\textrm{i}\psi _2\) by \(\psi _2\). Now, consider the case \(\lambda _i> 0\). By the previous lemma, we infer that for all \(\lambda _i \ge 2\gamma \) we find \(-\lambda _i, -\lambda _i + \textrm{i}\lambda _r \in \rho (A_+)\) and

$$\begin{aligned} \Vert (A_+ + \lambda _i)^{-1}\Vert _{H \rightarrow H}, \Vert (A_+ + \lambda _i - \textrm{i}\lambda _r)^{-1}\Vert _{H \rightarrow H} \le \frac{2}{\lambda _i}, \quad \Vert (A_+ + \lambda _i - \textrm{i}\lambda _r)^{-1}\Vert _{H \rightarrow H} \le \frac{1}{|\lambda _r|}. \end{aligned}$$

In particular, we can solve the first equation in (3.7) for \(\phi _1\):

$$\begin{aligned} \phi _1 =- (A_+ + \lambda _i - \textrm{i}\lambda _r)^{-1} B \phi _2 + (A_+ + \lambda _i - \textrm{i}\lambda _r)^{-1} \psi _1 \end{aligned}$$

and substituting the expression for \(\phi _1\) into the second equation amounts to

$$\begin{aligned} (A_- - \lambda _i + \textrm{i}\lambda _r ) \phi _2 - B^* (A_+ + \lambda _i - \textrm{i}\lambda _r)^{-1} B \phi _2 = -B^* (A_+ + \lambda _i - \textrm{i}\lambda _r)^{-1} \psi _1 + \psi _2. \end{aligned}$$

By the resolvent identity, we find

$$\begin{aligned} (A_+ + \lambda _i - \textrm{i}\lambda _r)^{-1} - (A_+ + \lambda _i )^{-1} = \textrm{i}\lambda _r (A_+ + \lambda _i - \textrm{i}\lambda _r)^{-1}(A_+ + \lambda _i )^{-1} \end{aligned}$$

and consequently

$$\begin{aligned} \big (A_- - B^* (A_+ + \lambda _i )^{-1} B - \lambda _i + \textrm{i}\lambda _r \big ) \phi _2 - \textrm{i}\lambda _r B^* (A_+ + \lambda _i - \textrm{i}\lambda _r)^{-1}(A_+ + \lambda _i )^{-1} B\phi _2 \quad \\ = - B^* (A_+ + \lambda _i - \textrm{i}\lambda _r)^{-1} \psi _1 + \psi _2. \end{aligned}$$

The operator \(B^* (A_+ + \lambda _i )^{-1} B:H \rightarrow H\) is bounded and symmetric and thus

$$\begin{aligned} {\mathcal {A}}:= A_- - B^* (A_+ + \lambda _i )^{-1} B: D \rightarrow H \end{aligned}$$

is self-adjoint. From the previous lemma on resolvent bounds of self-adjoint operators, we have \(\Vert ({\mathcal {A}} - \lambda _i + \textrm{i}\lambda _r)^{-1}\Vert _{H \rightarrow H} \le |\lambda _r|^{-1}\). Hence, we infer

$$\begin{aligned}&\big [I - \textrm{i}\lambda _r ({\mathcal {A}} - \lambda _i + \textrm{i}\lambda _r)^{-1} B^* (A_+ + \lambda _i - \textrm{i}\lambda _r)^{-1}(A_+ + \lambda _i )^{-1} B\big ] \phi _2 \\&\qquad = -({\mathcal {A}} - \lambda _i + \textrm{i}\lambda _r)^{-1} B^* (A_+ + \lambda _i - \textrm{i}\lambda _r)^{-1} \psi _1 + ({\mathcal {A}} - \lambda _i + \textrm{i}\lambda _r)^{-1}\psi _2. \end{aligned}$$

Now observe that

$$\begin{aligned} \Vert \textrm{i}\lambda _r ({\mathcal {A}} - \lambda _i + \textrm{i}\lambda _r)^{-1} B^* (A_+ + \lambda _i - \textrm{i}\lambda _r)^{-1}(A_+ + \lambda _i )^{-1} B\Vert _{H \rightarrow H} \lesssim \lambda _i^{-2}. \end{aligned}$$

Thus for \(\lambda _i>0\) sufficiently large, the operator

$$\begin{aligned} I - \textrm{i}\lambda _r ({\mathcal {A}} - \lambda _i + \textrm{i}\lambda _r)^{-1} B^* (A_+ + \lambda _i - \textrm{i}\lambda _r)^{-1}(A_+ + \lambda _i )^{-1} B: H \rightarrow H \end{aligned}$$

is invertible as a small perturbation of the identity and

$$\begin{aligned} \Big \Vert \big [I - \textrm{i}\lambda _r ({\mathcal {A}} - \lambda _i + \textrm{i}\lambda _r)^{-1} B^* (A_+ + \lambda _i - \textrm{i}\lambda _r)^{-1}(A_+ + \lambda _i )^{-1} B\big ]^{-1} \Big \Vert _{H \rightarrow H} \le \frac{1}{2} \end{aligned}$$

uniformly in \(\lambda _i \gg 1\). For this reason and using \(\Vert ({\mathcal {A}} - \lambda _i + \textrm{i}\lambda _r)^{-1}\Vert _{H \rightarrow H} \le |\lambda _r|^{-1}\), we find

$$\begin{aligned} \Vert \phi _2\Vert \lesssim |\lambda _r|^{-1} (\Vert \psi _1\Vert + \Vert \psi _2\Vert ) \end{aligned}$$

as well as

$$\begin{aligned} \Vert \phi _1\Vert \lesssim |\lambda _r|^{-1} (\Vert \psi _1\Vert + \Vert \psi _2\Vert ) \end{aligned}$$

and both estimates are independent of \(\lambda _i\) provided \(\lambda _i \gg 1\). In summary for \(\lambda = \lambda _r + \textrm{i}\lambda _i \in \mathbb {C}\) with \(\lambda _r \not = 0\) and \(\lambda _i \gg 1\), the resolvent in (3.6) exists and is uniformly bounded in \(\lambda _i\). In the same way, one can show the existence and boundedness of the resolvent for \( \lambda _i \ll -1\) and the claim follows. \(\square \)

3.2.3 Asymptotic orbital stability

The proof of the nonlinear stability follows as a direct consequence of the exponential decay estimate in Lemma 7 and Theorem 4.3.5 in [30] applied to (1.5). Notice that the nonlinearity in (1.5) is locally Lipschitz, so that all assumptions of the theorem in [30] are satisfied. In conclusion, the solitary wave bifurcating from \(\phi _{\theta _0}\) with \(\sin \theta _0>0\) is asymptotically orbitally stable against localized perturbations in \(H^1(\mathbb {R})\) and the proof of Theorem 3 is completed.