Skip to main content
SpringerLink
Log in

Generalized Tresca yield condition as a family of elliptic curves with application to mode I crack problems

  • Published:
Zeitschrift für angewandte Mathematik und Physik Aims and scope Submit manuscript

Abstract

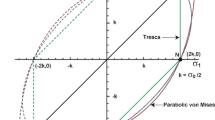
By appending a constant to the Weierstrass form of the conventional Tresca yield condition, a new yield condition is generated that allows a continuous transition of yield criteria spanning the Tresca to the von Mises and beyond. The Weierstrass form of the Tresca yield condition is defined by a cubic algebraic relationship between the second and third invariants of the deviatoric stress tensor. In general, the Weierstrass form is commonly associated with a family of plane curves called elliptic, which have special group properties. The additional parameter of the generalized Tresca yield condition is determined from an analytical expression that relates the yield strength of a material in tension to the yield strength of a material in pure shear. Solutions of plane stress, perfectly plastic, mode I crack problems are then obtained for the generalized Tresca yield condition for variations in this parameter. Through insight gained by varying this parameter, an analytical mode I perfectly plastic solution is proposed for the traditional Tresca yield condition under plane stress loading conditions. Unlike the corresponding mode I perfectly plastic solution for the von Mises yield condition, which has three distinct sectors in the upper half plane of symmetry, the solution for the Tresca yield condition requires a fourth distinct sector.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14

Similar content being viewed by others

References

  1. Ambramowitz, M., Stegun, I.A.: Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, National Bureau of Standards, Applied Mathematics Series 55. US Government Printing Office, Washington, DC (1964)

    Google Scholar 

  2. Unger, D.J.: Yield criteria representable by elliptic curves and Weierstrass form. Procedia Struct. Integ. 35, 2–9 (2022). https://doi.org/10.1016/j.prostr.2021.12.041

    Article  Google Scholar 

  3. Drucker, D.C.: Relationship of experiments to mathematical theories of plasticity. J. Appl. Mech. 16, 349–357 (1949). https://doi.org/10.1115/1.4010009

    Article  MathSciNet  MATH  Google Scholar 

  4. Hutchinson, J.W.: Plane stress and strain fields at a crack tip. J. Mech. Phys. Solids 16, 337–347 (1968). https://doi.org/10.1016/0022-5096(68)90021-5

    Article  Google Scholar 

  5. Kendig, K.: A Guide to Plane Algebraic Curves, Dolciani Mathematical Expositions 46 / MAA Guides 7. Mathematical Association of America, Washington, DC (2011)

    Book  Google Scholar 

  6. Mendelson, A.: Plasticity: Theory and Applications, pp. 80–87. Macmillan, New York (1968)

  7. Unger, D.J.: Analytical Fracture Mechanics. Academic Press, San Diego (1995), Reprinted Dover, Mineola (2001), (2010)

  8. Chakrabarty, J.: Theory of Plasticity. McGraw-Hill, New York (1987)

    Google Scholar 

  9. Hosford, W.F.: A generalized isotropic yield criterion. J. Appl. Mech. 32, 607–609 (1972). https://doi.org/10.1115/1.3422732

    Article  Google Scholar 

  10. Karafillis, A.P., Boyce, M.C.: A general anisotropic yield criterion using bounds and a transformation weighting tensor. J. Mech. Phys. Solids 41, 1859–1886 (1993). https://doi.org/10.1016/0022-5096(93)90073-O

    Article  MATH  Google Scholar 

  11. Carney, K., Du Bois, P., Sengoz, K., Wang, L., Kan, C.-D.: Development of a Generalized Yield Surface for Isotropic, Pressure-Insensitive Metal Plasticity with Differing Tension, Compression, and Shear Yield Strengths, DOT/FAA/TC-19/42. US NTIS, Springfield, VA (2020)

    Google Scholar 

  12. Kachanov, L.M.: Fundamentals of the Theory of Plasticity. Dover, Mineola (2004)

    Google Scholar 

  13. Ghomi, M.: Class notes (online), Lecture 5, Corollary 16, p. 6, Math 4441 Differential Geometry, Georgia Institute of Technology, Atlanta (2007). https://people.math.gatech.edu/~ghomi/LectureNotes/LectureNotes5U.pdf

  14. Unger, D.J.: A plane stress perfectly plastic mode I crack problem for a yield condition based on the second and third invariants of the deviatoric stress tensor. J. Mech. Mater. Struct. 3, 795–807 (2008). https://doi.org/10.2140/jomms.2008.3.795

    Article  Google Scholar 

  15. Unger, D.J.: A plane stress perfectly plastic mode I crack problem for a yield condition based on the second and third invariants of the deviatoric stress tensor. II. J. Mech. Mater. Struct. 4, 1651–1656 (2009). https://doi.org/10.2140/jomms.2009.4.1651

    Article  Google Scholar 

  16. Timoshenko, S.P., Goodier, J.N.: Theory of Elasticity, 3\(^{rd}\) edition. McGraw-Hill, New York (1970)

    Google Scholar 

  17. Unger, D.J.: A plane stress perfectly plastic mode I crack solution with continuous stress field. J. Appl. Mech. 72, 62–67 (2005). https://doi.org/10.1115/1.1828061

    Article  MATH  Google Scholar 

  18. Ince, E.L.: Ordinary Differential Equations, pp. 39–40. Dover, Mineola (1956)

  19. Davis, H.T.: Introduction to Nonlinear Differential and Integral Equations, pp. 49–51. Dover, Mineola (1962)

  20. Zwillinger, D.: Handbook of Differential Equations. Academic Press, Boston (1989)

    MATH  Google Scholar 

  21. Weisstein. E.W.: CRC Concise Encyclopedia of Mathematics, 2nd ed. Chapman & Hall/CRC, Boca Raton (2002)

  22. Hershey, A.V.: The plasticity of an isotropic aggregate of anisotropic face centered cubic crystals. J. Appl. Mech. 21, 241–249 (1954). https://doi.org/10.1115/1.4010900

    Article  MATH  Google Scholar 

  23. Hellan, K.: Introduction to Fracture Mechanics, pp. 166–169. McGraw-Hill, New York (1984)

  24. Unger, D.J.: Perfectly plastic caustics for the opening mode of fracture. Theoret. Appl. Fract. Mech. 44, 82–94 (2005). https://doi.org/10.1016/j.tafmec.2005.05.007

    Article  Google Scholar 

  25. Broberg, K.B: Cracks and Fracture, pp. 308–327. Academic Press, San Diego (1999)

Download references

Author information

Authors and Affiliations

  1. Mechanical and Civil Engineering, University of Evansville, Evansville, IN, 47722, USA

    David J. Unger

Authors
  1. David J. Unger
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to David J. Unger.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Unger, D.J. Generalized Tresca yield condition as a family of elliptic curves with application to mode I crack problems. Z. Angew. Math. Phys. 73, 184 (2022). https://doi.org/10.1007/s00033-022-01825-6

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s00033-022-01825-6

Keywords

Mathematics Subject Classification

Search

Navigation