Skip to main content
SpringerLink
Log in

Nonlinear surface SH waves in a half-space covered by an irregular layer

  • Published:
Zeitschrift für angewandte Mathematik und Physik Aims and scope Submit manuscript

Abstract

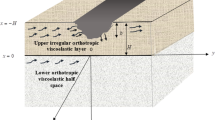
Research on the shear horizontal (SH) waves propagating in a nonlinear elastic half-space coated with a nonlinear elastic layer having slow variation in the boundary surfaces is presented. It is assumed that both the free surface and interface change as a function of the distance in the direction of propagation of the waves. By employing a perturbation method, nonlinear self-modulation of the surface SH waves for a general geometry is characterized by a generalized nonlinear Schrödinger (GNLS) equation with variable coefficients depending on functions representing the irregularities of boundary surfaces in addition to linear and nonlinear material parameters of the medium. The solitary wavelike solutions of this GNLS equation are obtained for certain special cases of the irregular boundary surfaces. It has been demonstrated by graphs that the propagation characteristics of SH waves are significantly affected by slowly varying layer and nonlinear properties of the media.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

References

  1. Noyer, J.: The effect of variations in layer thickness on Love waves. Bull. Seismol. Soc. Am. 51, 227–235 (1961)

    Article  MathSciNet  Google Scholar 

  2. Sato, R.: Love waves in case the surface layer is variable in thickness. J. Phys. Earth 9, 19–36 (1961)

    Article  Google Scholar 

  3. Mal, A.K.: On the frequency equation for Love waves due to abrupt thickening of the crustal layer. Geophys. Pure. Appl. 52, 59–68 (1962)

    Article  Google Scholar 

  4. Takahashi, T.: Transmission of Love waves in a half-space with a surface layer whose thickness varies hyperbolically. Bull. Seismol. Soc. Am. 54, 611–625 (1964)

    Article  Google Scholar 

  5. Wolf, B.: Propagation of Love waves in surface layers of varying thickness. Pure Appl. Geophys. 67, 76–82 (1967)

    Article  Google Scholar 

  6. Wolf, B.: Propagation of Love waves in layers with irregular boundaries. Pure Appl. Geophys. 73, 48–57 (1970)

    Article  Google Scholar 

  7. Woodhouse, J.H.: Surface waves in a laterally varying layered structure. Geophys. J. R. Astron. Soc. 37, 461–490 (1974)

    Article  Google Scholar 

  8. Gjevik, B.: A variational method for Love waves in nonhorizontally layered structures. Bull. Seismol. Soc. Am. 63(3), 1013–1023 (1973)

    Article  Google Scholar 

  9. Markenscoff, X., Lekoudis, S.G.: Love waves in slowly varying layered media. Pure Appl. Geophys. Math. 114, 805–810 (1976)

    Article  Google Scholar 

  10. Ben-Hador, R., Buchen, P.: Love and Rayleigh waves in non-uniform media. Geophys. J. Int. 137, 521–534 (1999)

    Article  Google Scholar 

  11. Whitham, G.B.: A general approach to linear and nonlinear dispersive waves using a Lagrangian. J. Fluid Mech. 22, 273–283 (1965)

    Article  MathSciNet  Google Scholar 

  12. Ahmad, M., Nolde, E., Pichugin, A.V.: Explicit asymptotic modelling of transient Love waves propagated along a thin coating. Z. Angew. Math. Phys. 62(1), 173–181 (2011)

    Article  MathSciNet  Google Scholar 

  13. Acharya, D.P., Roy, I.: Effect of surface stress and irregularity of the interface on the propagation of SH-waves in the magneto-elastic crustal layer based on a solid semi space. Sadhana 34(2), 309–330 (2009)

    Article  Google Scholar 

  14. Singh, S.S.: Love wave at a layer medium bounded by irregular boundary surfaces. J. Vib. Control 17(5), 789–795 (2010)

    Article  MathSciNet  Google Scholar 

  15. Kaplunov, J., Prikazchikov, D., Sultanova, L.: Rayleigh-type waves on a coated elastic half-space with a clamped surface. Philos. Trans. R. Soc. A 377, 2156 (2019)

    Article  MathSciNet  Google Scholar 

  16. Kaplunov, J., Prikazchikov, D.A., Prikazchikova, L.: On integral and differential formulations in nonlocal elasticity. Eur. J. Mech. A Solids 104497 (2022). https://doi.org/10.1016/j.euromechsol.2021.104497

  17. Teymur, M.: Nonlinear modulation of Love waves in a compressible hyperelastic layered half space. Int. J. Eng. Sci. 26, 907–927 (1988)

    Article  MathSciNet  Google Scholar 

  18. Maugin, G.A., Hadouaj, H.: Solitary surface transverse waves on an elastic substrate coated with a thin film. Phys. Rev. B 44(3), 1266–1280 (1991)

    Article  Google Scholar 

  19. Teymur, M., Demirci, A., Ahmetolan, S.: Propagation of surface SH waves on a half space covered by a nonlinear thin layer. Int. J. Eng. Sci. 85, 150–162 (2014)

    Article  Google Scholar 

  20. Deliktas, E., Teymur, M.: Surface shear horizontal waves in a double-layered nonlinear elastic half space. IMA J. Appl. Math. 83(3), 471–495 (2018)

    Article  MathSciNet  Google Scholar 

  21. Johnson, R.S.: A Modern Introduction to the Mathematical Theory of Water Waves. Cambridge University Press, Cambridge (1997)

    Book  Google Scholar 

  22. Eringen, A.C., Suhubi, E.S.: Elastodynamics, vol. I. Academic Press, New York (1974)

    MATH  Google Scholar 

  23. Knowles, J.K.: The finite anti-plane shear field near the tip of a crack for a class of incompressible elastic solids. Int. J. Fract. 13(5), 611–639 (1977)

    Article  MathSciNet  Google Scholar 

  24. Djordjevic, D., Redekopp, G.: On the development of packets of surface gravity waves moving over an uneven bottom. J. Appl. Math. Phys. 29, 950–962 (1978)

    MathSciNet  MATH  Google Scholar 

  25. Mei, C.C.: The Applied Dynamics of Ocean Surface Waves. Wiley, Hoboken (1983)

    MATH  Google Scholar 

  26. Whitham, G.: Linear and Nonlinear Waves. Wiley, New York (1974)

    MATH  Google Scholar 

  27. Ewing, W.M., Jardetzky, W.S., Press, F.: Elastic Waves in Layered Media. McGraw-Hill, New York (1957)

    Book  Google Scholar 

  28. Serkin, V.N., Hasegawa, A.: Soliton management in the nonlinear Schrödinger equation model with varying dispersion, nonlinearity, and gain. J. Exp. Theor. Phys. Lett. 72(2), 89–92 (2000)

    Article  Google Scholar 

  29. Serkin, V.N., Belyaeva, T.L.: High-energy optical Schrödinger solitons. JETP Lett. 74, 573–577 (2001)

    Article  Google Scholar 

  30. Serkin, V.N., Hasegawa, A.: Exactly integrable nonlinear Schrodinger equation models with varying dispersion, nonlinearity and gain: application for soliton dispersion. IEEE J. Sel. Top. Quantum Electron. 8(3), 418–431 (2002)

    Article  Google Scholar 

  31. Hao, R.Y., Li, L., Li, Z.H., Xue, W.R., Zhou, G.S.: A new approach to exact soliton solutions and soliton interaction for the nonlinear Schrödinger equation with variable coefficients. Opt. Commun. 236, 79–86 (2004)

    Article  Google Scholar 

  32. Yang, J.: Nonlinear Waves in Integrable and Nonintegrable Systems. Society for Industrial and Applied Mathematics, Philadelphia (2010)

    Book  Google Scholar 

  33. Trefethen, L.N.: Spectral Methods in MATLAB. Society for Industrial and Applied Mathematics, Philadelphia (2000)

    Book  Google Scholar 

  34. Mei, C.C., Li, Y.: Evolution of solitons over a randomly rough seabed. Phys. Rev. E 70(1), 016302 (2004)

    Article  MathSciNet  Google Scholar 

  35. Love, A. E. H. : Some Problems of Geodynamics, Vol. 911. Cambridge University Press, (1911)

Download references

Author information

Authors and Affiliations

  1. Department of Naval Architecture and Marine Engineering, Faculty of Engineering, Piri Reis University, 34940, Tuzla, Istanbul, Turkey

    Ekin Deliktas-Ozdemir

  2. Department of Mathematics, Faculty of Science and Letters, İstanbul Technical University, 34469, Maslak, Istanbul, Turkey

    Mevlüt Teymür

Authors
  1. Ekin Deliktas-Ozdemir
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Mevlüt Teymür
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ekin Deliktas-Ozdemir.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendices

Appendices

A.1

$$\begin{aligned} {\mathcal {D}}_{1}= & {} 2iR_{1} {\mathcal {M}}_{2}^{(1)}+2 \Lambda _{1}\frac{\partial }{\partial \tau }{\mathcal {M}}_{1}^{(1)}+R_{1}{\mathcal {N}}^{(1)}+2iR_{1}c_1^2 k \frac{\partial \textit{A}_1}{\partial \xi } -{\mathcal {P}}_{1}+2i\mathcal {\zeta }_{1}^{(1)}{} \textit{A}_1, \\ {\mathcal {D}}_{2}= & {} (-2iR_{1}/pkc_{1}^{2})\left( -\omega + \frac{kc_{1}^{2}}{V_g}\right) \frac{\partial }{\partial \tau }{\mathcal {M}}_{1}^{(1)}+2c_1^2\frac{k}{p} \frac{\partial k}{\partial \xi }{} \textit{A}_1 R_{1}, \\ {\mathcal {D}}_{3}= & {} 2iR_{2} {\mathcal {M}}_{2}^{(1)}+2 \Lambda _{2}\frac{\partial }{\partial \tau }{\mathcal {M}}_{1}^{(1)}+R_{2}{\mathcal {N}}^{(1)}+2iR_{2}c_1^2 k \frac{\partial \textit{A}_1}{\partial \xi }-{\mathcal {P}}_{2}+2i\mathcal {\zeta }_{2}^{(1)}{} \textit{A}_1,\\ {\mathcal {D}}_{4}= & {} (2iR_{2}/pkc_{1}^{2})\left( -\omega +\frac{kc_{1}^{2}}{V_g}\right) \frac{\partial }{\partial \tau }{\mathcal {M}}_{1}^{(1)}-2c_1^2\frac{k}{p} \frac{\partial k}{\partial \xi }{} \textit{A}_1 R_2, \\ {\mathcal {D}}_{5}= & {} {\mathcal {Q}}_{1},\quad {\mathcal {D}}_{6}={\mathcal {Q}}_{2} \\ {\mathcal {D}}_{7}= & {} 2iR_{3} {\mathcal {M}}_{2}^{(2)}+2 \Lambda _{3}\frac{\partial }{\partial \tau }{\mathcal {M}}_{1}^{(2)}+R_{3}{\mathcal {N}}^{(2)}+2iR_{3}c_2^2 k \frac{\partial \textit{A}_1}{\partial \xi }+2i\mathcal {\zeta }_{3}^{(2)}{} \textit{A}_1, \\ {\mathcal {D}}_{8}= & {} (2R_{3}/vkc_{2}^{2})\left( -\omega +\frac{kc_{2}^{2}}{V_g}\right) \frac{\partial }{\partial \tau }{\mathcal {M}}_{1}^{(2)}+2ic_2^2\frac{k}{v} \frac{\partial k}{\partial \xi }{} \textit{A}_1 R_3,\\ {\mathcal {D}}_{9}= & {} n_{2}k^{4}(-3+2v^{2}+9v^{4})|R_{3}|^{2}R_{3}|\textit{A}_{1}|^{2}{} \textit{A}_{1} , \end{aligned}$$

with

$$\begin{aligned} {\mathcal {M}}_{\beta }^{(\alpha )}=\left( -\omega +\frac{kc_{\alpha }^{2}}{V_g}\right) \frac{\partial \textit{A}_{\beta } }{\partial \tau }, \quad {\mathcal {N}}^{(\alpha )}=\left( \frac{c_{\alpha }^{2}}{V_g^2}-1\right) \frac{\partial ^{2}{} \textit{A}_{1} }{\partial \tau ^{2}}, \quad \Lambda _{\alpha }=\left( \frac{1}{V_g}\frac{\partial R_{\alpha }}{\partial k}+\frac{\partial R_{\alpha }}{\partial \omega }\right) \end{aligned}$$
$$\begin{aligned} {\mathcal {P}}_{1}= & {} n_{1}k^{4}\left( |R_{1}|^{2}R_{1}(9+2p^{2}+9p^{4})\right) |\textit{A}_{1}|^{2}{} \textit{A}_{1}, \quad {\mathcal {P}}_{2}=n_{1}k^{4}\left( |R_{2}|^{2}R_{2}(9+2p^{2}+9p^{4})\right) |\textit{A}_{1}|^{2}{} \textit{A}_{1}, \\ \mathcal {\zeta }_{\beta }^{(\alpha )}= & {} k c_{\alpha }^{2} \frac{\partial R_{\beta }}{\partial \xi }+\frac{R_{\beta }}{2}c_{\alpha }^{2} \frac{\partial k}{\partial \xi }, \\ {\mathcal {Q}}_{1}= & {} n_{1}k^{4}|\textit{A}_{1}|^{2}{} \textit{A}_{1}R_{1}^{3}(-3-2p^{2}+9p^{4}),\quad {\mathcal {Q}}_{2}=n_{1}k^{4}|\textit{A}_{1}|^{2}{} \textit{A}_{1}R_{2}^{3}(-3-2p^{2}+9p^{4}), \end{aligned}$$

A.2

$$\begin{aligned} F_{1}= & {} - \frac{1}{8}{\mathrm{{e}}^{3f_2kv}}\left( {f_1 + h} \right) {k^4}\left( {9 + 2{p^2} + 9{p^4}} \right) \beta _1 \sec {\left[ {\left( {f_1 - f_2 + h} \right) kp} \right] ^3}, \\ F_{2}= & {} \frac{1}{32pv}{\mathrm{{e}}^{3f_2kv}}{k^3}\{4p\left( {9 + 2{v^2} - 3{v^4}} \right) \beta _2\gamma - 4f_2 kp\left( {9 + 2{p^2} + 9{p^4}} \right) v\beta _1\sec {\left[ {\left( {f_1 - f_2 + h} \right) kp} \right] ^2}\\&-\, 4\left( { - 9 + 2{p^2} + 3{p^4}} \right) v\beta _1\tan \left[ {\left( {f_1 - f_2 + h} \right) kp} \right] \\&+\, \left( {27 + 2{p^2} - 33{p^4}} \right) v\beta _1\sec {\left[ {\left( {f_1 - f_2 + h} \right) kp} \right] ^2} \tan \left[ {\left( {f_1 - f_2 + h} \right) kp} \right] \},\\ F_{3}= & {} -\frac{{\mathrm{{e}}^{3f_2kv}}{k^2}\sec {\left[ {\left( {f_1 - f_2 + h} \right) kp} \right] ^3}}{32 p^2 v^2}\{ 3{p^2}\beta _2\left( { - 3 + 2{v^2} + 9{v^4}} \right) \cos \left[ {\left( {f_1 - f_2 + h} \right) kp} \right] \\&+\, \left( { - 3{v^2}\beta _1 + {p^2}\left( { - 3\beta _2 + 9{v^4}\beta _2 + {v^2}\left( { - 2\beta _1 + 9{p^2}\beta _1 + 2\beta _2} \right) } \right) } \right) \cos \left[ {3\left( {f_1 - f_2 + h} \right) kp} \right] \\&-\,4f_2kp {v^2}\beta _1\left( {9 + 2{p^2} + 9{p^4}} \right) \sin \left[ {\left( {f_1 - f_2 + h} \right) kp} \right] \}. \end{aligned}$$

A.3

$$\begin{aligned} G_{1}= & {} \frac{{}{\mathrm{{e}}^{f_2kv}}\left( {f_1 + h} \right) \sec \left[ {\left( {f_1 - f_2 + h} \right) kp} \right] }{2p^2v}\{2{k^2}{p^2}v\left( {p\tan \left[ {\left( {f_1 - f_2 + h} \right) kp} \right] \left( {f{_1^\prime } - f{_2^\prime }} \right) + vf{_2^\prime }} \right) \\&+\, \left( {v + p\left( {2f_2kp + v\left( {p - 2\left( {f_1 - f_2 + h} \right) k\tan \left[ {\left( {f_1 - f_2 + h} \right) kp} \right] } \right) } \right) } \right) k'\}, \\ G_{2}= & {} \frac{1}{{2k{p^3}{v^3}}}{}{\mathrm{{e}}^{f_2kv}}\{2{k^2}{p^2}{v^3}(- f_2k{p^2}\tan \left[ {\left( {f_1 - f_2 + h} \right) kp} \right] f{_2^\prime } - v\tan \left[ {\left( {f1 - f_2 + h} \right) kp} \right] f{_2^\prime } \\&+\,2{k^2}{p^3}{v^3}\left( {\left( {f_2kv - \gamma } \right) f{_2^\prime } + \sec {{\left[ {\left( {f_1 - f_2 + h} \right) kp} \right] }^2}\left( { - f{_1^\prime } + f{_2^\prime }} \right) } \right) ) \\&+\,p\left( {f_2k{v^3} + {p^2}\left( {\gamma + v\left( { - f{_2^2}{k^2}v\left( { - 2 + \gamma } \right) - v\gamma - f_2k\left( {{v^2}\left( { - 1 + \gamma } \right) + \gamma } \right) } \right) } \right) } \right) k' \\&+\, 2\left( {f_1 - f_2 + h} \right) kp{v^3}\sec {\left[ {\left( {f_1 - f_2 + h} \right) kp} \right] ^2}\\&+ {v^2}\left( { - v + {p^2}\left( { - v + f_2k\left( { - 2 + f_2kv} \right) } \right) } \right) \tan \left[ {\left( {f_1 - f_2 + h} \right) kp} \right] k' \}, \\ G_{3}= & {} -\frac{{}{\mathrm{{e}}^{f_2kv}}f_2}{2kp^3v^3}\{ 2{k^2}{p^3}{v^3}f{_2^\prime } + p\left( { - f_2k{v^3} + {p^2}\left( { - 1 + f_2kv + {v^2}} \right) } \right) k' \\&+\,2kp{v^3}\sec {\left[ {\left( {f_1 - f_2 + h} \right) kp} \right] ^2}\left( {k{p^2}\left( {f{_1^\prime } - f{_2^\prime }} \right) - \left( {f_1 - f_2 + h} \right) k'} \right) \\&+\,{v^2}\tan \left[ {\left( {f_1 - f_2 + h} \right) kp} \right] \left( {2{k^2}{p^2}{v^2}f{_2^\prime } + \left( {v + {p^2}\left( {2f_2k + v} \right) } \right) k'} \right) \}. \end{aligned}$$

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Deliktas-Ozdemir, E., Teymür, M. Nonlinear surface SH waves in a half-space covered by an irregular layer. Z. Angew. Math. Phys. 73, 145 (2022). https://doi.org/10.1007/s00033-022-01783-z

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s00033-022-01783-z

Keywords

Mathematics Subject Classification

Search

Navigation